•
•
•
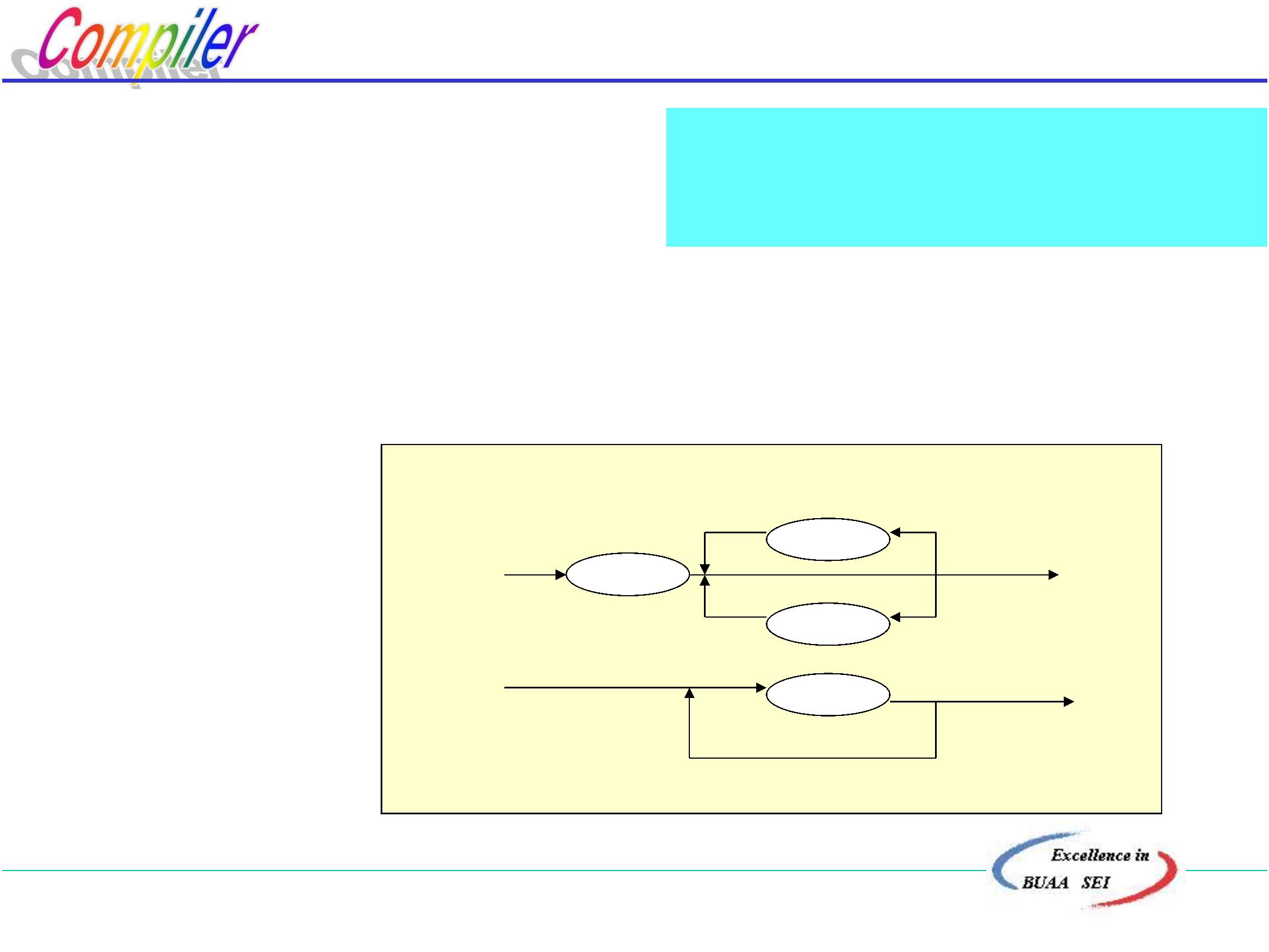
编译的起源:程序设计语言的发展
基本概念
编译过程和编译程序构造
•
编译技术的应用
北京航空航天大学计算机学院
1

机器语言
(机器指令)
面向用户
的语言
面向问题
的语言
汇编语言
低级语言
高级语言
北京航空航天大学计算机学院
2
•
•
低级语言(Low level Language)
–
字位码、机器语言、汇编语言
特点:与特定的机器有关,效率高、灵活,但使用复
杂、繁琐、编写费时、易出错
–
高级语言
-- Fortran、Pascal、C 语言等
–特点:不依赖具体机器,移植性好、便于描述问题处
理过程和算法、易使用、易维护等。
用高级语言编制的程序,计算机不能立即执行,
必须通过一个“翻译程序”加工,转化为与其等价的
机器语言程序,机器才能执行。
这种翻译程序,称之为“编译程序”。
北京航空航天大学计算机学院
3

•
•
源程序
用汇编语言或高级语言编写的程序称为源程序。
目标程序
用目标语言所表示的程序。
目标语言:可以是某种机器的机器语言或汇编语言,
也可以是介于源语言和机器语言之间的“中间语言”,
甚至可以是另一种高级语言。
•
翻译程序
将源程序转换为目标程序的程序称为翻译程序。
它是指各种语言的翻译器,包括汇编程序和编译程序,
是汇编程序、编译程序以及各种变换程序的总称。
北京航空航天大学计算机学院
4

源程序、翻译程序、目标程序三者关系:
源程序
翻译程序
目标程序
OBJECT
PROGRAM
SOURCE
PROGRAM
TRANSLATER
即源程序是翻译程序的输入,目标程序是翻译程序的输出
北京航空航天大学计算机学院
5
•
汇编程序
若源程序用汇编语言书写,经过翻译程序得到用机器语言
表示的程序,这时的翻译程序就称之为汇编程序,这种翻译过
程称为“汇编”(Assemble)
•
编译程序
若源程序是用高级语言书写,经加工后得到目标程序,
这种翻译过程称“编译”(Compile)
汇编程序与编译程序都是翻译程序,主要区别是加工对象的
不同。
北京航空航天大学计算机学院
6

•
•
编译或汇编阶段
编译程序
或汇编程序
源程序
目标程序
输出数据
运行阶段
目标程序
+
运行子程序
输入数据
北京航空航天大学计算机学院
7
•
解释程序(Interpreter)
对源程序进行解释执行的程序。
•
工作过程
源程序
输入数据
输出数据
解释程序
北京航空航天大学计算机学院
8
源程序
编译程序
源程序的中间形式
输入数据
输出数据
解释程序
北京航空航天大学计算机学院
9
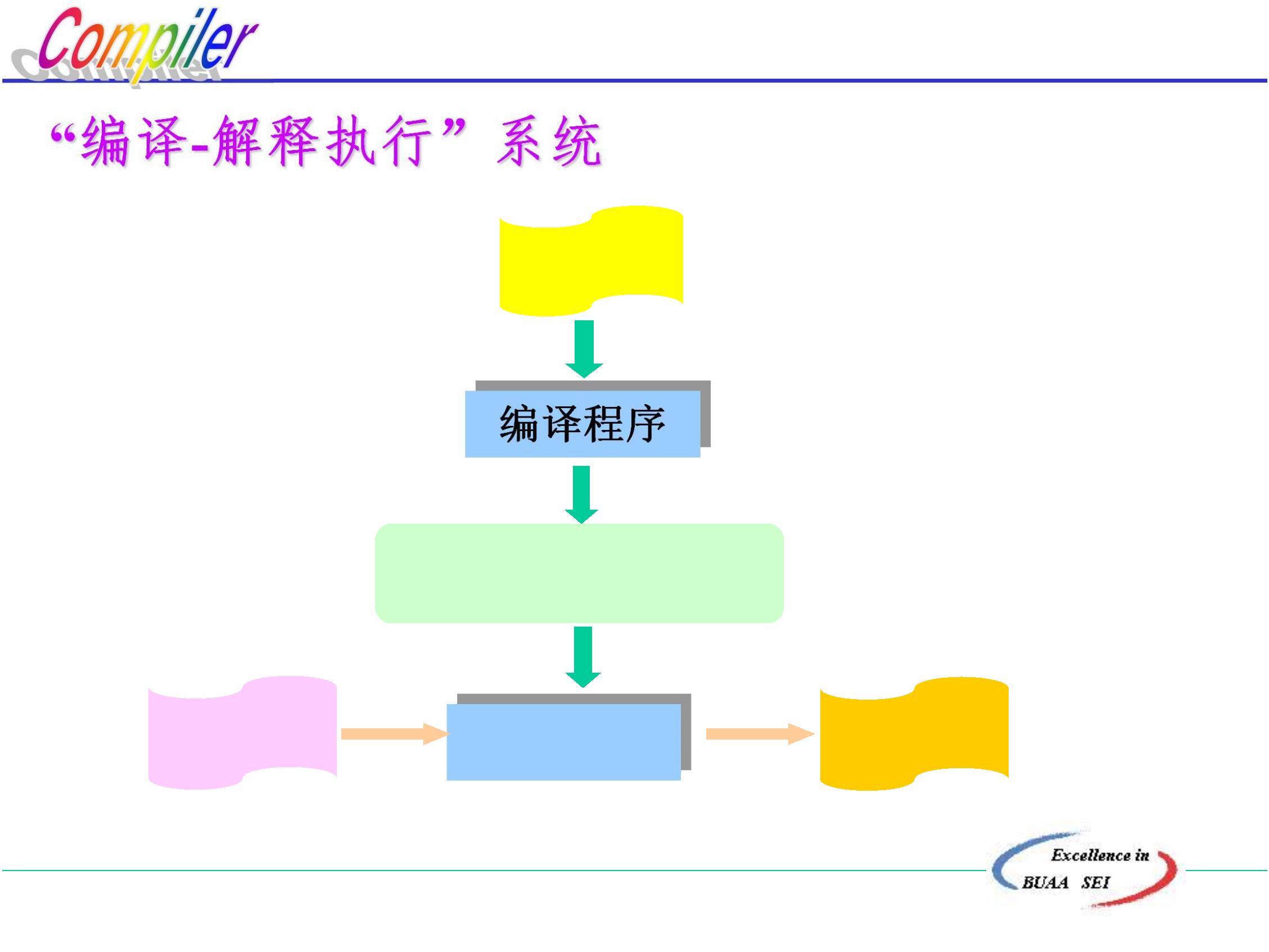
编译过程是指将高级语言程序翻译为等价的目标程
序的过程。
习惯上是将编译过程划分为5个基本阶段:
词法分析
语法分析
语义分析、生成中间代码
代码优化
生成目标程序
北京航空航天大学计算机学院
1
0
一、词法分析
任务:分析和识别单词。
源程序是由字符序列构成的,词法分析扫描源程序
(字符串),根据语言的词法规则分析并识别单词,并以某
种编码形式输出 。
•单词:是语言的基本语法单位,一般语言有四大类单词
<
<
<
<
1>语言定义的关键字或保留字(如BEGIN、END、IF)
2>标识符
3>常数
4>分界符(运算符) (如+、-、*、/、;、(、) ……)
北京航空航天大学计算机学院
11

二、语法分析
任务:根据语法规则(即语言的文法),分析并识别出
各种语法成分,如表达式、各种说明、各种语句、
过程、函数等,并进行语法正确性检查。
X1:= ( 2.0 + 0.8 ) * C1
赋值语句的文法 :
<
<
<
<
赋值语句>→<变量><赋值操作符><表达式>
变量>→<简单标识符>
赋值操作符>→:=
表达式>→ ……
北京航空航天大学计算机学院
1
2

三、语义分析、生成中间代码
任务:对识别出的各种语法成分进行语义分析,
并产生相应的中间代码。
•
•
中间代码:一种介于源语言和目标语言之间的中间语言形式
生成中间代码的目的:
<
<
1> 便于做优化处理;
2> 便于编译程序的移植。
•
中间代码的形式:编译程序设计者可以自己设计,常用的有
四元式、三元式、逆波兰表示等。
北京航空航天大学计算机学院
1
3

四元式(三地址指令)
X1:= ( 2.0 + 0.8 ) * C1
运算符 左运算对象 右运算对象 结果
(1) +
(2) *
(3) :=
2.0
T1
X1
0.8
C1
T2
T1
T2
其中T1和T2为编译程序引入的工作单元
四元式的语义为: 2.0 + 0.8 → T1
T1 * C1 → T2
T2 → X1
这样所生成的四元式与原来的赋值语句在语言的
形式上不同,但语义上等价。
北京航空航天大学计算机学院
1
4

四、代码优化
目的: 是为了得到高质量的目标程序。
例如:前面的四元式中第一个四元式是计算常
量表达式值,该值在编译时就可以算出并存放在工
作单元中,不必生成目标指令来计算,这样四元式
可优化为:
编译时: 2.0 + 0.8 → T1
(
(
1) * T1 C1 T2
2) := X1 T2
北京航空航天大学计算机学院
1
5

五、生成目标程序
由中间代码很容易生成目标程序(地址指令序列)。这
部分工作与机器关系密切 ,所以要根据机器进行。在做这
部分工作时(要注意充分利用累加器),也可以进行优化
处理。
X1:= ( 2.0 + 0.8 ) * C1
注意:在翻译成目标程序的过程中,要切记保持
语义的等价性。
北京航空航天大学计算机学院
1
6

1.3.2 编译程序构造
一、 编译程序的逻辑结构
按逻辑功能不同,可将编译过程划分为五个基本阶段,
与此相对应,我们将实现整个编译过程的编译程序划分为
五个逻辑阶段(即五个逻辑子过程)。
语义分析
生成中间
代码
词法分析 语法分析
程序 程序
代码优化 生成目标
程序 程序
S.P
O.P
北京航空航天大学计算机学院
1
7
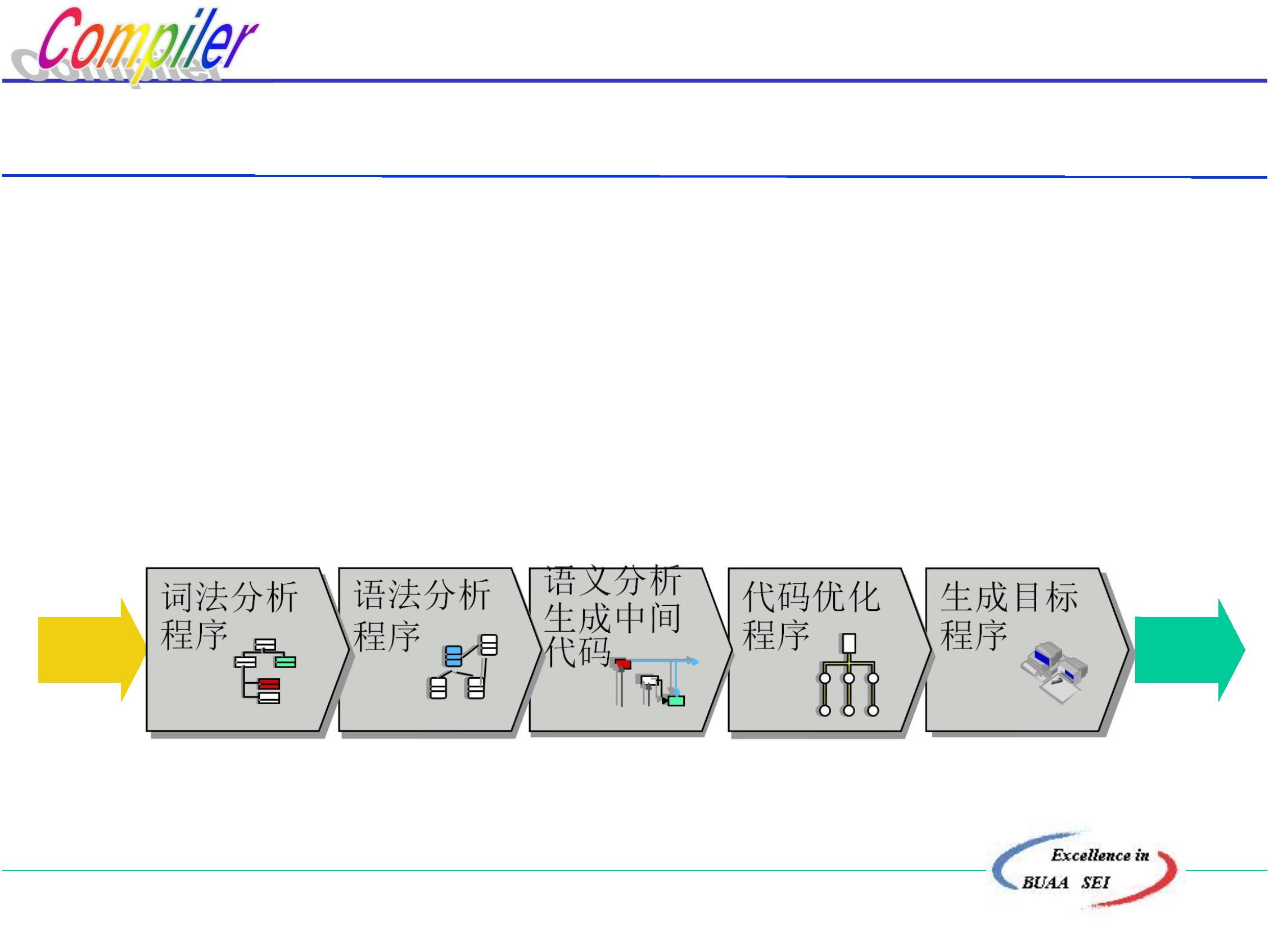
在上列五个阶段中都要做两件事:
(1)建表和查表;(2)出错处理;
所以编译程序中都要包括符号表管理和出错处理两部分
符号表管理
在整个编译过程中始终都要贯穿着建表(填表)和查表的工
作。即要及时地把源程序中的信息和编译过程中所产生的信息登
记在表格中,而在随后的编译过程中同时又要不断地查找这些表
格中的信息。
出错处理
规模较大的源程序难免有多种错误,编译程序必须要有出错
处理的功能。即能诊察出错误,并能报告用户错误的性质和位
置,以便用户修改源程序。出错处理能力的大小是衡量编译程
序质量好坏的一个重要指标。
北京航空航天大学计算机学院
1
8

典型的编译程序具有7个逻辑部分
S.P
词法分析程序
语法分析程序
语义分析、生成中间代码
代码优化程序
符
号
表
管
理
出
错
处
理
生成目标程序
O.P
北京航空航天大学计算机学院
1
9
二、 遍(PASS)
遍:对源程序(包括源程序中间形式)从头到尾扫描一次,
并做有关的加工处理 ,生成新的源程序中间形式或目标程序,
通常称之为一遍。
第一遍
第二遍
…
…
S.P
中间形式1
S.P
中间形式2
S.P
C1
C2
O.P
一遍
要注意遍与基本阶段的区别
五个基本阶段:是将源程序翻译为目标程序在逻辑上要完成的
工作。
遍:是指完成上述5个基本阶段的工作,要经过几次扫描处理。
北京航空航天大学计算机学院
2
0
一遍扫描即可完成整个编译工作的称为一遍扫描编译程序
其结构为:
语法成分
语义分析生成
目标程序
语法分析
S.P.
返回分析结果
取单词
返回单词
词法分析
整理目标程序
停机
O.P.
北京航空航天大学计算机学院
2
1
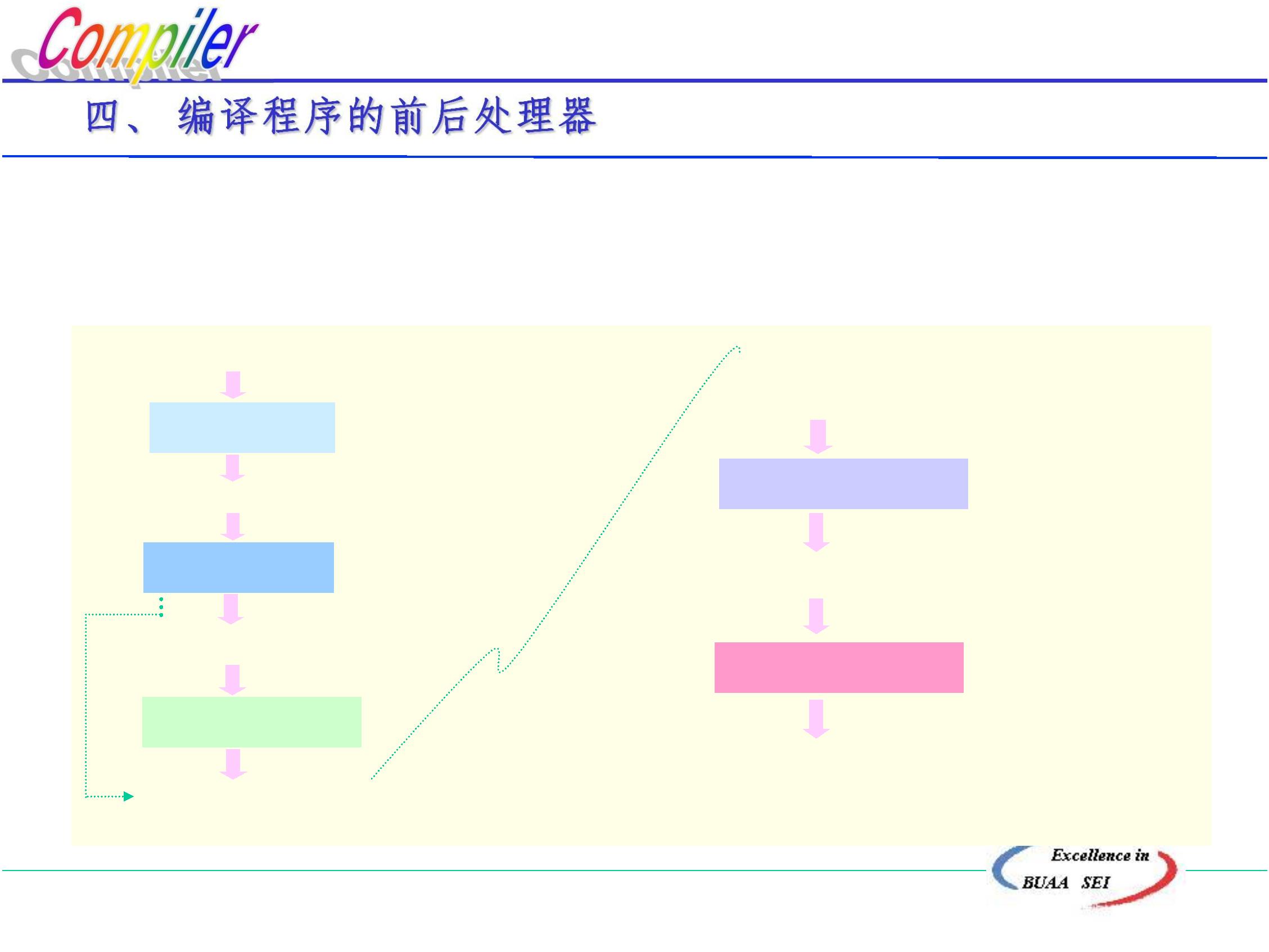
三、前端和后端
根据编译程序各部分功能,将编译程序分成前端和后端。
前端:通常将与源程序有关的编译部分称为前端。
词法分析、语法分析、语义分析、中间代码生成、
代码优化 -------分析部分
特点:与源语言有关
后端:与目标机有关的部分称为后端。
目标程序生成(与目标机有关的优化)
-------综合部分
特点:与目标机有关
北京航空航天大学计算机学院
2
2

源程序:多文件、宏定义和宏替换(调用),包含文件
目标程序:一般为汇编程序或可重定位的机器代码
框架源程序
可重定位机器码
(文件组)
预处理器
源程序
库目标、可重
定位目标文件
连接编辑
编译程序
可重定位机器码
目标程序(汇编)
加载器
汇编程序
可运行的机器代码
可重定位机器码
(Obj文件)
北京航空航天大学计算机学院
2
3
语法制导的结构化编辑器
程序格式化工具
软件分析与测试工具
程序理解工具
高级语言的翻译工具
等等
北京航空航天大学计算机学院
2
4

第二章 文法和语言的概念和表示
•
•
•
•
•
预备知识 - 形式语言基础
文法和语言的定义
若干术语和重要概念
文法的表示:扩充的BNF范式和语法图
文法和语言的分类
北京航空航天大学计算机学院
1
2
.1 预备知识
一、字母表和符号串
字母表: 符号的非空有限集 例:={a,b,c}
符号: 字母表中的元素 例: a,b,c
符号串: 符号的有穷序列 例:a, aa, ac, abc,..
空符号串:无任何符号的符号串(ε)
符号串的形式定义
有字母表,定义:
(
(
(
1)ε是上的符号串;
2)若x是上的符号串,且a ,则ax或xa是上的符号串;
3)y是上的符号串,iff(当且仅当)y可由(1)和(2)产生。
符号串集合:由符号串构成的集合。

•
通常约定:
–
用英文字母表开头的小写字母和字母表靠近末尾
的大写字母来表示符号
如:a, b, c, d, … , r 和 S, T , U, V , W,X, Y, Z
–
–
用英文字母表靠近末尾的小写字母来表示符号串
如:s, t, u, v, w , x, y, z
用英文字母表开头的大写字母来表示符号串集合
如:A, B, C, D, … , R
北京航空航天大学计算机学院
3

二、符号串和符号串集合的运算
1
.符号串相等:若x、y是集合上的两个符号串,则x=y
iff(当且仅当)组成x的每一个符号和组成y的每一个符号
依次相等。
2.符号串的长度:x为符号串,其长度|x|等于组成该符
号串的符号个数。
例: x=STV , |x|=3
北京航空航天大学计算机学院
4

3
.符号串的联接:若x、y是定义在Σ上的符号串, 且
x=XY,y=YX,则x和y的联接 xy=XYYX也是Σ上的符号
串。
注意:一般xy≠yx,而εx=xε
4
. 符号串集合的乘积运算:令A、B为符号串集合,
定义 AB={ xy |x∈A, y∈B}
例:A={s, t}, B = {u,v}, AB= ?
su,sv,tu,tv}
{
因为εx=xε=x,所以{ε}A=A {ε} =A
北京航空航天大学计算机学院
5

5
. 符号串集合的幂运算:有符号串集合A,定义
A0 ={ε}, A1=A, A2=AA, A3=AAA,
… …… An=An-1A=AAn-1 ,n>0
…
6
.符号串集合的闭包运算:设A是符号串集合,定义
A+=A1 ∪ A2 ∪ A3 ∪……∪ An ∪……
称为集合A的正闭包。
A*=A0 ∪A+
称为集合A的闭包。
例:A={x,y}
A ={x,y, xx,xy,yx,yy , xxx,xxy,xyx,xyy,yxx,yxy,yyx,yyy, ……}
+
A1
A2
A3
{
ε, x,y, xx,xy,yx,yy , xxx,xxy,xyx,xyy,yxx,yxy,yyx,yyy, ……}
A* =
A0 A1
A2
A3
北京航空航天大学计算机学院
6

为什么对符号、符号串、符号串集合以及它们的运算感兴趣?
若A为某语言的基本字符集 ( 把字符看作符号)
A={a, b, ……z, 0, 1, ……, 9, +, -, ×, _, /, ( , ), =, ……}
B为单词集
(单词是符号串)
B ={begin, end, if, then, else, for, ……,<标识符>,<常量>, ……}
则B A* 。
(
把单词看作符号,句子便是符号串)
语言的句子是定义在B上的符号串。
若令C为句子集合,则C B * , 程序 C
北京航空航天大学计算机学院
7

2
.2文法的非形式讨论
1.什么是文法:文法是对语言结构的定义与描述。即从形式上
用于描述和规定语言结构的称为“文法”(或称为“语法”)。
例:有一句子:“我是大学生” 。这是一个在语法、
语义上都正确的句子,该句子的结构(称为语法结构)是由
它的语法决定的 。在本例中它为“主谓结构”。
如何定义句子的合法性?
•
•
有穷语言
无穷语言
北京航空航天大学计算机学院
8
2.语法规则:我们通过建立一组规则,来描述句子的语法结构。
规定用“::=”表示“由...组成”(或“定义为...”)。
<
句子>::=<主语><谓语>
<
<
<
<
<
<
主语>::=<代词>|<名词>
代词> ::=你|我|他
名词>::= 王民|大学生|工人|英语
谓语>::=<动词><直接宾语>
动词>::=是|学习
直接宾语>::=<代词>|<名词>
北京航空航天大学计算机学院
9

3
. 由规则推导句子:有了一组规则之后,可以按照一定的方式
用它们去推导或产生句子。
推导方法:从一个要识别的符号开始推导,即用相应规则的
右部来替代规则的左部,每次仅用一条规则去进行推导。
<
句子> => <主语><谓语>
<
主语> <谓语> => <代词> <谓语>
…
… ……
这种推导一直进行下去,直到所有带< >的符号都由终结符号
替代为止。
北京航空航天大学计算机学院
1
0

推导方法:从一个要识别的符号
开始推导,即用相应规则的
右部来替代规则的左部,
每次仅用一条规则去进行推导。
<
句子> => <主语><谓语>
=
=
> < 代词><谓语>
> 我<谓语>
=
=
=
=
>我<动词><直接宾语>
>我是<直接宾语>
>我是<名词>
>我是大学生
北京航空航天大学计算机学院
11

例:有一英语句子:The big elephant ate the peanut.
<
句子>::=<主语><谓语>
<
<
<
<
<
<
<
<
主语>::=<冠词><形容词><名词>
冠词> ::=the
形容词>::=big
名词>::=elephant
谓语>::=<动词><宾语>
动词>::=ate
宾语>::=<冠词><名词>
名词> ::=peanut
北京航空航天大学计算机学院
1
2

<
句子> => <主语><谓语>
=
=
=
=
=
=
=
=
=
> <冠词><形容词><名词><谓语>
> the <形容词><名词><谓语>
> the big <名词> <谓语>
> the big elephant <谓语>
> the big elephant <动词><宾语>
> the big elephant ate <宾语>
> the big elephant ate <冠词><名词>
> the big elephant ate the <名词>
> the big elephant ate the peanut
北京航空航天大学计算机学院
1
3

+
上述推导可写成<句子> => the big elephant ate the peanut
说明:
(1) 有若干语法成分同时存在时,我们总是从最左的语法成
分进行推导,这称之为最左推导,类似的有最右推导(还有一般
推导)。
(2) 从一组语法规则可推出不同的句子,如以上规则还可推出
大象吃象”、“大花生吃象”、“大花生吃花生”等句子,
“
它们 在语法上都正确,但在语义上都不正确。
所谓文法是在形式上对句子结构的定义与描述,而未
涉及语义问题。
北京航空航天大学计算机学院
1
4

4
.语法(推导)树:我们用语法(推导)树
来描述一个句子的语法结构。
<
句子>
<
主语>
<谓语>
<
冠词> <形容词> <名词> <动词>
<
宾语>
冠词> <名词>
the peanut
<
The
big
elephant ate
北京航空航天大学计算机学院
1
5
2.3 文法和语言的形式定义
2
.3.1文法的定义
定义1. 文法G=(Vn,Vt,P,Z)
Vn:非终结符号集
Vt:终结符号集
P:产生式或规则的集合
Z:开始符号(识别符号) Z∈Vn
规则的定义:
规则是一个有序对(U, x), 通常写为:
U :: x 或U x , | U| = 1 |x| 0
北京航空航天大学计算机学院
1
6

例:无符号整数的文法:
G[<无符号整数>]=(Vn,Vt,P,Z)
Vn={<无符号整数>,<数字串>, <数字>}
Vt = {0, 1, 2, 3, …… 9}
P = {<无符号整数> →<数字串> ,
<
<
<
<
数字串> → <数字串> <数字>,
数字串> →<数字> ,
数字> →0,
数字> →1,
…
………
<
数字> →9}
Z = <无符号整数>
北京航空航天大学计算机学院
1
7

几点说明:
产生式左边符号构成集合Vn,且Z ∈Vn
有些产生式具有相同的左部,可以合在一起
例:<无符号整数> →<数字串>
<
<
数字串> → <数字串> <数字> | <数字>
数字> →0| 1 | 2 | 3 | …… | 9
给定一个 文法,需给出产生式(规则)集合,并指定识别符号
例:G[<无符号整数>]:
<
<
<
无符号整数> →<数字串>
数字串> → <数字串> <数字> | <数字>
数字> →0| 1 | 2 | 3 | …… | 9
北京航空航天大学计算机学院
1
8

2
.3.2 推导的形式定义
定义2:文法G:v=xUy,w=xuy,
其中x、y ∈V* ,U∈Vn , u ∈V*,
若U :: u∈P,则v w。
G
若x=y=ε,有U :: u,则U u
G
根据文法和推导定义,可推出终结符号串,所谓通过文法
能推出句子来。
北京航空航天大学计算机学院
1
9

例如:G[<无符号整数>]
(4) <数字> →0
(5) <数字> →1
…………
(1) <无符号整数> →<数字串>
(2) <数字串> → <数字串> <数字>
(3) <数字串> → <数字>
(13) <数字> →9
<
无符号整数>==> <数字串> ==> <数字串> <数字>
(1)
(2)
<
1
数字><数字> =(4=) > 1 <数字>
=
=>
(3)
=
=>
0
(5)
当符号串已没有非终结符号时,推导就必须终止。因为
终结符不可能出现在规则左部,所以将在规则左部出现的符
号称为非终结符号。
北京航空航天大学计算机学院
2
0

定义3:文法G,u , u , u , ……,u ∈V+
0
1
2
n
=
=> ==>
==>
u ==>…… u =w
if v= u0
+
u
1
2
n
G
G
G
G
则v ==> w
G
例:<无符号整数>==> <数字串> ==> <数字串> <数字>
=
=> <数字><数字> ==>1 <数字>
=
+
=>1 0
即<无符号整数>==> 10
G
北京航空航天大学计算机学院
2
1

定义4:文法G,有v,w ∈V+
+
*
if v w , 或v=w,则v => w
=
>
G
G
*
定义5:规范推导:有xUy ==> xuy, 若 y ∈V ,则此推导为规范
t
|
的,记为xUy ==> xuy
直观意义:规范推导=最右推导
最右推导:若规则右端符号串中有两个以上的非终结符时,先推右边的。
最左推导:若规则右端符号串中有两个以上的非终结符时,先推左边的。
+
若有v = u =|=> u =|=> u =|=>……=|=> u = w, 则 v =|=> w
0
1
2
n
北京航空航天大学计算机学院
2
2

2
.3.3 语言的形式定义
定义6:文法G[Z]
(
(
(
1)句型:x是句型 Z * x , 且x∈V* ;
+
2)句子:x是句子 Z x , 且x∈V * ;
t
+
3)语言:L(G[Z])={x | x∈V *, Z x } ;
t
形式语言理论可以证明以下两点:
(
(
1)G →L(G);
2)L(G) →G1,G2,……,Gn;
已知文法,求语言,通过推导;
已知语言,构造文法,无形式化方法,更多是凭经验。
北京航空航天大学计算机学院
2
3

例:{ abna | n≥1},构造其文法
G1[Z]:
Z→aBa,
B→b | bB
G2[Z]:
Z→aBa,
B→b | Bb
定义7. G和G’是两个不同的文法,若L(G) = L(G’) ,
则G和G’为等价文法。
北京航空航天大学计算机学院
2
4

编译感兴趣的问题是:
•
给定句子 x 以及文法 G , 求x L(G) ?
G
yes
x 算法1
算法2 停机
x L(G) ?
no
出错处理
北京航空航天大学计算机学院
2
5
2
.3.4 递归文法
1
.递归规则:规则右部有与左部相同的符号(非终结符)
对于U::= xUy
若x=ε, 即U::= Uy, 左递归
若y=ε, 即U::= xU, 右递归
若x, y≠ε,即U::= xUy,自嵌入递归
2
.递归文法:文法G,存在U ∈Vn
+
if U==>…U…, 则G为递归文法;
+
if U==>U…, 则G为左递归文法;
+
if U==>…U, 则G为右递归文法。
北京航空航天大学计算机学院
2
6

3
. 递归文法的优点:可用有穷条规则,定义无穷语言
会造成死循环(后面将详细论述)
4
. 左递归文法的缺点:不能用自顶向下的方法来进行语法分析
例:对于前面给出的无符号整数的文法是左递归文法,用13
条规则就可以定义出所有的无符号整数。若不用递归文法,那
将要用多少条规则呢?
<
<
<
无符号整数> →<数字串>
数字串> → <数字串> <数字> | <数字>
数字> →0| 1 | 2 | 3 | …… | 9
北京航空航天大学计算机学院
2
7
2
.3.5 句型的短语、简单短语和句柄
定义8. 给定文法G[Z], w = xuy∈V+,为该文法的句型,
*
+
若Z ==> xUy, 且U ==>u, 则u是句型w相对于U的短语;
*
若Z ==> xUy, 且U ==>u, 则u是句型w相对于U的简单短语。
其中U ∈Vn,u ∈V+,x , y ∈V*
直观理解:短语是前面句型中的某个非终结符所能推
出的符号串。
任何句型本身一定是相对于识别符号Z的短语
北京航空航天大学计算机学院
2
8

定义9. 任一句型的最左简单短语称为该句型的句柄。
给定句型找句柄的步骤:
短语
简单短语 句柄
例: 文法G[<无符号整数>], w = <数字串>1
<
无符号整数> => <数字串> => <数字串><数字>
=> <数字串>1
短语:<数字串>1,1 ; 简单短语:1;句柄:1
注意:短语、简单短语是相对于句型而言的,一个句型
可能有多个短语、简单短语,而句柄只能有一个。
北京航空航天大学计算机学院
2
9
Z
2.4 语法树与二义性文法
U
V
2
.4.1 推导与语法(推导)树
a
b c
d
(
1)语法(推导)树:句子( 句型)结构的图示表示法,
它是有向图,由结点和有向边组成。
结点:符号
根结点: 识别符号(非终结符)
中间结点:非终结符
叶结点: 终结符或非终结符
有向边:表示结点间的派生关系
北京航空航天大学计算机学院
3
0
( 2 ) 句型的推导及语法树的生成(自顶向下)
给定G[Z],句型w:
*
G
可建立推导序列,Z ==> w
可建立语法树,以Z为树根结点,每步推导生成语法树
的一枝,最终可生成句型w的语法树。
注意一个重要事实:文法所能产生的句子,可以
用不同的推导序列(使用产生式顺序不同)将其
推导出来。语法树的生长规律不同,但最终生成的语
法树形状完全相同。某些文法有此性质,而某些文法
不具此性质。
北京航空航天大学计算机学院
3
1

G[<无符号整数>]:
<
<
<
无符号整数> →<数字串>
数字串> →<数字串> <数字> | <数字>
数字> →0 | 1 | 2 | 3 | …… | 9
一般推导:
<
无符号整数>
(1)
数字串>
<
(2)
<
数字串> <数字>
(3)
(4)
<
数字>
0
(5)
1
北京航空航天大学计算机学院
3
2
最左推导:
<
无符号整数>
(1)
数字串>
<
(2)
<
数字串> <数字>
(3)
(5)
<
数字>
0
(4)
1
北京航空航天大学计算机学院
3
3
最右推导
<
无符号整数>
(1)
数字串>
<
(2)
<
数字串> <数字>
(4)
(3)
<
数字>
0
(5)
1
北京航空航天大学计算机学院
3
4
( 3 ) 子树与短语
子树:语法树中的某个结点(子树的根)连同它向下
派生的部分所组成。
某子树的末端结点按自左向右顺序为句型中的符
定理
号串,则该符号串为该句型的相对于该子树根的短语。
只需画出句型的语法树,然后根据子树找短语→
简单短语→句柄。
北京航空航天大学计算机学院
3
5

( 4 ) 树与推导
句型推导过程<==> 该句型语法树的生长过程
由推导构造语法树
1
从识别符号开始,自左向右建立推导序列。
由根结点开始,自上而下建立语法树。
北京航空航天大学计算机学院
3
6
由语法树构造推导
2
自下而上地修剪子树的某些末端结点(短语),直至
把整棵树剪掉(留根),每剪一次对应一次归约。
从句型开始,自右向左地逐步进行归约,建立推导序列。
北京航空航天大学计算机学院
3
7
定义12. 对句型中最左简单短语(句柄)进行的归约称为
规范归约。
定义13. 通过规范推导或规范归约所得到的句型称为规范句型。
句型<数字><数字>不是文法的规范句型,因为:
<
无符号整数>==><数字串>
=
=
=><数字串><数字>
=><数字><数字>
不是规范推导
北京航空航天大学计算机学院
3
8
2
.4.2 文法的二义性
定义14.1 若对于一个文法的某一句子(或句型)
存在两棵不同的语法树,则该文法是二义性文法,
否则是无二义性文法。
换而言之,无二义性文法的句子只有一棵语法树,尽管推
导过程可以不同。
二义性文法举例:
G[E]:
E ::= E+E | E*E | (E) | i
Vn={E}
Vt={ +, * , ( , ) , i }
北京航空航天大学计算机学院
3
9

对于句子S=i+i * i ∈ L( G[E] ),存在不同的规
范推导:
(1) E==>E+E==>E+E*E ==>E+E*i ==>E+i*i ==> i+i * i
(2) E==> E*E ==> E*i ==> E+E*i ==> E+i*i ==> i+i * i
这两种不同的推导对应了两棵不同的语法树:
E
E
E + E
E * E
i
i
E
i
E
i
E
i
E
i
*
+
北京航空航天大学计算机学院
4
0
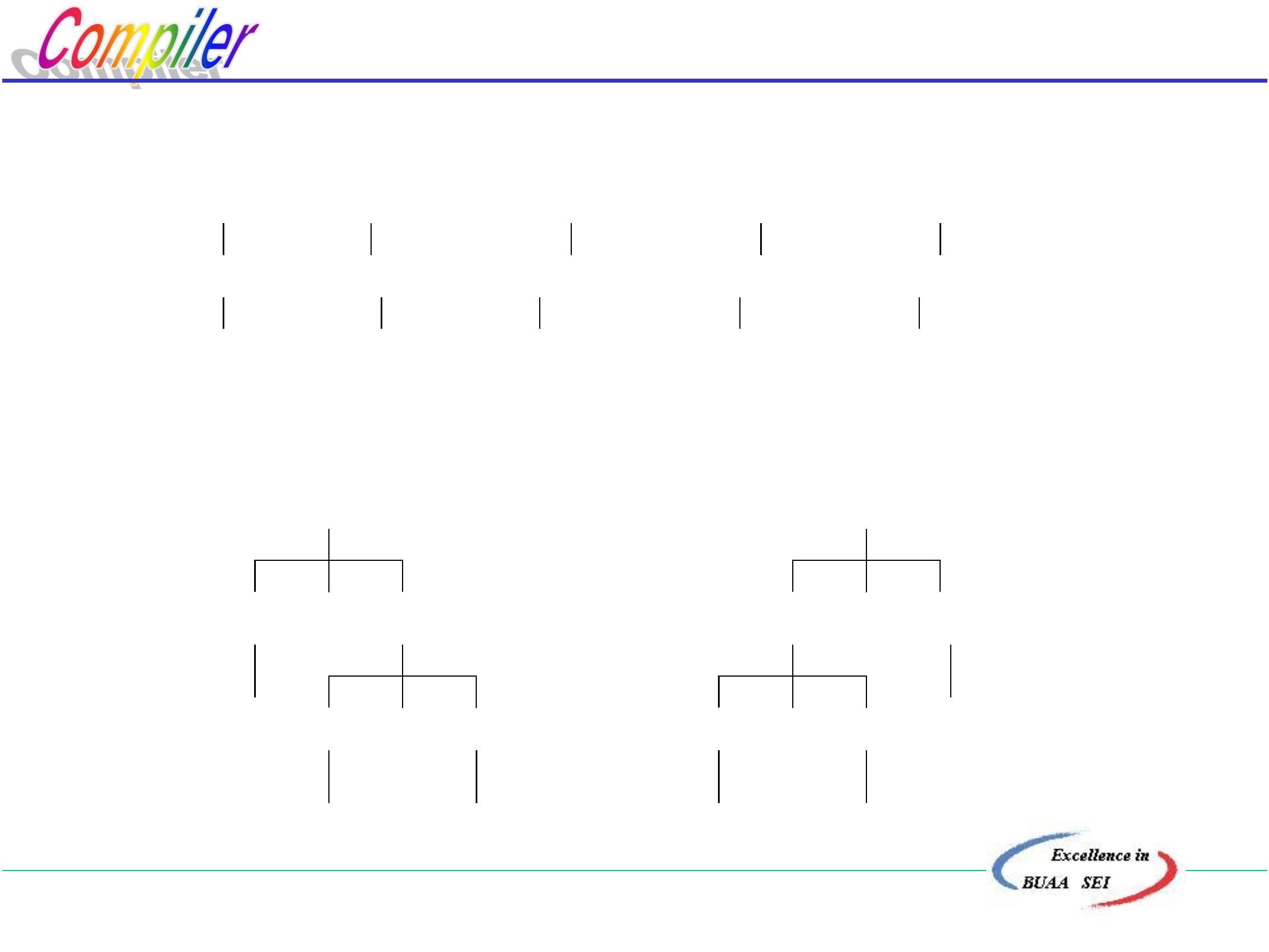
定义14.2 若一个文法的某句子存在两个不同的规范推导,则
该文法是二义性的,否则是无二义性的。
(1) E=|=>E+E=|=>E+E*E =|=>E+E*i =|=>E+i*i =|= > i+i * i
|
|
|
|
|
(2) E==> E*E ==> E*i ==> E+E*i ==> E+i*i ==> i+i * i
从自底向上的归约过程来看,上例中规范句型
E+E*i 是由i+i * i通过两步规范归约得到的,但对于同
一个句型E+E* i,它有两个不同的句柄(对应上述两棵
不同的语法树):i 和E+E。因此,文法的二义性意味
着句型的句柄不唯一。
北京航空航天大学计算机学院
4
1

E
E
E + E
E * E
E
E
i
*
i
E + E
句柄:i
句柄:E+E
定义14.3 若一个文法的某规范句型的句柄不唯一,则该文法
是二义性的,否则是无二义性的。
北京航空航天大学计算机学院
4
2
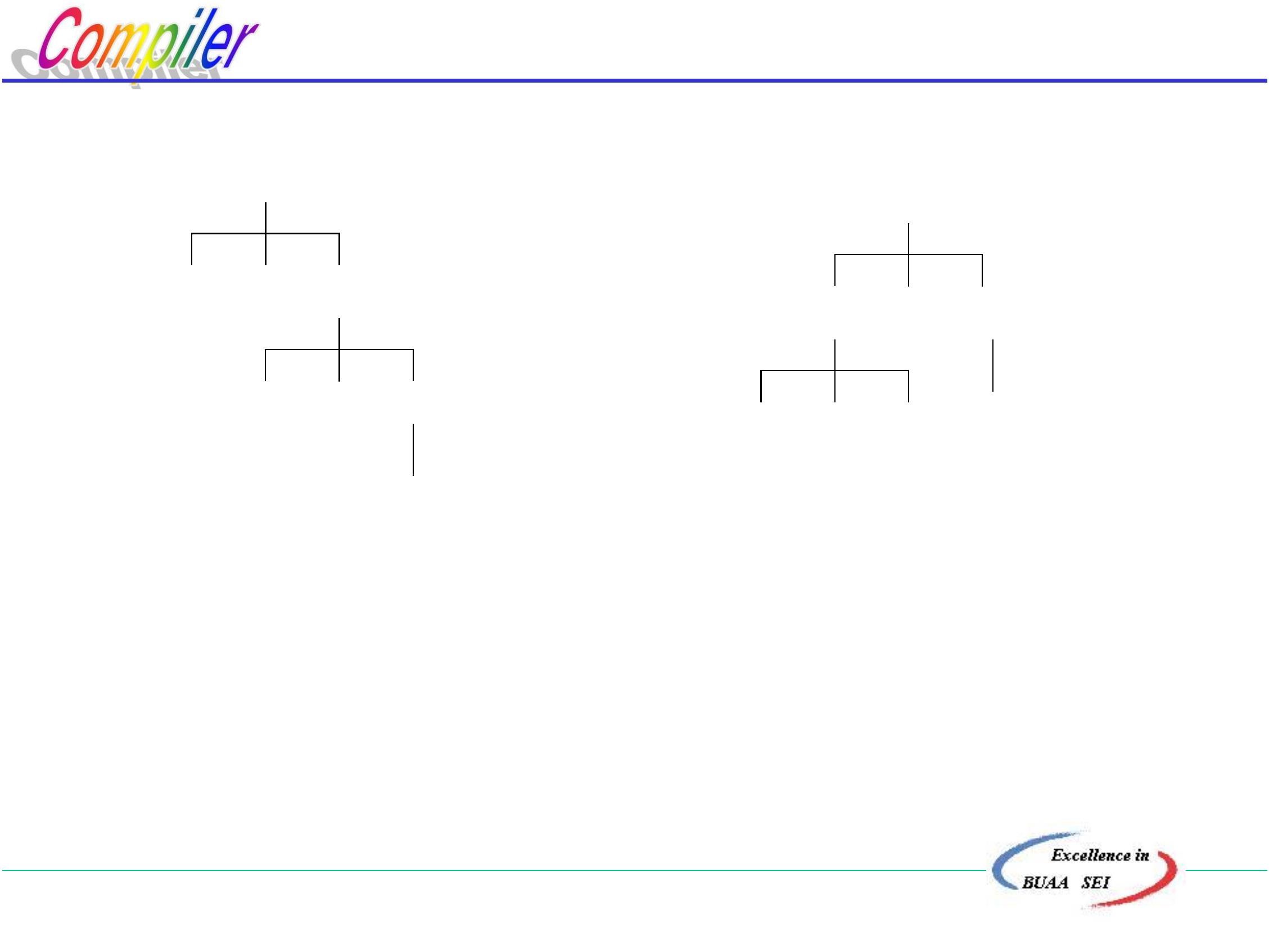
若文法是二义性的,则在编译时就会产生不确定性,
遗憾的是在理论上已经证明:文法的二义性是不可判定的,
即不可能构造出一个算法,通过有限步骤来判定任一文法
是否有二义性。
现在的解决办法是:提出一些限制条件,称为无二义性
的充分条件,当文法满足这些条件时,就可以判定文法是无
二义性的。
例:算术表达式的文法
E::= E+T | T
T ::= T*F | F
F ::= (E) | i
E::= E+E | E*E | (E) | i
北京航空航天大学计算机学院
4
3
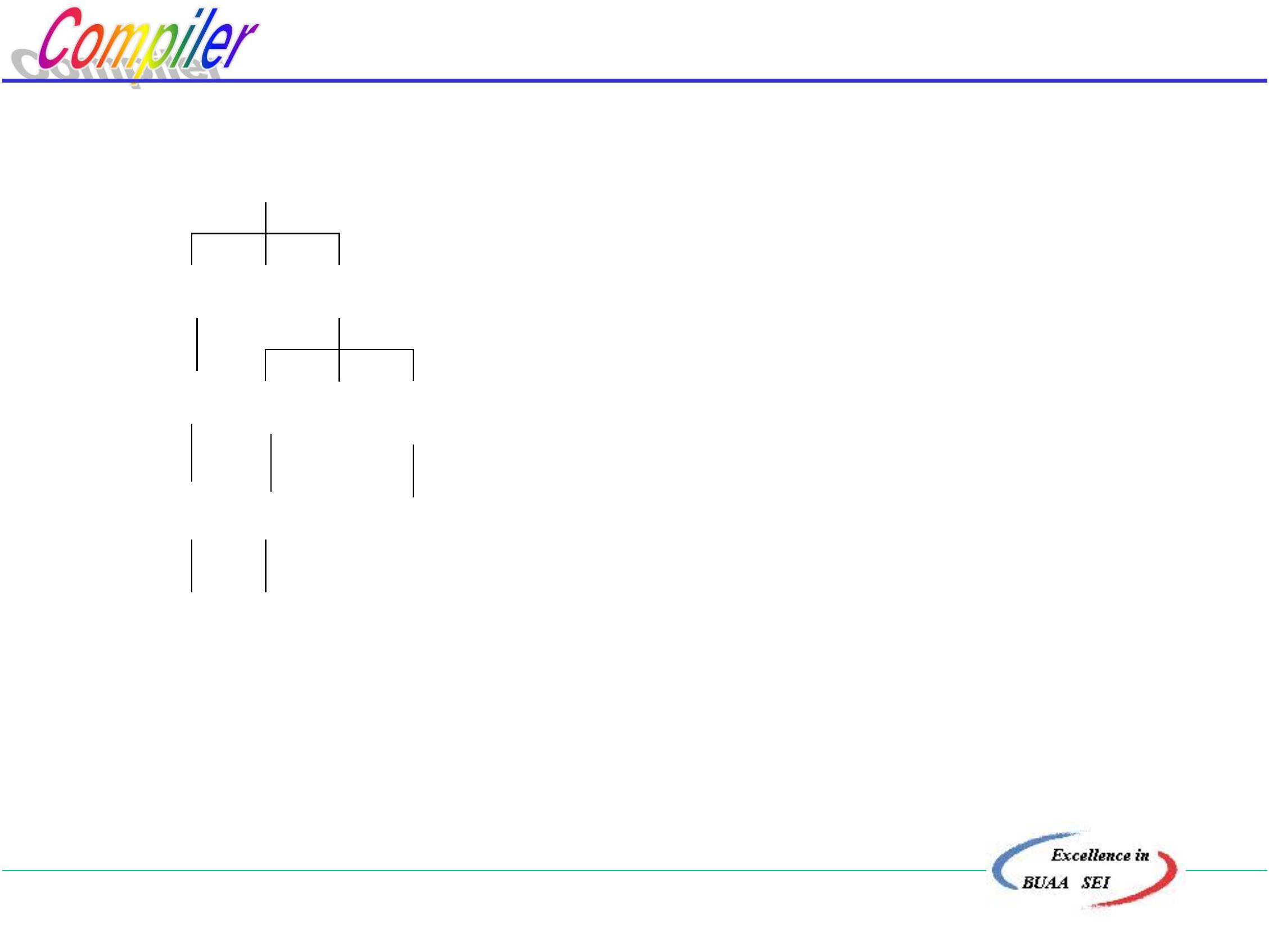
句子:i+ i * i
E
E + T
E =|=> E+T =|=> E+T*F =|=> E+T*i
=
=
|=> E+F*i =|=> E+i*i =|=> T+i*i
|=> F+i*i =|=> i+i*i
T
F
T
F
F
i
*
i i
北京航空航天大学计算机学院
4
4
也可以采用另一种解决办法:即不改变二义性文法,而是确
定一种编译算法,使该算法满足无二义性充分条件。
例: Pascal 条件语句的文法
<
条件语句>::= If <布尔表达式>then<语句> |
If <布尔表达式> then <语句> else <语句>
<
语句> ::= <条件语句> | <非条件语句> |…….
If B then If B then stmt else stmt
北京航空航天大学计算机学院
4
5

2.5 句子的分析
任务:给定G[Z]: S ∈ Vt*, 判定是否有S L (G[Z] ) ?
这是词法分析和语法分析所要做的工作,将在第三、
第四章中详细介绍。
北京航空航天大学计算机学院
4
6

2.6 有关文法的实用限制
若文法中有如U::=U的规则,则这就是有害规则,它会引
起二义性。
例如存在U::=U,U::= a | b,则有两棵语法树:
U
U
a
U
a
北京航空航天大学计算机学院
4
7
多余规则:(1)在推导文法的所有句子中,始终用不到的规则。
即该规则的左部非终结符不出现在任何句型中(不可达符号)
(
2)在推导句子的过程中,一旦使用了该规则,将推
不出任何终结符号串。即该规则中含有推不出任何终结符号串
的非终结符(不活动符号)
例如给定G[Z],若其中关于U的规则只有如下一条:
U::=xUy
若还有U::=a,则此规则
并非多余
该规则是多余规则。
若某文法中无有害规则或多余规则,则称该文法是压缩过的。
北京航空航天大学计算机学院
4
8
例1:G[<Z>] :
例2: G[S] :
S ::= ccc
<
<
<
<
<
Z> ::= <B> e
A> ::= <A> e | e
B> ::= <C> e | <A> f
C> ::= <C> f
D> ::= f
S ::= Abccc
A ::= Ab
A ::= aBa
B ::= aBa
B ::= AD
D ::= Db
D ::= b
北京航空航天大学计算机学院
4
9
2
.7 文法的其它表示法
<
<
标识符>::=字母{字母|数字}
无符号整数>::=数字{数字}
1
、扩充的BNF表示
•
BNF的元符号:< , >, ::= , |
•
扩充的BNF的元符号:< , >, ::= , | , { , } , [ , ] , ( , )
标识符
2
、语法图
字母
字母
数
字
无符号整数
数字
北京航空航天大学计算机学院
5
0
2.8 文法和语言分类
形式语言:用文法和自动机所描述的没有语义的语言。
文法定义:乔姆斯基将所有文法都定义为一个四元组:
G=(Vn,Vt,P,Z)
Vn:非终结符号集
Vt:终结符号集
P:产生式或规则的集合
Z:开始符号(识别符号) Z∈Vn
+
语言定义: L(G[Z])={x| x∈Vt*, Z==>x }
北京航空航天大学计算机学院
5
1

文法和语言分类:0型、1型、2型、3型
这几类文法的差别在于对产生式(语法规则)施加不同的限制。
0
型: P:u ::= v
其中 u∈V+,v∈V* V = Vn∪ Vt
0型文法称为短语结构文法。规则的左部和右部都可
以是符号串,一个短语可以产生另一个短语。
0
型语言:L0 这种语言可以用图灵机(Turing)接受。
北京航空航天大学计算机学院
5
2

1
型: P:xUy ::= xuy
其中U∈Vn,
x、y、u∈V*
称为上下文敏感或上下文有关。也即只有在x、y这样的
上下文中才能把U改写为u
1
型语言:L1 这种语言可以由一种线性界限自动机接受。
北京航空航天大学计算机学院
5
3

2
型: P:U ::= u
其中U∈Vn,
u∈V*
称为上下文无关文法。也即把U改写为u时,不必考虑上下文。
(1型文法的规则中x,y均为 ε 时即为2型文法)
注意:2型文法与BNF表示相等价。
2
型语言:L2 这种语言可以由下推自动机接受。
北京航空航天大学计算机学院
5
4

3
型文法:
(
左线性)
P:U ::= t
(右线性)
P:U ::= t
或 U ::= Wt
其中U、W∈Vn
t∈Vt
或 U ::= tW
其中U、W∈Vn
t∈Vt
3
型文法称为正则文法。它是对2型文法进行进一步限制。
3型语言:L3 又称正则语言、正则集合
这种语言可以由有穷自动机接受。
北京航空航天大学计算机学院
5
5

•
•
•
•
根据上述讨论,L0 L1 L2 L3
0型文法可以产生L0、L1、L2、L3,
但2型文法只能产生L2,L3不能产生L0,L1
3型文法只能产生L3
北京航空航天大学计算机学院
5
6

第三章 词法分析
•
•
词法分析程序的功能及实现方案
单词的种类及词法分析程序的输出形式
正则文法和状态图
•
•
•
•
词法分析程序的设计与实现
正则表达式与有穷自动机
词法分析程序的自动生成器
北京航空航天大学计算机学院
1

3
.1 词法分析程序的功能及实现方案
词法分析程序的功能
¨
¨
¨
词法分析:根据词法规则识别及组合单词,进行词法检查。
对数字常数完成数字字符串到二进制数值的转换。
删去空格字符和注释。
北京航空航天大学计算机学院
2

实现方案:基本上有两种
1
.词法分析单独作为一遍
单词串
第二遍
第一遍
S.P.(字符串)
词法分析
S.P.(符号串)
语法分析
优点: 结构清晰、
各遍功能单一
缺点:效率低
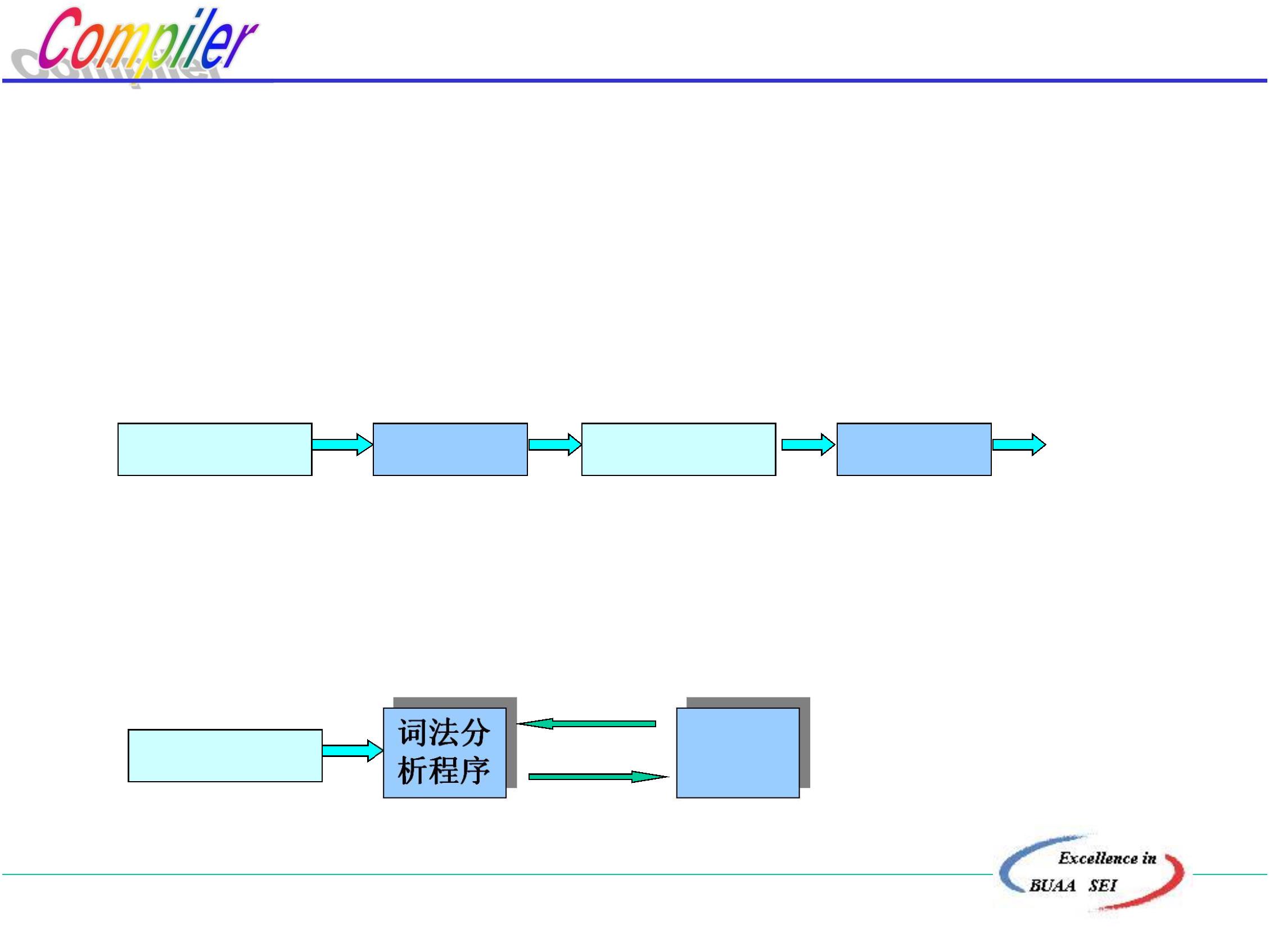
2
.词法分析程序作为单独的子程序
取单词
词法分
析程序
语法分
析程序
S.P.(字符串)
单词
优点: 效率高
北京航空航天大学计算机学院
3
3
.2 单词的种类及词法分析程序的输出形式
单词的种类
1
2
3
4
. 保留字:begin、end、for、do...
. 标识符:由用户定义,表示各种名字
. 常 数:无符号数、布尔常数、字符串常数等
. 分界符:+、-、*、/、...
北京航空航天大学计算机学院
4

词法分析程序的输出形式-----单词的内部形式
单词类别 单词值
几种常用的单词内部形式:
1
2
3
、按单词种类分类
、保留字和分界符采用一符一类
、标识符和常数的单词值又为指示字(指针值)
北京航空航天大学计算机学院
5
1
、按单词种类分类
单词名称
单词值
类别编码
标识符
1
2
3
4
5
6
7
内部字符串
整数值
无符号常数(整)
无符号浮点数
布尔常数
字符串常数
保留字
数值
0 或 1
内部字符串
保留字或内部编码
分界符或内部编码
分界符
北京航空航天大学计算机学院
6

2
、保留字和分界符采用一符一类
类别编码
单词名称
单词值
1
2
3
4
5
6
7
8
9
标识符
内部字符串
整数值
无符号常数(整)
无符号浮点数
布尔常数
字符串常数
BEGIN
END
FOR
DO
数值
0 或 1
内部字符串
-
-
-
-
…
2
2
2
2
….
…
:
+
*
,
……
…..
-
-
-
0
1
2
3
-
…
….
(
--
北京航空航天大学计算机学院
7

3
.3 正则文法和状态图
•
状态图的画法(根据文法画出状态图)
例如:正则文法
Z::= U0 |V1
U ::=Z1 |1
V ::=Z0 | 0
左线性文法。该文法所定义的语言为:
L(G[Z]) = { Bn | n>0 }, 其中B= {01,10}
北京航空航天大学计算机学院
8

左线性文法的状态图的画法:
1
2
. 令G的每个非终结符都是一个状态;
. 设一个开始状态S;
T
3
. 若Q::=T, Q ∈Vn,T ∈Vt, 则:
Q
S
T
4
. 若Q::=RT, Q、R∈Vn,T ∈Vt, 则:
Q
R
5
. 按自动机方法,可加上开始状态和终止状态标志。
北京航空航天大学计算机学院
9
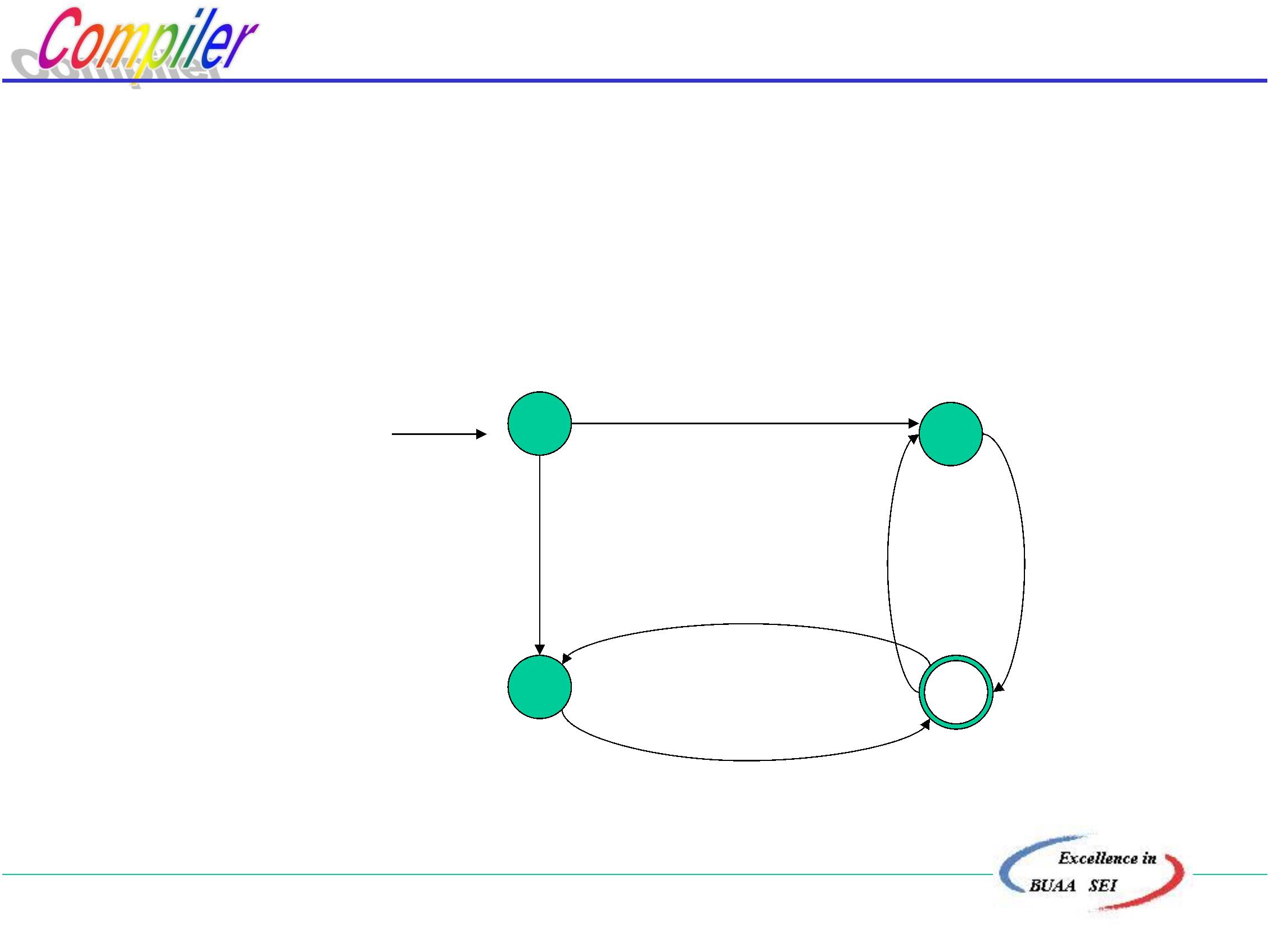
例如:正则文法
Z::= U0 |V1
U ::=Z1 |1
V ::=Z0 | 0
1
Start
其状态图为:
S
U
Z
0
1
0
0
V
1
北京航空航天大学计算机学院
1
0
•
识别算法
利用状态图可按如下步骤分析和识别字符串x:
1
、置初始状态为当前状态,从x的最左字符开始,
重复步骤2,直到x右端为止。
2
、扫描x的下一个字符,在当前状态所射出的弧中
找出标记有该字符的弧,并沿此弧过渡到下一个状
态;如果找不到标有该字符的弧,那么x不是句子,
过程到此结束;如果扫描的是x的最右端字符,并
从当前状态出发沿着标有该字符的弧过渡到下一个
状态为终止状态Z,则x是句子。
例:x=0110 和1011
北京航空航天大学计算机学院
11

•问题:
1、上述分析过程是属于自底向上分析?还是自顶向下
分析?
Z
2
、怎样确定句柄?
V
Z
U
Z =|=> V1 =|=>Z01 =|=>U001 =|=> 1001
1
0 0 1
北京航空航天大学计算机学院
1
2
3
.4 词法分析程序的设计与实现
词法规则 状态图 词法分析程序
北京航空航天大学计算机学院
1
3
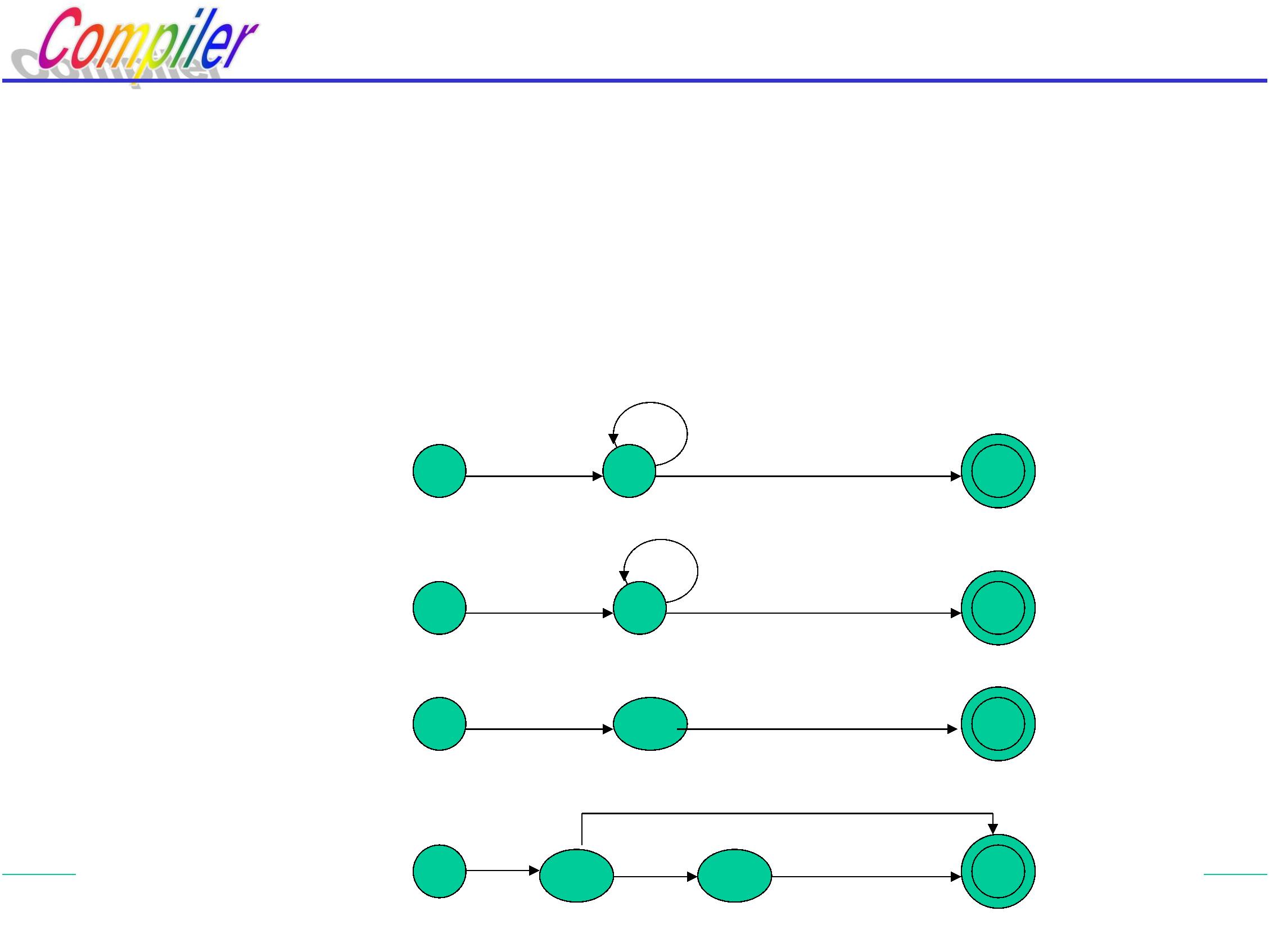
3
.4.1 文法及其状态图
语言的单词符号
标识符
保留字(标识符的子集)
无符号整数
单分界符 + * :,( )
双分界符 :=
两点说明:1. 空格的作用
2. 实数的表示
北京航空航天大学计算机学院
1
4

•
文法:1. <标识符>::= 字母| <标识符>字母| <标识符>数字
2. <无符号整数>::=数字| <无符号整数>数字
3. <单字符分界符>::= : | + | * | , | ( | )
4. <双字符分界符>::= <冒号>=
5. <冒号>::= :
字母、数字
字母
数字
非字母数字
非数字
标识符
S
标
数字
无符号整数
S
S
数
单字符分界符
其他字符
+ * ,
( )
单界
非 =
双字符分界符
:
=
S
双界
冒号
其他字符
查保留字表
字母、数字
非字母数字
标
读字符
字母
数字
S
标识符
数字
非数字
数
无符号整数
其他字符
+
* ,
( )
单界
单字符分界符
双字符分界符
非 =
:
=
冒号
双界
其他字符
其他
出错
返回S
北京航空航天大学计算机学院
1
6
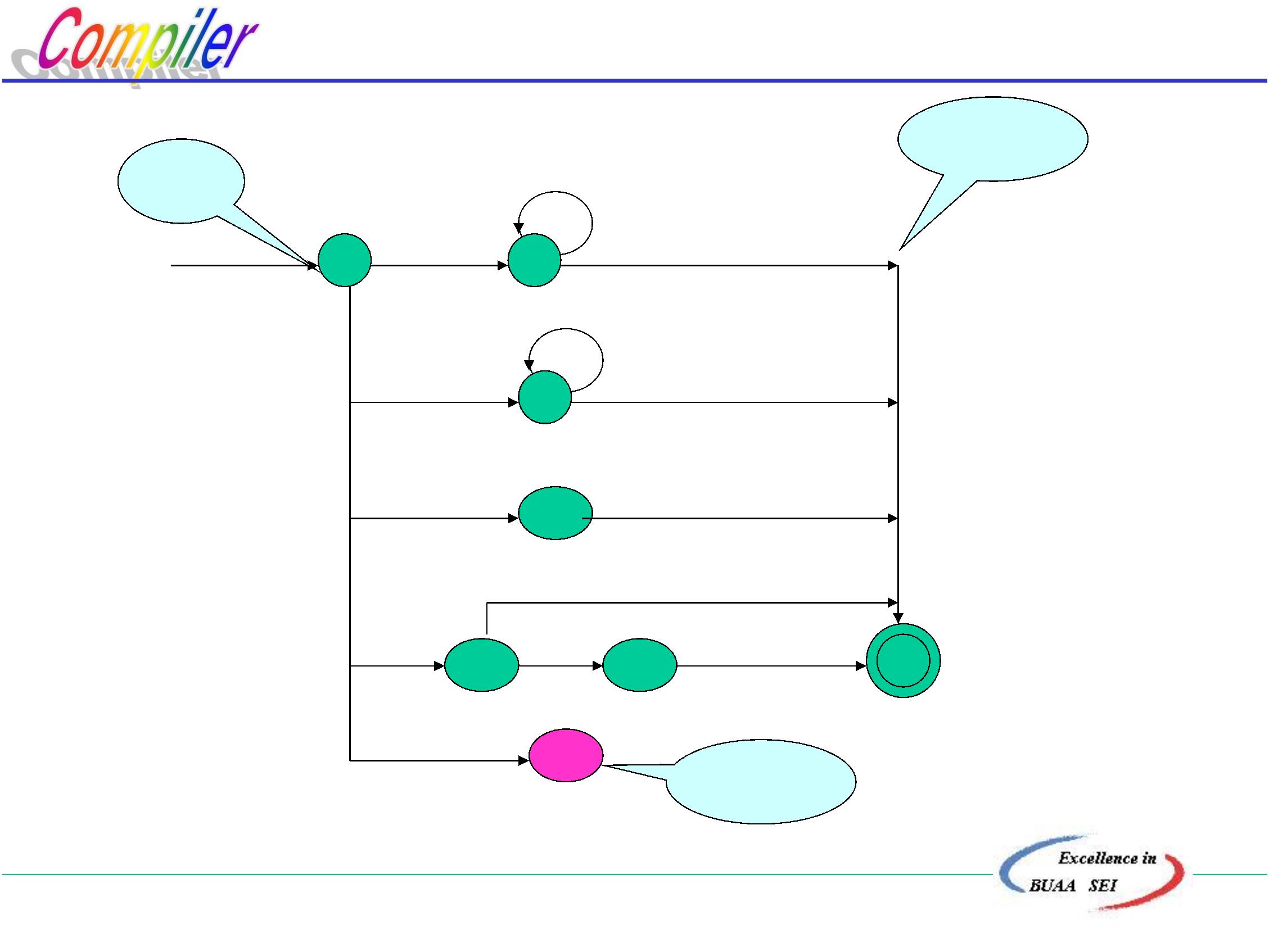
3
.4.2 状态图的实现——构造词法分析程序
1
2
3
. 单词及内部表示
. 词法分析程序需要引用的公共(全局)变量和过程
. 词法分析程序算法
北京航空航天大学计算机学院
1
7

1
.单词及内部表示: 保留字和分界符采用一符一类
单词名称
类别编码
记忆符
单词值
BEGIN
END
FOR
DO
1
2
3
4
BEGINSY
ENDSY
FORSY
DOSY
-
-
-
-
IF
5
IFSY
-
THEN
ELSE
标识符
6
7
8
THENSY
ELSESY
IDSY
-
-
内部字符串
整数值
常数(整)
9
INTSY
:
10
11
12
13
14
15
16
COLONSY
PLUSSY
STARSY
COMSY
LPARSY
RPARSY
ASSIGNSY
-
-
-
-
-
-
-
+
*
,
(
)
:
=
北京航空航天大学计算机学院
1
8

2
.词法分析程序需要引用的公共(全局)变量和过程
名称
类别
功能
4
4
4
4
CHAR
TOKEN
GETCHAR
GETNBC
字符变量
字符数组
存放当前读入的字符
存放单词字符串
读字符过程 读字符到CHAR,移动指针
过程
反复调用GETCHAR,
直至CHAR进入一个非空白字符
CHAR与TOKEN连接
判断
4
4
CAT
ISLETTER 和
过程
布尔函数
过程
ISDIGIT
4
4
读字符指针后退一个字符
判断TOKEN中的字符串
是保留字, 还是标识符
字符串到数字的转换
出错处理
UNGETCH
RESERVE
布尔函数
函数
过程
4
4
ATOI
ERROR
北京航空航天大学计算机学院
1
9

3
、词法分析程序算法
S TA RT: TOKEN := ‘ ‘; /*置TOKEN为空串*/
GETCHAR; GETNBC;
CASE CHAR OF
‘
A’..’Z’: BEGIN
WHILE ISLETTER OR ISDIGET DO
BEGIN CAT; GETCHAR END;
UNGETCH;
C:= RESERVE;
IF C=0 THEN RETURN(‘IDSY’: TOKEN)
ELSE RETURN (C,-) /*C为保留字编码*/
END;
0’..’9’: BEGIN
WHILE DIGIT DO
BEGIN CAT; GETCHAR END;
‘
UNGETCH;
RETURN (‘INTSY’,ATOI)
END;
‘
+’ : RETURN(‘PLUSSY’,-) ;
北京航空航天大学计算机学院
2
0

‘
‘
‘
‘
‘
*’ : RETURN(‘STARSY’,-) ;
,’ : RETURN(‘COMMASY’,-) ;
(’ : RETURN(‘LPARSY’,-) ;
)’ : RETURN(‘RPARSY’,-) ;
:’ : BEGIN
GETCHAR;
if CHAR=‘=‘ THEN RETURN(‘ASSIGNSY’,-) ;
UNGETCH;
RETURN(‘COLONSY’,-) ;
END
END OF CASE;
ERROR;
GOTO START;
北京航空航天大学计算机学院
2
1

3
.5.1 正则表达式和正则集合的递归定义
有字母表, 定义在 上的正则表达式和正则集合递归定义如下:
1
2
3
. 和都是 上的正则表达式, 其正则集合分别为:{}和;
. 任何a , a是 上的正则表达式,其正则集合为:{a};
. 假定U和V是 上的正则表达式, 其正则集合分别记为L(U)
和L(V), 那么U|V, U•V和U*也都是 上的正则表达式, 其
正则集合分别为L(U) L(V)、 L(U) • L(V)和L(U)*;
. 任何 上的正则表达式和正则集合均由1、2和3产生。
4
北京航空航天大学计算机学院
2
2

正则表达式中的运算符:
|
*
-----或(选择) • ----连接
或 { } ---重复 () ----括号
运算符的优先级:
先*, 后• , 最后 |
• 在正则表达式中可以省略.
正则表达式相等 这两个正则表达式表示的语言相等
如:b{ab} = {ba}b
{a|b} = {{a} {b}} = (a*b*)*
北京航空航天大学计算机学院
2
3

例:设 = { a,b },下面是定义在上的正则表达式和正则集合
正则集合
正则表达式
ba*
a(a|b)*
(a|b)*(aa|bb)(a|b)*
北京航空航天大学计算机学院
2
4

正则表达式的性质:
设e1, e2和e3均是某字母表上的正则表达式, 则有:
单位正则表达式:
e = e = e
交换律: e1 | e2 = e2 | e1
结合律: e1|(e2|e3) = (e1|e2)|e3
e1(e2e3) = (e1e2)e3
分配律: e1(e2|e3) = e1e2|e1e3
(e1|e2)e3 = e1e3|e2e3
此外: r* = (r|)* r** =r*
(r|s)* = (r*s*)*
北京航空航天大学计算机学院
2
5

正则表达式与3型文法等价
例如:
正则表达式:ba*
a(a|b)*
3
型文法: Z ::= Za|b
Z::=Za|Zb|a
例:
3
型文法
正则表达式
S::= aS|aB
B::= bC
aS|aba*a
ba*a
a*aba*a
C::= aC|a
a*a
北京航空航天大学计算机学院
2
6
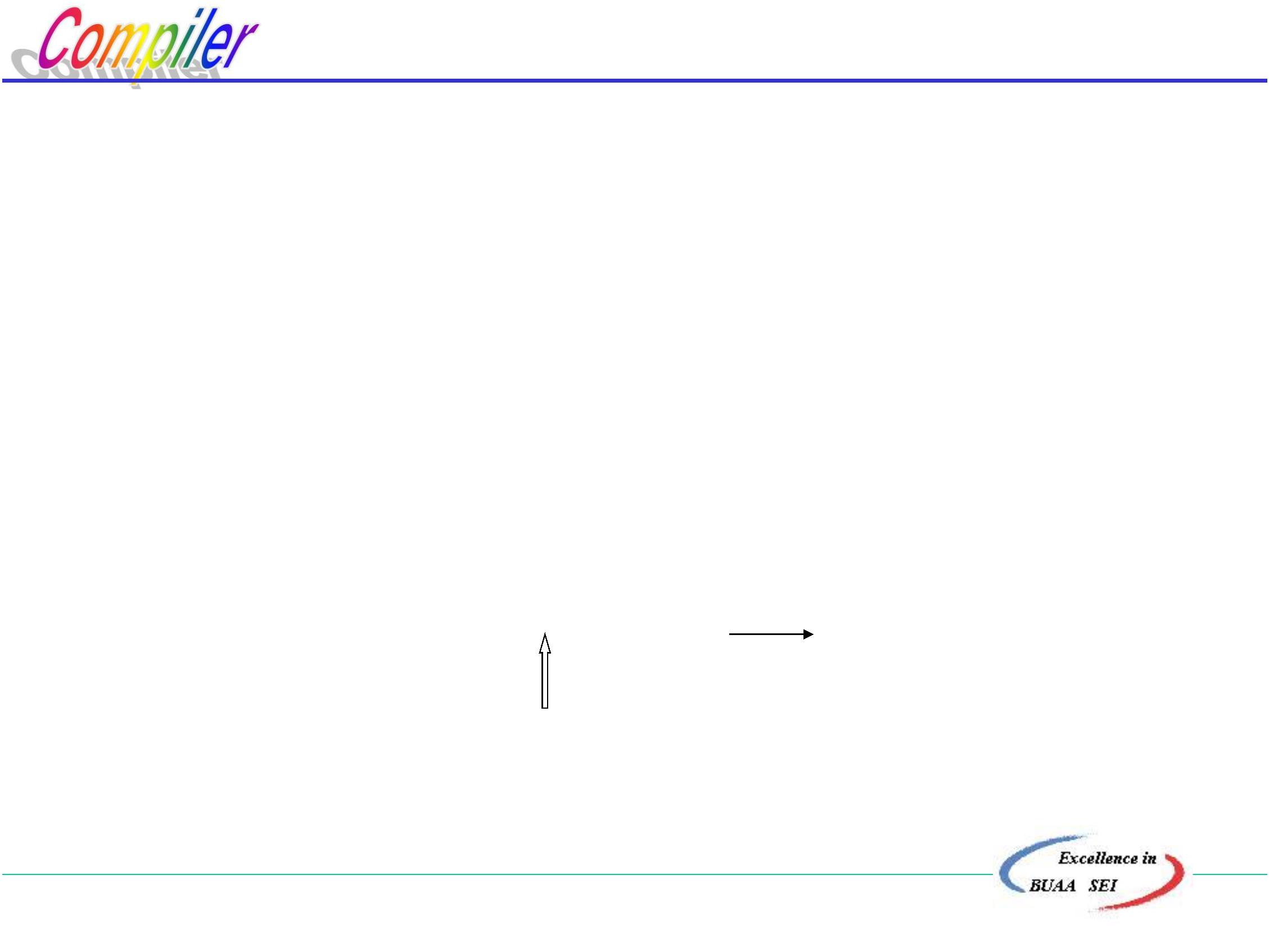
3
.5.2 确定的有穷自动机(DFA)— 状态图的形式化
(Deterministic Finite Automata)
一个确定的有穷自动机(DFA)M是一个五元式:
M=(S, Σ,δ,s0, Z)
其中:
1
2
3
. S —有穷状态集
. Σ—输入字母表
. δ—映射函数(也称状态转换函数)
S×Σ→S
δ(s,a)=s’ , s, s’ ∈S, a∈Σ
4
5
. s0 —初始状态
. Z—终止状态集
s
0
∈S
ZS
北京航空航天大学计算机学院
2
7

例如: M:({0,1,2,3},{a,b},δ,0,{3})
δ(0,a)=1 δ(0,b)=2
δ(1,a)=3 δ(1,b)=2
δ(2,a)=1 δ(2,b)=3
δ(3,a)=3 δ(3,b)=3
状态转换函数δ可用一矩阵来表示:
输入
字符
所谓确定的状
态机,其确定
性都表现在状
态转换函数是
单值函数!
状态
a
b
0
1
2
3
1
2
3
1
3
2
3
3
北京航空航天大学计算机学院
2
8
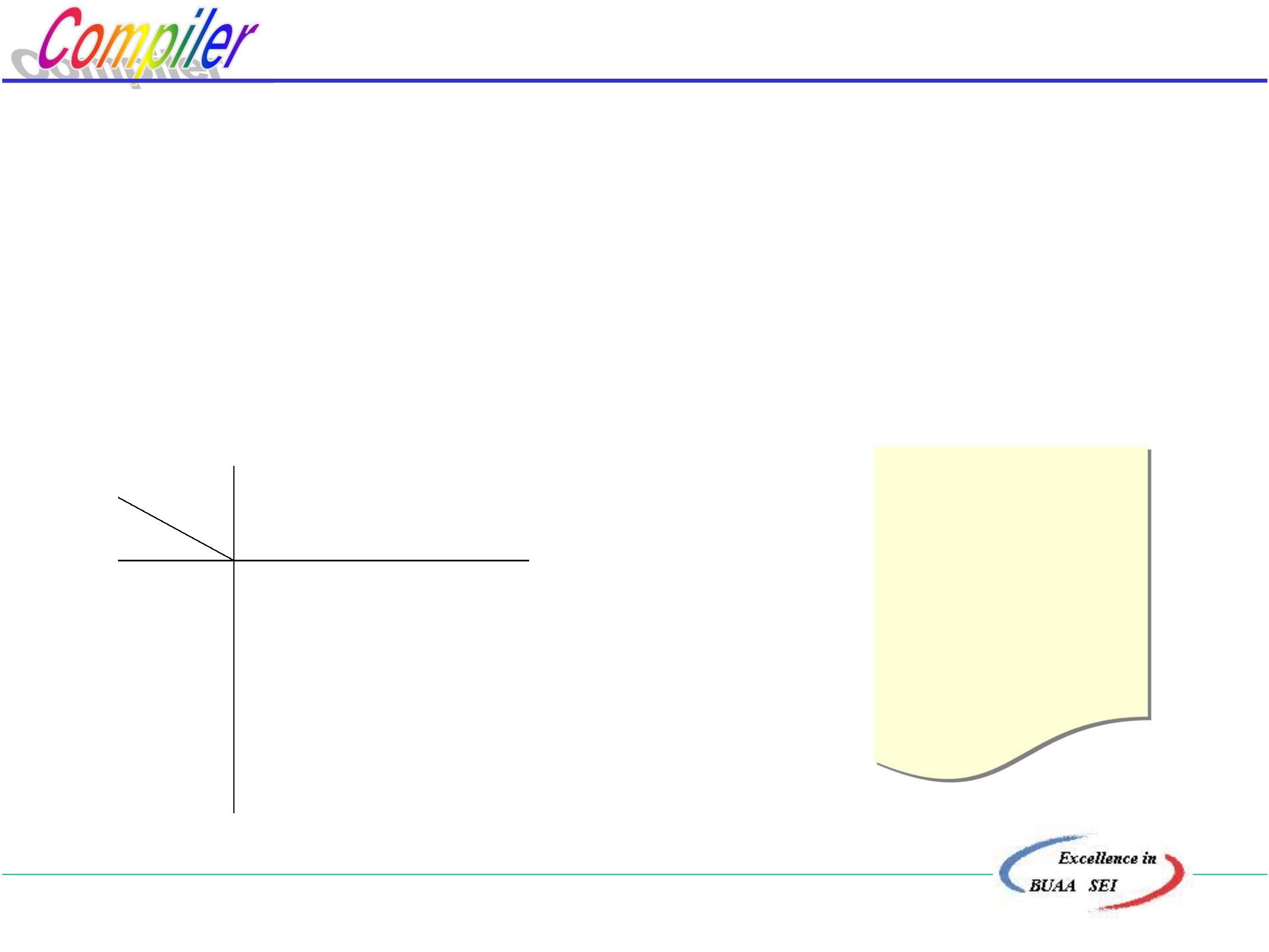
DFA也可以用一状态转换图表示:
DFA的状态图表示:
a
a
1
2
start
0
b
a
3
a,b
b
b
北京航空航天大学计算机学院
2
9
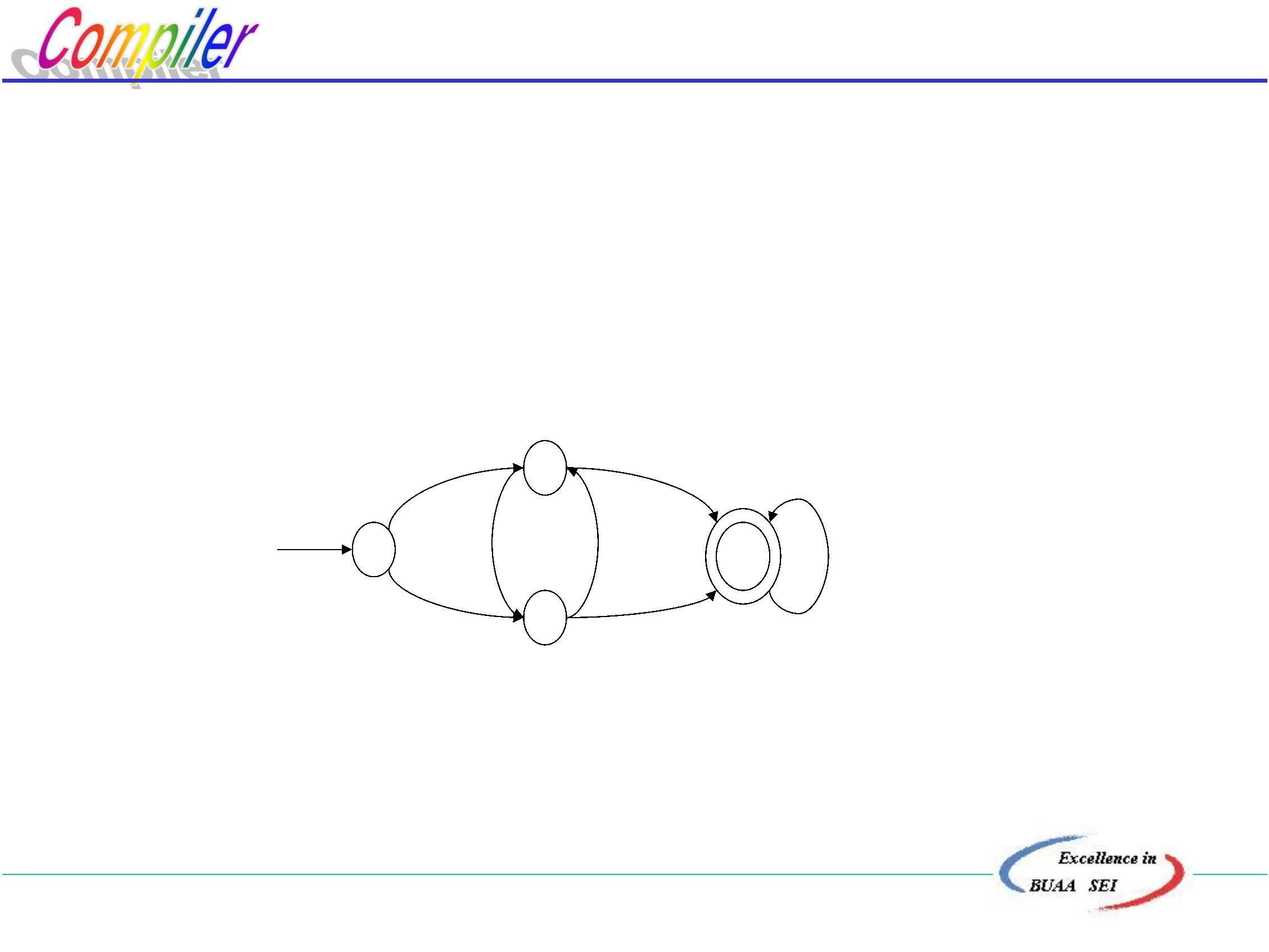
DFA M所接受的符号串:
令α= a1a2¨¨¨an,α∈Σ,若*δ(δ(¨¨ δ(s0, a1),a2)¨¨),
an-1),an) = Sn ,且Sn ∈Z,则可以写成δ(s0, α)= Sn,我们称α可为
M所接受。
δ(s0, a1)= S1
换言之:若存在一条
初始状态到某一终止
状态的路径,且这条
路径上能有弧的标记
符号连接成符号串α,
则称α为DFA M(接受)
识别。
δ(s1, a2)= S2
…
……
δ(sn-2, an-1)= Sn-1
δ(sn-1, an)= Sn
DFA M所接受的语言为:L(M)={α|δ(s0, α)= Sn , Sn∈Z}
北京航空航天大学计算机学院
3
0

3
.5.3 不确定的有穷自动机(NFA)
(Nondeterministic Finite Automata)
若δ是一个多值函数,且输入可允许为ε,则有穷自动机是不确定的,
即在某个状态下,对于某个输入字符存在多个后继状态。
ꢀ
从同一状态出发,有以同一字符标记的多条边,或者有
以ε标记的特殊边的自动机。
北京航空航天大学计算机学院
3
1

NFA的形式定义为:
一个非确定的有穷自动机NFA M’是一个五元式:
NFA M’=(S, Σ∪{ε}, δ, s0, Z)
其中 S—有穷状态集
Σ∪{ε}—输入符号加上ε,
即自动机的每个结点所射出的弧可以是Σ中的一个字符或是ε
s0—初态
s
0
∈S
Z—终态集
δ—转换函数
ZS
S×Σ∪{ε} →2S
(2S --S的幂集—S的子集构成的集合)
北京航空航天大学计算机学院
3
2

NFA M’所接受的语言为:
L(M’)={α|δ(S0,α)=S’ S’∩Z≠Φ}
例:NFA M’=({1,2,3,4},{a,b,c} ∪{ε},δ,1,{4})
北京航空航天大学计算机学院
3
3

上例题相应的状态图为:
a
b
a
2
start
ε
4
1
c
a 3
c
M’所接受的语言(用正则表达式) R=aa*b|ac*c|ε
北京航空航天大学计算机学院
3
4
3
.5.4 NFA的确定化
已证明:不确定的有穷自动机与确定的有穷自动机从功能
上来说是等价的,也就是说能够从:
NFA M ’构造成一个DFA M
使得 L(M)=L(M’)
北京航空航天大学计算机学院
3
5

为了使得NFA确定化,首先给出两个定义:
定义1、集合I的ε-闭包:
令I是一个状态集的子集,定义ε-closure(I)为:
1
2
)若s∈I,则s∈ε-closure(I);
)若s∈I,则从s出发经过任意条ε弧能够到达的任何
状态都属于ε-closure(I)。
状态集ε-closure(I)称为I的ε-闭包。
可以通过一例子来说明状态子集的ε-闭包的构造方法
北京航空航天大学计算机学院
3
6

ε
例:
2
3
4
6
5
a
如图所示的状态图:
令I={1},
1
ε
a
求ε-closure(I)=?
a
根据定义:
ε-closure(I)= {1,3}
北京航空航天大学计算机学院
3
7
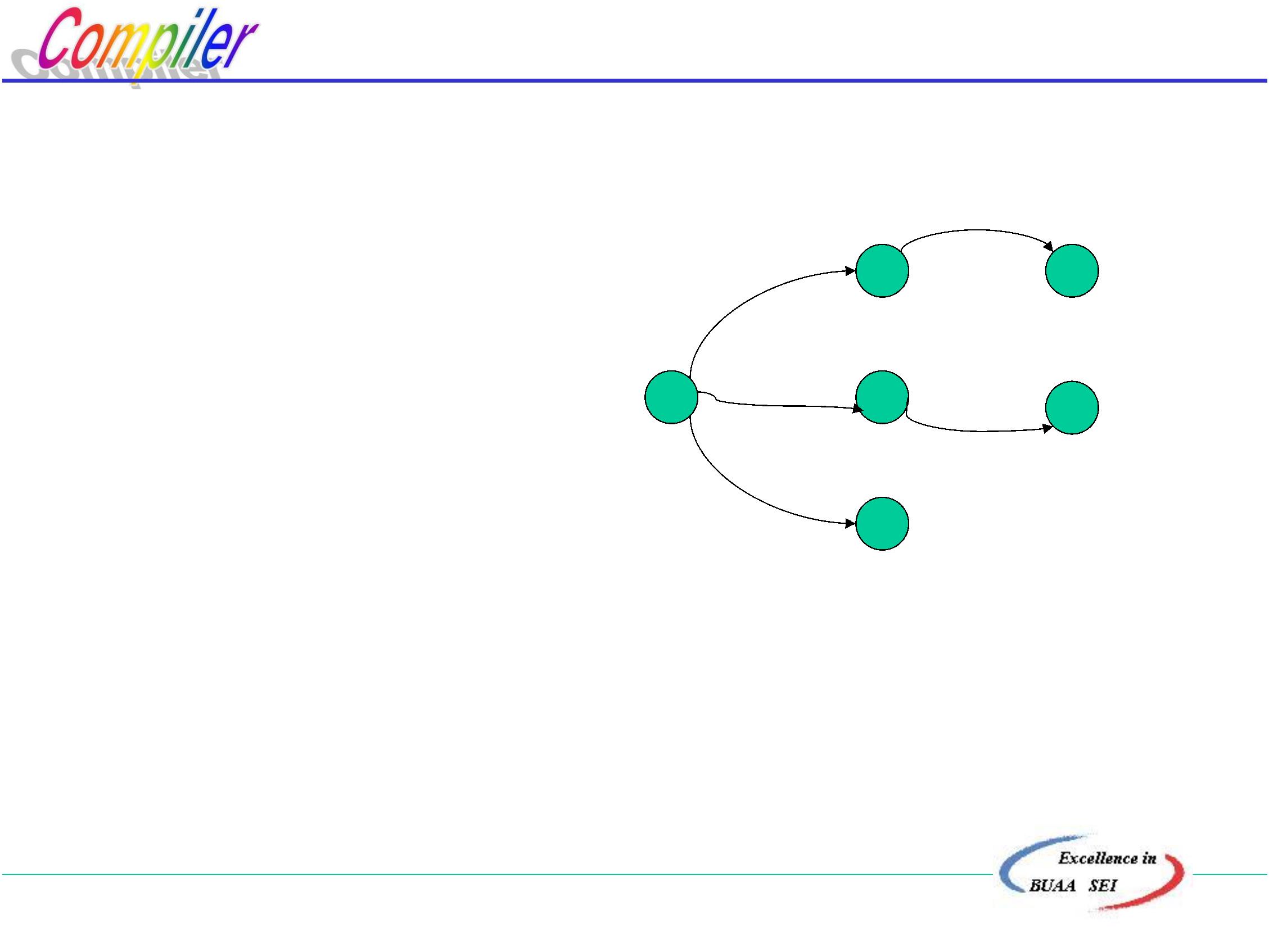
定义2: 令I是NFA M’的状态集的一个子集, a∈Σ
定义: Ia=ε-closure(J)
其中J = ∪δ(s,a)
S∈I
-- J是从状态子集I中的每个状态出发,经过标记为a的弧而
达到的状态集合。
-
- Ia是状态子集,其元素为J中的状态,加上从J中每一个
状态出发通过ε弧到达的状态。
同样可以通过一例子来说明上述定义,仍采用前面给定的
状态图为例
北京航空航天大学计算机学院
3
8

例:令 I={1}
Ia =ε-closure(J)
=
=
=
ε-closure(δ(1,a))
ε-closure({2,4})
{2,4,6}
根据定义1,2,可以将上述的M’确定化(即可构造出状态
转换矩阵)
北京航空航天大学计算机学院
3
9

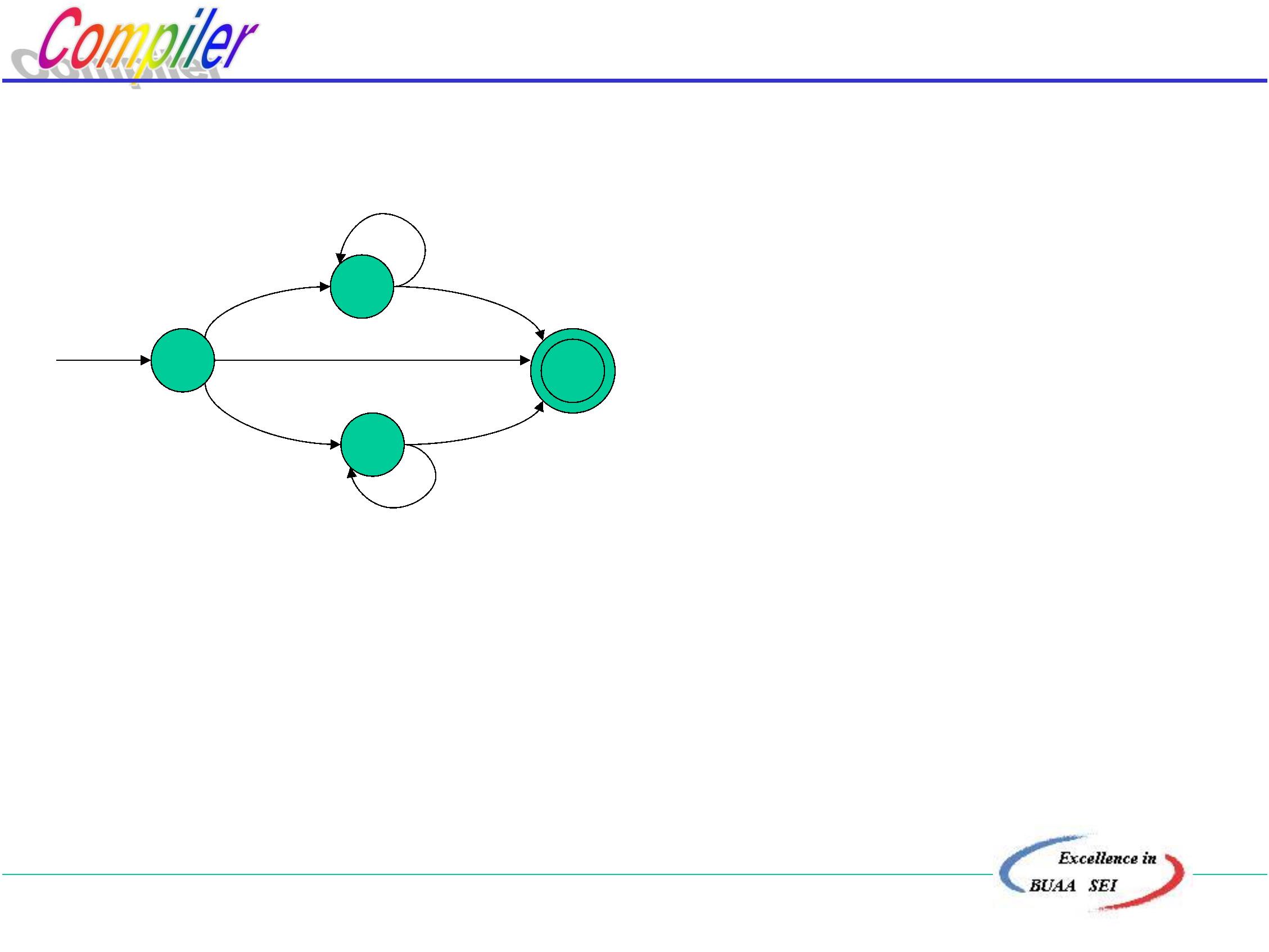
例:有NFA M’
I=ε-closure({1})={1,4}
Ia=ε-closure(δ(1,a)∪δ(4,a))
a
b
a
2
=
=
=
ε-closure({2,3}∪φ)
ε-closure ({2,3})
{2,3}
start
ε
1
4
c
a 3
Ib= ε-closure(δ(1,b)∪δ(4,b))
c
=
=
ε-closure(φ)
φ
Ic= ε-closure(δ(1,c)∪δ(4,c))
=
φ
I={2,3}, I ={2},I ={4},I ={3,4}…
a
b
c
北京航空航天大学计算机学院
4
0
I
Ia
1,4} {2,3} φ
2,3} {2} {4}
2} {2}
Ib
Ic
{
{
{
{
{
φ
{3,4}
{4} φ
4} φ
φ
φ
φ
3,4} φ
{3,4}
北京航空航天大学计算机学院
4
1
将求得的状态转换矩阵重新编号
DFA M状态转换矩阵:
符号
a
b
_
c
状态
_
0
1
2
3
4
1
2
2
3
3
4
_
_
_
_
_
_
4
北京航空航天大学计算机学院
4
2
DFA M的状态图:
{2,3}
a
c
{1,4}
1
start
0
4
b
3
a
c
{3,4}
a
2
{2}
{4}
b
注意:包含原初始状态1的状态子集为DFA M的初态
包含原终止状态4的状态子集为DFA M的终态。
北京航空航天大学计算机学院
4
3
3
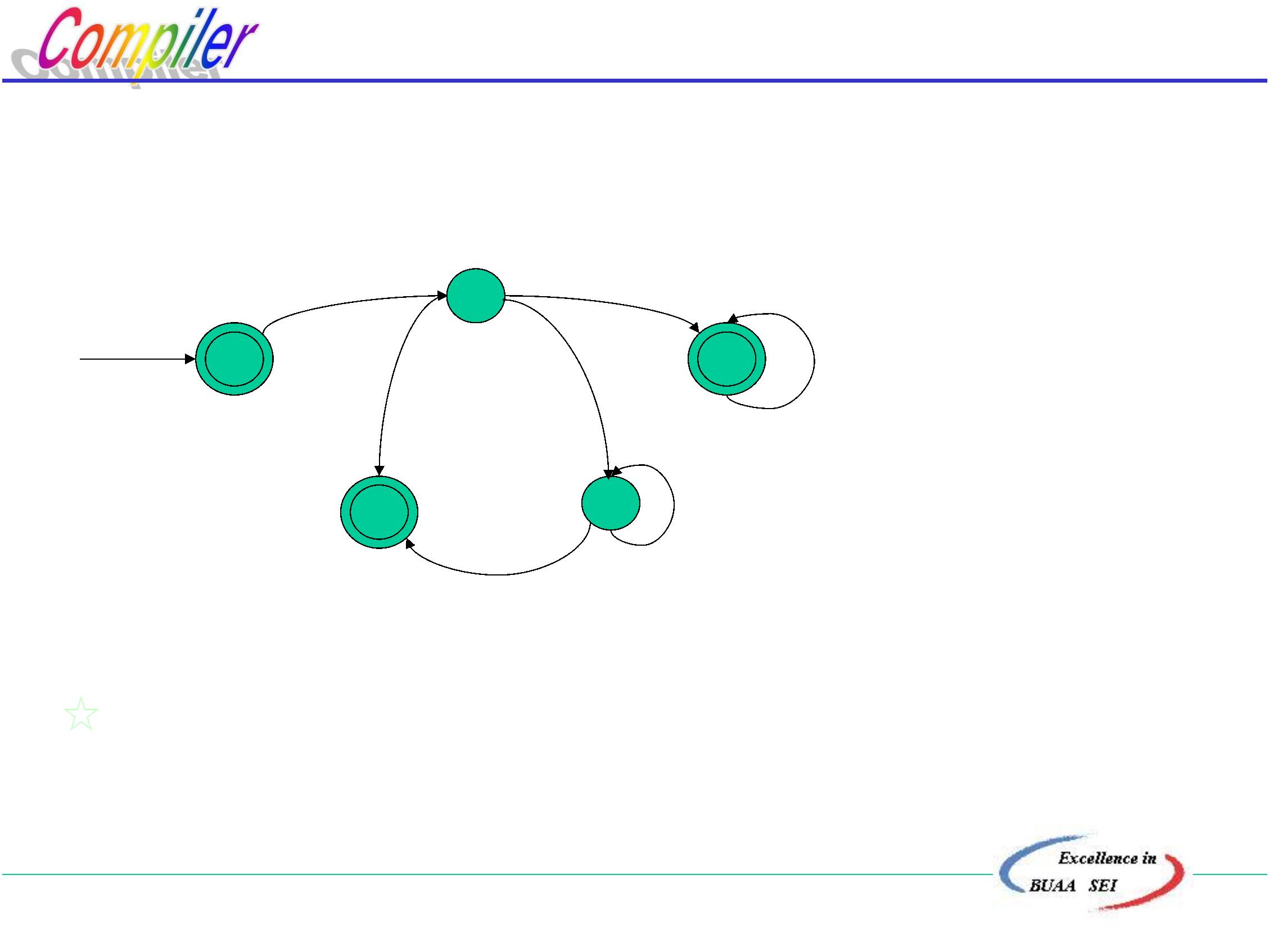
.5.5 正则表达式与DFA的等价性
定理:在Σ上的一个子集V ( VΣ* )是正则集合,当且仅当
存在一个DFA M,使得V=L(M)
V是正则集合,
R是与其相对应的正则表达式 DFA M
V=L(R)
L(M)=L(R)
所以 正则表达式R NFA M’ DFA M
L(R) = L(M’) = L(M)
证明: 根据定义。
北京航空航天大学计算机学院
4
4

start
start
start
a
a
φ
φ
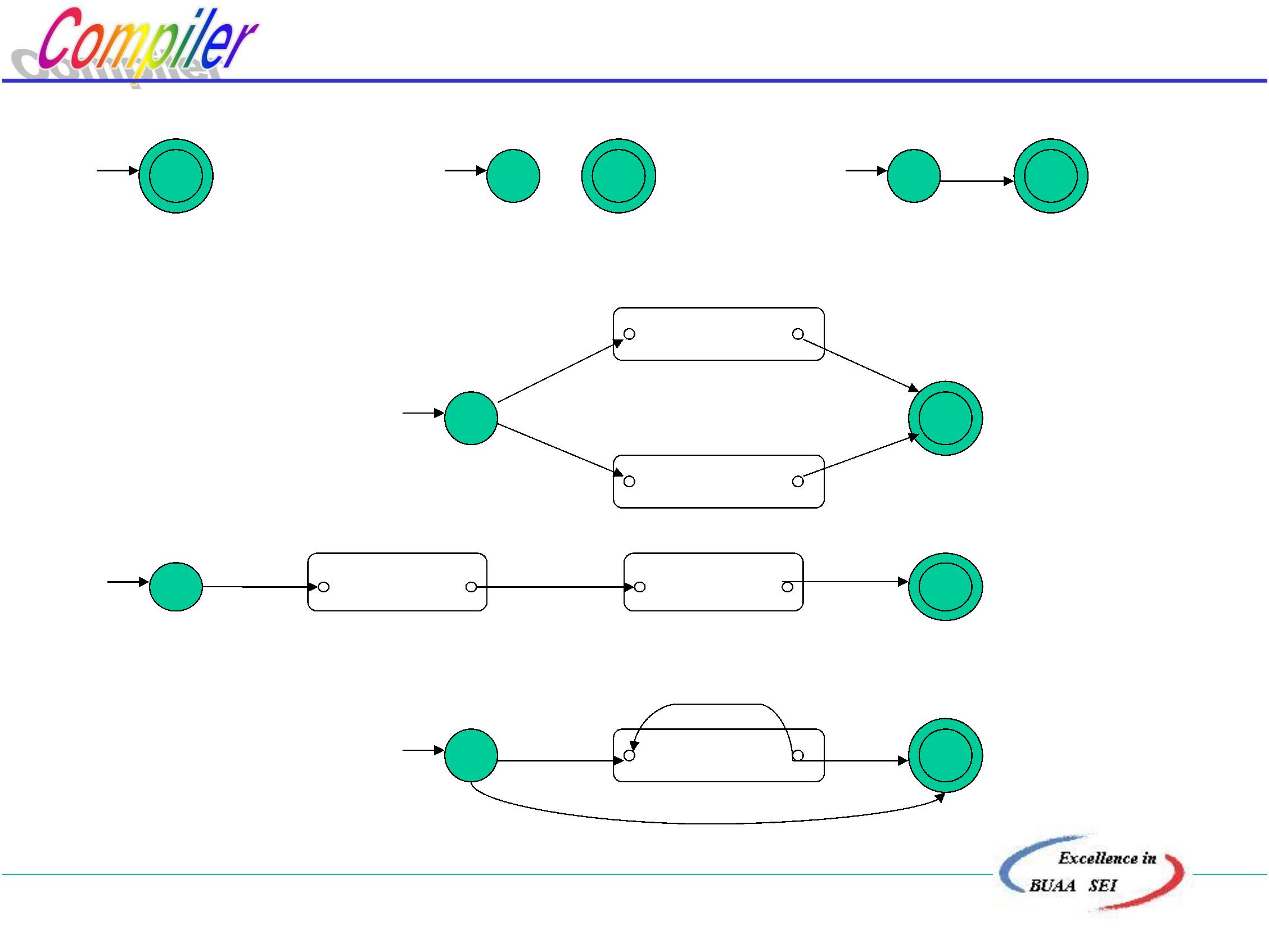
正则表达式 ε
正则集合 {ε}
{
a}
N(s)
ε
ε
R=s|t NFA(R):
start
x
x
y
y
ε
ε
ε
ε
N(t)
N(t)
ε
R=st NFA(R):
start ε
N(s)
x
R=s* NFA(R):
start
ε
ε
N(s) y
ε
北京航空航天大学计算机学院
4
5
3
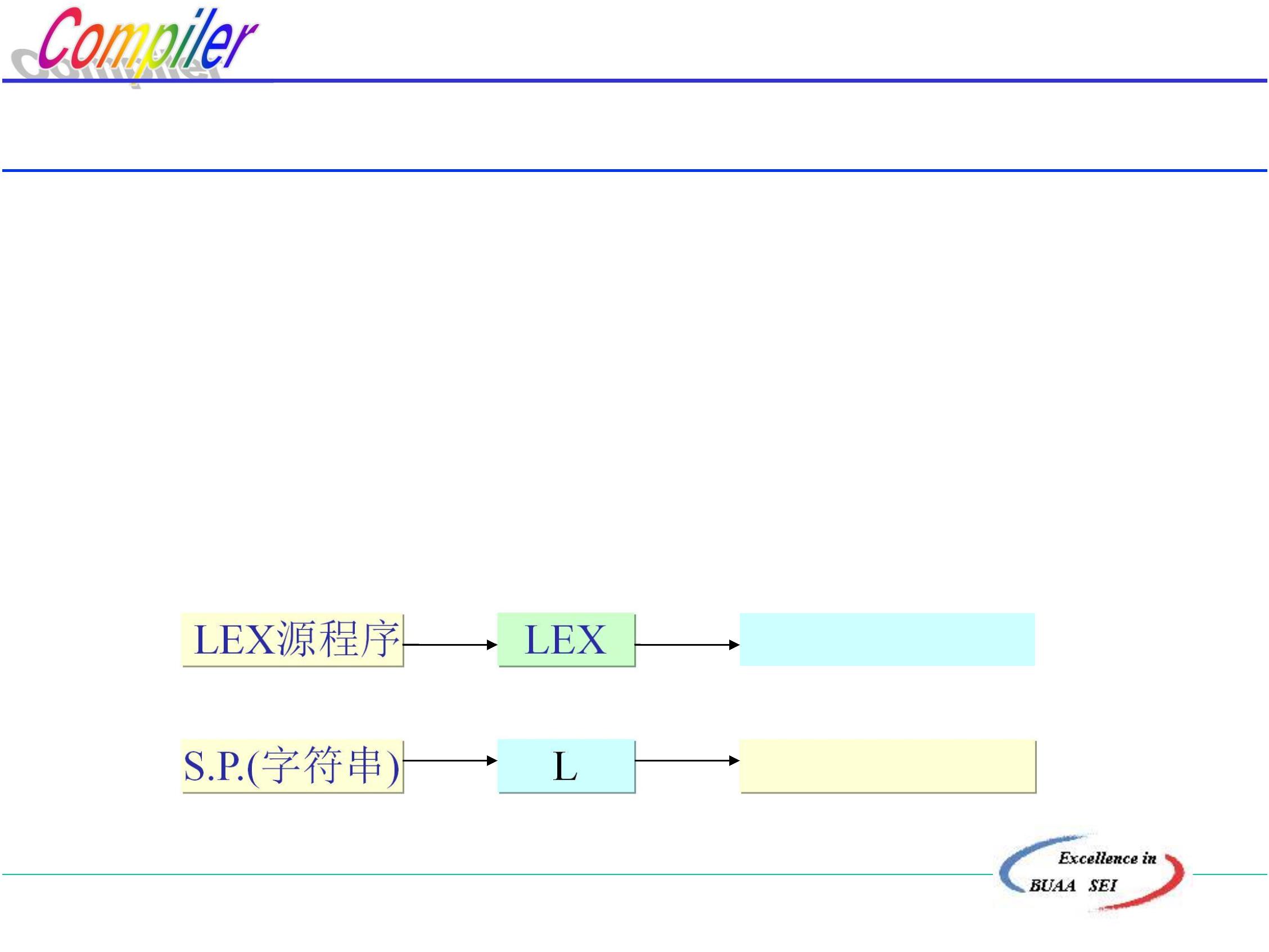
.6 词法分析程序的自动生成器—LEX(LEXICAL)
LEX的原理:
正则表达式与DFA的等价性
根据给定的正则表达式自动生成相应的词法分析程序。
LEX的功能:
LEX源程序
S.P.(字符串)
LEX 词法分析程序L
S.P.单词(符号串)
L
北京航空航天大学计算机学院
4
6
3
.6.1 LEX源程序
一个LEX源程序主要由三个部分组成:
1
2
3
. 辅助定义式
. 识别规则
. 用户子程序
各部分之间用%%隔开
北京航空航天大学计算机学院
4
7

辅助定义式是如下形式的LEX语句:
D
D
1
2
R
R
1
2
∶
∶
D
n
R
n
其中:
R1,R2,……,Rn 为正则表达式。
D1,D2,……,Dn 为正则表达式名字,称简名。
北京航空航天大学计算机学院
4
8
例:标识符: letter→A|B|¨¨¨|Z
digit →0|1| ¨¨¨|9
iden →letter(letter|digit)*
带符号整数:integer→digit (digit)*
sign →+| - |ε
sign_integer →sign integer
北京航空航天大学计算机学院
4
9

识别规则:是一串如下形式的LEX语句:
P
P
1
{A1}
{A2}
2
∶
∶
P
m
{Am}
P
i
:定义在Σ∪{D1,D2,¨¨Dn}上的正则表达式,也称词形。
{Ai}:Ai为语句序列,它指出,在识别出词形为Pi的单词以
后,词法分析器所应作的动作。
其基本动作是返回单词的类别编码和单词值。
北京航空航天大学计算机学院
5
0

下面是识别某语言单词符号的LEX源程序:
例:LEX 源程序
AUXILIARY DEFINITIONS /*辅助定义*/
letter A|B|¨¨|Z
digit 0|1|¨¨|9
%
%
RECOGNITION RULES
/*识别规则*/
1
2
3
.BEGIN
.END
{RETURN(1,─) }
{RETURN(2,─) }
{RETURN(3,─) }
.FOR
北京航空航天大学计算机学院
5
1

4
5
6
7
8
9
.DO
{RETURN(4,─) }
{RETURN(5,─) }
{RETURN(6,─) }
{RETURN(7,─) }
{RETURN(8,TOKEN) }
{RETURN(9,DTB }
{RETURN(10,─) }
{RETURN(11,─) }
{RETURN(12,─) }
.IF
.THEN
.ELSE
.letter(letter |digit)*
.digit(digit)*
1
0. :
1. +
2. “*”
1
1
北京航空航天大学计算机学院
5
2

1
1
1
1
1
3. ,
{RETURN(13,─) }
{RETURN(14,─) }
{RETURN(15,─) }
4. “(”
5. “)”
6. :=
{RETURN(16,─) }
{RETURN(17,─) }
7. =
北京航空航天大学计算机学院
5
3

3
.6.2 LEX的实现
LEX的功能是根据LEX源程序构造一个词法分析程序,
该词法分析器实质上是一个有穷自动机。
LEX生成的词法分析程序由两部分组成:
状态转换矩阵(DFA)
词法分析程序
控制执行程序
∴
LEX的功能是根据LEX源程序生成状态转换矩阵和控制程序
北京航空航天大学计算机学院
5
4
LEX的工作过程:
·
¨
·
扫描每条识别规则Pi,构造相应的不确定有穷自动机Mi
将各条规则的有穷自动机Mi合并成一个新的NFA M
¨确定化
NFADFA
生成该DFA的状态转换矩阵和控制执行程序
北京航空航天大学计算机学院
5
5

LEX二义性问题的两条原则:
1
.最长匹配原则
P
j
P
i
在识别单词过程中,有一字符串 x x x x x
根据最长匹配原则,应识别为这是
P
k
一个符合Pk规则的单词,而不是Pj和Pi规则的单词。
2
.优先匹配原则
如有一字符串,有两条规则可以同时匹配时,那么用规则
序列中位于前面的规则相匹配,所以排列在最前面的规则优先
权最高。
北京航空航天大学计算机学院
5
6

P
1
例:字符串·¨begin·¨
P
8
根据原则,应该识别为关键字begin,所以在写LEX源程序
时应注意规则的排列顺序。另要注意的是,优先匹配原则
是在符合最长匹配的前提下执行的。
可以通过一个例子来说明这些问题:
北京航空航天大学计算机学院
5
7

start
a
例: LEX源程序
a { }
1
2
4
8
start a
b
b
3
7
5
6
abb { }
a
b
start
b
a*bb
*
{ }
一.读LEX源程序,分别生成NFA,用状态图表示为:
a
二.合并成一个NFA:
1
3
7
2
4
8
ε
start ε
a
b
b
0
5
6
a
ε
b
b
北京航空航天大学计算机学院
5
8
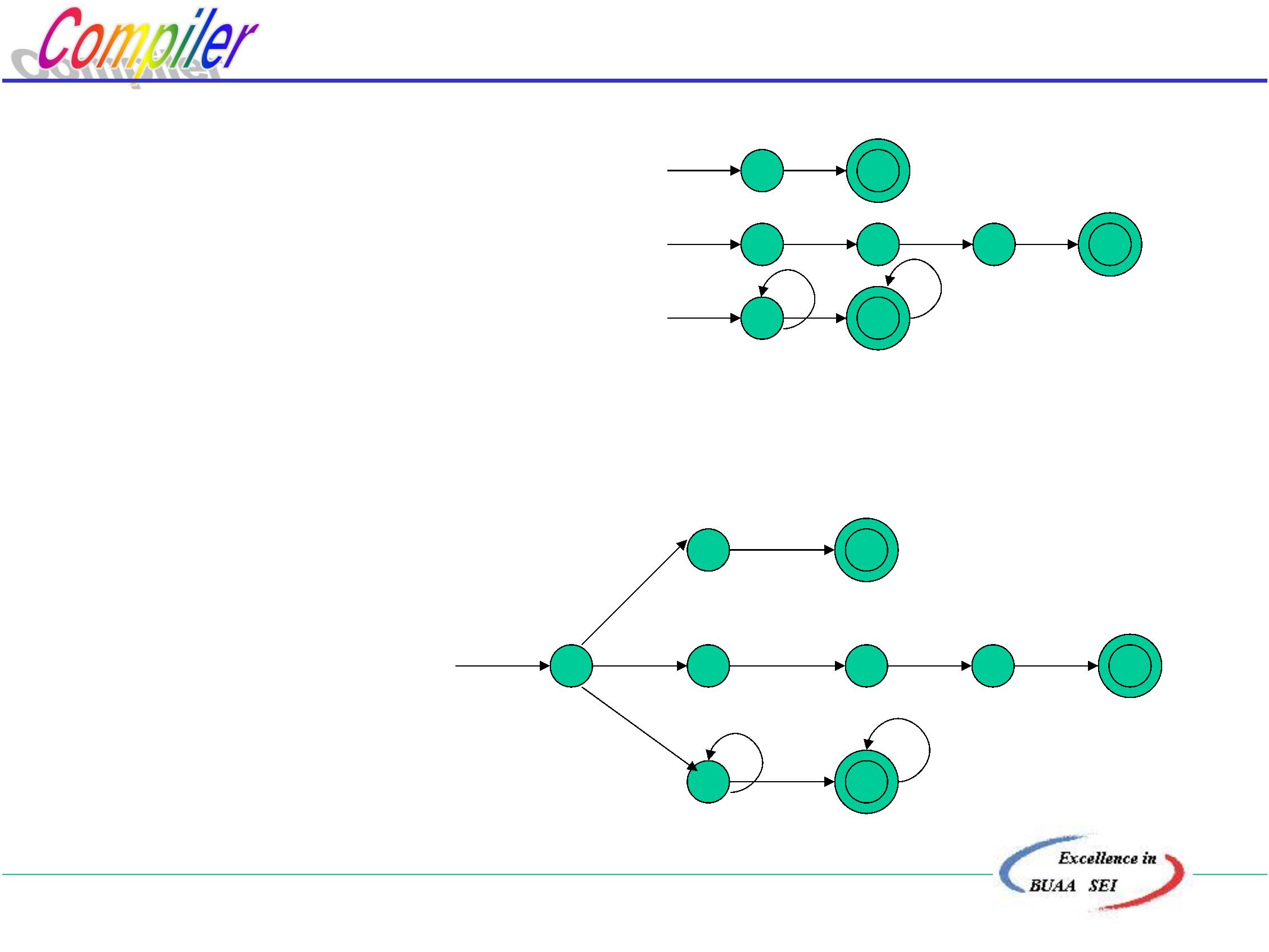
三.确定化 给出状态转换矩阵
状态
a
b 到达终态所识别的单词
初态
{2,4,7} {8}
{0,1,3,7}
终态 {2,4,7}
{7}
8} φ
7} {7}
{5,8}
{8}
{8}
{6,8}
a
*
{
a* bb
终态
{
*
终态
终态
{5,8} φ
{6,8} φ
a bb
*
{8}
abb
在此DFA中 初态为{0,1,3,7}
终态为{2,4,7},{8},{5,8},{6,8}
北京航空航天大学计算机学院
5
9
读入字符 进入状态
开始 {0,1,3,7}
词法分析程序的分析过程
令输入字符串为aba…
a
{2,4,7}
(1) 吃进字符ab
(2) 按反序检查状态子集
检查前一次状态是否含有原
b {5,8}
a 无后继状态(退
掉输入字符a)
NFA的终止状态
·即检查{5,8},含有终态8,因此断定所识别的单词ab是属于
a*bb*中的一个。
··若在状态子集中无NFA的终态,则要从识别的单词再退掉
一个字符(b),然后再检查上一个状态子集。
··若一旦吃进的字符都退完,则识别失败,调用出错程序,
一般是跳过一个字符然后重新分析。(应打印出错信息)
·
北京航空航天大学计算机学院
6
0
三点说明:
1
) 以上是LEX的构造原理,虽然是原理性的,但据此就
不难将LEX构造出来。
2
) 所构造出来的LEX是一个通用的工具,用它可以生成
各种语言的词法分析程序,只需要根据不同的语言书
写不同的LEX源文件就可以了。
3
) LEX不但能自动生成词法分析器,而且也可以产生多
种模式识别器及文本编辑程序等。
北京航空航天大学计算机学院
6
1

正则文法
1
5
2
6
4
3
NFA
DFA
正则表达式
最小化
北京航空
6
2
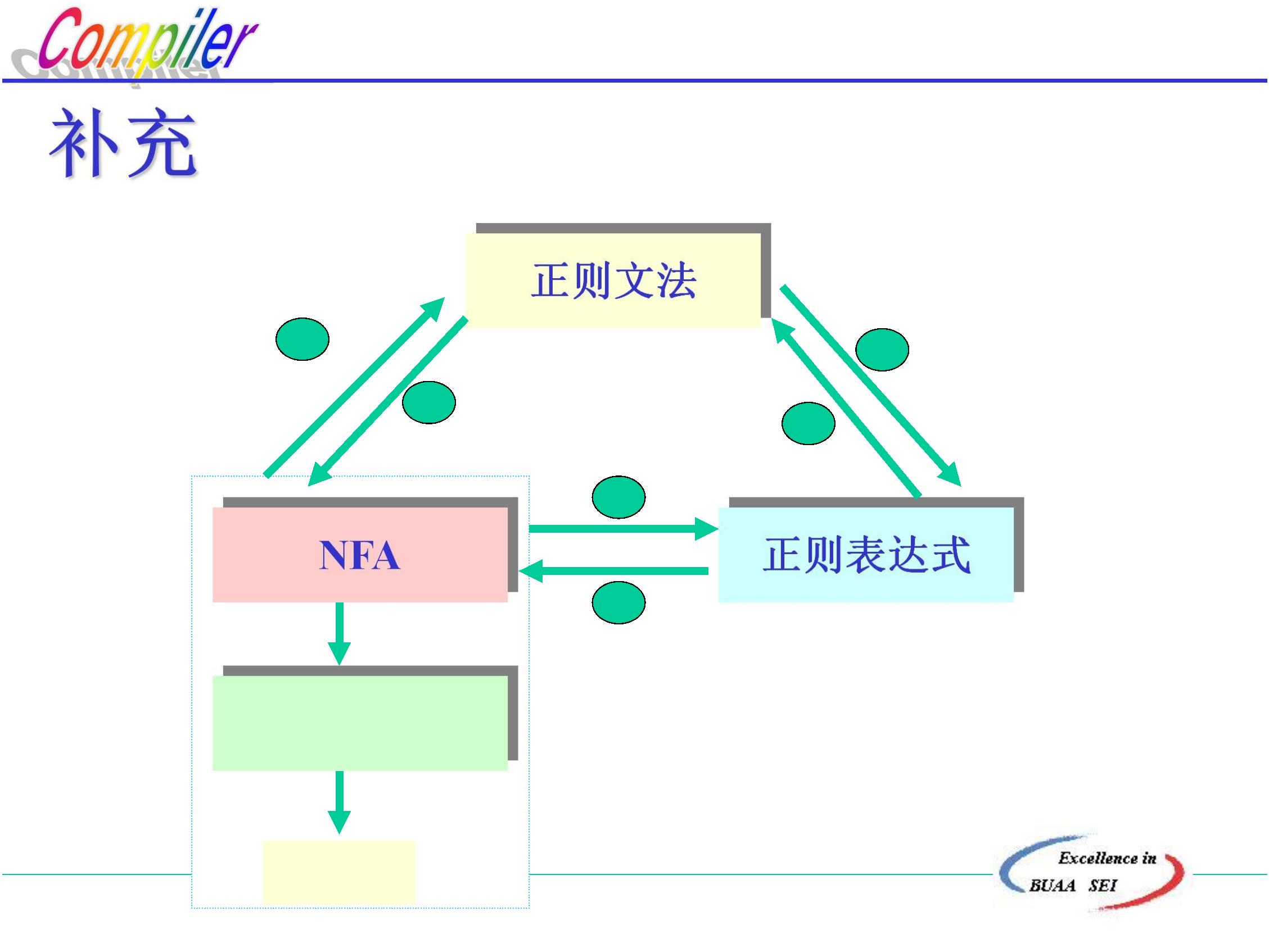
(
1)有穷自动机正则文法
算法:
t
A
B
1
2
3
.对转换函数f(A,t)=B,可写成一个产生式:A→tB
.对可接受状态Z,增加一个产生式:Z→ε
.有穷自动机的初态对应于文法的开始符号(识别符号),
有穷自动机的字母表为文法的终结符号集。
北京航空航天大学计算机学院
6
3
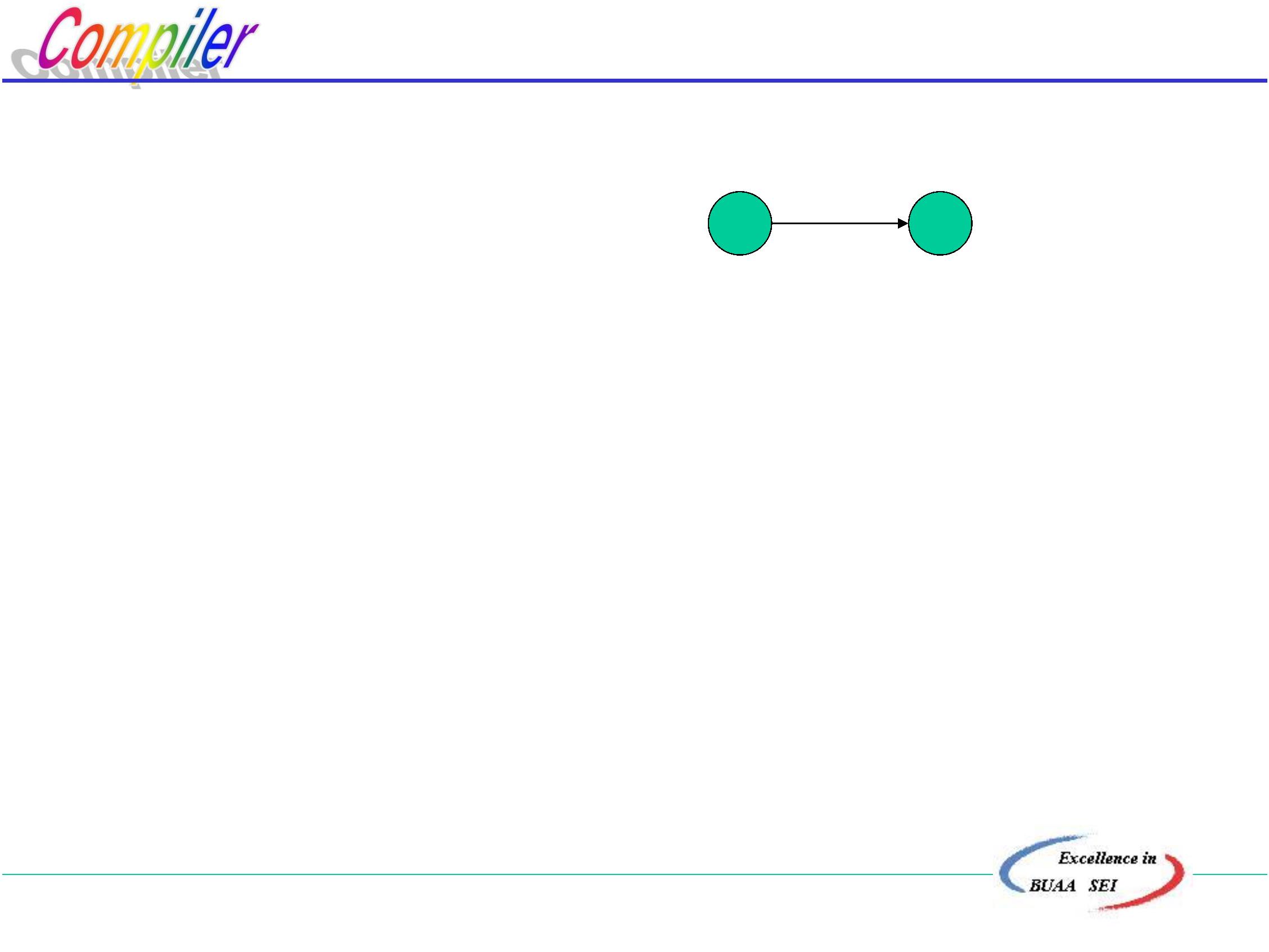
a
例:给出如图NFA等价的正则文法G
start
a
b
C
A
B
a
G=({A,B,C,D},{a,b},P,A)
b
b
其中P: A aB
→
D
A→bD
B→bC
b
C aA
→
C bD
→
→
C ε
D→aB
D→bD
D ε
→
北京航空航天大学计算机学院
6
4
(
2)正则文法有穷自动机M
算法:
1
2
.字母表与G的终结符号相同;
.为G中的每个非终结符生成M的一个状态,G的开始符号S
是开始状态S;
3
4
.增加一个新状态Z,作为NFA的终态;
.对G中的形如A→tB,其中t为终结符或ε,A和B为非终结
符的产生式,构造M的一个转换函数f(A,t)=B;
5
.对G中的形如A→t的产生式,构造M的一个转换函数
f(A,t)=Z。
北京航空航天大学计算机学院
6
5

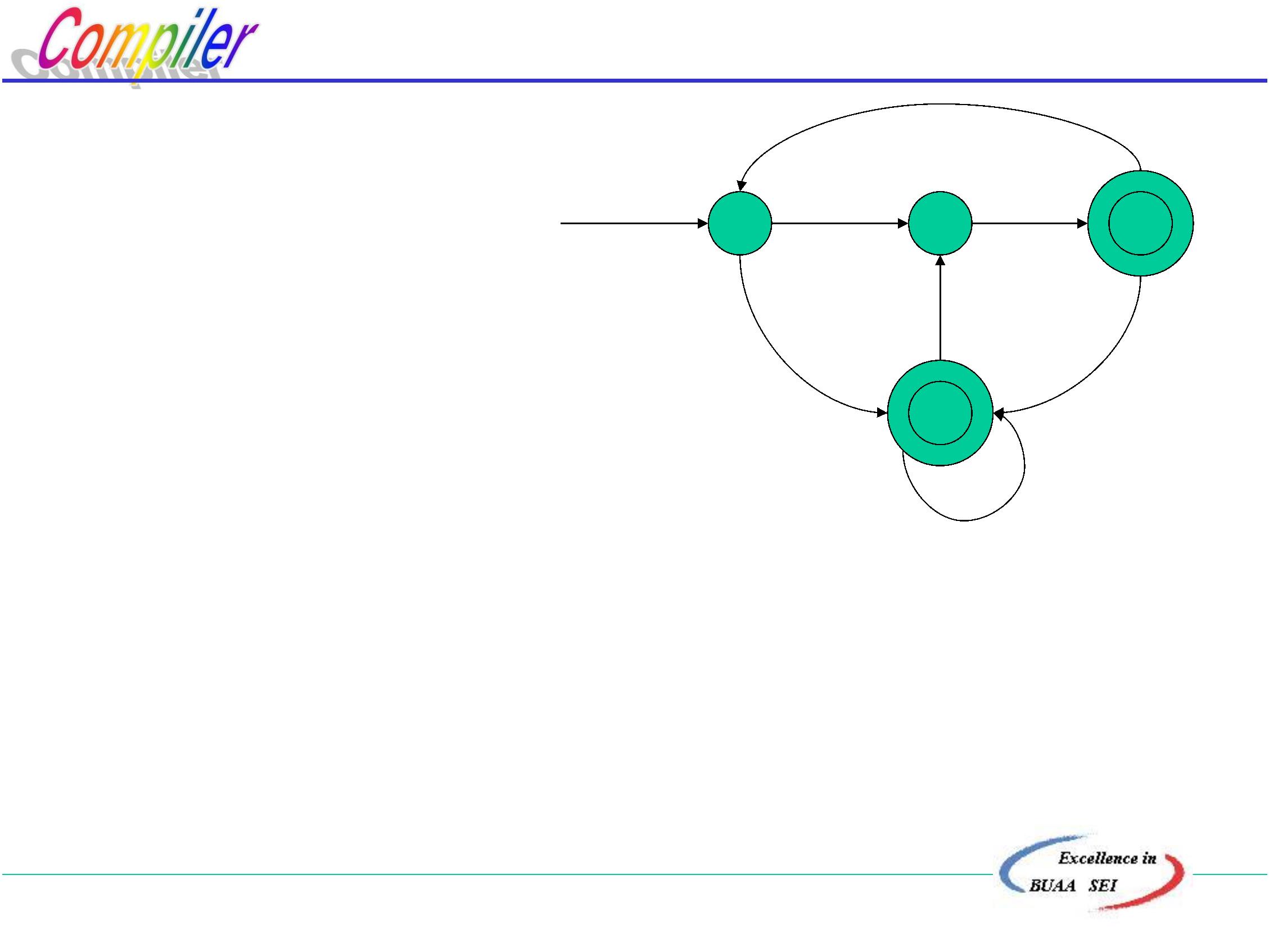
例:求与文法G[S]等价的NFA
G[S]: S→aA|bB|ε
A→aB|bA
B→aS|bA|ε
b
A
a
a
求得:
b
start
b
S
B
a
ε
ε
Z
北京航空航天大学计算机学院
6
6
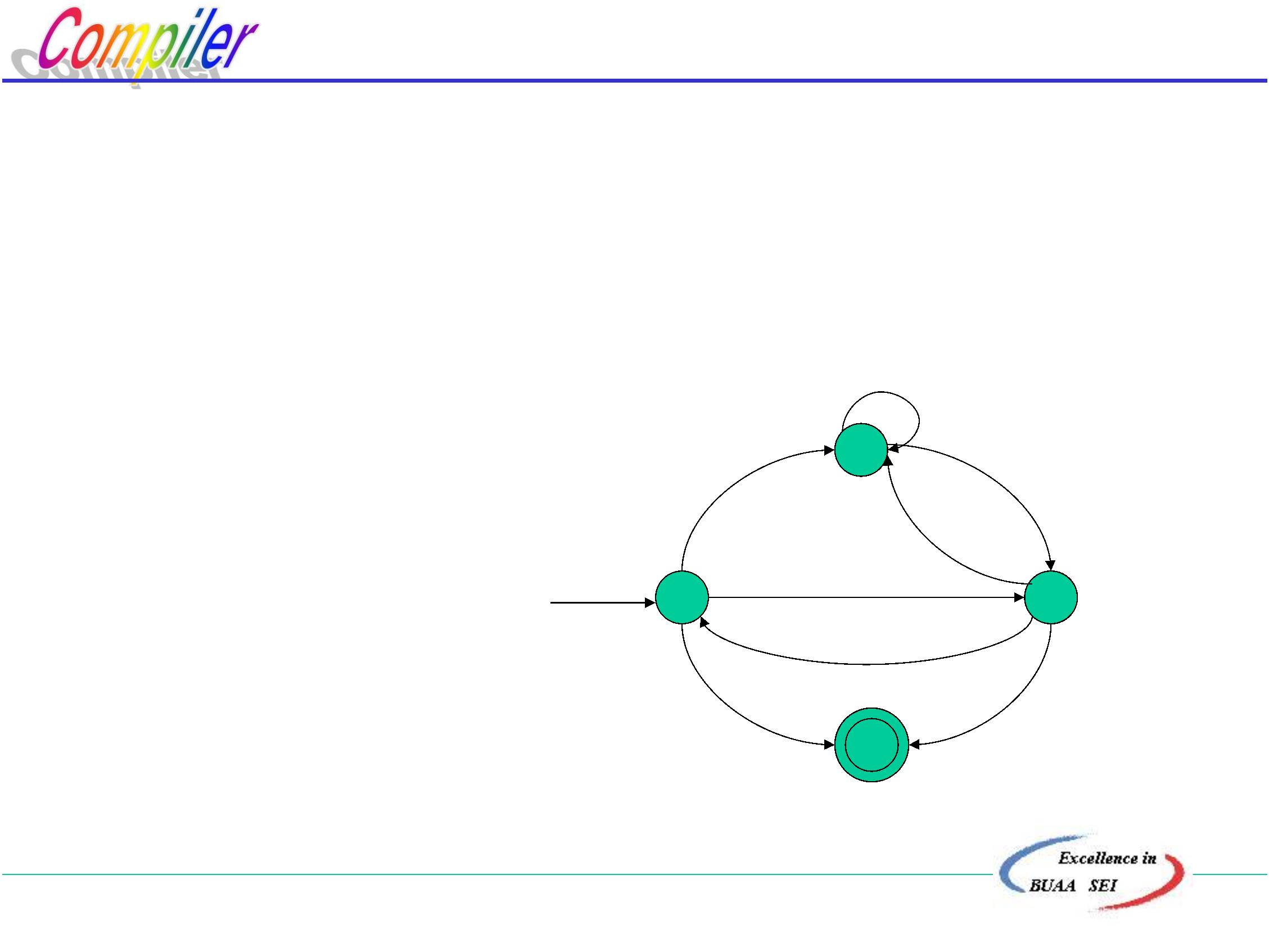
(
3)正则式有穷自动机
语法制导方法
.(a)对于正则式φ,所构造NFA:
1
x
x
y
y
ε
(b)对于正则式ε,所构造NFA:
(c)对于正则式a,a∈Σ,则NFA:
a
x
y
北京航空航天大学计算机学院
6
7
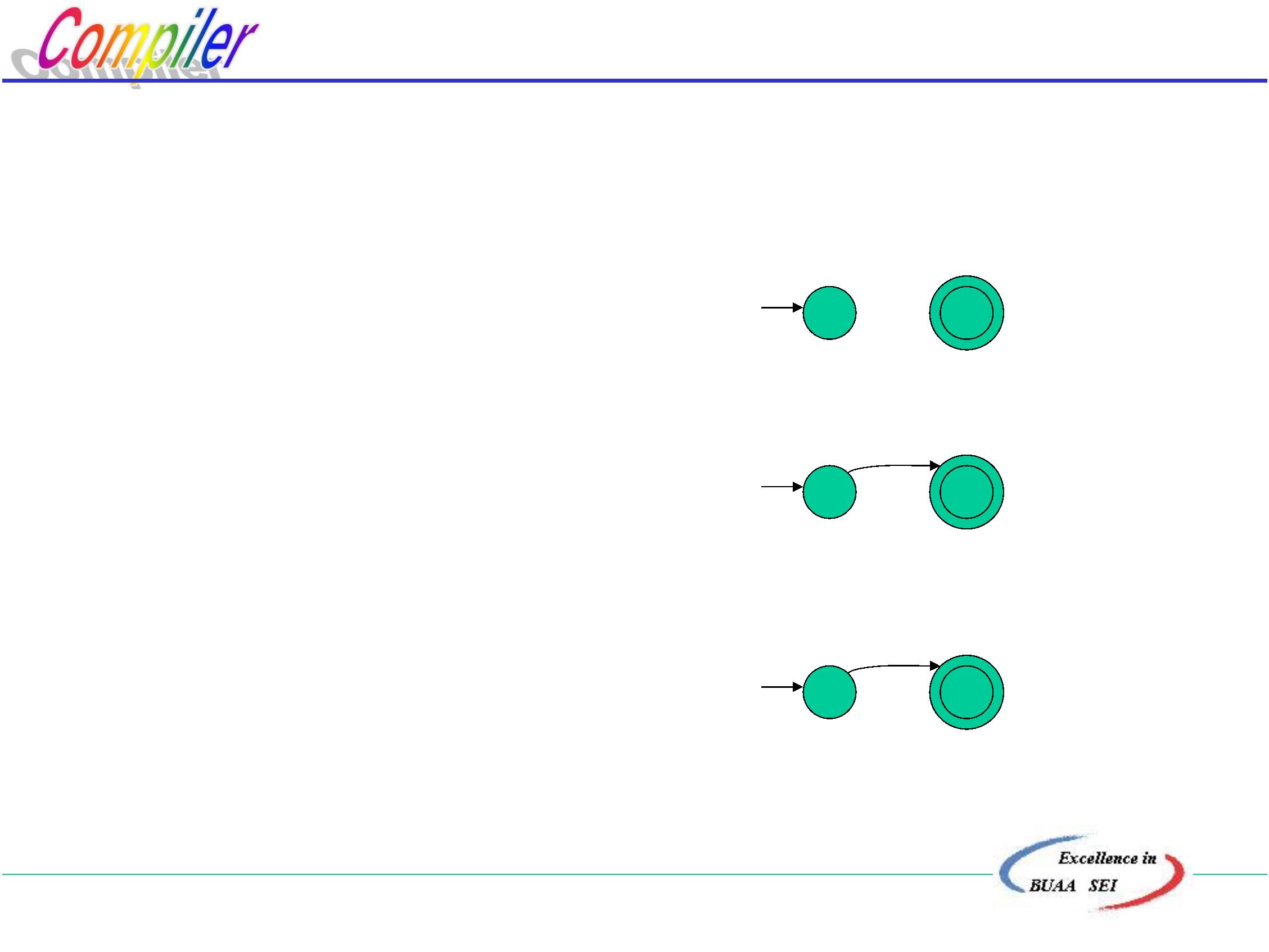
2
.若s,t为Σ上的正则式,相应的NFA分别为N(s)和N(t);
(a)对于正则式R=s|t, NFA(R)
ε
N(s)
N(t)
ε
ε
x
y
ε
(b)对正则式R=st, NFA(R)
ε
ε
ε
N(s)
N(t)
x
y
或:
x N(s) N(t) y
北京航空航天大学计算机学院
6
8
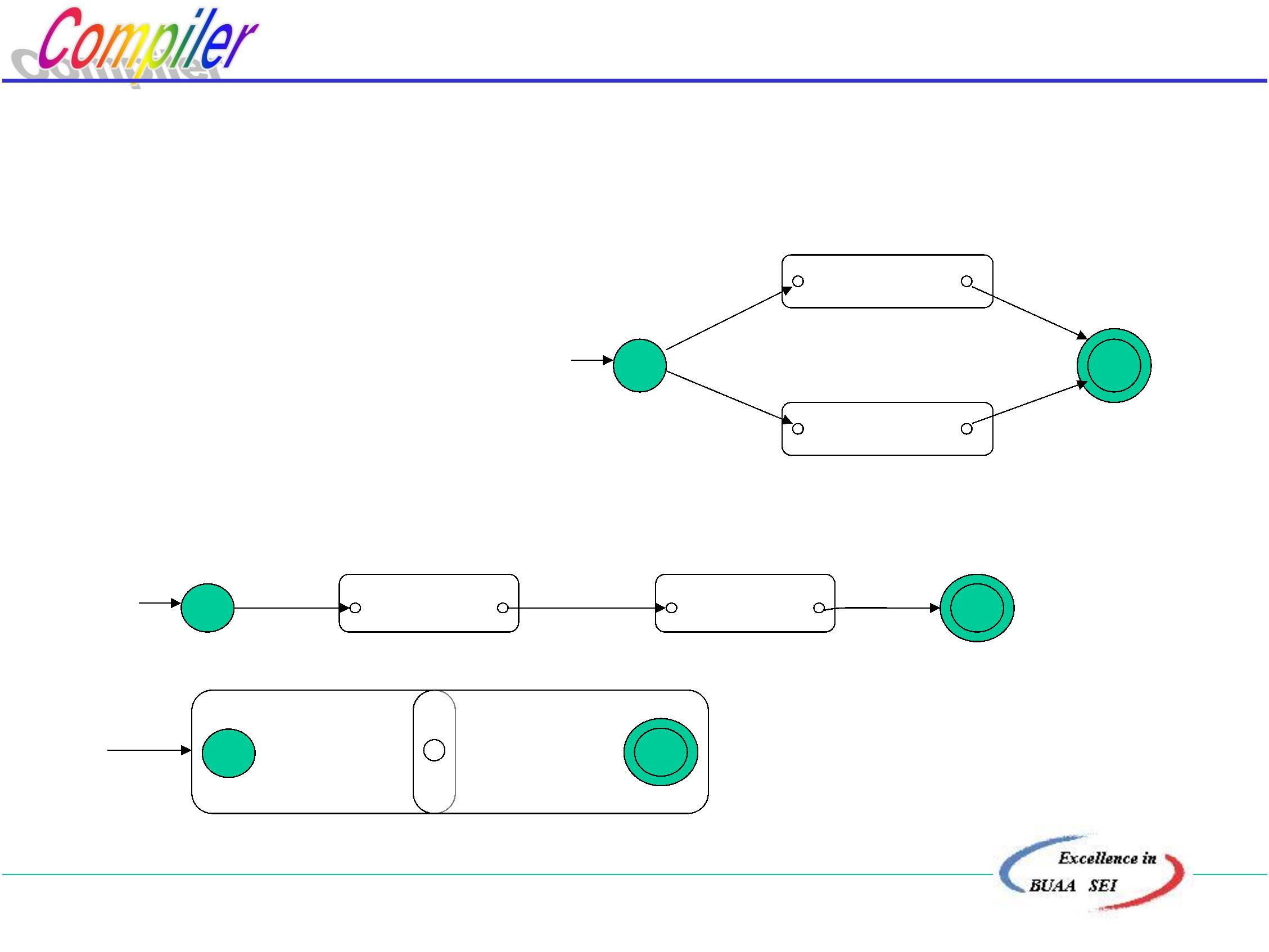
(c)对于正则式R=s*, NFA(R)
ε
ε
ε
x
N(s) y
ε
(d)对R=(s),与R=s的NFA一样.
北京航空航天大学计算机学院
6
9
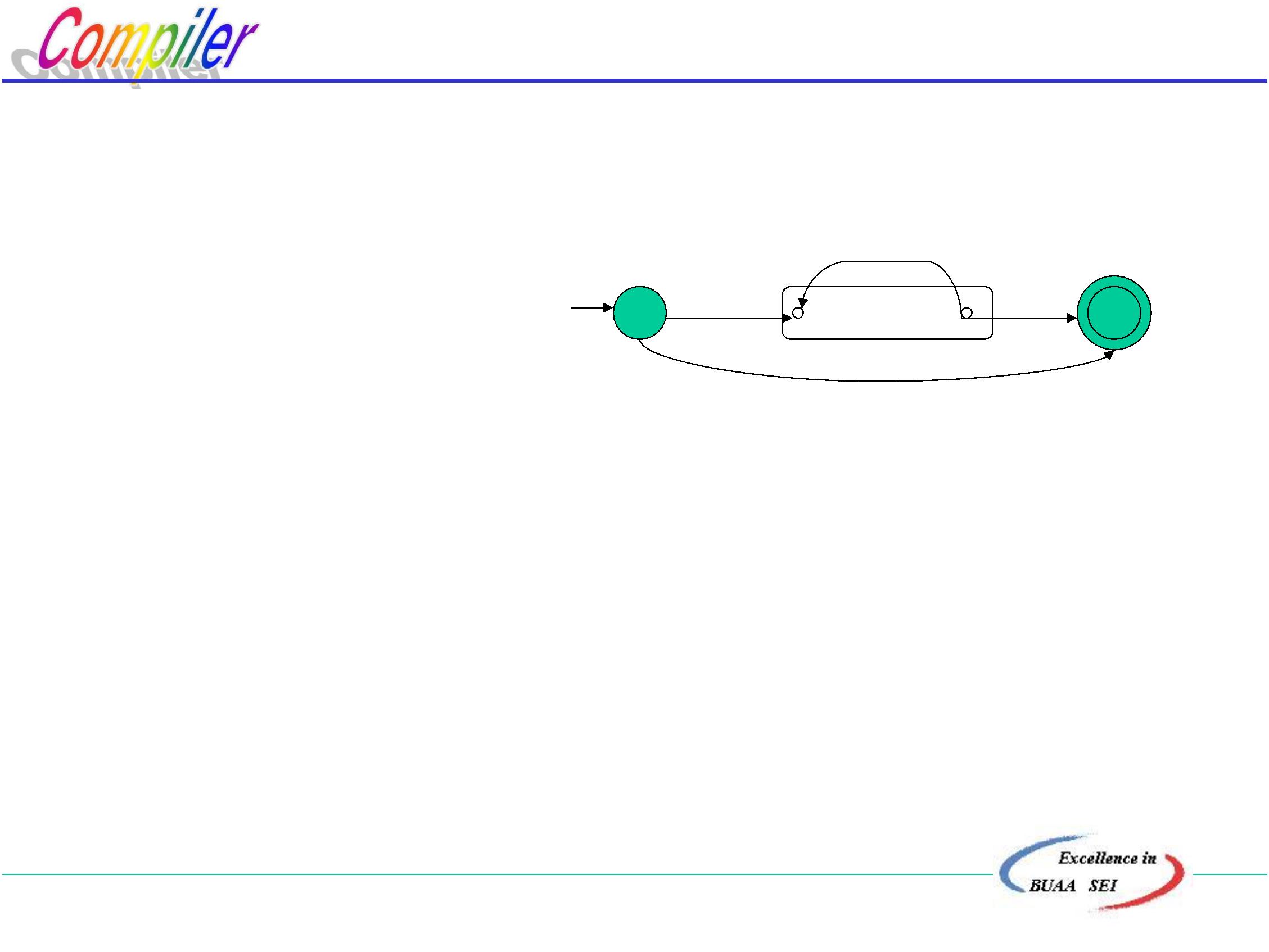
*
例:为R=(a|b) abb构造NFA N,使得L(N)=L(R)
a
从左到右分解R,令r1=a,第一个a,则有 2
3
b
令r2=b,则有 4
5
a
令r3= r1 |r2,则有
ε
ε
ε
ε
2
4
3
5
1
6
b
北京航空航天大学计算机学院
7
0
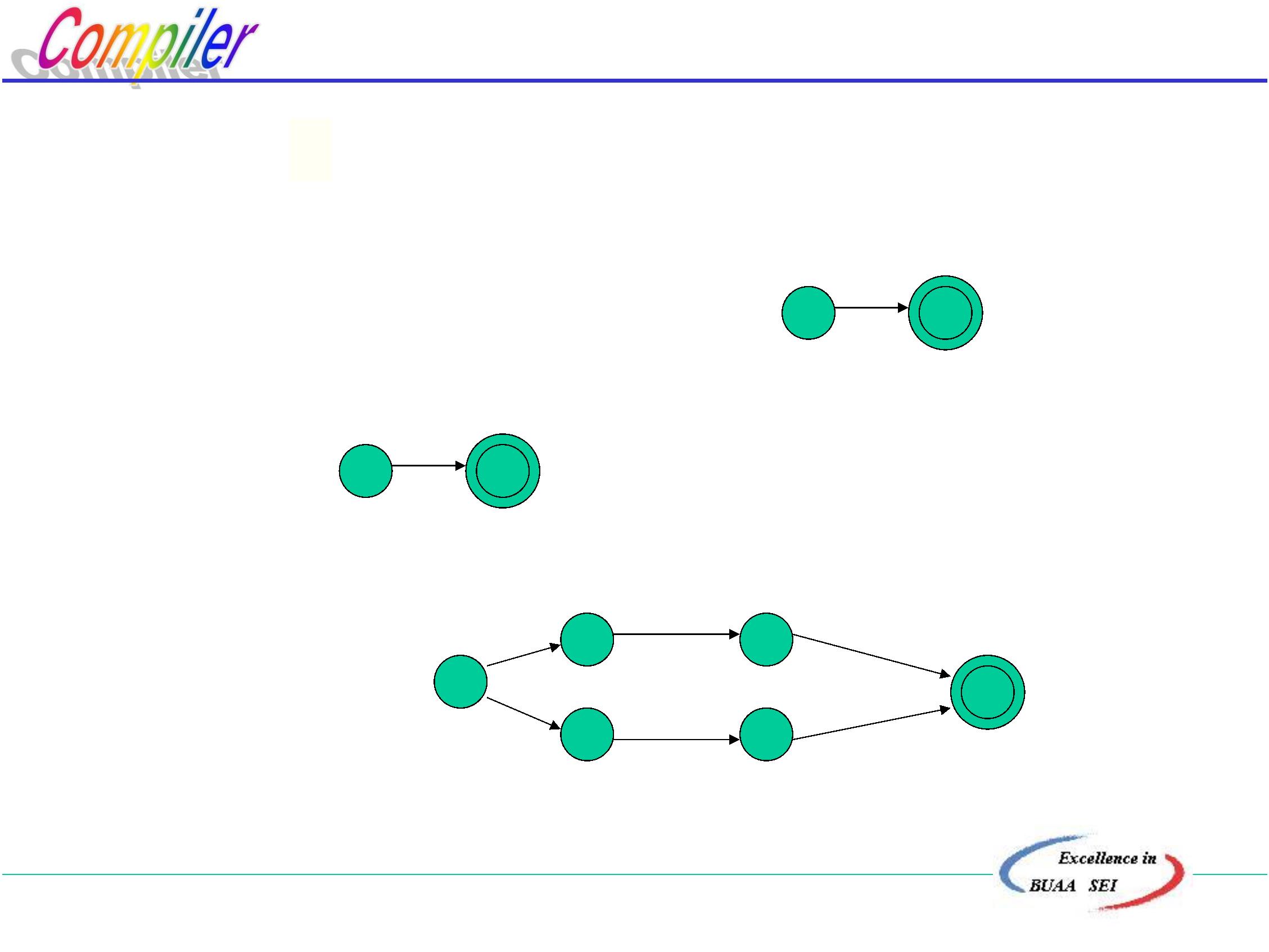
令r4= r3* 则有:
ε
a
ε
ε
ε
ε
2
4
3
5
ε
ε
0
1
6
7
b
ε
令r5=a,
令r6=b
令r7=b
令r8= r5 r6
令r9= r8 r7 则有
a
b
b
7
8
9
10
北京航空航天大学计算机学院
7
1
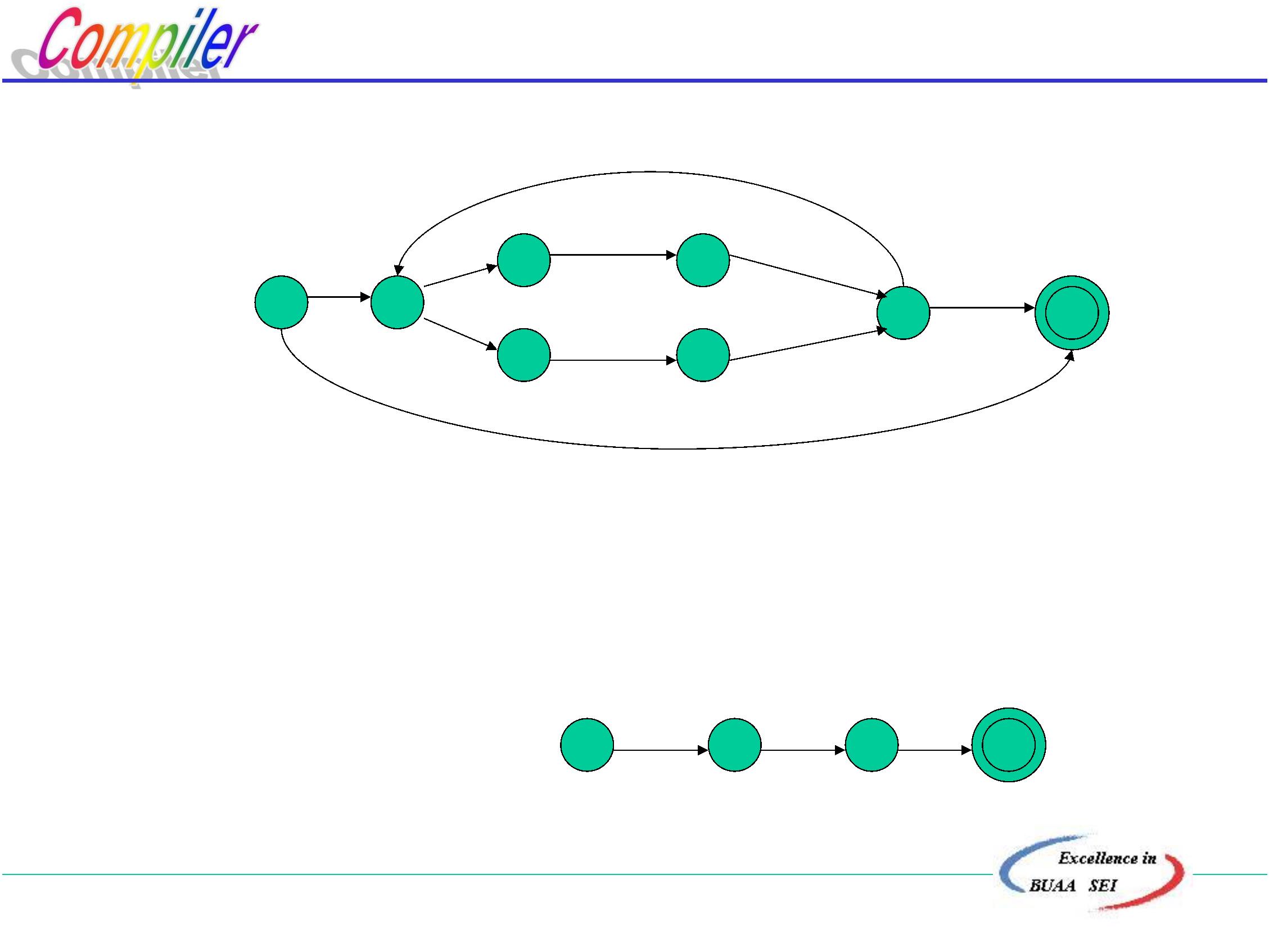
令r10= r4 r9 则最终得到NFA N:
ε
a
ε
ε
ε
ε
2
4
3
5
ε
ε a b b
7 8 9 10
0
1
6
b
ε
分解R的方法有很多种,下面给出另一种分解方式和所构成的NFA
北京航空航天大学计算机学院
7
2
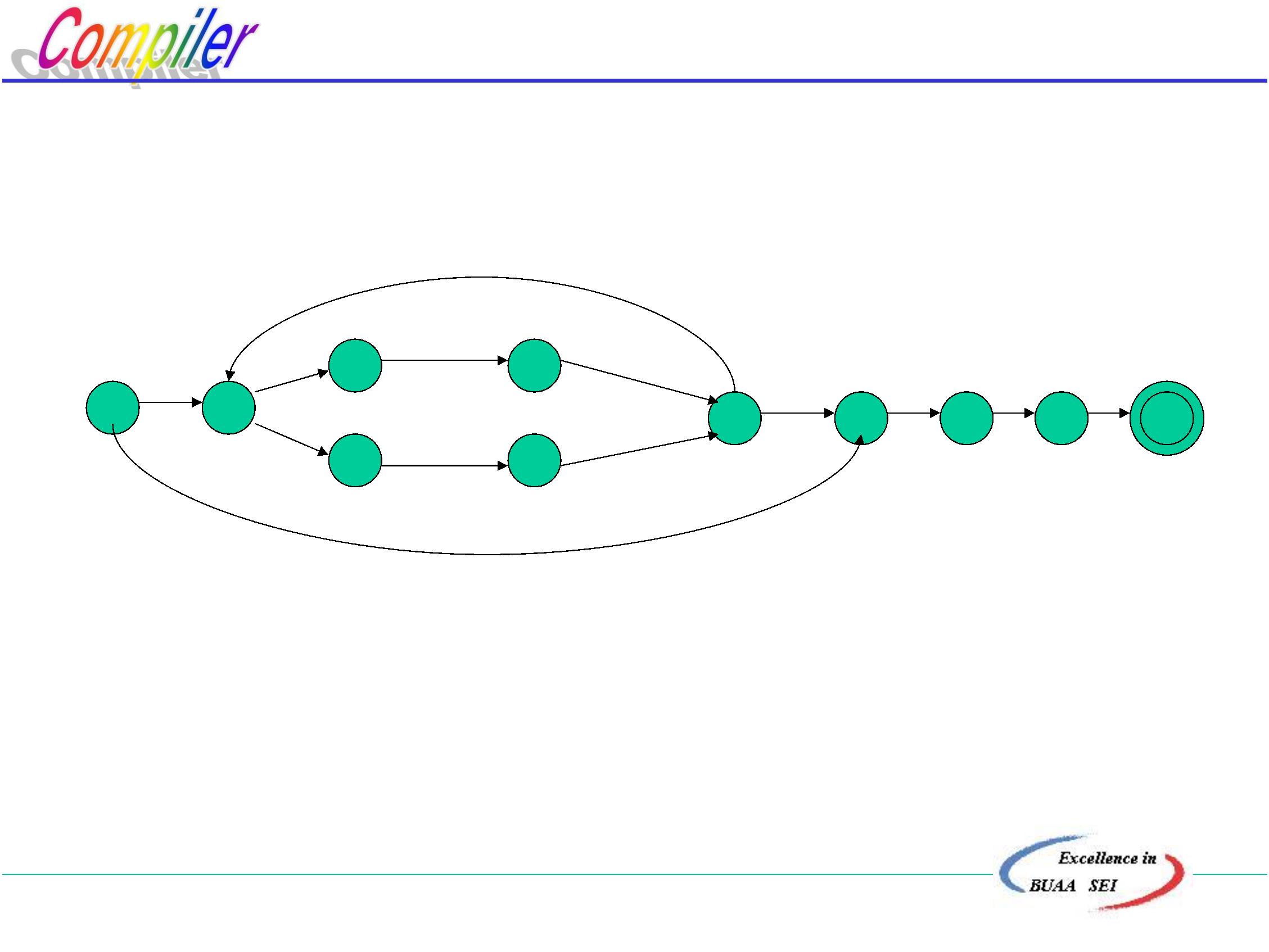
(a|b)*
abb
(a)
(b)
x
x
x
i
y
j
a|b
ε ε
abb
abb
i
y
y
a
ε ε
i
j
(c)
(d)
b
a
ε ε
a
b
b
x
i
j
k
l
y
b
北京航空航天大学计算机学院
7
3
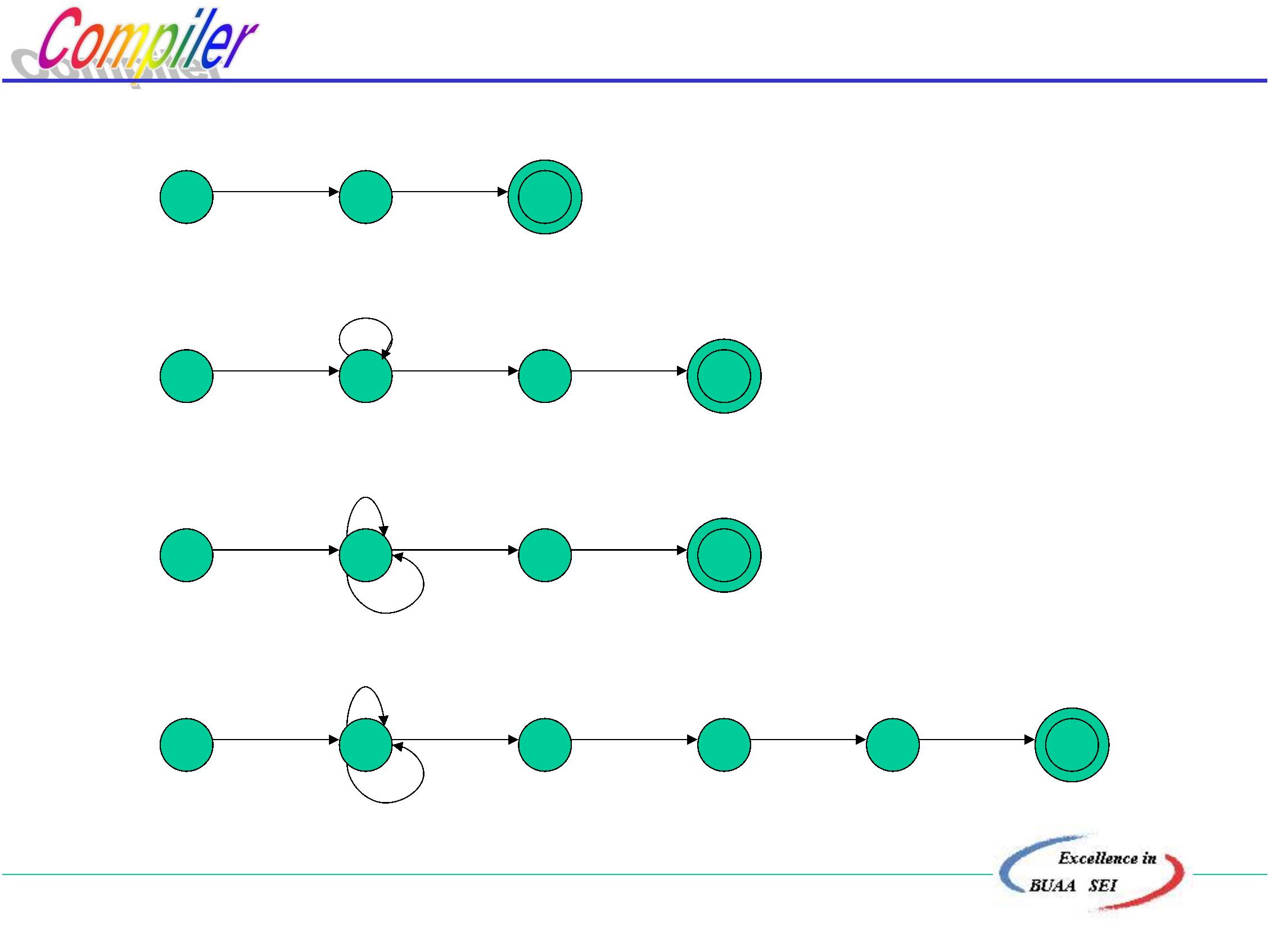
(
4)有穷自动机正则式R
算法:
1
)在M上加两个结点x,y,从x结点用ε弧到M的所
有初态,从M的所有终态用ε到y结点形成与M等
价的M’,M’只有一个初态x和一个终态y。
)逐步消去M’中的所有结点,直至剩下x和y结点,在
消结过程中,逐步用正则式来记弧,其消结规则如
下:
2
R
1
R
2
2 3
RR
1 2
1
2
3
.对于
代之为
1
1 3
R
1
2 代之为 1 R1|R2 2
.对于 1
R
2
R
2
.对于
代之为
R
1
R
3
2 3
R1R2*R3
1
1
3
北京航空航天大学计算机学院
7
4
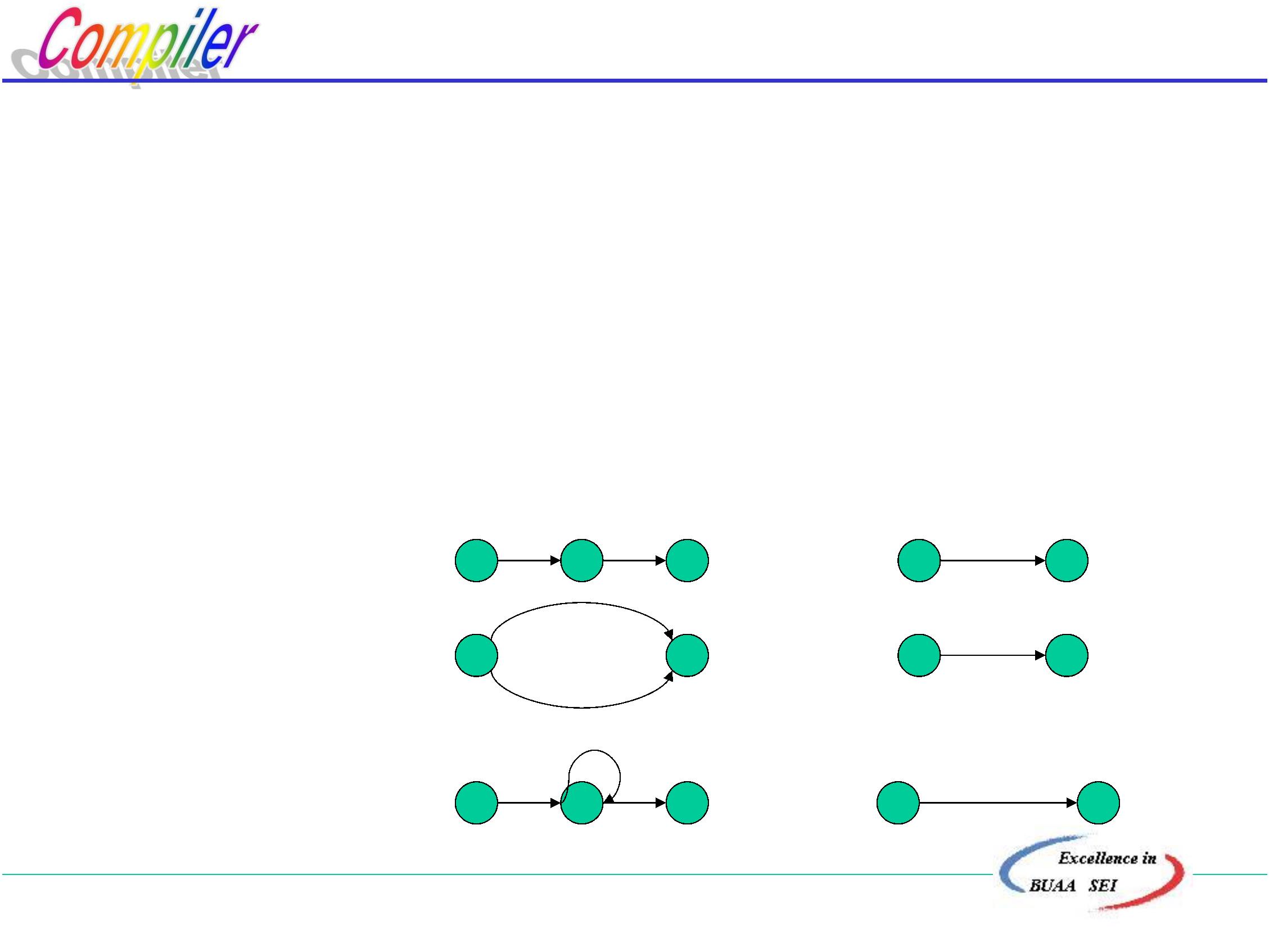
a,b
a,b
例:M:
start
a
a
0
3
4
b
1
b
2
a,b
a,b
解: (1)加x,y
a
a
3
1
4
a,b
0
ε
ε
y
x
ε
b
2
b
a,b
北京航空航天大学计算机学院
7
5
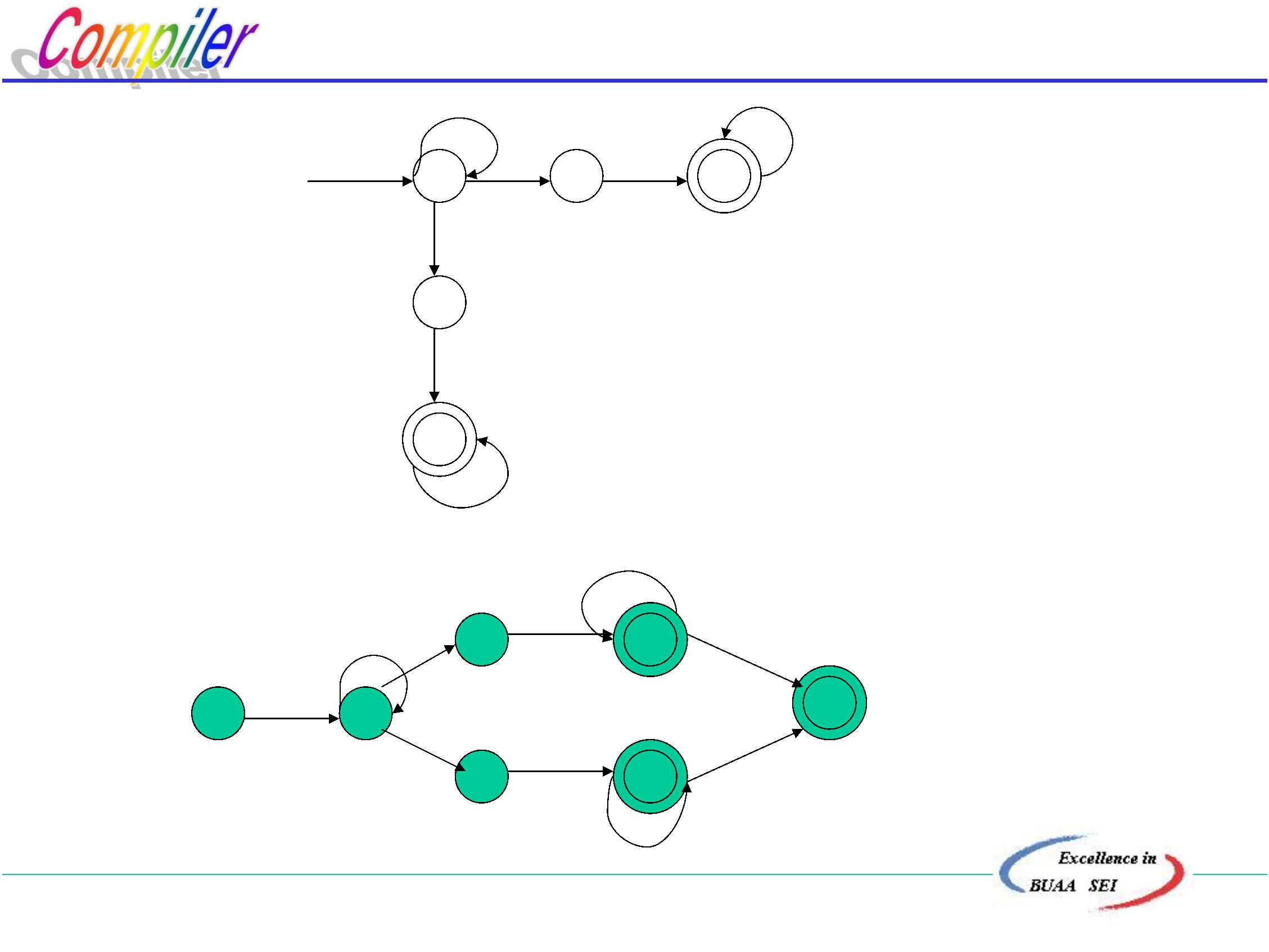
(2)消除M中的所有结点
a|b
aa(a|b) *
4
a|b
a|b
aa ε
x
0
y
x
0
y
ε
ε
bb ε
2
bb(a|b) *
a|b
(a|b)*(aa|bb)(a|b)*
x
y
北京航空航天大学计算机学院
7
6
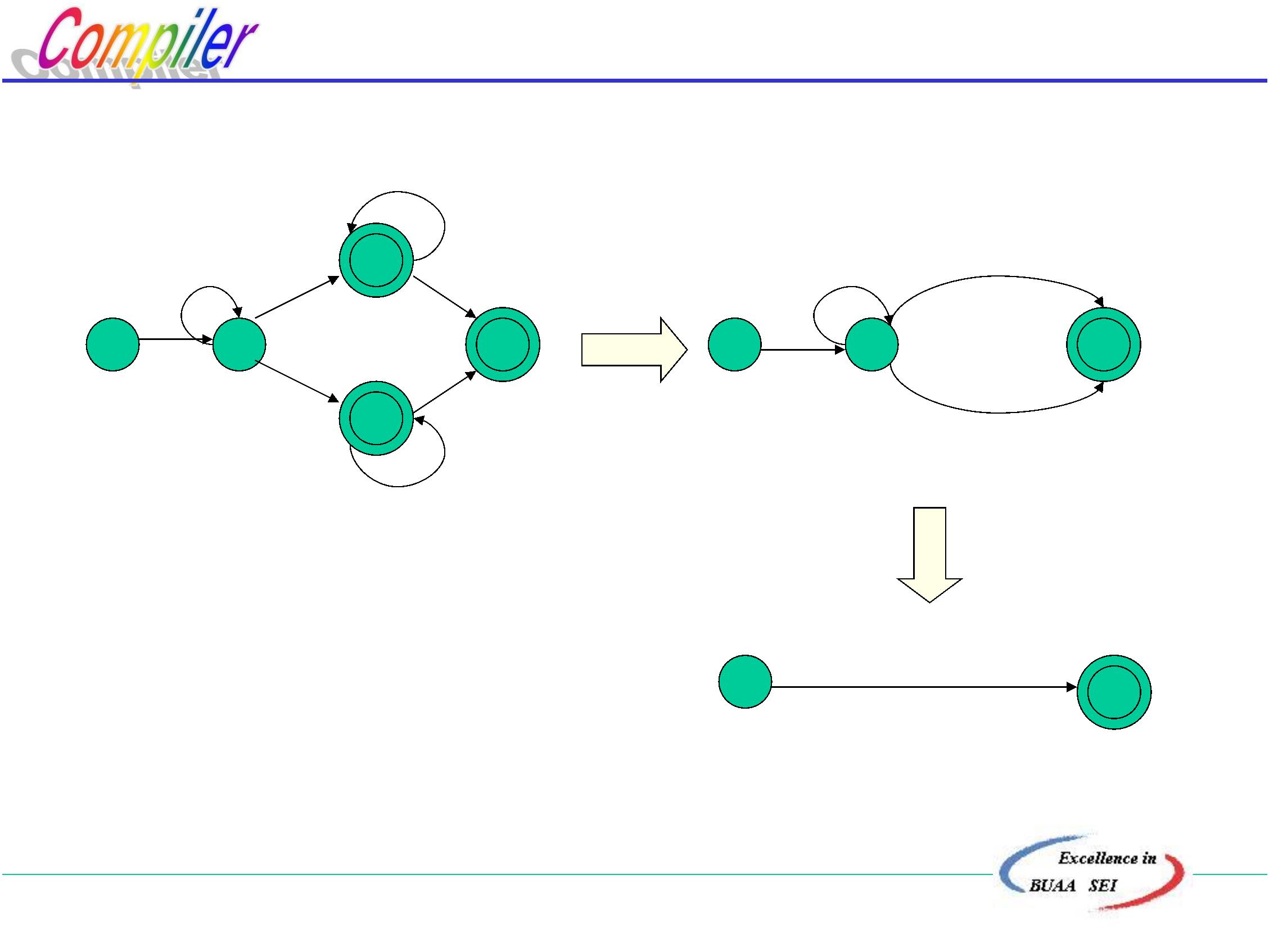
(
5)正则文法正则式
利用以下转换规则,直至只剩下一个开始符号定义的产
生式,并且产生式的右部不含非终结符。
规则 文法产生式 正则式
规则1 A→xB,B→y A=xy
规则2
规则3
A→xA|y
A=x*y
A→x,A→y A=x|y
北京航空航天大学计算机学院
7
7
例:有文法G[s]
S→aA|a,
A→aA|dA|a|d
于是: S=aA|a
A=(aA|dA)|(a|d)A=(a|d)A|(a|d)
由规则二: A=(a|d)*(a|d)
代入:S=a(a|d)*(a|d)|a
于是:S=a((a|d)*(a|d)|ε)
北京航空航天大学计算机学院
7
8

(
6)正则式正则文法
算法:
1
) 对任何正则式r,选择一个非终结符S作为识别符号,
并产生产生式 S→r
2
) 若x,y是正则式,对形为A→xy的产生式,重写为
A→xB B→y,其中B为新的非终结符,B∈Vn
同样: 对于 A→x*y A→xA A→y
A→x|y A→x A→y
例:将R=a(a|d)*转换成相应的正则文法
解:1) S→a(a|d)*
3
) S→aA
A→(a|d)A
A→ε
4) S→aA
A→aA|dA
A→ε
2
) S→aA
A→(a|d)*
北京航空航天大学计算机学院
7
9

补充: DFA的简化(最小化)
“对于任一个DFA,存在一个唯一的状态最少的等价的DFA”
一个有穷自动机是化简的 它没有多余状态并且它的状态
中没有两个是互相等价的。
一个有穷自动机可以通过消除多余状态和合并等价状态
而转换成一个最小的与之等价的有穷自动机
北京航空航天大学计算机学院
8
0

定义:
(1) 有穷自动机的多余状态:从该自动机的开始状态出发,任
何输入串也不能到达那个状态
0
1
例:
画状态图可
以看出s4,s6,s8
为不可达状
态应该消除
s
s
s
s
s
s
s
s
s
0
1
2
3
4
5
6
7
8
s
s
s
s
s
s
s
s
s
1
s
s
s
s
s
s
s
s
s
5
0
1
2
2
5
5
3
8
0
3
7
5
7
6
1
0
1
6
s
s
s
s
s
s
0
1
2
3
5
7
s
s
s
s
s
s
1
s
s
s
s
s
s
5
2
2
5
3
0
7
5
7
1
1
北京航空航天大学计算机学院
8
1
(2)等价状态 状态s和t的等价条件是:
1
2
)一致性条件:状态s和t必须同时为可接受状态或
不接受状态。
)蔓延性条件:对于所有输入符号,状态s和t必须
转换到等价的状态里。
对于所有输入符号c,Ic(s)=Ic(t),即状态s、t对于c具有相同
的后继,则称s,t是等价的。
(任何有后继的状态和任何无后继的状态一定不等价)
有穷自动机的状态s和t不等价,称这两个状态是可区别的。
北京航空航天大学计算机学院
8
2
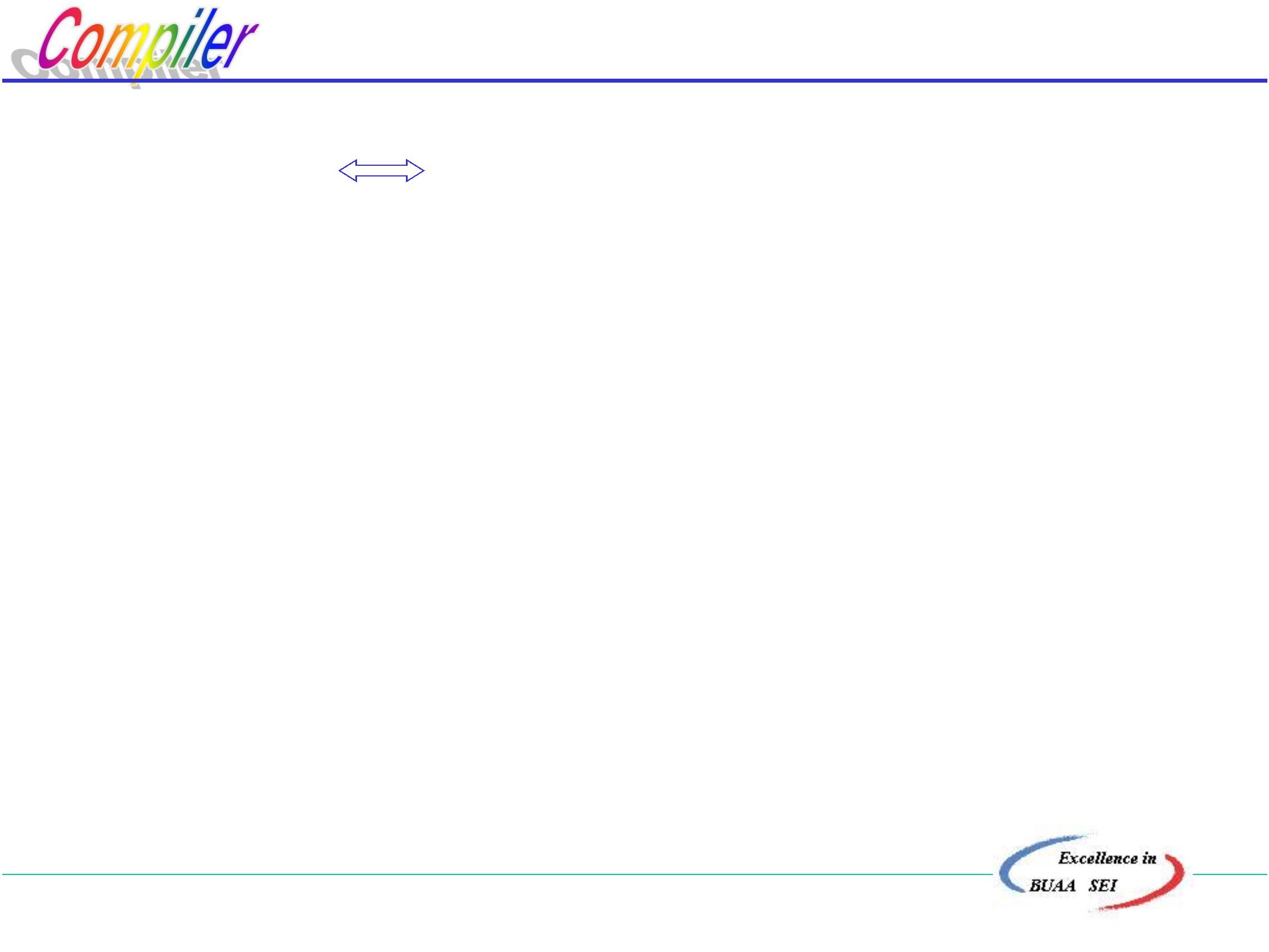
“
分割法”:把一个DFA(不含多余状态)的状态分割成一些
不相关的子集,使得任何不同的两个子集状态
都是可区别的,而同一个子集中的任何状态都
是等价的。
b
例:最小化
a
a
6
4
a
a
a
b
start
7
1
5
a
b
a
b
b
b
2
3
b
北京航空航天大学计算机学院
8
3
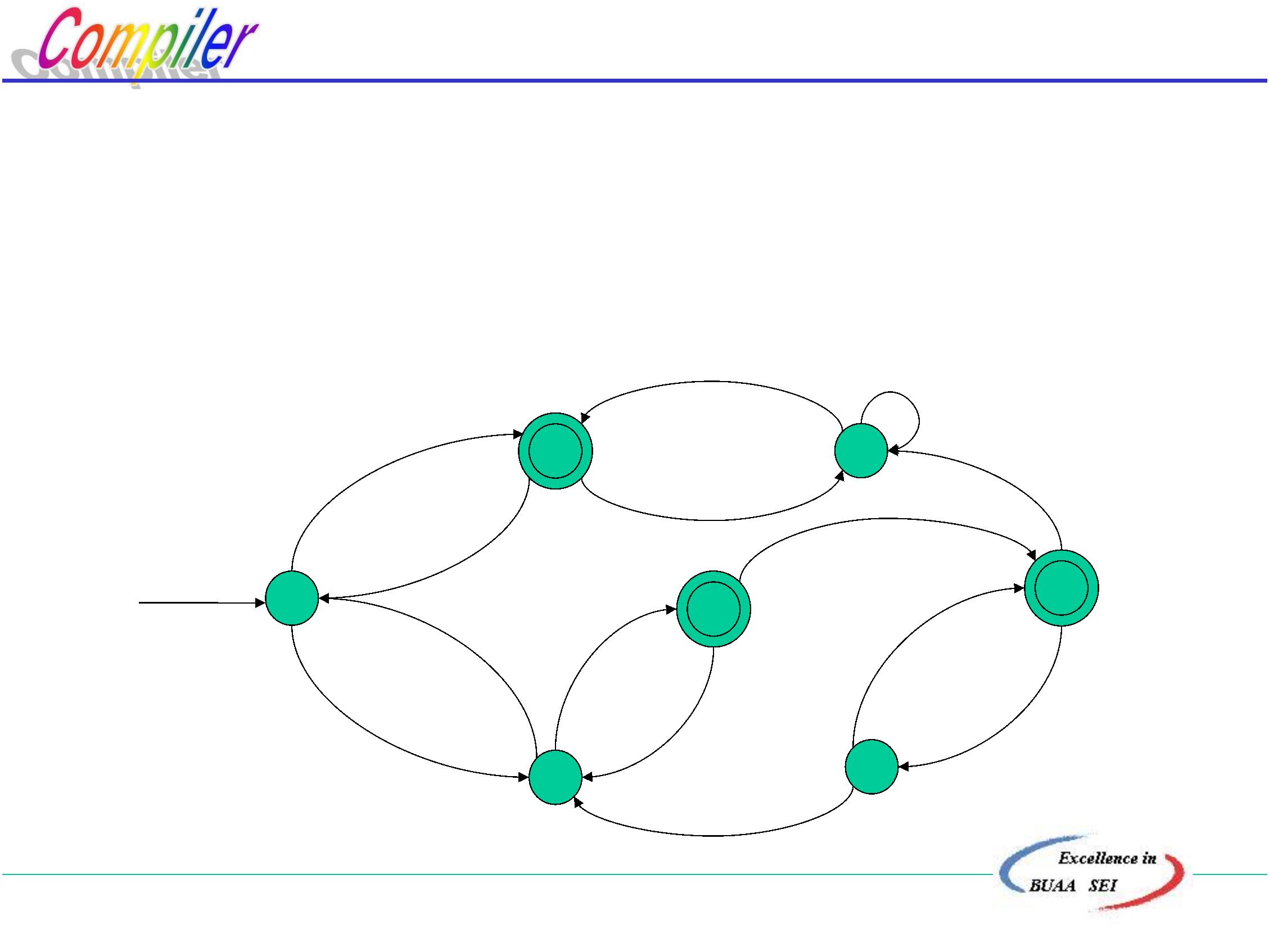
解:
(一)区分终态与非终态
a
6
7
b 区号
区号
a
6
7
b
3
3
1
2
3
3
1
2
1
1
3
4
1
4
5
6
3
3
4
1
4
5
6
3
2
5
6
7
4
5
6
7
4
1 2
1 3
7
4
2
7
4
2
北京航空航天大学计算机学院
8
4
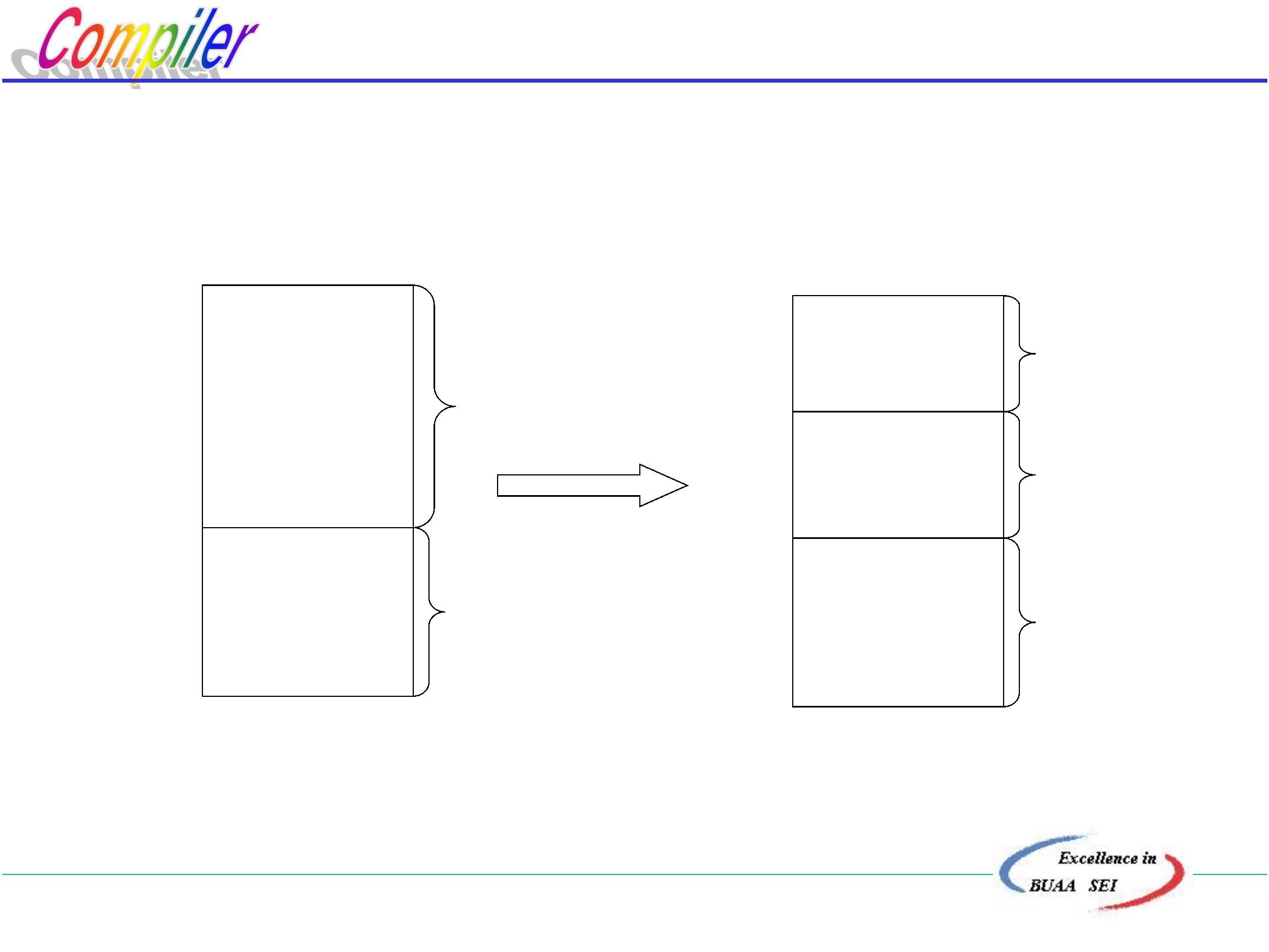
区号
区号
a
6
7
b
3
3
a
1 6
2 7
b
3
3
1
2
1
1
3
4
1
4
5 2
6 3
3 1
4 4
5 2
6 3
4
5
6
7
4
3
5 7
6 4
3
1
1 4
5
7
4
2
7 4
2
北京航空航天大学计算机学院
8
5
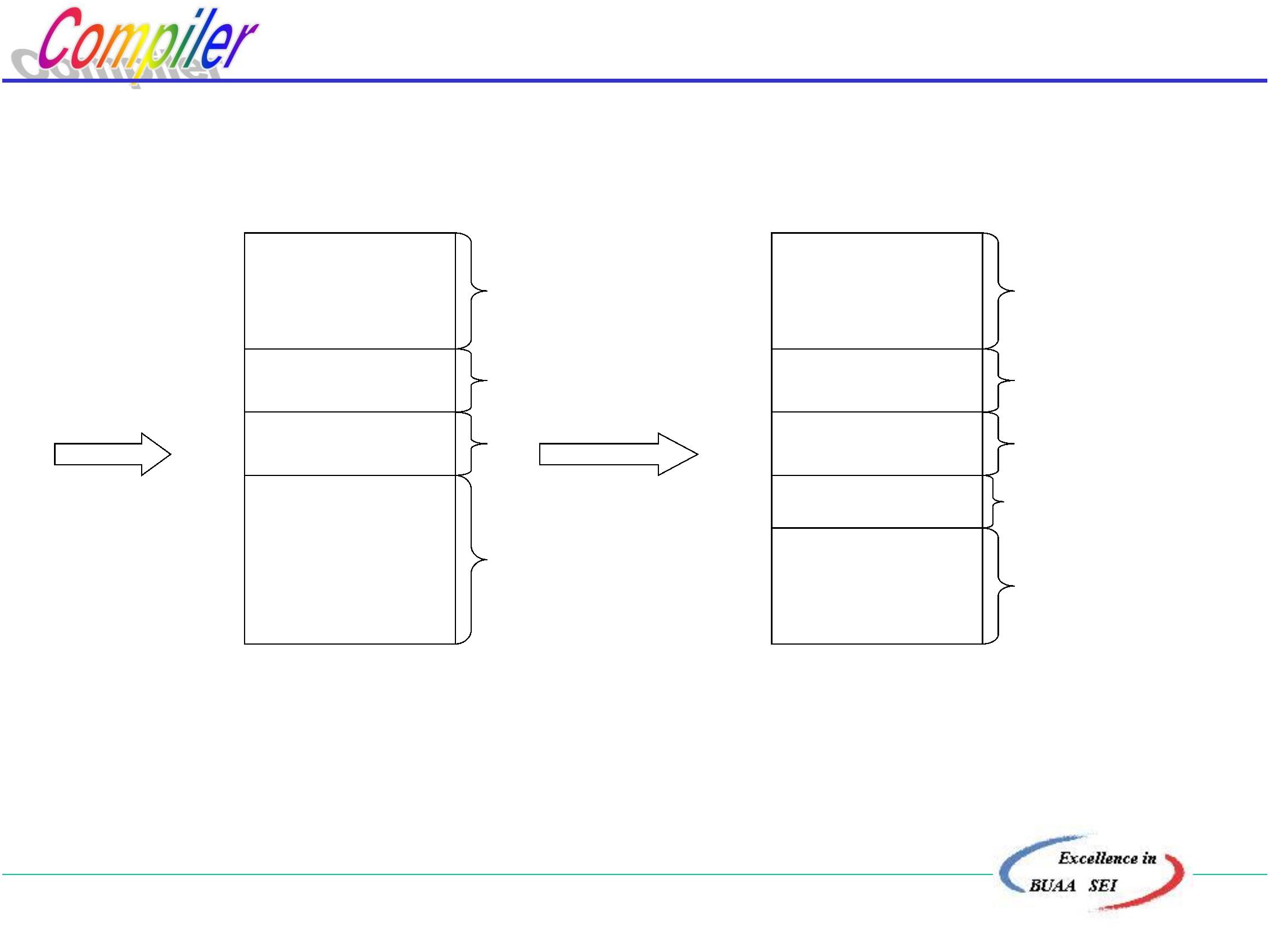
将区号代替状态号得:
a
b
b
a
a
5
a
1
2
3
4
5
5
1
3
5
3
2
4
5
2
1
3
a
b
1
a
b
b
2
4
b
北京航空航天大学计算机学院
8
6
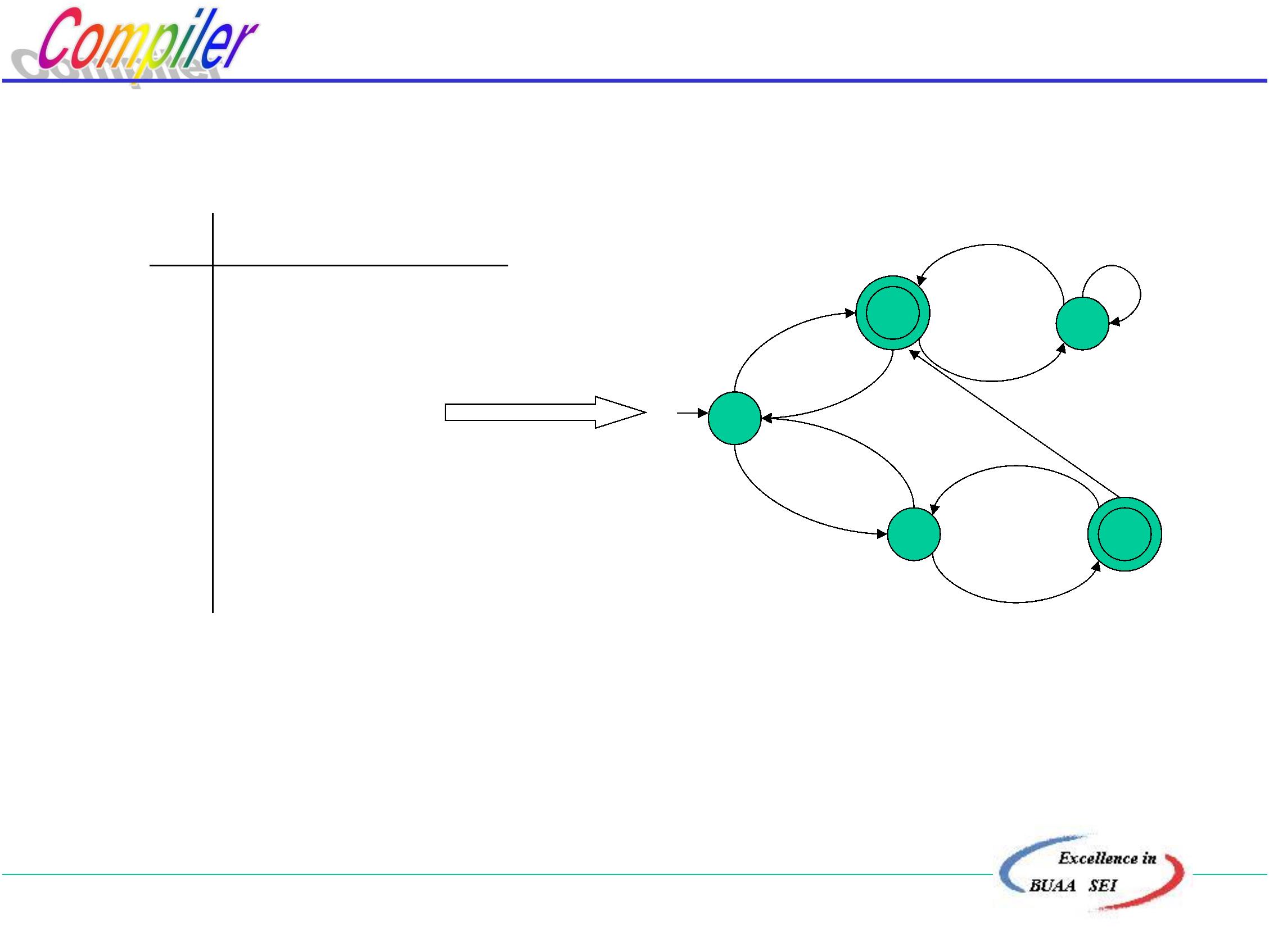
•
•
•
语法分析的功能、基本任务
自顶向下分析法
自底向上分析法
北京航空航天大学计算机学院
1

4.1 语法分析概述
功能:根据文法规则,从源程序单词符号串中识别出语法
成分,并进行语法检查。
基本任务:识别符号串S是否为某语法成分。
两大类分析方法:
自顶向下分析
自底向上分析
北京航空航天大学计算机学院
2

自顶向下分析算法的基本思想为:
+
若Z S 则 S L(G[Z]) 否则 S L(G[Z])
G[Z]
s 主要问题:
Ø 左递归问题
§ 主要方法:
•
•
递归子程序法
LL分析法
Ø 回溯问题
北京航空航天大学计算机学院
3

自底向上分析算法的基本思想为:
+
若Z S
则 S L(G[Z]) 否则 S L(G[Z])
G[Z]
s 主要问题:
§ 主要方法:
•
•
算符优先分析法
LR分析法
Ø 句柄的识别问题
北京航空航天大学计算机学院
4

4.2 自顶向下分析
4
.2.1 自顶向下分析的一般过程
给定符号串S,若预测是某一语法成分,则可根据该
语法成分的文法,设法为S构造一棵语法树,
若成功,则S最终被识别为某一语法成分,即
SL(G[Z]),其中G[Z]为某语法成分的文法
若不成功, 则 SL(G[Z])
•
可以通过一例子来说明语法分析过程
北京航空航天大学计算机学院
5

例:
S = cad
G[Z]:
分析过程是设法建立一
棵语法树,使语法树的末端结
点与给定符号串相匹配。
Z∷ =cAd
A∷ =ab|a
求解 SL(G[Z]) ?
Z
1
2
. 开始:令Z为根结点
·
Z
. 用Z的右部符号串去匹配输入串
·
完成一步推导ZcAd
检查, c-c匹配
c A d
A是非终结符,将匹配任务交给A
北京航空航天大学计算机学院
6
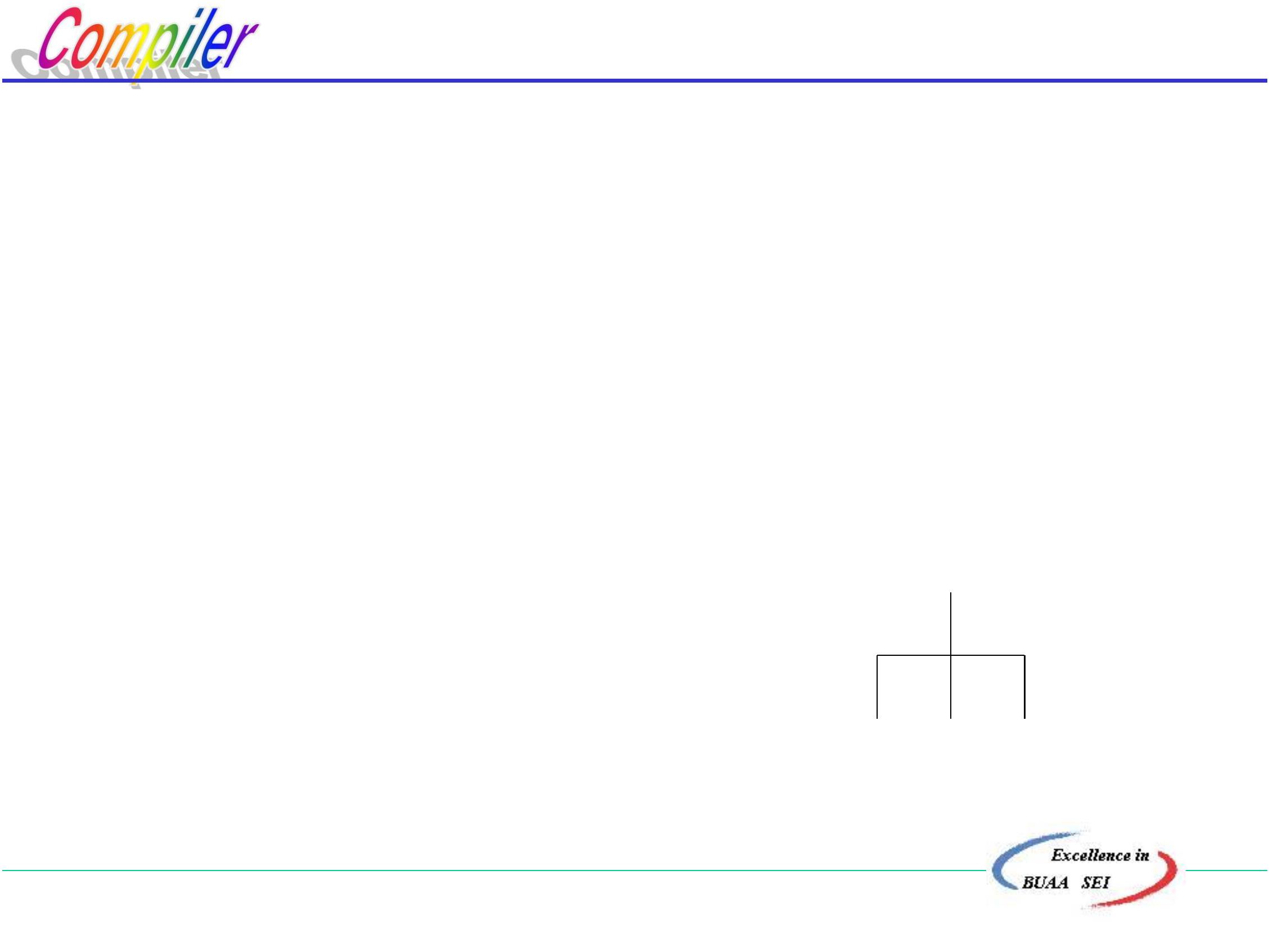
Z
·
3
. 选用A的右部符号串匹配输入串
A有两个右部,选第一个
c A d
完成进一步推导Aab
检查,a-a匹配,b-d不匹配(失败)
但是还不能冒然宣布SL(G[Z])
a b
Z
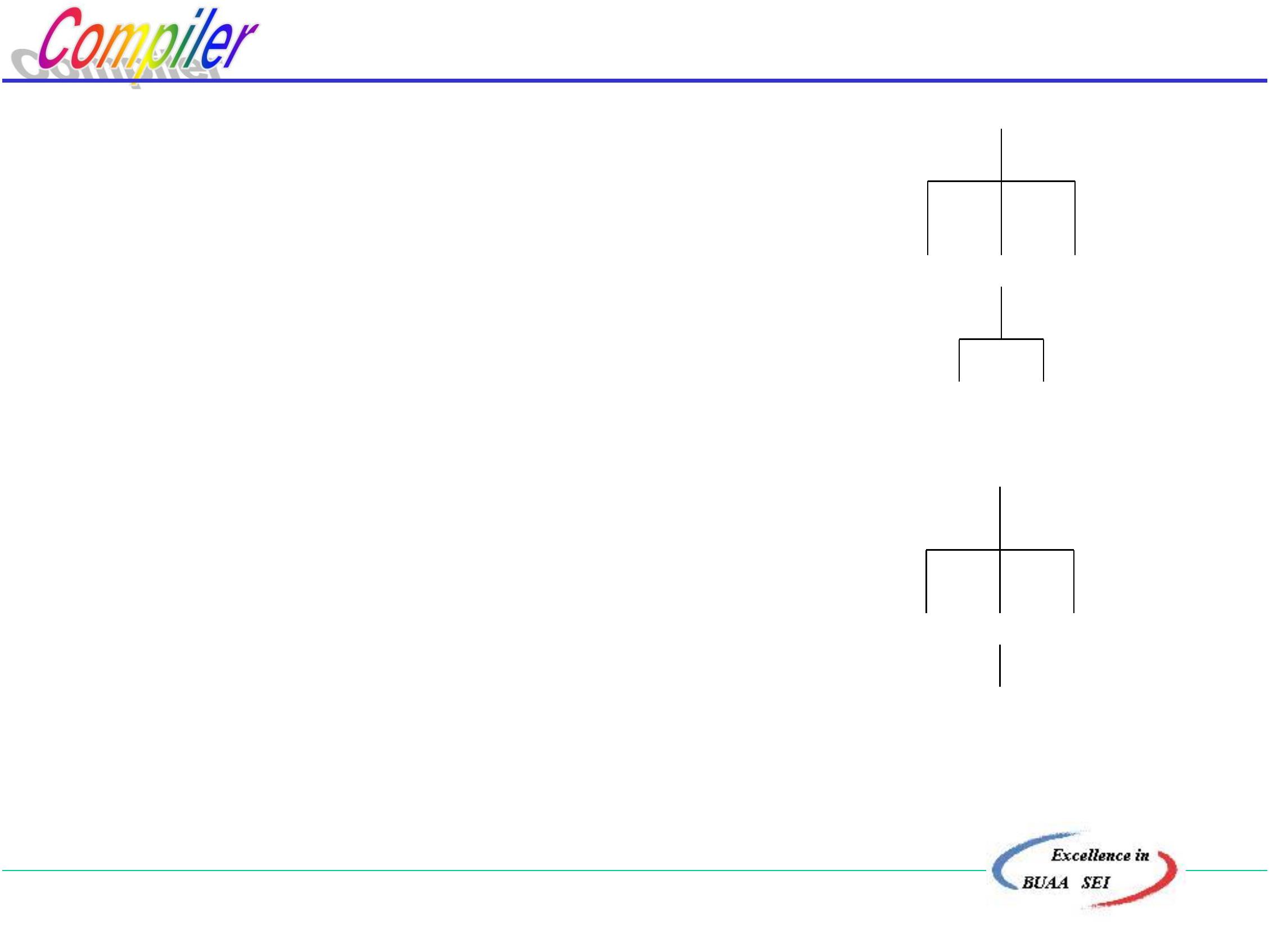
4
. 回溯 即砍掉A的子树
改选A的第二右部
·
Aa 检查 a-a匹配
d-d匹配
c A d
a
建立语法树,末端结点为cad,与输入cad相匹配,
建立了推导序列 ZcAdcad
∴
cadL(G(Z))
北京航空航天大学计算机学院
7
自顶向下分析方法特点:
1
2
. 分析过程是带预测的,对输入符号串要预测属于什么
语法成分,然后根据该语法成分的文法建立语法树。
. 分析过程是一种试探过程,是尽一切办法(选用不同
规则) 来建立语法树的过程, 由于是试探过程, 难免
有失败, 所以分析过程需进行回溯, 因此也称这种方法
是带回溯的自顶向下分析方法。
3
. 最左推导可以编写程序来实现, 但带溯的自顶向下分
析方法在实际上价值不大, 效率低。
北京航空航天大学计算机学院
8

4
.2.2 自顶向下分析存在的问题及解决方法
1
、 左递归文法:
有如下文法:
令U是文法的任一非终结符,文法中有规则
+
U∷ =U¨¨或者U U¨¨
这个文法是左递归的。
自顶向下分析的基本缺点是:
不能处理具有左递归性的文法
为什么?
北京航空航天大学计算机学院
9

如果在匹配输入串的过程中,假定正好轮到要用非终结
符U直接匹配输入串,即要用U的右部符号串U¨¨去匹配,
为了用U¨¨去匹配,又得用U去匹配,这样无限的循环下
去将无法终止。
如果文法具有间接左递归,则也将发生上述问题,只不
过环的圈子兜得更大。
要实行自顶向下分析,必须要消除文法的左递归,下面
将介绍直接左递归的消除方法,在此基础上再介绍一般左递
归的消除方法。
北京航空航天大学计算机学院
1
0

消除直接左递归
方法一,使用扩充的BNF表示来改写文法
例:(1) E∷ =E+T|T E∷ =T{+T}
(2) T∷ =T*F|T/F|F T ∷ =F{*F|/F}
a. 改写以后的文法消除了左递归。
b. 可以证明,改写前后的文法是等价的,表现在
L(G改前) = L(G改后)
如何改写文法能消除左递归,又前后等价,
可以给出两条规则:
北京航空航天大学计算机学院
11

规则一(提因子)
若:U∷ =xy|xw|….|xz
则可改写为:U∷ =x(y|w|….|z)
若:y=y y , w=y w
1
2
1 2
则 U∷ =x(y (y |w )|….|z)
1
2
2
若有规则:U∷ =x|xy
则可以改写为:U∷ =x(y|ε)
注意:不应写成U∷ =x(ε|y)
使用提因子法,不仅有助于消除直接左递归,而且有
助于压缩文件的长度,使我们能更有效地分析句子。
北京航空航天大学计算机学院
1
2

规则二
若有文法规则:U∷ =x|y|……|z|Uv
其特点是:具有一个直接左递归的右部并位于最后,
这表明该语法类U是由x或y……或z其后随有零个
或多个v组成。
UUv Uvv Uv vv ……
∴
可以改写为U∷ =(x|y|……|z){v}
通过以上两条规则,就能消除文法的直接左递归,
并保持文法的等价性。
北京航空航天大学计算机学院
1
3

方法二,将左递归规则改为右递归规则
规则三
若:P∷ =P|
则可改写为:P ∷ = P’
P’ ∷ = P’| ε
北京航空航天大学计算机学院
1
4

例1 E∷ =E+T|T
右部无公因子,所以不能
用规则一。
例2 T∷ =T*F|T/F|F
T∷ =T(*F|/F) | F 规则一
T∷ =F|T(*F|/F)
为了使用规则二,
令E∷ =T|E+T
T∷ =F{(*F|/F)} 规则二
即T∷ =F{*F|/F}
∴
由规则二可以得到
E∷ =T{+T}
右递归:
T ::= FT’
T’ ::= *FT’ | /FT’ | ε
北京航空航天大学计算机学院
1
5

消除一般左递归
一般左递归也可以通过改写文法予以消除。
消除所有左递归的算法:
1
. 把G的非终结符整理成某种顺序A1,A2,……An ,使得:
A
1
::= δ1|δ2|……δk
::= A1 r……
::= A2u |A1v…..
A
A
2
3
…
….
北京航空航天大学计算机学院
1
6

2
. For i:=1 to n do
begin
for j :=1 to i-1 do
把每个形如Ai∷ =Ajr的规则替换成
∷ =(δ1|δ2|……|δk) r ,
A
i
其中Aj ∷ =δ1|δ2|……|δk是当前全部Aj 的规则;
消除Ai规则中的直接左递归
end
3
. 化简由2得到的文法即可。
北京航空航天大学计算机学院
1
7

例:文法G[s]为
S ∷ = Qc|c
Q ∷ = Rb|b
R ∷ = Sa|a
该文法无直接左递归,但有间接左递归
+
SQc Rbc Sabc
∴ S Sabc
R∷ =Sa|a
Q∷ =Rb|b
S∷ =Qc|c
非终结符顺序重新排列
北京航空航天大学计算机学院
1
8

1
2
3
4
5
. 检查规则R是否存在直接左递归 R∷ =Sa|a
. 把R代入Q的有关选择,改写规则Q
. 检查Q是否存在直接左递归
Q∷ =Sab|ab|b
. 把Q代入S的右部选择
. 消除S的直接左递归
S∷ =Sabc|abc|bc|c
S∷ =(abc|bc|c){abc}
北京航空航天大学计算机学院
1
9

最后得到文法为:
S∷ =(abc|bc|c){abc}
Q∷ =Sab|ab|b
R∷ =Sa|a
可以看出其中关于Q和R的规则是多余的规则
∴经过压缩后 S∷ =(abc|bc|c){abc}
可以证明改写前后的文法是等价的
应该指出,由于对非终结符的排序不同,最后得到的文法在形
式上可能是不一样的,但是不难证明它们的等价。
北京航空航天大学计算机学院
2
0

2
、回溯问题
什么是回溯?
分析工作要部分地或全部地退回去重做叫回溯。
造成回溯的条件:
文法中,对于某个非终结符号的规则其右部
有多个选择,并根据所面临的输入符号不能准确
地确定所要的选择时,就可能出现回溯。
回溯带来的问题:
严重的低效率,只有在理论上的意义而无实际意义
北京航空航天大学计算机学院
2
1

效率低的原因
1
FIRST(α1)
1
2
) 语法分析要重做
FIRST(α2)
U
2
) 语义处理工作要推倒重来
FIRST(α2)
设文法G(不具左递归性),U Vn
U::= | |
3
1
2
3
[
定义] FIRST(αi) = {a | αi*
a…, a Vt }
为避免回溯,对文法的要求是:
FIRST(αi) ∩ FIRST(αj)=φ (ij)
北京航空航天大学计算机学院
2
2
消除回溯的途径:
.改写文法
对具有多个右部的规则反复提取左因子
1
例1 U∷ =xV|xW
改写为U∷ =x(V|W)
更清楚地表示为:
U∷ =xZ
U, V, W∈Vn, x∈Vt+
注意:问题到此并没有结束,还需要
进一步检查V和W的首符号是否相交
若V∷ =ab|cd FIRST(V) = {a,c}
W∷ =de|fg FIRST(W) = {d,f}
只要不相交就可以根据输入符号确定
目标,若相交,则要代入,并再次提
取左因子。如:V::= ab w::= ac
Z∷ =V|W
则:Z::= a (b|c)
北京航空航天大学计算机学院
2
3
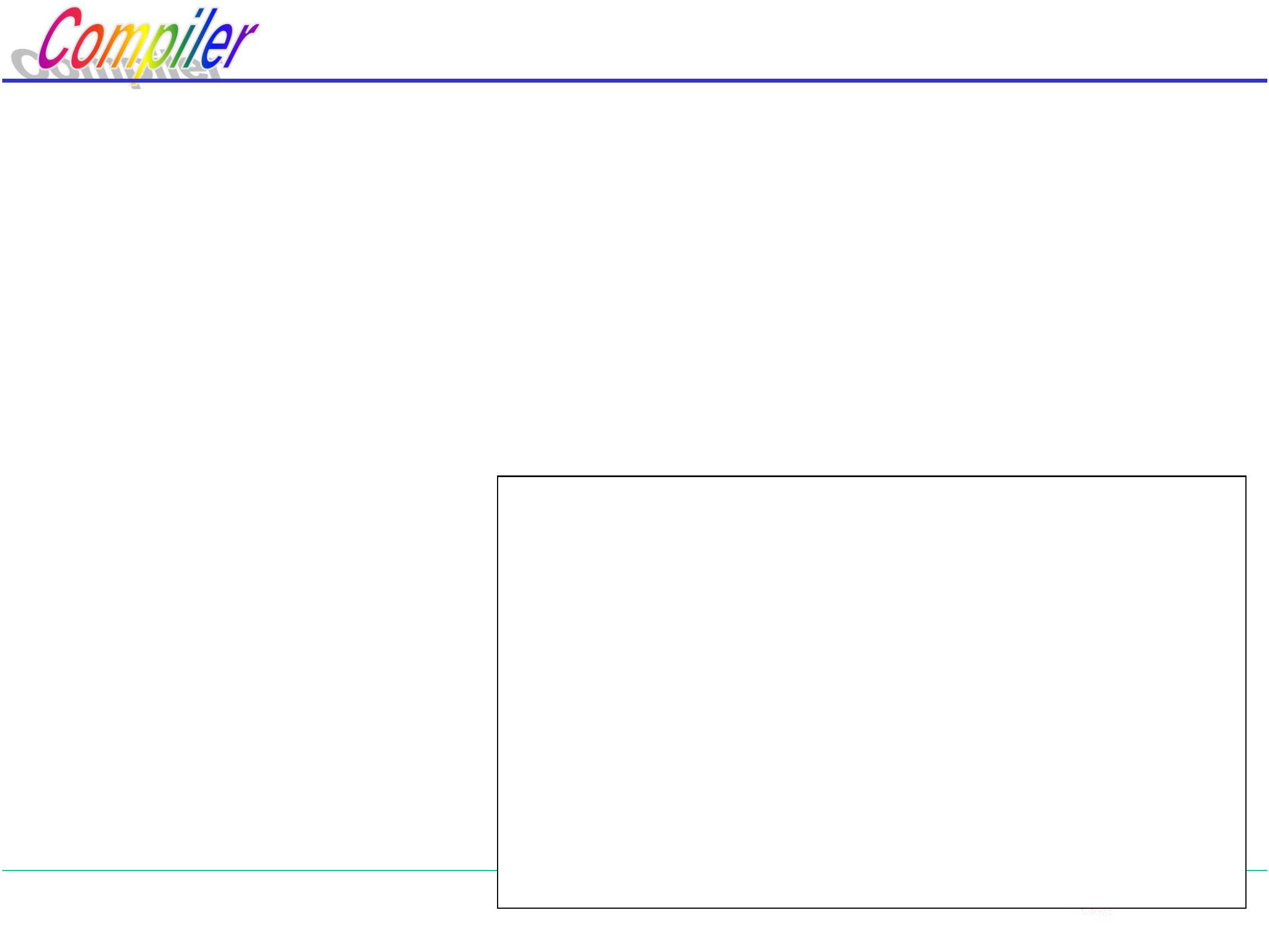
例2:文法G[<程序>]
<
<
<
程序> ∷ = <分程序>| <复合语句>
分程序>∷ = begin<说明串>;<语句串> end
复合语句>∷ = begin<语句串> end
FIRST(<分程序>) = {begin }
FIRST(<复合语句>) = {begin }
改写文法:
<
程序> ∷ = begin (<说明串>;<语句串> end |
语句串> end )
<
引入 <程序*>
<
<
程序> ∷ = begin <程序*>
程序*> ∷ = <说明串>;<语句串> end | <语句串> end
北京航空航天大学计算机学院
2
4

<
<
程序> ∷ = begin <程序*>
程序*> ∷ = <说明串>;<语句串> end | <语句串> end
对于:<程序*>
FIRST( <说明串>;<语句串> end)
=
{real, integer, boolean, array, function, procedure }
FIRST( <语句串>end )
{标识符,goto, begin, if, for}
=
不相交。
北京航空航天大学计算机学院
2
5

2
.超前扫描
当文法不满足避免回溯的条件时,即各选择的首符号相
交时,可以采用超前扫描的方法,即向前侦察各输入符
号串的第二个、第三个符号来确定要选择的目标
这种方法是通过向前多看几个符号来确定所选择的目
标,从本质上来讲也有回溯的味道,因此比第一种方
法费时,但是假读仅仅是向前侦察情况,不作任何语
义处理工作。
北京航空航天大学计算机学院
2
6

例:
<
<
<
程序> ∷ = <分程序>| <复合语句>
分程序>∷ = begin<说明串>;<语句串> end
复合语句>∷ = begin<语句串> end
这两个选择的首符号是相交的,故读到begin时并不能确定
该用哪个选择,这时可采用向前假读进行侦察,此例题只
需假读一次就可以确定目标。
因为<说明串>的首符集为{real,integer,……,procedure}
而<语句串>的首符集为{标识符,if ,for,……,begin}
∴只要超前假读得到的是“说明”的首符,便是第一个选择;
若是“语句”的首符,就是第二个选择。
北京航空航天大学计算机学院
2
7

文法的两个条件
为了在不采取超前扫描的前提下实现不带回溯的自顶向
下分析,文法需要满足两个条件:
1、文法是非左递归的;
2、 对文法的任一非终结符,若其规则右部有多个选择时, 各选择
所推出的终结符号串的首符号集合要两两不相交。
[
定义] 设文法G(不具有左递归性),UVn
U::= | |
1
2
3
*
FIRST(αi) = {a | αi a…, a Vt }
为避免回溯,对文法的要求是:
FIRST(αi) ∩ FIRST(αj)=φ (ij)
在上述条件下,就可以根据文法构造有效的、不带回溯的
自顶向下分析器。
北京航空航天大学计算机学院
2
8

4
.2.3 递归子程序法(递归下降分析法)
具体做法:对语法的每一个非终结符都编一个分析程序,
当根据文法和当时的输入符号预测到要用某个非终结符
去匹配输入串时,就调用该非终结符的分析程序。
下面通过举例说明如何根据文法构造该文法的
语法分析程序
北京航空航天大学计算机学院
2
9

如文法G[Z]: Z ::= UV
U ::= ….
V ::= ….
Z的分析程序
U的分析程序
V的分析程序
U
V
注:消除左递归后,可有其它递归:
U ::= …U…
U ::= …W…
W::= …U…
北京航空航天大学计算机学院
3
0
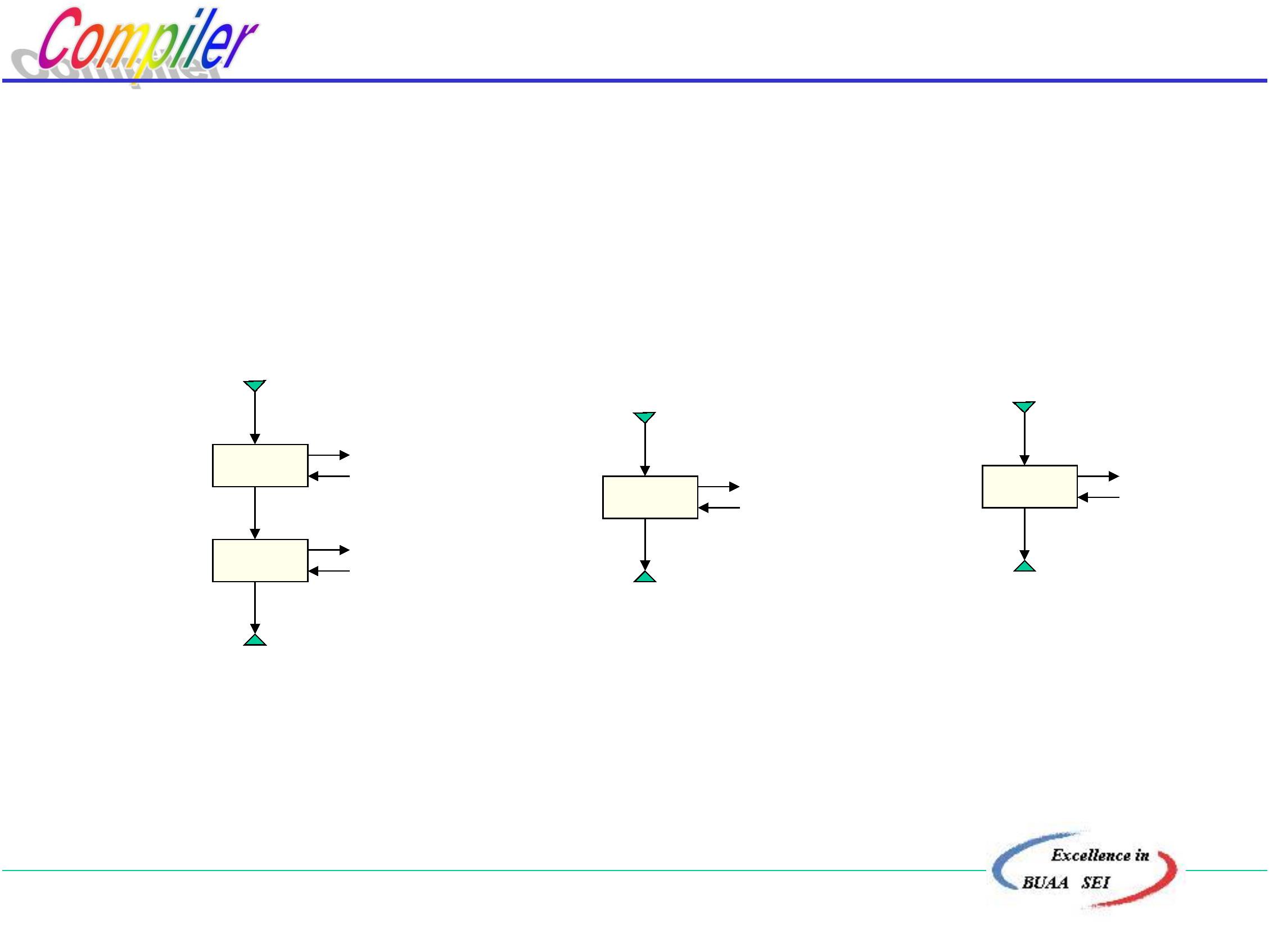
例:文法G[Z]
Z∷ =‘(’U‘)’|aUb
U∷ =dZ|Ud|e
1
.检查并改写文法
改写后无左递归且首符集不相交:
Z∷ =‘ (’U‘) ’|aUb
U∷ =(dZ|e){d}
{
{
(}∩{a}=φ
d}∩{e}=φ
2
.检查文法的递归性
+
Z¨·U¨·¨·Z¨·
U¨·Z¨·¨·U¨·
∴Z¨·Z¨·
+
∴U¨·U¨·
因此,Z和U的分析程序要编成递归子程序
北京航空航天大学计算机学院
3
1

3
.算法框图
非终结符号的分析子程序的功能是:
用规则右部符号串去匹配输入串。
以下是以框图形式给出的两个子程序:
北京航空航天大学计算机学院
3
2

入口
F
F
F
error
(sym)=‘(’
(sym) =‘a’
Y
T
读符号
读符号
U
U
F
error
(sym) =‘)’
T
(sym) =‘b’
T
读符号
出口
北京航空航天大学计算机学院
3
3
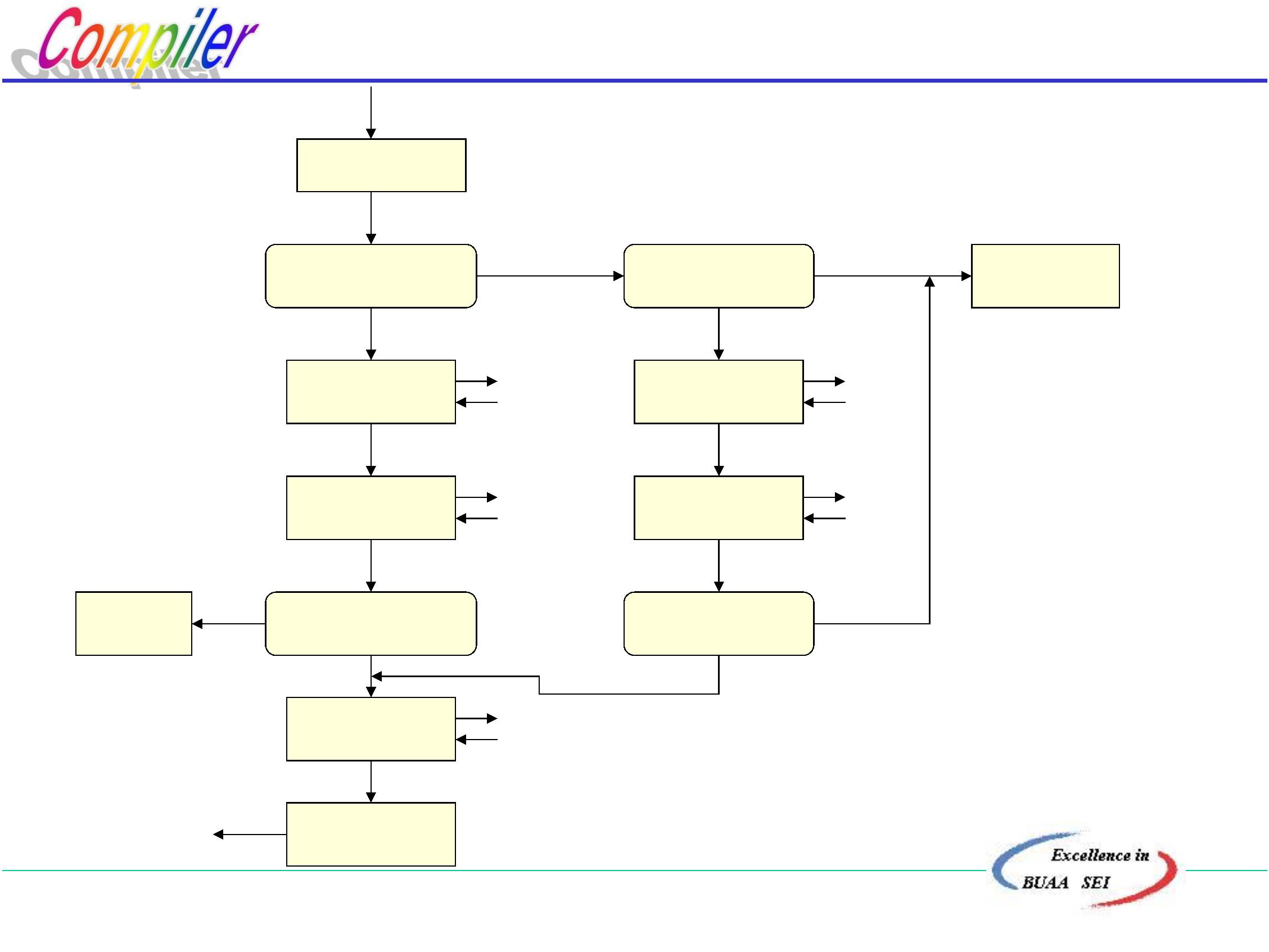
入口
F
F
error
(sym)=‘d’
(sym) =‘e’
Y
T
读符号
读符号
Z
(sym) =‘d’
T
F
读符号
出口
北京航空航天大学计算机学院
3
4
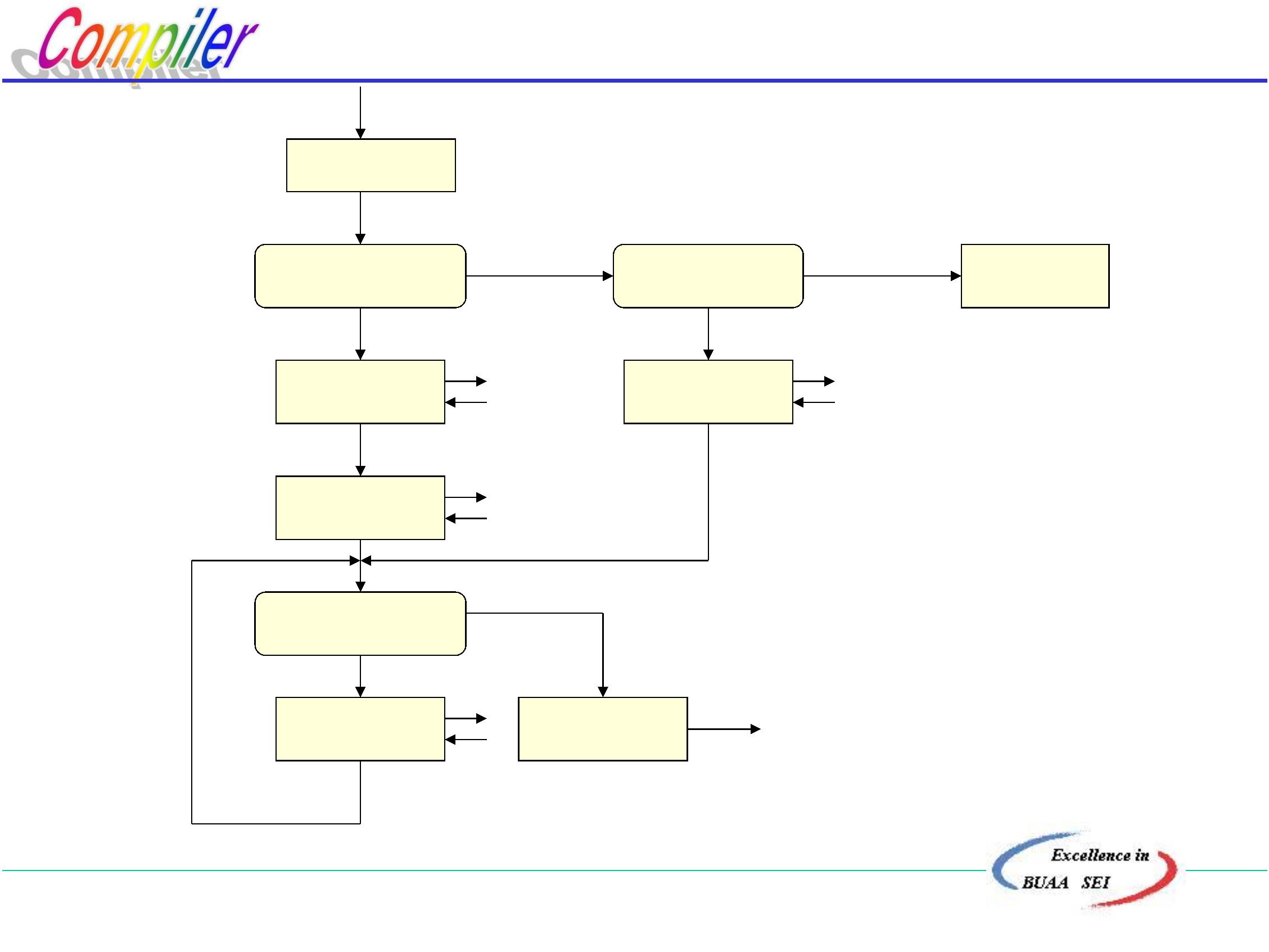
说明
要注意子程序之间的接口,在程序编制时进入某个非终结
•
符的分析程序时其所要分析的语法成分的第一个符号已
读入sym中。
递归子程序法对应的是最左推导过程
北京航空航天大学计算机学院
3
5

4
.2.4 用递归子程序法构造语法分析程序的例子
文法: <语句>∷ = <变量>∶ =<表达式>
IF <表达式> THEN <语句>
IF <表达式> THEN <语句> ELSE <语句>
|
|
<
<
<
<
变量>∷ = i | i ‘[’<表达式>‘]’
表达式>∷ = <项>| <表达式> + <项>
项>∷ = <因子>| <项>* <因子>
因子>∷ = <变量>| ‘(’<表达式>‘)’
改写文法: <语句>∷ = <变量>∶ =<表达式>
|
IF<表达式>THEN<语句>[ELSE <语句>]
<
<
<
<
变量>∷ = i[‘[’<表达式>‘]’]
表达式>∷ = <项>{+<项>}
项>∷ = <因子>{*<因子>}
因子>∷ = <变量>|‘(’<表达式>‘)’
北京航空航天大学计算机学院
3
6

语法分析程序所要调用的子程序:
nextsym: 词法分析程序, 每调用一次读进一个单词,
单词的类别码放在sym中。
error:
出错处理程序。
北京航空航天大学计算机学院
3
7

PROCEDURE state;
IF sym =‘IF’ THEN
/*语句分析子程序*/
BEGIN nextsym; expr;
IF sym≠‘THEN’ THEN error
ELSE BEGIN nextsym; state;
IF sym= ‘ELSE’
THEN BEGIN
nextsym;
state;
END
END
END
ELSE BEGIN var;
IF sym≠‘∶ =’
THEN error
ELSE BEGIN
nextsym;
expr;
END
END
北京航空航天大学计算机学院
3
8

PROCEDURE var;
IF sym ≠‘i’ THEN error
ELSE BEGIN nextsym;
IF sym=‘[’ THEN
BEGIN nextsym;
expr;
/*变量*/
IF sym ≠‘]’
THEN error
ELSE nextsym;
END
END
北京航空航天大学计算机学院
3
9

<语句>∷ = <变量>∶ =<表达式>
|
IF<表达式>THEN<语句>[ELSE <语句>]
<
<
<
<
变量>∷ =i[‘[’<表达式>‘]’]
表达式>∷ =<项>{+<项>}
项>∷ =<因子>{*<因子>}
因子>∷ =<变量>|‘(’<表达式>‘)’
PROCEDURE expr;
BEGIN term;
/*表达式*/
WHILE sym=‘+’ DO
BEGIN nextsym;
term;
END
END;
北京航空航天大学计算机学院
4
0

PROCEDURE term;
BEGIN factor;
/*项*/
WHILE sym=‘*’ DO
BEGIN nextsym; factor END
END;
PROCEDURE factor;
BEGIN
/*因子*/
IF sym=‘(’ THEN
BEGIN nextsym; expr;
IF sym ≠‘)’
THEN error
ELSE nextsym
END
ELSE var;
END
北京航空航天大学计算机学院
4
1

4
.2.5 LL分析法
LL-自左向右扫描、自左向右地分析和匹配输入串。
分析过程表现为最左推导的性质。
1
、LL分析程序构造及分析过程
输入串
#
由三部分组成:
分析表
执行程序
符号栈
#
执行程序 (总控程序)
符号栈 (分析栈)
分析表
北京航空航天大学计算机学院
4
2
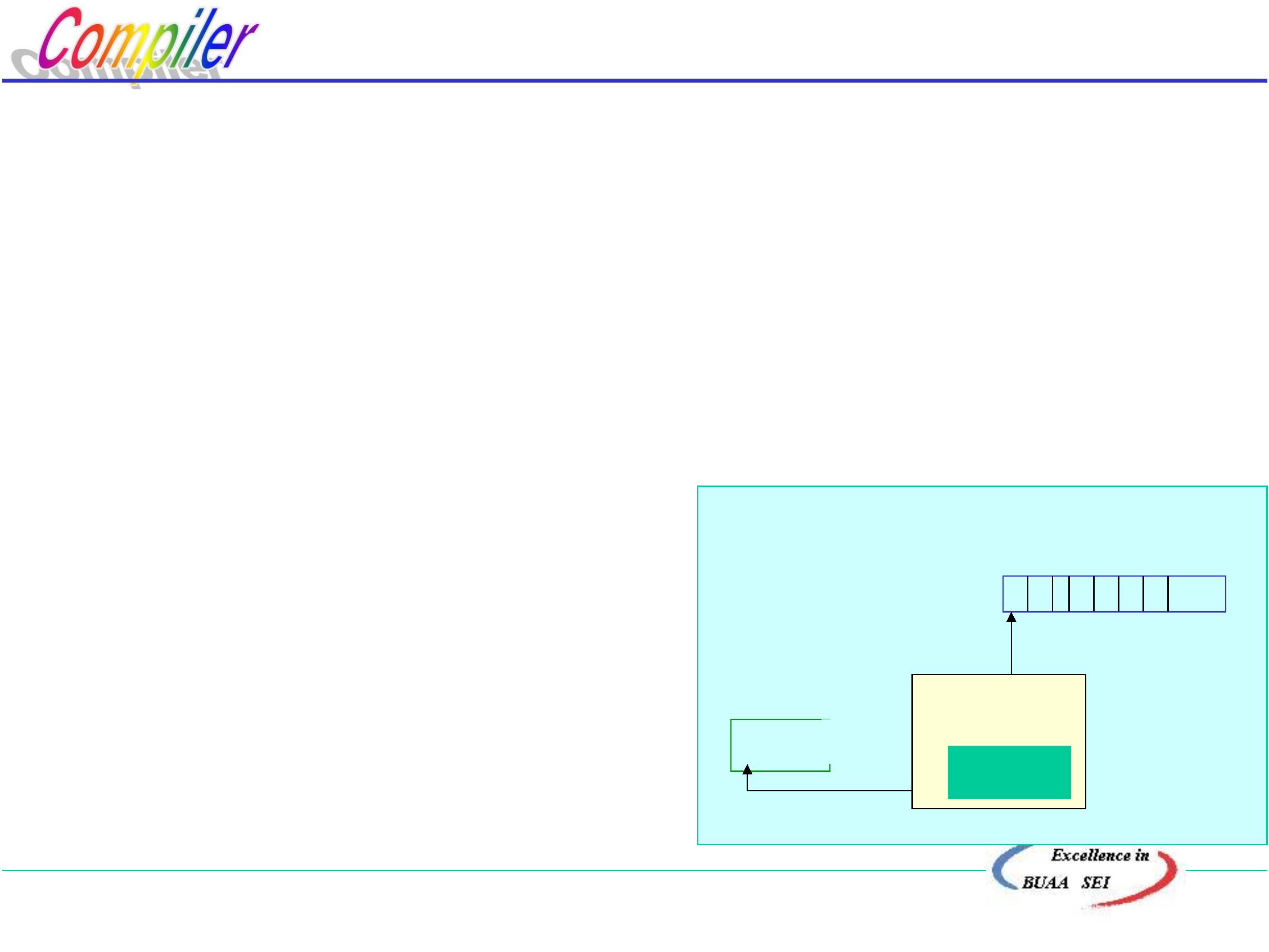
在实际语言中,每一种语法成分都有确定的左右界
符,为了研究问题方便,统一以‘#’表示。
(
1)、分析表:二维矩阵M
A∷ =αi
αi∈V*
A ∈Vn
M[A,a]= 或
error
a ∈ Vt or #
北京航空航天大学计算机学院
4
3

M[A,a] = A∷ =αi
表示当要用A去匹配输入串时,且当前输
入符号为a时,可用A的第i个选择去匹配。
*
即 当αi≠ε时,有αi a…;
当αi=ε时,则a为A的后继符号。
M[A,a] = error
表示当用A去匹配输入串时,若当前输入符
号为a,则不能匹配,表示无Aa…,或a不是A的
*
后继符号。
北京航空航天大学计算机学院
4
4

(
2)符号栈: 有四种情况
•
开始状态
xxxxxx#
符号栈
#
E
E#
a
•
工作状态
X
i
X::=
a……#
查分析表得:
X ∈Vn, M[X,a] = X∷ =αi
X+ a…
符号栈
#
…..X
X….#
X ∈Vt, X = a
北京航空航天大学计算机学院
4
5
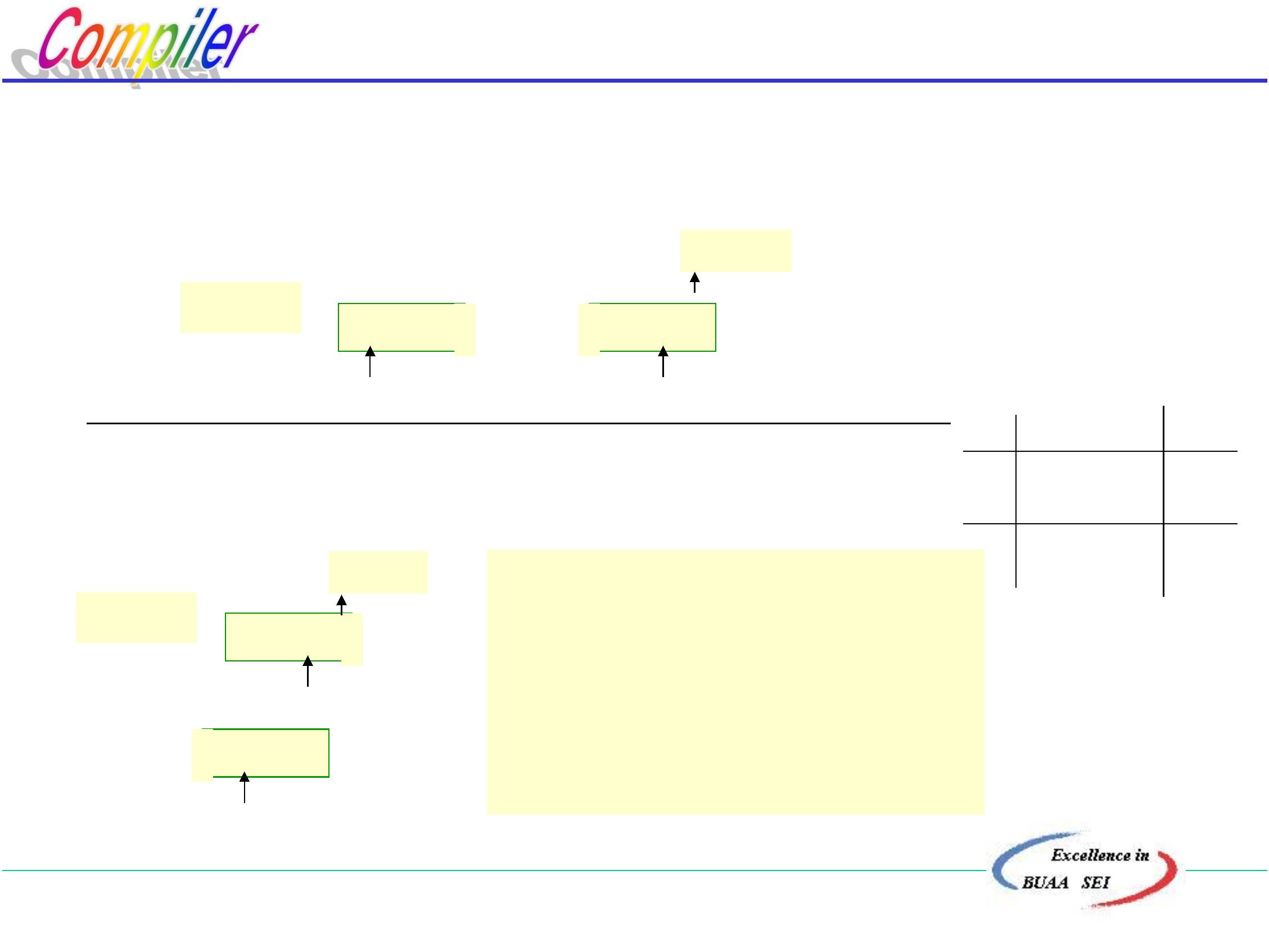
a
•
出错状态
X error
a……#
查分析表得:
X ∈Vn, M[X,a] = error
无X+ a…
符号栈
#
…..X
X….#
X ∈Vt, X a
•
结束状态
#
符号栈
#
#
北京航空航天大学计算机学院
4
6
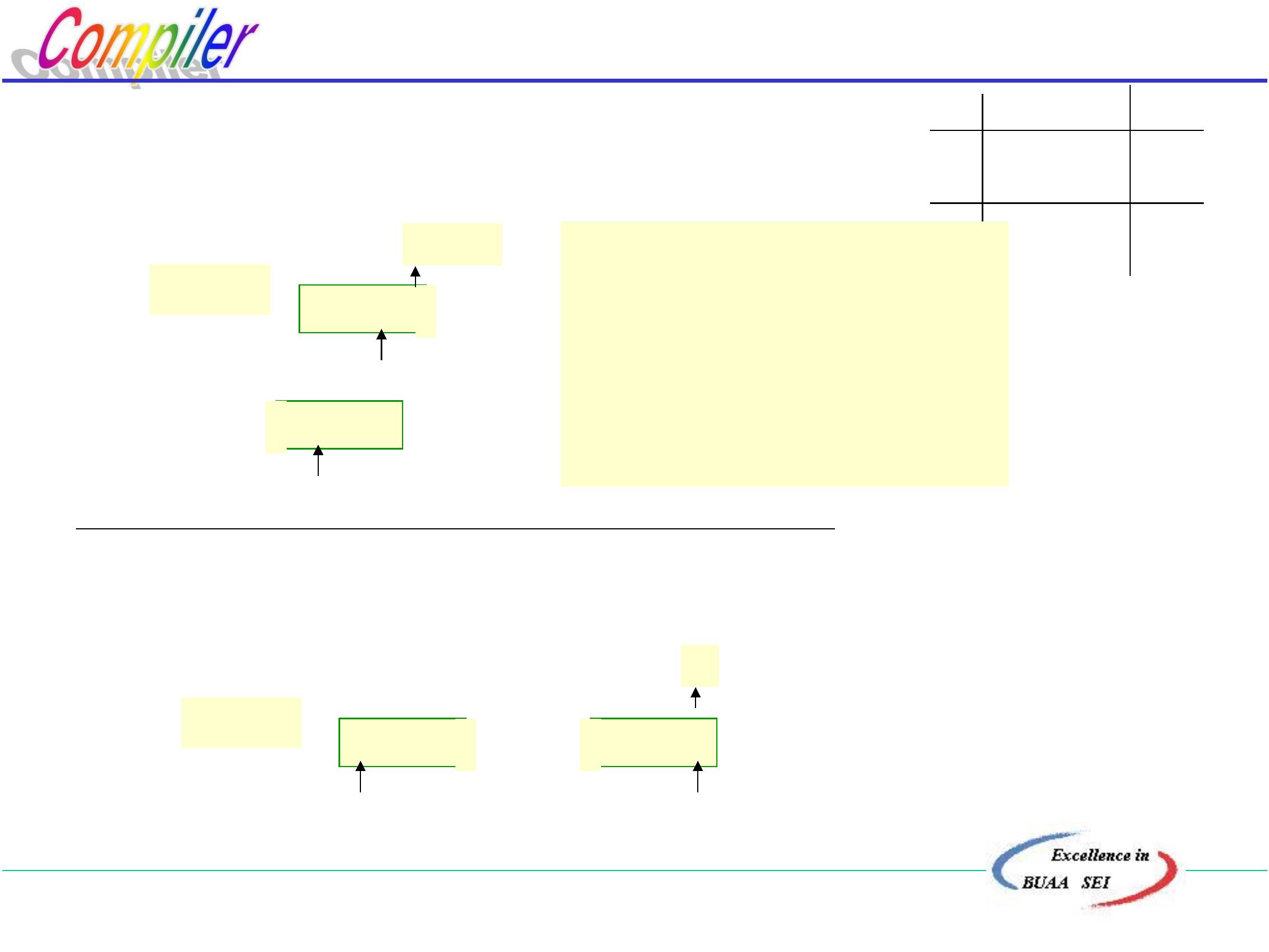
a……#
符号栈
#
…..X
(
3)执行程序
X….#
执行程序主要实现如下操作:
1
2
. 把#和文法识别符号E推进栈, 读入下一个符号,
重复下述过程直到正常结束或出错。
. 测定栈顶符号X和当前输入符号a,执行如下操作:
(1) 若X=a=#,分析成功,停止。E匹配输入串成功。
(2) 若X=a≠#,把X推出栈,再读入下一个符号。
(3) 若X∈Vn,查分析表M。
北京航空航天大学计算机学院
4
7
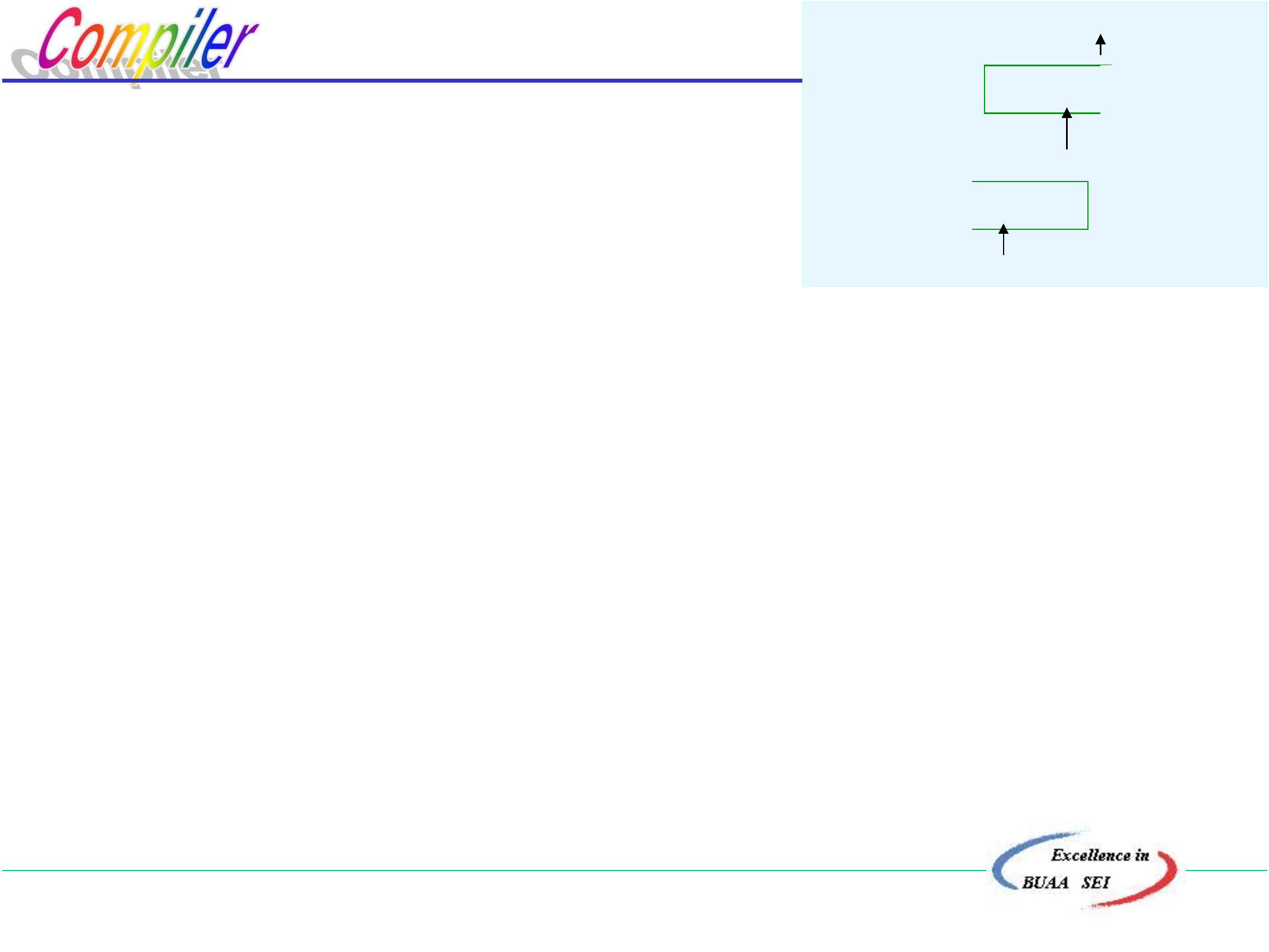
(3) 若X∈Vn,查分析表M
a) M[X,a] = X∷ = UVW
#
…..X
#…..WVU
UVW….#
则将X弹出栈,将UVW压入
注:U在栈顶 (最左推导)
X….#
b) M[X, a] = error 转出错处理
c) M[X, a] = X::=ε,
a
—
a为X的后继符号
X
X::=UVW
则将X弹出栈 (不读下一符号)
继续分析。
北京航空航天大学计算机学院
4
8
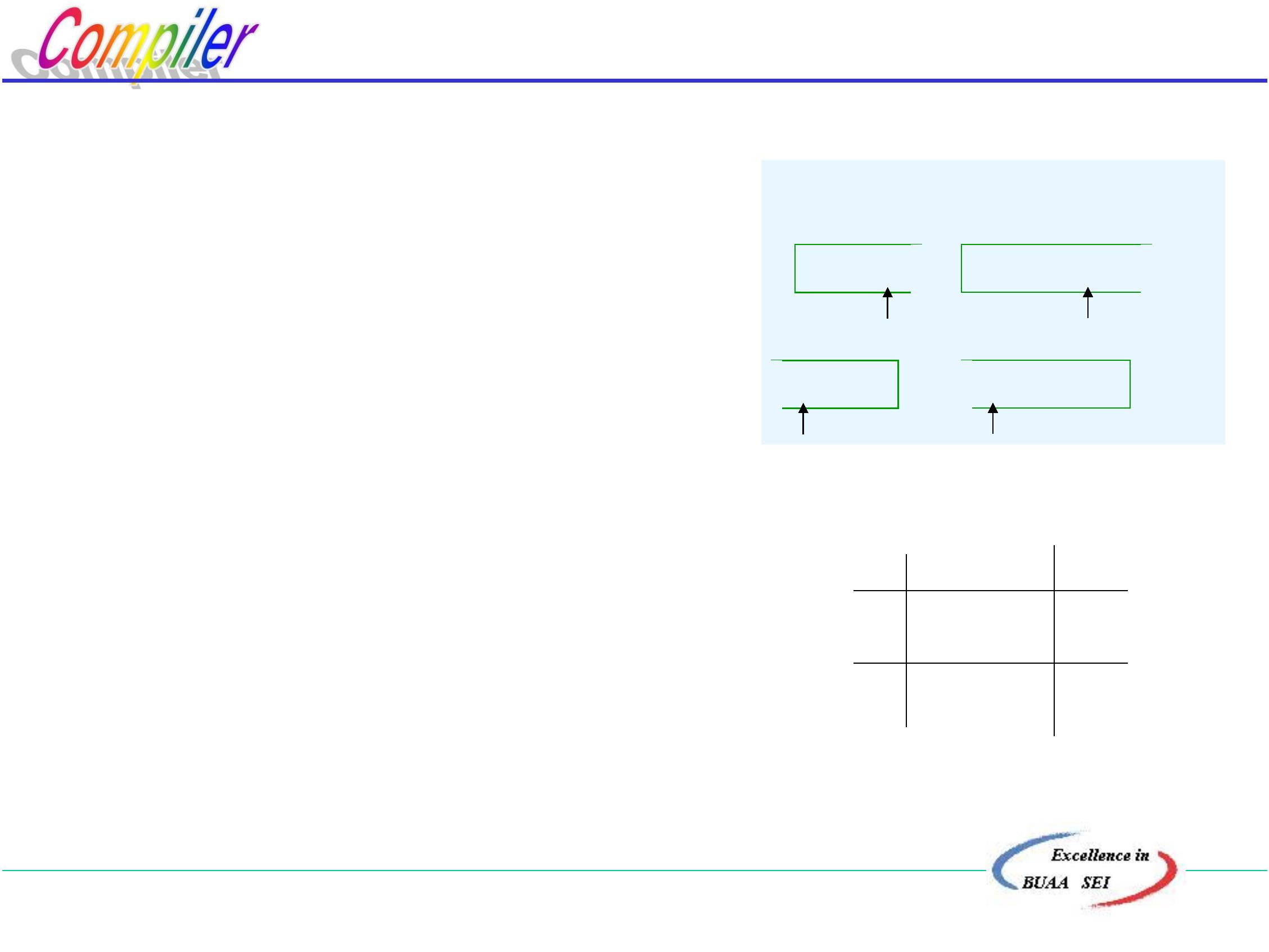
例:文法G[E]
E ::= E +T | T
消除左递归
E ::= TE’
T ::= T * F | F
F ::= (E)|i
E ::= +TE’|ε
T ::= FT’
T’ ::= *FT’|ε
F ::= (E)|i
北京航空航天大学计算机学院
4
9
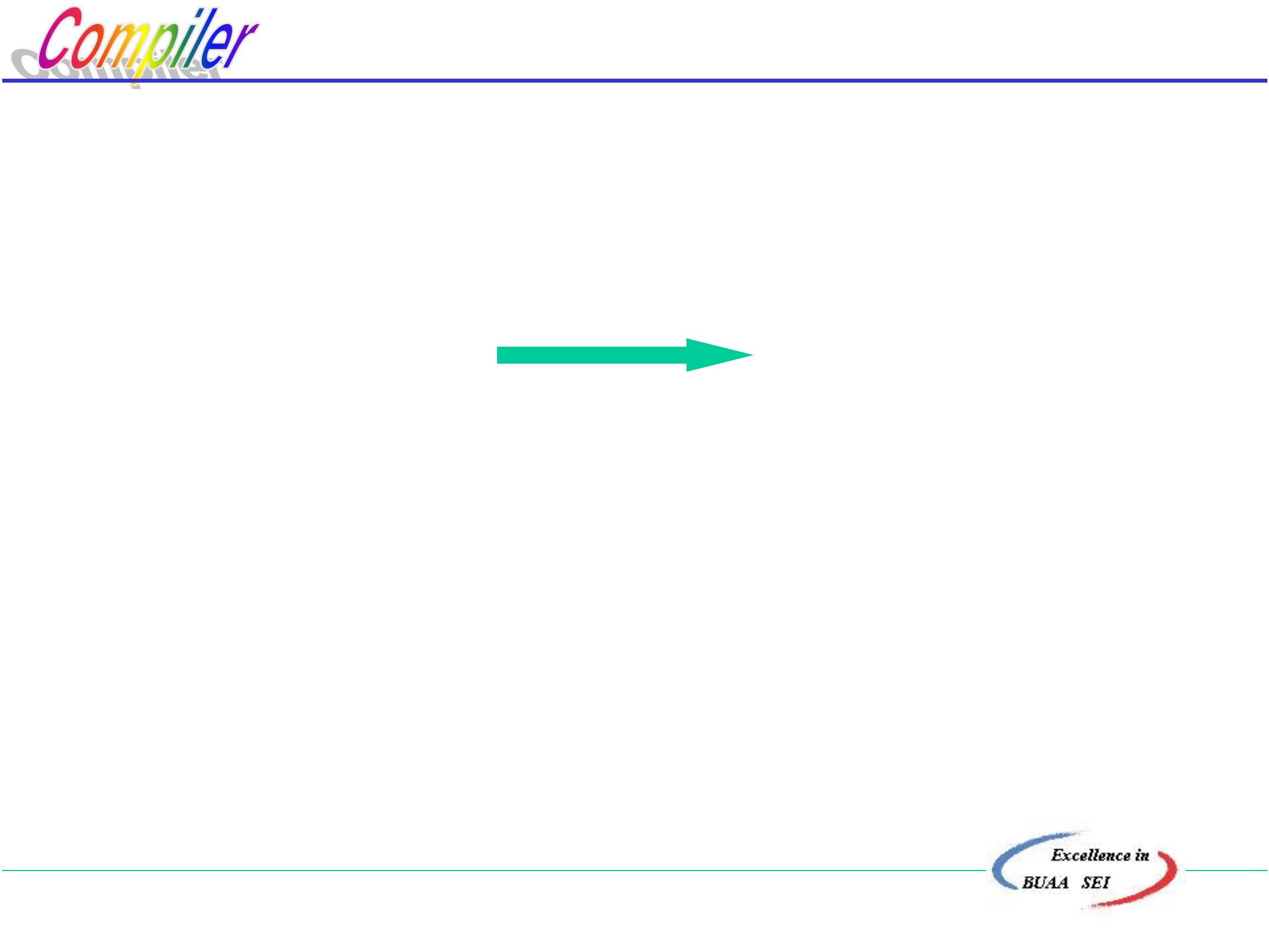
分析表
i
+
*
(
)
#
E E ::= T E '
E ::=
T E '
E '
E '::=
E '::=ε E '::=ε
T '::=ε T '::=ε
+
T E '
T T::= F T '
T '
T::=
FT '
T '::= T '::=
FT '
*
ε
F
F ::=
F ::= i
(E )
注:矩阵元素空白表示Error
北京航空航天大学计算机学院
5
0

输入串为: i+i*i#
步骤
符号栈
#E
读入符号
剩余符号串
+i*i#
使用规则
1
2
3
4
5
6
7
.
.
.
.
.
.
.
E#
i
i
#E’T
TE’#
+i*i#
E::=TE’
T::=FT’
F::= i
#E’T’F FT’E’#
#E’T’ i iT’E’#
#E’T’ T’E’#
i
+i*i#
i
+i*i#
+
+
+
i*i#
i*i#
i*i#
(出栈,读下一个符号)
T::= ε
#E’
E’#
#E’T+ +TE’#
E’::=+TE’
北京航空航天大学计算机学院
5
1

步骤
符号栈
#E’T
读入符号
剩余符号串
使用规则
8
9
1
.
i
*i#
*i#
*i#
i#
.
#E’T’F
#E’T’ i
#E’T’
#E’T’F*
#E’T’F
#E’T’ i
#E’T’
#E’
i
T::=FT’
F::= i
0.
i
11.
*
*
i
1
1
1
1
1
1
2.
3.
4.
5.
6.
7.
i#
T’::=*FT’
F::= i
#
i
#
#
#
#
T’::= ε
E’::= ε
#
北京航空航天大学计算机学院
5
2

推导过程:
E TE' FT'E' iT'E' iE'
i+TE' i+FT'E' i+iT'E'
i+i*FT'E' i+i*iT'E'
i+i*iE' i+i*i
最左推导。
北京航空航天大学计算机学院
5
3

2
、分析表的构造
设有文法G[Z]:
*
定义:FIRST(α)={a| αa…,a∈Vt}
α∈V* , 若αε,则ε∈FIRST(α)
*
该集合称为α的头符号集合。
*
定义:FOLLOW(A)={a| Z…Aa…,a∈Vt}
A∈Vn , Z识别符号
该集合称为A的后继符号集合。
*
特殊地:若Z ...A 则 #∈FOLLOW(A)
北京航空航天大学计算机学院
5
4

构造集合FIRST的算法
设α=X X ...X ,
X ∈V V
t
1
2
n
i
n
求FIRST(α)=?
首先求出组成α的每一个符号Xi的FIRST集合
(1) 若Xi∈Vt,则 FIRST(Xi) = {Xi}
(2) 若Xi ∈Vn 且 Xi∷ =a…..|ε, a ∈Vt
则 FIRST(Xi)={a,ε}
北京航空航天大学计算机学院
5
5

(3) 若Xi ∈Vn 且Xi∷ =y1 y2 …yk,则按如下顺序计算FIRST(Xi)
FIRST(Xi) FIRST(y1) –{ε};
若ε∈FIRST(y1) 则将FIRST(y2)-{ε}加入FIRST(Xi);
若ε∈FIRST(y1)
ε∈FIRST(y2) 则将FIRST(y3)-{ε}加入FIRST(Xi)
.
.......
若ε∈FIRST(yk-1) 则将FIRST(yk)-{ε}加入FIRST(Xi)
若ε ∈FIRST(y1) ~ FIRST(yk)
则将ε加入FIRST(Xi)
注意:要顺序往下做,一旦不满足条件,过程就要中断进行
得到FIRST(Xi),即可求出FIRST(α)
北京航空航天大学计算机学院
5
6

2
.构造集合FOLLOW的算法
设S, A, B∈Vn ,
算法:连续使用以下规则,直至FOLLOW集合不再扩大
(1) 若S为识别符号,则把“#”加入FOLLOW(S)中
(2) 若A∷ =αBβ (β≠ε),则把FIRST(β)-{ε}加入FOLLOW(B)
*
(3) 若A∷ =αB 或A∷ =αBβ, 且βε则把FOLLOW(A)加
入FOLLOW(B)
注:FOLLOW集合中不能有ε
北京航空航天大学计算机学院
5
7

2
、构造分析表
基本思想是:
终结符号
当文法中某一非终结符
呈现在栈顶时,根据当前
的输入符号,分析表应指
示要用该非终结符的哪
一条规则去匹配输入串
(即进行一步最左推导)
非
终
结
符
号
根据这个思想, 不难把构造分析表算法构造出来!
北京航空航天大学计算机学院
5
8
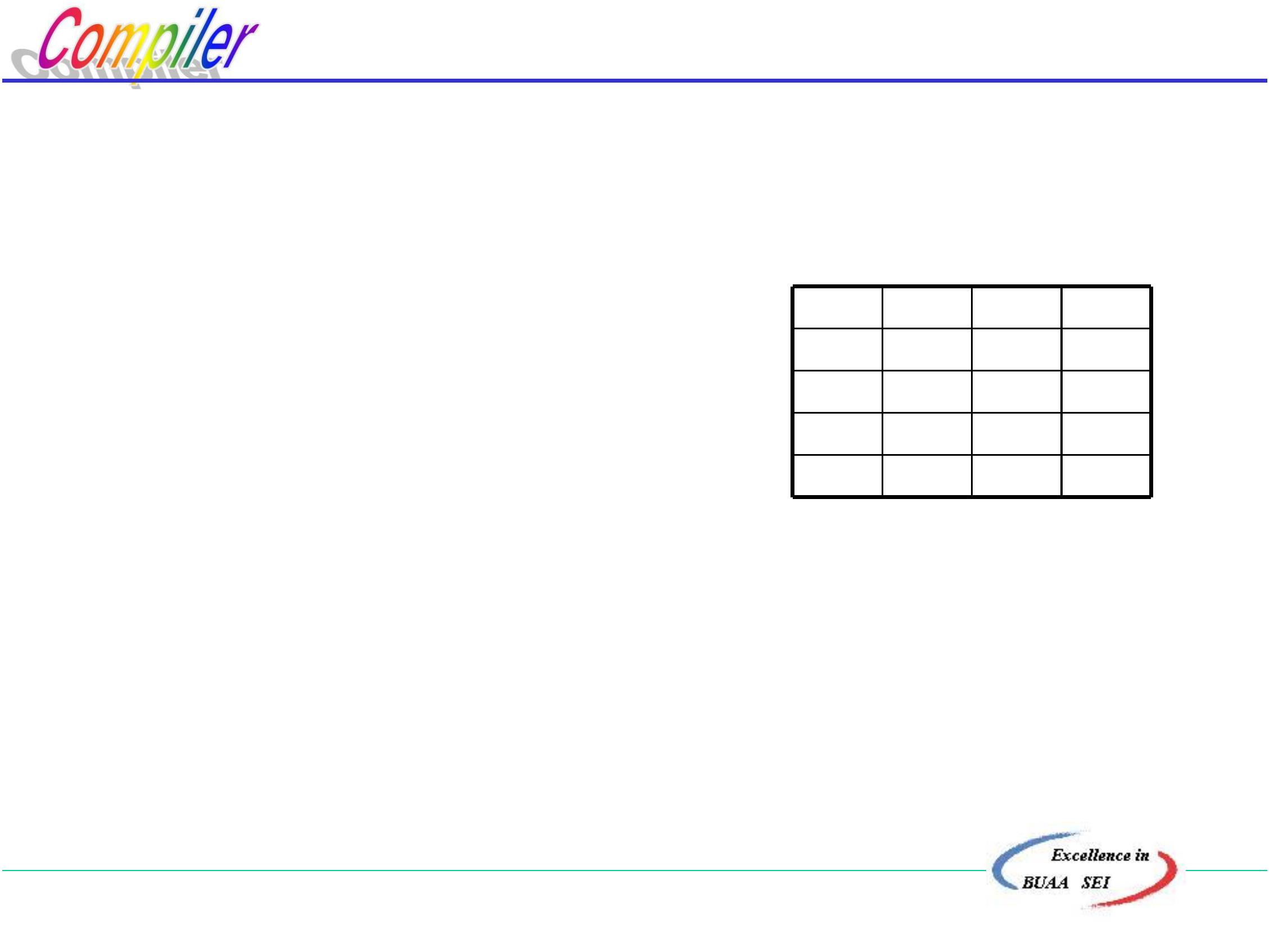
算法:
设A∷ =αi为文法中的任意一条规则,a为任一终结符或#。
1
、若a ∈FIRST(αi ),则A::= αi ==> M[A,a]
表示:A在栈顶,输入符号是a,应选择αi 去匹配
、若αi =ε或αi + ε,而且a ∈FOLLOW(A),
则A::= αi ==>M[A,a],表示A已经匹配输入串成功,
其后继符号终结符a由A后面的语法成分去匹配。
、把所有无定义的M[A,a]都标上error
2
3
北京航空航天大学计算机学院
5
9

例:G[E]分析表的构造
E∷ =TE’
E’∷ =+TE’|ε
T∷ =FT’
求FIRST :
FIRST(F)={(,i}
T’∷ =*FT’|ε
F∷ =(E)|i
FIRST(T’)={*,ε}
FIRST(T)=FIRST(F)-{ε}={(,i}
FIRST(E’)={+,ε}
FIRST(E)= FIRST(T)-{ε}={(,i}
∴
FIRST(TE’)=FIRST(T)-{ε}={(,i}
FIRST(+TE’)={+}
FIRST(ε)={ε}
FIRST(FT’)= FIRST(F)-{ε}={(,i}
FIRST(*FT’)={*}
FIRST((E))={(}
FIRST(ε)={ε}
FIRST(i)={i}
北京航空航天大学计算机学院
6
0

E∷ =TE’
E’∷ =+TE’|ε
T∷ =FT’
T’∷ =*FT’|ε
F∷ =(E)|i
求FOLLOW
FOLLOW(E)={#, )} ∵因为E是识别符号∴#∈FOLLOW(E)
又F∷ =(E) ∴ )∈FOLLOW(E)
FOLLOW(E’)={#, )} ∵E∷ =TE’ ∴FOLLOW(E)加入
FOLLOW(E’)
FOLLOW(T)={+, ), #} ∵E’∷ =+TE’ ∴FIRST(E’)-{ε}加入FOLLOW(T)
又E’ε,∴ FOLLOW(E’)加入FOLLOW(T)
FOLLOW(T’)= FOLLOW(T)= {+,),#}
∵T∷ =FT’ ∴ FOLLOW(T)加入FOLLOW(T’)
FOLLOW(F)={*, + , ), #} ∵T∷ =FT’ ∴ FOLLOW(F)=FIRST(T’)-{ε}
*
又T’ε∴ FOLLOW(T)加入FOLLOW(F)
北京航空航天大学计算机学院
6
1
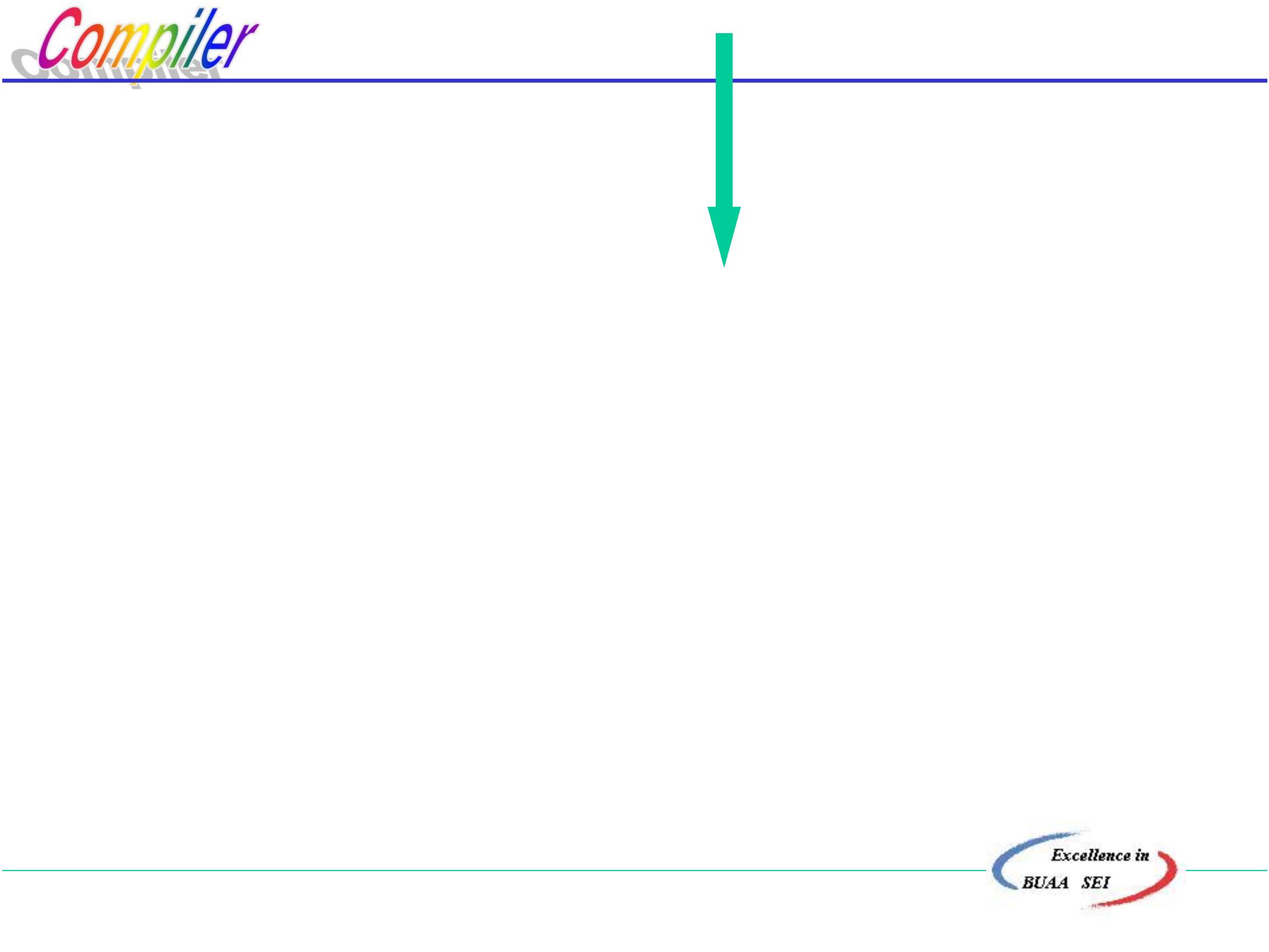
构造分析表
i
+
*
(
)
#
E E::=TE’
E
E::=TE’
E’∷ =+TE’
E’∷ =εE’∷ =ε
T’∷ =εT’∷ =ε
’
T T::=FT’
T::=FT’
T
’
T’∷ =ε T’∷ =*FT’
F F∷ =i
F∷ =(E)
注意:用上述算法可以构造出任意给定文法的分析表,但不是所有
文法都能构造出上述那种形状的分析表即M[A,a]=一条的规则或
Error。对于能用上述算法构造分析表的文法称为LL(1)文法
北京航空航天大学计算机学院
6
2
3
、LL(1)文法
定义:一个文法G,其分析表M不含多重定义入口(即分
析表中无二条以上规则),则称它是一个LL(1)文法.
定理:文法G是LL(1)文法的充分必要条件是:对于G的
每一个非终结符A的任意两条规则A::=α|β,下列条件成立:
1
2
、FIRST(α) ∩FIRST(β) = Ф
*
、若β==> ε, 则FIRST(α) ∩FOLLOW(A) = Ф
北京航空航天大学计算机学院
6
3

用此构造分析表的算法,可以构造任何文法的分析表,
但对于某些文法,有些M[A,a]中可能有若干条规则,这称
为分析表的多重定义或者多重入口。
可以证明: 如果G是左递归的,或者是二义性的文法,则至少有一
个多重入口。
U∷ =U…| a …
则有:FIRST(U…)∩FIRST(a…)≠φ
左递归:
∴
M[U,a]={U∷ =U…, U∷ =a…}
对文法所定义的某些句子存在着两个最左推导,
即在推导的某些步上存在多重定义,有两条规则
可用,所以分析表是多重定义的。
二义文法:
北京航空航天大学计算机学院
6
4

4
、LL分析的错误恢复----补充(不要求)
当符号栈顶的终结符和下一个输入符号不匹配,或栈
顶是非终结符A, 输入符号a,而M[A,a]为空白(即error)时,
分析发现错误。
错误恢复的基本思想是: 跳过一些输入符号,直到期望
的同步符号之一出现为止。
同步符号(可重新开始继续分析的输入符号)集合通
常可按以下方法确定:
北京航空航天大学计算机学院
6
5

1
2
) 把FOLLOW(A)的所有符号加入A的同步符号集合,跳过输
入符号直到出现FOLLOW(A)的元素, 便把A从栈中弹出,
继续往下分析。
) 为了避免仅按1)来确定同步符号集合会使跳读过多(如输入
串中缺少语句结束符号“;”),可将程序高层语法结构(成分)的
开始符号(通常是关键词)加入到低层语法结构的同步集合中。
3
4
5
) 把FOLLOW(A)的符号加入A的同步集合中。
) 如果栈顶的非终结符号A可以产生空串,可以将A从栈中弹出。
) 如果终结符在栈顶而不能匹配,则可弹出该终结符,继续分析,
这好比把所有其他符号均作为该符号的同步集合元素。
北京航空航天大学计算机学院
6
6

4.3 自底向上分析
基本算法思想:
若采用自左向右的描述和分析输入串,那么自
底向上的基本算法是:
从输入符号串开始,通过重复查找当前句型的句
柄(最左简单短语),并利用有关规则进行归约,若能
归约为文法的识别符号,则表示分析成功,输入符号
串是文法的合法句子,否则有语法错误。
北京航空航天大学计算机学院
6
7

分析过程是重复以下步骤:
1
、找出当前句型的句柄 x (或句柄的变形)
2
3
、找出以 x 为右部的规则 X::= x
、把 x 归约为X,产生语法树的一枝
关键:找出当前句型的句柄 x (或其变形),这不是很容易。
北京航空航天大学计算机学院
6
8

主要内容:
•
•
•
自底向上分析的一般过程(移进-归约分析)
算符优先分析法
LR分析法
北京航空航天大学计算机学院
6
9

4
.3.1 移进—归约分析(Shift-reduce parsing)
要点:建立符号栈,用来记录分析的历史和现状,
并根据所面临的状态,确定下一步动作是移
进还是归约。
输入串
#
符号栈
S.R.P
#
北京航空航天大学计算机学院
7
0
分析过程:把输入符号串按扫描顺序一一地移进
符号栈(一次移一个),检查栈中符号,当在栈顶的若
干符号形成当前句型的句柄时,就根据规则进行归约,
将句柄从符号栈中弹出,并将相应的非终结符号压入
栈内(即规则的左部符号),然后再检查栈内符号串是
否形成新的句柄,若有就再进行归约,否则移进符号。
分析一直进行到读到输入串的右界符为止。最后,若栈
中仅含有左界符号和识别符号,则表示分析成功,否则
失败。
北京航空航天大学计算机学院
7
1

例:G[S]:
S ∷ = aAcBe
A∷ = b
输入串为:
abbcde
A∷ = Ab
B∷ = d
输入串为abbcde,检查是否是该文法的合法句子:
若采用自底向上分析,即能否一步步归约当前句型的
句柄 ,最终归约到识别符号S。先设立一个符号栈,将
符号“#”作为待分析的符号串的左右分界符。
作为初始状态,先将符号串的左分界符推进符号栈,作
为栈底符号。
分析过程如下表:
北京航空航天大学计算机学院
7
2

步骤
符号栈
输入符号串
动作
1
#
abbcde#
准备,初始化
2
3
4
5
6
7
8
9
#a
#ab
bbcde#
bcde#
bcde#
cde#
cde#
de#
e#
移进
移进
#aA
归约(A∷ =b)
移进
#aAb
#aA
归约(A∷ =Ab)
移进
#aAc
#aAcd
#aAcB
#aAcBe
#S
移进
e#
归约(B∷ =d)
移进
10
#
11
#
归约(S∷ =aAcBe)
成功
12
#S
#
北京航空航天大学计算机学院
7
3

这一方法简单明了,不断地进行移进归约,关键是确定
当前句型的句柄。
说明: 1) 例子的分析过程是一步步地归约当前句型的句柄
S
该句子的唯一语法树为:
A
B
A
a b b c d e
北京航空航天大学计算机学院
7
4
注意两点:
(
1)栈内符号串 + 未处理输入符号串 = 当前句型
2)句柄都在栈顶
(
实际上,以上分析过程并未真正解决句柄的识别问题
北京航空航天大学计算机学院
7
5

2
) 未真正解决句柄的识别。
上述分析过程是怎样识别句柄的,主要看栈顶符号串
是否形成规则的右部。
这种做法形式上是正确的,但在实际上不一定正确。
举例的分析过程可以说是一种巧合。
因为不能认为: 对句型 xuy 而言
若有U∷ = u,即Uu 就断定u是简单短语,
*
u 就是句柄,而是要同时满足 Z xUy
北京航空航天大学计算机学院
7
6

4
.3.2 算符优先分析(Operator-Precedence Parsing)
1
) 这是一种经典的自底向上分析法,简单直观,并被广泛使
用,开始主要是对表达式的分析,现在已不限于此。可以
用于一大类上下无关的文法。
2
) 称为算符优先分析是因为这种方法是仿效算术式的四则运算
而建立起来的,作算术式的四则运算时,为了保证计算结果
和过程的唯一性,规定了一个统一的四则运算法则,规定运
算符之间的优先关系。
1
2
3
.乘除的优先级大于加减
.同优先级的运算符左大于右
.括号内的优先级大于括号外
运算法则:
于是: 4+8-6/2*3 运算过程和结果唯一
北京航空航天大学计算机学院
7
7

3
) 算符优先分析的特点:
仿效四则运算过程,预先规定相邻终结符之间的优
先关系,然后利用这种优先关系来确定句型的“句柄” ,
并进行归约。
4
) 分析器结构:
输入串
#
分析程序
符号栈
#
优先关系矩阵
北京航空航天大学计算机学院
7
8
例: G[E]
E∷ =E+E | E*E | (E) | i
Vt={+, *, (, ), i}
这是一个二义文法,要用算符优先法分析由该文法所确定的
语言句子, 如:i+i*i
(1) 先确定终结符之间的优先关系
优先关系的定义:
设 a, b 为可能相邻的终结符
定义: a =. b
a的优先级等于b
a的优先级小于b
a的优先级大于b
.
a< b
.
a > b
北京航空航天大学计算机学院
7
9

1
) 例中文法终结符之间的优先关系可以用一个矩阵M来表示
b(右,栈外)
+
*
i
(
)
#
a(左,栈内)
.
. . . . .
+
>
<
<
<
>
>
.
. . . . .
*
i
>
>
<
<
>
>
.
.
.> .
>
>
>
.
. . . .
(
<
<
<
<
=
.
.
.> .
)
>
>
>
.
. . .
#
<
<
<
<
北京航空航天大学计算机学院
8
0
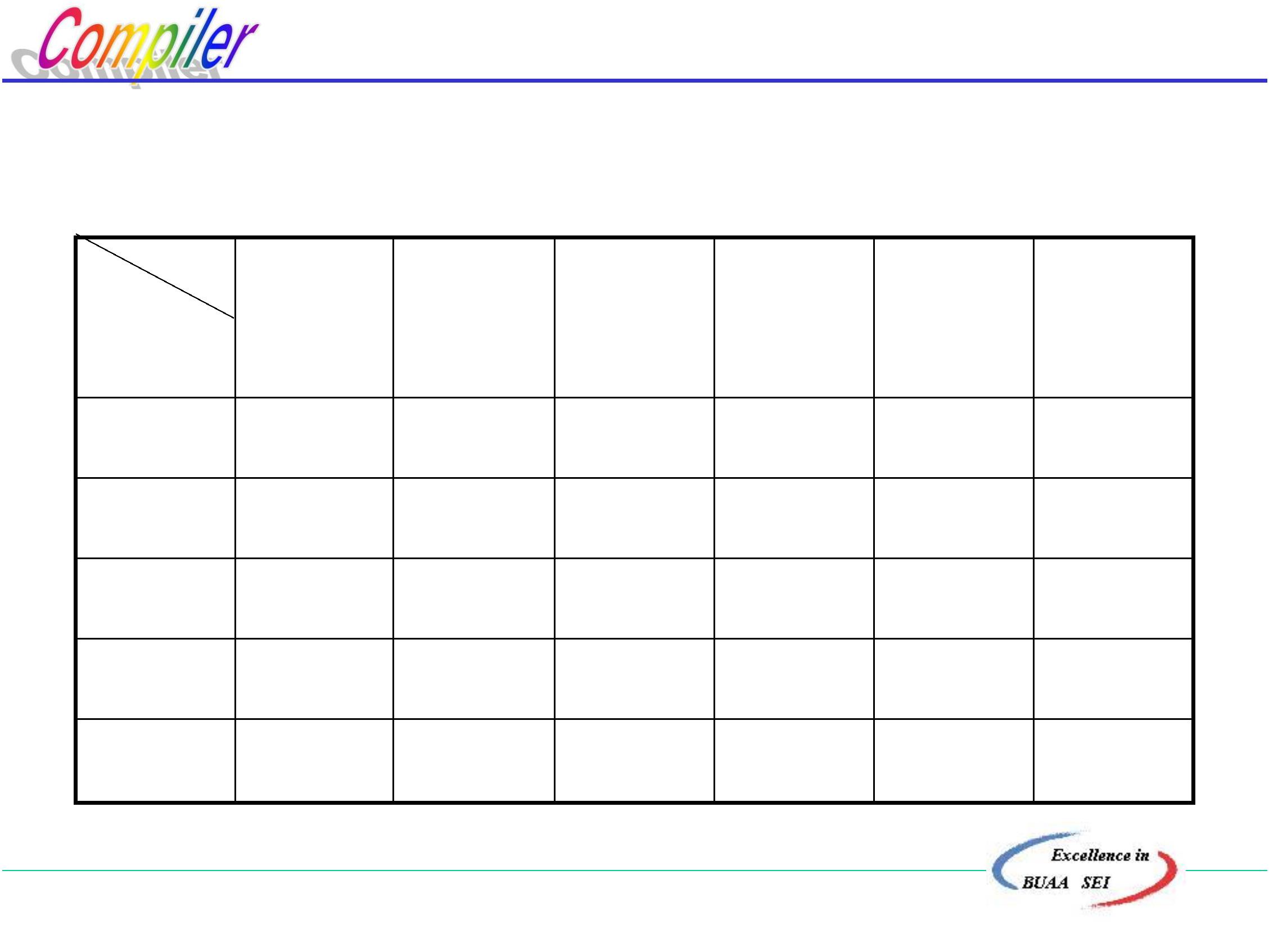
2
) 矩阵元素空白处表示这两个终结符不能相邻,故没有
优先关系
(2) 分析过程
算法:
i+i*i
当栈顶项(或次栈顶项)终结符的优先级大于
栈外的终结符的优先级,则进行归约,否则
移进。
北京航空航天大学计算机学院
8
1

E∷ =E+E | E*E | (E) | i
步骤
符号栈
输入串
i+i*i#
+i*i#
+i*i#
i*i#
优先关系
#<i
动作
移进
归约
移进
移进
归约
1
#
2
3
4
5
#i
i>+
#E
#<+
#E+
#E+i
+<i
*i#
i>*
6
7
8
#E+E
#E+E*
#E+E*i
*i#
i#
#
+<*
*<i
i>#
移进
移进
归约
9
#E+E*E
#E+E
#E
#
#
#
*>#
+>#
归约
归约
接受
10
11
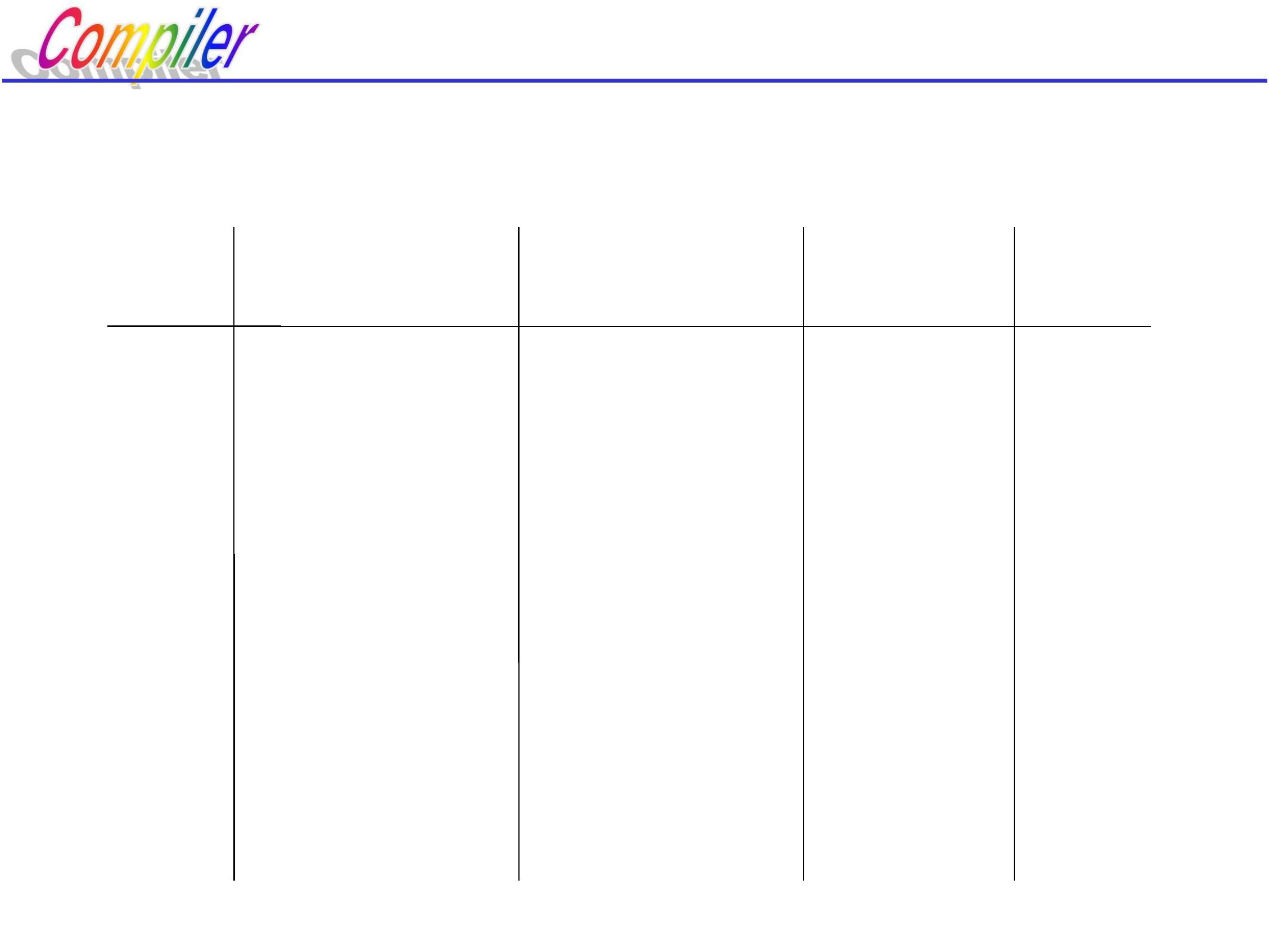
分析过程是从符号串开始,根据相邻终结符之间的优先
关系确定句型的“句柄”,并进行归约,直到识别符号E,最
后分析成功: i+i*i∈L(G[E])
出错情况:
1
2
3
. 相邻终结符之间无优先关系
. 对双目运行符进行归约时,符号栈中无足够项
. 非正常结束状态
北京航空航天大学计算机学院
8
3

重要说明
(1) 上述分析过程不一定是严格的最左归约(即不一定是
规范归约)也就是每次归约不一定是归约当前句型的
句柄,而是句柄的变形,但也是短语。
(2) 文法的终结符优先关系可以用一个矩阵表示,也可以用
两个优先函数来表示:
f—栈内优先函数
g—栈外优先函数
若 a < b 则令 f(a) < g(b)
.
.
.
a = b
a > b
f(a) = g(b)
f(a) > g(b)
北京航空航天大学计算机学院
8
4

根据这些原则,构造出上述文法的优先函数:
算符优先函数值的确定方法
1
2
. 把各算符优先级由小到大定为j=0~n
#
( + * ) i
0
0 1 2 3
. 对于各算符的优先顺序
若为左结合,则 f (op)=2j g (op)=2j-1
若为右结合,则 f (op)=2j g (op)=2j
设m>2n, 则 f (j) = f (i) = m+1
g (j) = g (i) = m,其他为0
f(#) = f(() = g(#) = g()) = 0
北京航空航天大学计算机学院
8
5

+
*
(
) i
0 5 5 0
6 0 6 0
#
f(栈内) 2 4
g(栈外) 1 3
f(+) > g(+)
f(+) < g(*)
f(+) < g(()
:
左结合
先乘后加
先括号内后括号外
:
北京航空航天大学计算机学院
8
6
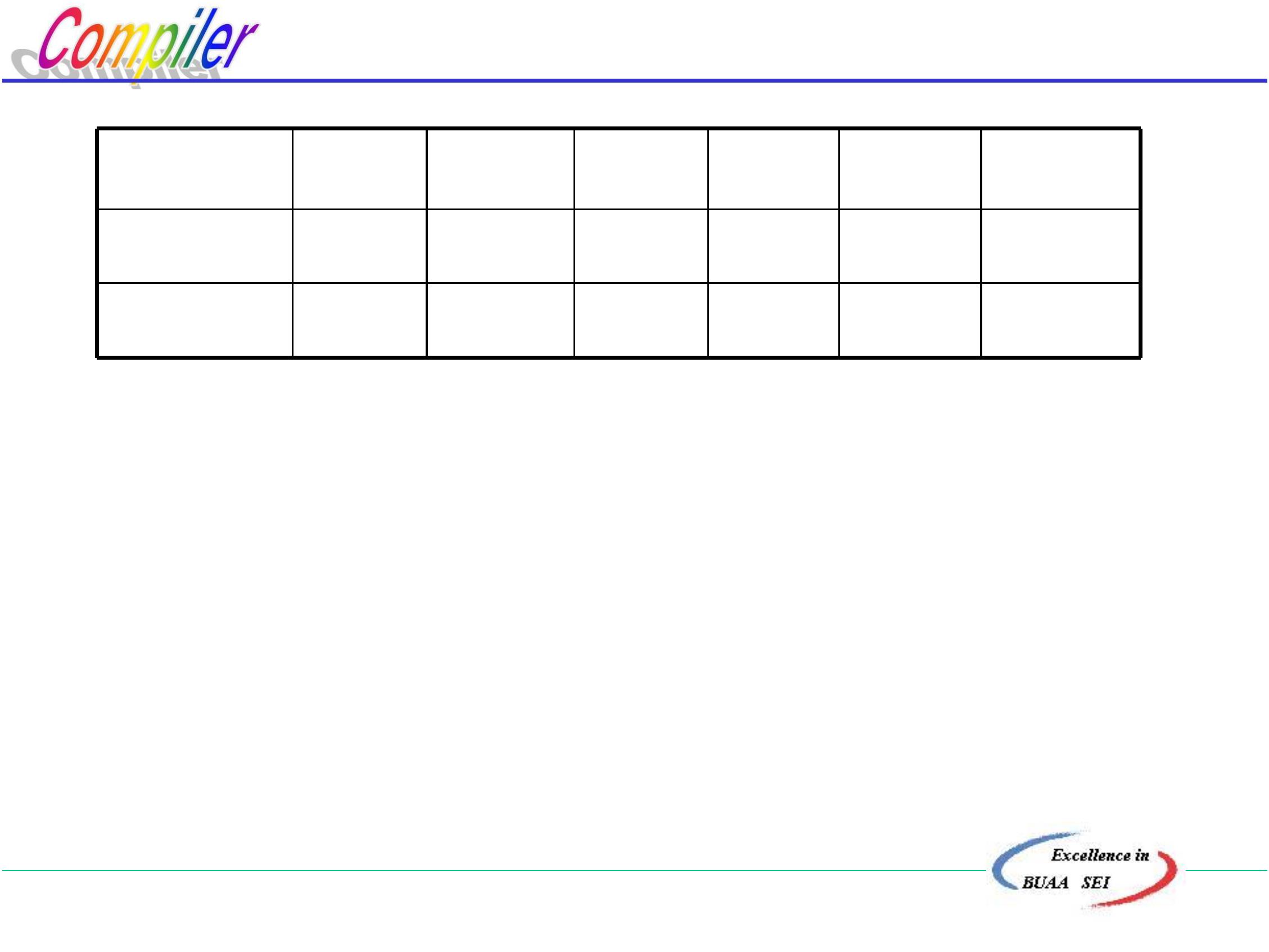
特点:
(1) 优先函数值不唯一
(2) 优点:
•
节省内存空间
若文法有n个终结符,则关系矩阵为n2
而优先函数为2n
•
易于比较:算法上容易实现,数与数比,不必
查矩阵。
(3) 缺点:可能掩盖错误。
北京航空航天大学计算机学院
8
7

(3) 可以设立两个栈来代替一个栈
运算对象栈(OPND)
运算符栈(OPTR)
优点:便于比较,只需将输入符号与运算符栈的
栈顶符号相比较
(4) 使用算符优先分析方法可以分析二义性文法所产生的语言
二义性文法按规范分析,其句柄不唯一
例: G[E]
这是一个二义性文法,
i+i*i有两棵语法树
E∷ =E+E|E*E|(E)|i
Vt={+, *, (, ), i}
北京航空航天大学计算机学院
8
8

E
E
5
5
E
+
E
E
*
E
4
3
1
4
E * E
E + E
i
i
2
3
1
2
i
i
i
i
按规范归约,句柄不唯一, E+E*i 所以整个归约过程就
不唯一,编译所得的结果也将不唯一。
北京航空航天大学计算机学院
8
9
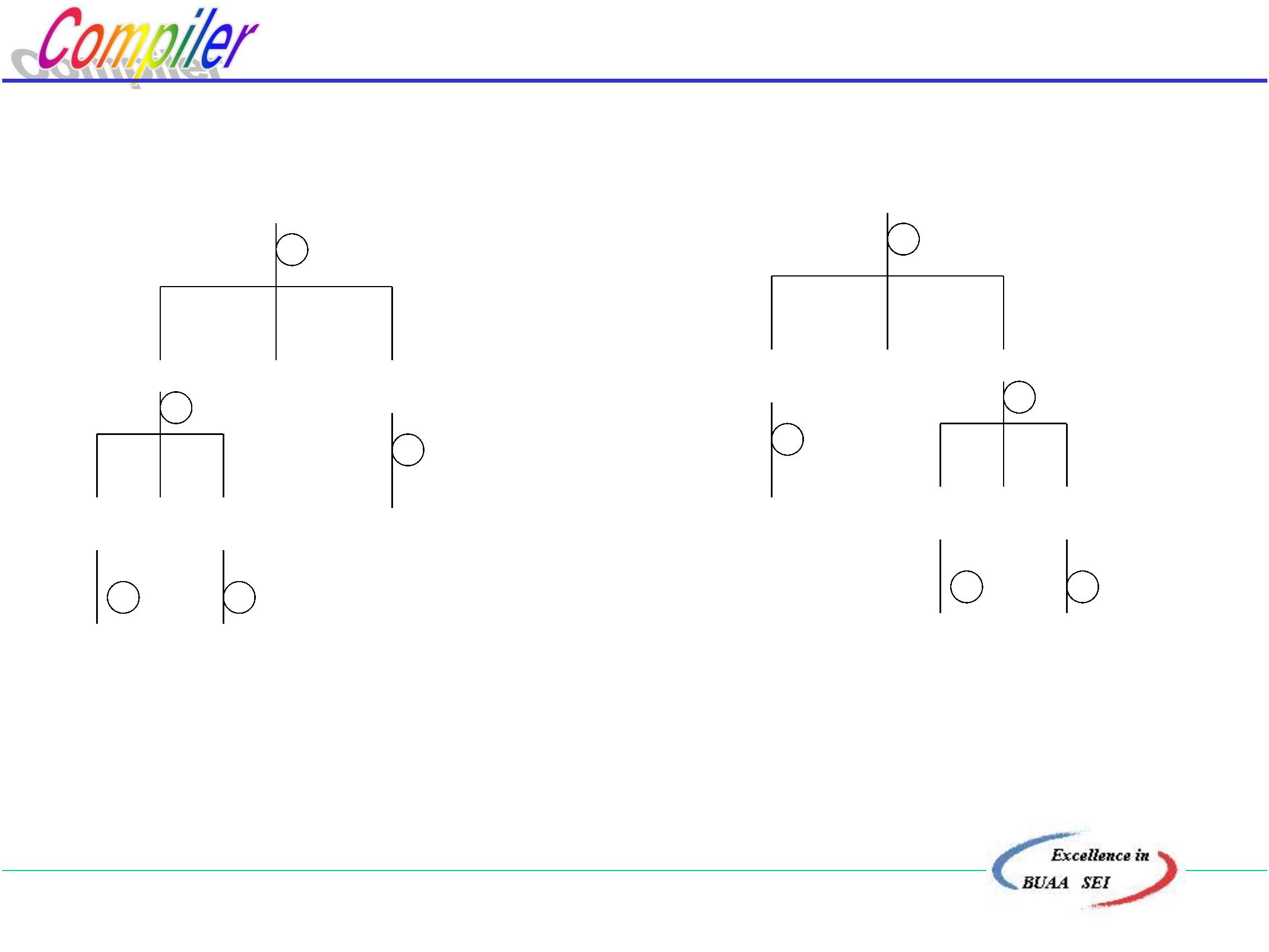
4
.3.3 算符优先分析法的进一步讨论
三个问题:
(1) 算符优先文法(OPG)
(2) 构造优先关系矩阵
(3) 算符优先分析算法的设计
北京航空航天大学计算机学院
9
0

(
1)算符优先文法(OPG-Operator Precedence Grammar)
算符文法(OG)的定义
若文法中无形如U∷ = ·¨VW·¨的规则,这里V,W∈Vn
则称G为OG文法,也就是算符文法。
优先关系的定义
若G是一OG文法,a,b∈Vt , U,V,W∈Vn
分别有以下三种情况:
北京航空航天大学计算机学院
9
1

.
1
2
3
) a=b iff 文法中有形如 U∷ = ·¨ab·¨或U∷ = ·¨aVb·¨
的规则。
.
) a<b iff 文法中有形如 U∷ =·¨aW·¨的规则,其中
W b·¨或W Vb·¨ 。
+
+
.
) a>b iff 文法中有形如 U∷ =·¨Wb·¨的规则, 其中
+
+
W ·¨a或W ·¨aV 。
北京航空航天大学计算机学院
9
2

例:文法G[E]
E::= E + T | T
T::= T * F | F
F::= ( E ) | i
E::=E + T
E => E + T ∴ + >· +
T => T * F ∴ + <· *
T =>F =>( E ) ∴ + (
<
·
T =>F =>i ∴ + i
<
·
F::= ( E )
E => E + T ∴ + ·> )
∴
∴
( )
( <· +
=
·
北京航空航天大学计算机学院
9
3

算符优先文法(OPG)的定义
设有一OG文法,如果在任意两个终结符之间,至多只有
上述关系中的一种,则称该文法为算符优先文法(OPG)
对于OG文法的几点说明:
(1) 运算是以中缀形式出现的
(2) 可以证明,若文法为OG文法,则不会出现两个非
终结符相邻的句型。
(3) 算法语言中的表达式以及大部分语言成分的文法均
是OG文法
北京航空航天大学计算机学院
9
4

(
2)构造优先关系矩阵
.
•
求 “ = ” 检查每一条规则,若有U::=…ab…或
.
U::=…aVb…, 则 a=b
.
.
•
求“ < ”、“ > ” ,需定义两个集合
+
+
FIRSTVT( U ) = {b|Ub…或UVb…,b∈Vt, V∈Vn}
+
+
LASTVT( U ) = {a|U…a或U…aV,a∈Vt, V∈Vn}
北京航空航天大学计算机学院
9
5

.
.
•
求“ < ”、“ > ”:
若文法有规则
W∷ =...aU... ,对任何b, b∈FIRSTVT(U)
.
则有:a < b
若文法有规则
W∷ =...Ub... ,对任何a, a∈LASTVT(U)
.
则有:a > b
北京航空航天大学计算机学院
9
6

构造FIRSTVT(U)的算法
+
+
1
) 若有规则U∷ = b…或U∷ = Vb…(存在Ub…或UVb…)
则b∈FIRSTVT(U)
2
) 若有规则U∷ = V…且b∈FIRSTVT(V), 则b∈FIRSTVT(U)
+
+
+
说明:因为Vb…或VWb…, 所以有UV…b…或
UV… + Wb…
北京航空航天大学计算机学院
9
7

具体方法如下:
设一个栈S和一个二维布尔数组F
F[U,b]=TRUE iff b∈FIRSTVT(U)
PROCEDURE INSERT(U,b)
IF NOT F[U,b] THEN
BEGIN
F[U,b]:=TRUE;
把(U,b)推进S栈 /* b∈FIRSTVT(U) */
END
BEGIN {main}
FOR 每个非终结符号U和终结符b DO
F[U,b]:=FALSE;
FOR 每个形如U::=b…或U::=Vb… 的规则 DO
INSERT(U,b);
北京航空航天大学计算机学院
9
8

WHILE S栈非空 DO
BEGIN
把S栈的栈顶项弹出,记为 (V,b) /* b∈FIRSTVT(V)*/
FOR 每条形如U::=V…的规则 DO
INSERT (U,b); /* b∈FIRSTVT(U)*/
END OF WHILE
END
上述算法的工作结果是得到一个二维的布尔数组F,从F
可以得到任何非终结符号U的FIRSTVT
FIRSTVT(U) = { b | F[U,b] = TRUE }
北京航空航天大学计算机学院
9
9

构造LASTVT(U)的算法
1
2
. 若有规则U::=…a或U::=…aV,则a∈LASTVT(U)
. 若有规则U::=…V,且a∈LASTVT(V), 则a∈LASTVT(U)
设一个栈ST,和一个布尔数组B
PROCEDURE INSERT(U,a)
IF NOT B[U,a] THEN
BEGIN
B[U,a]::=TRUE; 把(U,a)推进ST栈;
END;
北京航空航天大学计算机学院
1
00

BEGIN
FOR 每个非终结符号U和终结符号a DO
B[U,a]:=FALSE;
FOR 每个形如U::=…a或U::=…aV的规则 DO
INSERT (U,a);
WHILE ST栈非空 DO
BEGIN
把ST栈的栈顶弹出,记为(V,a);
FOR 每条形如U::=…V的规则 DO
INSERT(U,a);
END OF WHILE;
END;
北京航空航天大学计算机学院
1
01

构造优先关系矩阵的算法
FOR 每条规则U::=x1x2…xn DO
FOR i:=1 TO n-1 DO
BEGIN
IF xi和xi+1均为终结符,THEN 置 xi=. xi+1
IF i≤n-2,且xi和xi+2都为终结符号但
xi+1为非终结符号 THEN 置 xi=.xi+2
IF xi为终结符号,xi+1为非终结符号 THEN
FOR FIRSTVT(xi+1)中的每个b DO
.
置xi<b
IF xi为非终结符号,xi+1为终结符号 THEN
FOR LASTVT(xi)中的每个a DO
置a>. xi+1
END
北京航空航天大学计算机学院
1
02

(
3)算符优先分析算法的实现
先定义优先级,在分析过程中通过比较相邻运算符之
间的优先级来确定句型的“句柄”并进行归约。
[
定义] 素短语:文法G的句型的素短语是一个短语,
它至少包含有一个终结符号,并且除它自身以外不再
包含其他素短语。
北京航空航天大学计算机学院
1
03
例: 文法G[E]
E::=E+T|T
文法的语法树:
T::=T*F|F
F::=(E)|i
求句型T+T*F+i 的素短语
E
+
E
T
F
短语:T+T*F+i, T+T*F
T(最左), T*F, i
E + T
其中T不包含终结符,T是句柄
而T+T*F+i和T+T*F包含其他
素短语。
i
T T * F
只有T*F和i为素短语,其中T*F为最左素短语,而该句型句
柄为T。
北京航空航天大学计算机学院
1
04
句型:T + T + i
短语:T+T+i
T +T
T
i
句柄:T
素短语:T+T, i
北京航空航天大学计算机学院
1
05
算符优先分析法如何确定当前句型的最左素短语?
设有OPG文法句型为:
#
N1a1N2a2…NnanNn+1#
其中Ni为非终结符(可以为空), ai为终结符
定理:一个OPG句型的最左素短语是满足下列条件的
最左子串:aj-1Njaj…NiaiNi+1ai+1
其中 aj-1<. aj
.
.
.
.
aj=aj+1, aj+1= aj+2 ,…, ai-2= ai-1, ai-1= ai
.
ai> ai+1
北京航空航天大学计算机学院
1
06

根据该定理,要找句型的最左素短语就是要找满足
上述条件的最左子串。
Njaj…NiaiNi+1
注意:出现在aj左端和ai右端的非终结符号一定
属于这个素短语,因为运算是中缀形式给
出的(OPG文法的特点)NaNaNaN NaWaN
例: 文法G[E]
E::=E+T|T
T::=T*F|F
F::=(E)|i
分析文法的句型T+T*F+i
北京航空航天大学计算机学院
1
07

步骤
句型
关系
. . . .
. . .
最左子串 归约符号
.
1
2
3
4
#T+T*F+i# #<+<*>+<i># T*F
T
E
F
E
.
#T+T+i#
#E+i#
#<+>+<i># T+T
.
. .
#<+<i>#
i
.
.
#E+F#
#<+>#
E+F
可以看出:
1
2
3
. 每次归约最左子串,确实是当前句型的
最左素短语(语法树)
. 归约的不都是真句柄(仅i归约为F是句柄,
但它是最左素短语)
. 没有完全按规则进行归约,因为素短语不一
定是简单短语
北京航空航天大学计算机学院
1
08
E
E
E
+
T
F
+
E
T
F
E + T
E
+
T
T * F
i
T
i
T
T
.
. . . .
. . . .
#
<+<*>+<i>#
#<+>+<i>#
E
E
+
T
F
E
+
T
E
FF
.
.
.
. .
i
#<+>#
#
<+<i>#
北京航空航天大学计算机学院
1
09
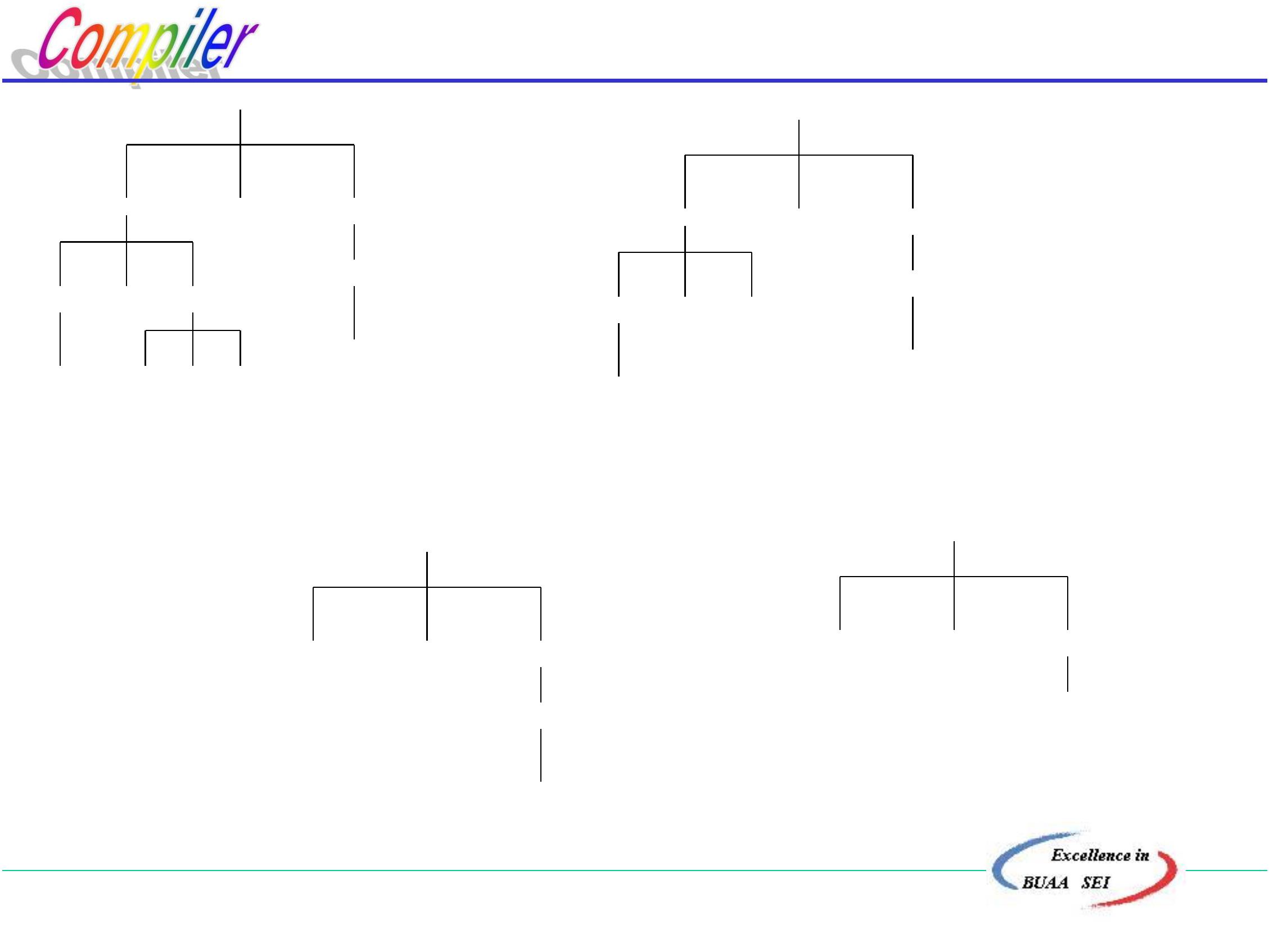
算符优先分析法的实现:
基本部分是找句型的最左子串(最左素短语)
并进行归约。
输入串
#
分析程序
符号栈
#
优先关系矩阵
当栈内终结符的优先级<=栈外的终结符的优先级时,移
进;栈内终结符的优先级>栈外的终结符的优先级时,表
明找到了素短语的尾,再往前找其头,并进行归约。
北京航空航天大学计算机学院
110
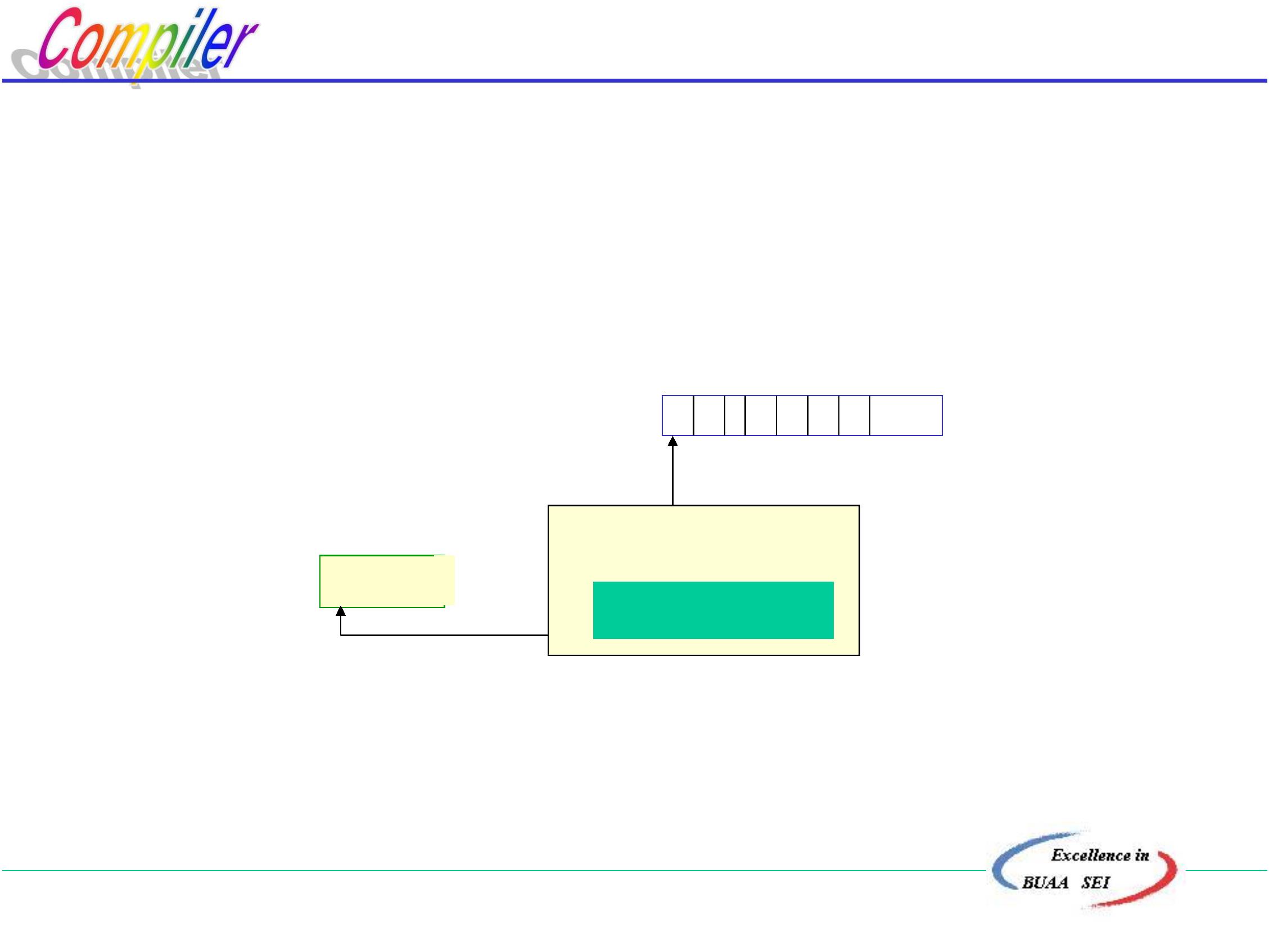
4
.3.4 LR分析法
、概述
1
什么是LR分析:从左到右扫描(L)自底向上进行归约(R)
(是规范归约), 是自底向上分析方法的高度概括和集中
历史 + 展望 + 现状 => 句柄
(1) LR分析法的优缺点:
1
2
3
4
5
) 适合文法类足够大
) 分析效率高
) 报错及时
) 可以自动生成
) 手工实现工作量大
北京航空航天大学计算机学院
111

(2) LR分析器有三部分: 状态栈 分析表 控制程序
输入串
#
状态栈:放置分析
器状态和文法符号。
状态栈
控制程序
#
分析表
分析表:由两个矩阵组成,其功能是指示分析器的动作,
是移进还是归约,根据不同的文法类要采用不同
的构造方法。
控制程序:执行分析表所规定的动作,对栈进行操作。
北京航空航天大学计算机学院
112
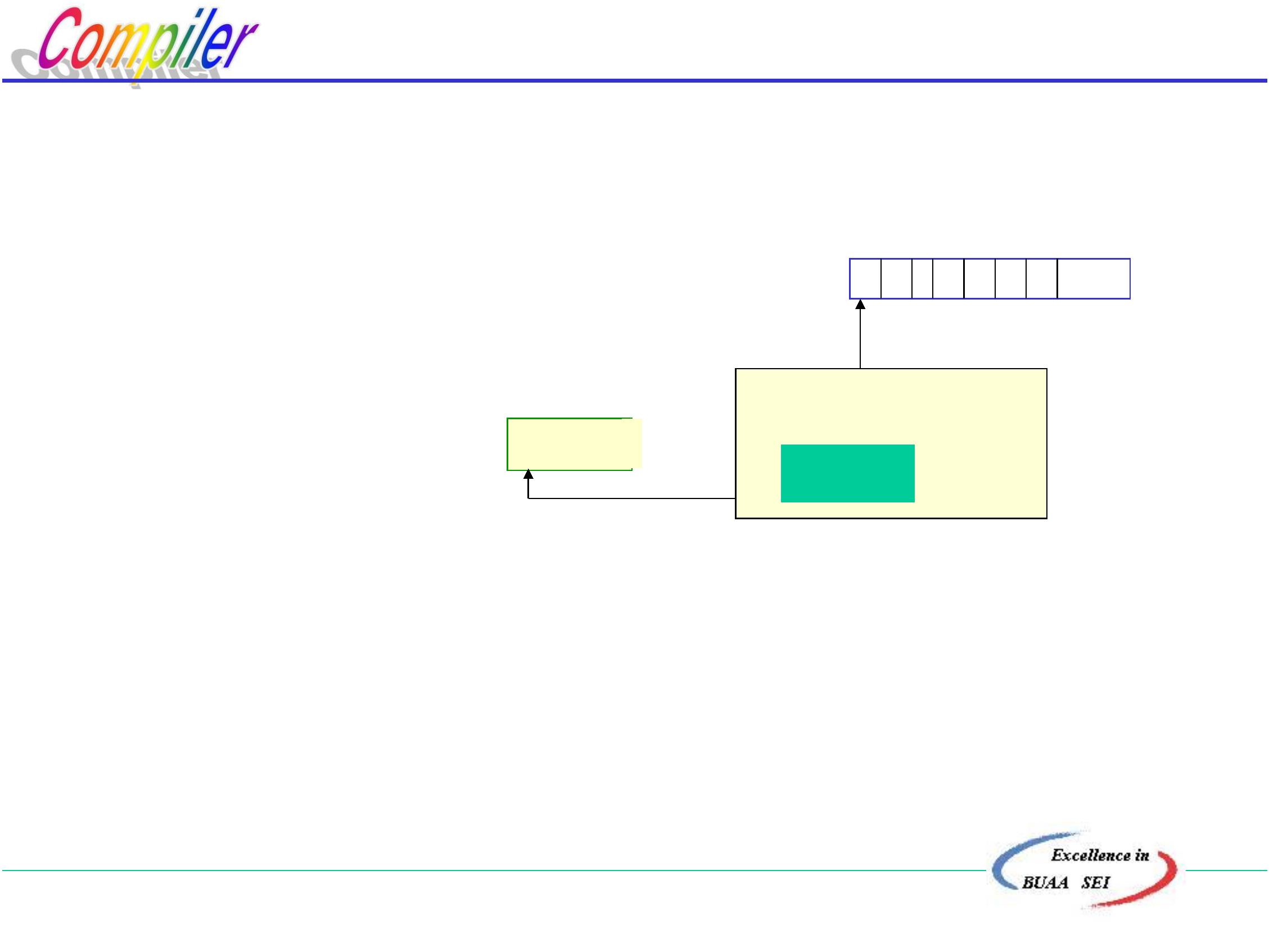
(3) 分析表的种类
a) SLR分析表(简单LR分析表)
构造简单,最易实现,大多数上下文无关文法都
可以构造出SLR分析表,所以具有较高的实用
价值。使用SLR分析表进行语法分析的分析器
叫SLR分析器。
b) LR分析表(规范LR分析表)
适用文法类最大,几乎所有上下文无关文法都能
构造出LR分析表, 但其分析表体积太大,实
用价值不大。
北京航空航天大学计算机学院
113

c) LALR分析表(超前LR分析表)
这种表适用的文法类及其实现上难易在上面
两种之间,在实用上很吸引人。
使用LALR分析表进行语法分析的分析器叫LALR分析器。
例:UNIX----YACC
文法规则文件
YACC源文件
某语言的
LALR分析器
YACC
北京航空航天大学计算机学院
114
(4) 几点说明
1
2
3
. 三种分析表对应三类文法
. 一个SLR文法必定是LALR文法和LR文法
. 仅讨论SLR分析表的构造方法
北京航空航天大学计算机学院
115

2
、LR分析
(1)逻辑结构
输入串:#a a ... a ... a #
1
2
i
n
状态栈
S x S x
分 状
析 态 LR分析器
动 转
作 移
表 表
#
......
x S
m m
0
1 1 2
控
制
程
序
北京航空航天大学计算机学院
116
S S ...... Sm
#
S x S x
......
x S
m m
0 1
0
1 1 2
#
x1x2..... xm
S0,S1,…,Sm 状态
状态栈:
S0---初始状态
Sm---栈顶状态
栈顶状态概括了从分析开始到该状态的
全部分析历史和展望信息。
符号串: X X ..... X
m
1
2
为从开始状态(S0)到当前状态(Sm)所识别
的规范句型的活前缀。
北京航空航天大学计算机学院
117
规范句型: 通过规范归约得到的句型。
规范句型前缀: 将输入串的剩余部分与其连接起来就
构成了规范句型。
如: x1x2..... x a ... a 为规范句型
m
i
n
活前缀: 若分析过程能够保证栈中符号串均是规范句型
的前缀,则表示输入串已分析过的部分没有语
法错误,所以称为规范句型的活前缀。
北京航空航天大学计算机学院
118

规范句型的活前缀:
对于句型αβt, β表示句柄,如果αβ= u1u2…ur
那么符号串u1u2…ui(1≤i≤r)即是句型αβt的活前
缀
例: 有文法G[E]: E→T|E+T|E-T
T→i|(E)
拓广文法G’[S]: S→E#
E→T|E+T|E-T
T→i|(E)
句型E-(i+i) #
活前缀:E, E-, E-(, E-(i 是句型E-(i+i)# 的活前缀。
北京航空航天大学计算机学院
119

•
分析表
a. 状态转移表 (GOTO表)
GOTO表
符号
E T F i + * ( ) #
状态
S
S
S
:
0
1
2
是一个矩阵:
行---分析器的状态
列---文法符号
S
n
北京航空航天大学计算机学院
1
20
GOTO表
符号
E T F i + * ( ) #
状态
S
S
S
:
0
1
2
S
n
GOTO[Si-1, xi]=Si
Si-1---当前状态(栈顶状态)
xi--- 新的栈顶符号
Si----新的栈顶状态(状态转移)
#
S x S x x S x S
......
1 1 2 i-1 i-1 i i
0
Si需要满足条件是:
若X1 X2…. Xi-1是由S0到Si-1所识别的规范句型的
活前缀,则X1 X2…. Xi是由S0到Si所识别的规范句型
的活前缀。
北京航空航天大学计算机学院
1
21
通过对有穷自动机的了解, 可以看出:
状态转移函数GOTO是定义了一个以文法符
号集为字母表的有穷自动机,该自动机识别文法所
有规范句型的活前缀。
M=(S, V, GOTO, S0, Z )
xi-1
Si-1
S
2
x
2
x
i
S
1
x
1
S
i
S
0
北京航空航天大学计算机学院
1
22
b. 分析动作表(ACTION表)
ACTION表
输入符号a
状态s
+
*
i
( ) #
S
S
S
:
0
1
2
S
n
ACTION[Si,a] = 分析动作 a∈Vt
北京航空航天大学计算机学院
1
23
分析动作:
(1) 移进(shift)
ACTION[Si,a] = s
动作: 将a推进栈,并设置新的栈顶状态Sj
= GOTO[Si,a],将指针指向下一个
输入符号
S
j
(2) 归约(reduce)
ACTION[Si,a] = rd
d:文法规则编号 (d) A→β
动作: 将符号串β(假定长度为n)连同状态从栈内
弹出, 把A推进栈, 并设置新的栈顶状态Sj
S
j
= GOTO[Si-n,A]
北京航空航天大学计算机学院
1
24

(3) 接受(accept)
ACTION[Si,#]=accept
(4) 出错(error)
ACTION[Si,a]=error
北京航空航天大学计算机学院
1
25

控制程序: (Driver Routine)
1
2
、 根据栈顶状态和现行输入符号,查分析动
作表(ACTION表),执行由分析表所规定
的操作;
、并根据GOTO表设置新的栈顶状态(即实现
状态转移)。
北京航空航天大学计算机学院
1
26

(
2) LR分析过程
例:文法G[E]
(1) E ::= E+T
(2) E ::= T
(3) T ::= T*F
(4) T ::= F
(5) F ::= (E)
(6) F ::= i
该文法是SLR文法,故可以构
造出SLR分析表(ACTION表
和GOTO表)
北京航空航天大学计算机学院
1
27

GOTO表
文法符号
状态
E
1
T
2
F
i
+
6
*
(
)
0
1
2
3
4
5
6
7
8
9
1
(S0)
(S1)
3
5
4
(S2)
(S3)
(S4)
(S5)
(S6)
(S7)
(S8)
(S9)
0(S10)
7
8
2
9
3
5
4
3
5
5
4
4
10
6
11
7
11(S11)
北京航空航天大学计算机学院
1
28
ACTION 表
GOTO 表
输入符号
状态
北京航空航天大学计算机学院
1
29
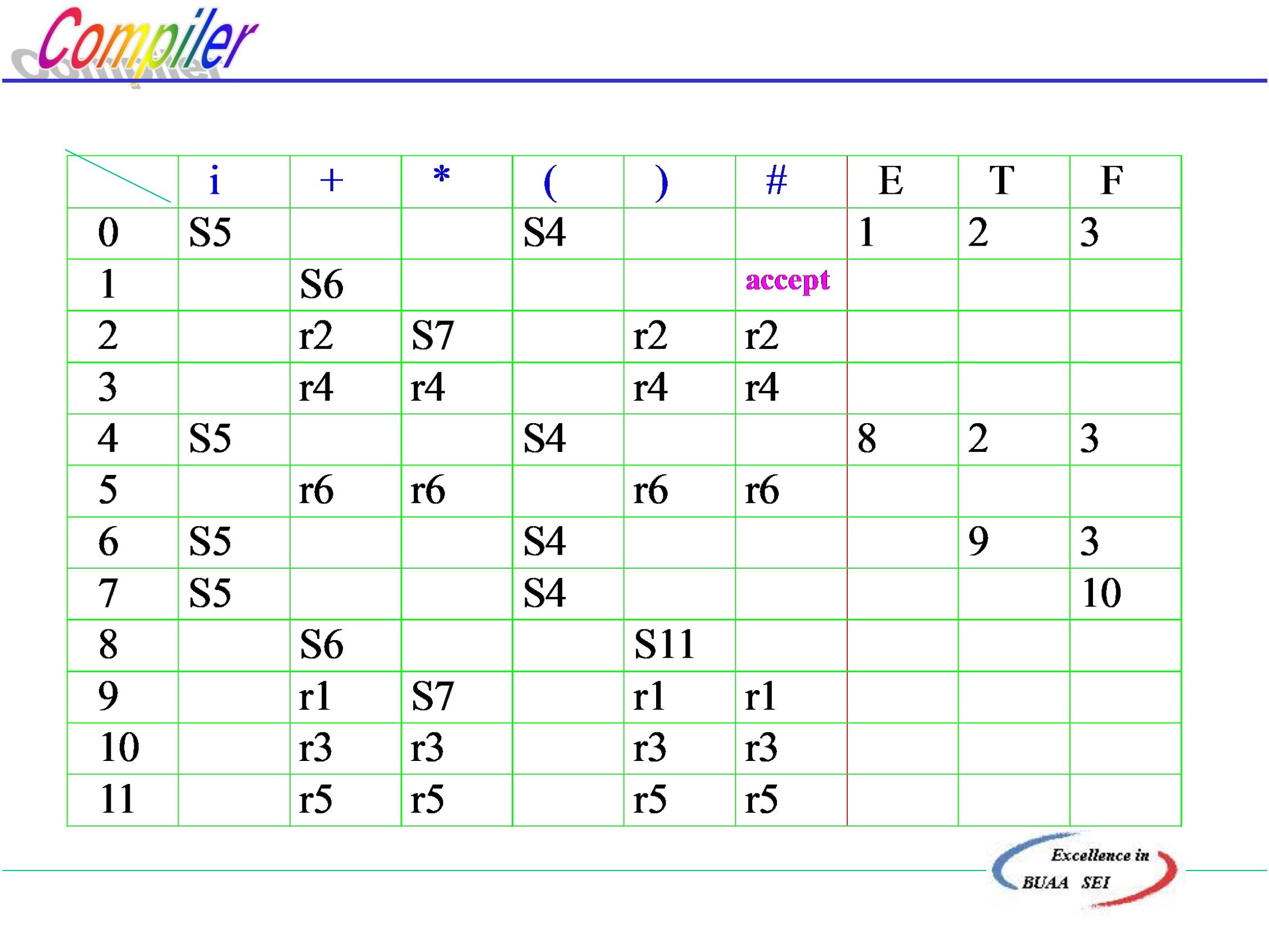
分析过程 i*i+i
步骤 状态栈
符号
#
输入串
i*i+i#
*i+i#
*i+i#
*i+i#
i+i#
动作
初始化
1
2
3
4
5
6
7
#0
#0i5
#i
S
#0F3
#0T2
#0T2*7
#F
#T
#T*
r6
r4
S
#0T2*7i5 #T*i
#0T2*7F10 #T*F
+i#
S
+i#
r6
北京航空航天大学计算机学院
1
30

8
9
#0T2
#T
#E
+i#
+i#
i#
#
r3
#0E1
r2
1
0
#0E1+6
#E+
S
11
#0E1+6i5 #E+i
#0E1+6F3 #E+F
#0E1+6T9 #E+T
S
1
2
3
4
5
#
r6
1
1
1
#
r4
#0E1
#E
#E
#
r1
accept
北京航空航天大学计算机学院
1
31

由分析过程可以看到:
E
8
(1) 每次归约总是归约当前句型的句柄,是
规范归约。
E + T
7
5
(算符优先分析归约最左素短语)
T
F
4
6
i
T * F
(2) 分析的每一步栈内符号串均是规范句
型的活前缀,与输入串的剩余部分构成
规范句型。
2
3
i
F
1
i
北京航空航天大学计算机学院
1
32
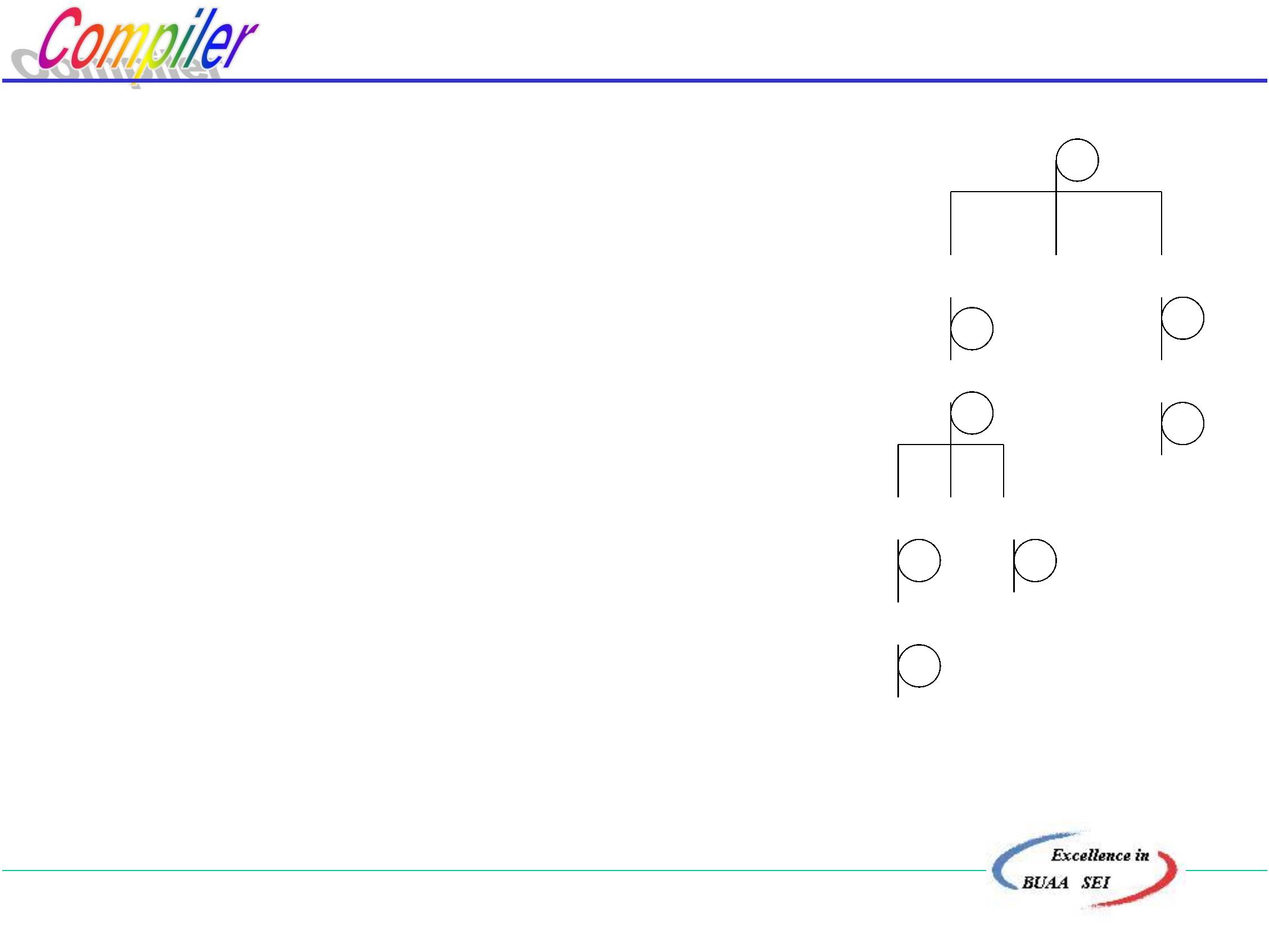
3
、构造SLR分析表
构造LR分析器的关键是构造其分析表。
构造LR分析表的方法是:
(
1)根据文法构造识别规范句型活前缀的有穷
自动机DFA
(
2)由DFA构造分析表
北京航空航天大学计算机学院
1
33

(1) 构造DFA
DFA 是一个五元式
1
M=(S, V, GOTO, S0, Z)
S:有穷状态集
在此具体情况下,S = LR(0) ,项目集规范族。
项目集规范族:其元素是由项目所构成的集合。
V:文法字汇表
S0:初始状态 S0∈S
北京航空航天大学计算机学院
1
34

GOTO: 状态转移函数
GOTO[Si,X]=Sj
S
i
,Sj∈S
S
i
,Sj为项目集合
X∈Vn∪Vt
表示当前状态Si面临文法符号为X时,应将状态转移到Sj
Z:终态集合 Z = S-{S0}
即除S0以外,其余全部是终态
构造DFA:
一、确定S集合,即LR(0)项目集规范族,
同时确定S0
二、确定状态转移函数GOTO
北京航空航天大学计算机学院
1
35

2
构造LR(0)的方法
LR(0) 是DFA的状态集,其中每个状态又都是项目的集合。
项目:文法G的每个产生式(规则)的右部添加一个圆点
就构成一个项目。
例:产生式:A→XYZ
项 目: A→.XYZ
A→X.YZ
A→XY.Z
A→XYZ.
项目的直观意义: 指明在分
析过程中的某一时刻已经归
约的部分和等待归约部分。
产生式:A→ε
项 目: A→.
北京航空航天大学计算机学院
1
36

构造LR(0)的方法(三步)
) 将文法拓广
1
目的:使构造出来的分析表只有一个接受状态,这是
为了实现的方便。
方法:修改文法,使识别符号的规则只有一条。
G[E]
E→···
E→···
G'[E']
E'→E
E→···
E→···
拓广
·
··
·
··
L(G(E))=L(G'[E'])
北京航空航天大学计算机学院
1
37
2
) 根据文法列出所有的项目
3
) 将有关项目组合成集合,即DFA中的状态;
所有状态再组合成一个集合,即LR(0)项目集规范族
通过一个具体例子来说明LR(0)的构造以及DFA
的构造方法。
例:G[E]
E→E+T | T
T→T*F | F
F→(E) | i
北京航空航天大学计算机学院
1
38

1
2
将文法拓广为G’[E’]
(0) E’→E
(1) E→E+T
(2) E→T
(4) T→F
(5) F→(E)
(6) F→i
(3) T→T*F
列出文法的所有项目
(1) E’→.E
(2) E’→E.
(6) E→E+T. (11)T→T*.F (16)F→(.E)
(7) E→.T (12)T→T*F. (17)F→(E.)
(3) E→.E+T (8) E→T.
(13)T→.F
(18)F→(E).
(19)F→.i
(4) E→E.+T (9) T→.T*F (14)T→F.
(5) E→E+.T (10) T→T.*F (15)F→.(E) (20) F→i.
北京航空航天大学计算机学院
1
39

3
将有关项目组成项目集,所有项目集构成的集合即为LR(0)
为实现这一步,先定义:
•
•
项目集闭包closure
状态转移函数GOTO
北京航空航天大学计算机学院
1
40

A.项目集闭包closure的定义和计算:
令I是文法G’的任一项目集合,定义closure(I)为项目
集合I的闭包,可用一个过程来定义并计算closure(I):
Procedure closure(I);
begin
将属于I的项目加入closure(I);
repeat
for closure(I)中的每个项目A→α.Bβ(B∈Vn) do
将B→.r(r∈V* )加入closure(I)
until closure(I)不再增大
end
北京航空航天大学计算机学院
1
41

B. 状态转移函数GOTO的定义:
GOTO(I,X) = closure(J)
I:项目集合
X:文法符号,X∈V
J:项目集合
J = { 任何形如A→αX.β的项目| A→α.Xβ∈I }
closure(J):项目集J的闭包, 仍是项目集合
所以,GOTO(I,X) = closure(J) 的直观意义是:
它规定了识别文法规范句型活前缀的DFA, 从状态
I(项目集)出发,经过X弧所应该到达的状态(项目集合)
北京航空航天大学计算机学院
1
42

例:
I={E’→E. , E→E.+T} 求GOTO(I , + ) =?
GOTO(I , +) = closure(J)
∵
∴
J = {E→E+.T}
GOTO(I , +) = {E→E+.T , T→.T*F , T→.F ,
F→.(E) , F→.i }
北京航空航天大学计算机学院
1
43

LR(0)和GOTO的构造算法:
G'→LR(0), GOTO
Procedure ITEMSETS(G')
begin
LR(0) := {closure({E'→.E})};
repeat
for LR(0)中的每个项目集I和G'的每个符号X do
if GOTO(I , X)非空,且不属于LR(0)
then 把GOTO(I , X)放入LR(0)中
until LR(0)不再增大
end
北京航空航天大学计算机学院
1
44

例:求G'[E']的LR(0)
G'[E']共有20个项目
V={E, T, F, i, +, *, (, )}
LR(0)={I0,I1,I2,…I11} 由12个项目集组成:
I
0
:
E'→.E
E→.E+T
E→.T
closure({E’→.E}) = I0
T→.T*F
T→.F
F→.(E)
F→.i
GOTO(I0,E) = closure({E’→E.
E→E.+T})
I1: E'→E.
E→E.+T
=
I
1
北京航空航天大学计算机学院
1
45
I
2
:
E→T.
GOTO(I0,T) = closure({E→T. T→T.*F}) = I2
T→T.*F
T→F.
F→(.E)
E→.E+T
E→.T
T→.T*F
T→.F
GOTO(I0,F) = closure({T→F.}) = I3
GOTO(I0,() = closure({F→(.E)}) = I4
I
I
3
:
:
4
F→.(E)
F→.i
I5: F→i.
GOTO(I0,i) =closure({F→i.})= I5
GOTO(I0,*) =φ
GOTO(I0,+) =φ
GOTO(I0,)) =φ
北京航空航天大学计算机学院
1
46
I
6
:
E→E+.T
T→.T*F
T→.F
GOTO(I1,+) = closure({E→E+.T}) = I6
GOTO(I1,其他符号)为空
F→.(E)
F→.i
I
7
:
T→T*.F
F→.(E)
F→.i
GOTO(I2,*) = closure({T→T*.F}) = I7
GOTO(I2,其他符号)为空
GOTO(I3,所有符号)为空
北京航空航天大学计算机学院
1
47
I
8
:
F→(E.)
E→E.+T
GOTO(I4,E) = closure({F→(E.),E→E.+T}) = I8
GOTO(I4,T) = I2 ∈LR(0)
GOTO(I4,F) = I3 ∈LR(0)
GOTO(I4,() = I4 ∈LR(0)
GOTO(I4,i) = I5 ∈LR(0)
GOTO(I4,+) =φ
GOTO(I4,*) =φ
GOTO(I4,)) =φ
GOTO(I5,所有符号) =φ
I
9
:
E→E+T.
T→T.*F
GOTO(I6,T) = closure({E→E+T.,T→T.*F}) = I9
GOTO(I6,F) = I3
GOTO(I6,() = I4
GOTO(I6,i) = I5
北京航空航天大学计算机学院
1
48

I10:T→T*F. GOTO(I7,F) = closure({T→T*F .}) = I10
GOTO(I7,() = I4
GOTO(I7,i) = I5
I11:F→(E). GOTO(I8,)) =closure({F→(E) .}) = I11
GOTO(I8,+) = I6
GOTO(I9,*)= I7
GOTO(I10,所有符号) =φ, GOTO(I11,所有符号) =φ
北京航空航天大学计算机学院
1
49

3
构造DFA
M = (S, V, GOTO, S0, Z)
S = {I0, I1, I2, …, I11} = LR(0)
V = {+, *, i, (, ), E, T, F}
GOTO(Im , X) = In
S
0
= I0
Z = S-{I0} = {I1, I2, …, I11}
M的图解表示如下:
北京航空航天大学计算机学院
1
50

+
T
I
I
I
1
5
3
4
2
I
I
6
i
I
9
E
i
+
i
i
*
start
F
F
I
0
(
8
I11
(
F
I
(
)
E
T
I
7
I10
T
I
(
F
*
北京航空航天大学计算机学院
1
51
关于自动机的说明:
除I0以外,其余状态都是终态,从I0到每一状态的每条
1
路径都识别和接受一个规范句型的活前缀
如对文法句子i+i*i 进行规范归约
所得到的规范句型的活前缀都可
以由该自动机识别,如:
I0~I1 识别规范句型的活前缀E(+i*i)
I0~I6 识别规范句型的活前缀E+(i*i)
I0~I7 识别规范句型的活前缀E+T*(i)
I0~I9 识别规范句型的活前缀E+T(*i)
I0~I10 识别规范句型的活前缀E+T*F
北京航空航天大学计算机学院
1
52

2
3
状态中每个项目对该状态能识别的活前缀都是
有效的。
有效项目定义:若项目A→β1 .β2 对活前缀αβ1
有效,其条件是存在规范推导
*
E’αAw αβ1β2 w
其中α,β1,β2 ∈ V *, w ∈ Vt *
注意:项目中圆点前的符号串成为活前缀的后缀
有效项目能预测分析的下一步动作:
E→E+T. 表示已将输入串归约为E+T,下一步应
该将E+T归约为E
*
E’ (E)(E+T)
T→T.*F 表示已将输入串归约为T,下一步动作
是移进输入符号*
注意:经移进或归约后,在栈内仍是规范句型的活前缀
北京航空航天大学计算机学院
1
53
4
DFA中的状态,既代表了分析历史又提供了展望信息
每条规范句型的活前缀都代表了一个确定的
的规范归约过程,故由状态可以代表分析历史。
由于状态中的项目都是有效项目,所以提供了
下一步可能采取的动作。
历史+展望+现实 句柄
北京航空航天大学计算机学院
1
54

(
2)由DFA构造SLR分析表
*
GOTO表在求LR(0)时已求出
GOTO表
文法符号
E
1
T
2
F
3
i
5
+
*
(
4
)
状态
0
1
2
3
4
5
6
7
8
9
1
(S0)
(S1)
(S2)
(S3)
(S4)
(S5)
(S6)
(S7)
(S8)
(S9)
0(S10)
6
7
8
2
9
3
5
4
3
10
5
5
4
4
6
11
7
11(S11)
北京航空航天大学计算机学院
1
55
*
求ACTION表
设k为状态编号,E为原文法识别符号,
E’为扩充文法识别符号
1
、求出文法每个非终结符的FOLLOW集合
2
、若项目A→α.aβ∈k,且a ∈Vt ,则置
ACTION[k,a] = s (移进)
北京航空航天大学计算机学院
1
56

3
、若项目A→α.∈k, 那么对输入符号a,若
a∈FOLLOW(A),则置ACTION[k,a]=rj
其中A→ α为文法G’的第j个产生式。
4
、若项目E’→E.∈k, 则置
ACTION[ k , # ] =accept
5
、ACTION表中不能用步骤2~4填入信息的
空白格,均置error
北京航空航天大学计算机学院
1
57

在状态中可有三种类型的项目,其中只有两种有移
进或归约动作:
A→α.aβ a∈Vt
A→α.
移进项目 分析动作:移进
归约项目 分析动作:归约
A→α.Bβ B∈Vn 待约项目 无动作
根据上述算法,可以构造出文法G’[E’]的ACTION
北京航空航天大学计算机学院
1
58

对文法G’[E’]
k=2 (I2)
有效项目 E→T.
k=1 (I1)
E’→E.
k=0 (I0)
E’→.E
T→T.*F
E→E.+T
E→.E+T
FOLLOW(E)={#, +, )} FOLLOW(E’)={#} E→.T
T→.T*F
T→.F
F→.(E)
F→.i
根据算法造出的ACTION表为:
北京航空航天大学计算机学院
1
59

ACTION表
输入符号a
状态s
i
+
*
(
)
#
0
1
2
3
4
5
6
S
5
S
4
S
6
accpet
r
2
S
7
r
2
r
2
7
8
9
1
0
1
1
北京航空航天大学计算机学院
1
60
两点说明:
1
. 由DFA构造出的SLR分析表,在造表时, 只需
向前看一个符号就能确定分析的动作是移进还
是归约,所以称为SLR(1)分析表,简称SLR分
析表,使用SLR分析表的分析器叫SLR分析器。
. 对文法G,若应用上述算法所造出的分析表
具有多重定义入口,分析动作不唯一, 则文法
G就不是SLR的,需要用别的方法来构造分析表。
2
北京航空航天大学计算机学院
1
61

复 习
+
自顶向下分析法 Z S
S∈L[Z]
语法分析方法:
+
自底向上分析法 SZ
(一) 自顶向下分析
概述自顶向下分析的一般过程
1
左递归问题 消除左递归的方法
存在问题
无回溯的条件
改写文法
回溯问题
超前扫描
北京航空航天大学计算机学院
1
62
两种常用方法:
2
a) 改写文法,消除左递归,回溯
b) 写递归子程序
(1) 递归子程序法
LL(1)分析器的逻辑结构及工作过程
LL(1)分析表的构造方法
1
2
3
.构造FIRST集合的算法
.构造FOLLOW集合的算法
.构造分析表的算法
(2) LL(1)分析法
LL(1)文法的定义以及充分必要条件
北京航空航天大学计算机学院
1
63
(二) 自底向上分析
归约过程:
(1)一般过程: 移进-归约过程
问题:如何寻找句柄
(2)算法:
i)算符优先分析法:
1
.分析器的构造,分析过程
根据算符优先关系矩阵来决定
是移进还是归约。
北京航空航天大学计算机学院
1
64

2
.算符优先法的进一步讨论
1
2
3
) 适用的文法类--------------引出的算符优先法的定义
) 优先关系矩阵的构造
) 什么是“句柄”,如何找
由句柄引出的最左素短语的概念。
最左素短语的定理,如何找。
ii)LR分析法
1
.概述----概念、术语 (活前缀、项目)
北京航空航天大学计算机学院
1
65

状态栈
分析表
GOTO表
1
2
)逻辑结构
)分析过程
分析动作表
控制程序
2
3
.LR分析
1
2
)构造DFA
.如何构造SLR分析表
)由DFA构造分析表
北京航空航天大学计算机学院
1
66
除了递归子程序法,其他几种方法逻辑结构很象:
输入串
符号栈(状态栈)
分析表
控制程序
(1) 对于LL(1)分析法
终结符
LL(1)分析表
符号栈
α
i
非
终
结
符
A::=αi
α
i
A
error
(自顶向下,保证最左推导)
首字符
北京航空航天大学计算机学院
1
67
栈外终结符
栈
内
终
结
符
(2)对于算法优先分析:
符号栈
.
<
.
>
.
=
error
(3)LR分析:
状态转移GOTO表
符号栈
S0,S1…Sm
分析表
#
X1…Xm
分析动作表
北京航空航天大学计算机学院
1
68
符号
GOTO表
根据栈顶状态和栈
顶符号推导出下一
状态
状
态 下一
状态
终结符号
分析动作表
根据栈顶状态和输入
符号推导出下一动作
状
态 移进S
归约(rj)
北京航空航天大学计算机学院
1
69
将GOTO表和分析动作表压缩后得:
非终结符号
终结符号
GOTO表
状
态
S
i
i(下一状态数)
r
j
北京航空航天大学计算机学院
1
70
第五章 符号表管理技术
•
•
•
•
概述
符号表的组织与内容
非分程序结构语言的符号表组织
分程序结构语言的符号表组织
北京航空航天大学计算机学院
1

5.1 概述
(1) 什么是符号表?
在编译过程中,编译程序用来记录源程序中各种
名字的特性信息, 所以也称为名字特性表。
名 字: 程序名、过程名、函数名、用户定义类型名、
变量名、常量名、枚举值名、标号名等。
特性信息: 上述名字的种类、类型、维数、参数个数、
数值及目标地址(存储单元地址)等。
北京航空航天大学计算机学院
2

(2)建表和查表的必要性(符号表在编译过程中的作用)
•
•
源程序中变量要先声明,然后才能引用。
用户通过声明语句,声明各种名字,并给出它们的类型、
维数等信息,编译程序在处理这些声明语句时,应该将声
明中的名字及其信息登录到符号表中,同时编译程序还要
给变量分配存储单元,而存储单元地址也必须登录在符号
表中。
•
当编译程序编译到引用所声明的变量时(赋值或引用其值),
要进行语法语义正确性检查(类型是否符合要求)和生成相
应的目标程序,这就需要查符号表以取得相关信息。
北京航空航天大学计算机学院
3

符号表
数据区
x 简单变量 整型
a 简单变量 整型
建表,
例:int x, a, b;
分配存贮 b 简单变量 整型
L 标号
.
.
..
..
L: x := a + b;
..
1
. 语法分析和语义分析
• 说明语句、赋值语句的语法规则
.
•
•
上下文有关分析:是否声明
类型一致性检查
2
. 生成目标代码
LOAD a的地址
ADD b的地址
STO x的地址
北京航空航天大学计算机学院
4
(3)有关符号表的操作:填表和查表
填表:当分析到程序中的说明或定义语句时,应将说明或
定义的名字,以及与之有关的信息填入符号表中。
例:Procedure P( )
查表:(1) 填表前查表,检查在程序的同一作用域内名字
是否重复定义;
(2) 检查名字的种类是否与说明一致;
(3) 对于强类型语言,要检查表达式中各变量的类型
是否一致;
(4) 生成目标指令时,要取得所需要的地址。
.
........
北京航空航天大学计算机学院
5

5.2 符号表的组织与内容
(1)符号表的结构与内容
符号表的基本结构:
名字 特性(信息)
“
名字”域: 存放名字,一般为标识符的符号串,也可
为指向标识符字符串的指针。
北京航空航天大学计算机学院
6
名字
特性(信息)
“
特性”域: 可包括多个子域, 分别表示标识符的有
关信息,如:
名字(标识符)的种类:简单变量、函数、过程、
数组、标号、参数等
类型:如整型、浮点型、字符型、指针等
性质:变量形参、值形参等
值: 常量名所代表的数值
地址:变量所分配单元的首址或地址位移
大小:所占的字节数
作用域的嵌套层次:
北京航空航天大学计算机学院
7
对于数组: 维数、上下界值、计算下标变量地址所用的
信息(数组信息向量)以及数组元素类型等。
对于记录(结构、联合):域的个数,每个域的域名、
地址位移、类型等。
对于过程或函数:形参个数、所在层次、函数返回值类型、
局部变量所占空间大小等。
对于指针:所指对象类型等。
北京航空航天大学计算机学院
8

(2)符号表的组织方式
1
.统一符号表:不论什么名字都填入统一格式的符号表中
符号表表项应按信息量最大的名字设计,填表、
查表比较方便, 结构简单, 但是浪费大量空间。
2
3
.对于不同种类的名字分别建立各种符号表
节省空间, 但是填表和查表不方便。
.折中办法:大部分共同信息组成统一格式的符号表,
特殊信息另设附表,两者用指针连接。
北京航空航天大学计算机学院
9

例: begin
A : real;
B : array [1:100] of real;
:
:
end
A 简变 实型 地址
B 数组 实型
指针连接
补充
维数 上下界 首地址
北京航空航天大学计算机学院
1
0
5.3 非分程序结构语言的符号表组织
(1)非分程序结构语言: 每个可独立进行编译的程序单
元是一个不包含有子模块的单
一模块,如FORTRAN语言。
FORTRAN程序构造
主程序
主程序和子程序中可
定义common语句
子程序
或函数
北京航空航天大学计算机学院
11
(2)标识符的作用域及基本处理办法
1
. 作用域: 全局:子程序名,函数名和公共区名。
局部: 程序单元中定义的变量。
2
. 符号表的组织:
全局符号表
局部符号表
3
. 基本处理办法:
<
1> 子程序、函数名和公共区名填入全局
符号表。
北京航空航天大学计算机学院
1
2
<
<
2> 在子程序(函数)声明部分读到标识符,
造局部符号表。
有,重复声明,报错
查本程序单元局部符
号表,有无同名?
无,造表
3> 在语句部分读到标识符,查表:
有,即已声明
查本程序单元局部符
号表,有无同名?
有,全局量
无,查全局变量表
无, 无定义
标识符
北京航空航天大学计算机学院
1
3
4
5
. 程序单元结束: 释放该程序单元的局部符号表。
. 程序编译完成: 释放全部符号表。
(3)符号表的组织方式
1
. 无序符号表: 按扫描顺序建表,查表要逐项查找
查表操作的平均长度为n+1 2
北京航空航天大学计算机学院
1
4

2
3
. 有序符号表:符号表按变量名进行字典式排序
线性查表: n+1 2
Log -
折半查表:
n
1
2
. 散列符号表(Hash表):符号表地址= Hash(标识符)
解决:冲突
北京航空航天大学计算机学院
1
5

5.4 分程序结构语言的符号表组织
(1) 分程序结构语言:模块内可嵌入子模块
(2) 标识符的作用域和基本处理方法:
作用域:标识符局部于所定义的模块(最小模块)
模块中所定义的标识符作用域是定义该标识
1
符的子程序
北京航空航天大学计算机学院
1
6

1
real A;
1
real A;
2
2
A为内分程序局部变量
A为可作用于内分程序的全局变量
real A;
real A;
2
1
1
real A;
2
real A;
2
B:=A;
都是局部变量
北京航空航天大学计算机学院
1
7
过程或函数说明中定义的标识符(包括形参)其
作用域为本过程体。
2
例
begin
procedure P (i,j);
begin
:
2
1
L:
×
end
goto L;
P(3,5);
end ;
北京航空航天大学计算机学院
1
8
3
循环语句中定义的标识符,其作用域为该循环语句。
for … … do
begin
:
L:
×
end
Goto L;
:
北京航空航天大学计算机学院
1
9
基本处理办法:
建查符号表均要遵循标识符的作用域规定进行。
建表:不能重复,不能遗漏
查表:按标识符作用域
real x, A, B;
定义重复错误
必须填表
integer
y;
real ;
A:= + 2.0;
查表,是本层的x
:
:
B:= + 2.0
查表,是本层的x(外层的x)
北京航空航天大学计算机学院
2
0
处理方法:
a. 在程序声明部分读到标识符时(声明性出现),建表:
有,重复声明,报错
查本层符号表,有无同名?
无,填入符号表
b. 在语句中读到标识符(引用性出现),查表:
有,即已声明, 取该名字信息
是,未声明标识
符,报错
否,转到直接
外层
(局部量)
无,是否是最外层?
查本层符号表,有无同名?
(n-1)
北京航空航天大学计算机学院
2
1
c. 标准标识符的处理
主要是语言定义的一些标准过程和函数的名字,
它们是标识符的子集。
如sin con abs….
特点:1) 用户不必声明,就可全程使用
2
) 设计编译程序时,标准名字及其数目已知
处理方法:1) 单独建表:使用不便,费时。
) 预先将标准名填入名字表中
最外层
2
北京航空航天大学计算机学院
2
2

例:Pascal程序的分程序结构示例如下:
0
program main (…);
var
0
1
main
M1
P2
x, y : real; i, k: integer;
name: array [1…16] of char;
2
P33
1
:
procedure M1 (ind:integer);
var x : integer
2
q2 2
procedure P2 (j : real);
:
3
procedure P3;
var
f : array [1…5] of integer
test1: boolean;
begin
:
end; {P3}
:
北京航空航天大学计算机学院
2
3
0
program main (…);
var
x, y : real; i, k: integer;
name: array [1…16] of char;
0
1 2
begin
:
1
procedure M1 (ind:integer);
var x : integer
:
2
end;{P2}
procedure q2;
var r1,r2 : real;
begin
procedure P2 (j : real);
2
:
3
procedure P3;
var
f : array [1…5] of integer
test1: boolean;
:
begin
:
end; {P3}
P2(r1+r2);
:
end; {q2}
0
1 2
begin
:
end;{P2}
2
begin
procedure q2;
var r1,r2 : real;
:
begin
P2(x/y);
:
:
p2(r1+r2);
:
end;{M1}
end; {q2}
begin
begin
:
:
P2(x/y);
:
end;{M1}
M1(i+k);
:
begin
:
end {main}
M1(i+k);
:
北京航空航天大学计算机学院
2
4
end {main}
栈式符号表结构
主程序符号表main
M1符号表
main符号表
main符号表
M1符号表
M1符号表
P2符号表
P2符号表
P2符号表
P3符号表
栈顶
main符号表
M1符号表
q2
main符号表
M1符号表
main符号表
释放
符号表
北京航空航天大学计算机学院
2
5
name kind
type lev other inf
real
real
int
int
array
符
号
x
y
i
var
var
var
var
1
0
0
0
0
0
0
1
1
1
2
2
3
3
表
2
3
4
5
6
7
8
9
main
k
分程序索
引表
name var
M
ind
x
1
proc
para
var
0 1
1
2
3
7
10
12
int
int
M
1
P
j
P
2
proc
para
proc
var
real
1
0
P
P
2
1
1
3
f
array
1
1
2
3 test1
var boolean
3
北京航空航天大学计算机学院
2
6
编译q2说明部分后:
7
8
9
ind para int 1
var int 1
x
M
1
P
2
proc
para
1
real 1
1
1
0
11 q2
proc
1
1
2 r1
3 r2
var real 2
var real 2
q
2
北京航空航天大学计算机学院
2
7
编译完q2过程体:
7
8
9
ind para
int
int
x
var
P
2
proc
para
proc
10
1
real
q
2
1
当过程和函数体编译完成后,应将与之相应的
参数名和局部变量名以及后者的特性信息从符号表
中删去。
要求:给出一段程序,会画出其栈式符号表
北京航空航天大学计算机学院
2
8
第七章 源程序的中间形式
•
•
•
波兰表示
N-元表示
抽象机代码
北京航空航天大学计算机学院
1
7.1 波兰表示
一般编译程序都生成中间代码,然后再生成目
标代码,主要优点是可移植(与具体目标程序无关),
且易于目标代码优化。有多种中间代码形式:
波兰表示
波兰表示
算术表达式:
N-元组表示 抽象机代码
F*3.1416*R*(H+R)
转换成波兰表示: F3.1416*R*HR+*
赋值语句: A := F * 3.1416 * R * ( H + R )
波兰表示:
AF3.1416 * R * HR + * :=
北京航空航天大学计算机学院
2

#
a+b#
ab+
+
#
操作符栈
#
优先级最低
算法:
设一个操作符栈;当读到操作数时,立即输出该操作数,
当扫描到操作符时,与栈顶操作符比较优先级,若栈顶操作
符优先级高于栈外,则输出该栈顶操作符,反之,则栈外操
作符入栈。
北京航空航天大学计算机学院
3
if 语句的波兰表示
label
label
1
if 语句 :if <expr> then <stmt > else <stmt >
2
1
2
波兰表示为 :<expr><label >BZ<stmt ><label >BR<stmt >
1
1
2
2
BZ: 二目操作符
若<expr>的计算结果为0 (false),
则产生一个到<label1>的转移
BR: 一目操作符
产生一个到< label2>的转移
北京航空航天大学计算机学院
4

波兰表示为 :<expr><label >BZ<stmt ><label >BR<stmt >
1
1
2
2
由if语句的波兰表示可生成如下的目标程序框架:
<
expr>
BZ label1
stmt1>
<
BR label2
label :<stmt >
1
2
label2:
其他语言结构也很容易将其翻译成波兰表示,
使用波兰表示优化不是十分方便。
北京航空航天大学计算机学院
5

7.2 N-元表示
在该表示中,每条指令由n个域组成,通常第一
个域表示操作符,其余为操作数。
常用的n元表示是: 三元式 四元式
三元式
操作符 左操作数 右操作数
表达式的三元式:w * x + ( y + z )
第三个三元
式中的操作数(1)
(2)表示第(1)和第
(2)条三元式的计
算结果。
(1) *, w, x
(2) +, y, z
(3) +, (1), (2)
北京航空航天大学计算机学院
6
条件语句的三元式:
if x > y then
z := x;
else z := y+1;
(1) -, x, y
其中:
(2) BMZ, (1), (5)
(3) :=, z, x
(4) BR, , (7)
(5) +, y, 1
(6) :=, z, (5)
(7)
BMZ:是二元操作符,测试第二
个域的值,若≤0,则按
第3个域的地址转移,
若>0,则顺序执行。
BR: 一元操作符,按第3个域
作无条件转移。
:
:
北京航空航天大学计算机学院
7
使用三元式不便于代码优化,因为优化要删除
一些三元式,或对某些三元式的位置要进行变更,由
于三元式的结果(表示为编号),可以是某个三元式的
操作数,随着三元式位置的变更也将作相应的修改,
很费事。
间接三元式:
为了便于在三元式上作优化处理,可使用间接三元式
三元式的执行次序用另一张表表示,这样在优化时,
三元式可以不变,而仅仅改变其执行顺序表。
北京航空航天大学计算机学院
8

例: A:=B+C*D/E
F:=C*D
用间接三元式表示为:
操作
三元式
1
2
3
4
5
6
. (1)
. (2)
. (3)
. (4)
. (1)
. (5)
(1) * , C, D
(2) / , (1), E
(3) + , B, (2)
(4) := , A, (3)
(5) := , F, (1)
北京航空航天大学计算机学院
9

操作符 操作数1 操作数2 结果
四元式表示
结果:通常是由编译引入的临时变量,可由编译程序
分配一个寄存器或主存单元。
例:
( A + B ) * ( C + D ) - E
+
+
, A, B, T1
, C, D, T2
式中T1,T2,T3,T4
为临时变量,由四
元式优化比较方便
*
, T1, T2, T3
一, T3, E, T4
北京航空航天大学计算机学院
1
0
7.3 抽象机代码
许多pascal编译系统生成的中间代码是一种称为
P-code的抽象代码,P-code的“P”即“Pseudo”
抽象机:
寄存器
保存程序指令的存储器
堆栈式数据及操作存储
北京航空航天大学计算机学院
11

寄存器有:
1
2
. PC-程序计数器
. NP-New指针,指向“堆”的顶部。“堆”用来存放由New
生成的动态数据。
3
. SP- 运行栈指针,存放所有可按源程序的数据声明直接
寻址的数据。
4
5
. BP-基地址指针,即指向当前活动记录的起始位置指针。
. 其他,(如MP-栈标志指针,EP-极限栈指针等)
北京航空航天大学计算机学院
1
2

计算机的存储大致情况如下:
栈底
运行栈
P-code指令
BP
SP
当前模块活
动记录
(数据段)
NP
PC
堆
堆底
常量区
程序指令存储器
北京航空航天大学计算机学院
1
3
运行P-code的抽象机没有专门的运算器或
累加器,所有的运算(操作)都在运行栈的栈顶进
行,如要进行d:=(a+b)*c的运算,生成P-code序
列为:
取a LOD a
取b LOD b
栈底:
运行栈
a单元
b单元
c单元
d单元
a
+
ADD
取c
*
送d
LOD c
MUL
STO d
SP
P-code实际上是波兰表示形式的中
间代码
b
栈顶
北京航空航天大学计算机学院
1
4
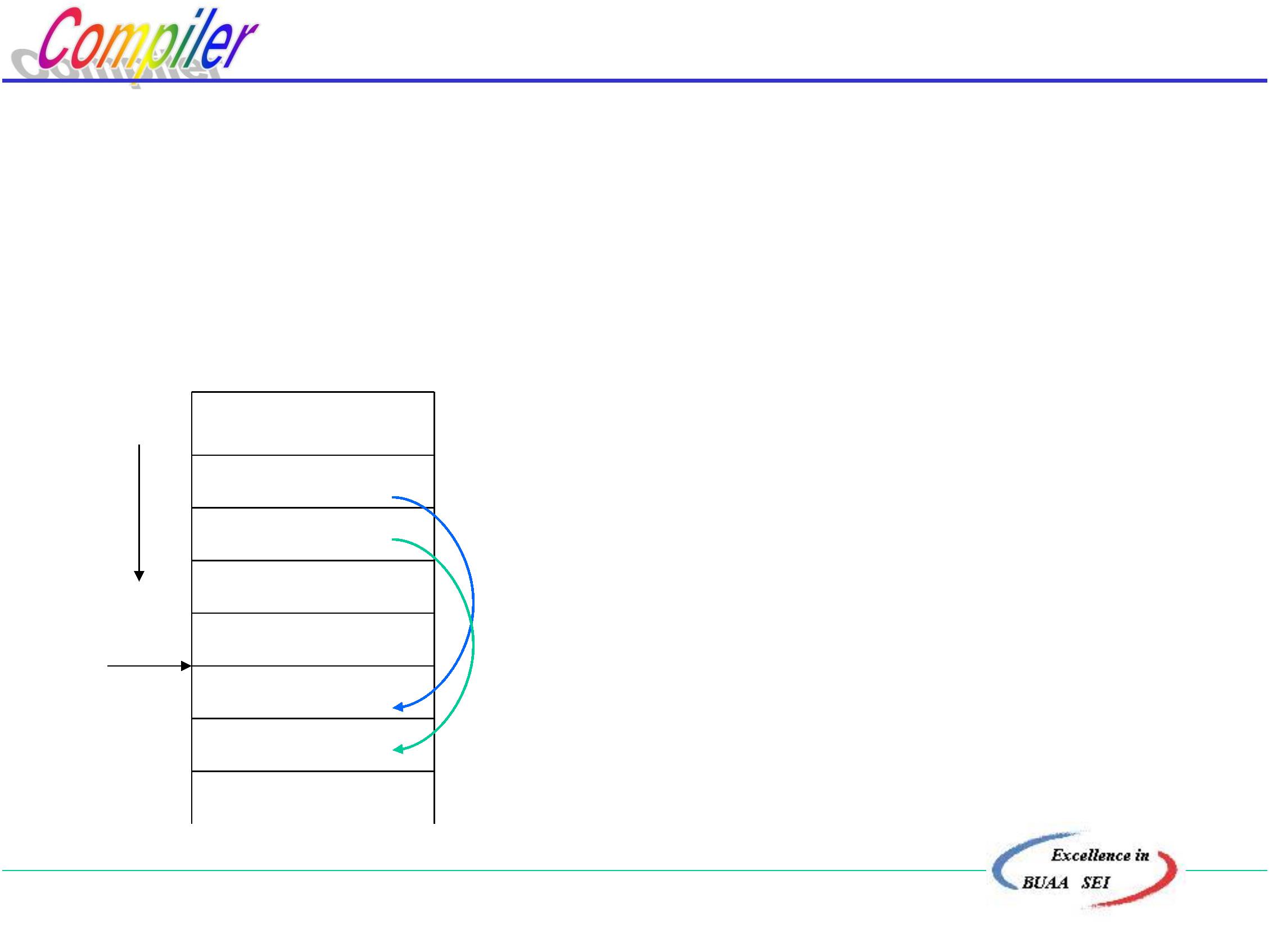
第八章 错误处理
•
•
•
•
概述
错误分类
错误的诊察和报告
错误处理技术
北京航空航天大学计算机学院
1
8.1 概述
1
. 必备功能之一
正确的源程序:通过编译生成目标代码
错误的源程序:通过编译发现并指出错误
. 错误处理能力
2
(1) 诊察错误的能力
(2) 报错及时准确
(3) 一次编译找出错误的多少
(4) 错误的改正能力
(5) 遏止重复的错误信息的能力
北京航空航天大学计算机学院
2

8.2 错误分类
从编译角度,将错误分为两类:语法错误和语义错误
语法错误:源程序在语法上不合乎文法
如:
A[ I,J := B +* C
语义错误主要包括:程序不符合语义规则或
超越具体计算机系统的限制
北京航空航天大学计算机学院
3
语义规则:
•
标识符先说明后引用
•
•
•
•
标识符引用要符合作用域规定
过程调用时实参与形参要一致
参与运算的操作数类型一致
下标变量下标不能越界
超越系统限制:
•
•
•
数据溢出错误
符号表、静态存储分配数据区溢出
动态存储分配数据区溢出
北京航空航天大学计算机学院
4

8.3 错误的诊察和报告
错误诊察:
1
. 违反语法和语义规则以及超过编译系统限制的错误。
编译程序: 语法和语义分析时
语义分析要借助符号表)
(
2
. 下标越界,计算结果溢出以及动态存储数据区溢出。
目标程序: 目标程序运行时
对此,编译程序要生成相应的目标程序作检查
和进行处理
北京航空航天大学计算机学院
5

错误报告:
. 出错位置:即源程序中出现错误的位置
实现:行号计数器 line_no
单词序号计数器 char_no
一旦诊察出错误,当时的计数器内容就是出错位置
1
2
. 出错性质:
可直接显示文字信息
可给出错误编码
北京航空航天大学计算机学院
6

3
. 报告错误的两种方式:
(1) 分析完以后再报告(显示或者打印)
编译程序可设一个保存错误信息的数据区(可
用记录型数组),将语法语义分析所诊察到的错误
送数据区保存,待源程序分析完以后,显示或打印
错误信息。
例:A[x , y :=B+*C
源程序行号 错误序号 错误性质
x x
x x
6
缺少“]”
10 表达式语法错误
北京航空航天大学计算机学院
7
(2) 边分析边报告
可以在分析一行源程序时若发现有错,立即输
出该行源程序,并在其下输出错误信息。
Line-no A[x , y
:= B+ *C
缺“]”orn 表达式语法错 m
有时候报错不一定十分准确
位置和性质),需进一步分析
(
错误编号
例
begin
.......
i := 1 step 1 until n do
...........
.
.
end
北京航空航天大学计算机学院
8
8.4 错误处理技术
发现错误后,在报告错误的同时还要对错误进行
处理,以方便编译能进行下去。目前有两种处理办法:
1
. 错误改正:指编译诊察出错误以后,根据文法进
行错误改正。
如:A[i , j :=B+*C
要正确地改正错误
是很困难的
但不是总能做到,如A:=B-C*D+E)
2
. 错误局部化处理:指当编译程序发现错误后,尽可
能把错误的影响限制在一个局部
的范围,避免错误扩散和影响
程序其他部分的分析。
北京航空航天大学计算机学院
9

(1) 一般原则
当诊察到错误以后,就暂停对后面符号的
分析, 跳过错误所在的语法成分然后继续往下分析。
词法分析:发现不合法字符,显示错误,并跳
过该标识符(单词)继续往下分析。
语法语义分析:跳过所在的语法成分(短语或语
句),一般是跳到语句右界符,
然后从新语句继续往下分析。
北京航空航天大学计算机学院
1
0

(2) 错误局部化处理的实现(递归下降分析法)
cx: 全局变量,存放错误信息。
•用递归下降分析时,如果发现错误,便将有
关错误信息(字符串或者编号)送CX,然后转出
错误处理程序;
•出错程序先打印或显示出错位置以及出错信息,
然后跳出一段源程序, 直到跳到语句的右界符
(如:end)或正在分析的语法成分的合法后继符号
为止, 然后再往下分析。
北京航空航天大学计算机学院
11

if<B> then <stmt>[else< stmt >];
例:条件语句分析:
有如下分析程序:
procedure if_stmt;
begin
nextsym;
B;
/*读下个单词符号*/
/*调用布尔表达式处理程序*/
if not class=‘then’ then
begin
cx :=‘缺then’
error;
/*错误性质送cx*/
/*调用出错处理程序*/
end;
else
begin
nextsym;
statement
end;
if class=‘else’then
begin
nextsym;
statement;
end
北京航空航天大学计end if_stmt;
2

局部化处理的出错程序为:
procedure error;
begin
write(源程序行号, 序号, cx)
repeat
nextsym;
until class = ‘;’ or class = ‘end’ or class = ‘else’
end error;
跳过太多
real x, 3a, a, bcd, 2fg;
北京航空航天大学计算机学院
1
3

(3) 提高错误局部化程度的方法
设S1: 合法后继符号集(某语法成分的后继符号)
S2: 停止符号集
(跳读必须停止的符号集)
进入某语法成分的分析程序时:
S1:= 合法后继符号
S2:= 停止符号
北京航空航天大学计算机学院
1
4

当发现错误时: error(S1,S2)
procedure error(S1,S2)
begin
write(line_no, char_no, cx);
repeat
nextsym
until(class in S1 or class in S2 );
end
if<B> then <stmt>[else< stmt >]
若<B>有错,则可跳到then,
若<stmt>有错,则可跳到else。
北京航空航天大学计算机学院
1
5

3
.目标程序运行时错误检测与处理.
下标变量下标值越界
计算结果溢出
动态存储分配数据区溢出
·
在编译时生成检测该类错误的代码。
对于这类错误,要正确的报告出错误位置很难,因为
目标程序与源程序之间难以建立位置上的对应关系
一般处理办法:
当目标程序运行检测到这类错误时,就调用异常
处理程序,打印错误信息和运行现场(寄存器和存储
器中的值)等, 然后停止程序运行。
北京航空航天大学计算机学院
1
6

第九章 语法制导翻译技术
•
•
•
翻译文法(TG)和语法制导翻译
属性翻译文法(ATG)
自顶向下语法制导翻译
•
•
翻译文法的自顶向下语法制导翻译
属性文法的自顶向下语法制导翻译
•
自底向上的语法制导翻译(自学)
北京航空航天大学计算机学院
1

9
.0 本章导言
词法分析,语法分析:解决单词和语言成分的识别
及词法和语法结构的检查。语法结构可形式化地用
一组产生式来描述。给定一组产生式,能够很容易
地将其分析器构造出来。
本章要介绍的是语义分析和代码生成技术。
程序语言的语义形式化描述目前有三种基本描述方
法,即:
•
•
•
操作语义
指称语义
公理语义
北京航空航天大学计算机学院
2

9.1 翻译文法和语法制导翻译
有上下无关文法G[E]:
1
2
3
. E →E+T
. E →T
. T →T*F
4. T →F
5. F →(E)
6. F →i
此文法是一个中缀算术表达式文法
翻译的任务是: 中缀表达式 逆波兰表示
a+b*c abc*+
假如翻译任务是要将中缀表达式简单变换为波兰后
缀表示,只需在上述文法中插入相应的动作符号。
北京航空航天大学计算机学院
3
1
2
3
. E →E+T@+
. E →T
. T →T*F @*
4. T →F
5. F →(E)
6. F →i@i
其中:
@+,@*,@i 为动作符号。@为动作符号标记,后面为字符串。
在本例中,其对应语义子程序的功能是要输出打印动作
符号标记后面的字符串。
所以,产生式1:E→E+T@+ 的语义是分析E, + 和T,输出+
产生式6:F→i @ i的语义是分析i,输出i
北京航空航天大学计算机学院
4

下面给出输入文法和翻译文法的概念:
输入文法:未插入动作符号时的文法。
由输入文法可以通过推导产生输入序列。
翻译文法:插入动作符号的文法。
由翻译文法可以通过推导产生活动序列。
输入序列
动作序列
北京航空航天大学计算机学院
5

例:( i+i ) * i
可以用输入文法推导:
E T T*F F*F (E)*F (E+T)*F
* (i+i)*i
用相应的翻译文法推导,可得:
E T
T*F@*
F*F@*
(E)*F@*
(E+T@+)*F@* * (i@i+i@i @+)*i@i@*
北京航空航天大学计算机学院
6

活动序列:由翻译文法推导出的符号串,由终结符和动作
符号组成。
●
●
从活动序列中,抽去动作符号,则得输入序列(i+i)*i
从活动序列中,抽去输入序列,则得动作序列,执行动
作序列,则完成翻译任务:
@
i@i@+@i@* ii+i*
定义9.1
翻译文法是上下文无关文法,其终结符号集由输入符
号和动作符号组成。由翻译文法所产生的终结符号串称为
活动序列。
北京航空航天大学计算机学院
7

上例题中的翻译文法为:
G = (V , V , P, E)
T
n
t
Vn = {E, T, F}
Vt = {i, +, *, (, ), @ +, @ *, @i}
P = {E→E+T@ +, E→T, T→T*F@*, T→F, F→(E),
F→i@i}
符号串翻译文法:若插入文法中的动作符号对应的语义子
程序是输出动作符号标记@后的字符串的文法。
语法导制翻译:按翻译文法进行的翻译。
给定一输入符号串,根据翻译文法获得翻译该符号串的动作
序列,并执行该序列所规定的动作的过程。
北京航空航天大学计算机学院
8

语法导制翻译的实现方法:
在文法的适当位置插入语义动作符号,当按文法分析到动作
符号时就调用相应的语义子程序,完成翻译任务。
翻译文法所定义的翻译是由输入序列和动作序列组成的对偶集。
如:(i+i)*i, @i@i@+@i@* →ii+i*
i+i*i @i@i@i@*@+
因此,给定一个翻译文法,就给定了一个对偶集。
北京航空航天大学计算机学院
9

9.2 属性翻译文法
在翻译文法的基础上,可以进一步定义属性文法,
翻译文法中的符号,包括终结符、非终结符和动作符号
均可带有属性,这样能更好的描述和实现编译过程。
属性可以分为两种:
综合属性
继承属性
北京航空航天大学计算机学院
1
0
9
.2.1 综合属性
基本操作数带有属性的表达式文法G[E]
1
2
3
.E→E+F
.E→T
.T→T*F
4.T→F
5.F→(E)
6.F→i
C
其中↑C是综合属性符号,↑为综合属性标记,
c为属性变量或者属性值。
此文法能够产生如下的输入序列:
i
(
3 +i 9) * i 2
北京航空航天大学计算机学院
11

根据给定的文法,可写出该输入序列的语法树
E
T
E
T
24
24
T
F
F
i
T
F
*
*
12
2
自底向上
F
E
12
2
i
2
(
)
的属性计算
(
)
E
12
E + T
E + T
3
3
9
9
T F 所以,用表示属性 T
计算是自底向上的,
F
F
F
3
i
9
i
称为综合属性。
9
i
3
i 3
北京航空航天大学计算机学院
1
2
为了形式地表示上述表达式的属性求值过程,可以改写上述文法:
产生式 求值规则
1
2
3
4
5
6
.E
.E
.T
.T
.F
.F
p4
p3
p2
p2
p1
p1
E
T
q5
q4
+ T
r2
p
p
4:=q 5+r
3:=q
2:=q 3*r
2
;
4
;
T
q3
* F
r1
p
1
;
F
q2
p
p
p
2:=q
2
1
1
;
;
;
(E q1)
1
:=q
:=q
i
q1
1
说明:
•
求值规则:综合属性是自右向左,
自底向上求值。
•
•
p,q,r为属性变量名。
属性变量名局部于每个产生
式,也可使用不同的名字。
北京航空航天大学计算机学院
1
3
9
.2.2 继承属性
考虑下列文法:G[<说明>]:
1. <说明> → Type id <变量表>
2. <变量表> →,id <变量表>
3
. <变量表> →ε
其中
Type: 类型名(值:int, real, bool等)
id: 变量名(值:指向该变量符号表项的指针)
符号表
上述文法所产生的语句:int A,BC
A 整型
该文法的翻译任务:将声明的变量填入符号表
完成该工作的动作符号:@set_table
BC 整型
北京航空航天大学计算机学院
1
4
翻译文法:
1
. <说明> →Type id @set_table <变量表>
. <变量表> →,id @set_table <变量表>
2
3
. <变量表> →ε
填表时需要的信息:类型,名字,以及填的位置(可以用全程
变量或指针)
如何得到?
类型和名字在词法分析时得到,可设两个综合属性。
北京航空航天大学计算机学院
1
5

Type t
id n
t中放类型值
n中放变量名
填表动作符号也可带有属性:
@set_table↓t1 , n1
↓t ,n 可从前面得到,所以称为继承属性,
1
1
继承前面的值
↓t2 同上
<变量表> ↓t
2
属性翻译文法:
1
2
3
.<说明> →Type id @set_table
<变量表>
t ,t := t; n := n;
2 1
t
n
↓t1,n1
↓t2
1
.<变量表> →,id @set_table
<变量表>↓t3 t ,t := t ; n := n;
3 1
↓
t2
n
↓t1,n1
2
1
.<变量表> →ε
↓
t2
北京航空航天大学计算机学院
1
6

例:int A,BC Type
id A , idBC
int
语法树:
<说明>
Type int
id A
@ set_table↓int,A
<变量表> ↓int
,
idBC @ set_table ↓int BC <变量表> ↓int
ε
继承属性求值:自左向右,自顶向下
综合属性求值:自右向左,自底向上
北京航空航天大学计算机学院
1
7
int A, BC 的分析翻译过程:
<
说明> Type id @ set_table <变量表>
↓t
t
n1
↓t,n1
+
Type id @ set_table
t
n1
↓t,n1
,
id @ set_table
n2 ↓t,n2
符号表
A int
BC int
p
北京航空航天大学计算机学院
1
8
9
.2.3 ( 1 ) L-属性翻译文法(L-ATG)
这是属性翻译文法中较简单的一种。其输入文法要求是LL(1)
文法,可用自顶向下分析构造分析器。在分析过程中可进行属性求
值。
定义9.2:
L-属性翻译文法是带有下列说明的翻译文法:
1. 文法中的终结符,非终结符及动作符号都带有属性,且每个属性都有一个
值域。
2. 非终结符及动作符号的属性可分为继承属性和综合属性。
3. 开始符号的继承属性具有指定的初始值。
4. 输入符号(终结符号)的每个综合属性具有指定的初始值。
5. 属性的求值规则:
北京航空航天大学计算机学院
1
9

属性的求值规则:
继承属性:
(
1) 产生式左部非终结符号的继承属性值,取前面产生式
右部该符号已有的继承属性值。
2)产生式右部符号的继承属性值,用该产生式左部符号
的继承属性或出现在该符号左部的符号的属性值进行
计算。
(
北京航空航天大学计算机学院
2
0

综合属性:
(
1)产生式右部非终结符号的综合属性值,取其下部产
生式左部同名非终结符号的综合属性值。
2)产生式左部非终结符号的综合属性值,用该产生式
左部符号的继承属性或某个右部符号的属性进行计
算。
(
(
3)动作符号的综合属性用该符号的继承属性或某个右
部符号的属性进行计算。
适合在自顶向下分析过程中求值
北京航空航天大学计算机学院
2
1

例:A→BC
求值顺序:
1
) A的继承属性 (若A为开始符号,则有指定值,否则由上面
产生式右部符号的继承属性求得)
2
) B的继承属性 (由A的继承属性求得)
3
) B的综合属性 (由下面产生式中左部符号为B的综合属性
求得)
4
) C的继承属性 (由A的继承属性和B的属性求得)
5
) C的综合属性 (由下面产生式中左部符号为C的综合属性
求得)
6
) A的综合属性 (由前述(2),即A的继承属性或产生式某
右部符号属性计算)
北京航空航天大学计算机学院
2
2

(2) 简单赋值形式的L_属性翻译文法(SL-ATG)
•
一般属性值计算: x:=f ( y , z )
SL-ATG属性值计算: x:=某符号的属性值或常量。
例 x:=y, x,y,z:=17 —— 称为复写规则
为了实现上的方便,常希望文法符号的属性求值规则为上述简
单形式的。为此,对现有的L-ATG的定义做一点改变,
从而形成一个称为简单赋值形式的L-ATG。
北京航空航天大学计算机学院
2
3

•定义9.4 一个L-ATG被定义为简单赋值形式的(SL-ATG),
当且仅当满足如下条件:
1
. 产生式右部符号的继承属性是一个常量,它等于左部符号
的继承属性值或等于出现在所给符号左边符号的一个综合
属性值。
2
.产生式左部非终结符号的综合属性是一个常量,它等于左
部符号的继承属性值或等于右部符号的综合属性值。
因此,一个简单赋值形式的L-ATG除动作符号外,其余符号的
属性求值规则其右部是属性或是常量。
北京航空航天大学计算机学院
2
4

•
L-ATG SL-ATG
给定一个L-ATG,如何找一个等价的赋值形式的L-ATG?
考虑产生式:
<
A > → a < B > < C > ,
I : = f ( R , S )
↓
I
R
S
显然: 该属性求值规则不是简单赋值形式的,因为它需要
对f求值。
北京航空航天大学计算机学院
2
5

第一步:设动作符号“@ f ” 表示函数f求值,该动作符
号有两个继承属性和一个综合属性。
@f
且 S := f ( I , I )
1 2
I ,I S
1
1
2
1
第二步:修改产生式
1
2
3
. 插入“@ f ” (在适当位置)
. 引进新的复写规则(将R , S 赋给I 和I , f值赋给S )
1
2
1
. 删去原有包含f 的规则
北京航空航天大学计算机学院
2
6

<
A >→a < B > @ f
< C > ↓I,
↓I , I S
R
S
1
2
1
I := R , I := S, S := f(I I ), I := S
1
2
1
1, 2
1 .
该文法是简单赋值形式的L-ATG.
注意: 无参函数过程作为常数处理,如
<
A > → < B > < C >
x ,y := NEWT
x
y
北京航空航天大学计算机学院
2
7

9.3 自顶向下语法制导翻译
9
9
.3.1 翻译文法的自顶向下翻译
—递归下降翻译器
—
.3.2 属性翻译文法的自顶向下翻译的实现
—递归下降属性翻译器
—
北京航空航天大学计算机学院
2
8

9
.3.1 翻译文法的自顶向下翻译——递归下降翻译器
按翻译要求,在文法中插入语义动作符号,在分析过程
中调用相应的语义处理程序,完成翻译任务。
例:输入文法
翻译文法(符号串翻译文法)
1
2
3
. < S >
. < S >
. < A >
a< A >< S >
b
< S >
< S >
< A >
a < A > @ x < S >
b @ z
c< A >< S >b
c @ y < A > < S > @ v b
@ w
<
A >
4
. < A > ε
北京航空航天大学计算机学院
2
9
主程序
if CLASS = a or b
PROCS;
主程序
if CLASS = a or b
then
then
PROCS;
if CLASS ≠ #
ERROR;
if CLASS ≠ 右界符 then
ERROR;
then
ACCEPT;
ACCEPT;
过程 PROCS
case CLASS of
a : P1;
过程 PROCS
case CLASS of
a : P1 ;
b : P2;
b : P2 ;
其它:ERROR;
其它:ERROR;
end of
case;
end of
case.
北京航空航天大学计算机学院
3
0

P :
/ *产生式1的代码* /
NEXTSYM;
P1:
/ *产生式1的代码* /
NEXTSYM;
1
PROCA;
PROCS;
RETURN;
PROCA;
OUT( x ) ;
PROCS;
P :
/ *产生式2的代码* /
RETURN;
2
NEXTSYM;
RETURN;
P :
/ *产生式2的代码* /
2
NEXTSYM;
OUT( z ) ;
RETURN;
过程 PROCA
…
过程 PROCA
…
北京航空航天大学计算机学院
3
1
9
.3.2 属性文法自顶向下翻译的实现——递归下降翻译器
方法:
• 对于每个非终结符号都编写一个翻译子程序(过程)。根据该
非终结符号具有的属性数目,设置相应的参数。
U↓x, y→ …
继承属性:声明为赋值形参
综合属性:声明为变量形参
Procedure U(x,y);
x—赋值形参
y—变量形参
北京航空航天大学计算机学院
3
2

•
过程调用语句的实参:
继承属性 : 继承属性值
综合属性 : 属性变量名(传地址,返回时有值)
•
关于属性名的约定:
1
)产生式左部的同名非终结符使用相同的属性名。
<
L> →e <R>
<L> →e <R>
↑x↓y ↓I ↓J
(
递归下降分析法所必须)
↑a↓b ↓I
↓J
<L> →<H>
<L> →<H>
↑
x↓y
)具有相同值的属性取相同的属性名。
↓z↑w
↑x↓y
↓z↑w
2
具有简单赋值形式的属性变量名取相同的属性名,可删
去属性求值规则。
<
S>→I <B> <C> b,c:= a
↑
a
↓b
↓c
<
S>→I <B> <C>
↑
x
↓x
↓x
北京航空航天大学计算机学院
3
3

下面通过一个例子,较详细地介绍如何构造属性文法 的递归下降翻
译器。
例:有如下属性翻译文法G[< S>]
R2:= R1
T2:= T1
Q2:= Q1
1.
< S >↓R1 → a T < A > Q @ x
T , R < S >
Q
2
↓
↓
1
1
2
2
2
.
.
< S >↓R1 →b @ z↓R2 ,
R2 : = R1
3
< A > P → CU @ y < A > Q < S > ↓z @ v ↓P b
↓
U
1
2
U := U , P := Q + U , z := U -3
2
1
1
1
4.
< A > P →@ w P := 8
对简单赋值形式的属性变量取相同的属性名,其求值规则可
以删去。开始符号的继承属性R1=7。
北京航空航天大学计算机学院
3
4

1.
< S >↓R → a T < A > Q @ x ↓T , R < S >
Q
↓
2
.
.
< S >↓R →b @ z↓R ,
3
< A > P→ Cu @ y↓u < A > Q < S > ↓z @ v ↓P b
P := Q + U, z := U-3
4.
< A > P →@ w P := 8
北京航空航天大学计算机学院
3
5

全局变量和过程声明:
CLASS;
TOKEN;
/ * 存放单词类别码* /
/ * 存放单词值*/
NEXTSYM;
/ *词法分析程序,每调用一次单词类别码 CLASS,
单词值 TOKEN,该符号指针指向下一个单词*/
主程序:
NEXTSYM;
PROCS(7);
if CLASS ≠ 右界符 then
ERROR;
ACCEPT
过程 PROCS(R)
R;
/* 值形参声明*/
北京航空航天大学计算机学院
3
6

case
a:
CLASS
P1 ;
of
b:
P2 ;
其它: ERROR;
end of case;
P1 :
T , Q ;
/ * 产生式1的代码* /
/ * 局部变量声明* /
T := TOKEN;
NEXTSYM;
PROCA(Q)
/ * 单词值赋给终结符的综合属性* /
OUT(X ↓T,R);
PROCS(Q)
RETURN;
北京航空航天大学计算机学院
3
7

P :
/ * 产生式2的代码* /
NEXTSYM;
2
OUT(Z ↓R );
RETURN;
过程 PROCA(P)
P;
/*变量形参声明*/
case CLASS of
C : p3
其它: p4
end of
case;
北京航空航天大学计算机学院
3
8

P3:
U , Q , Z ;
P4:
P := 8;
/*局部变量声明*/
U := TOKEN;
NEXTSYM;
Z := U – 3 ;
OUT(y↓U);
OUT(w);
RETURN;
插在U已知,使用Z之前
PROCA(Q); 返回时有值
插在Q,U已知,使用P之前。
P := Q+U;
PROCS(Z);
OUT(V↓P );
if CLASS ≠ b then ERROR;
NEXTSYM;
RETURN;
北京航空航天大学计算机学院
3
9

一个例子
例:构造将算术表达式翻译成四元式的属性翻译文法,并写出递
归下降分析程序。由该属性翻译文法来描述翻译过程。
翻译的输入: 算术表达式
翻译的输出: 四元式
a + b
ADD , P , P , P
r
a
b
其中P , P , P 为变量a , b和结果单元的地址。
a
b
r
表达式:
输入:
(a + b) * c
( Id + Id ) * Id
4
1
2
Id由词法分析程序返回,
.....综合属性,变量在数据区地址。
1
输出:
ADD, 1, 2, 3
MULT, 3, 4, 5
北京航空航天大学计算机学院
4
0

数据区:
a
1
2
b
3
4
部分结果
c
部分结果
5
北京航空航天大学计算机学院
4
1
(⑴)翻译文法设计:
E →E+T@ADD
T →F
E →T
F →(E)
F →Id
T →T*F @MULT
@
ADD为输出ADD四元式的动作符号
MULT为输出MULT四元式的动作符号
对应于完成翻译
的语义动作程序
@
在文法中的插入位置:在分别处理完成两个操作数之后
输入序列:(a+b)*c
翻译文法产生的活动序列: (a+b@ADD)*c@MULT
动作符号序列:@ADD @MULT 反映生成四元式的顺序,语法分析过
程中语义程序的调用顺序。
北京航空航天大学计算机学院
4
2

(2) 属性翻译文法的设计
•
•
•
输入符号(操作数)有一个综合属性,它是该符号在数据区
的地址。
每个非终结符有一个综合属性,该属性是由它产生的代表该
子表达式在数据区的地址。
动作符号有三个继承属性,它们分别是左右操作数和运算结
果在数据区地址。
这样可得表达式的属性翻译文法
—
—可将中缀表达式翻译成四元式
北京航空航天大学计算机学院
4
3

x, p := NEW y := q z := r
1
2
3
4
5
6
. E x →E q +T r @ADD↓y , z , p
x := p
. E
x p
→ T
x, p := NEW y := q z := r
. T x →T q *F r @MULT↓y , z , p
x := p
x := p
x := p
. T
. F
. F
x
x
x
→ F
→(E
→Id
p
p
)
p
说明:
Id的综合属性p是数据区地址,NEWT为系统过程,
返回数据区地址。
北京航空航天大学计算机学院
4
4

反映属性求值的语法树:
E
T
5
5
*
T
F
3
3
3
F
4
Id
4
@MULT
↓3 , 4 , 5
( E
1
)
E
T
F
+ T
F
2
2
1
1
Id
2
@ADD
↓1 , 2 , 3
Id
1
北京航空航天大学计算机学院
4
5
语义动作程序如何设计在后面介绍
@
ADD ↓y , z , p fprintf(objfile, “ADD %d %d %d \n”, y, z, p)
(⑶)写递归下降翻译程序
(留作作业)
北京航空航天大学计算机学院
4
6

小结:
本章介绍了语法制导翻译的概念和技术,是在抽象层次上讲的。
第十章对过程语言的编译就是采用该法。
翻译文法:在输入文法中插入语义动作符号(完成翻译任务的语义
子程序)
属性翻译文法:文法符号(包括动作符号)可带有属性,并定义相
应的属性求值规则,就成为属性翻译文法。比翻译
文法能更细地描述翻译过程。(属性有综合属性和
继承属性之分)
北京航空航天大学计算机学院
4
7

自顶向下的语法制导翻译(递归下降翻译)
翻
译
文
法
属
性
文
法
在本章的基础上,第十章将介绍典型的过程语言的语法制
导翻译。
本章未讲的部分不要求
北京航空航天大学计算机学院
4
8
第十章 语义分析和代码生成
•
•
•
•
•
•
•
语义分析的概念
栈式抽象机及其汇编指令
声明的处理
表达式的处理
赋值语句的处理
控制语句的处理
过程调用和返回
北京航空航天大学计算机学院
1
假定:
•
源语言: 通用的过程语言
•
•
•
生成代码:栈式抽象机的(伪)汇编程序
翻译方法:自顶向下的属性翻译
语法成分翻译子程序参数设置:
–
–
继承属性为值形参
综合属性为变量形参
•
语法成分翻译动作子程序参数设置:
–
–
继承属性为值形参
综合属性不设形参,而作为动作子程序的返回值
(
由RETURN语句返回)
北京航空航天大学计算机学院
2

1
0.1 语义分析的概念
1
2
3
、上下文有关分析:即标识符的作用域
、类型的一致性检查
、语义处理:
声明语句:其语义是声明变量的类型等,并不要求
做其他的操作。
编译程序的工作是填符号表,登录名字
的特征信息,分配存储。
执行语句:语义是要做某种操作。
语义处理的任务:按某种操作的目标结构
生成代码。
北京航空航天大学计算机学院
3

用上下文无关文法只能描述语言的语法结构,
而不能描述其语义。
例如,对于有嵌套子程序结构的程序段:
BEGIN … BEGIN αINT I βI END … I … END
若存在文法规则:VAR ::= I
第一次I的归约正确
第二次I的归约错误
BEGIN … <BLOCK> … I ... END
BEGIN … δVAR ... END
δ∈V*且不包含变量I的声明
文法规则应改为:INT I βVAR ::= INT I βI
北京航空航天大学计算机学院
4
然而上下文有关文法不仅构造困难,
而且其分析器十分复杂,分析效率又低,
显然是不实用的
因此,通常我们把与语义相关的上下文有关
信息填入符号表中,并通过查符号表中的这些信
息来分析程序的语义是否正确
北京航空航天大学计算机学院
5

1
0.2 栈式抽象机及其汇编指令
栈式抽象机:由三个存储器、一个指令寄存器
和多个地址寄存器组成。
存储器: 数据存储器 (存放AR的运行栈)
操作存储器 (操作数栈)
指令存储器
北京航空航天大学计算机学院
6
计算机的存储大致情况如下:
栈底
运行栈
P-code指令
BP
SP
当前模块活动
记录(数据段)
NP
PC
堆
(堆底)
程序指令存储器
北京航空航天大学计算机学院
7
栈式抽象机指令代码如下:
指令名称
加载指令
操作码
地址
指令意义
LOD
D
将D 的内容→栈顶
立即加载
地址加载
存储
LDC
LDA
STO
ST
常量
(D)
D
常量→栈顶
变量D 的地址→栈顶
存入
栈顶内容 →变量D
间接存
间接存
加
@D
将栈顶内容→D 所指单元
将栈顶内容→次栈顶所指单元
栈顶和次栈顶内容相加,结果留栈顶
次栈顶内容减栈顶内容
STN
ADD
SUB
MUL
减
乘
…
……
北京航空航天大学计算机学院
8

指令名称
等于比较
操作码
地址
指令意义
EQL
不等比较
大于比较
小于比较
大于等于
小于等于
NEQ
GRT
LES
GTE
LSE
次栈顶内容与栈顶内容比较,
结果(1 或0)留栈顶
逻辑与
逻辑或
逻辑非
转子
AND
ORL
NOT
JSR
lab
M
分配
ALC
在运行栈顶分配大小为M 的活动记录区
北京航空航天大学计算机学院
9
1
0.3 声明的处理
语义的表示:
给出语言结构的属性翻译文法来说明其语义及语义动作,
并把这些语义动作插入属性翻译文法产生式中的适当位置。
编译程序的任务:
•
•
编译程序处理声明语句要完成的主要任务为:
1
2
) 分离出每一个被声明的实体,并把它们的名字填入符号表中
) 把被声明实体的有关特性信息尽可能多地填入符号表中
对于已声明的实体,在处理对该实体的引用时要做的事情:
1
2
) 检查对所声明的实体引用(种类,类型等)是否正确
) 根据实体的特征信息,例如类型,所分配的目标代码地址(可能
为数据区单元地址,或目标程序入口地址)生成相应的目标代码
北京航空航天大学计算机学院
1
0

声明有常量声明,变量(包括简单变量,数组变量
和记录变量等)和过程(函数)声明等,这里主要讨论
常量声明和简单变量、数组声明的处理。
声明的两种方式:
(1) 类型说明符放在变量的前面。如:C语言: int a;
在填表时已知类型和a的值(名字):直接填入符号表。
(2) 类型说明符放在变量的后面,如:Pascal, PL/1,Ada
等,需要返填。
如PL/I声明语句:
DECLARE( X, Y(N), YTOTAL) FLOAT;
北京航空航天大学计算机学院
11

声明语句的输入文法为:
<
<
<
declaration>→DECLARE ‘ (’<entity list>‘)’<type>
entity list>→<entity name> | <entity name> , <entity list>
type>→FIXED | FLOAT | CHAR
属性翻译文法为:
declaration>→DECLARE @dec_on ‘ (’<entity list> ‘)’
<
↑
x
<
type> @fix_up
↑
t
↓x, t
<
<
entity list>→<entity name> @name_defn
↑
n
↓n
|
<entity name> , @name_defn <entity list>
↑
n
↓n
type> →FIXED | FLOAT | CHAR
↑
t
↑t
↑t
↑t
北京航空航天大学计算机学院
1
2

动作程序
dec_on 是把符号表当前可用表项的入口地址(指向符
@
↑
x
号表入口的指针,或称 表项下标值)赋给属性变量x 。
@
name_defn 是将由各实体名所得的n继承属性值,依次填
↓
n
入从x开始的符号表中。
注:显然应有内部计数器或内部指针,指向下一个该填的符号表项。
@
fix_up 是将类型信息t 和相应的数据存储区分配地址填入
↓
x, t
从x 位置开始的符号表中。(反填)
当然,如果声明语句中,类型说明符放在头上,就无需“反填”处理了。
北京航空航天大学计算机学院
1
3

1
0.3.1 常量类型声明处理
常量标识符通常被看作是全局名。
常量声明的ATG如下:
const del> →constant <type> <entity> :=<const expr>
↑c, s
<
↑
t
↑n
@insert↓
;
t,n,c,s
<
<
type> →real |integer |string
↑t ↑t ↑t
↑
t
const expr> →<integer const > |<real const>
↑
c, s
↑c, s
↑c, s
|
<string const>↑c, s
由该文法产生的一个声明实例为:
constant integer SYMBSIZE := 1024;
北京航空航天大学计算机学院
1
4

翻译处理过程为:
const del> →constant <type> <entity> :=
<
↑
t
↑n
<
const expr> @insert
c, s
↓t,n,c,s ;
↑
先识别类型(integer),将它赋给属性t;然后识别常量名字
SYMBSIZE), 将它赋给属性n;最后识别常量表达式,并将
(
其值赋给c,其类型赋给属性s 。
★
@insert 的功能是:
①
检查声明的类型t 和常量表达式的类型s 是否一致,若
不一致,则输出错误信息
②
把名字n,类型t 和常量表达式的值c 填入符号表中
北京航空航天大学计算机学院
1
5

1
0.3.2 简单变量声明处理
ATG文法:
svar del> →<type> <entity> @svardef
<
↑
t , i
↑n
↓t, i, n
@
allocsv↓
;
i
<
type> →real |integer |character (<number>)
↑
t, i ↑t, i ↑t, i ↑t ↑i
|
logical
↑
t, i
n: 变量名
t: 类型值
简单变量声明的例子:
real x ;
i: 该类型变量所需
数据空间的大小
integer j;
character ( 20 ) s ;
北京航空航天大学计算机学院
1
6

@svardef动作符号是把n,i 和t 填入符号表中。
procedure svardef( t, i, n );
j := tableinsert ( n, t, i ); /*将有关信息填入符号表*/
if j = 0
then errmsg ( duplident , statementno);
else if j = -1 //符号表已满
then errmsg( tblovflow, statementno);
end svardef;
//填表时要检查是否重名
procedure allocsv( i );
codeptr := codeptr + i ; //codeptr 为分配地址指针
end allocsv;
@allocsv 和@svardef 可以合并
北京航空航天大学计算机学院
1
7

对于变长字符串(或其它大小可变的数据实体),往往需要
采用动态申请存储空间的办法把可变长实体存储在堆中。我们可
通过指向存放该实体数据区的指针来引用该实体,有时还应得到
该实体存储空间的大小信息,并一起填入符号表内。
1
0.3.3 数组变量声明的处理
对于静态数组,即数组的大小在编译时是已知的,编译程序
在处理数组声明时,可建立一个数组模板(又称为数组信息向量)
以便以后的程序中引用该数组元素时,可按照该模板提供的信
息,计算数组元素(下标变量)的存储地址。
对于动态数组,其大小只有在运行时才能最后确定。我们
在编译时仅为该模板分配一个空间,而模板本身的内容将在运
行时才能填入。
北京航空航天大学计算机学院
1
8

大部分程序设计语言,数组元素是按行(优先)存放在存储器
中的*,如声明数组 array B ( N, -2: 1 ) char ;
B:
实际数组B各元素的存储次序为:
LOC→
LOC是数组首地址
(该数组第一个元素的地址)
FORTRAN 例外,
它按列(优先)存放数组元素
*
北京航空航天大学计算机学院
1
9
a)n维数组的地址计算公式
设数组的维数为n, 各维的下界和上界为L(i)和U(i)
例如, 上例二维数组B
L(1) = 1 (隐含值), U(1) = N
L(2) = -2 ,
U(2) = 1
还假定n维数组元素的下标为V(1), V(2),…, V(n)
则该数组元素的地址计算公式为:
注:E为数组元素
大小(字节数)
n
ADR LOC [V ( i ) L( i )] P ( i ) E
i 1
其中
1
当i =n时
P(i) =
n
[
U( j) L( j) 1]
当1 ≤i <n 时
ji1
北京航空航天大学计算机学院
2
0
L(3)
U(3)
U(1)
v2
P(1)
v3
A(v1,v2,v3)
v1
L(2)
U(2)
[
V(1)-L(1) ]*[U(2)-L(2)+1]*[U(3)-L(3)+1]*E+
V(2)-L(2) ]*[U(3)-L(3)+1]*E+
V(3)-L(3) ]*1*E
[
[
L(1)
n
P(2)
ADR LOC [V ( i ) L( i )] P ( i ) E
i 1
其中
1
当i =n时
P(3)
P(i) =
n
[
U( j) L( j) 1]
当1 ≤i <n 时
ji1
北京航空航天大学计算机学院
2
1
(不变部分)
若令
n
RC L(i) P(i) E
i1
n
则地址
ADR LOC RC V(i) P(i) E
i1
RC为数组元素地址计算公式中的不变部分。因为,只要知道
数组的维数和每一维的上下界值,便可求得RC值。
以前面所举的二维数组B为例,若N = 3
2
RC = L(i)P(i)* E
则 P(1) = [U(2) - L(2) +1]
1- (-2)+1
P(2) = 1
i1
=
=
=
-[ 1×4 +(-2)×1]×E
-2E
=
4
因此, 若有数组元素B( 2 , 1 ), 则它的地址为:
2
ADR LOC 2E V(i) p(i) E =
=
LOC + 7×E
北京航空航天大学计算机学院
LOC – 2E+(2×4+1×1)×E
i1
2
2

L(3)
U(3)
U(1)
数组模板的一般形式如
下左图所示,而对于数组
B的模板如下右图所示:
v2
v3
A(v1,v2,v3)
v1
L(2)
U(2)
array B (3, -2: 1 ) char ;
1
-
2
L(1)
1
三维数组的例子
3
1
4
2
数组信息向量表
-
2
北京航空航天大学计算机学院
2
3
b) 数组信息向量表(模板)
U(n)
L(n)
P(n)
上界
下界
计算地址用
常量
功能:1、用于计算下标变量地址
2
、检查下标是否越界
.
..
.
...
一般形式:
U(1)
L(1)
P(1)
n
大小:3n + 2
RC
注:1、数组模板所需的空间大小取决于数组的维数,即3n+2
无论是常界或变界数组,在编译时就能确定数组模板的大小
、常界数组,在编译时就可造信息向量表;而变界数组信息向量
2
表要在目标程序运行时才能造。编译程序要生成相应的指令
北京航空航天大学计算机学院
2
4
以前面所举的二维数组B为例,若N = 3
P(2) = 1
数组信息向量表
P(1) = [U(2) - L(2) +1]
=
=
1- (-2)+1
4
1
U(2)--上界
L(2)--下界
-
2
1
3
1
4
2
P(2)--计算地址常量
U(1)--
L(1)--下界
2
RC =
L(i)P(i)
上界
i1
P(1)--
计算地址常量
=
=
-[ 1×4 +(-2)×1]
n---维数
-2
-
2
RC
北京航空航天大学计算机学院
2
5
数组声明的ATG文法:
<
<
<
array del> →array @init <entity> ( <sublist> )
↑
k
↑j
↑n
↑j
<
type> @symbinsert
↑
t
↓j, n, t
sublist> →<subscript> @dimen#
↑
j
↑j
|
<subscript>, <sublist> @dimen#
↑
j
↑j
subscript> →<integer expr> @bannds
↑
u
↓u
|
<integer expr> : @lowerbnd
↑
l
↓l
<
integer expr> @upperbnd
↑
u
↓u, l
1
) 动作程序@init 的功能为在分配给数组模板区中保留两个存
储单元,用来放RC 和n, 并将维数计数器j 清0。
2
) @dimen# : j := j + 1, 即统计维数
↑
j
北京航空航天大学计算机学院
2
6

1
) @init:
p:= p+2;
j := 0; /*维数计数器*/
U(n)
L(n)
P(n)
.
..
活动
记录
数组
信息表
....
U(1)
L(1)
P(1)
n
RC
运行栈指针p
北京航空航天大学计算机学院
2
7
3
) @bannds将省略下界表达式情况的u => U(i),但应把相应的L(i)
置成隐含值1, 然后计算P(i )
实际P(i)计算公式可利用P(i)=[ U(i+ 1) - L(i +1) +1]×P(i+1)
1
当i =n 时
P(i) =
n
[
U( j) L( j) 1]
当1 ≤i <n 时
ji1
注:由于P(i)的计算要依赖于P(i +1 ), 所以实际P(i)的值是反填的
4
) @lowerbnd 把l => L(i )
@
upperbnd 把u => U(i ), 并计算P(i )
5
) 最后的动作程序@symbinsert是把数组名n,数组维数j 和数
组
间
元素类型t 及数组标志k 填入符号表中 ;为数组分配存储空
北京航空航天大学计算机学院
2
8

对于变界数组:
4
) @lowerbnd↓l
生成将l => L(i ) 的代码
upperbnd↓u
@
生成把u => U(i )的代码,
生成计算P(i )的代码;
生成将P(i )的值送模板区的代码;
5
) @symbinsert↓j, n, t
a) 把n, j, t, 填入符号表中
b) 生成调用运行子程序代码(计算RC, 并将计算结果和数组
名一起存入模板区;计算数组所需数据区大小,为数组分
配存储空间,并将头地址填入符号表。)
北京航空航天大学计算机学院
2
9

1
0.4 表达式的处理
分析表达式的主要目的是生成计算该表达式值的代码。通
常的做法是把表达式中的操作数装载(LOAD)到操作数栈
或运行栈)栈顶单元或某个寄存器中,然后执行表达式所指
(
定的操作,而操作的结果保留在栈顶或寄存器中。
注:操作数栈即操作栈,它可以和前述的运行栈
(动态存储分配)合而为一,也可单独设栈。
本章中所指的操作数栈实际应与动态运行(存储分配)栈分开。
请看下面的整型表达式ATG文法:
北京航空航天大学计算机学院
3
0

1
2
3
4
5
6
7
8
9
1
.<expression>→<expr>
.<expr>→<term><terms>
.<terms>→ε
procedure lookup(n);
string n; integer j;
j:= symblookup( n);
.
.
| +<term>@add<terms>
| - <term>@sub<terms>
/*名字n表项在符号表中的位置*/
if j < 1
then /*error*/
else return (j);
.<term>→<factor><factors>
.<factors>→ε
.
.
| *<factor>@mul<factors>
| /<factor>@div<factors>
end;
0.<factor>→<variable> @lookup
↑
n
↓n↑j
procedure push(j);
@
push↓j
integer j;
1
1.
| <integer> @pushi
↑
i
↓i
emit(‘LOD’, symbtbl (j).objaddr);
end;
12.
| (<expr>)
有关的语义动作为:
procedure pushi(i); /*压入整数*/
procedure add;
emit(‘ADD’);
end;
integer i;
emitl(‘LDC’, i) ;
end;
procedure mul;
emit(‘MUL’);
end;
北京航空航天大学计算机学院
3
1

对于输入表达式x + y * 3, 可以生成如下目标代码:
LOD, < ll, on> x
LOD, < ll, on> y
LDC, 3
MUL
ADD
上面所述的表达式处理实际上忽略了出现在表达式中各操
作数类型的不同,且变量也仅限于简单变量。
下面假定表达式中允许整型和实型混合运算,并允许在
表达式中出现下标变量(数组元素)。因此应该增加有关类
型一致性检查和类型转换的语义动作,也要相应产生计算下
标变量地址和取下标变量值的有关指令。
北京航空航天大学计算机学院
3
2

<
<
<
expression>→<expr>
↑
t
expr> →<term> <terms>
↑
t
↑s
↓s ↑t
terms> →@echo
↓
s ↑u
↓s ↑u
|
|
+ <term> @add
<terms>
<terms>
↑
t
↓t, s ↑v
- <term> @sub
↓t, s ↑v
↓v ↑u
↓v ↑u
↑
t
<
term> →<factor> <factors>
↑
u
↑s ↓s ↑u
<
factors> →@echo
↓
s ↑u
↓s ↑u
|
|
*<factor> @mul
<factors>
↓t, s ↑v ↓v ↑u
↑
t
/<factor> @div
<factors>
↑
t
↓t, s ↑v
↓v ↑u
<
factor> →<variable> @type
↑
t
↑i ↓i↑t
|
|
<integer> @pushi
↑
i
↓i ↑t
<real> @pushi
↑
r
↓r ↑t
<
variable> →<identifier> @lookup ↓n ↑j @push ↓j
↑
j
↑n
|
<identifier> @lookup (@template ↓j ↑k<sublist> ↓k, j)
↓n ↑j
↑
n
<
sublist> →<subscript> @offset ↓k, t ↑i <subscripts>
k, j ↑t ↓i, j
↓
<
subscripts> →@checkdim
↓
k, j
↓k, j
|
, <subscript> @offset ↓k, t ↑i <subscripts>
↓i, j
↑
t
<
subscript> →<expr>
↑
t
↑t
北京航空航天大学计算机学院
3
3

procedure offset( k, t );
integer k; string t;
k := k+1;
语义动作add等应作相应改变:
procedure add( t, s);
string t, s;
if t = ‘real ’ and s = ‘integer’
then begin
if t ≠ ‘ integer’
then errmsy(‘数组下标应为整
型表达式’, statno);
else emitl( ‘OFS’, k );
return (k);
emit( ‘CVN’); /*次栈顶转为实数*/
emit( ‘ADD’);
return ( ‘real’);
end;
procedure checkdim( k, j);
integer k, j;
end;
if k ≠ symbtbl (j).dim
then errmsy(‘数组维数与
声明不匹配’, statno);
else begin
if t = ‘integer ’ and s = ‘real’
then begin
emit( ‘CNV’); /*栈顶转为实数*/
emit( ‘ADD’);
return ( ‘real’);
emit( ‘ARR’);
emit( ‘DER’);
end;
end;
emit( ‘ADD’);
return ( t);
end;
procedure template(j);
integer j;
end;
emitl( ‘TMP’, symbtbl (j). objaddr);
k:= 0; /*维数计数器初始化*/
return(k);
北京航空航天大学计
3
4
end;
★
过程template发送一条目标机指令‘TMP’, 该指令把数组的模
板地址加载到操作数栈顶,并将下标(维数)计数器k清0。
★offset过程要确保每一个下标都是整型,而且发送一条‘OFS’
指令,该指令在运行时要完成以下功能:
1
2
. 检查第k个下标值是否在栈顶并是否在上下界范围内
.使用下列递归函数,计算地址计算公式中可变部分:
VP(0) = 0;
VP(k) = VP(k-1) + V(k) *P(k) 1≤k≤n
n
该VP函数是由计算公式
V (k) P(k)
导出的
k 1
北京航空航天大学计算机学院
3
5

(d)
下面以数组元素B(2,1)为例,说明
B(2,1)值
→
(
(
(
(
a)执行TMP指令并形成第一个下标值的情况
b)执行第一 个OFS指令并形成第二个下标值的情况
c)执行第二个OFS指令及ARR指令后的情况
.
.
.
d)执行DER指令,最后在栈顶形成下标变量B(2,1)的值
数据栈
(c)
1
U(2)
L(2)
P(2)
U(1)
L(1)
P(1)
#dim
RC
(a)
V(2)→
1
-
2
8
+1=9
VP(2)→
1
3
1
4
2
LOC+(-2)+9
=LOC+7
locB
.
.
.
V(1)→
VP(0) →
2
0
locB
(b)
locB
栈底
-2
.
.
.
.
.
.
V(2)→
VP(1)→
1
2*4=8
locB
栈底
B的模板
.
.
.
操作数栈
栈底
北京航空航天大学计算机学院
3
6
处理逻辑表达式(关系表达式)的方法与处理算术表达式
的方式基本相同。下面是逻辑表达式~( x =y & y≠z | z<x)
生成的指令序列:
LOD, ( ll, on )x
LOD, ( ll, on )y
EQL
LOD, ( ll, on )y
LOD, (ll, on )z
NEQ
AND
LOD, ( ll, on )z
LOD, ( ll, on )x
LES
ORL
NOT
北京航空航天大学计算机学院
3
7

1
0.5 赋值语句的处理
X:= Y+X;
<
assignstat >→@setL ↑L<variable>↓L↑t:=
LDA ( ll, on )x
LOD ( ll, on )y
LOD ( ll, on )x
ADD
@resetL <expr> @storin ;
↑
L
↑s
↓t,s
STN
@
setL是设置变量为“左值”(被赋变量),即将属性L置true
resetL是设置变量为非被赋变量,即把属性L置成false
@
procedure setL;
return (true );
end;
procedure resetL; procedure storin(t,s);
return (false );
end;
string t, s;
if t ≠ s
指示取变量地址 指示取变量之值
then /*生成进行类型转换的指令*/
emit(‘STN’);
北京航空航天大学计算机学院
end;
3
8

1
0.6 控制语句的处理
0.6.1 if语句
1
JMF, labA
IF <log_expr> THEN <stat_list> labA:
JMF, labA
IF <log_expr> THEN <stat_list> ELSE labA: <stat_list> labB:
JMP, labB
其属性翻译文法及相应的语义动作程序:
1
2
3
. <if_stat>→<if_head> <if_tail>
↑
y
↓y
. <if_head> →IF <log_expr>@brf THEN <stat list>
↑
y
↑y
. <if_tail> →@labprod
↓
y
↓y
|
ELSE @br @labprod <stat_list>@labprod
z
↓y ↓z
39
↑
动作程序@brf的功能是生成
JMF指令,并将转移标号返回给属性y
动作程序@br是是生成JMP指
令,并将转移标号返回给属性z
procedure brf;
string labx;
labx := genlab;
procedure br;
string labz;
labz := genlab;
emitl( ‘JMP’, labz);
return( labz);
end;
/*产生一标号赋给labx*/
emitl(‘JMF’, labx);
return (labx);
end;
动作程序@labprod是把从继承属
性y得到的标号设置到目标程序中
procedure labprod(y);
string y;
setlab(y);
/*在目标程序当前位置设标号*/
end;
北京航空航天大学计算机学院
4
0

1
0.6.4 for 循环语句
ATG文法
for 语句例子:
for i:= 1 to n by z do
<
statement>
..
end for;
.
1
2
.<for loop>→<for head>↑a, f, r < rest of loop>↓a, f, r
.<for head> →for <id> := <expr> @initload
↑
a, f, r
↑a
↑s
to @labgen <expr> by
↑
r
@
loadid <expr> @compare
↓
a
↓a, s↑f
3
.<rest of loop> →do <stat list> end for
↓
a, f, r
@
retbranch @labemit
↓
r
↓f
@initload 只生成给循环变量赋初值的指令。
北京航空航天大学计算机学院
4
1

for <id> := <expr1> to <expr2> by <expr3> do <stat list>
LDA, (<id>)
LOD, (expr1)
STN
@
initload↑s
JMP, start
loop:
@labgen↑
r
LOD, (expr2)
@
loadid↓aLOD, (id)
LOD, (expr3)
ADD
STO, (id)
@
compare
↓
a,s↑f
BGT, end_loop
start: <statement>
…
@
retbranch↓r
JMP, loop
labprod↓
end_ loop:
f
4
2
@
procedure compare( a, s);
address a; string f, s;
emit( ‘ADD’);
emitl( ‘STO’, a );
f := genlab;
procedure labgen
string r;
r := genlab;
setlab(r);
return ( r );
end;
emitl( ‘BGT’, f );
setlab( s );
return( f );
end;
procedure loadid( a )
address a;
emitl( ‘LOD’, a);
end;
procedure labprod( f ) // 即labemit
string f;
setlab( f );
end;
北京航空航天大学计算机学院
4
3

1
0.7 过程调用和返回
1
1
0.7.1 参数传递的基本形式
.传值(call by value) — 值调用
实现:
调用段(过程语句的目标程序段):
计算实参值=> 操作数栈栈顶
被调用段(过程说明的目标程序段):
从栈顶取得值=> 形参单元
过程体中对形参的处理:
对形参的访问等于对相应实参的访问
特点:
如C语言,
Ada语言的in参数,
Pascal 的值参数。
数据传递是单向的
北京航空航天大学计算机学院
4
4

2
.传地址(call by reference) — 引用调用
实现:
调用段:
如:FORTRAN,
Pascal 的变量形参。
计算实参地址=> 操作数栈栈顶
被调用段:
从栈顶取得地址=> 形参单元
过程体中对形参的处理:
通过对形参的间接访问来访问相应的实参
特点:
结果随时送回调用段
如:ALGOL 的
换名形参。
3
. 传名(call by name )
又称“名字调用”。即把实参名字传给形参。这样在过程体中引用形参
时,都相当于对当时实参变量的引用。
当实参变量为下标变量时,传名和传地址调用的效果可能会完全不同。
传名参数传递方式,实现比较复杂,其目标程序运行效率较低, 现已很少
采用。
北京航空航天大学计算机学院
4
5

1
0.7.2 过程调用处理
例:有过程调用:
process_symb(symb, cursor,replacestr);
与调用有关的动作如下:
调用该过程生成的目标代码为:
1. 检查该过程名是否已定
义(过程名和函数名不能
LOD, (addr of symb )
传值调用
LOD, (addr of cursor )
用错) 实参和形参在类型、 LOD, (addr of replacestr)
JSR, ( addr of process_symb)
顺序、个数上是否一致。
(查符号表)
<retaddr>:….
若实参并非上例中所示变量,
而是表达式,则应生成相应计算
实参表达式值的指令序列。
2
3
4
. 加载实参(值或地址)
. 加载返回地址
JSR指令先把返回地址压入操
作数栈,然后转到被调过程入口
地址。
.转入过程体入口地址
北京航空航天大学计算机学院

设过程说明的首部有如下形式:
procedure process_symb(string:symbal, int: cur, string: repl);
则过程体目标代码的 ALC, 4 + x /* x为定长项空间*/
STO, <actrec loc1> /* 保存返回地址*/
STO, <actrec loc4> /* 保存replacestr */
STO, <actrec loc3> /* 保存cursor */
STO, <actrec loc2> /* 保存symb */
开始处应生成以下指令,
以存储返回地址和形参
的值。
过程调用时,实参加载指令是把实参变量内容(或地址)
送入操作数栈顶,过程声明处理时,应先生成把操作数栈顶的实参
送运行栈AR中形参单元的指令。
将操作数栈顶单元内容存入运行栈(动态存储分配的数据区)
当前活动记录的形式参数单元。
可认为此时运行栈和操作数栈不是一个栈(分两个栈处理)
北京航空航天大学计算机学院
4
7

过程调用的ATG文法:
<
<
<
<
<
proc call>→<call head>↑i , z @initm↑m<args>
call head> →<id> @lookupproc
@genjsr↓i
↓i , z
↑
i , z
↑n
↓n↑i, z
args> →@chklength | (<arg list>↓i, z)
↓i , z
↓
i,z
arg list> →<expr> @chktype
<exprs>↓i , z
<exprs>↓i , z
↓
i , z
↑t
↓t, i, m, z↑z
exprs> →@chklength
↓
i , z
↓i , z
|
, <expr> @chktype
↑
t
↓t, i, m, z↑z
procedure lookupproc(n);
string n; integer i, z;
i := lookup(n); /*查符号表*/
if i < 1
then begin
error( ‘过程’, n ,‘未定义’, statno);
errorrecovery( panic ); /*应急处理过程*/
return ( i := 0, z:= 0);
end
else return( i , z:= symtbl [i].dim); /* z为形参数目*/
end;
48

LOD, (addr of symb )
LOD, (addr of cursor )
LOD, (addr of replacestr)
JSR, ( addr of process_symb)
procedure chktype(t, i, m, z);
string t; integer m, i, z;
if z < 1
<retaddr>:….
then begin
error( ‘实参数大于形参数’, symtbl [i].name, statno);
return ( z);
end
m := m+1;
/* 实参计数*/
if t ≠symtbl [i+m].type
then error(‘实参和形参类型不匹配’, symtbl [i+m].name, statno);
z := z-1;
return (z);
/* 减去已匹配的形参数*/
/* 剩下待匹配的形参数*/
end;
@
@
chklenth 应检验z最后值为0。否则表示实参数目小于形参数目。
genjsr 生成JSR指令。该指令转移地址为symbtbl [i] .addr
北京航空航天大学计算机学院
4
9

过程说明(定义)的ATG文法如下:
<
proc defn>→<proc defn head> @initcnt↑j
parameters>↓j↑k @emitstores↓k
proc defn head>→procedure <id> @tblinsert
↓t, n
<
<
<
<
↑
t
↑n
parameters> →@echo | (<parm list>↓j↑k)
↓j↑k
↓
j↑k
parm list> →<type> : <id> @tblinsert
↓
j↑l
↑t
↑n
↓t, n
@
upcnt↓j↑k <parms>↓k↑l
<
parms> →@echo
| , <type> : <id> @tblinsert
↓j↑l ↑t ↑n ↓t, n
↓
j↑l
@
upcnt↓j↑k <parms>↓k↑l
@tblinsert 是把过程名和它的形参名填入符号表中:
procedure tblinsert( t, n );
string t, n; integer hloc;
if lookup ( n ) > 0
hashtbl[hloc] := s; /*s为符号表指针
(下标), 为全局量*/
symbtbl [s].name:= n;
symbtbl [s].type:= t;
s := s+1;
then error( ‘名字定义重复’, statno);
else begin
hloc := hashfctn(n); /*求散列函数值*/ end;
5
0

symbtbl
procedure emitstores(k);
integer k;
hashtbl
5
1
2
3
4
1
2
3
4
5
.
emitl( ‘ALC’, k + x +… );
emitl( ‘STO’, < ll, x+1 >);
s: 5 n
6
t
…← s
/
*保存返回地址*/
for i := k + x+1 down to x+2
*保存参数值*/
emitl( ‘STO’, < ll , i > )
end;
end;
.
.
.
.
.
.
.
.
.
.
.
/
m
ALC, 4 + x /* x为定长项空间*/
STO, <actrec loc1> /* 保存返回地址*/
STO, <actrec loc4> /* 保存replacestr */
STO, <actrec loc3> /* 保存cursor */
STO, <actrec loc2> /* 保存symb */
注:实际ALC指令所分配的空间应在
所有局部变量定义处理完以后,并考
虑固定空间(前述‘x’)大小,反填
回去。
北京航空航天大学计算机学院
5
1
1
0.7.3 返回语句和过程体结束的处理
其语义动作有:
1
) 若为函数过程,应将操作数栈(或运行栈)顶的函数
结果值送入(存回)函数值结果单元
2
3
) 生成无条件转移返回地址的指令(JMP RA)
) 产生删除运行栈中被调用过程活动记录的指令
(
只要根据DL—活动链,把abp退回去即可)
北京航空航天大学计算机学院
5
2

第十一章 代 码 优 化
•
•
•
•
概述
优化的例子
基本块的优化
循环优化
北京航空航天大学计算机学院
1

1
1.1 概述
代码优化(code optimization)
指编译程序为了生成高质量的目标程序而做的
各种加工和处理。
时间效率(减少运行时间)
目的:提高目标代码运行效率
空间效率(减少内存容量)
原则:进行优化必须严格遵循“不能改变原有程序语义”原则。
北京航空航天大学计算机学院
2

分类:
从优化的层次,与机器是否有关,分为:
独立于机器的优化:即与目标机无关的优化,通常是在中间代码上进
行的优化。
与机器有关的优化:充分利用系统资源,(指令系统,寄存器资源)。
从优化涉及的范围,又分为:
局部优化:是指在基本块内进行的优化。
循环优化:对循环语句所生成的中间代码序列上所进行的优化。
全局优化:顾名思义,跨越多个基本块的全局范围内的优化。因此
它是指在非线性程序段上(包括多个基本块, GOTO, 循
环)的优化。需要进行全局控制流和数据流分析,复杂。
北京航空航天大学计算机学院
3

[
定义] 基本块( basic block )
满足以下三个条件的程序段,称为基本块:
•
只有一个入口和一个出口,且语句为顺序执行的
程序段。
•
所有转移语句的目的语句都是基本块的第一条语
句。
•
•
转移语句的下一条语句是基本块的第一条语句。
如果块中任一语句被执行,则该块内的所有语句
也将被执行(无分支),且执行次数一样(无循
环)。
北京航空航天大学计算机学院
4

例:书上的例子
1. FACTOR = 2
基本块
基本块
1⊕
2. EXP 1 =…
2
3
⊕
⊕
3. IF ( )GO TO 10
4. BASE = 2.0
⊕
⊕
⊕
4
5. FACTOR = FACTOR**2
1
0
⊕
⊕
6
. GO TO 20
0. BASE =…
5
11
6
1
基本块
基本块
⊕
⊕
2
0
1
11. FACTOR…
20. Q =
2
21. RETURN
(
先编号,后画图→决定基本块)
北京航空航天大学计算机学院
5
优化所花费的代价和优化产生的效果可用下图表示:
优化的
效果
局部优化 循环优化 全局优化
优化的
代价
北京航空航天大学计算机学院
6
•
图的左部表示只要做些简单的处理,便能得到明显
的优化效果。这相当于局部优化。
若要进一步提高优化效果,就要逐步付出更大的代
价——循环优化。
•
•
全局优化进一步提高。
北京航空航天大学计算机学院
7

为什么要优化?
•
有的大型计算程序一运行就要花上几十分钟,甚至好几
小时,这时为优化即使付出些代价也是值得的。
另外,程序中的循环往往要占用大量的计算时间。所以
为减少循环执行时间所进行的优化对减少整个程序的运
行时间有很大的意义。——尤其有实时要求的程序。如
市场决策,供需及求益的平衡
•
•
至于(像学生作业之类的)简单小程序(占机器内存,运行
速度均可接受),或在程序的调试阶段,花费许多代价
去进行一遍又一遍的优化就毫无必要了。
北京航空航天大学计算机学院
8

1
1.2 优化的基本方法和例子
注:实际的优化应在中间代码或目标代码上进行。但为
了便于说明,这里用源程序形式举例。
(
1)利用代数性质(代数变换)
•
编译时完成常量表达式的计算,整数类型与实型的转换。
例: a := 5+6+x → a := 11+x
又如: 设x为实型,x := 3+1 可变换成x := 4.0
• 下标变量引用时,其地址计算的一部分工作可在编译时
预先做好(运行时只需计算“可变部分”即可)。
北京航空航天大学计算机学院
9

• 运算强度削弱:用一种需要较少执行时间的运算代替另一
种运算,以减少运行时的运算强度时、空开销)
如
x**2 →x*x
3
8
*x →x+x+x
*x , 4*x 等换成左移运算
x/2 , x/16 等换成右移运算
x:=x+1 变为INC x指令
x/5 → x*0.2
等
利用机器硬件所提供的一些功能,如左移,右移操作,
利用它们做乘法或除法,具有更高的代码效率。
北京航空航天大学计算机学院
1
0

(
2) 复写(copy)传播
如x:=y这样的赋值语句称为复写语句。由于x和y值相同,所以当
满足一定条件时,在该赋值语句下面出现的x可用y来代替。
例如:
x:=y ;
u:=2*x ; → u:=2*y ;
v:=x+1 ; v:=y+1 ;
x:=y ;
这就是所谓的复写传播。(copy propagation )
若以后的语句中不再用到x时,则上面的x:=y可删去。
北京航空航天大学计算机学院
11

若上例中不是x := y而是x := 3。则复写传播变成了常量传播,即
u := 6;
v := 4;
x := y;
x := 3;
u := 2*x;
v := x+1;
u := 2*x;
v := x+1;
又如
t1 := y/z;
x := t1;
若这里t1为暂时(中间)变量,以后不再使用,则可变换为
x := y/z;
此外常量传播,引起常量计算,如:
pi = 3.14159
r = pi/180.0
此时:pi = 3.14159
r = 0.0174644 (常量计算)
北京航空航天大学计算机学院
1
2
(
3) 删除公共子表达式
具有相同值的子表达式在两个以上地方出现时,称它为
公共子表达式(common subexpression)
如赋值语句:
x := ( -y + z ) * z/2 - ( -y + z )
其中: (-y+z)是公共子表达式。
可用DAG (directed acyclic graph,有向无循环图)
来表示具有公共子表达式的抽象语法树。
北京航空航天大学计算机学院
1
3

x := (-y+z)*z/2-(-y+z)
:
=
x
-
显然,对于公共子表达
式只要计算1次即可
*
/
+
Y
Z
2
-
北京航空航天大学计算机学院
1
4
(
4) 删除冗余代码
冗余代码就是毫无实际意义的代码,又称死代码(dead code)或
无用代码(useless code)。
例如: x := x + 0 ;
x := x * 1 ; 等
又例:
FLAG := TRUE
IF FLAG
…
THEN…
FLAG永真
ELSE…
另外在程序中为了调试常有如下:
if debug then … 的语句。
但当debug为false时,then后面的语句便永远不会执行,
( 可用条件编译#if DEBUG 编写
程序,而源代码中还应留着)
这就是可删去的冗余代码。
北京航空航天大学计算机学院
1
5

(
5) 循环优化
经验规则告诉我们:“程序运行时间的80%是由仅占源程
序20%的部分执行的”。这20%的源程序就是循环部分,
特别是多重循环的最内层的循环部分。因为减少循环部
分的目标代码对提高整个程序的时间效率有很大作用。
for i = 1 to
for j = 1
10
to
100
x := x+0 ;
y := 5+7+x ;
优化一条,少10*100次运算
北京航空航天大学计算机学院
1
6
除了对循环体进行优化,还有专用于循环的优化
a) 循环不变式的代码外提
不变表达式:
不随循环控制变量改变而改变的表达式或子表达式。
如:FOR I := E STEP E TO E DO
1
2
3
BEGIN
不变表达式
可外提
S := 0.2*3.1416*R
P := 0.35*I
不能外提
V := S*P
…
…
北京航空航天大学计算机学院
1
7
如
while …
do
x := … (b*b - 4.0*a*c) …
若a,b,c的值在该循环中不改变时,则可将循环不变式
移到循环之外,即变为:
t1 := b*b - 4.0*a*c
while … do
x:= …( t1) …
从而减少计算次数——也称为频度削弱
北京航空航天大学计算机学院
1
8

b) 循环展开
循环展开是一种优化技术 。它将构成循环体的代码(不包括控制
循环的测试和转移部分),重复产生许多次(这可在编译时确
定),而不仅仅是一次,以空间换时间。
例 PL/1中的初始化循环 DO I = 1
TO
30
A[ I ] = 0.0
END
展开
I := 1
L1: IF I > 30 THEN 代码5条语句
A[1] = 0.0
30条语句
A[2] = 0.0 (指令)执行
GOTO L2
A[ I ] = 0.0
I = I+1
共执行5*30
……
也是30条语句
条语句
A[30] = 0.0
GOTO L1
1
9
L2:
•
循环一次执行5条语句才给一个变量赋初值。展开后,一条语句就能赋一
个值,运行效率高。
•
•
•
优化在生成代码时进行,并不是修改源程序。
必须知道循环的终值,初值及步长。
但并不是所有展开都是合适的。如上例中循环展开后节省执行了转移和
测试语句:2*30=60语句(其实,还不止节省60条)。
∴
增加29条省60条
但若循环体中不是一条而是40条语句,则展开后将有40*30条=1200,但省
的仍是60条,就不算优化了。
∴
判断准则:1. 主存资源丰富
循环展开有利
(大型机)
处理机时间昂贵
2. 循环体语句越少越好
北京航空航天大学计算机学院
2
0
实现步骤:
1
2
3
. 识别循环结构,确定循环的初值,终值和步长。
. 判断。以空间换时间是否合算来决定是否展开。
. 展开。重复产生循环体所需的代码个数。
比较复杂:
在对空间与时间进行权衡时,还可以考虑一种折衷的办法,即部分展开循
∵
环。如上例展为:
DO I = 1 TO 30 BY 3
A[I] = 0.0
空间只多二条,
但省了20次测
试时间
A[I+1] = 0.0
A[I+2] = 0.0
(只循环10次)
END;
北京航空航天大学计算机学院
2
1
c) 归纳变量的优化和条件判断的替换
归纳变量(induction varable): 在每一次执行循环迭代的
过程中,若某变量的值固定增加(或减少)一个常量值,
则称该变量为归纳变量(induction variable)。即若当前
执行循环的第j次迭代。归纳变量的值应为c*j+c’, 这里c
和c’都循环不变式。
例: for i := 1 to 10
do
a[i] := b[i] + c[i]
北京航空航天大学计算机学院
2
2

for i:= 1
to
10 do
1
)
i := 1
a[i] := b[i] + c[i]
2
3
4
5
6
)
labb:
1
)
u := 4
)
if i > 10 goto labe
t1 := 4*i
2
3
4
5
)
labb:
)
)
)
)
if u >40 goto labe
tb := b [u]
t := b [ t ]
2
优化:
1
)
)
t3 := 4*i
7
)
t := c [ t ]
4
tc := c [u]
3
8
)
t := t + t
4
5
2
6)
t := tb + tc
a [ u] := t
•
t6 := 4*i
a[t6] := t5
i := i+1
7
8
9
1
)
7
8
9
1
)
)
u := u+4
)
)
goto
labb
)
goto labb
0)
labe :
3) labe:
中间变量t1 ,t3 ,t6 都是归纳变量
t1 := 4*i , t3 := 4*i , t6 := 4*i
d) 其它循环优化方法
•
把多重嵌套的循环变成单层循环。
•
把n个相同形式的循环合成一个循环等。
对于循环优化的效果是很明显的。某FORTRAN 77 编译程序,在
进行不同级别的优化后所得的目标代码指令数为:
优化级别 循环内的指令数(包括循环条件判断)
0
1
2
3
(不优化)
21
16
6
5
北京航空航天大学计算机学院
2
4

(
6)in_line 展开
把过程(或函数)调用改为in_line展开可节省许多处理过程
(函数)调用所花费的开销。
如:procedure m( i , j : integer ; max : integer);
begin if i > j then max:=i else max:=j end;
若有过程调用 m ( k , 0, max );
则内置展开后为:
if k > 0 then max := k else
max := 0;
省去了函数调用时参数压栈,保存返回地址等指令。
这也仅仅限于简单的函数。
北京航空航天大学计算机学院
2
5

(
7)其他, 如控制流方法
如
BR L
…
无条件转移
——为不可达代 码
L :
又如:转移到转移指令的指令
BR L1
BR L2
优化
…
L1: BR
L2
L1: BR
L2
北京航空航天大学计算机学院
2
6
还有:
BRCC
BR
L1
L2
当条件CC成立,转到L1
L1: ….
可改进为:
BR ’
L2
当条件不能成立时 ,转到L2
CC
(L1:) …
北京航空航天大学计算机学院
2
7

总结:
局部优化: (一个入口,一个出口,线性)——基本块
方法:常数合并
冗余子表达式的削除等
与机器无关的
优化,即独立
于机器的(中
间)代码优化
循环优化:对循环语句所生成的中间代码序列上所进行的
优化
方法:循环展开
优化
分为
两大
类
频度削弱
循环不变表达式的外提
强度削弱
全局优化:顾名思义,跨越多个基本块的全局范围内的优
化。因此它是在非线性程序段上(包括多个基
本块,GOTO循环)的优化。
与机器有关的
优化,即目标
代码上的优化
(与具体机器
有关)
北京航空航天大学计算机学院
2
8
第十二章 编译程序生成方法和工具
•
•
•
•
•
编译程序的书写语言
自编译性
自展
编译程序的移植
编译程序的自动生成
北京航空航天大学计算机学院
1
12.1 编译程序的书写语言
•机器语言或汇编语言
主要优点:编出来的程序效率高。
主要缺点:编程效率低,可读性差,不便于修改和移植。
高级程序设计语言已基本取代汇编语言
优点:编程效率高,可读性好,利于移植。
缺点:编译程运行效率较低。
•
北京航空航天大学计算机学院
2

12.2 自编译性
自编译性:如果一个高级语言能用来书写自己的编译程序,则
该语言具有自编译性,并称该语言为自编译语言。
两点说明:
1
. 通常用自编译语言除可编写本语言的编译程序以外,也可用
来编写别的语言的编译程序。
∴如果某台机器上已配备有某种自编译语言,则可利用这种
语言为本台机器配置其它的高级语言。
北京航空航天大学计算机学院
3

例:A机上有自编译语言L1的编译程序
L1 . AO
L ——语言L 的编译程序
1
1
AO——以A机的机器指令形式给出
利用语言L 可为A机生成语言L 的编译程序
1
2
L2. L1
L1.AO
L2.AO
L1源程序
L2可执行的编译程序
A机
L2源程序
L2.AO
L2目标程序
A机
可在A机上运行
北京航空航天大学计算机学院
4
源语
言
目标语
言
书写语
言
(d)程序
(b)解释程序
(c)计算机
(a)编译程序
北京航空航天大学计算机学院
5
L2
Ao
L1
L2
Ao
L1
Ao
Ao
用Ao描述的L2语
言的编译器L2.Ao
用L1写的L2语言
的编译器L2.L1
Ao
Ao
运行Ao的
计算机
用Ao描述的L1语
言的编译器L1.Ao
f
f
L2
Ao
L2
Ao
Ao
Ao
北京航空航天大学计算机学院
6
2
.自编译性不是绝对的,只是强弱不同
数据类型丰富的语言
自编译性强
控制结构丰富的语言
数据类型:除一般的外还有字符串类型,数组,结构,枚举,指
针等类型。
控制结构:应适于进行多分支的程序设计,如有CASE语句等
FORTRAN , ALGOL——自编译性差
PASCAL , C , ADA,C++,JAVA——自编译性强
实践示例:用PASCAL语言编写一个简单的编译程序,就是利用
PASCAL的自编译性。
北京航空航天大学计算机学院
7

12.3 自展
利用高级语言的自编译性,还可以通过自展方式生成语言的
编译程序。
设L为自编译语言,自展生成
L. Ao(A机目标形式的语言L的编译器,可在A机上运行)
步骤:1.首先,将语言划分为N个部分:
L = L + L +…+ L
n
1
2
L1 ——核心部分
L ~L ——扩充部分
2
n
北京航空航天大学计算机学院
8

2
3
.先用A机上的汇编编写L 的编译程序,L .Aa
1
1
L .Aa→Assember→L .Ao
1
1
.用L 编写L +L 的编译程序
1
1
2
(L +L ). L
L1.Ao
(L +L ).Ao
1
2
1
1
2
4
.用(L +L )编写L +L +L 的编译程序
1
2
1
2
3
…
5
.
L. (L +L …+L )
(L +L …+L ).Ao
L.Ao
1
2
n-1
1
2
n-1
北京航空航天大学计算机学院
9
L.Ao
滚雪球式
…
….
用自展方式进行编译,可提高生产率。因核心语言小,可用汇
编实现。其余部分高级语言编写。比全用低级语言效率高。
北京航空航天大学计算机学院
1
0
12.4 编译程序的移植
移植:将某台机上的成熟软件移植到另一台机器上,也就是将
宿主机上的软件移植到目标机上。如果使用具有自编译性的高
级语言来书写程序,则移植是方便的。
移植
L. L
L.Ao
宿主机A
目标机B
L.Bo
通过移植,在B机上可得到语言L
的编译程序,具B机目标形式,可
在B机上运行。
北京航空航天大学计算机学院
11
移植步骤:
. 将L. L分为两部分:
1
一部分与机器无关F.L 一部分与机器有关 A.L
∴
L. L = F.L+ A.L
2
. 根据目标机用语言L改写与具体机器有关的部分:
L
A.L
B.L
产生A机代码 产生B机代码
∴交叉编译器: I.L= F.L+ B.L
用A机上的L语言所写的能生成B机目标代码的语言L的编译程序。
北京航空航天大学计算机学院
1
2

3
. 第一次编译
将I.L在宿主机A上用L的编译程序进行编译,生成能在宿主机A上
运行的语言L的交叉编译器,它能生成目标机B的代码。
I.L
L.Ao
I. Ao
语言L的交
叉编译器,
能在宿主机
A上运行,生
成目标机B的
代码
用L所写的生
成目标机B
代码的L语言
交叉编译器源
程序
宿主机A
的L编译
程序
北京航空航天大学计算机学院
1
3
4
. 第二次编译(交叉编译)
I.L
I. Ao
L.Bo
可在目标机B
上运行并生
成目标机B代
码的L编译
程序
A机
交叉编译程序:在宿主机A上运行,
但所生成的目标只能在目标机B
(
另一台机器)上运行。
北京航空航天大学计算机学院
1
4
L
Bo
L
Bo
L
Ao语言描述
的交叉编译
器I.Ao
L
Ao
Ao
L语言描述
的交叉编译
Ao
Ao
器
I.L
可在B机上运
行的L语言编
译器L.Bo
L
Bo
L
L
Bo
L
Bo
Bo
Ao语言描述
的交叉编译
Ao
L语言描述
的交叉编译
器I.L
Ao
器I.Ao
北京航空航天大学计算机学院
1
5
可以设想,只要在某台机器上为某目标机配置一个L语言的
交叉编译程序,就能将宿主机上的L语言所写的所有软件移植到
其他目标机上。
采用软件移植的办法来开发软件,可提高软件生产率,并提
高软件的可靠性。由于上述优点,所以软件的可移植性是软件开
发所追求的目标之一。
目前有许多编译程序都考虑到可移植性的要求。
例如有:可移植的PASCAL编译程序。
P.J.Brown , Software Portablility.
朱关铭等译,1982.12
北京航空航天大学计算机学院
1
6

12.5 编译程序的自动生成
理想的编译程序自动生成工具:
L源程序
该语言(L)
的编译程序
编译程序
生成工具
L语言规格说明
L语义描述和机器规格说明
目标代码
北京航空航天大学计算机学院
1
7
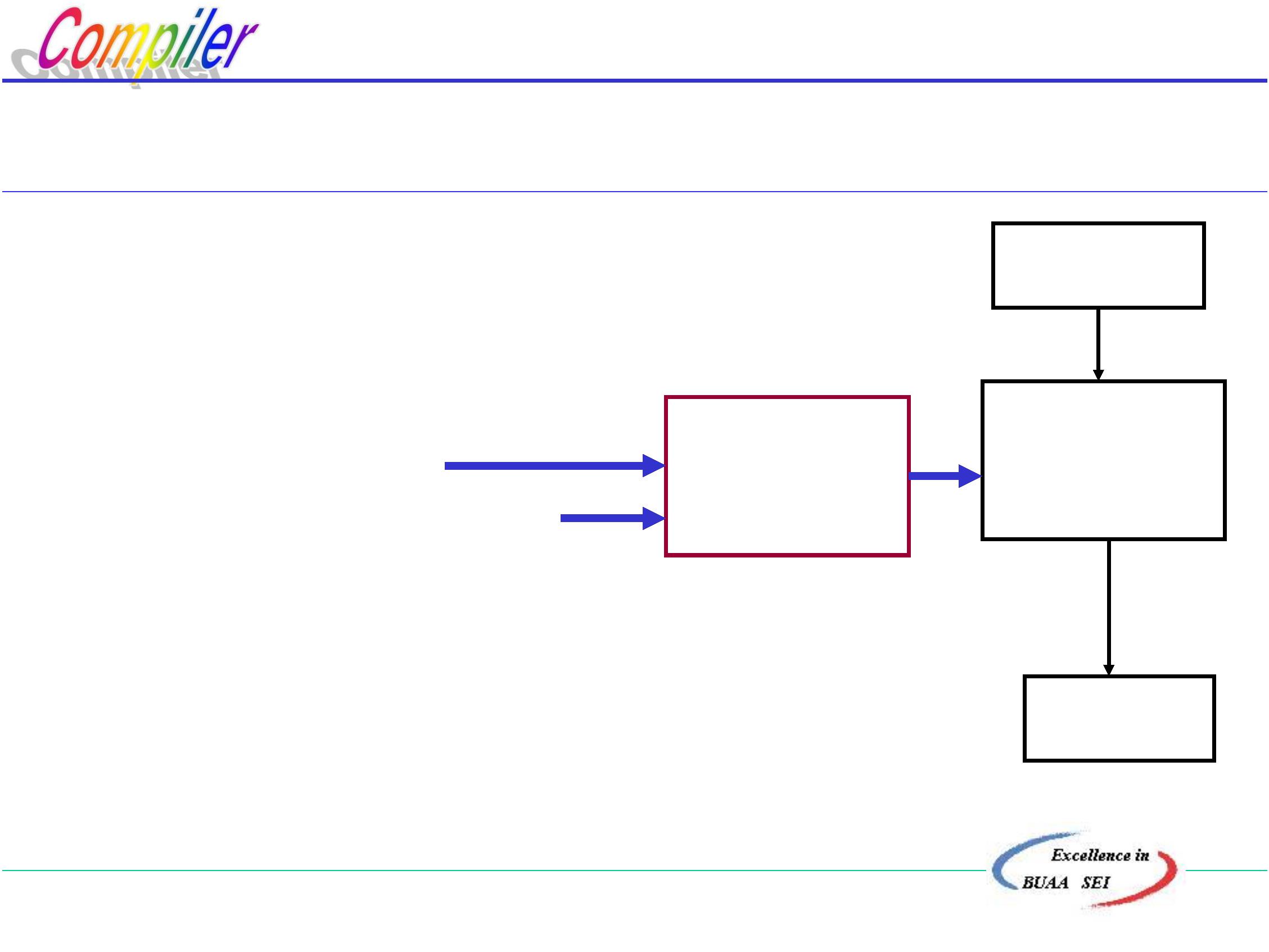
目前还没有一个系统能自动生成整个编译系统。
早期的工作集中在分析部分,即针对语法规则的形式化描述。
对编译程序后端,即与目标机有关的代码生成与代码优化部分,
由于对语义和目标机进行形式化描述方面所存在的困难,最近
有所突破,但未见到流行的产品。(样机——未形成真正产品)
•
有词法分析器的自动生成器和语法分析器的自动生成器。
词法分析器生成器(在第三章已作介绍)LEX:
LEX
词法分析器
lex.yy.c 文件)
(自动机)
LEX源文件(. l 文件)
(
(
构造识别单词符
号的自动机)
(正则表达式表示的单词符号)
北京航空航天大学计算机学院
1
8
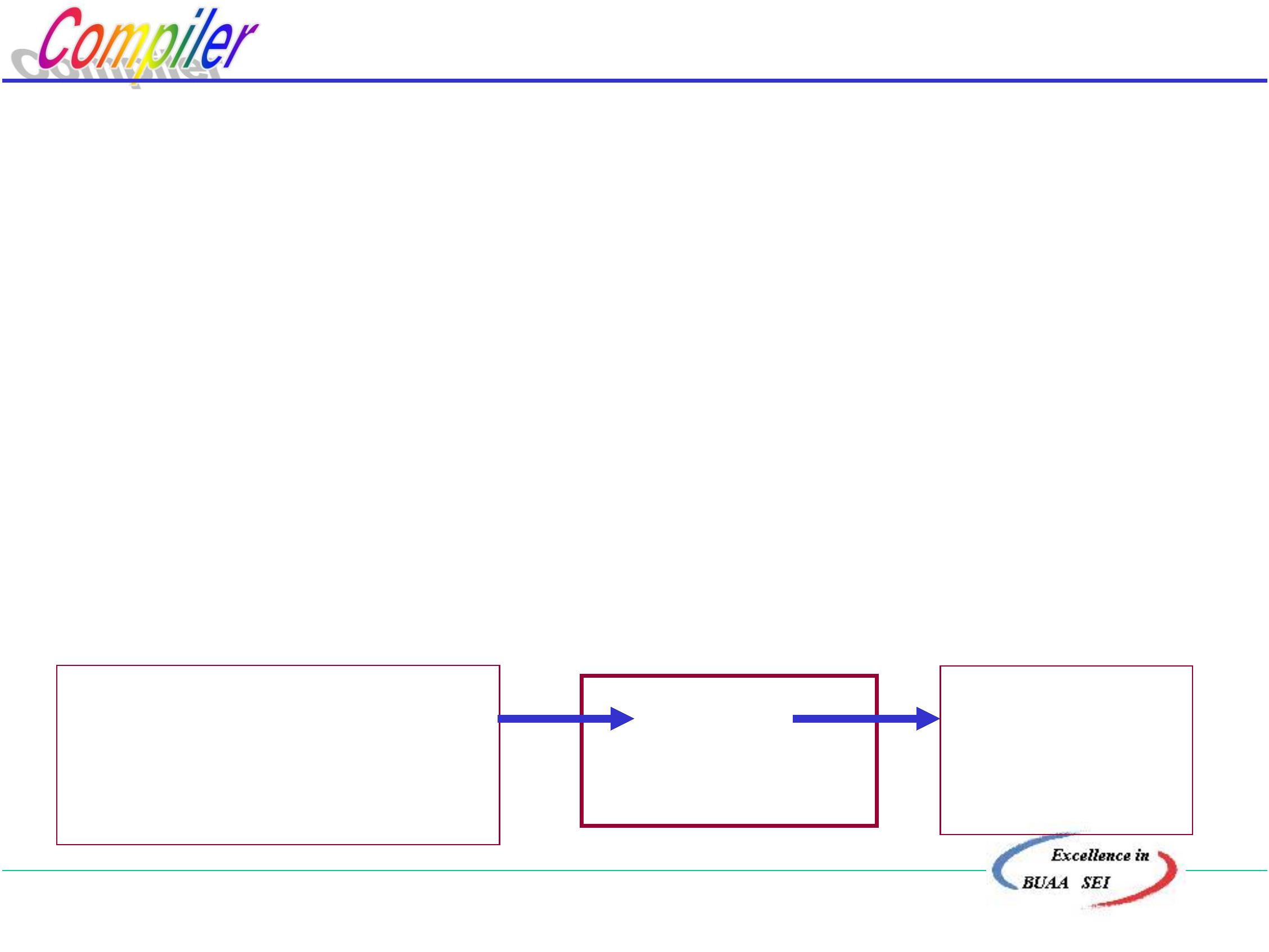
语法分析器生成器:
YACC ( YET ANOTHER COMPILER - COMPILER )
YACC
.
(
y 文件
语法分析器
BNF表示的语
(
y.tab. c文件)
构造分析表和
控制执行程序 (LALR(1)分析器)
法描述可插入语
义动作)
Bison: 美国GNU开发的语法分析器生成器)和YACC一样都在
UNIX系统下运行。(已有PC版)
北京航空航天大学计算机学院
1
9
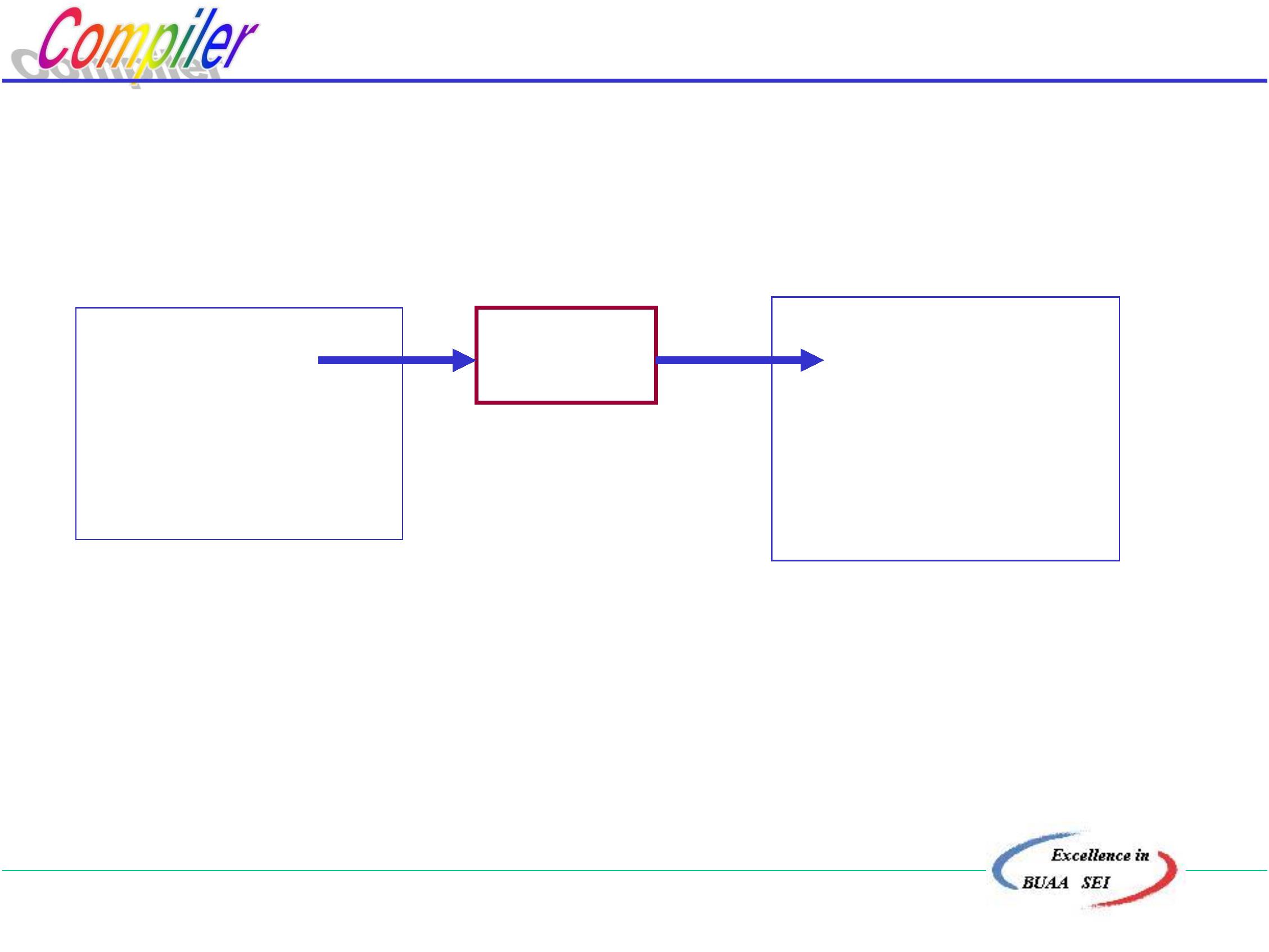
用yacc建立翻译程序
yacc源程序:translate.y
1
. 键入命令:
ꢀ
yacc translate.y
2
. 生成进行LALR分析的翻译
程序: y.tab.c
3
. 对生成的分析器进行编译:
ꢀ
cc y.tab.c -ly
(ly为使用LR分析器的库)
生成可执行的 翻译程序a.out
北京航空航天大学计算机学院
2
0
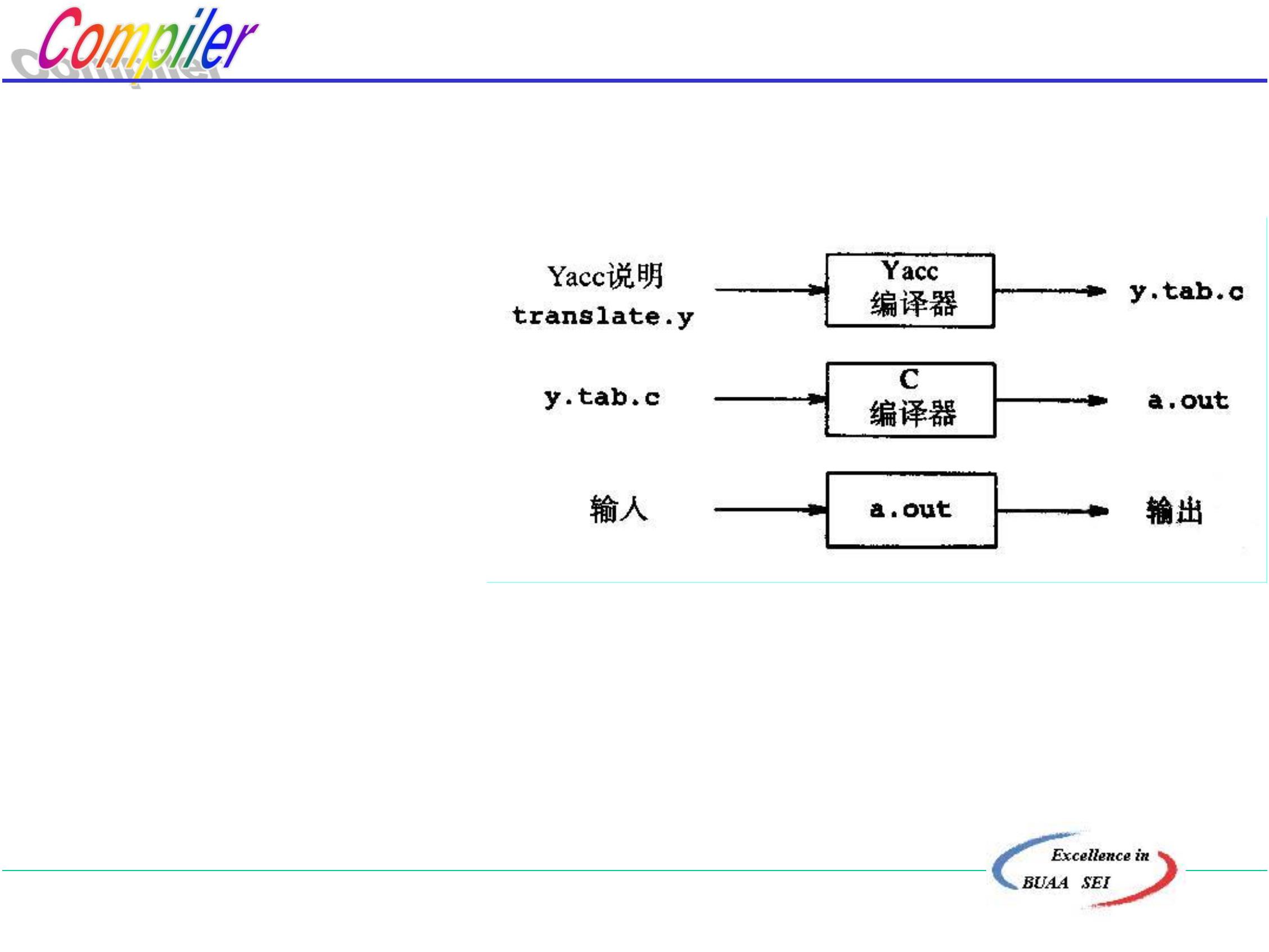
语法分析表
声明部分
头文件
y.tab.h
%%
yyparse()
{
语法分析函数
Yacc
翻译规则部分
编译程序
}
%
%
y.output
处理记录
函数定义部分
(拷贝)
函数定义部分
yacc源程序
y.tab.c
( *. y )
北
计算机学院
2
1
1
2
3
4
5
6
7
8
9
1
1
1
1
1
1
1
.
.
.
.
.
.
.
.
.
/* 表达式计算 */
%%
% token NUM
#include <ctype.h>
%%
yylex( )
{
line : expr ‘\n’
{ printf (‘\n’, $1);}
;
int c;
expr : expr ‘+’ term
{ $$ = $1 + $3; }
{ $$ = $1 - $3; }
/* $$ = $1 */
while (( c = getchar( )) == ‘ ’ );
| expr ‘-’ term
if ( isdigit ( c ) ) {
| term
;
yylval = c – ‘0’;
while ( isdigit( c = getchar ( ) ) )
yylval = yylval*10 + ( c-‘0’ );
ungetc ( c, stdin );
0. term : term ‘*’ factor
{ $$ = $1 * $3; }
{ $$ = $1 / $3; }
/* $$ = $1 */
1.
2.
3.
| term ‘/’ factor
| factor
;
retun NUM;
}
else return c;
4. factor: ‘(’ espr ‘)’
{ $$ = $2; }
/* $$ = $1 */
}
5.
6.
| NUM
;







