常用数据挖掘算法总结及 Python 实现
目录
第六部分 数据结构与算法...................................................................................... 错误!未定义书签。
一、二叉树(前、中、后遍历).................................................................... 错误!未定义书签。
二、几种基本排序方法.................................................................................... 错误!未定义书签。
第七部分 SQL 知识............................................................................................... 错误!未定义书签。
案例四 KNN 算法实现葡萄酒价格模型预测及交叉验证........................................................126
第一部分 数据挖掘与机器学习数学基础
第一章 机器学习的统计基础
1
.1 概率论
1
.概率论基本概念
样本空间
我们将随机实验 E 的一切可能基本结果组成的集合称为 E 的样本空间,记为 S。样本空间的元素,即
E 的每一个可能的结果,称为样本点。样本空间又叫基本事件空间。
例:拍拍贷用户的学历 S={‘研究生或以上’,‘本科’,‘大专’,‘高中’,‘中专’,‘初中及以下’},A={‘研
究生或以上’,‘本科’,‘大专’}
S
A
事件
事件 A 是样本空间的子集,可分为四种类型
空事件: 样本空间的空子集;
原子事件: 仅包含一个元素的样本空间;
混合事件: 包含多个元素的样本空间;
样本空间本身也是一个事件.
集合
概率论定义
概率用来描述一件事的不确定性。假设 A 是投硬币的一个结果(比如正面朝上),如果重复投硬币很
多次,直到 A 出现的机会逼近一个极限 p。那么可以说出现 A 的概率是 p
对于事件 A 和 B,联合概率 Pr(AB)表示事件 A 和 B 同时发生的概率。
概率定律
P( A ) P(A )
事件的概率: P(A)
满足: P(A) 0 ;P(S) = 1;对于一连串的互斥事件:
i
i
i
i


条件概率
发生事件 A 的情况下,发生 B 的概率称作条件概率 P(B|A).
P(B A)
P(B | A)
P(A)
独立性
事件发生和其它事件无关。
P(A B) P(A)P(B)
如果 P(B|A)=P(B), 我们称 B 和 A 统计独立,当且仅当:
如果 A 和 B 统计独立,那么 B 与 A 也统计独立
总概率
P(A) = P(퐴 ∩ 퐵) + P(A ∩ 퐵̅ ) = P(A|B)P(B) + P(A|퐵̅)P(퐵̅)
贝叶斯理论
P(A| B)P(B)
P(B | A)
P(A)
P(B) : B 的先验概率,非条件概率,或者边际概率
P(A|B): 给定 B 条件下的 A 的条件概率,也被称作“似然”
P(A): A 的边际概率,也作为 B 的后验概率的归一化常量
P(B|A):B 的后验概率
2
.随机变量,期望,方差
随机变量 X 是随机试验的数值型结果
相关概念:
观测值:其中一个结果成为观测值
数据:多个观测值集合为数据
总体:所有的结果称为总体
有两种类型的随机变量
离散变量:值数目可数
对于离散型随机变量,我们关心每个特定数值出现的概率 eg.客户的婚姻情况
连续变量:数值在一定范围内
对于连续性变量,某一个特定值出现的概率为 0,我们只关心区间的概率
Eg.客户的投资金额
概率分布
随机变量的分布就是它所有可能的输出以及它们的概率集合
概率密度函数
随机变量的概率密度函数描述该随机变量在某个取值发生的可能性
离散变量:P(X=x)=p(x)
b
P(a X b) p(x )dx
连续变量:
a


累积分布函数
x 处的累积分布函数是负无穷到 x 点的概率密度函数的累加和
期望
期望是指所有可能值的加权和。其权重对于离散值而言就是该值出现的概率,而对于连续值而言就是
其密度函数。
离散情况:
E(X ) x p(x )
连续情况:
E(X ) xp(x)dx
i
i
all x
all x
方差
用来描述该随机变量值和平均值的离散程度
离散情况
连续情况
Var(X ) (x E(X ))2p(xi)
( )
Var X x E X p(x)dx
(
( ))2
i
all x
all x
3
.常用概率分布
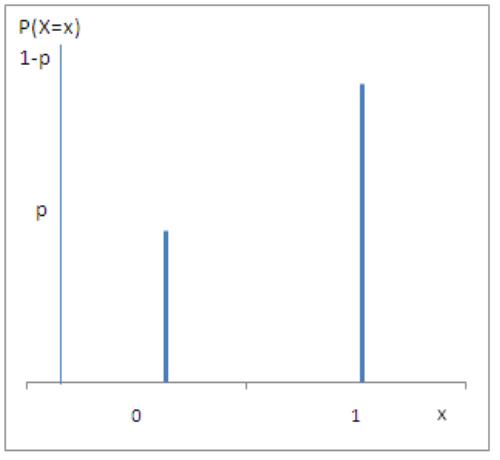
离散分布:伯努利分布(二项分布)
概率密度函数:
p(x) px(1 p)1x
均值:
E(X) p
方差:
Var(X) p(1 p)
连续分布
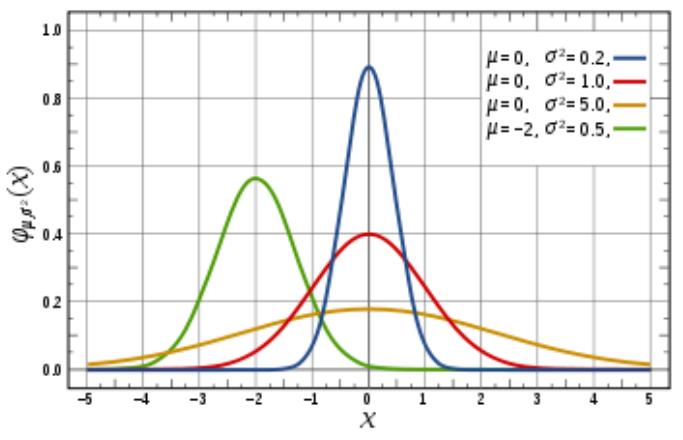
正态分布是最常用的一种连续分布。密度函数的特点是:关于均值 μ 对称,并在 μ 处取最大值,
在正(负)无穷远处取值为 0,图像是一条位于 x 轴上方的钟形曲线。期望值 μ 决定了分布的位置,
标准差 σ 决定了分布的幅度。当 μ=0,σ^2 =1 时,称为标准正态分布,记为 N(0,1)。
概率密度函数
(x)2
2 2
1
f(x )
e
2
2
期望
E(X )
方差
Var(X) 2


4
.统计量估计和中心极限定理
从一个数据集(样本)估计它的分布情况
统计直方图:直观地显示了数据的分布
描述性指标:
衡量据中趋势
∑
푋푖
期望值的估计:푋̅ =
푛
最大值 /最小值:2500 万用户的最大/最小借款金额
中值:按照借款金额排序,最中间的值
众数::出现次数最多的借款金额
衡量变化性
范围:最大最小的借款金额之差
方差的估计:
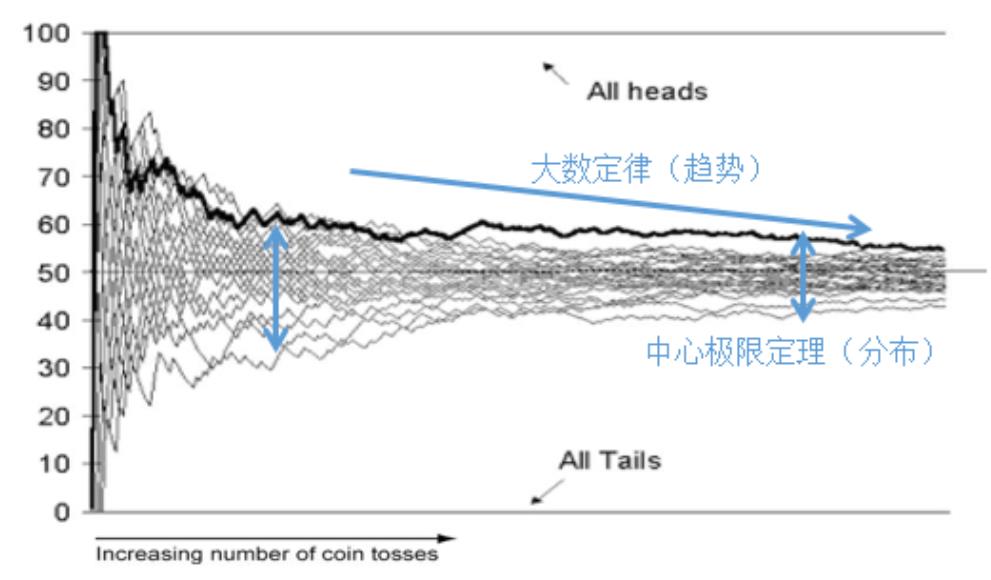
两个重要定理
大数定律
中心极限定理
大数定理
大数定理描述的是一组独立同分布随机变量的均值的极限。在这些随机变量个数趋于无穷时,其均值
依概率收敛于这些随机变量的数学期望
指明样本均值的收敛趋势
中心极限定理
设随机变量 X1,X2,......Xn 相互独立,服从同一分布,且具有数学期望和方差
E(X ) ,Var(X ) 2 0
i
i
푋 +푋 +⋯+푋
则随机变量的均值푋̅ =
1
2
푛
渐进地服从正态分布,并且期望和方差分别为
푛
E(X ) ,Var(X ) 2 0
i
i
指明样本均值的分布与样本量的关系


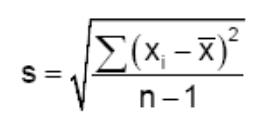
1
.2 假设检验
1
.假设检验概述
作用:检查观察到的样本究竟是否支持对总体的假设,帮助进行决策
假设检验在数据分析中的应用
理解分析建模的结果
需要读懂相关性分析,归回等建模的结果
AB Test
什么是假设检验
假设检验是数理统计学中根据一定假设条件由样本推断总体的一种方法。
-
-
对总体做假设
由样本做检验
假设检验的要素
原假设(Null Hypothesis)
备择假设(Alternative Hypothesis):即与原假设相悖的陈述
检验统计量:用采样数据基于原假设计算出的统计量,用来检验原假设和备择假设
拒绝域:在该区间,拒绝原假设,而趋向于备择假设
错误类型
类型 I: 在给定原假设是正确的情况下拒绝原假设的概率(False positive)
α = P(reject H | H true) 拒真
0
0
类型 II: 在给定备择假设是正确的情况下接受原假设的概率(False negative)
β = P(accept H | H true) 取伪
0
1
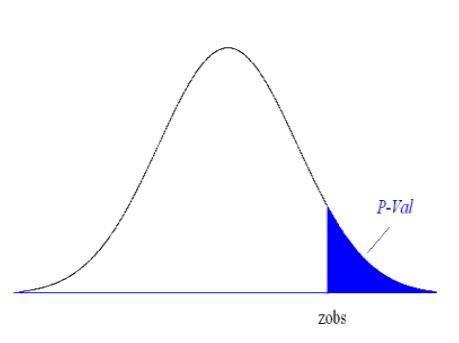
P-value
比观测值更极端的情况出现的概率,衡量样本数据相对于原假设的置信强,也称作观测的显著性水平
P val: p P(Z zobs)
用于做拒绝决定:
如果 p-value ³ a, 不拒绝原假设
如果 p-value < a, 拒绝 H0

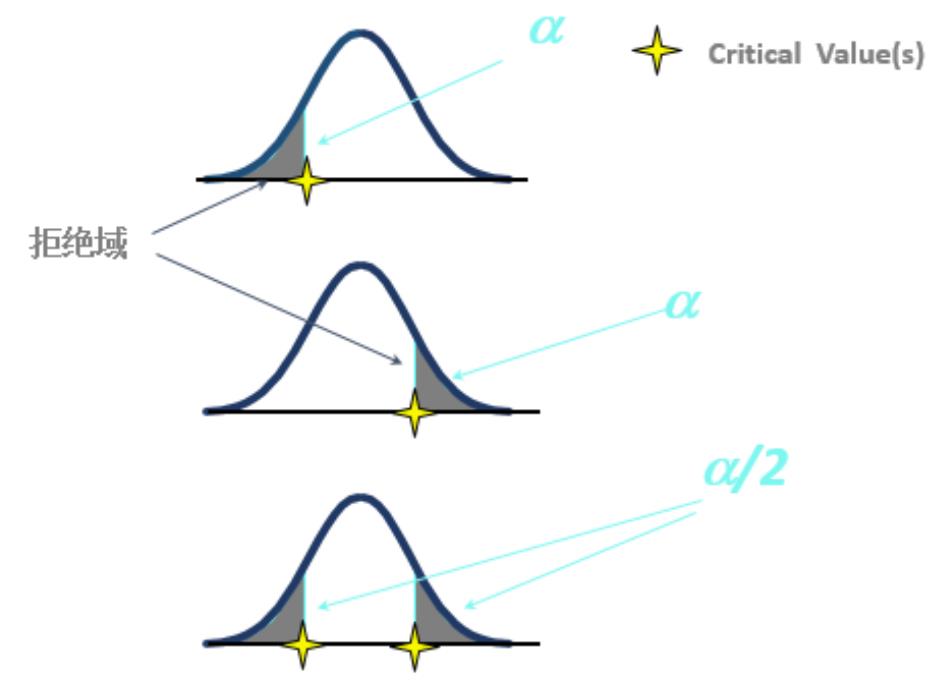
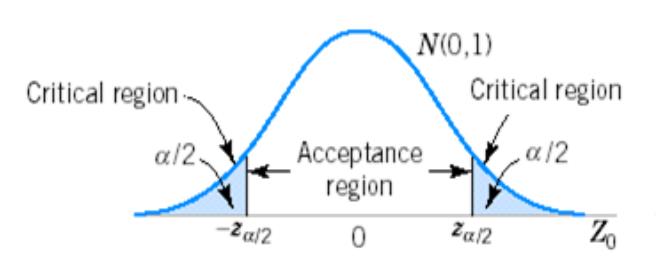
拒绝域
单边检测 I
单边检测 II
双边检测
2
.如何选择合适的检验
两组检验类型
参数检测:假定数据遵从某些特定的分布(例如:高斯分布),对总体参数进行估计或检验。
例如 : z 检测,t 检测,ANOVA,chi-square 等
非参数检测:并没有假定数据遵从某种分布。 往往直接对分布的某种特性(如对称性,分位数大小)
做检验。
例如: Kolmogorov-Smirnov 检测,Wilcoxon 检测, Mann-Whitney 检测, Kruskal-Wallis 检测等。
一个样本和多个样本
单个样本检验:仅仅基于一个采样样本,通常基于均值、方差和分布的假设
例如,正态分布检验,z 检验,t 检验
多个样本检验:目标是比较多个组别的均值方差是不是相等。
例如:ANOVA 检验, Kruskal-Wallis 检验, Chi- square 检验等等。
3
.假设检验
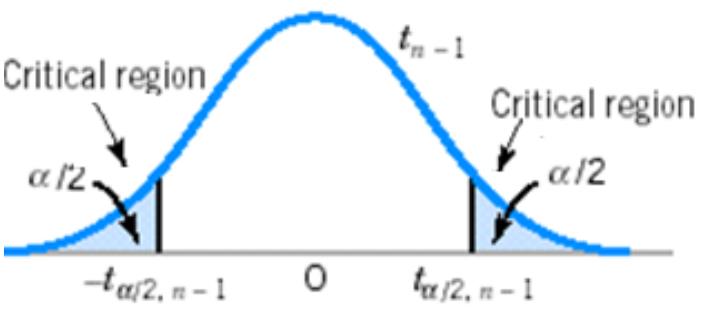
正态性检验
评估一个数据集{x1, …, xn} 服从正态分布的可
能性。
H0 : {x1, …, xn } ~N(μ, σ2)
H1 : {x1, …, xn} 服从任意分布
Q-Q plot(图形检验):
用图形的方法来比较两个概率分布:把他们的相应百分位数画在一张图里,图中任意一点(x,y),
x 和 Y 坐标分别是这两个分布的百分位数。如果这两个分布很相似, Q-Q plot 上的点会近似地位于
对角线 y = x 附近
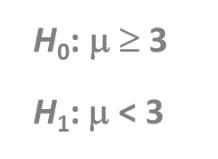
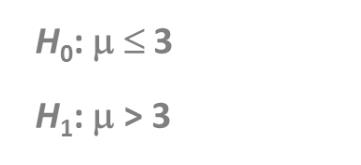
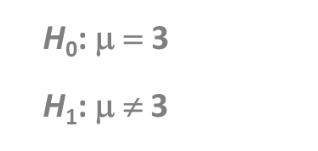
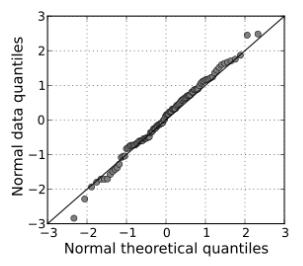
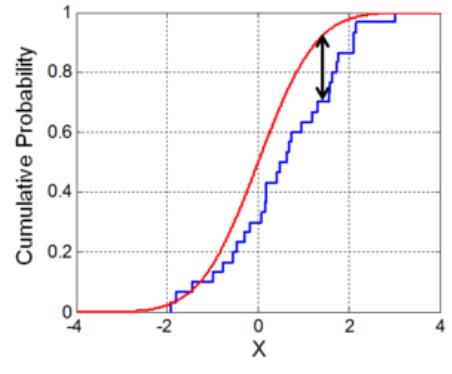
Kolmogorov-Smirnov(非参数检验)
以样本数据的累计频数分布与特定理论分布比较,
若两者间的差距很小,则推论该样本取自某特定分布。只
对连续分布适用。
-
Z 检验
原假设下的统计量近似为正态分布。
该正态分布方差已知,或可以从大样本里估计出来(近似 Z 检验)
-
检验统计量:
(X 0)
Z
/ n
拒绝 H0 : Z > Z/2 or Z < - Z/2
T 检验
-
-
-
-
-
数据严格遵从正态分布
不要求方差已知,可以从数据中估算
尤其适用于评估小样本相对总体的差异
较 Z 检验复杂
大样本与 Z 检验结果相似
检验统计量:
(X 0)
T
S / n
拒绝 H0 :T > t/2 or T < - t /2
检验步骤
1
2
3
4
5
6
7
8
) 根据问题,判定感兴趣的参数
) 给定原假设, H0
) 给定备择假设 H1
) 选择一个置信水平 .
) 选择合适的假设检验
) 推导出拒绝域
) 计算需要的统计变量
) 决定拒绝或接收原假设 H0
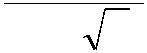

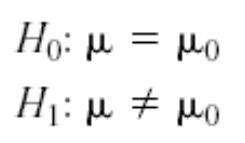
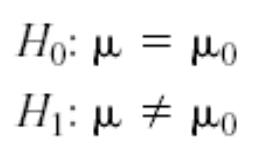
4
.AB Test
-
-
-
-
假设检验的一个重要应用;
多个方案并行测试——大多数情况是两个方案;
每个方案只有一个变量不同——必须是单变量;
以某种规则优胜劣汰——规则不同可能结果完全不同。
第二章 探索性数据分析(EDA)
1
.EDA 定义:探索性数据分析是对调查、观测所得到的一些初步的杂乱无章的数据,在尽量少的先
验假定下进行处理,通过作图、制表等形式和方程拟合、计算某些特征量等手段,探索数据的结构
和规律的一种数据分析方法
2
.数据类型
结构化数据
非结构化数据
二分类型:如性别
多分类型:如职业
有序类型:如收入水平
文本
音频
视频
图片
3
.单变量分析
频数和众数:针对于无序的分类的变量
百分位数:针对于有序的或连续的变量
位置度量:均值和中位数
散布度量:方差、标准差、偏度、峰度、四分位数、极差
(
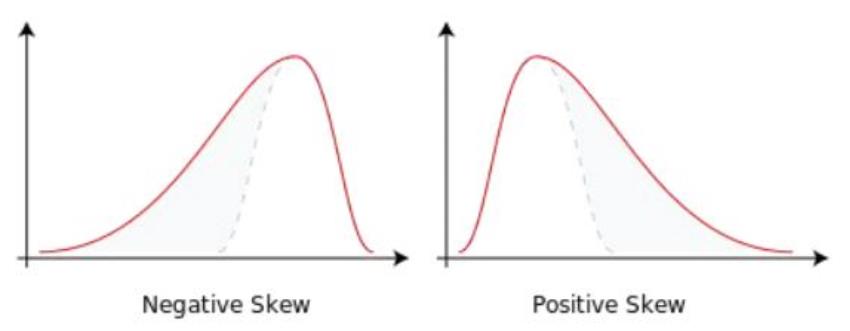
1)偏度----刻画数据对称性的指标
计算公式:
性质: 关于均值对称的数据其偏度为 0
呈现右偏的数据偏度大于 0
呈现左偏的数据偏度小于 0
(
2)峰度----刻画分布状态的陡缓程度的指标
性质:峰度=0,分布呈正态; 峰度>0,分布呈尖峰状态;峰度<0,分布呈平峰状态
(
3)四分位数极差
定义:푅 = 푄 − 푄
1
3
1
判断数据异常点的方法:称푸 − ퟏ. ퟓ푹 ,푸 + ퟏ. ퟓ푹 为数据的下、上截断点,大于上截断点或小于
ퟏ
ퟏ
ퟑ
ퟏ
下截断点的数据均为异常点
(
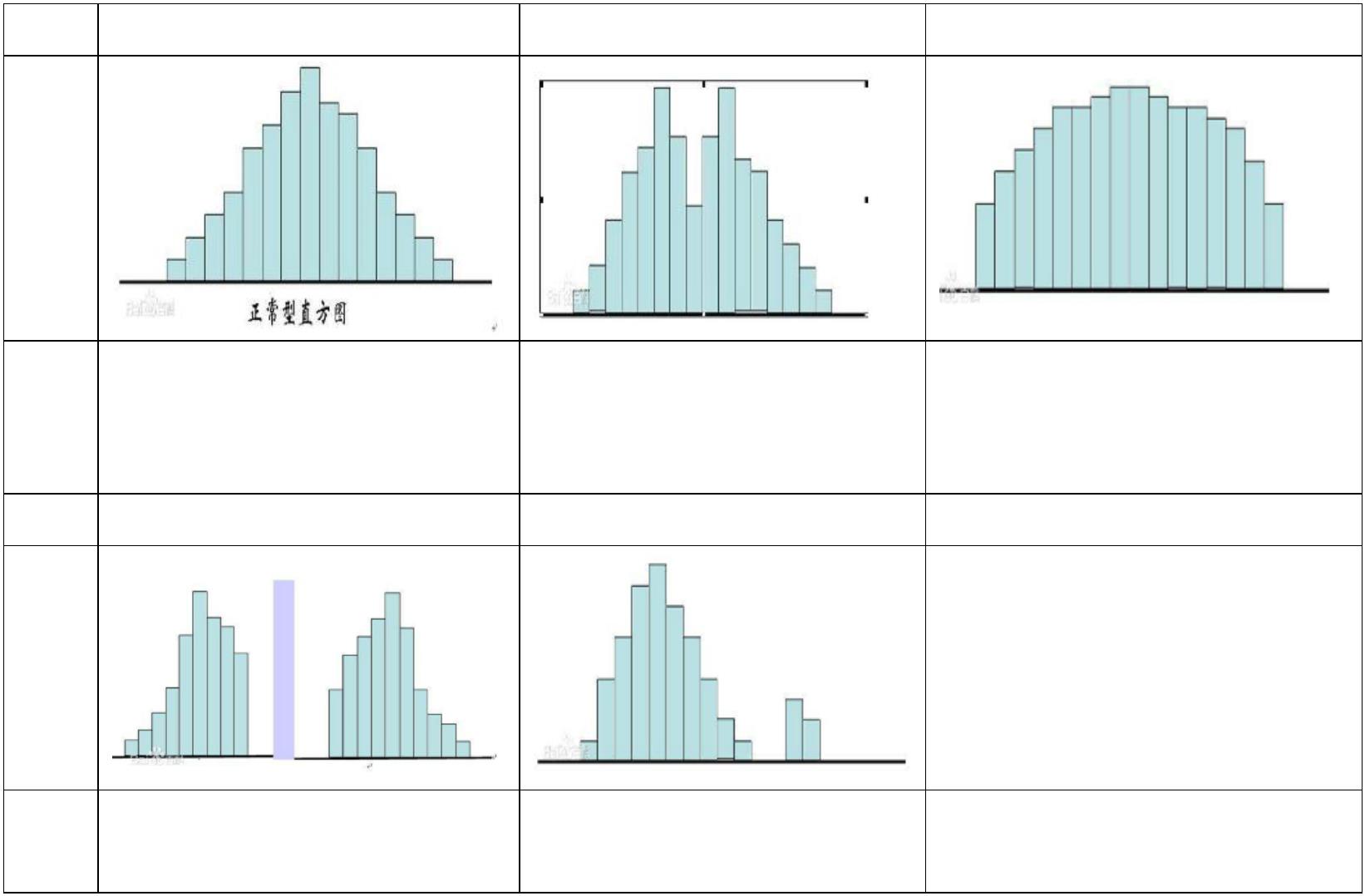
4)直方图
类型 正常型直方图
图形
双峰型直方图
平顶型直方图
特点 中间高,两边低,左右近似
对称
直方图出现两个峰,由于观 多个总体多个分布混合在一
测值来自两个总体、两个分 起;变量在某个区间均匀变化
布的数据混合在一起
类型 偏态型直方图
图形
孤岛型直方图
特点 图的顶峰有时向左偏,有时
在直方图旁边有孤立的小岛
出现
向右偏
直方图作用:
数据是否接近对称
数据分散性如何
数据是否有异常值
数据中是否有间隙
5)箱线图
(
概念:是一种现实一维数值属性值分布的图形,它有 6 个数据节点:上边缘、上四分位数、中位
数、下四分位数、下边缘、异常值
作用:识别异常值;判断数据的偏态;比较几批数据的形状
(
5)正态性检验
正态分布式许多检验的基础,比如 F 检验,t 检验,卡方检验等。因此对于一个样本是否来自正
态总体的检验是至关重要的
图示法
直方图:是否以钟型分布
箱线图:观测矩形位置和中位数,若矩形位于中间位置且中位数位于矩形的中间位置,则分布较为
对称
QQ 图:
http://wenku.baidu.com/link?url=Hu_Y5MSYZHa25LZm2k3rx6k1Kyz6Jw1BWZXPdqvnfW2yelnTZuzxe
L3E0-7urY6TufsWZ3RyG-w-2IyFdZ_kPTMake259biSbiT5S7iPynm
非参数检验法
4
.两个变量的关系
(
1)两个数值型变量线性相关(服从二元正态分布)
计算 Pearson 样本相关系数
γ取值: -1~1 之间;
>
<
=
=
=
0,表示两变量存在正的线性相关关系;
0,表示两变量存在负的线性相关系数
1,两变量存在完全正相关
-1,两变量存在完全负相关
0,两变量不存在线性相关关系
绝对值>0.8 表示两变量之间具有较强的线性关系
绝对值<0.3 表示两变量之间的线性相关关系较弱
相关系数的假设检验
提出零假设:两变量无线性相关关系
훾√푛−2
选择检验统计量:Pearson 相关系数的检验统计量为 t 统计量,即t =
,其中 t 统计量服从 n-2
√1−훾2
个自由度的 t 分布
计算检验统计量的观测值和 p 值
决策:若 p 值小于显著水平α,应拒绝原假设,即两变量存在线性相关关系,否则拒绝
相关性分析注意事项:
进行线性相关分析前,可以先绘制散点图
要求两变量都来自正态总体的随机变量
出现异常值时甚用
(
(
2)秩相关(两个有序的分类变量)
3)两个无序分类变量关联性分析---휒2检验


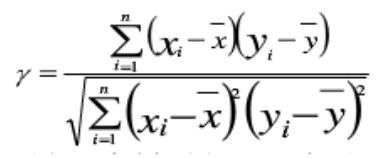
第二部分 机器学习概述
第三章 机器学习概述
3
.1 机器学习概述
机器学习方法主要分为有监督学习(supervised learning)和无监督学习(unsupervised learning),半
监督学习和强化学习
监督学习就是分类,通过已有的训练样本去训练得到一个最优模型,然后利用这个最优模型将
所有输入映射为相应的输出,对于输出进行判断实现分类,这就对未知数据进行了分类。监督
学习中的典型例子是 KNN 和 SVM。
无监督学习与监督学习的不同之处,主要是它没有训练样本,而是直接对数据进行建模。典型
案例就是聚类了,其目的是把相似的东西聚在一起,而不关心这一类是什么。聚类算法通常只
需要知道如何计算相似度就可以了,它可能不具有实际意义。
如果在分类过程中有训练样本,则可以考虑采用监督学习的方法,否则不能使用监督学习。
3
.2 数据挖掘常用 Python 库
Python 科学计算包: Numpy
数据处理工具包:pandas
绘图和可视化:matplotlib
统计包:statsmodels
Python 算法库和工具包:SciPy
机器学习模块 scikit-learn: 基于 Numpy 和 SciPy,包括分类、回归、聚类系列算法,主要算法
有 SVM、逻辑回归、朴素贝叶斯、Kmeans、DBSCAN 等,目前由 INRI 资助,偶尔 Google 也
资助一点
3
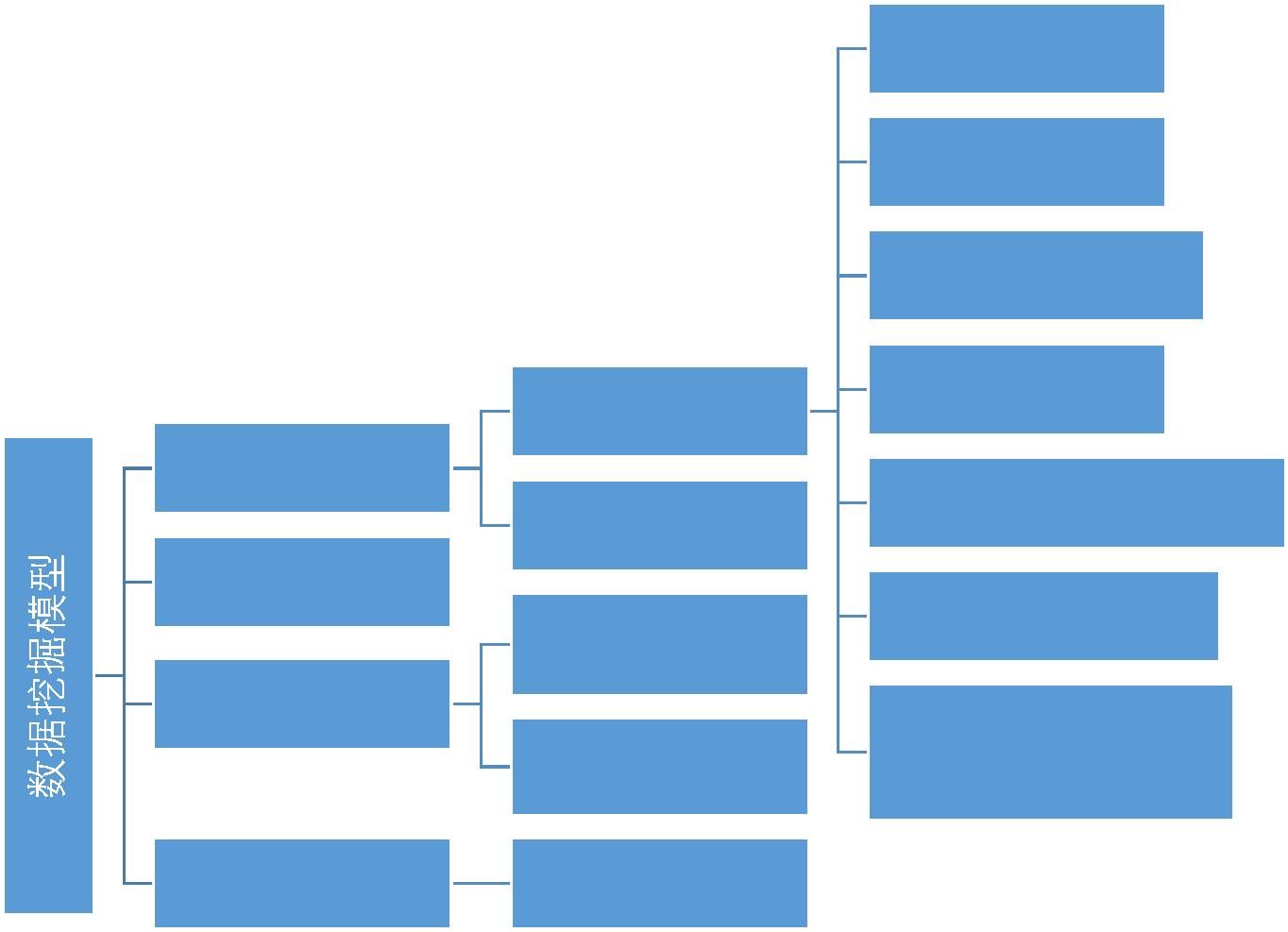
.3 数据挖掘常用模型
KNN
决策树
朴素贝叶斯分类
Logistic回归
CART分类回归树
SVM支持向量机
分类
回归
监督学习
半监督学习
聚类分析--
Kmeans
非监督学习
数据降维
集成学习(Bagging,
Adaboost)
关联分析—Apriori
PCA
第三部分 监督学习---分类与回归
有监督就是给的样本都有标签,分类的训练样本必须有标签,所以分类算法都是有监督算法。监
督机器学习无非就是“minimize your error while regularizing your parameters”,也就是在规则化参数的
同时最小化误差。最小化误差是为了让我们的训练数据,而规则化参数是防止我们的模型过分拟合我
们的训练数据,提高泛化能力
第四章 KNN(k 最邻近分类算法)
1
.算法思路
通过计算每个训练样例到待分类样品的距离,取和待分类样品距离最近的 K 个训练样例,K 个
样品中哪个类别的训练样例占多数,则待分类样品就属于哪个类别
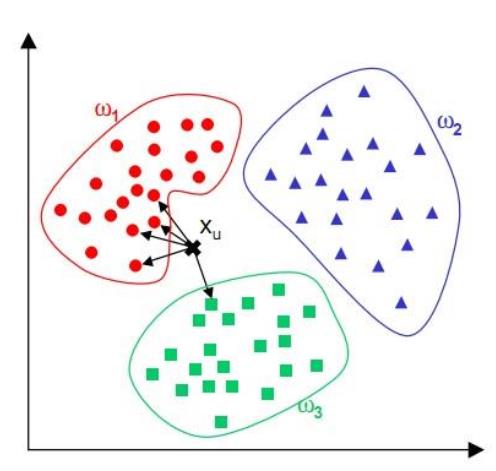
核心思想:如果一个样本在特征空间中的 k 个最相邻的样本中的大多数属于某一个类别,则该样本
也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或
者几个样本的类别来决定待分样本所属的类别。 kNN 方法在类别决策时,只与极少量的相邻样本
有关。由于 kNN 方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,
因此对于类域的交叉或重叠较多的待分样本集来说,kNN 方法较其他方法更为适合。
2
3
4
.算法描述
1
2
3
. 算距离:给定测试对象,计算它与训练集中的每个对象的距离
依公式计算 Item 与 D1、D2 … …、Dj 之相似度。得到 Sim(Item, D1)、Sim(Item, D2)… …、
Sim(Item, Dj)。
. 将 Sim(Item, D1)、Sim(Item, D2)… …、Sim(Item, Dj)排序,若是超过相似度阈值 t 则放入邻居
案例集合 NN。
找邻居:圈定距离最近的 k 个训练对象,作为测试对象的近邻
. 自邻居案例集合 NN 中取出前 k 名,依多数决,得到 Item 可能类别。
做分类:根据这 k 个近邻归属的主要类别,来对测试对象分类
.算法步骤
•
•
•
•
•
•
•
step.1---初始化距离为最大值
step.2---计算未知样本和每个训练样本的距离 dist
step.3---得到目前 K 个最临近样本中的最大距离 maxdist
step.4---如果 dist 小于 maxdist,则将该训练样本作为 K-最近邻样
step.5---重复步骤 2、3、4,直到未知样本和所有训练样本的距离
step.6---统计 K-最近邻样本中每个类标号出现的次数
step.7---选择出现频率最大的类标号作为未知样本的类标号
该算法涉及 3 个主要因素:训练集、距离或相似的衡量、k 的大小。
. k 邻近模型三个基本要素
三个基本要素为距离度量、k 值的选择和分类决策规则
距离度量:
푇
푇
设特征空间χ是 n 维实数向量空间푅푛,푥 , 푥 ∈ 휒,푥 = (푥(1), 푥푖(2), … , 푥푖 ) , 푥 = (푥(1), 푥(2), … , 푥(푛))
(푛)
푖
푗
푖
푖
푗
푗
푗
푗

1/푝
(푙)
(푙)
푗
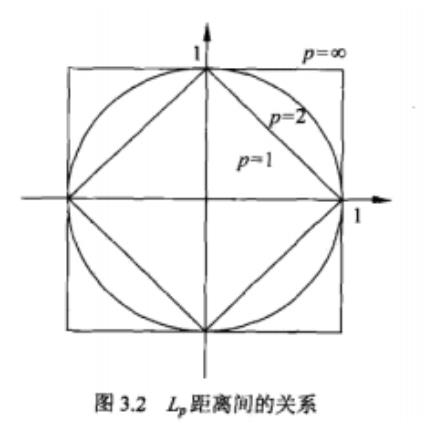
풙 , 풙 的퐿 距离定义为:퐿 (푥 , 푥 ) = (∑ |푥푖 − 푥 | )
푛
푝
p ≥ 1
풊
풋
푝
푝
푖
푗
푙=1
1/2
p=2 时为欧式距离:퐿 (푥 , 푥 ) = (∑푛 |푥푖 − 푥(푙)|2)
(푙)
2
푖
푗
푙=1
푗
p=1 时为曼哈顿距离:퐿 (푥 , 푥 ) = ∑푛 |푥푖 − 푥(푙)|
(푙)
1
푖
푗
푙=1
푗
(푙)
푖
(푙)
푗
p=∞时,它是各个坐标距离的最大值 퐿 (푥 ,푥 ) = max|푥 − 푥 |
∞
푖
푗
푙
5
.算法优缺点
) 优点
1
简单,易于理解,易于实现,无需估计参数,无需训练;
适合样本容量比较大的分类问题
特别适合于多分类问题(multi-modal,对象具有多个类别标签),例如根据基因特征来判断其功能
分类,kNN 比 SVM 的表现要好
2
) 缺点
懒惰算法,对测试样本分类时的计算量大,内存开销大,评分慢;
可解释性较差,无法给出决策树那样的规则
对于样本量较小的分类问题,会产生误分
6
.常见问题
1
)K 值设定为多大
k 太小,分类结果易受噪声点影响;k 太大,近邻中又可能包含太多的其它类别的点。(对距离加
权,可以降低 k 值设定的影响)
k 值通常是采用交叉检验来确定(以 k=1 为基准)
经验规则:k 一般低于训练样本数的平方根
2
)类别如何判定最合适
投票法没有考虑近邻的距离的远近,距离更近的近邻也许更应该决定最终的分类,所以加权投票法
更恰当一些。
3
)如何选定合适的距离衡量
高维度对距离衡量的影响:众所周知当变量数越多,欧式距离的区分能力就越差。
变量值域对距离的影响:值域越大的变量常常会在距离计算中占据主导作用,因此应先对变量进行
标准化。
4
)训练样本是否要一视同仁
在训练集中,有些样本可能是更值得依赖的。
可以给不同的样本施加不同的权重,加强依赖样本的权重,降低不可信赖样本的影响。
5
)性能问题
kNN 是一种懒惰算法,平时不好好学习,考试(对测试样本分类)时才临阵磨枪(临时去找 k 个近
邻)。
懒惰的后果:构造模型很简单,但在对测试样本分类地的系统开销大,因为要扫描全部训练样本并
计算距离。
已经有一些方法提高计算的效率,例如压缩训练样本量等。
6
)能否大幅减少训练样本量,同时又保持分类精度?
浓缩技术(condensing)
编辑技术(editing)
6
.KNN 算法 Python 实现实例之电影分类
电影名称 打斗次数 接吻次数 电影类型
California Man
3
104
100
81
10
5
Romance
Romance
Romance
Action
He’s Not Really into Dudes
Beautiful Woman
Kevin Longblade
Robo Slayer 3000
Amped II
2
1
101
99
98
18
Action
2
Action
未知
90
Unknown
任务描述:通过打斗次数和接吻次数来界定电影类型
调用 Python 的 sklearn 模块求解
1
2
3
4
.
.
.
.
import numpy as np
from sklearn import neighbors
knn = neighbors.KNeighborsClassifier() #取得 knn 分类器
data = np.array([[3,104],[2,100],[1,81],[101,10],[99,5],[98,2]]) # <span style="font-family:Arial, Helvetica, sans-serif;">data 对应着
打斗次数和接吻次数</span>
5
6
7
8
9
1
.
.
.
.
.
labels = np.array([1,1,1,2,2,2]) #<span style="font-family:Arial, Helvetica, sans-serif;">labels 则是对应 Romance 和 Action</span>
knn.fit(data,labels) #导入数据进行训练'''
#Out:KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform')
0. knn.predict([18,90])
说明:
首先,用 labels 数组中的 1 和 2 代表 Romance 和 Aciton,因为 sklearn 不接受字符数组作为标志,只
能用 1,2 这样的 int 型数据来表示,后面处理可以将 1 和 2 映射到 Romance 和 Action 上来。fit 则是
用 data 和 labels 进行训练,data 对应的是打斗次数和接吻次数构成的向量,称之为特征向量。labels
则是这个数据所代表的电影所属的类型。调用 predict 进行预测,将未知电影的特征向量代入,则能
分析出该未知电影所属的类型。此处计算结果为 1,也就是该未知电影属于 Romance,和直觉相符。

第五章 决策树
5
.1. 决策树基本概念及算法优缺点
1
. 什么是决策树
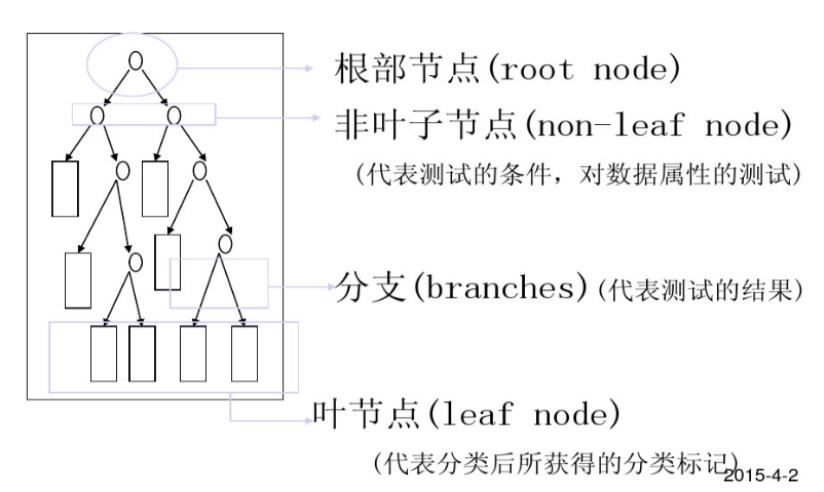
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两
种类型:内部结点和叶结点。内部结点表示一个特征或属性,叶结点表示一个类。
决策树(Decision Tree),又称判定树,是一种以树结构(包括二叉树和多叉树)形式来表达的预
测分析模型。
通过把实例从根节点排列到某个叶子节点来分类实例
叶子节点即为实例所属的分类
树上每个节点说明了对实例的某个属性的测试,节点的每个后继分支对应于该属性的一个可能值
2
. 决策树结构
3
. 决策树种类
分类树---对离散变量做决策树
回归树---对连续变量做决策树
4
. 决策树算法(贪心算法)
•
•
•
•
有监督的学习
非参数学习算法
自顶向下递归方式构造决策树
在每一步选择中都采取在当前状态下最好/优的选择
决策树学习的算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得各
个子数据集有一个最好的分类的过程。
在决策树算法中,ID3 基于信息增益作为属性选择的度量,C4.5 基于信息增益比作为属性选择的
度量,CART 基于基尼指数作为属性选择的度量
5
.决策树学习过程
•
•
•
特征选择
决策树生成:递归结构,对应于模型的局部最优
决策树剪枝:缩小树结构规模、缓解过拟合,对应于模型的全局选择
6
. 决策树优缺点
优点:
(1) 速度快:计算量相对较小,且容易转化成分类规则。只要沿着树根向下一直走到叶,沿途的分裂
条件就能够唯一确定一条分类的谓词。
(2) 准确性高:挖掘出的分类规则准确性高,便于理解,决策树可以清晰的显示哪些字段比较重要,
即可以生成可以理解的规则。
(3)可以处理连续和种类字段
缺点:
(1) 对于各类别样本数量不一致的数据,信息增益偏向于哪些具有更多数值的特征
(2) 易于过拟合
(3) 对连续的字段比较难预测
(4) 不是全局最优
5
.2 决策树数学知识
1
.信息论:若一事假有 k 种结果,对应的概率为푃푖,则此事件发生后所得到的信息量 I 为:
푘
I = −(푝 ∗ 푙표푔 (푝 ) + 푝 ∗ 푙표푔 (푝 ) + ⋯ + 푝 ∗ 푙표푔 (푝 )) = − ∑ 푝 푙표푔 푝
푖
1
2
1
2
2
2
푘
2
푘
푖
2
푖=1
2
. 熵:给定包含关于某个目标概念的正反样例的样例集 S,那么 S 相对这个布尔型分类的熵为:
Entropy(S) ≡ −푝 푙표푔 푝 − 푝 푙표푔 푝 其中 P+代表正样例,p-代表反样例
⊕
2
⊕
⊝
2
⊝
3
. 条件熵:假设随机变量(X,Y),其联合分布概率为 P(X=xi,Y=yi)=Pij,i=1,2,⋯,n;j=1,2,⋯,m
则条件熵 H(Y|X)表示在已知随机变量 X 的条件下随机变量 Y 的不确定性,其定义为 X 在给定条件下
Y 的条件概率分布的熵对 X 的数学期望
5
.3 决策树算法 Hunt
在 Hunt 算法中,通过递归的方式建立决策树。
1
2
)如果数据集 D 中所有的数据都属于一个类,那么将该节点标记为为节点。
)如果数据集 D 中包含属于多个类的训练数据,那么选择一个属性将训练数据划分为较小的子集,
对于测试条件的每个输出,创建一个子女节点,并根据测试结果将 D 中的记录分布到子女节点中,
然后对每一个子女节点重复 1,2 过程,对子女的子女依然是递归的调用该算法,直至最后停止。
5
.4. 决策树算法 ID3
1
2
. 分类系统信息熵
.条件熵
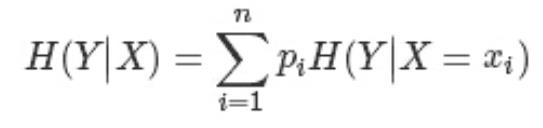
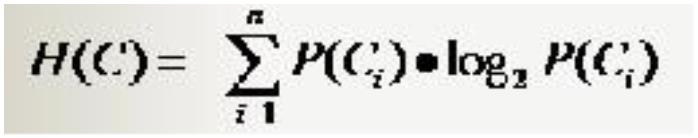
分类系统中的条件熵指的是当样本的某一特征 X 固定时的信息熵
因此样本特征 X 取值为 xi 的概率是 Pi,该特征被固定为值 xi 时的条件信息熵就是 H(C|X=xi),那么
H(C|X)就是分类系统中特征 X 被固定时的条件熵(X=(x1,x2,……,xn)):
3
.信息增益 Gain(S,A)定义
4
. 属性选择度量
使用信息增益,选择最高信息增益的属性作为当前节点的测试属性
5.算法不足
使用 ID3 算法构建决策树时,若出现各属性值取值数分布偏差大的情况,分类精度会大打折扣
ID3 算法本身并未给出处理连续数据的方法
ID3 算法不能处理带有缺失值的数据集,故在算法挖掘之前需要对数据集中的缺失值进行预处理
ID3 算法只有树的生成,所以该算法生成的树容易产生过拟合
6
. 算法流程
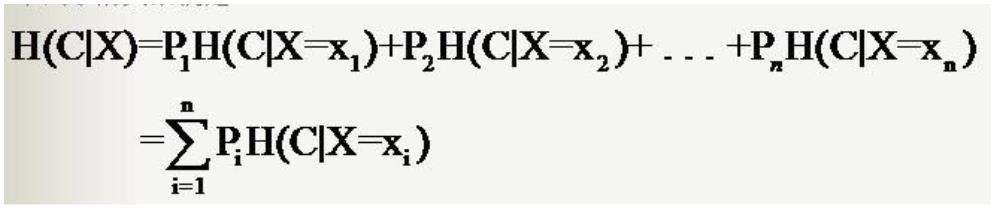
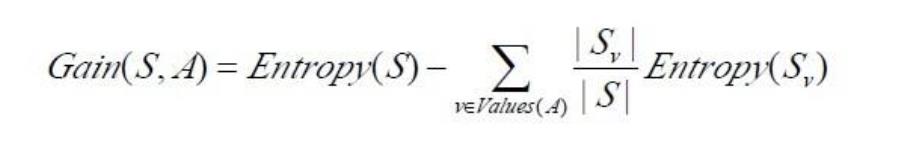
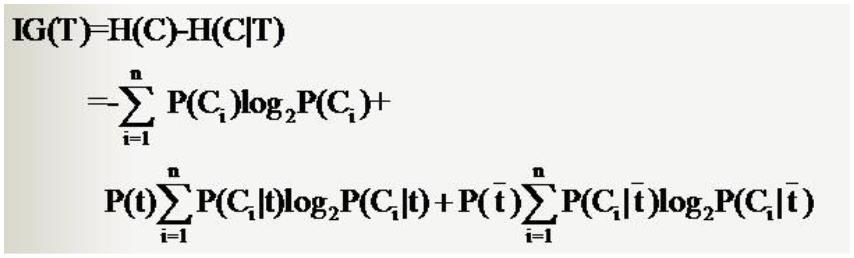

7
. 算法 Python 实现
1
)Python 实现熵的计算
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob*log(prob,2)
return shannonEnt
2
)Sklearn.tree 参数介绍及使用建议
官网:http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html
class sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2,min_samples_leaf=1, max_f
eatures=None, random_state=None, min_density=None, compute_importances=None,max_leaf_nodes=None)
比较重要的参数:
criterion :规定了该决策树所采用的的最佳分割属性的判决方法,有两种:“gini”,“entropy”。
max_depth :限定了决策树的最大深度,对于防止过拟合非常有用。
min_samples_leaf :限定了叶子节点包含的最小样本数,这个属性对于防止上文讲到的数据碎片问
题很有作用
模块中一些重要的属性方法:
n_classes_ :决策树中的类数量。
classes_ :返回决策树中的所有种类标签。
feature_importances_ :feature 的重要性,值越大,越重要。
fit(X, y, sample_mask=None, X_argsorted=None, check_input=True, sample_weight=None)
将数据集 x,和标签集 y 送入分类器进行训练,这里要注意一个参数是:sample_weight,它和样本
的数量一样长,所携带的是每个样本的权重。
get_params(deep=True)
得到决策树的各个参数。
set_params(**params)
调整决策树的各个参数。
predict(X)
送入样本 X,得到决策树的预测。可以同时送入多个样本。
transform(X, threshold=None)
返回 X 的较重要的一些 feature,相当于裁剪数据。
score(X, y, sample_weight=None)


返回在数据集 X,y 上的测试分数,正确率。
使用建议
当我们数据中的 feature 较多时,一定要有足够的数据量来支撑我们的算法,不然的话很容易
overfitting
PCA 是一种避免高维数据 overfitting 的办法。
从一棵较小的树开始探索,用 export 方法打印出来看看。
善用 max_depth 参数,缓慢的增加并测试模型,找出最好的那个 depth。
善用 min_samples_split 和 min_samples_leaf 参数来控制叶子节点的样本数量,防止 overfitting。
平衡训练数据中的各个种类的数据,防止一个种类的数据 dominate。
3
) Sklearn.tree 实战
测试数据 data.txt
1
1
1
1
1
1
1
1
1
1
.5 50 thin
.5 60 fat
.6 40 thin
.6 60 fat
.7 60 thin
.7 80 fat
.8 60 thin
.8 90 fat
.9 70 thin
.9 80 fat
Python 实战代码
#
-*- coding: utf-8 -*-
import numpy as np
from sklearn import tree
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import classification_report
from sklearn.cross_validation import train_test_split
#
数据读入
data=[]
labels=[]
with open('C:\Users\Allen\Desktop\data.txt') as ifile:
for line in ifile:
tokens=line.strip().split(' ')
data.append([float(tk) for tk in tokens[:-1]])
labels.append(tokens[-1])
x=np.array(data)
labels=np.array(labels)
y=np.zeros(labels.shape)
#
标签转化为 0,1
y[labels=='fat']=1
拆分训练数据和测试数据
x_train,x_test,y_train,y_test=train_test_split(x, y, test_size = 0.2)
#
#
使用信息熵作为划分标准,对决策树进行训练
clf=tree.DecisionTreeClassifier(criterion='entropy')
print clf
#
DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=None,
#
#
#
max_features=None, max_leaf_nodes=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
clf.fit(x_train,y_train)
#
把决策树写入文件
with open("tree.dot", 'w') as f:
f = tree.export_graphviz(clf, out_file=f)
#
#
#
#
#
#
#
#
#
#
#
#
#
digraph Tree {
node [shape=box] ;
0 [label="X[1] <= 75.0\nentropy = 0.9544\nsamples = 8\nvalue = [3, 5]"] ;
1 [label="X[0] <= 1.65\nentropy = 0.971\nsamples = 5\nvalue = [3, 2]"] ;
0 -> 1 [labeldistance=2.5, labelangle=45, headlabel="True"] ;
2 [label="entropy = 0.0\nsamples = 2\nvalue = [0, 2]"] ;
1 -> 2 ;
3 [label="entropy = 0.0\nsamples = 3\nvalue = [3, 0]"] ;
1 -> 3 ;
4 [label="entropy = 0.0\nsamples = 3\nvalue = [0, 3]"] ;
0 -> 4 [labeldistance=2.5, labelangle=-45, headlabel="False"] ;
}
系数反映每个特征的影响力。越大表示该特征在分类中起到的作用越大
print(clf.feature_importances_)
#
测试结果的打印
answer=clf.predict(x_train)
print(x_train)
print(answer)
print(y_train)
print(np.mean(answer==y_train))
#
#
#
#
#
#
5
#
准确率与召回率
准确率:某个类别在测试结果中被正确测试的比率
召回率:某个类别在真实结果中被正确预测的比率
测试结果:array([ 0., 1., 0., 1., 0., 1., 0., 1., 0., 0.])
真实结果:array([ 0., 1., 0., 1., 0., 1., 0., 1., 0., 1.])
分为 thin 的准确率为 0.83。是因为分类器分出了 6 个 thin,其中正确的有 5 个,因此分为 thin 的准确率为
/6=0.83。
分为 thin 的召回率为 1.00。是因为数据集中共有 5 个 thin,而分类器把他们都分对了(虽然把一个 fat 分成了
thin!),召回率 5/5=1。
#
#
分为 fat 的准确率为 1.00。不再赘述。
分为 fat 的召回率为 0.80。是因为数据集中共有 5 个 fat,而分类器只分出了 4 个(把一个 fat 分成了 thin!),召
回率 4/5=0.80。
#
本例中,目标是尽可能保证找出来的胖子是真胖子(准确率),还是保证尽可能找到更多的胖子(召回率)。
precision, recall, thresholds = precision_recall_curve(y_train, clf.predict(x_train))
answer = clf.predict_proba(x)[:,1]
print(classification_report(y, answer, target_names = ['thin', 'fat']))

5
.5 决策数算法 C4.5
1
. 属性选择度量
C4.5 算法用信息增益率来选择属性,即选用信息增益比选择最佳特征
. 信息增益比率度量
2
信息增益比率度量是用 ID3 算法中的增益度量 Gain(D,X)和分裂信息度量 SplitInformation(D,X)来
共同定义的。分裂信息度量 SplitInformation(D,X)就相当于特征 X(取值为 x ,x ,……,x ,各
1
2
n
自的概率为 P ,P ,...,P ,P 就是样本空间中特征 X 取值为 X 的数量除上该样本空间总数)的熵。
1
2
n
k
k
SplitInformation(D,X) = -P log (P )-P log (P)-,...,-P log (P )
1
2
1
2
2
n
2
n
GainRatio(D,X) = Gain(D,X)/SplitInformation(D,X)
. 对连续分布特征的处理
C4.5 先把连续属性转换为离散属性再进行处理。如果有 N 条样本,那么我们有 N-1 种离散化的方法:
=vj 的分到左子树,>vj 的分到右子树。计算这 N-1 种情况下最大的信息增益率。
3
<
1
2
)对特征的取值进行升序排序
)两个特征取值之间的中点作为可能的分裂点,将数据集分成两部分,计算每个可能的分裂点的信
息增益(InforGain)。优化算法就是只计算分类属性发生改变的那些特征取值。
3
4
)选择修正后信息增益(InforGain)最大的分裂点作为该特征的最佳分裂点
)计算最佳分裂点的信息增益率(Gain Ratio)作为特征的 Gain Ratio。
以每个数据
为阈值划分
数据集
使用阈值对
数据集进行
划分
对数据集排
序
计算各划分
的信息增益
根据最大增
益选择阈值
4
.相比 ID3 算法的改进
使用信息增益比例而非信息增益作为分裂标准
处理含有带缺失值的样本方法为将这些值并入最常见的某一类中或以最常用的值代替
处理连续值属性
规则的产生:规则集存储于一个二维数组中,每一行代表决策树的一个规则
交互验证:训练开始之前,预留一部分数据,训练之后,使用这部分数据对学习的结果进行验证
5
.6 叶子裁剪
1
.剪枝的原因和目的
解决决策树对训练样本的过拟合问题
.决策树常用剪枝方法
预剪枝(Pre-Pruning)和后剪枝(Post-Pruning)
. 预剪枝:预剪枝是根据一些原则及早的停止树增长,如树的深度达到用户所要的深度、节点中样本
个数少于用户指定个数、不纯度指标下降的最大幅度小于用户指定的幅度等。
. 后剪枝:通过在完全生长的树上剪去分枝实现的,通过删除节点的分支来剪去树节点,可以使用的
2
3
4
后剪枝方法有多种,比如:代价复杂性剪枝、最小误差剪枝、悲观误差剪枝等等
修剪方式有:1)用叶子节点来替换子树,叶节点的类别由子树下面的多类决定
2
)用子树最常用的分支来替代子树


5
.7 决策树算法 CART
参考:http://wenku.baidu.com/view/286c19dae009581b6bd9eb59.html
1.分类与会归树(calssification and regression tree,CART)是在给定输入随机变量 X 条件下输出随机
变量 Y 的条件概率分布的学习方法。CART 假设决策树是二叉树,内部结点特征的取值为‘是’和‘否’。
这样的决策树等同于递归地二分每个特征,将输入控件即特征空间划分为有限个单元,并在这些单元
上确定预测地概率分布。
2
.决策树的生成就是递归地构建二叉决策树的过程,对回归树用平方误差最小化准则,对分类树用
GINI 指标(基尼指数)最小化准则进行特征选择,生成二叉树。
.最小二乘回归树生成算法
3
已知 X,Y 分别为输入和输出变量,并且 Y 是连续变量
输入:训练数据集 D
输出:回归树 f(x)
在训练数据集所在的输入空
间中,递归地将每个区域划分为两
个子区域并决定每个子区域的输
出值,构建二叉决策树
4
. 基尼指数
分类问题中,假设有 K 个类,样本点属于第 k 类的概率为푝푘,则概率分布的基尼指数定义为:
Gini(푝) = ∑퐾 푝 (1 − 푝 ) = 1 − ∑
퐾
푘=1
2
푝
푘
푘=1
푘
푘
2
对于给定的样本集合,其基尼指数为Gini(D) = 1 − ∑퐾 (|
퐶 |
) ,其中 Ck 是 D 中属于第 k 类的
푘
푘=1
|
퐷|
样本子集,K 是类的个数。
若样本集合 D 根据特征 A 是否取某一可能值 a 被分割成 D 和 D 两部分,即
1
2
퐷 = {(푥, 푦) ∈ 퐷|퐴(푥) = 푎}, 퐷 = 퐷 − 퐷
1
2
1
则在特征 A 的条件下,集合 D 的基尼指数定义为:
|
퐷 |
|퐷2|
1
Dini(D, A) =
퐺ꢀꢁꢀ(퐷1) +
퐺ꢀꢁꢀ(퐷2)
퐷
퐷
基尼指数 Gini(D)表示集合 D 的不确定性,基尼指数越大,样本的不确定性越大
5
6
.分类树用基尼指数选择最优特征,同时决定该特征的最优二值切分点。
.CART 生成算法
输入:训练数据集 D,停止计算得条件
输出:CART 决策树
根据训练数据集,从根节点开始,递归地对每个节点进行以下操作,构建二叉决策树:
(
1)设终点训练数据集为 D,计算现有特征对该数据集的基尼指数,此时对每个特征 A,其可能取





的每个值 a,样本点对 A=a 的测试为“是”或“否”将 D 分割成 D 和 D 两部分,计算 A=a 时的基尼指
1
2
数
(
2)在所有可能的特征 A 以及他们所有可能的切分点 a 中,选择基尼指数最小的特征及其对应的切
分点作为最优特征与最优切分点。依据最优特征与最优切分点,从现结点生成两个子节点,将训练数
据集依特征分配到两个子结点中。
(
(
3)对两个子结点递归地调用(1),(2),直到满足条件为止。
4)生成 CART 决策树
算法停止的条件是节点中的样本个数小于预订阈值或样本集的基尼指数小于预订阈值(样本属于同一
类),或者没有更多特征
5
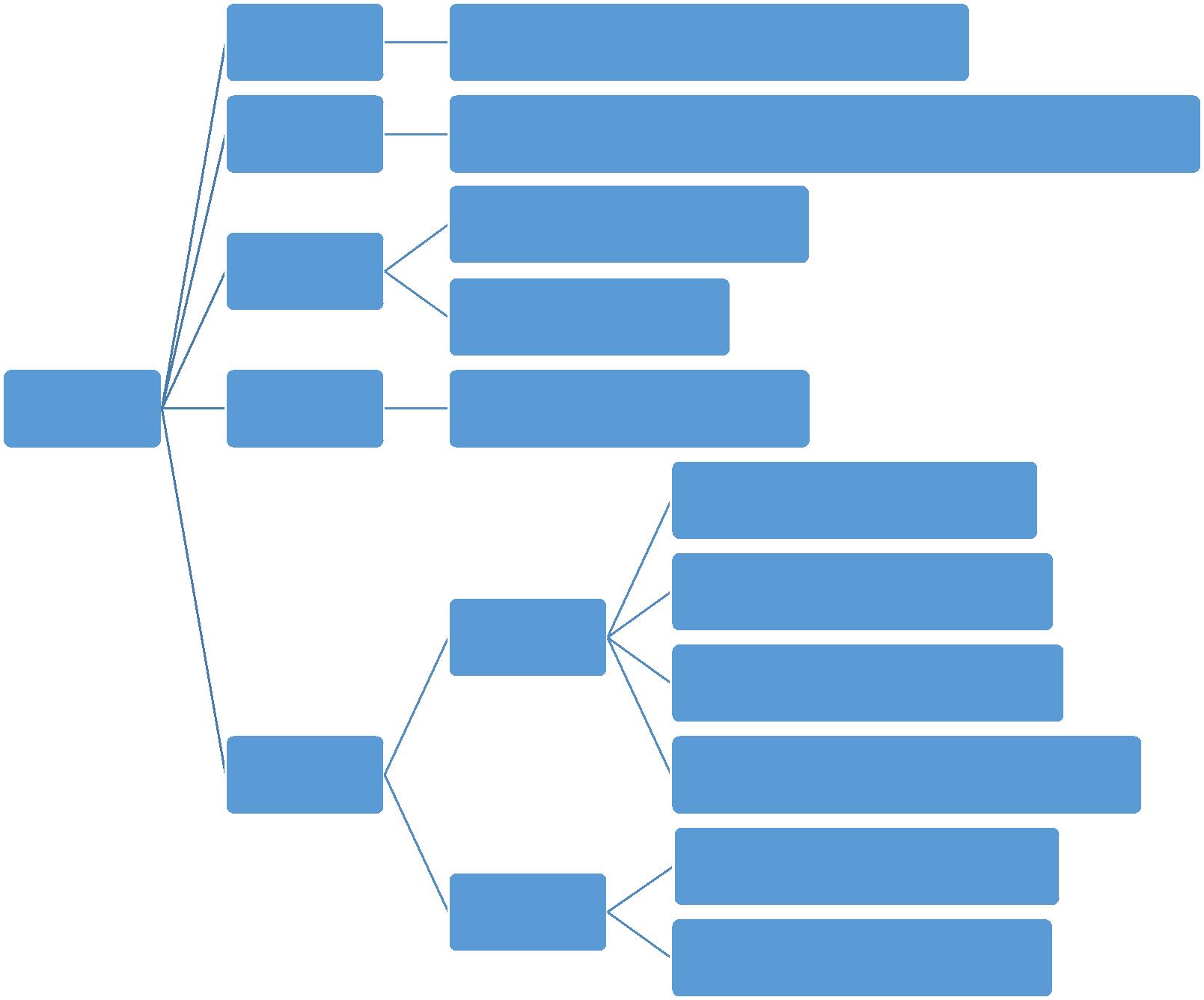
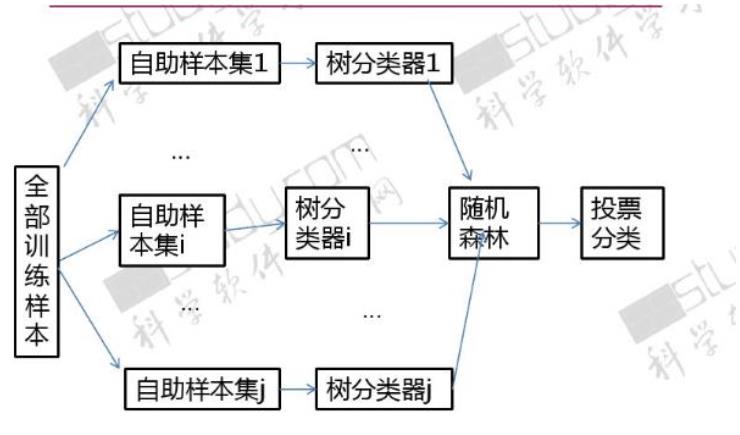
.8 随机森林
1
.概念:随机森林利用随机的方式将许多决策树组合成一个森林,每个决策树在分类的时候决定测试
样本的最终类别。在保持单颗树精度不变下,通过引入随机性,降低树与树之间的相关性,来提高预
测精度。
单棵决策树
精度低
组合算法,如bagging,
adaboost
随机森林
• 进一步提高精度
•
•
提高精度
2
.随机森林构造过程
1
.随机选择
给定训练样本集,数量为N,有放回采样
到N个样本(会重复)
样本
2
3
4
.随机选择
总量为M的特征向量中,随机选择(无放回)m个特征没然
后计算m个特征的增益(m<M),选择最佳特征
特征
Information Gain(ID3)
Gain Ratio(C4.5)
.构建决策
树
.随机森林
重复上述过程H次,投票机
随机森林
投票分类
制获取最终分类结果
能够处理高纬度的数据,并
且不做特征选择
每次学习使用不同训练集,一
定程度避免过拟合
优点
训练结束后,可以给出哪些
feature比较重要
5
.优缺点分
创建随机森林时,对generlization
error使用的是无偏估计
析
在某些噪音较大的分类或回归
问题上会过拟合
缺点
级别划分较多的属性会对随机
森林产生更大的影响
随机性体现在两个方面:
1
2
3
)每棵树的训练样本是随机的,样本容量与原始训练集一样
)树中每个节点的分类属性也是随机选择的
.随机森林参数
随机森林有两个参数需要人为控制,一个是森林中树的数量,一般建议取很大;一个是特征 m 的大
小,推荐 m 的值为 M 的均方根


4
.随机特征的选取
为了使每棵树之间的关联性尽可能的小,在构造树的过程中要对它的特征进行恰当的选择,主要有两
种方法:
随机选取特征变量
在每一个节点随机选取以小组(比如 m 个)输入变量进行分割,这样决策树的节点分割就是根据
这 F 个选定的特征,而不是考察所有的特征来决定
随机选取特征变量的线性组合
若 M 值不大,随机选择 m 个特征,这样可能提高模型的强度,但同时也扩大相关系数。
解决方法:有 L 个变量线性组合作为一个输入特征。在一个给定的节点,L 个变量是随机选择的,
以他们的系数作为权重想家,每一个系数都是在[-1,1]之间的均匀分布随机数。
5
Python 实现
使用 scikit-learn 自带的 iris 数据来进行随机森林的预测
#
Import Lib
From sklearn.ensemble import RandomForestClassifier
#
#
#
use RandomForestRegressor for regression problem
Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
Create Random Forest object
model= RandomForestClassifier(n_estimators=1000)
Train the model using the training sets and check score
model.fit(X, y)
Predict Output
predicted= model.predict(x_test)
#
#


第六章 朴素贝叶斯分类
6
.1 朴素贝叶斯分类数学基础
1
.贝叶斯定理
假设对于某个数据集,随机变量 C 表示样本为 C 类的概率,F1 表示测试样本某特征出现的概率,套
用基本贝叶斯公式,则如下所示:
上式表示对于某个样本,特征 F1 出现时,该样本被分为 C 类的条件概率。
对于该公式,需要熟知的概念:
先验概率(Prior):P(C)是 C 的先验概率,可以从已有的训练集中计算分为 C 类的样本占所有样本的
比重得出。
证据(Evidence):即上式 P(F1),表示对于某测试样本,特征 F1 出现的概率。同样可以从训练集中
F1 特征对应样本所占总样本的比例得出。
似然(likelihood):即上式 P(F1|C),表示如果知道一个样本分为 C 类,那么他的特征为 F1 的概率是
多少
对于多特征而言:
贝叶斯定理是基于假设的先验概率给定假设下观察到不同数据的概率,提供了一种计算后验概率的方
法
6
.2 朴素贝叶斯分类
1
.思想基础
对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项
属于哪个类别。
2
1
2
3
.假设条件
)特征之间相互独立
)每个特征同等重要
.朴素的概念
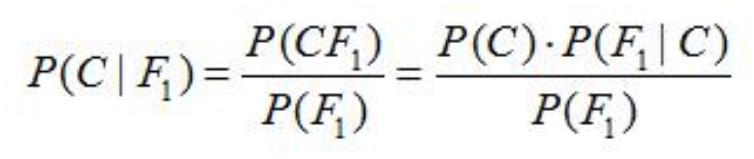
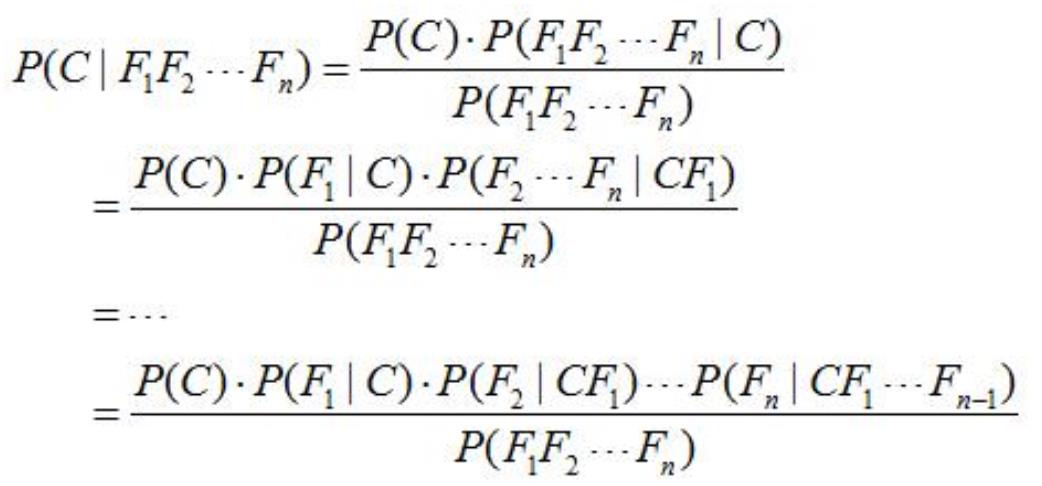
1
2
)“朴素的认为各个特征相互独立” 分子简化成 P(C)*P(F1|C)*P(F2|C)...P(Fn|C)
)工作原理为计算 P(C=0|F1...Fn)和 P(C=1|F1...Fn),并取最大值的那个作为其分类
而二者的分母是一模一样的。因此,我们又可以省略分母计算,从而进一步简化计算过程。
3
)贝叶斯公式推导能够成立有个重要前期,就是各个证据(evidence)不能为 0。也即对于任意特征
Fx,P(Fx)不能为 0。
处理方法:
A 把所有计数进行+1(加法平滑(additive smoothing,又叫拉普拉斯平滑(Laplace smothing))
B 如果通过增加一个大于 0 的可调参数 alpha 进行平滑,就叫 Lidstone 平滑。
4
)当特征很多的时候,大量小数值的小数乘法会有溢出风险。因此,通常的实现都是将其转换为 log:
log[P(C)*P(F1|C)*P(F2|C)...P(Fn|C)] = log[P(C)]+log[P(F1|C)] + ... +log[P(Fn|C)]
将乘法转换为加法,就彻底避免了乘法溢出风险。
4
.算法原理
5
.优缺点
优点
可以和决策树、神经网络分类算法相媲美,能运用于大型数据库
方法简单,分类准确率高,速度快,所需估计的参数少,对于缺失数据不敏感
缺点
假设一个属性对分类的影响独立于其他的属性值,这往往不成立(即实际上难以满足的相互独立)
需要知道先验概率



6
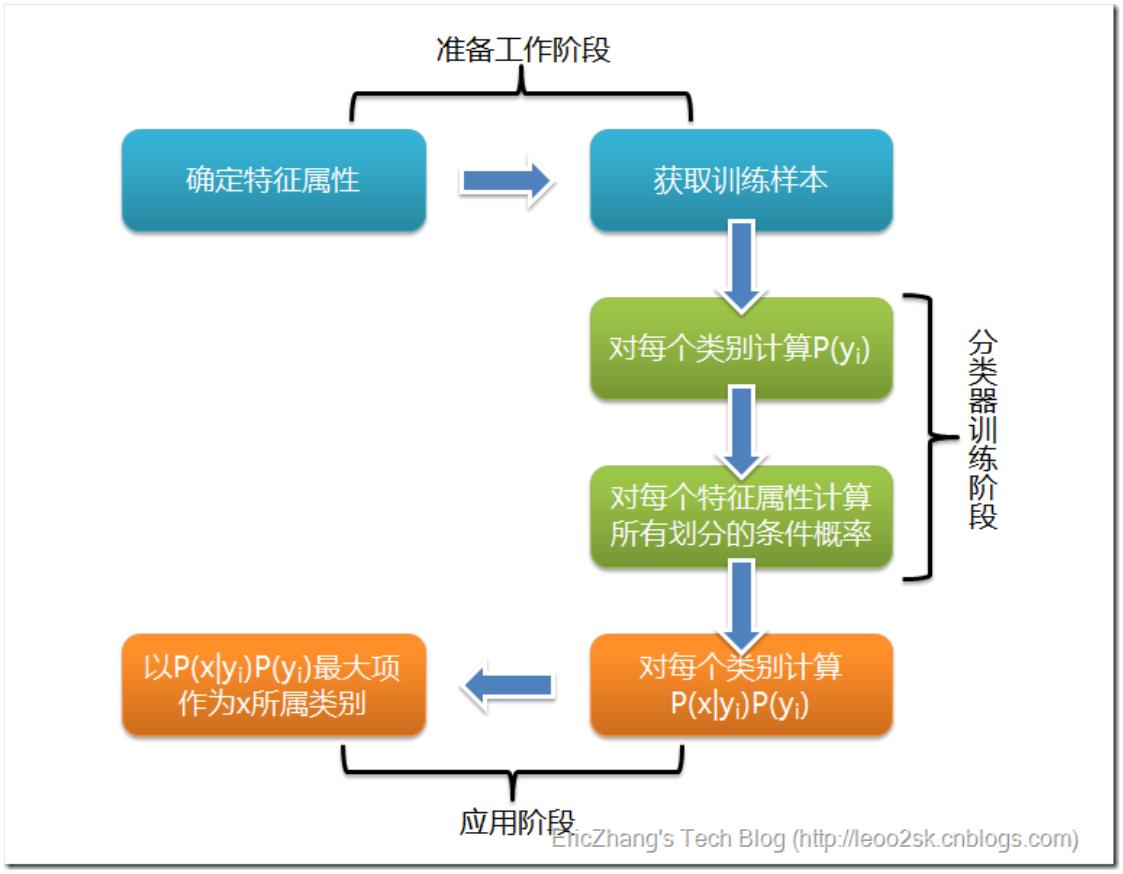
.3 朴素贝叶斯分类流程
6
.4 朴素贝叶斯分类 Python 实战
#
Import Library
from sklearn.naive_bayes import GaussianNB
#
#
Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
Create SVM classification object model = GaussianNB() # there is other distribution for multinomial classes like Bernoulli
Naive Bayes, Refer link
Train the model using the training sets and check score
model.fit(X, y)
Predict Output
predicted= model.predict(x_test)
#
#

第七章 Logistic 回归
7
.1.逻辑回归(LR)基本概念
1
.什么是逻辑回归
逻辑回归就是这样的一个过程:面对一个回归或者分类问题,建立代价函数,然后通过优化方
法迭代求解出最优的模型参数,然后测试验证我们这个求解的模型的好坏。
Logistic 回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只
有两种,分别代表两个类别)
回归模型中,y 是一个定性变量,比如 y=0 或 1,logistic 方法主要应用于研究某些事件发生的
概率
2
.逻辑回归优缺点
优点:
1
2
3
)速度快,适合二分类问题
)简单易于理解,直接看到各个特征的权重
)能容易地更新模型吸收新的数据
缺点:
对数据和场景的适应能力有局限性,不如决策树算法适应性那么强
.逻辑回归与多重线性回归区别
Logistic 回归与多重线性回归实际上有很多相同之处,最大的区别就在于它们的因变量不同,其
他的基本都差不多。正是因为如此,这两种回归可以归于同一个家族,即广义线性模型
generalizedlinear model)。
这一家族中的模型形式基本上都差不多,不同的就是因变量不同。
3
(
如果是连续的,就是多重线性回归;
如果是二项分布,就是 Logistic 回归;
如果是 Poisson 分布,就是 Poisson 回归;
如果是负二项分布,就是负二项回归。
4
.逻辑回归用途
寻找危险因素:寻找某一疾病的危险因素等;
预测:根据模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大;
判别:实际上跟预测有些类似,也是根据模型,判断某人属于某病或属于某种情况的概率有
多大,也就是看一下这个人有多大的可能性是属于某病。
5
6
. Regression 常规步骤
寻找 h 函数(即预测函数);
构造 J 函数(损失函数);
想办法使得 J 函数最小并求得回归参数(θ)
.构造预测函数 h
Logistic 函数(或称为 Sigmoid 函数),函数形式为:


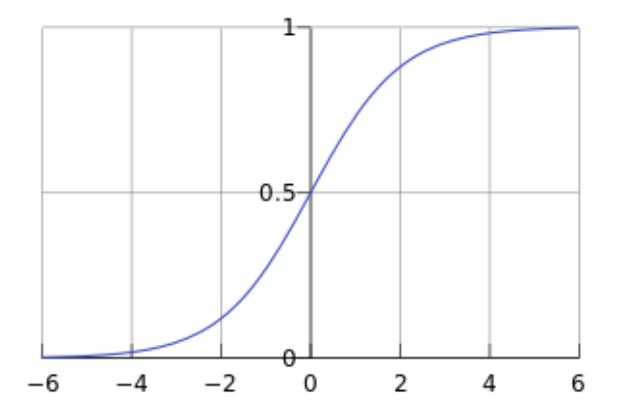
对于线性边界的情况,边界形式如下:
푛
푇
z = 휃 푥 = 휃 푥 + 휃 푥 + ⋯ + 휃 푥 = ∑ 휃 푥
0
0
1
1
푛
푛
푖
푖
푖=0
其中,训练数据为向量x = [푥 , 푥 , 푥 , 푥 , … , 푥 ]푇 ,最佳参数휃 = [휃 , 휃 , 휃 , … , 휃 ]푇
0
1
2
3
푛
0
1
2
푛
构造预测函数为:
1
ℎ (푥) = 푔(휃푇푥) =
휃
1
+ 푒−휃푇푥
函数
的值有特殊的含义,它表示结果取 1 的概率,因此对于输入 x 分类结果为类别 1 和类
别 0 的概率分别为:
푃(푦 = 1|푥; 휃) = ℎ휃(푥)
푃(푦 = 0|푥; 휃) = 1 − ℎ휃(푥)
(1)
7
.构造损失函数 J(m 个样本,每个样本具有 n 个特征)
Cost 函数和 J 函数如下,它们是基于最大似然估计推导得到的。
−
log(ℎ휃(푥)) ꢀ푓 푦 = 1
퐶표푠푡(ℎ휃(푥), 푦) = {
−
log(1 − ℎ휃(푥)) ꢀ푓 푦 = 0
푚
푚
1
1
퐽(휃) = ∑ 퐶표푠푡(ℎ (푥 ), 푦 ) = − [∑(푦 푙표푔ℎ (푥 ) + (1 − 푦 ) log(1 − ℎ (푥 )))]
휃
푖
푖
푖
휃
푖
푖
휃
푖
푚
푚
푖=1
푖=1
8
.损失函数详细推导过程
求代价函数
(
1)式综合起来可以写成:
取似然函数为:
对数似然函数为:
最大似然估计就是求使
要求的最佳参数。
取最大值时的 θ,其实这里可以使用梯度上升法求解,求得的 θ 就是
在 Andrew Ng 的课程中将
取为下式,即:



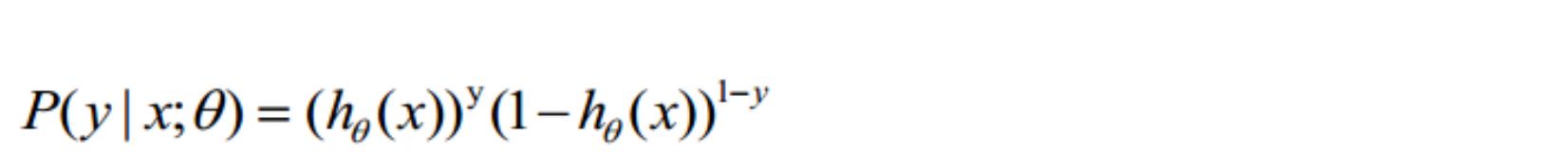
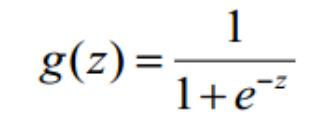
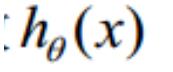
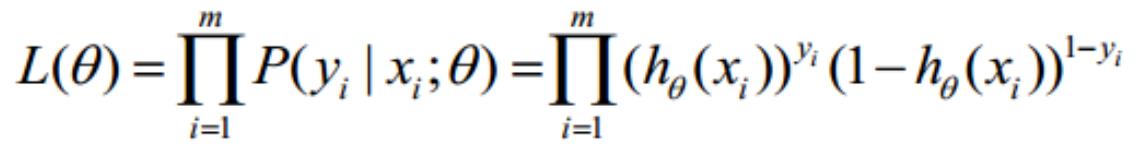
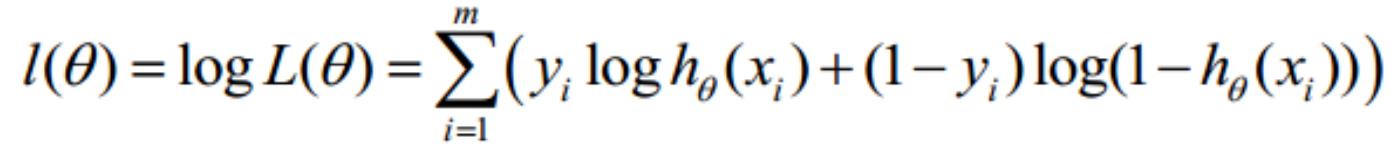
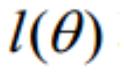
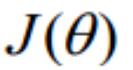
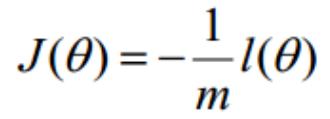
因为乘了一个负的系数-1/m,所以取
最小值时的 θ 为要求的最佳参数。
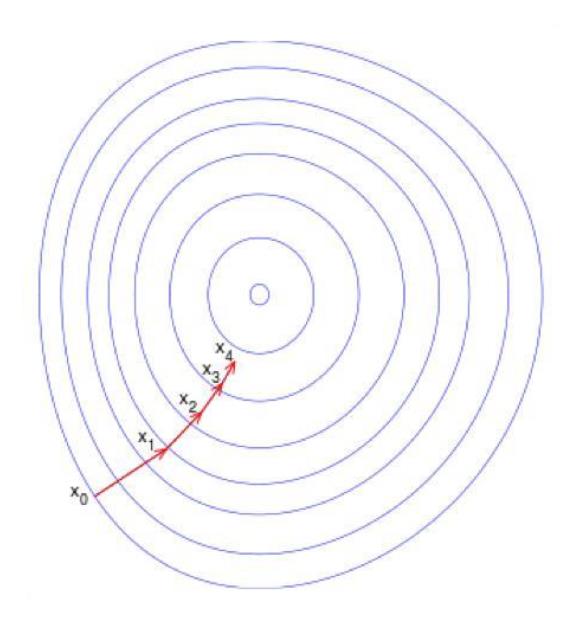
梯度下降法求解最小值
θ 更新过程:
θ 更新过程可以写成:
9
. 向量化 Vectorization
Vectorization 是使用矩阵计算来代替 for 循环,以简化计算过程,提高效率。
向量化过程:
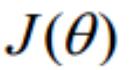
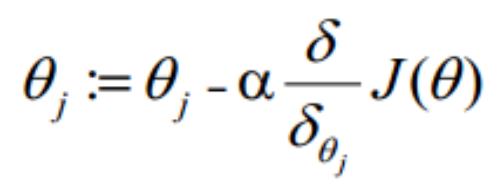
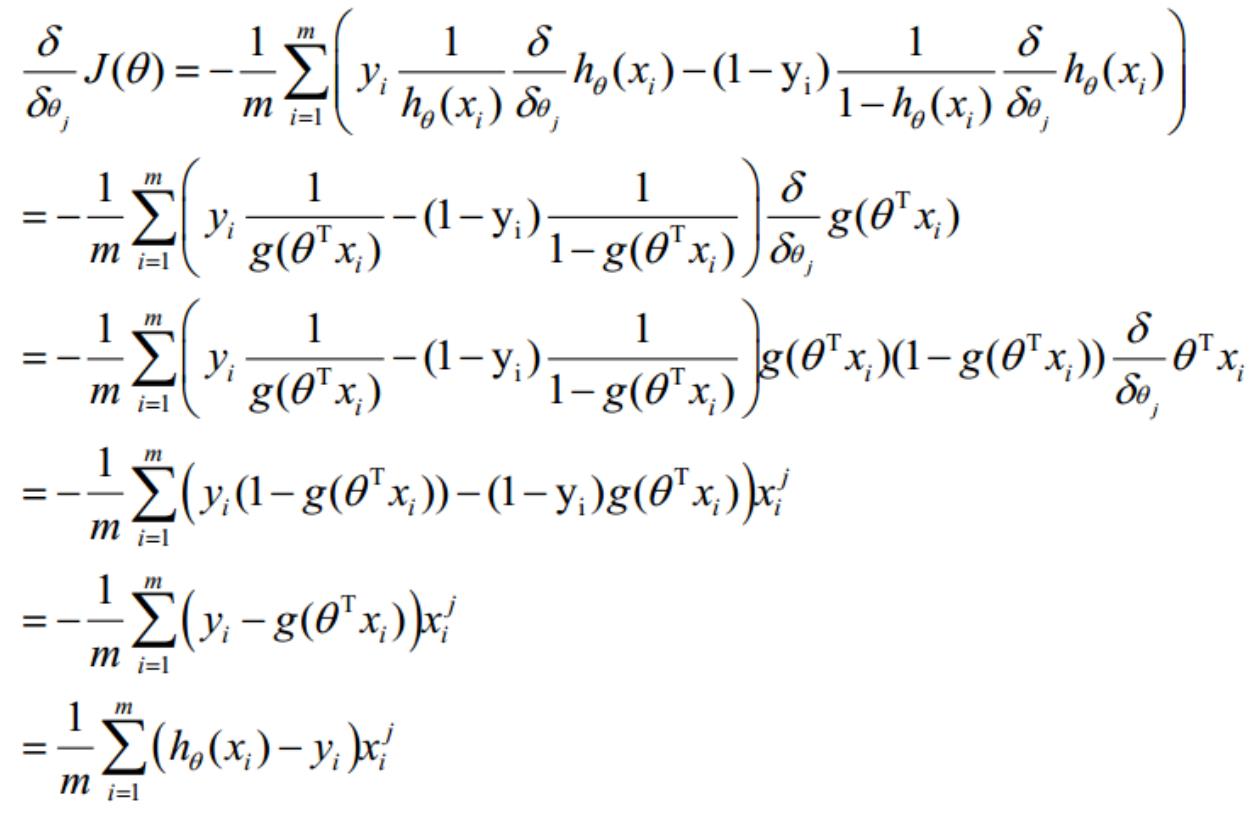
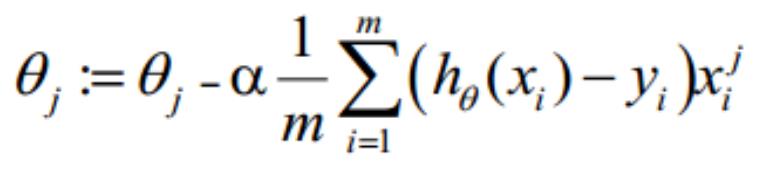
约定训练数据的矩阵形式如下,x 的每一行为一条训练样本,而每一列为不同的特称取值:
g(A)的参数 A 为一列向量,所以实现 g 函数时要支持列向量作为参数,并返回列向量。由上式可知
可由
一次计算求得。
θ 更新过程可以改为:
综上所述,Vectorization 后 θ 更新的步骤如下:
(
(
1)求
2)求
;
;
(
3) 求
。
1
0. 正则化 Regularization
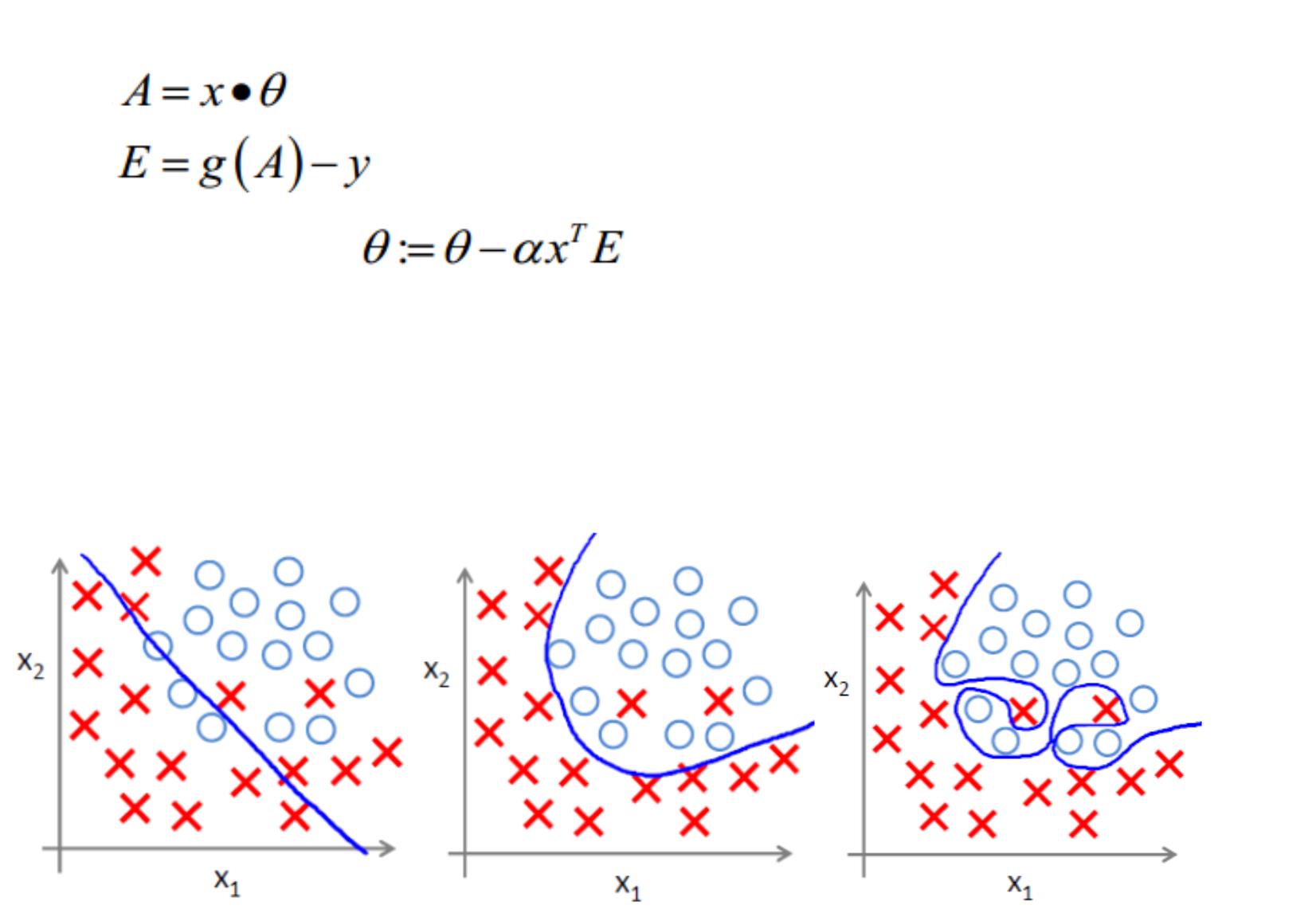
过拟合问题
过拟合即是过分拟合了训练数据,使得模型的复杂度提高,繁华能力较差(对未知数据的预测
能力)
下面左图即为欠拟合,中图为合适的拟合,右图为过拟合。


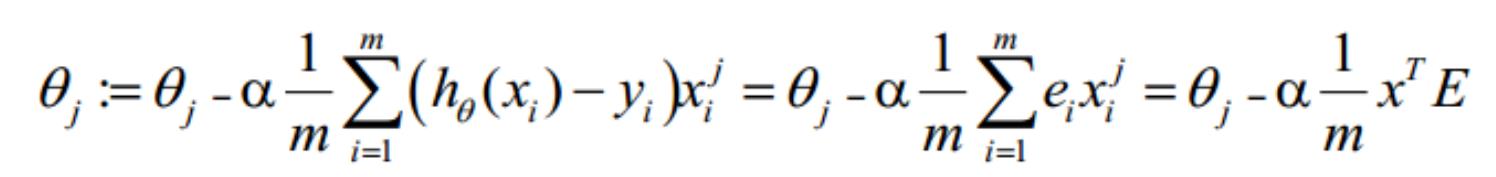
过拟合主要原因
过拟合问题往往源自过多的特征
解决方法
1
)减少特征数量(减少特征会失去一些信息,即使特征选的很好)
可用人工选择要保留的特征;
模型选择算法;
2
)正则化(特征较多时比较有效)
保留所有特征,但减少 θ 的大小
正则化方法
正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项或惩罚项。正则化项一般是
模型复杂度的单调递增函数,模型越复杂,正则化项就越大。
正则项可以取不同的形式,在回归问题中取平方损失,就是参数的 L2 范数,也可以取 L1 范数。取
平方损失时,模型的损失函数变为:
lambda 是正则项系数:
如果它的值很大,说明对模型的复杂度惩罚大,对拟合数据的损失惩罚小,这样它就不会过
分拟合数据,在训练数据上的偏差较大,在未知数据上的方差较小,但是可能出现欠拟合的
现象;
如果它的值很小,说明比较注重对训练数据的拟合,在训练数据上的偏差会小,但是可能会
导致过拟合。
正则化后的梯度下降算法 θ 的更新变为:
摘自博文:http://blog.csdn.net/pakko/article/details/37878837
7
.2 Python 算法包实现逻辑回归
以下内容摘自博文 http://www.powerxing.com/logistic-regression-in-python/
1
.使用算法包介绍
numpy: Python 的语言扩展,定义了数字的数组和矩阵
pandas: 直接处理和操作数据的主要 package
statsmodels: 统计和计量经济学的 package,包含了用于参数评估和统计测试的实用工具
pylab: 用于生成统计图
2
.逻辑回归实例
案例描述:辨别不同因素对研究生录取的影响



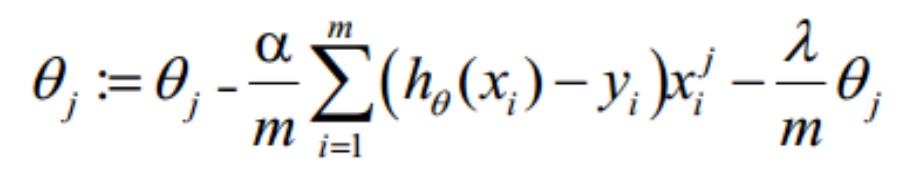
数据集中前三列作为预测变量(predictor variables):
gpa
gre 分数
rank 表示本科生母校的声望
第四列 admit 则是二分类目标变量,它表明考生最终是否被录用
3
.加载数据
使用 pandas.read_csv 加载数据,这样我们就有了可用于探索数据的 DataFrame。
#
-*- coding: utf-8 -*-
""
Created on Tue Sep 20 10:56:13 2016
author: Serana
""
"
@
"
import pandas as pd
import statsmodels.api as sm
import pylab as pl
import numpy as np
#
#
加载数据
备用地址: http://cdn.powerxing.com/files/lr-binary.csv
df = pd.read_csv("http://www.ats.ucla.edu/stat/data/binary.csv")
浏览数据集
print df.head()
#
#
#
#
#
#
#
#
admit gre
gpa rank
0
1
2
3
4
0
1
1
1
0
380 3.61
3
660 3.67
800 4.00
640 3.19
520 2.93
3
1
4
4
重命名'rank'列,因为 dataframe 中有个方法名也为'rank'
df.columns=["admit","gre","gpa","prestige"]
print df.columns
#
Index([u'admit', u'gre', u'gpa', u'prestige'], dtype='object')
4
.统计摘要(Summary Statistics)以及查看数据
#
使用 pandas 的函数 describe 来给出数据的摘要–describe
print df.describe()
#
#
#
#
#
#
#
#
admit
gre
gpa
prestige
count 400.000000 400.000000 400.000000 400.00000
mean
std
0.317500 587.700000
0.466087 115.516536
0.000000 220.000000
0.000000 520.000000
0.000000 580.000000
1.000000 660.000000
3.389900
0.380567
2.260000
3.130000
3.395000
3.670000
2.48500
0.94446
1.00000
2.00000
2.00000
3.00000
min
25%
50%
75%


#
#
max
1.000000 800.000000
4.000000
4.00000
查看每一列的标准差
print df.std()
#
#
#
#
#
admit
gre
0.466087
115.516536
0.380567
gpa
prestige
0.944460
频率表,表示 prestige 与 admin 的值相应的数量关系
print pd.crosstab(df['admit'], df['prestige'], rownames=['admit'])
#
#
#
#
#
prestige
1
2
3
4
admit
0
1
28 97 93 55
33 54 28 12
plot all of the columns
df.hist()
pl.show()
5
.虚拟变量(dummy variables)
虚拟变量,也叫哑变量,可用来表示分类变量、非数量因素可能产生的影响,通过构造 0-1 型的人工
变量来量化属性因素。
pandas 提供了一系列分类变量的控制。我们可以用 get_dummies 来将”prestige”一列虚拟化。
get_dummies 为每个指定的列创建了新的带二分类预测变量的 DataFrame,在本例中,prestige 有四
个级别:1,2,3 以及 4(1 代表最有声望),prestige 作为分类变量更加合适。当调用 get_dummies
时,会产生四列的 dataframe,每一列表示四个级别中的一个。
#
用 get_dummies 来将”prestige”一列虚拟化
dummy_ranks=pd.get_dummies(df['prestige'],prefix='prestige')

print dummy_ranks.head()
#
#
#
#
#
#
#
#
prestige_1 prestige_2 prestige_3 prestige_4
0
1
2
3
4
0
0
1
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
为逻辑回归创建所需的 data frame
除 admit、gre、gpa 外,加入了上面常见的虚拟变量(注意,引入的虚拟变量列数应为虚拟变量总列数减 1,减
去的 1 列作为基准)
cols_to_keep = ['admit', 'gre', 'gpa']
data = df[cols_to_keep].join(dummy_ranks.ix[:, 'prestige_2':])
print data.head()
#
#
#
#
#
#
#
admit gre
gpa prestige_2 prestige_3 prestige_4
0
1
2
3
4
0
1
1
1
0
380 3.61
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
660 3.67
800 4.00
640 3.19
520 2.93
需要自行添加逻辑回归所需的 intercept 变量
data['intercept'] = 1.0
#
#
#
将新的虚拟变量加入到了原始的数据集中后,就不再需要原来的 prestige 列了。在此要强调一点,
生成 m 个虚拟变量后,只要引入 m-1 个虚拟变量到数据集中,未引入的一个是作为基准对比的。
最后,还需加上常数 intercept,statemodels 实现的逻辑回归需要显式指定。
6
. 执行逻辑回归
本例中要预测的是 admit 列,使用 gre,gpa 和虚拟变量 prestige_2, prestige_3, prestige_4; prestige_1
作为基准,所以要排除掉。
#
指定作为训练变量的列,不含目标列`admit`
train_cols=data.columns[1:]
Index([gre, gpa, prestige_2, prestige_3, prestige_4], dtype=object)
logit=sm.Logit(data['admit'],data[train_cols])
拟合模型
result=logit.fit()
#
#
7
.使用训练模型预测数据
#
#
#
构建预测集
与训练集相似,一般也是通过 pd.read_csv() 读入
在这边为方便,我们将训练集拷贝一份作为预测集(不包括 admin 列)
import copy
combos=copy.deepcopy(data)
#
数据中的列要跟预测时用到的列一致
predict_cols = combos.columns[1:]
预测集也要添加 intercept 变量
combos['intercept'] = 1.0
进行预测,并将预测评分存入 predict 列中
combos['predict'] = result.predict(combos[predict_cols])
#
#



#
#
#
#
预测完成后,predict 的值是介于 [0, 1] 间的概率值
我们可以根据需要,提取预测结果
例如,假定 predict > 0.5,则表示会被录取
在这边我们检验一下上述选取结果的精确度
total=0
hit=0
for value in combos.values:
#
预测分数 predict, 是数据中的最后一列
predict =value[-1]
#
实际录取结果
admit=int(value[0])
假定预测概率大于 0.5 则表示预测被录取
#
if predict>0.5:
total+=1
#
表示预测命中
if admit==1:
hit+=1
#
输出结果
print 'Total: %d, Hit: %d, Precision: %.2f' % (total, hit, 100.0*hit/total)
#
#
6
Total: 49, Hit: 30, Precision: 61.22
假定预测概率大于 0.5 则表示预测被录取,一共预测有 49 个被录取,其中有 30 个预测命中,精确度为
1.22%。
8
.结果解释
#
#
statesmodels 提供了结果的摘要,如果你使用过 R 语言,你会发现结果的输出与之相似。
查看数据的要点
print result.summary()
#
#
Logit Regression Results
==========================================================================
=
===
#
#
#
#
#
#
#
#
Dep. Variable:
Model:
admit
Logit
MLE
No. Observations:
400
394
Df Residuals:
Method:
Date:
Df Model:
Pseudo R-squ.:
Log-Likelihood:
LL-Null:
5
Tue, 20 Sep 2016
14:03:05
0.08292
-229.26
-249.99
7.578e-08
Time:
converged:
True
LLR p-value:
==========================================================================
=
#
===
coef
std err
z
P>|z|
[95.0% Conf. Int.]
#
#
#
#
#
#
#
------------------------------------------------------------------------------
gre
0.0023
0.8040
0.001
0.332
2.070
2.423
0.038
0.015
0.000
0.154
0.004
1.454
-0.055
gpa
prestige_2
prestige_3
prestige_4
intercept
-0.6754
0.316
-2.134
0.033
-1.296
-1.3402
-1.5515
-3.9900
0.345
0.418
1.140
-3.881
-3.713
-3.500
0.000
0.000
0.000
-2.017
-2.370
-6.224
-0.663
-0.733
-1.756


#
==========================================================================
=
#
===
查看每个系数的置信区间
print result.conf_int()
#
0
1
#
#
#
#
#
#
gre
0.000120 0.004409
0.153684 1.454391
gpa
prestige_2 -1.295751 -0.055135
prestige_3 -2.016992 -0.663416
prestige_4 -2.370399 -0.732529
intercept -6.224242 -1.755716
9
.相对危险度(odds ratio)
使用每个变量系数的指数来生成 odds ratio,可知变量每单位的增加、减少对录取几率的影响。
#
输出 odds ratio
print np.exp(result.params)
#
#
#
#
#
#
#
#
gre
1.002267
2.234545
0.508931
0.261792
0.211938
0.018500
gpa
prestige_2
prestige_3
prestige_4
intercept
使用置信区间来计算系数的影响,来更好地估计一个变量影响录取率的不确定性。
odds ratios and 95% CI
params = result.params
conf = result.conf_int()
conf['OR'] = params
conf.columns = ['2.5%', '97.5%', 'OR']
print np.exp(conf)
#
#
#
#
#
#
#
2.5%
97.5%
OR
gre
1.000120 1.004418 1.002267
1.166122 4.281877 2.234545
0.273692 0.946358 0.508931
0.133055 0.515089 0.261792
0.093443 0.480692 0.211938
0.001981 0.172783 0.018500
gpa
prestige_2
prestige_3
prestige_4
intercept
1
0.结束语
逻辑回归是用于分类的优秀算法,尽管有一些更加性感的,或是黑盒分类器算法,如 SVM 和随机
森林(RandomForest)在一些情况下性能更好,但深入了解你正在使用的模型是很有价值的。很多
时候你可以使用随机森林来筛选模型的特征,并基于筛选出的最佳的特征,使用逻辑回归来重建模
型。


第八章 SVM 支持向量机
8
.1 SVM 基本思想
SVM 把分类问题转化为寻找分类平面的问题,并通过最大化分类边界点距离分类平面的距离来实现
分类
8
.2 SVM 优缺点
优点:
1
2
3
4
)可以解决小样本下机器学习的问题
)提高泛化性能
)可以解决文本分类、文字识别、图像分类等方面仍受欢迎
)避免神经网络结构选择和局部极小的问题
缺点:
1
2
)缺失数据敏感
)内存消耗大,难以解释
8
.3 SVM 与逻辑回归的区别
相同点:
1
2
)均是常见的分类算法
)两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的
权重
3
)两个方法都可以增加不同的正则化项,如 l1,l2 等等
区别:
1
2
)从目标函数来看:逻辑回归采用 logistical loss,SVM 采用 hinge loss
)损失函数处理:
SVM 只考虑 support vectors,也就是和分类最相关的少数点,去学习分类器
逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点
的权重
3
)logistic regression 是参数模型,SVM 更多的是属于非参数模型
补充:
参数模型:一类可以通过结构化表达式和参数集表示的模型.参数模型是以代数方程、微分方程、传递函数等形式
表达的,或采用机抑方法建立的模型。
非参数模型:指系统的数学模型中非显式地包含可估参数。例如,系统的频率响应、脉冲响应、阶
跃响应等都是非参数模型。


第九章 集成学习(Esemble Learning)
.1 关于集成学习的基本概念
9
1
.集成学习概念
集成学习是机器学习中一个非常重要且热门的分支,是用多个弱分类器构成一个强分类器,其哲学
思想是“三个臭皮匠赛过诸葛亮”。一般的弱分类器可以由决策树,神经网络,贝叶斯分类器,K-近
邻等构成。已经有学者理论上证明了集成学习的思想是可以提高分类器的性能的,比如说统计上的
原因,计算上的原因以及表示上的原因。
2
.为什么要集成
1
)模型选择
假设各弱分类器间具有一定差异性(如不同的算法,或相同算法不同参数配置),这会导致生成的分
类决策边界不同,也就是说它们在决策时会犯不同的错误。将它们结合后能得到更合理的边界,减
少整体错误,实现更好的分类效果。
2
)数据集过大或过小
数据集较大时,可以分为不同的子集,分别进行训练,然后再合成分类器。
数据集过小时,可使用自举技术(bootstrapping),从原样本集有放回的抽取 m 个子集,训练 m 个
分类器,进行集成。
3
)分治
若决策边界过于复杂,则线性模型不能很好地描述真实情况。因此先训练多个线性分类器,再将它
们集成。
4
)数据融合(Data Fusion)
当有多个不同数据源,且每个数据源的特征集抽取方法都不同时(异构的特征集),需要分别训练分
类器然后再集成
3
集成学习常用算法(Boosting / bagging / stacking)
boosting 的弱分类器形成是同一种机器学习算法,只是其数据抽取时的权值在不断更新,每次都是
提高前一次分错了的数据集的权值,最后得到 T 个弱分类器,且分类器的权值也跟其中间结果的数
据有关。
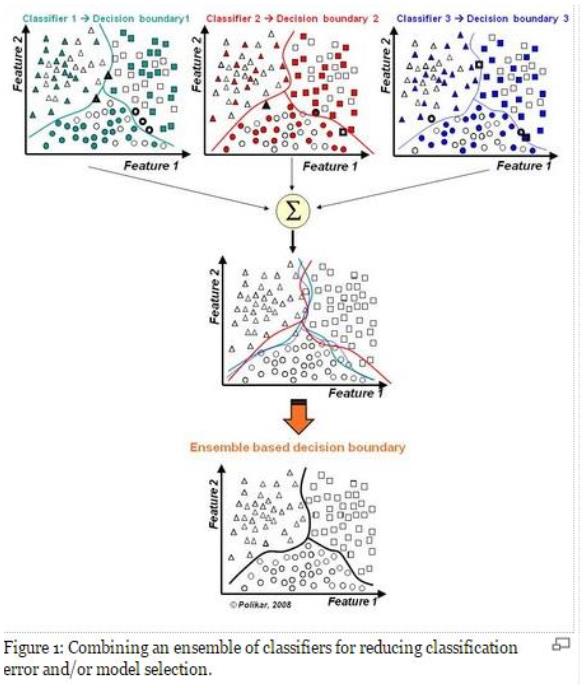
Bagging 算法也是用的同一种弱分类器,其数据的来源是用 bootstrap 算法得到的(有放回抽样,一
个 instance 被前面分错的越厉害,它的概率就被设的越高)。
Stacking 算法分为两个阶段,首先我们使用多个基础分类器来预测分类;然后,一个新的学习模块
与它们的预测结果结合起来,来降低泛化误差。
4
1
2
5
集成学习有效的前提
)每个弱分类器的错误率不能高于 0.5
)弱分类器之间的性能要有较大的差别,否则集成效果不是很好
集成学习分类
集成学习按照基本分类器之间的关系可以分为异态集成学习和同态集成学习。异态集成学习是指弱
分类器之间本身不同,而同态集成学习是指弱分类器之间本身相同只是参数不同。
6
不同算法的集成
同一种算法在不同设置下的集成
数据集的不同部分分配给不同分类器之后的集成
基本分类器之间的整合方式
简单投票,贝叶斯投票,基于 D-S 证据理论的整合,基于不同的特征子集的整合
7
目前有的一般性实验结论
Boosting 方法的集成分类器效果明显优于 bagging,但是在某些数据集 boosting 算法的效果还不如
单个分类器的。使用随机化的人工神经网络初始权值来进行集成的方法往往能够取得和 bagging
同样好的效果。
Boosting 算法一定程度上依赖而数据集,而 bagging 对数据集的依赖没有那么明显。
Boosting 算法不仅能够减少偏差还能减少方差,但 bagging 算法智能减少方差,对偏差的减少作
用不大。
9
.2 Boosting 中代表性算法 AdaBoost 元算法/集成算法
1
. AdaBoost 元算法
基于数据集多重抽样的分类器
Adaboost 是一种迭代算法,其核心思想是针对同一个训练集训练不同的分类器(弱分类器),然
后把这些弱分类器集合起来,构成一个更强的最终分类器(强分类器)
Adaboost 算法本身是通过改变数据权值分布来实现的,它根据每次训练集中每个样本的分类是
否正确,以及上次的总体分类的准确率,来确定每个样本的权值。将修改过权值的新数据送给
下层分类器进行训练,最后将每次得到的分类器最后融合起来,作为最后的决策分类器
关于弱分类器的组合,Adaboost 算法采用加权多数表决的方法。具体来说,就是加大分类误差
率小的弱分类器的权值,使其在表决中起较大的作用,减小分类误差率较大的弱分类器的权
值,使其在表决中起较小的作用
2
.Adaboost 算法思路
输入:分类数据;弱算法数组
输出:分类结果
流程:
Step1 给训练数据集中的每一个样本赋予权重,权重初始化相等值,这些权重形成向量 D
一般初始化所有训练样例的权重为 1 / N,其中 N 是样例数
Step2 在训练集上训练出弱分类器并计算该分类器的错误率
Step3 同一数据集上再次训练分类器,调整样本的权重,将第一次分对的样本权重降低,第一次分
错的样本权重提高
Step4 最后给每一个分类器分配一个权重值 alpha,alpha = 0.5*ln((1-错误率)/错误率)
Step5 计算出 alpha 值后,可以对权重向量 D 进行更新,以使得正确分类的样本权重降低而错分样
本的权重升高。D 的计算方法如下:
某样本被正确分类
某样本未被正确分类
(푡)
(푡)
퐷푖 푒−훼
퐷푖 푒훼
(푡+1)
(푡+1)
퐷푖
=
퐷푖
=
푆푢푚(퐷)
푆푢푚(퐷)
计算出 D 之后,AdaBoost 又开始进入下一轮迭代。Adaboost 算法会不断地重复训练和调整权重的过
程,知道训练错误率为 0 或者弱分类器的数目达到用户指定的值为止
3
.Adaboost 算法核心思想
“
关注”被错分的样本,“器重”性能好的弱分类器
实现:
不同的训练集调整样本权重
“关注”增加错分样本权重
“器重”好的分类器权重大
样本权重间接影响分类器权重
4
. Adaboost 算法优缺点
优点:
1
2
3
4
5
5
1
)Adaboost 是一种有很高精度的分类器
)可以使用各种方法构建子分类器,Adaboost 算法提供的是框架
)当使用简单分类器时,计算出的结果是可以理解的,而弱分类器构造及其简单
)简单,不用做特征筛选
)不用担心 overfitting(过拟合)问题
.Adaboost 算法应用场景
)用于二分类或多分类的应用场景





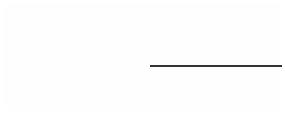
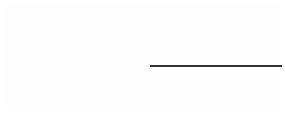


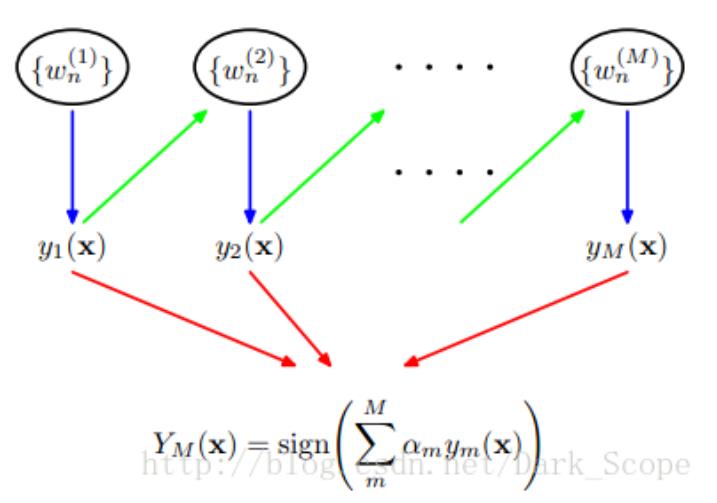
2
3
4
6
)用于做分类任务的 baseline--无脑化,简单,不会 overfitting,不用调分类器
)用于特征选择(feature selection)
)Boosting 框架用于对 badcase 的修正--只需要增加新的分类器,不需要变动原有分类器
.Adaboost 算法 Python 算法库实现
#
Import Library
from sklearn.ensemble import GradientBoostingClassifier
#
#
Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
Create Gradient Boosting Classifier object
model= GradientBoostingClassifier(n_estimators=100, learning_rate=1.0, max_depth=1, random_state=0)
Train the model using the training sets and check score
model.fit(X, y)
Predict Output
predicted= model.predict(x_test)
#
#
9
.2 Boosting 中代表性算法梯度提升(GBDT)
GBDT(Gradient Boosting Decision Tree) 又叫 MART(Multiple Additive Regression Tree),是一种迭代
的决策树算法,该算法由多棵决策树组成,所有树的结论累加起来做最终答案。
GBDT 主要由三个概念组成:
•
Regression Decision Tree(及 DT 回归决策树)
Gradient Boosting(即 GB)
•
•
Shrinkage(算法的一个重要演进分枝)
. DT:回归树 Regression Decision Tree
1
回归树总体流程也是类似,不过在每个节点(不一定是叶子节点)都会得一个预测值,以年龄为
例,该预测值等于属于这个节点的所有人年龄的平均值。分枝时穷举每一个 feature 的每个阈值找最
好的分割点,但衡量最好的标准不再是最大熵,而是最小化均方差--即(每个人的年龄-预测年龄)
^2 的总和 / N,或者说是每个人的预测误差平方和 除以 N。
2
.GB:梯度迭代,Gradient Boosting
Boosting,迭代,即通过迭代多棵树来共同决策。
GBDT 的核心就在于,每一棵树学的是之前所有树结论和的残差,这个残差就是一个加预测值后能
得真实值的累加量。比如 A 的真实年龄是 18 岁,但第一棵树的预测年龄是 12 岁,差了 6 岁,即残
差为 6 岁。那么在第二棵树里我们把 A 的年龄设为 6 岁去学习,如果第二棵树真的能把 A 分到 6 岁
的叶子节点,那累加两棵树的结论就是 A 的真实年龄;如果第二棵树的结论是 5 岁,则 A 仍然存在
1
岁的残差,第三棵树里 A 的年龄就变成 1 岁,继续学。这就是 Gradient Boosting 在 GBDT 中的意
义

9
.3 使用 sklearn 进行集成学习—理论
sklearn 提供了 sklearn.ensemble 库,支持众多集成学习算法和模型。
9
.4 使用 sklearn 进行集成学习---实践
http://www.cnblogs.com/jasonfreak/p/5657196.html
第十一章 模型评估
11.1 ROC 曲线
1
. ROC 曲线: 接收者操作特征(receiver operating characteristic),roc 曲线上每个点反映着对同一信
号刺激的感受性
横轴:负正类率(false positive rate,FPR)特异度 Specificity
代表分类器预测的正类中实际负实例占所有负实例的比例。1-Specificity
纵轴:真正类率(true positive rate,TPR)灵敏度 Sensitivity(正类覆盖率)
代表分类器预测的正类中实际正实例占所有正实例的比例。Sensitivity
2
. 针对二分类问题,将实例分成正类(postive)或者负类(negative)。但是实际中分类时,会出现四种
情况.
(1)若一个实例是正类并且被预测为正类,即为真正类(True Postive TP)
(2)若一个实例是正类,但是被预测成为负类,即为假负类(False Negative FN)
(3)若一个实例是负类,但是被预测成为正类,即为假正类(False Postive FP)
(4)若一个实例是负类,但是被预测成为负类,即为真负类(True Negative TN)
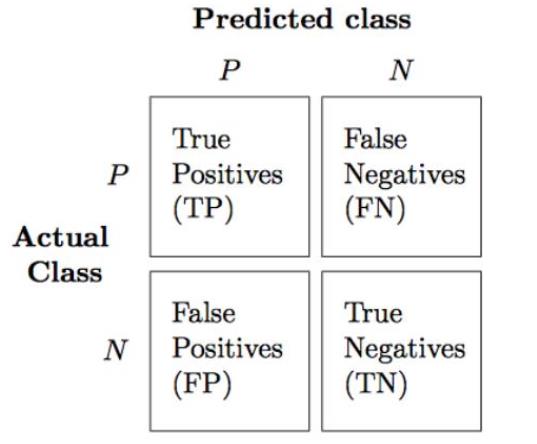
3
. 分类模型的性能根据模型正确和错误预测的检验记录计数进行评估,这些计数存放在称作混淆矩
阵(confusion matrix)的表格中
#
scikit-learn 计算混淆矩阵
from sklearn.metrics import confusion_matrix
Model.fit(X_train,y_train)
y_pred = Model.predict(X_test) # Model根据选择的不同模型,写法不同
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
print(confmat)
#
#
#
[[71 1]
[ 2 40]]
绘制混淆矩阵
fig,ax= plt.subplots()
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)
for i in range(confmat.shape[0]):
for j in range(confmat.shape[1]):
ax.text(x=j, y=i, s=confmat[i,j],va='center', ha='center')
plt.xlabel('predicted label')
plt.ylabel('true label')
plt.show()
列联表如下:
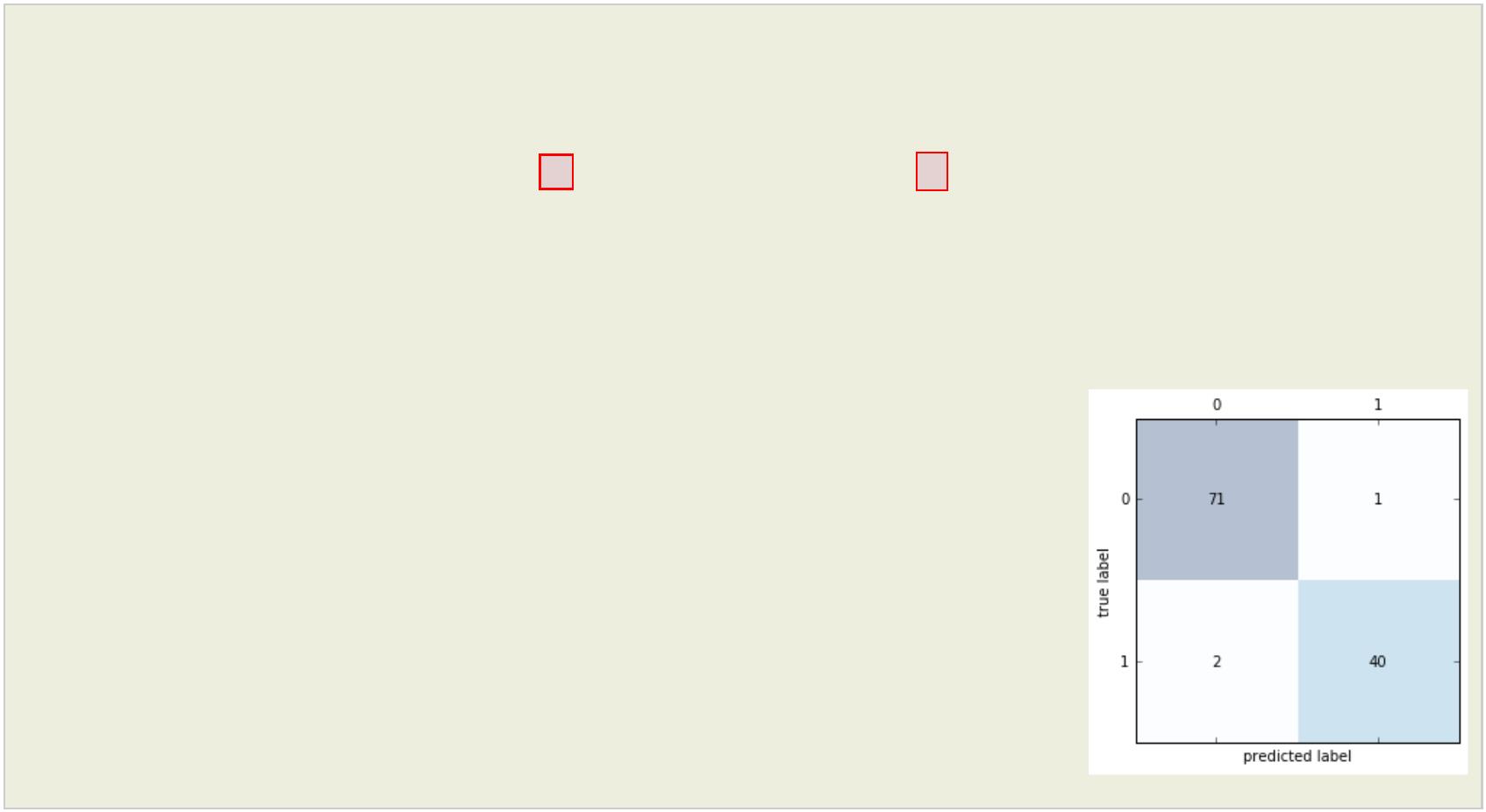

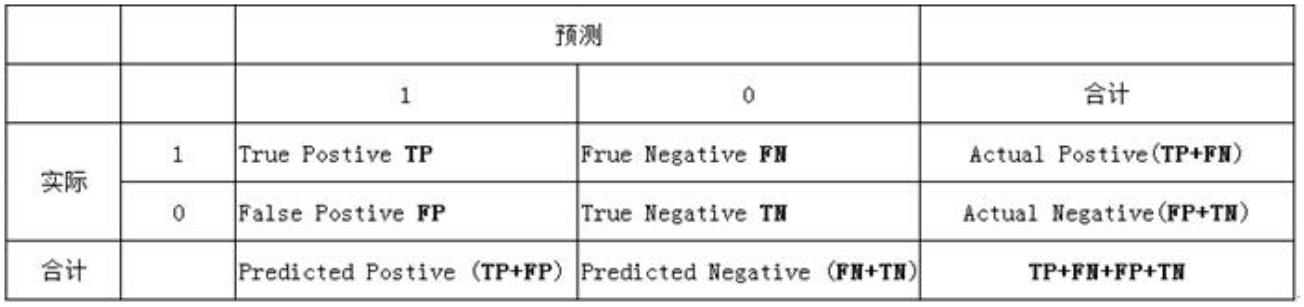
由上表可得出横,纵轴的计算公式:
(1)真正类率(True Postive Rate)TPR: TP/(TP+FN),代表分类器预测的正类中实际正实例占所有正实例
的比例。Sensitivity ------- 纵坐标
(2)负正类率(False Postive Rate)FPR: FP/(FP+TN),代表分类器预测的正类中实际负实例占所有负实
例的比例。1-Specificity ------ 横坐标
(3)真负类率(True Negative Rate)TNR: TN/(FP+TN),代表分类器预测的负类中实际负实例占所有负实
例的比例,TNR=1-FPR。Specificity
横轴 FPR:1-TNR,1-Specificity,FPR 越大,预测正类中实际负类越多。
纵轴 TPR:Sensitivity(正类覆盖率),TPR 越大,预测正类中实际正类越多。
理想目标:TPR=1,FPR=0,即图中(0,1)点,故 ROC 曲线越靠拢(0,1)点,越偏离 45 度对角线越好,Sensitivity、
Specificity 越大效果越好。
4
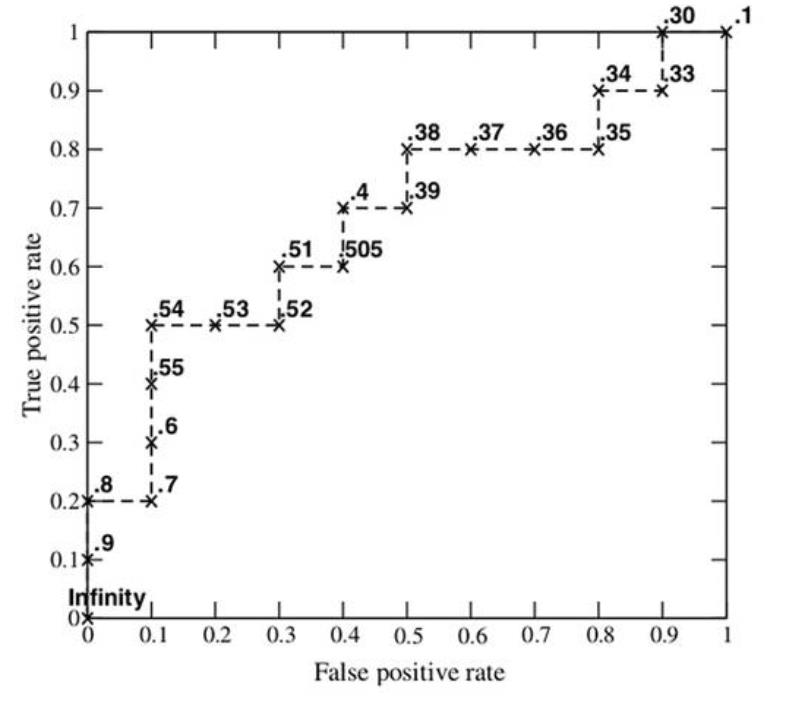
.绘制 ROC 曲线
假设已经得出一系列样本被划分为正类的概率,然后按照大小排序,下图是一个示例,图中共有 20
个测试样本,“Class”一栏表示每个测试样本真正的标签(p 表示正样本,n 表示负样本),“Score”表示
每个测试样本属于正样本的概率。


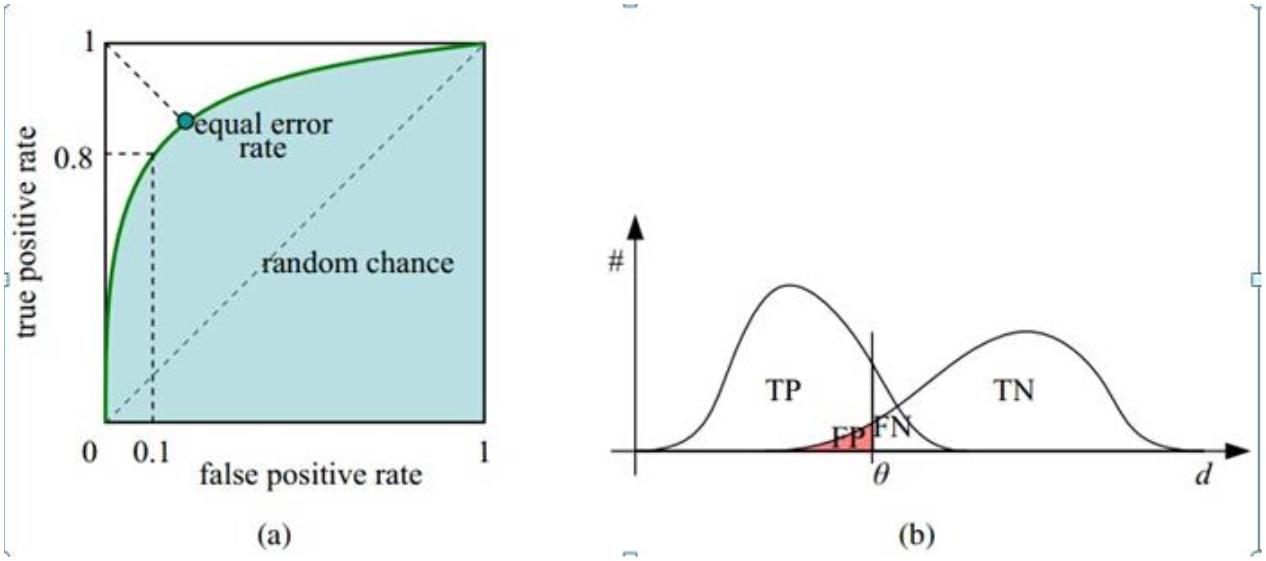
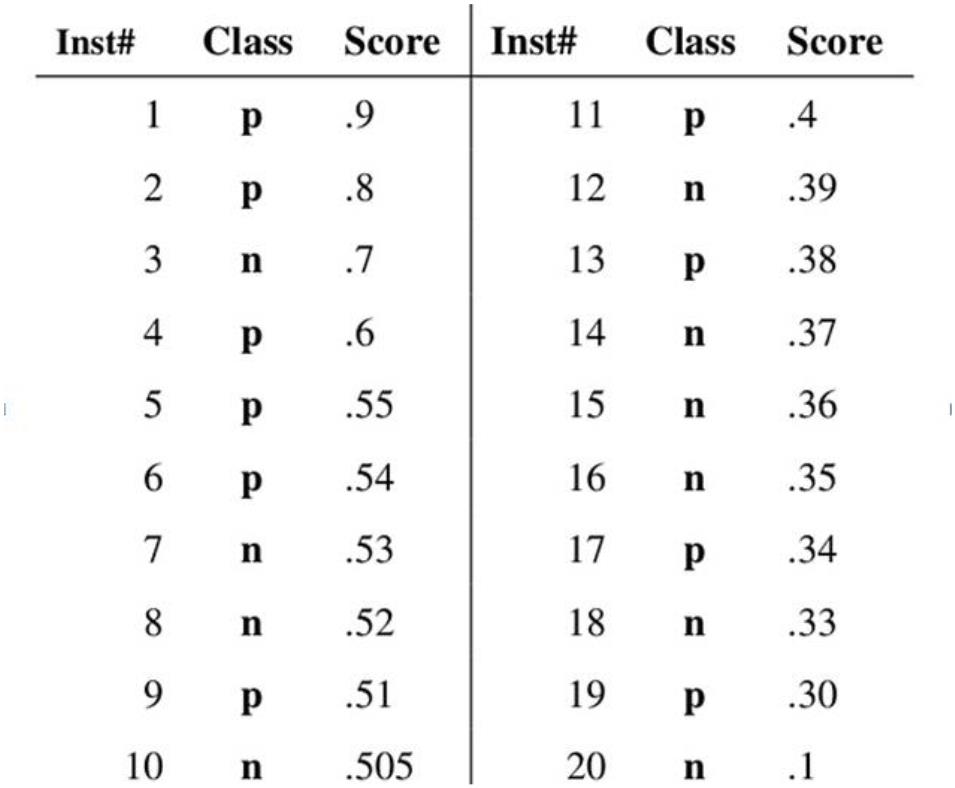
Step1 从高到低,依次将 Score 值作为阈值 threshold,Score>threshold 为正样本,Score<threshold 为
负样本
Step2 每次选取不同 threshold,得到一组 FPR 和 TPR,即 ROC 曲线上一点
Step3 绘制 ROC 曲线
摘自博文 http://blog.csdn.net/pzy20062141/article/details/48711355
5
. Python 实现 ROC 曲线绘制
from sklearn.metrics import roc_curve, auc
from scipy import interp # interp 线性插值
X_train2 = X_train[:, [4,14]]
cv = StratifiedKFold(y_train, n_folds=3, random_state=1)
fig = plt.figure()
mean_tpr=0.0
mean_fpr=np.linspace(0,1,100)
all_tpr = []
#
plot 每个 fold的 ROC曲线,这里 fold的数量为 3,被 StratifiedKFold指定
for i, (train,test) in enumerate(cv):
返回预测的每个类别(这里为 0或 1)的概率 probas[:,0] – 预测为 0的概率,probas[:,1]—预测为 1
的概率
probas = pipe_lr.fit(X_train2[train],y_train[train]).predict_proba(X_train2[test])
#
fpr,tpr,thresholds = roc_curve(y_train[test],probas[:,1],pos_label=1)
mean_tpr += interp(mean_fpr, fpr,tpr)
mean_tpr[0]=0.0
roc_auc=auc(fpr,tpr)
plt.plot(fpr,tpr,linewidth=1,label='ROC fold %d (area = %0.2f)' % (i+1, roc_auc))
plot random guessing line
#
plt.plot([0,1],[0,1],linestyle='--',color=(0.6,0.6,0.6),label='random guessing')
mean_tpr /= len(cv)
mean_tpr[-1] = 1.0
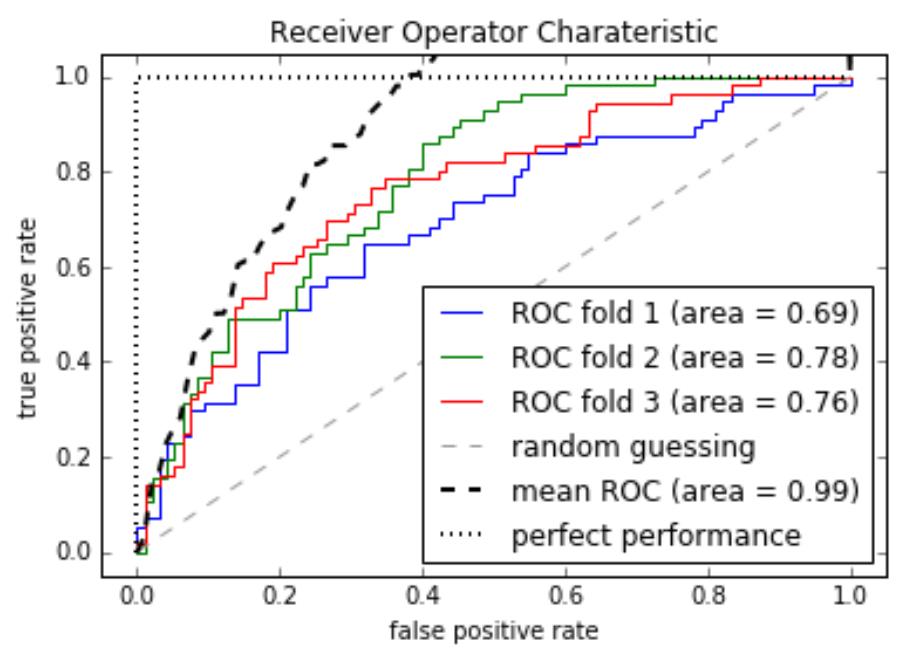
mean_auc = auc(mean_fpr, mean_tpr)
plt.plot(mean_fpr, mean_tpr, 'k--', label='mean ROC (area = %0.2f)' % mean_auc, lw=2)


#
plot perfect performance line
plt.plot([0, 0, 1], [0, 1, 1], lw=2, linestyle=':', color='black', label='perfect
performance')
#
设置 x,y坐标范围
plt.xlim([-0.05,1.05])
plt.ylim([-0.05,1.05])
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.title('Receiver Operator Charateristic')
plt.legend(loc='lower right')
plt.show()
11.2 AUC(Area under roc curve)--度量分类模型好坏的标准
1
. 首先 AUC 值是一个概率值,当你随机挑选一个正样本以及负样本,当前的分类算法根据计算得
到的 Score 值将这个正样本排在负样本前面的概率就是 AUC 值,AUC 值越大,当前分类算法越有
可能将正样本排在负样本前面,从而能够更好地分类。
2
. 计算 AUC 方法一
计算出 ROC 曲线下面的面积,就是 AUC 的值
3
. 计算 AUC 方法二
一个关于 AUC 的很有趣的性质是,它和 Wilcoxon-Mann-Witney Test 是等价的。而 Wilcoxon-
Mann-Witney Test 就是测试任意给一个正类样本和一个负类样本,正类样本的 score 有多大的概率大
于负类样本的 score。
具体来说就是统计一下所有的 M×N(M 为正类样本的数目,N 为负类样本的数目)个正负样本对
中,有多少个组中的正样本的 score 大于负样本的 score。当二元组中正负样本的 score 相等的时
候,按照 0.5 计算。然后除以 MN。实现这个方法的复杂度为 O(n^2)。n 为样本数(即 n=M+N)
4
.计算 AUC 方法三
首先对 score 从大到小排序,然后令最大 score 对应的 sample 的 rank 为 n,第二大 score 对应 sample
的 rank 为 n-1,以此类推。然后把所有的正类样本的 rank 相加,再减去 M-1 种两个正样本组合的情


况。得到的就是所有的样本中有多少对正类样本的 score 大于负类样本的 score。然后再除以 M×N。
即
公式解释:
1
) 为了求的组合中正样本的 score 值大于负样本,如果所有的正样本 score 值都是大于负样本的,
那么第一位与任意的进行组合 score 值都要大,我们取它的 rank 值为 n,但是 n-1 中有 M-1 是正样
例和正样例的组合这种是不在统计范围内的(为计算方便我们取 n 组,相应的不符合的有 M 个),
所以要减掉,那么同理排在第二位的 n-1,会有 M-1 个是不满足的,依次类推,故得到后面的公式
M*(M+1)/2,我们可以验证在正样本 score 都大于负样本的假设下,AUC 的值为 1
2
) 根据上面的解释,不难得出,rank 的值代表的是能够产生 score 前大后小的这样的组合数,但
是这里包含了(正,正)的情况,所以要减去这样的组(即排在它后面正例的个数),即可得到上
面的公式
另外,特别需要注意的是,再存在 score 相等的情况时,对相等 score 的样本,需要 赋予相同的
rank(无论这个相等的 score 是出现在同类样本还是不同类的样本之间,都需要这样处理)。具体操作
就是再把所有这些 score 相等的样本 的 rank 取平均。然后再使用上述公式。
11.3 准确率和召回率,以及 F1-score
1
.准确率(precision rate)
提取出的正确信息条数/提取出的信息条数
PRE = (TP + TN)/(TP + FP + FN + TN)
2
.召回率
正确提取出的正类信息条数/样本中的正类信息条数
REC = TP/(TP + FN)
3
. F1-score
F1=2* PRE * REC/(PRE + REC)
4
. Scikit-learn 计算实现
#
计算不同的误差评价标准。
from sklearn.metrics import precision_score, recall_score,f1_score
precision_score(y_true=y_test,y_pred=y_pred)
#
0.97560975609756095
recall_score(y_true=y_test,y_pred=y_pred)
0.95238095238095233
f1_score(y_true=y_test,y_pred=y_pred)
0.96385542168674698
#
#



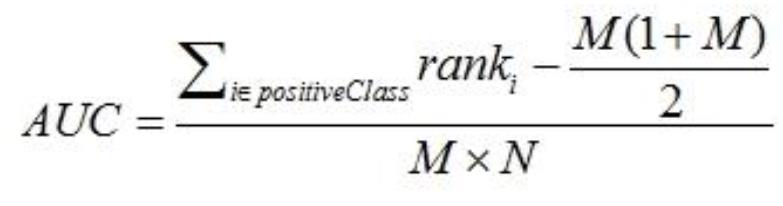
11.4 KS 值
1
. KS 曲线
逻辑回归举例,模型训练完成之后每个样本都会得到一个类概率值(注意是类似的类),把样本按这
个类概率值排序后分成 10 等份,每一份单独计算它的真正率和假正率,然后计算累计概率值。用
1
0 等份做为横坐标,用真正率和假正率的累计值分别做为纵坐标就得到两个曲线,这就是 KS 曲线
. KS 值
2
KS 曲线中两条曲线之间的最大间隔距离,KS 值表示了模型将+ 和 – 区分开来的能力,取值为
[0,1] 。
KS 值所代表的仅仅是模型的分隔能力,并不代表分隔的样本是准确的。换句话说,正负样本完全分
错,但 KS 值可以依旧很高。
3
. KS 曲线与 AUC 曲线的区别
横纵坐标不一样
KS 曲线:以 n 等份作为横坐标,真正率和假正率作为纵坐标,绘制去曲线
AUC 曲线: 以负正类率作为横坐标,真正类率作为纵坐标绘制
11.5 学习曲线和验证曲线
通过绘制模型训练和验证准确性关于训练集大小的函数,我们能很容易地诊断出模型是高方差还是
高偏差。
1
. 学习曲线
1
)左上角图



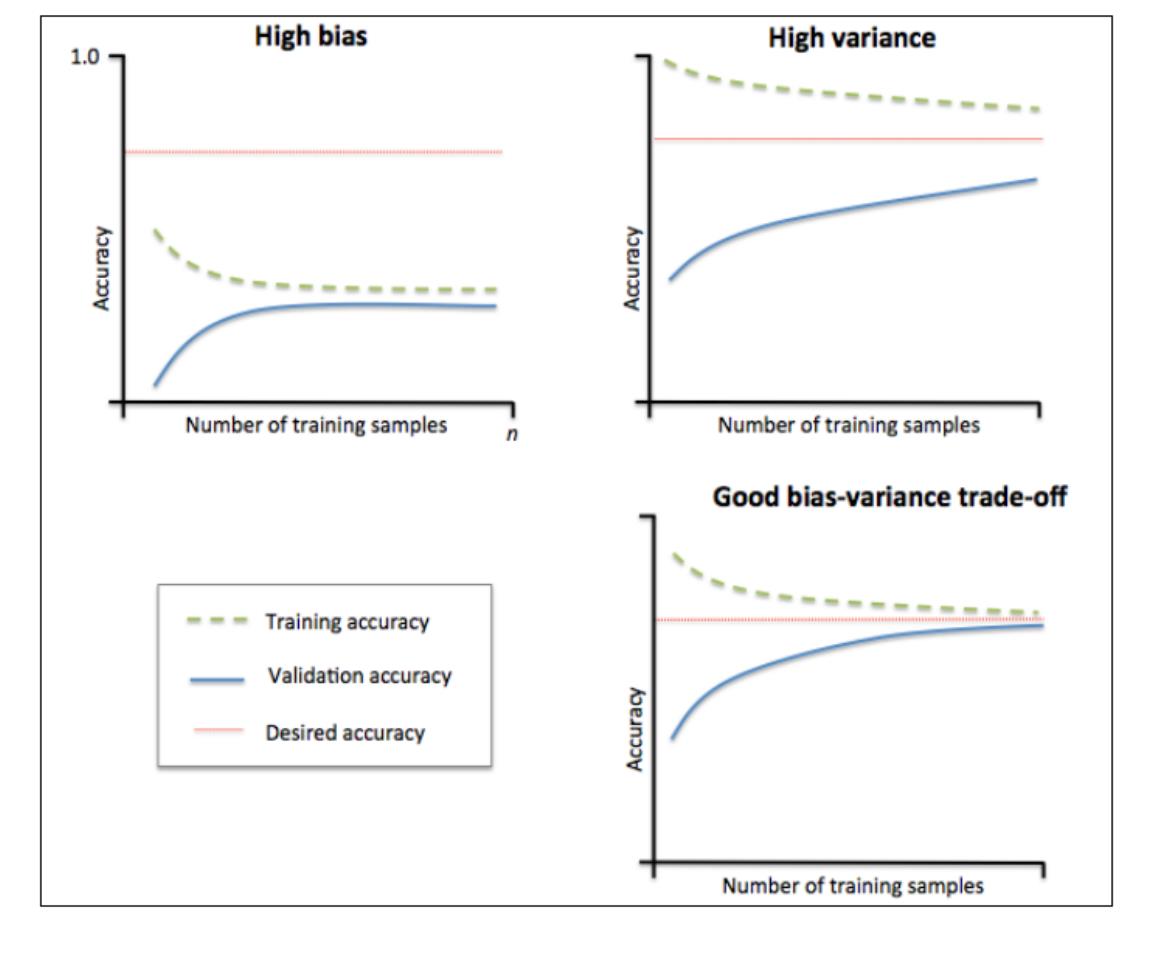
高偏差,代表这个模型的训练准确性和交叉验证准确性都很低,表明模型欠拟合。
解决高偏差(欠拟合)问题: 通常增加模型的参数,比如构造更多的样本特则会那个或减小正则化
的程度
2
)右上角图
高方差,该模型在训练集准确性和交叉验证集准确性之间有很大的缺口,这表明模型很好地拟合了
数据集,但对未见过的数据效果很差。说明模型存在过拟合问题。
解决高方差(过拟合)问题:收集更多的数据或者降低模型的复杂度
2
.绘制学习曲线
#
绘制学习曲线
from sklearn.learning_curve import learning_curve
import matplotlib.pyplot as plt
pipe_lr =
Pipeline([('scl',StandardScaler()),('clf',LogisticRegression(penalty='l2',random_state =
0
))])
train_sizes, train_scores, test_scores = learning_curve(estimator=pipe_lr, X=X_train,
y=y_train)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores,axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(train_sizes, train_mean, color='blue',marker='o',markersize=5, label='training
accuracy')
plt.fill_between(train_sizes, train_mean + train_std,train_mean - train_std, alpha=0.15,
color='blue' )
plt.plot(train_sizes, test_mean, color='green', linestyle='--',marker='s',markersize=5,
label='validation accuracy')
plt.fill_between(train_sizes, test_mean + test_std, test_mean - test_std, alpha=0.15,
color='green')
plt.grid()
plt.xlabel('Number of training samples')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.ylim([0.8, 1.0])
plt.show()
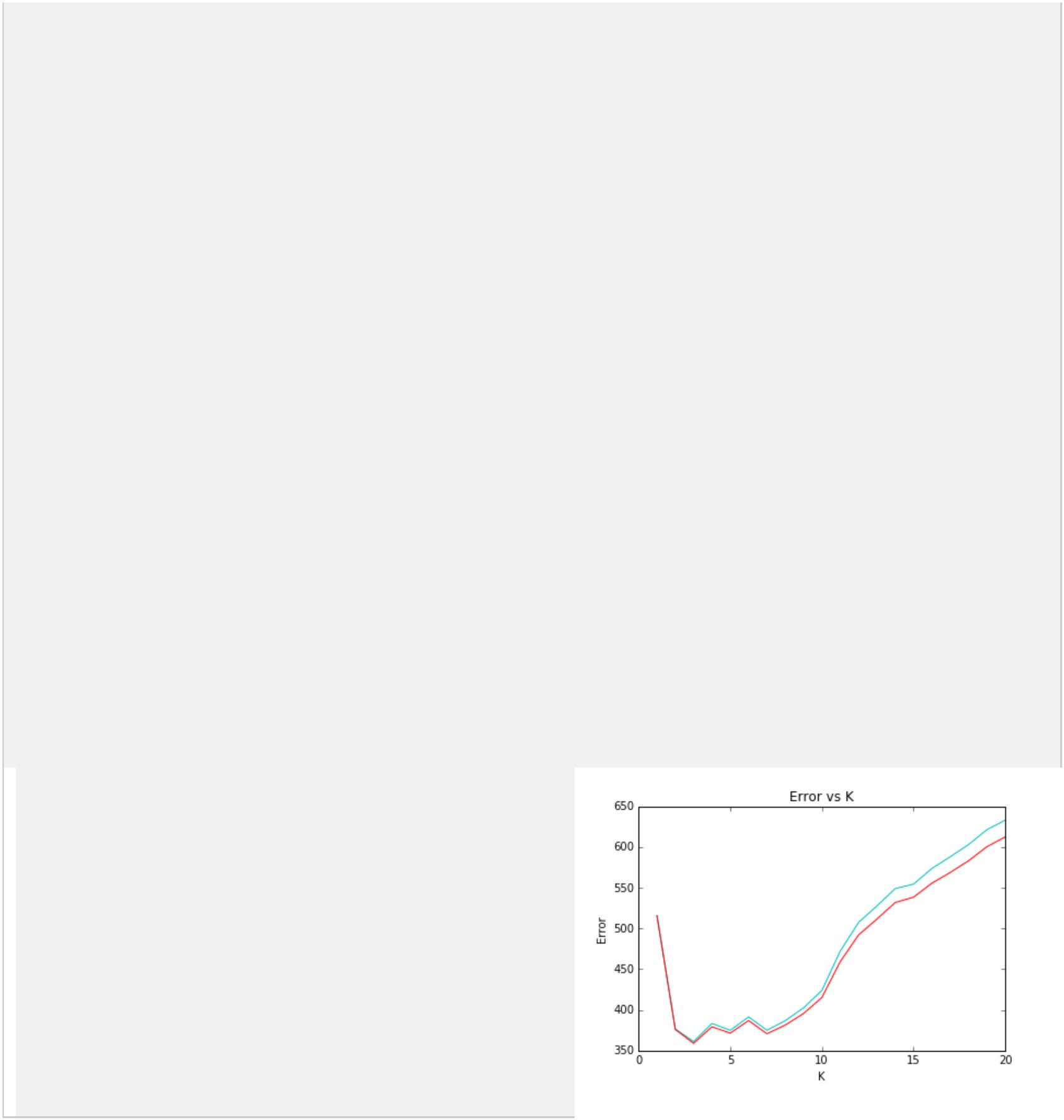
从左面的图形中我们可以看出,模型在交叉训练集上
表现地很好,但是有点过拟合,因为在两个曲线之间
有一点明显的间隔
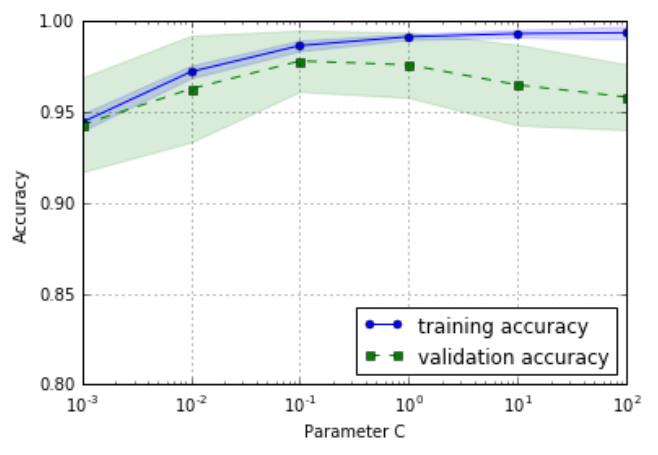
3
. 验证曲线





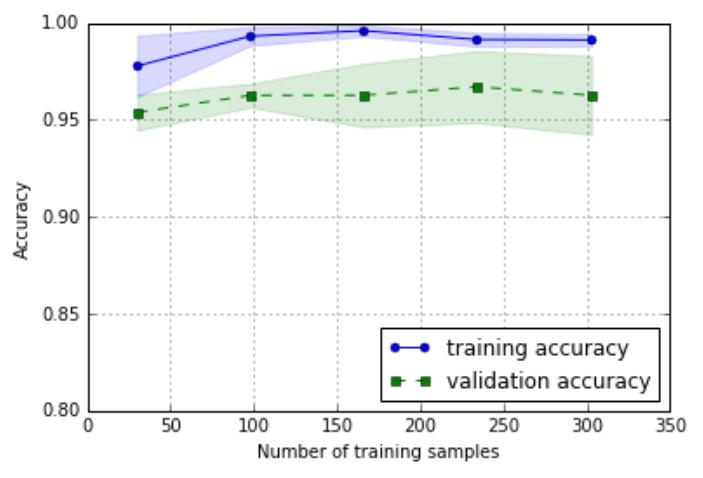
学习曲线是训练集数量与准确性之间的函数,而验证曲线是不同的模型参数与准确性之间的函数
从左图中可以看出,随着参数 C 的增大,模型
有点过拟合数据,因为 C 越大,就意味着正则
化的强度越小。然而对于小的参数 C 来说,正
则化的强度很大,模型有点欠拟合。从图形中
反馈得知,C 在 0.1 左右是最好的
#
绘制验证曲线
from sklearn.learning_curve import validation_curve
param_range = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0]
train_scores, test_scores = validation_curve(estimator=pipe_lr, X=X_train, y=y_train,
param_name='clf__C', param_range=param_range, cv=10)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(param_range, train_mean, color='blue', marker='o', markersize=5, label='training
accuracy')
plt.fill_between(param_range, train_mean + train_std, train_mean - train_std, alpha=0.15,
color='blue')
plt.plot(param_range, test_mean, color='green', linestyle='--', marker='s', markersize=5,
label='validation accuracy')
plt.fill_between(param_range, test_mean + test_std, test_mean - test_std, alpha=0.15,
color='green')
plt.grid()
plt.xscale('log')
plt.legend(loc='lower right')
plt.xlabel('Parameter C')
plt.ylabel('Accuracy')
plt.ylim([0.8, 1.0])
plt.show()


11.6 如何避免过拟合
过拟合表现在训练数据上的误差非常小,而在测试数据上误差反而增大。其原因一般是模型过于复
杂,过分得去拟合数据的噪声和 outliers
常见的解决办法是:增大数据集,正则化
11.7 交叉验证
1
.K-Folds 交叉验证
K 层交叉检验就是把原始的数据随机分成 K 个部分。在这 K 个部分中,选择一个作为测试数
据,剩下的 K-1 个作为训练数据。
交叉检验的过程实际上是把实验重复做 K 次,每次实验都从 K 个部分中选择一个不同的部分作
为测试数据(保证 K 个部分的数据都分别做过测试数据),剩下的 K-1 个当作训练数据进行实验,
最后把得到的 K 个实验结果平均。
Python 实现:
from sklearn import cross_validation
model = RandomForestClassifier(n_estimators=100)
#
Simple K-Fold cross validation. 10 folds.
cv = cross_validation.KFold(len(train), n_folds=10, indices=False)
results = []
#
"Error_function" can be replaced by the error function of your analysis
for traincv, testcv in cv:
probas = model.fit(train[traincv], target[traincv]).predict_proba(train[testcv])
results.append( Error_function )
print "Results: " + str( np.array(results).mean() )
11.8 Python 实现分类模型评估(逻辑回归预测垃圾短信)
1
. 读入样本集
df=pd.read_csv('C://Users//Allen//Desktop//smsspamcollection//SMSSpamCollection',delimiter='\t',names=['target','text'])
print(df.head())
df['Target']=df['target'].map({'ham':0,'spam':1}).astype(int)
df=df.drop('target',axis=1)
print('含 spam 垃圾短信数量:',df[df['Target']==1]['text'].count()) #spam=1 747
print('含 ham 正常短信数量:',df[df['Target']==0]['text'].count()) #ham=0 4825
2
.应用逻辑回归模型
classifier=LogisticRegression() #逻辑回归
classifier.fit(X_train,y_train)
predictions=classifier.predict(X_test)
for i,prediction in enumerate(predictions[-5:]):
print ('预测类型: %s. 信息:%s' % (prediction,X_test_raw.iloc[i]))



3
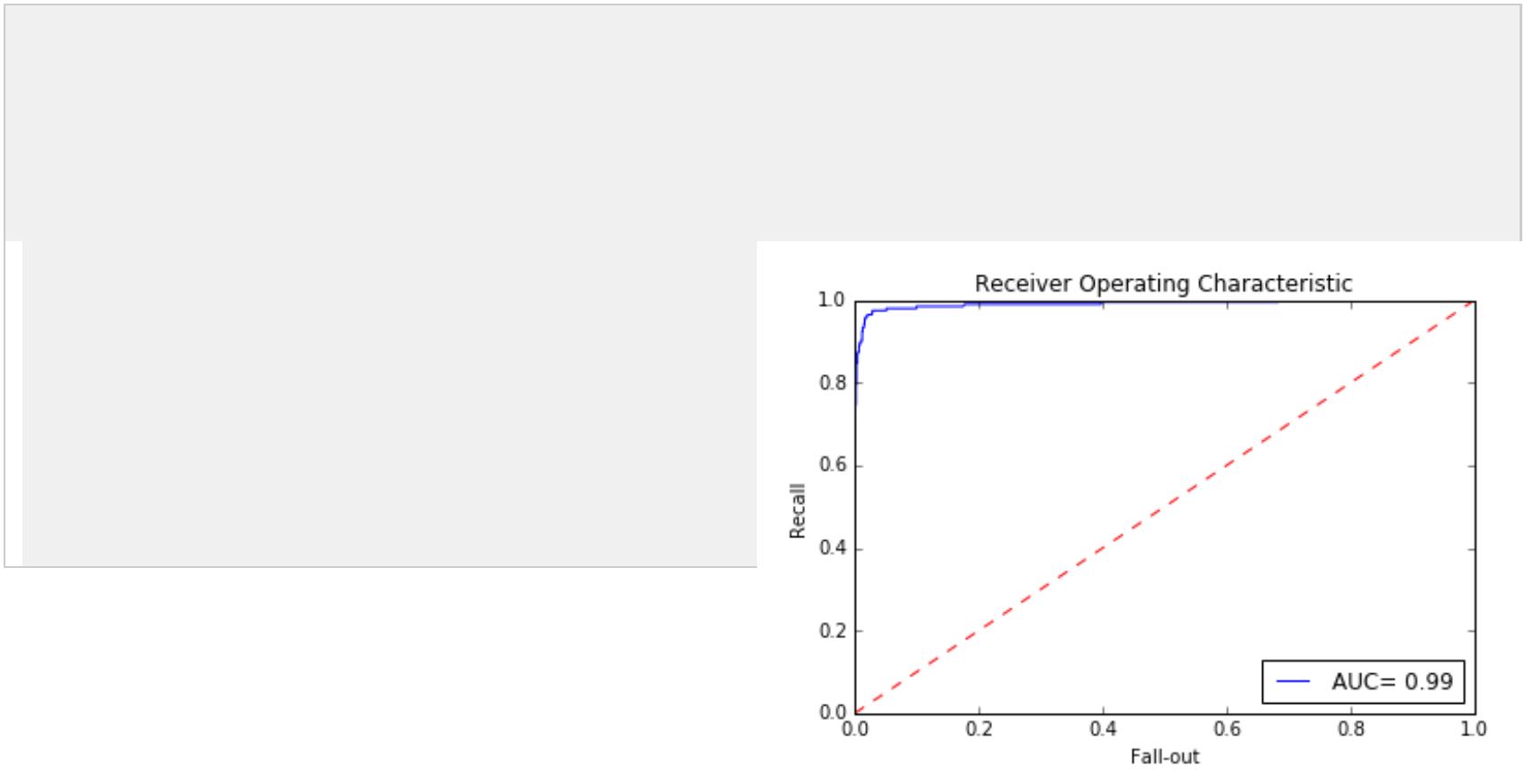
.绘制 ROC 曲线
predictions=classifier.predict_proba(X_test) #输出概率
false_positive_rate,recall,thresholds=roc_curve(y_test,predictions[:,1]) #predictions[:,1]表示结果为 1 的概率
roc_auc=auc(false_positive_rate,recall)
plt.title('Receiver Operating Characteristic')
plt.plot(false_positive_rate,recall,'b',label='AUC= %0.2f' % roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.0])
plt.ylabel('Recall')
plt.xlabel('Fall-out')
plt.show()
4
.计算准确率,精确率,召回率,综合评价指标
scores=cross_val_score(classifier,X_train,y_train,cv=5)
print('准确率:',np.mean(scores),scores)
precisions=cross_val_score(classifier,X_train,y_train,cv=5,scoring='precision')
print('精确率:',np.mean(precisions),precisions)
recalls=cross_val_score(classifier,X_train,y_train,cv=5,scoring='recall')
print('召回率:',np.mean(recalls),recalls)
fls=cross_val_score(classifier,X_train,y_train,cv=5,scoring='f1')
print('综合评价指标:',np.mean(fls),fls)
5
.概念说明
样本分类:
TP---True Positive 真阳性
TN---True Negative 真阴性
FP---False Positive 假阳性
FN---False Negative 假阴性
阳性与阴性指分类,真假指预测的正确与否
准确率:是指分类器预测正确性的指标
Acc=(TP+TN)/(TP+TN+FP+FN)
精确率:分类器预测出的垃圾短信中真的是垃圾短信的比例
P=TP/(TP+FP)



召回率:又称灵敏度。指所有真的垃圾短信被分类器正确找出的比例。
R=TP/(TP+FN)
精确率和召回率均不能从表现差的一种分类器中区分出好的分类器。
综合评价指标(F1 measure):是精确率和召回率的调和均值或加权平均值
F1 = 2푃푅⁄(푃 + 푅)
ROC 曲线:分类器的召回率 R 与误警率 F 的曲线。
误警率也称为假阳性率,是所有阴性样本中分类器识别为阳性样本的比例。
F = 퐹푃⁄(푇푁 + 퐹푃)
11.9 模型优化
Scikit—learn 中有 GridSerchCV()函数可以解决参数优化问题
#
模型参数优化
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.linear_model.logistic import LogisticRegression
from sklearn.grid_search import GridSearchCV
from sklearn.pipeline import Pipeline
from sklearn.cross_validation import train_test_split
from sklearn.metrics import precision_score,recall_score,accuracy_score
pipeline=Pipeline([
('vect',TfidfVectorizer(stop_words='english')),
('clf',LogisticRegression())
]
)
parameters={
'
'
'
'
'
'
'
'
vect__max_df':(0.25,0.5,0.75),
vect__stop_words':('english',None),
vect__max_features':(2500,5000,10000,None),
vect__ngram_range':((1,1),(1,2)),
vect__use_idf':(True,False),
vect__norm':('l1','l2'),
clf__penalty':('l1','l2'),
clf__C':(0.01,0.1,1,10)
}
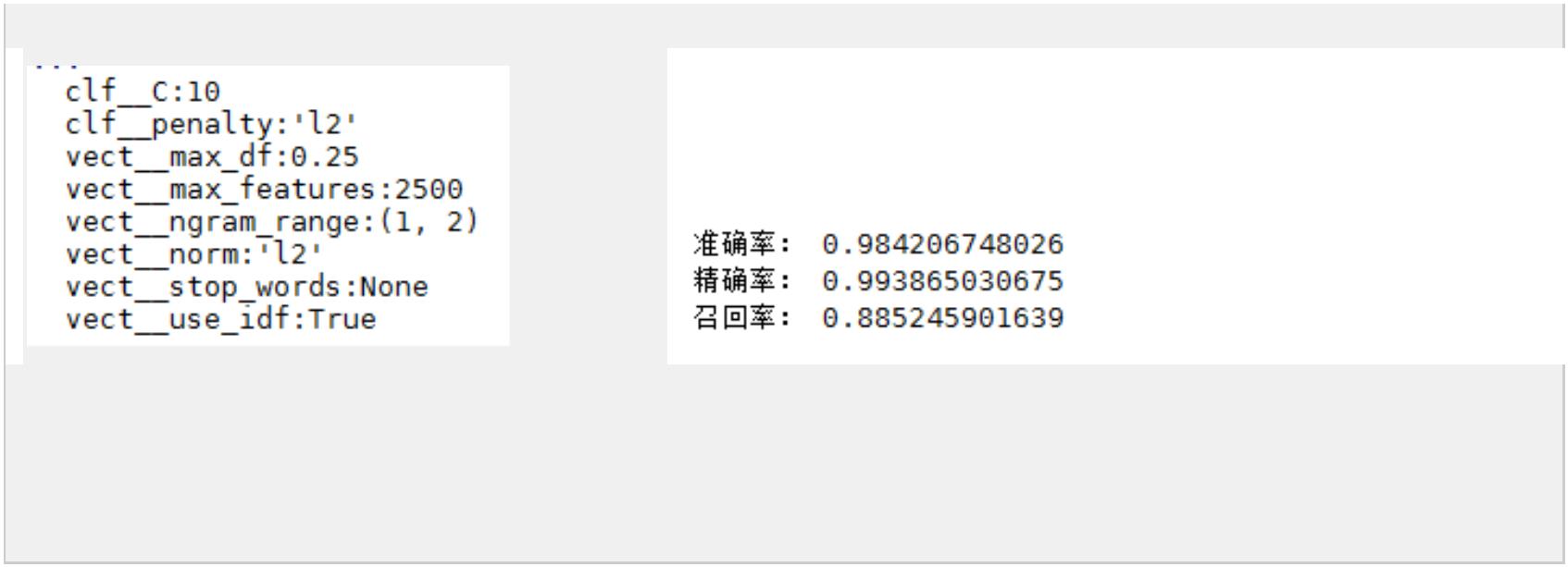
grid_search=GridSearchCV(pipeline,parameters,n_jobs=-1,verbose=1,scoring='accuracy',cv=3)
X,y=df['text'],df['Target']
X_train,X_test,y_train,y_test=train_test_split(X,y)
grid_search.fit(X_train,y_train)
print('最佳效果: %0.3f' % grid_search.best_score_)
#
最佳效果: 0.983
print('最优参数组合:')
best_parameters=grid_search.best_estimator_.get_params()
for param_name in sorted(parameters.keys()):
print('\t%s:%r' % (param_name,best_parameters[param_name]))

#
最优参数组合:
predictions=grid_search.predict(X_test)
print('准确率:',accuracy_score(y_test,predictions))
print('精确率:',precision_score(y_test,predictions))
print('召回率:',recall_score(y_test,predictions))
第四部分 非监督学习---聚类与关联分析
第十二章 Kmeans 聚类分析
2.1 聚类分析基本概念及常用算法
1
概念
聚类分析(cluster analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术。 聚
类分析也叫分类分析(classification analysis)或数值分类(numerical taxonomy)。聚类与分类的不同在
于,聚类所要求划分的类是未知的。
聚类度量方法
聚类之间类的度量是分距离和相似系数来度量的,
距离用来度量样品之间的相似性(KMeans 聚类,系统聚类中的 Q 型聚类)
相似系数用来度量变量之间的相似性(系统聚类的 R 型聚类)
聚类分析研究方法
层次的方法(hierarchical method)
划分方法(partitioning method)
基于密度的方法(density-based method)---DBSCAN (Density-Based Spatial Clustering of Applications
with Noise)
基于网格的方法(grid-based method)
基于模型的方法(model-based method)
常用聚类分析研究方法
K-pototypes 算法
K-Means 算法
CLARANS 算法(划分方法)
BIRCH 算法(层次方法)
CURE 算法(层次方法)
DBSCAN 算法(基于密度的方法)
CLIQUE 算法(综合了基于密度和基于网格的算法)
1
2.2 Kmeans 算法概述
1
. Kmeans 算法描述
适用于大样本,但需要事先制定分为 K 个类;
从 n 个数据对象任意选择 k 个对象作为初始聚类中心,对于剩下的其他对象,则根据它们与这
些聚类中心的相似度(距离),分别将它们分配给与其最相似的(聚类中心所代表的)聚类;再计算
每个所获新聚类的聚类中心(该聚类中所有对象的均值);不断重复这一过程,直到标准测度函数开
始收敛为止。K 个聚类具有以下特点:各聚类本身尽可能的紧凑,而各聚类之间尽可能的分开
2
. Kmeans 算法流程
Step1:从 n 个数据对象任意选择 k 个对象作为初始聚类中心
Step2:根据每个聚类对象的均值(中心对象),计算每个对象与这些中心对象的距离,并根据最小
距离重新对相应对象进行划分
Step3:重新计算每个(有变化)聚类的均值(中心对象)
重复下面过程直到收敛 {
对于每一个样例 i,计算其应该属于的类:
对于每一个类 j,重新计算该类的质心:
}
Step4:循环(2),(3)直到每个聚类不再发生变化为止
3
.Kmeans 算法伪代码
创建 k 个点作为初始的质心点(随机选择)
当任意一个点的簇分配结果发生改变时
对数据集中的每一个数据点
对每一个质心
计算质心与数据点的距离
将数据点分配到距离最近的簇
对每一个簇,计算簇中所有点的均值,并将均值作为质心
4
.Kmeans 算法优缺点
优点:
本算法确定的 K 个划分到达平方误差最小。当聚类是密集的,且类与类之间区别明显时,效果
较好。
对于处理大数据集,这个算法是相对可伸缩和高效的,计算的复杂度为 O(NKt),其中 N 是数据
对象的数目,K 是聚类中心,t 是迭代的次数。
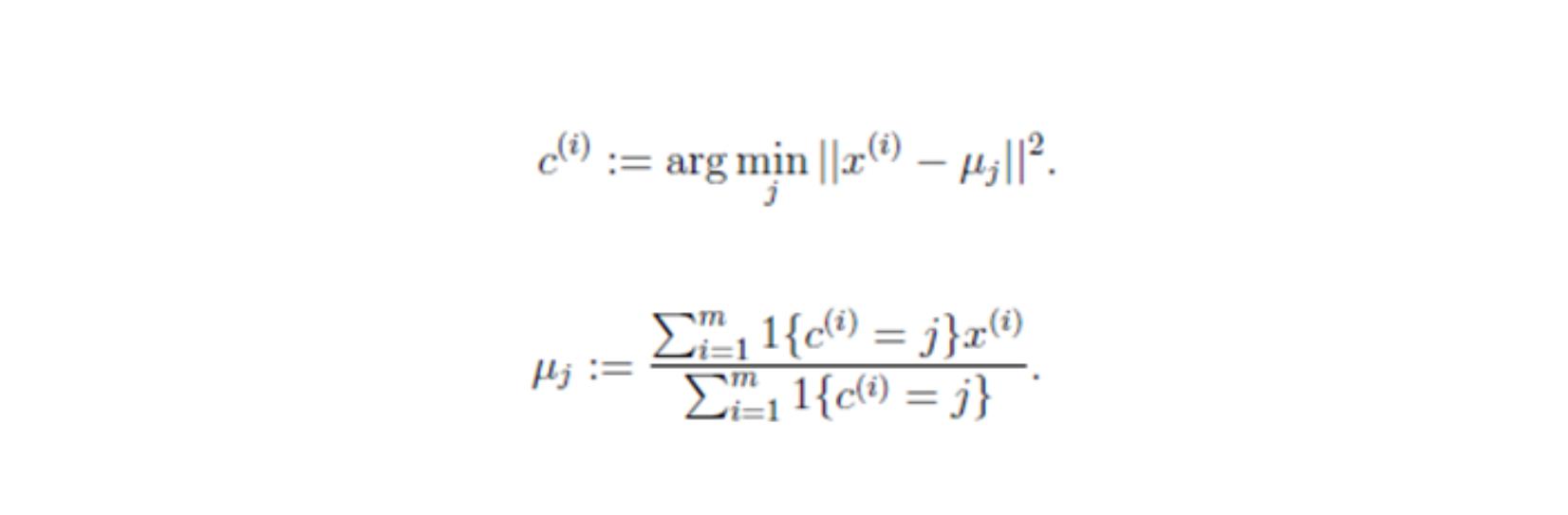
缺点:
K 是事先给定的,但非常难以选定
初始聚类中心的选择对聚类结果有较大的影响
5
.Kmeans 算法 Python 实现
from sklearn.cluster import KMeans
clf = KMeans(n_clusters=3, max_iter=300, n_init=10)
clf.fit(X)
ypred = clf.predict(X)
第十三章 关联分析 Apriori
1
3.1 关联分析基础概念
1
.关联规则定义
关联规则定义:假设
是项的集合。给定一个交易数据库 D,其中每个事务
(Transaction)t 是 I 的非空子集,即,每一个交易都与一个唯一的标识符 TID(Transaction ID)对应。
关联规则在 D 中的支持度(support)是 D 中事务同时包含 X、Y 的百分比,即概率;
置信度(confidence)是 D 中事务已经包含 X 的情况下,包含 Y 的百分比,即条件概率。如果满足最小
支持度阈值和最小置信度阈值,则认为关联规则是有趣的。
2
.信息熵--从信息传播的角度来看,信息熵可以表示信息的价值
1
)支持度
Support(A->B)=P(A U B)。支持度揭示了 A 与 B 同时出现的概率。如果 A 与 B 同时出现的概率小,
说明 A 与 B 的关系不大;如果 A 与 B 同时出现的非常频繁,则说明 A 与 B 总是相关的。
2
)置信度
Confidence(A->B)=P(A | B)=P(A U B)/P(A
。置信度揭示了 A 出现时,B 是否也会出现或有多大概率出现。如果置信度度为 100%,则 A 和 B
可以捆绑销售了。如果置信度太低,则说明 A 的出现与 B 是否出现关系不大
)k 项集事件
)
3
如果事件 A 中包含 k 个元素,那么称这个事件 A 为 k 项集事件,A 满足最小支持度阈值的事件称为
频繁 k 项集
4
)强规则
同时满足最小支持度阈值和最小置信度阈值的规则称为强规则
1
3.2 Apriori 算法
1
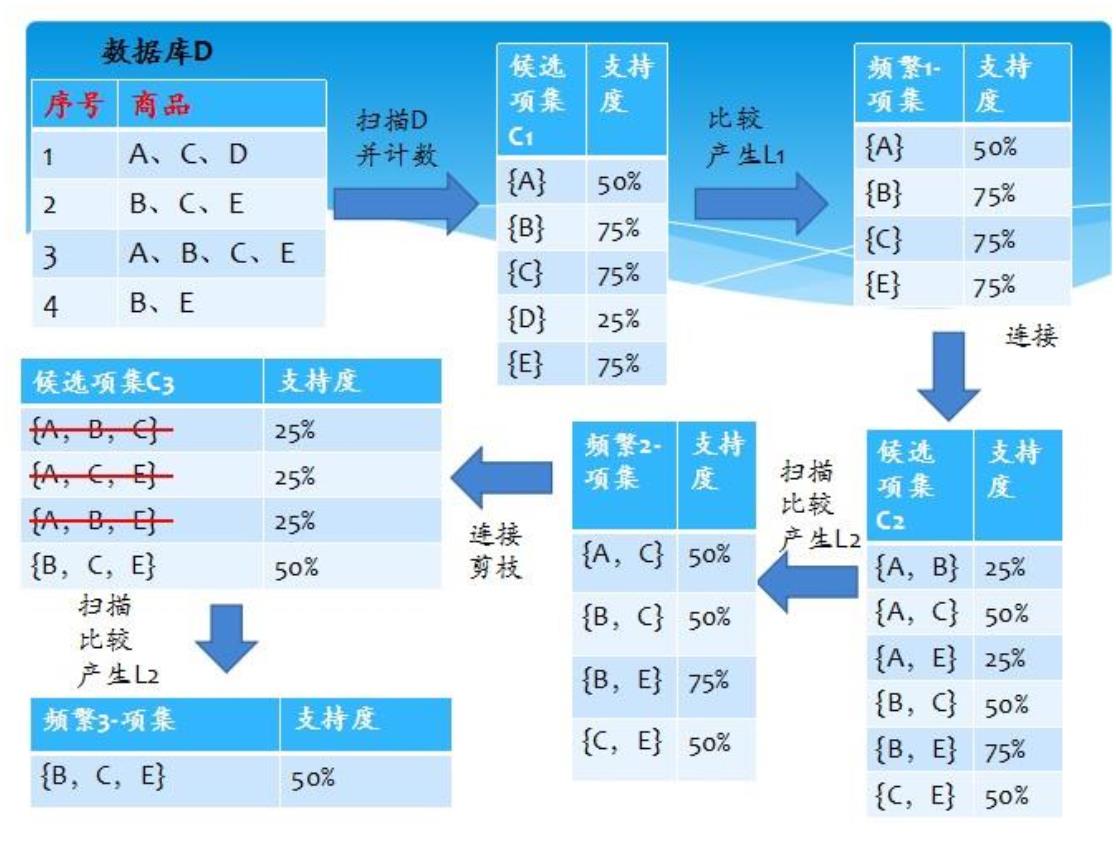
.Apriori 算法实现步骤
Step1 发现频繁项集,过程为(1)扫描(2)计数(3)比较(4)产生频繁项集(5)连接、剪枝,产
生候选项集 重复步骤(1)~(5)直到不能发现更大的频集
Step2 产生关联规则,过程为:
根据前面提到的置信度的定义,关联规则的产生如下:

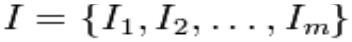
(
(
1)对于每个频繁项集 L,产生 L 的所有非空子集;
2)对于 L 的每个非空子集 S,如果
P(L)/P(S)≧min_conf 则输出规则“SàL-S”
注:L-S 表示在项集 L 中除去 S 子集的项集
2
.Apriori 算法 python 实现步骤
第十四章 数据预处理之数据降维
1
4.1 数据降维基本概念
1
2
1
2
3
3
.数据降维:又称数据约简,指采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中
.数据降维原因
)在原始的高维空间中,包含有冗余信息以及噪音信息
)feature 太多会造成模型复杂,训练速度过慢,因此要引入降维
)多维数据很难进行可视化分析,需要降维分析
.降维本质
学习一个映射函数 F:XY,其中 X 是原始数据点的表达,目前最多使用向量表达形式
4
.常用降维算法
PCA---主成分分析法(Principal component analysis),常用线性降维方法
LDA---线性判别分析(Linear Discriminant Analysis)
LLE---局部线性嵌入(Locally Linear Embedding)
Laplacian Eigenmaps --- 拉普拉斯特征映射
1
4.2 PCA 算法
参考:http://blog.csdn.net/abcjennifer/article/details/8002329
1.PCA 降维基本思想
Principal ComponentAnalysis(PCA)是最常用的线性降维方法,它的目标是通过某种线性投影,将高维
的数据映射到低维的空间中表示,并期望在所投影的维度上数据的方差最大,以此使用较少的数据维
度,同时保留住较多的原数据点的特性
2
.PCA 算法流程
假设有 m 个 samples (x(1),x(2),……,x(m)),每个数据有 n 个特征 x(1)= [x (1), x (1), x (1),……, x (1)]
1
2
3
n
Step 1 数据预处理
1
)计算各个 feature 的平均值,记为 μ ;(X (i)表示第 i 个样本的第 j 维特征的 value) μ = Σ X (i)/m
j
j
j
m
j
2
)将每一个 feature scaling:将在不同 scale 上的 feature 进行归一化(只有训练样本获得相应参数)
)将特征进行 zero mean normalization 零均值归一化 令 X (i)= (X (i)-μ )/s
3
j
j
j
j
Step 2 PCA 算法选取 k 个主分量
1
)求 N×N 的协方差矩阵∑
2
)根据 SVD 奇异值分解求取特征值和特征向量[U,S,V] = SVD(Σ) Σ = USV’=USU’
目的:从 N 维降到 K 维,即选出这 N 个特征中最重要的 K 个
)按特征值从大到小排列,重新组织 U
3
4
3
)选择 K 个分类
.从压缩数据汇总恢复原始数据

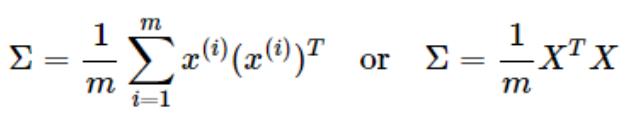
xapprox = (U')-1×z = (U-1)-1×z = UZ
这里恢复出的 xapprox 并不是原先的 x,而是向量 x 的近似值
4
.如何决定降维个数/主成分个数
1
푚
||푥(푖)−푥(푖)
||2
푎푝푝푟표푥
푘
푘
∑
∑
∑
푆푖푖
≥ 푡ℎ푟푒푠ℎ표푙푑 即∑
푆푖푖
푖=1
即Error Ratio =
푚
= 1 −
푖=1
푛
푖=1
≥ 1 − threshold
1
푚
푁
퐼=1
∑
||푥(푖)||2
푆푖푖
∑
푆퐼퐼
푖=1
푖=1
푚
5
.应用 PCA 进行降维的建议
)应用 PCA 提取主成分可能会解决一些 overfitting 的问题,但是不建议使用这种方法解决 overfitting
1
问题,建议加入 regularization 项(也称 ridge regression)来解决
2
3
6
)PCA 选择主成分的时候只应用 training data
)只有当在原数据上跑到了一个比较好的结果,但又嫌它太慢的时候才采取 PCA 进行降维
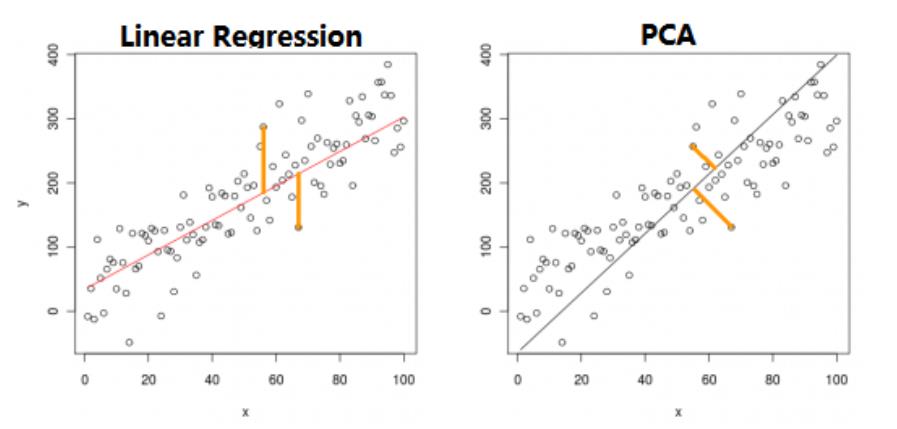
.PCA 与 Linear Regression 的区别
PCA cost function:样本点到拟合线的垂直距离
Linear Regresiion:计算样本上线垂直到拟合线的距离
7
.PCA 算法 Python 实现
函数:Scikit-Learn 中 sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)
参数说明:
n_components
.含义:PCA 算法中所要保留的主成分个数 n,也即保留下来的特征个数。也可以是设置解释变量
的比例。如:pca =PCA(n_components=.98)
1
2
.类型:int 或者 string,缺省时默认为 None,所有成分保留
int比如 n_components=1,将把原始数据降到一个维度
stringn_components=’mle’,将自动选取特征个数 n,使得满足所要求的方差百分比
copy
.含义:表示是否在运行运算时,将原始数据复制一份,若为 True,则在副本上运行 PCA 算法
后,原始数据的值不会有任何改变
.类型:bool,True 或者 False,缺省时默认为 True
Written
1
2
1
2
.含义:使得每个特征具有相同的方差
.类型:bool,缺省时默认为 False





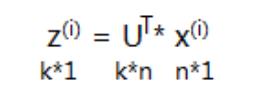
from sklearn.decomposition import PCA 引入 PCA()函数
import numpy as np
import pandas as pd
data=np.random.randn(10,4)
#
#
#
#
#
#
#
#
#
#
array([[ 2.27793149, 0.41199224, -1.80281988, 0.72065799],
[-0.80082211, 0.04550286, -0.70304146, 0.42561992],
[-0.16401835, -0.75932542, -0.81129943, 0.13719183],
[ 0.20487482, -0.98320166, 1.04128367, 2.85097795],
[ 1.29263802, -0.54013543, -0.19102035, -1.4808882 ],
[ 0.03716913, -2.08803088, 2.18752182, 0.28308089],
[ 0.33470243, 0.76565395, 0.91381749, -0.63045713],
[ 0.7814005 , 0.46238208, 0.76730049, 1.5696756 ],
[ 0.30049055, -2.04246298, -0.15875265, 0.79178319],
[-0.4805177 , 0.595143
,
1.08569314, -1.74164893]])
pca=PCA()
pca.fit(data)
pca.components_ #返回模型的各个特征向量
#
#
#
#
array([[-0.06417142, -0.44346869, 0.24356304, 0.86017126],
[-0.44837036, -0.23987254, 0.77443235, -0.37640367],
[ 0.08925189, -0.86101597, -0.37581387, -0.3308316 ],
[-0.88706265, 0.06669478, -0.44687305, 0.09474246]])
pca.explained_variance_ratio_ #返回各个成分各自的方差百分比(贡献率)
方差百分比越大,说明向量的权重越大
#
array([ 0.40107547, 0.33304522, 0.15769605, 0.10818325])
重新建立 PCA 模型
pca=PCA(3)
pca.fit(data)
low_d=pca.transform(data) #用这个方法来降低维度
pd.DataFrame(low_d).to_excel('result.xlsx') #保存结果
pca.inverse_transform(low_d) #必要时,可以用这个函数来复原数据。


第五部分 Python 数据预处理
第十五章 Python 数据分析基础
1
5.1 Python 常见数据结构整理
Python 中常见的数据结构可以统称为容器,主要包括序列(如列表和元组)、映射(如字典)以及集
合(Set)
(
一)序列(列表、元组和字符串)
Python 中有 6 中内建的序列,其中列表和元组是最常见的类型,其他包括字符串、Unicode 字符串、
buffer 对象和 xrange 对象
1
.列表 --- 可变的 – 中括号[ ]
1)创建列表
(
list1=['hello','world']
print list1
list2=[1,2,3]
print list2
(
2)list 函数
通过 list 函数对字符串创建列表
list3=list("hello")
print list3
输出:['h', 'e', 'l', 'l', 'o']
(
3)列表方法
append --- 用于在列表末尾追加新的对象
Input: lst=[1,2,3]
lst.append(4)
Output:[1,2,3,4]
count --- 统计某个元素在列表中出现的次数
Input: x=[1,2,1,1,2,2,3]
x.count(1)
Output: 3
extend --- 在列表的末尾一次性追加另一个序列中的多个值
Input:a=[1,2,3]
b=[4,5,6]
Output: [1,2,3,4,5,6]
a.extend(b)
Index --- 用于从列表中找到某个值第一个匹配项的索引位置
lst.index(‘A’)
insert --- 用于将对象插入到列表中
Input:numbers=[1,2,3,5,6,7]
Output: [1,2,3,’four’,5,6,7]
numbers.insert(3,’four’)



pop --- 移除列表中的一个元素(默认最后一个),并返回该元素的值
Input:x=[1,2,3,5,6,7]
Output: 7
x.pop( )
pop 方法是唯一一个既能修改列表又返回元素之(除了 None)的列表方法
remove --- 用于移出列表中某个值的第一个匹配项(修改列表但无返回值)
Input:x=[‘to’,’be’,’or’,’not’,’to’,’be’]
x.remove(‘be’)
Output: [‘to’,’or’,’not’,’to’]
reverse --- 将列表中的元素反向存放
Input:x=[1,2,3]
Output: x
[3,2,1]
x.reverse()
sort --- 用于在原位置对列表进行排序
Input:x=[4,6,2,1,7,9]
Output: [1,2,4,6,7,9]
x.sort( )
2
.元组 --- 不可变 --- 小括号()
(
1)创建
t1=1,2,3
t2="jeffreyzhao","cnblogs"
t3=(1,2,3,4)
t4=()
t5=(1,)
print t1,t2,t3,t4,t5
a、逗号分隔一些值,元组自动创建完成;
b、元组大部分时候是通过圆括号括起来的;
c、空元组可以用没有包含内容的圆括号来表示;
d、只含一个值的元组,必须加个逗号(,);
(
2)tuple 函数
tuple 函数和序列的 list 函数几乎一样:以一个序列(注意是序列)作为参数并把它转换为元组。如果
参数就算元组,那么该参数就会原样返回:
t1=tuple([1,2,3])
t2=tuple("jeff")
t3=tuple((1,2,3))
print t1
print t2
print t3
t4=tuple(123)
print t45
输出:
(1, 2, 3)
('j', 'e', 'f', 'f')
(1, 2, 3)
(
3)zip 函数
zip 函数接受任意多个(包括 0 个和 1 个)序列作为参数,返回一个 tuple 列表。
zip()是内置函数, 能把迭代对象进行聚合,返回值是迭代对象-聚合后的元组,用 list()函数把它转化
为列表
3
.字符串 --- 不可变 ---‘ ’
1)创建
(
str1='Hello world'
print str1
print str1[0]
for c in str1:
print c
(
2)格式化
符串格式化使用字符串格式化操作符即百分号%来实现。
.通用序列操作(方法)
4
从列表、元组以及字符串可以“抽象”出序列的一些公共通用方法(不是你想像中的 CRUD),这些操
作包括:索引(indexing)、分片(sliceing)、加(adding)、乘(multiplying)以及检查某个元素是否
属于序列的成员。除此之外,还有计算序列长度、最大最小元素等内置函数。
(
1)索引
索引从 0(从左向右)开始,所有序列可通过这种方式进行索引。神奇的是,索引可以从最后一个位
置(从右向左)开始,编号是-1
str1='Hello'
nums=[1,2,3,4]
t1=(123,234,345)
print str1[0]
print nums[1]
print t1[2]
输出:
O
3
123
(
2)分片
分片操作用来访问一定范围内的元素。分片通过冒号相隔的两个索引来实现:[a:b:c] 通常不包括索引
为 b‘的数据,c 为步长
分片的操作需要提供两个索引作为边界,第一个索引的元素是包含在分片内的,而第二个则不包含在
分片内。
(
3)序列相加
str1='Hello'
str2=' world'





print str1+str2
num1=[1,2,3]
num2=[2,3,4]
print num1+num2
print str1+num1
输出:
Hello world
[1, 2, 3, 2, 3, 4]
(
4)乘法 只能与数字相城,元素个数翻倍
print [None]*10
str1='Hello'
print str1*2
num1=[1,2]
print num1*2
print str1*num1
输出:
[
None, None, None, None, None, None, None, None, None, None]
HelloHello
1, 2, 1, 2]
5)成员资格
[
(
in 运算符会用来检查一个对象是否为某个序列(或者其他类型)的成员(即元素)
str1='Hello'
print 'h' in str1
print 'H' in str1
输出: False True True
(
6)长度、最大最小值
通过内建函数 len、max 和 min 可以返回序列中所包含元素的数量、最大(最后一个)和最小(第一
个)元素。
(
二)映射(字典)--- 可变 --- 大括号{ }
1
. 键类型
字典的键可以是数字、字符串或者是元组,键必须唯一。在 Python 中,数字、字符串和元组都被设
计成不可变类型,而常见的列表以及集合(set)都是可变的,所以列表和集合不能作为字典的键。键
可以为任何不可变类型
A={键:值,键:值} A[键]=值
2
.自动添加
即使键在字典中并不存在,也可以为它分配一个值,这样字典就会建立新的项。
.成员资格
表达式 item in d(d 为字典)查找的是键(containskey),而不是值(containsvalue)
3



(
三)集合
strs=set(['jeff','wong','cnblogs'])
nums=set(range(10))
. 副本是被忽略的,即元素的唯一性
1
2
3
1
. 集合元素的顺序是随意的
. 集合常用方法
) A.union(B) union 操作返回两个集合的并集,不改变原有集合。使用按位与(OR)运算符“|”可
以得到一样的结果 2) 其他常见操作包括&(交集),<=,>=,-,copy()等等
3
4
) b、add 和 remove
. frozenset
集合是可变的,所以不能用做字典的键。集合本身只能包含不可变值,所以也就不能包含其他集合
可以使用 frozenset 类型用于代表不可变(可散列)的集合
Set1.add(frozenset(set2)
1
5.2 Python 在函数中使用*和**接收元组和列表
当要使函数接收元组或字典形式的参数 的时候,有一种特殊的方法,它分别使用*和**前缀 。这
种方法在函数需要获取可变数量的参数 的时候特别有用。
注意:
[
1] 由于在 args 变量前有*前缀 ,所有多余的函数参数都会作为一个元组存储在 args 中 。如果
使用的是**前缀 ,多余的参数则会被认为是一个字典的健/值对 。
2] 对于 def func(*args):,*args 表示把传进来的位置参数存储在 tuple(元组)args 里面。例如,
调用 func(1, 2, 3) ,args 就表示(1, 2, 3)这个元组。
3] 对于 def func(**args):,**args 表示把参数作为字典的健-值对存储在 dict(字典)args 里面。
例如,调用 func(a='I', b='am', c='wcdj') ,args 就表示{'a':'I', 'b':'am', 'c':'wcdj'}这个字典 。
4] 注意普通参数与*和**参数公用的情况,一般将*和**参数放在参数列表最后。
元组:
[
[
[
#
#
#
! /usr/bin/python
Filename: tuple_function.py
2010-7-19 wcdj
def powersum(power, *args):
''''Return the sum of each argument raised
'
to specified power.'''
total=0
for i in args:
total+=pow(i,power)
return total
print 'powersum(2, 3, 4)==', powersum(2, 3, 4)
print 'powersum(2, 10)==', powersum(2, 10)
#
#
#
#######
output
#######
powersum(2, 3, 4)==25
powersum(2, 10)==100












字典
#
#
#
! /usr/bin/python
Filename: dict_function.py
2010-7-19 wcdj
def findad(username, **args):
''''find address by dictionary'''
'
print 'Hello: ', username
for name, address in args.items():
print 'Contact %s at %s' % (name, address)
findad('wcdj', gerry='gerry@byteofpython.info', /
wcdj='wcdj@126.com', yj='yj@gmail.com'
#
#
#
#######
output
#######
Hello: wcdj
Contact yj at yj@gmail.com
Contact gerry at gerry@byteofpython.info
Contact wcdj at wcdj@126.com

1
5.3 Python Numpy 常用方法
1
.Numpy Array 运算
数值化的 python,python list 的替代品:numpy array,对数组整体进行运算
Numpy 数组,元素只有一种类型
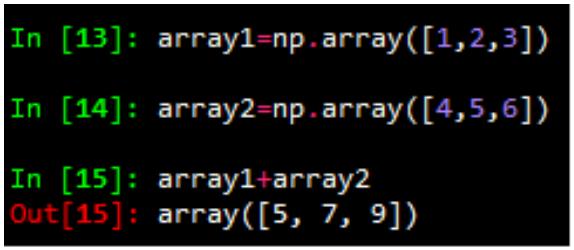
两个 array 相加,结果为对应元素相加
2
. numpy 的基本统计学
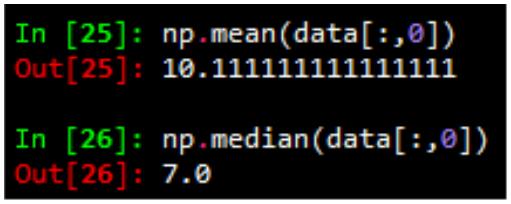
(
1)求平均值、中值
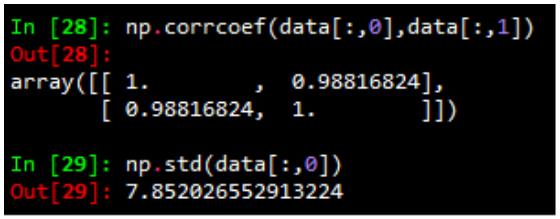
(2)相关系数和标准差
(
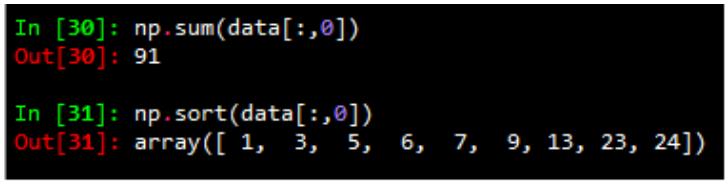
3)求和,排序
3
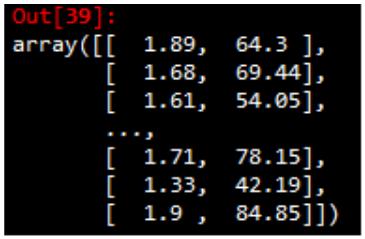
.数据的产生 – 随机抽样
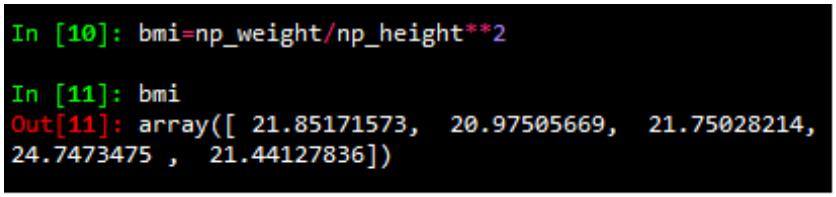
height=np.round(np.random.normal(1.75,0.20,5000),2)
weight=np.round(np.random.normal(60.32,15,5000),2)
np_city=np.column_stack((height,weight))
注:np.random.normal(均值,标准差,数量)
1
5.4 Python Pandas 常用方法
引入包 import pandas as pd;import numpy as np
(
一)创建对象
1
.通过传递一个 list 对象来创建一个 Series
2
.通过传递一个 numpy array,时间索引以及列标签来创建一个 DataFrame
3
.通过传递一个能够被转换成类似序列结构的字典对象来创建一个 DataFrame
4
.查看不同列的数据类型
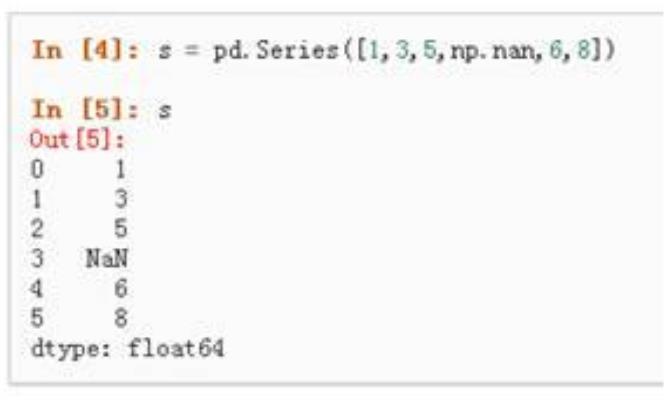
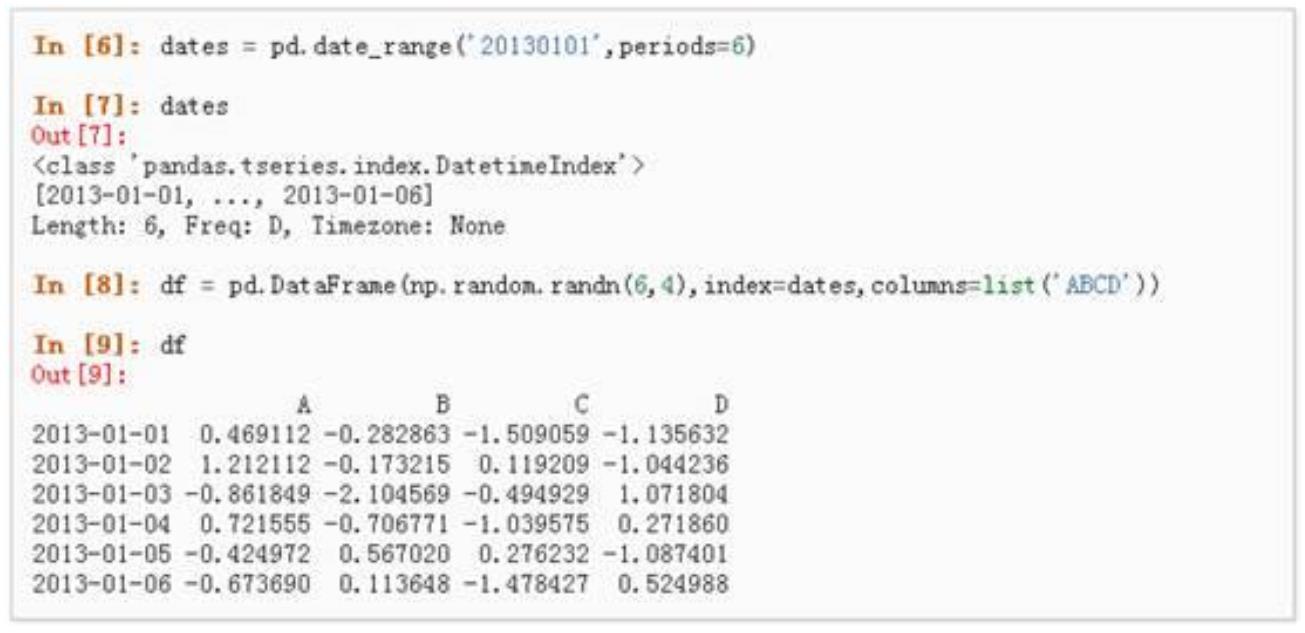
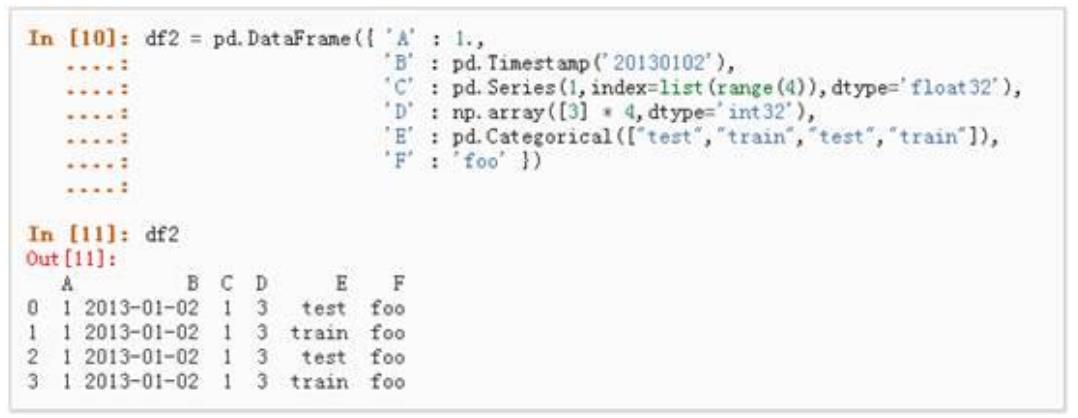

(
二)查看数据
1
. 查看 frame 中头部和尾部的行
2
.显示索引、列和底层的 numpy 数据:df.index df.columns df.values
3
4
. describe()函数对于数据的快速统计汇总 df.describe()
. 对数据的转置 df.T
5
6
.按轴进行排序 axis=1 按标签名降序排列
.按值进行排序




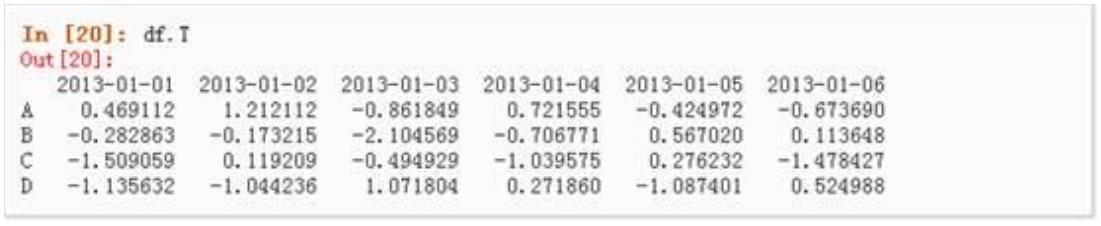
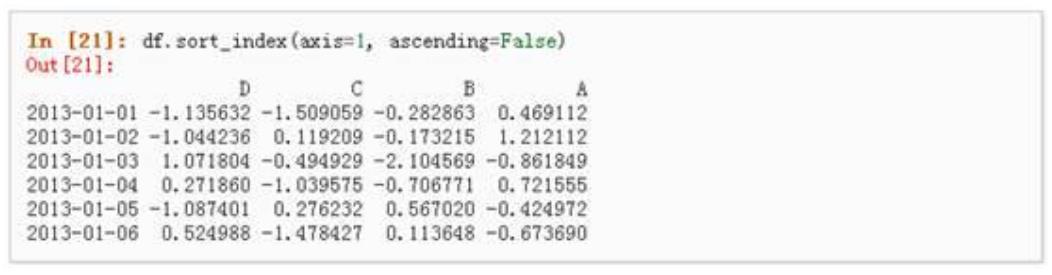
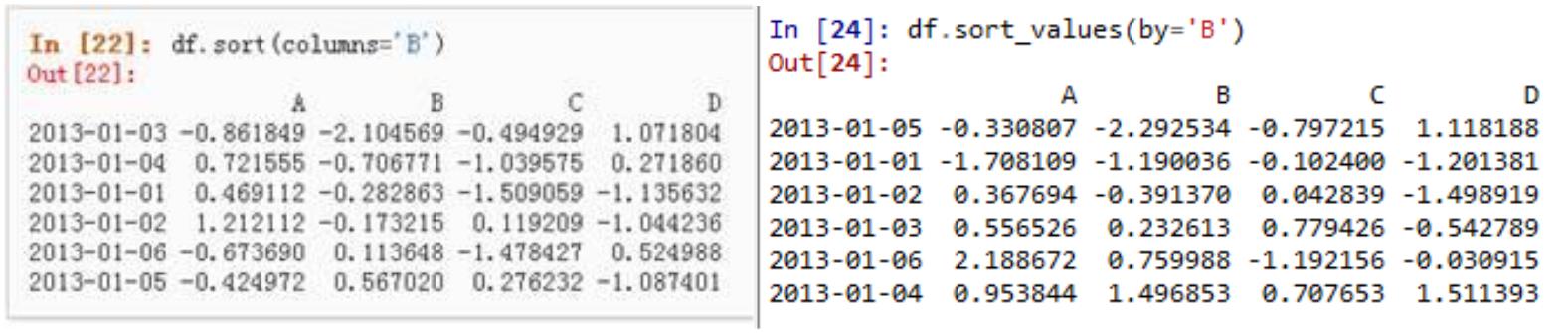
(
三)选择
推荐使用经过优化的 pandas 数据访问方式: .at, .iat, .loc, .iloc 和 .ix
1
.获取数据
1
)选择一个单独的列,这将会返回一个 Series,等同于 df.A
2
)通过[ ]进行选择,这将会对行进行切片
2
.通过标签进行选择 .loc[ ]
) 使用一个标签来获取一个交叉的区域
1
2)通过标签来在多个轴上进行选择
4)对于返回的对象进行维度缩减
6)快速访问一个标量
3
)标签切片
5
)获取一个标量



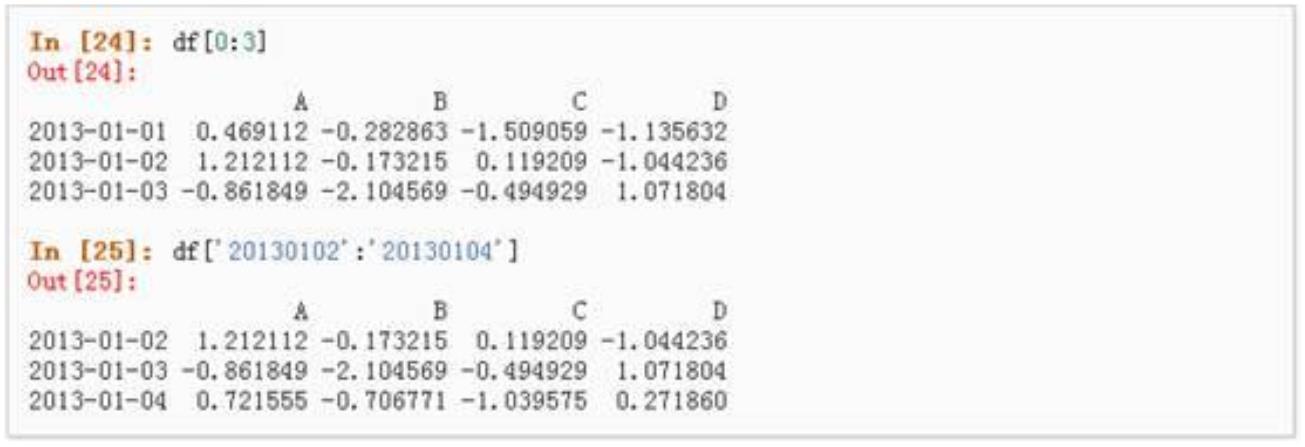
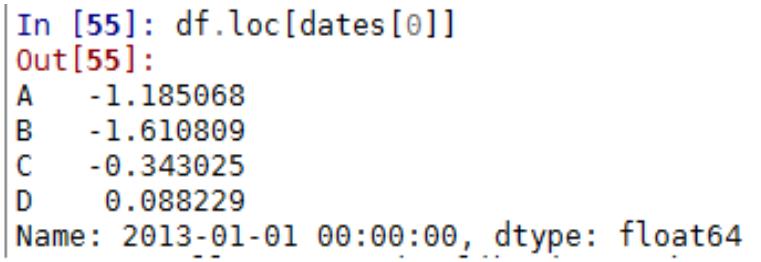
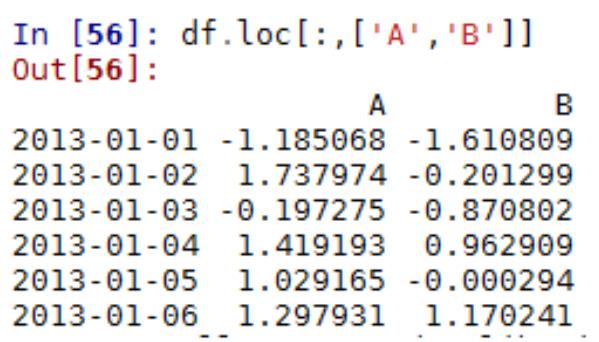
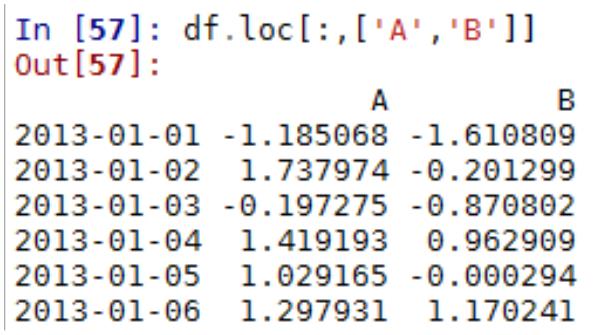
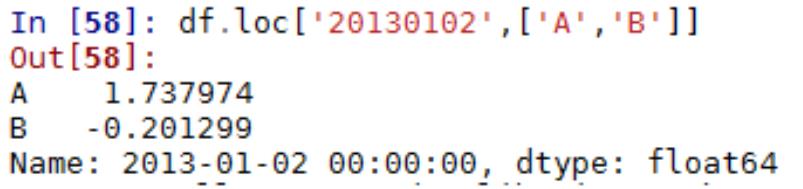


3
.通过位置选择 .iloc(:,:)
1
) 通过传递数值进行位置选择(选择的是行)
2)通过数值进行切片,与 numpy/python 情况类
似,不包含第二个值
3
5
)通过制定一个位置的列表
4)对行进行切片
6)获取特定的值
)对列进行切片
4
.布尔索引
1
)使用一个单独列的值来选择数据
2
)使用 where 操作来选择数据
3
)使用 isin()方法来过滤
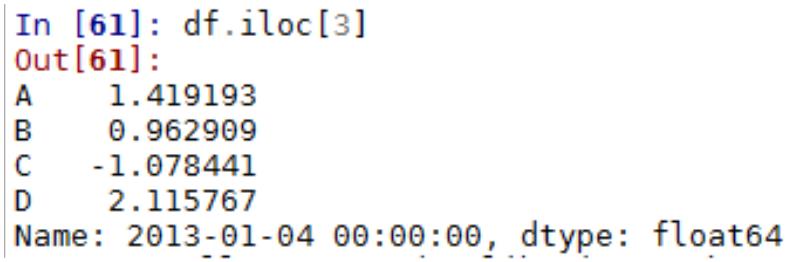
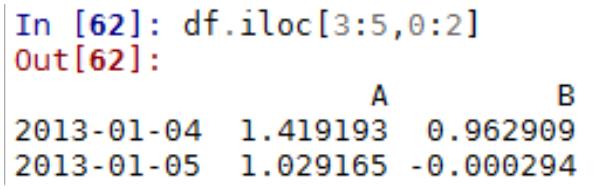





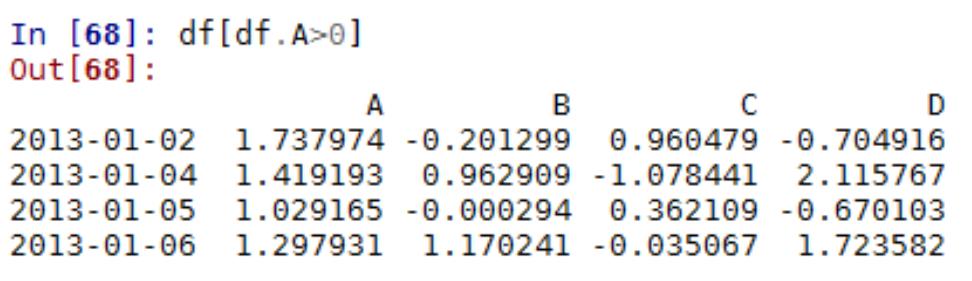

5
.设置
1
)设置一个新的列
2
)通过标签设置新的值
3)通过位置设置新的值
4
)通过 numpy 数组设置一组新值
5)where 操作来设置新的值
(
四)缺失值处理
在 pandas 中使用 np.nan 来代替缺失值
1. 使用 reindex()方法可以对指定轴上的索引进行改变/增加/删除操作,这将返回原始数据的一个拷贝
2
. 去掉包含缺失值的行,不改变原来的值

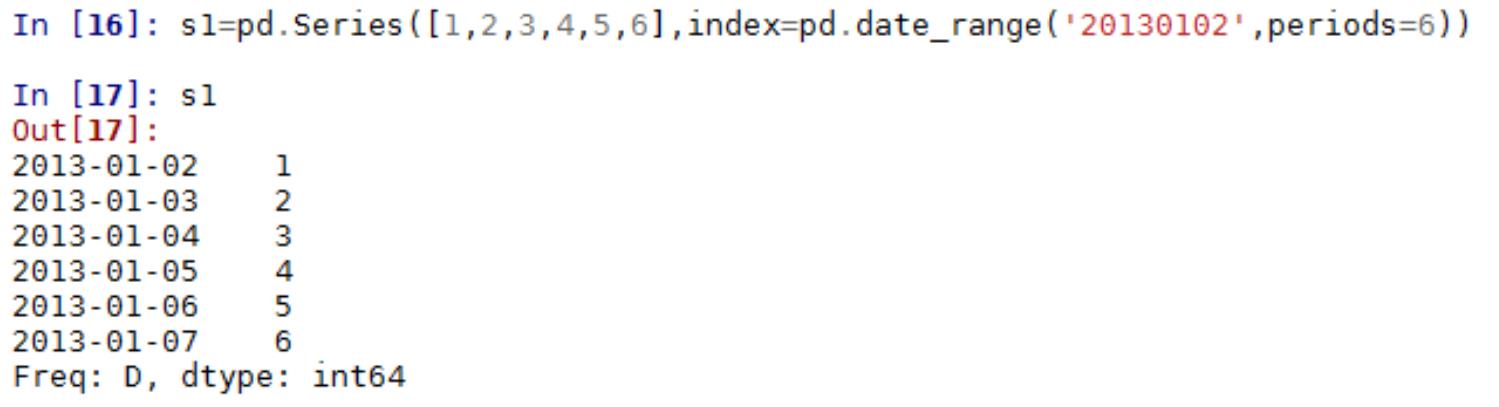

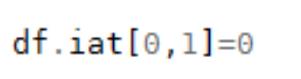

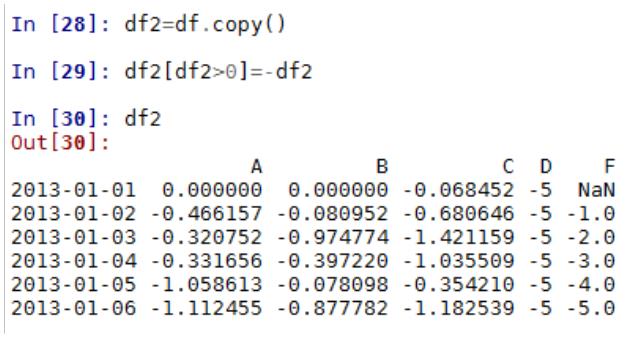
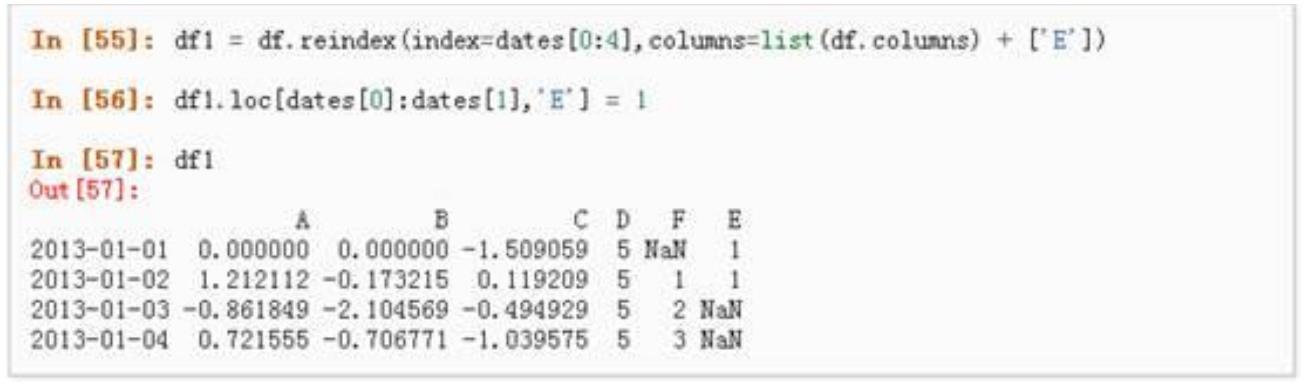

3
4
. 对缺失值进行填充
. 对数据进行布尔填充
(
五)相关操作
1
.统计(相关操作通常情况下不包括缺失值)
2)在其他轴上进行相同的操作
1
)执行描述性统计,默认统计各列的值情况
3
)对于拥有不同维度,需要对齐的对象进行操作.Pandas 会自动的沿着指定的维度进行广播
2
. Apply – 对数据应用函数
3
.直方图 value_counts()



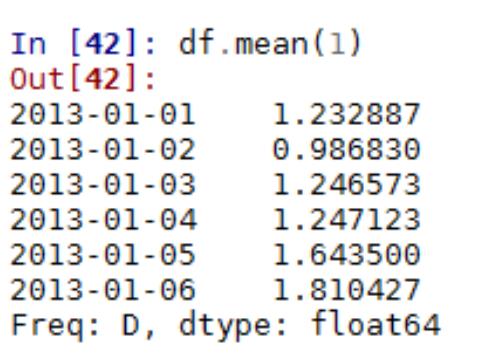
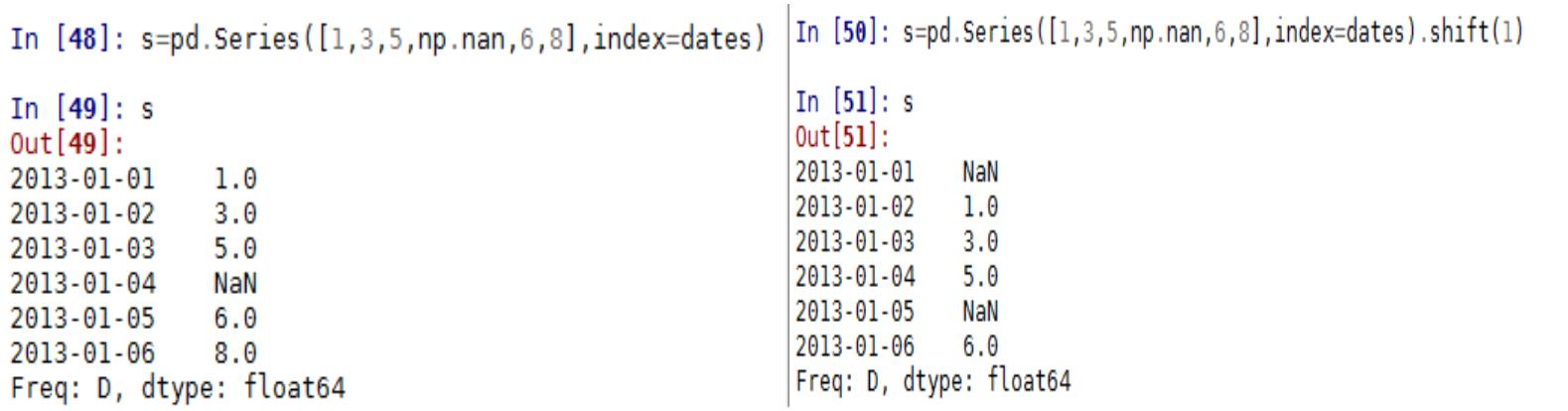
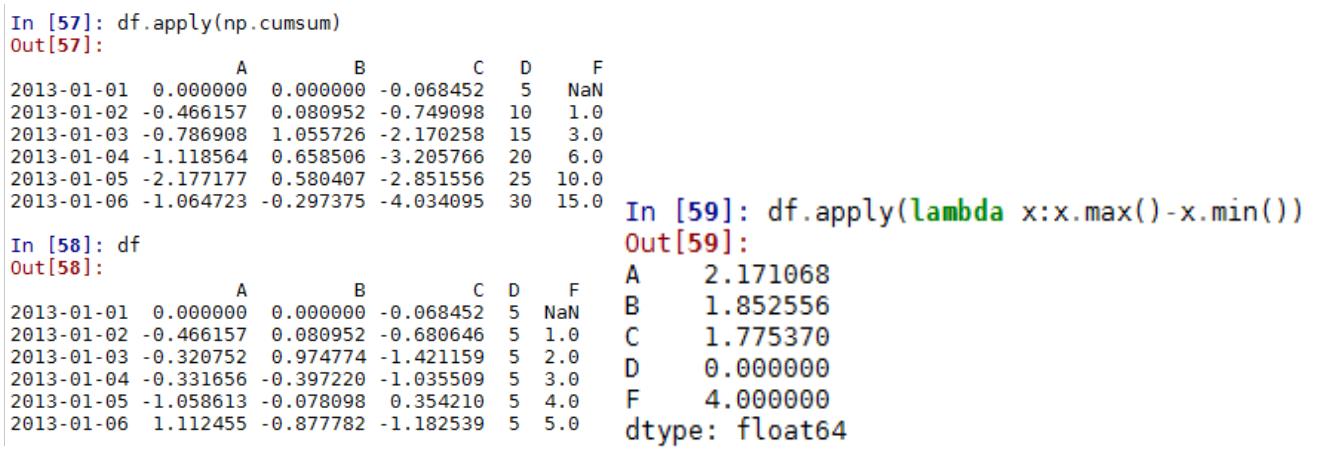
4
.字符串方法
(
六)合并
1
.concat ---- 类似于 SQL 中 union
2
. merge 类似于 SQL 类型的内连接(inner join)
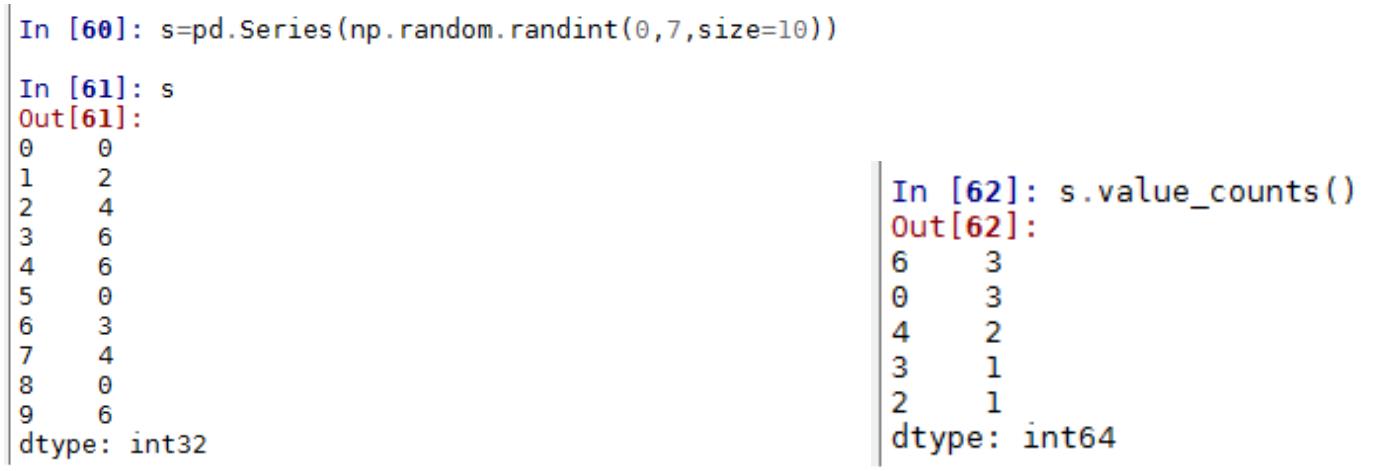

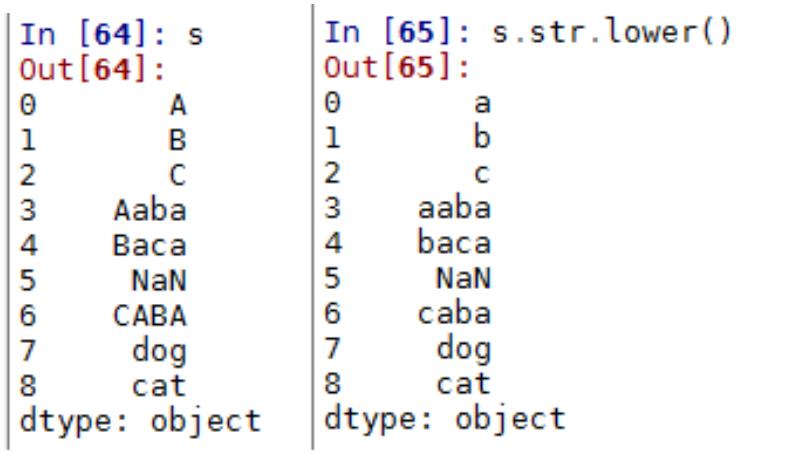



3
.Append 将一行连接到一个 DataFrame 上
(
七)分组
对于“group by”操作,我们通常指以下一个或多个操作
(
(
(
1
Splitting)按照一些规则将数据分为不同的组;
Applying)对于每组数据分别执行一个函数;
Combining)将结果组合到一个数据结构中;
.分组,并对每个分组执行 sum 函数
2.通过多个列进行分组形成一个层次索引
(
八)Reshaping
1
.Stack
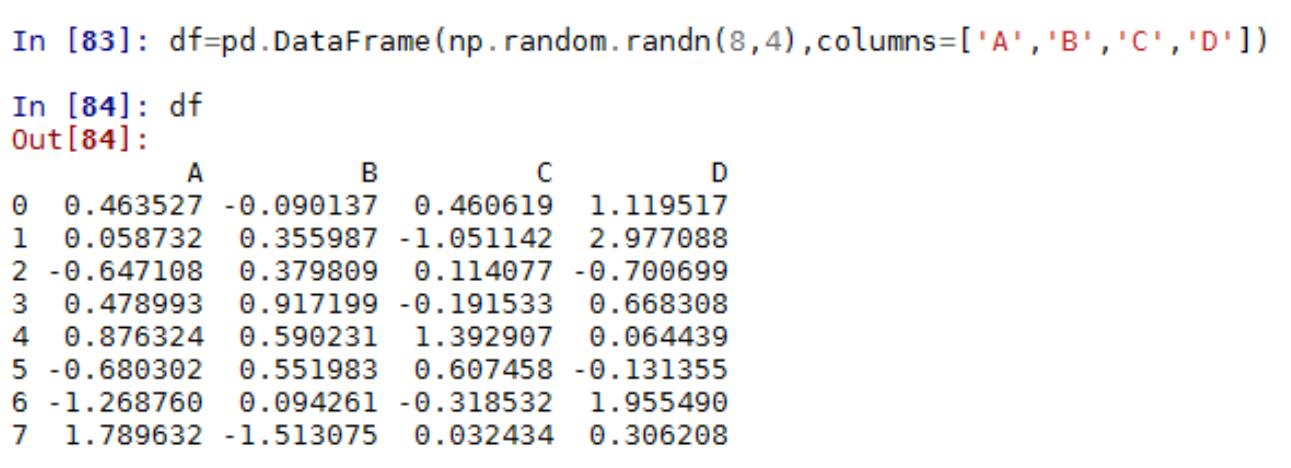
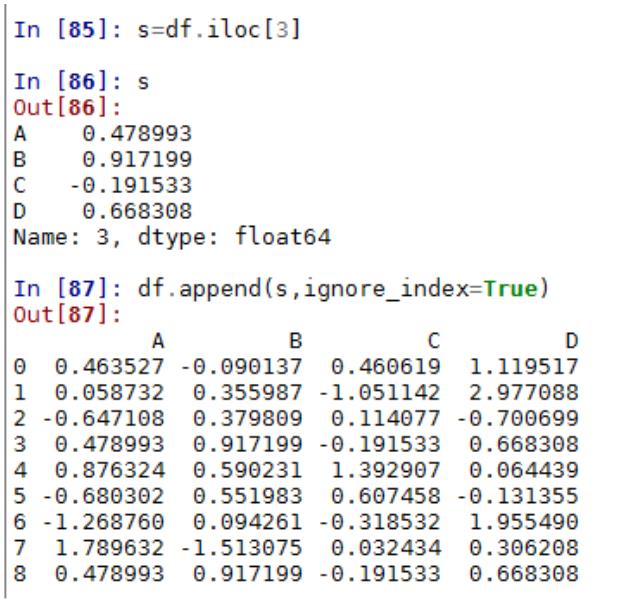
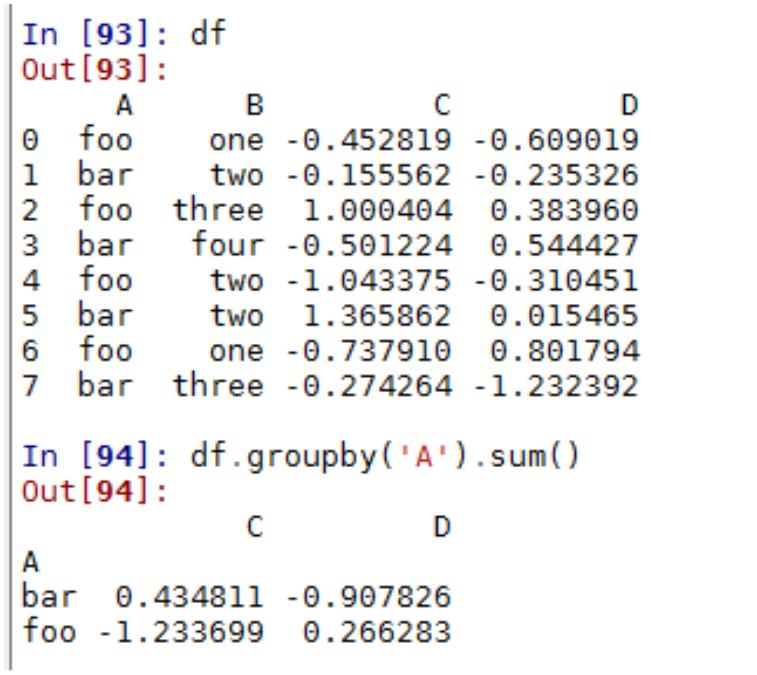
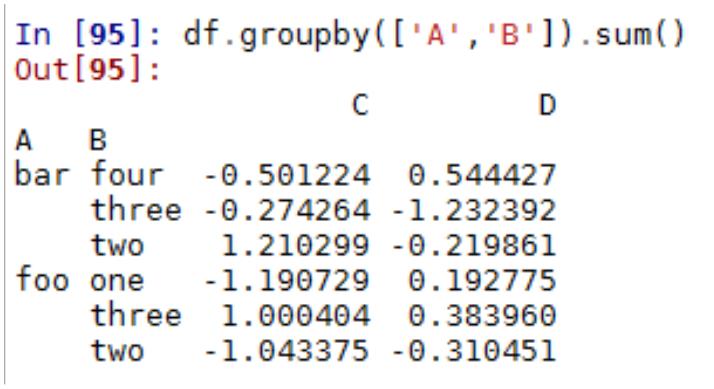
2
.数据透视表
(
九)时间序列

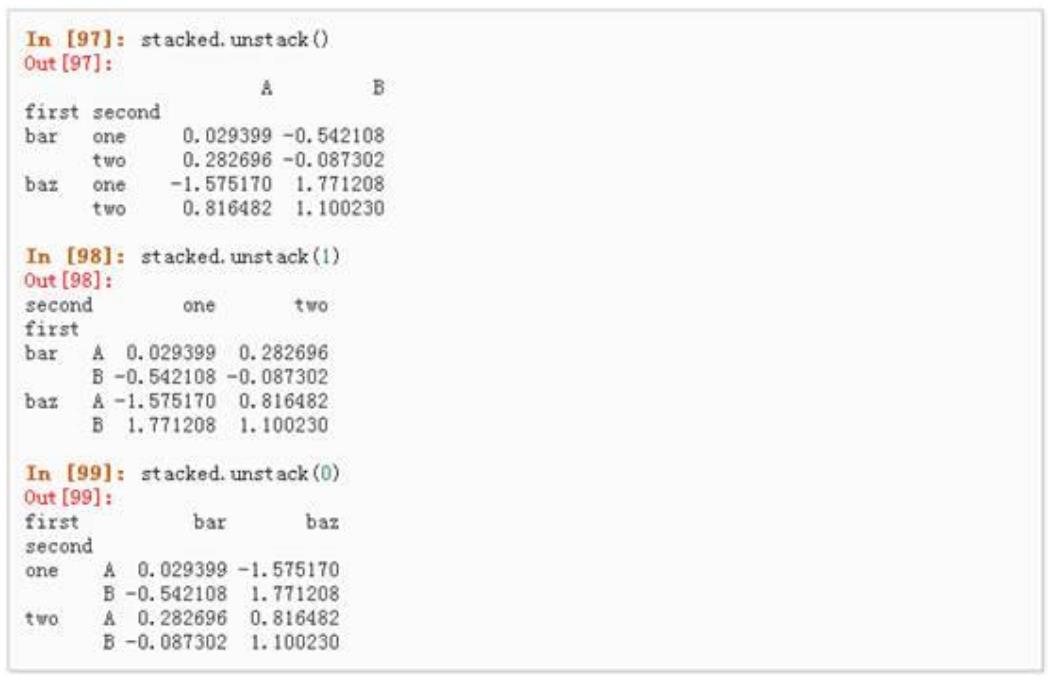
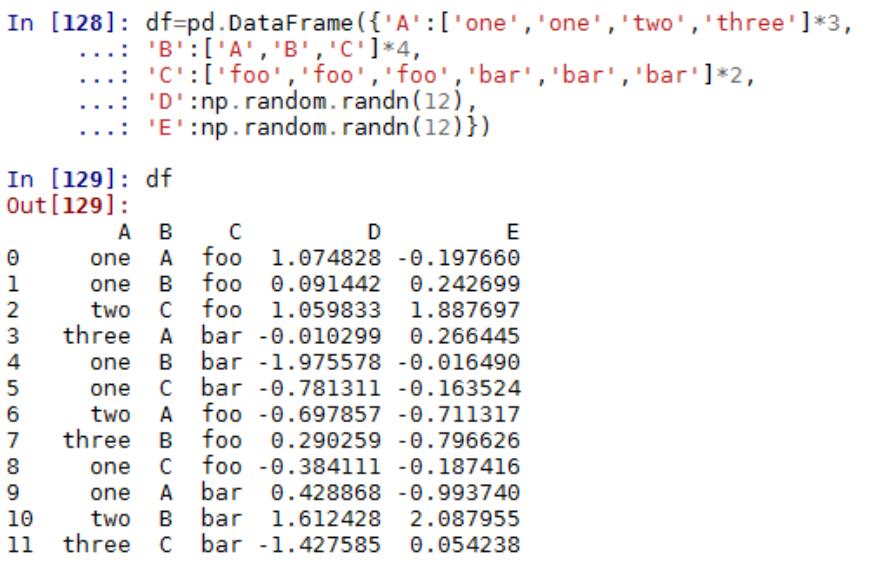
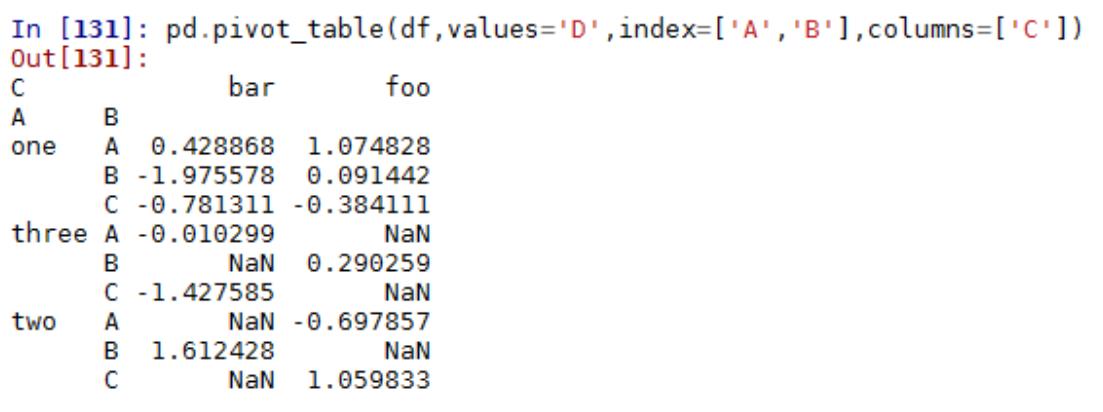
1
. 针对频率转换进行重采样
2
.时区表示
3
.时区转换
4
.时间跨度转换
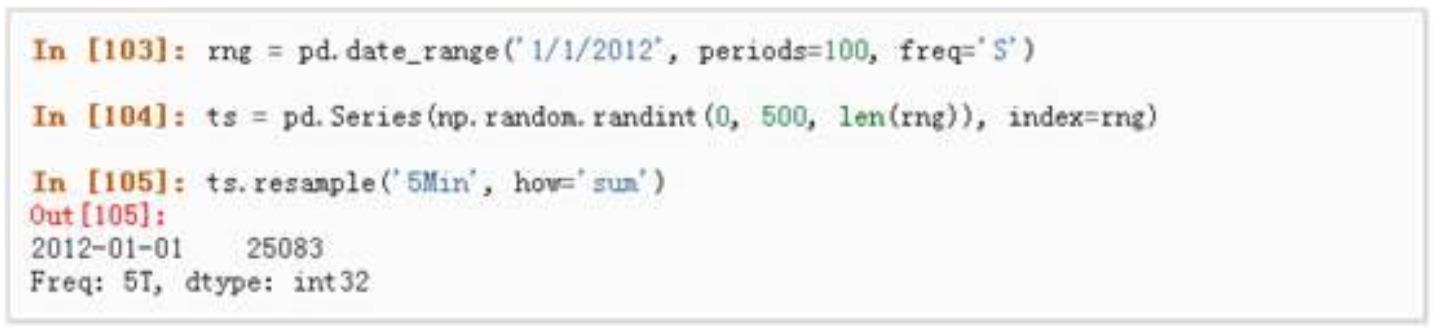
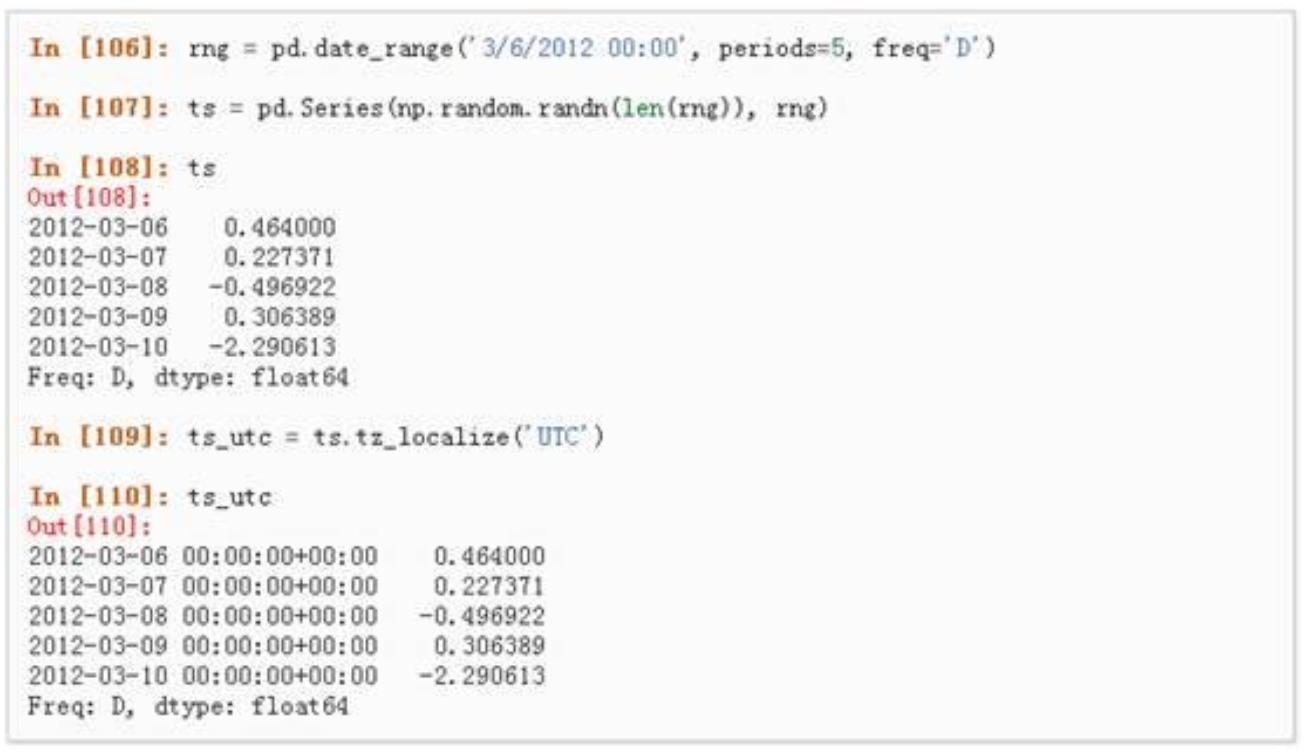
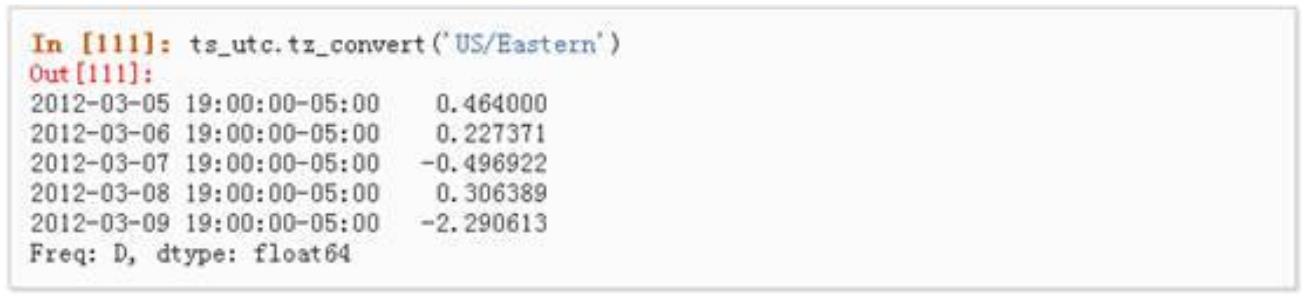
5
.时期和时间戳之间的转换可以使用一些方便的算术函数
(
十) Categorical
1
. 将原始的 grade 转换为 Categorical 数据类型
2
3
. Categorical 重命名为更有意义的名称
.对类别进行重新排序,增加缺失的类别
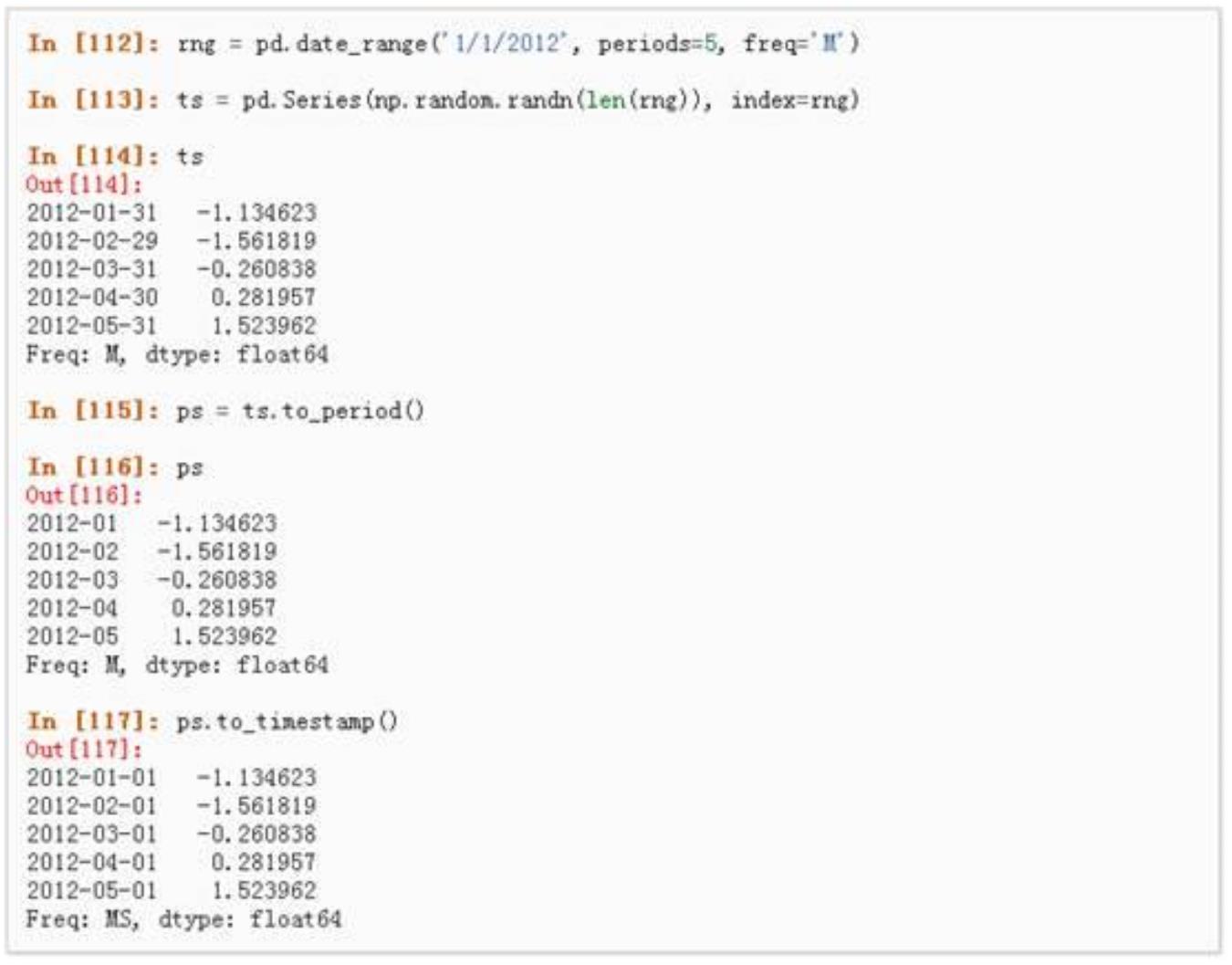

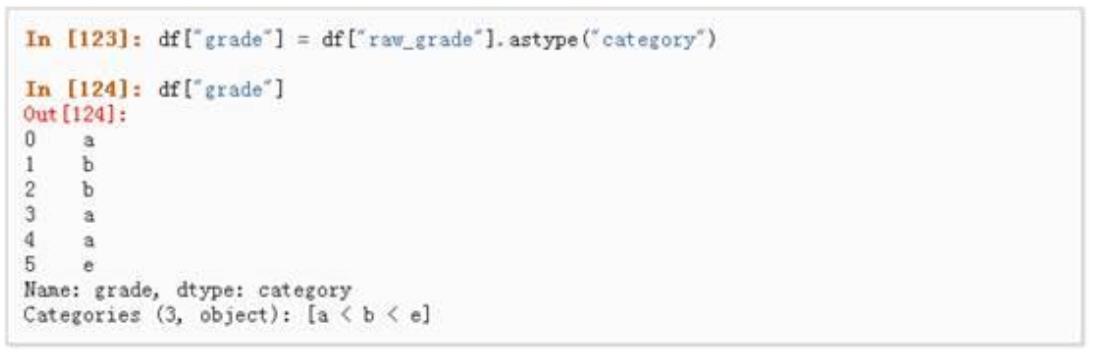

4
5
. 排序是按照 Categorical 的顺序进行的而不是按照字典顺序进行
.对 Categorical 列进行排序存在空的类别
(
十一)导入和保存数据
1
.CSV
写入 CSV
读取 CSV
2
.HDF5
写入 HDF5 存储


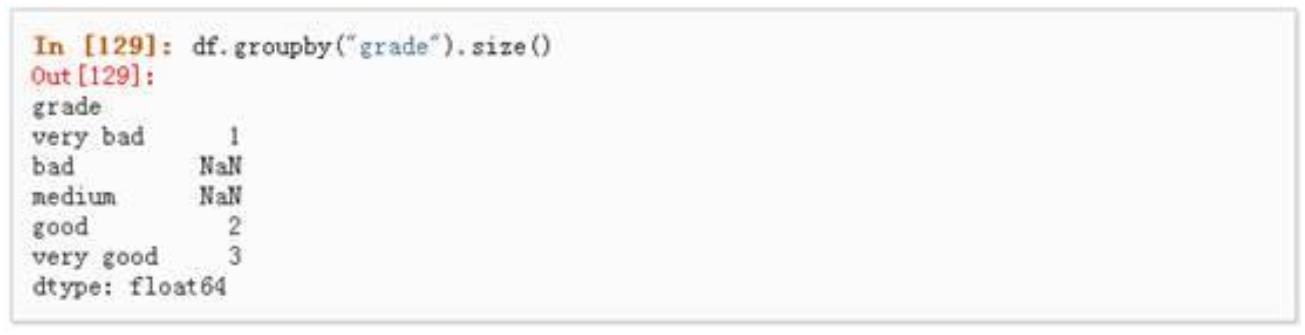

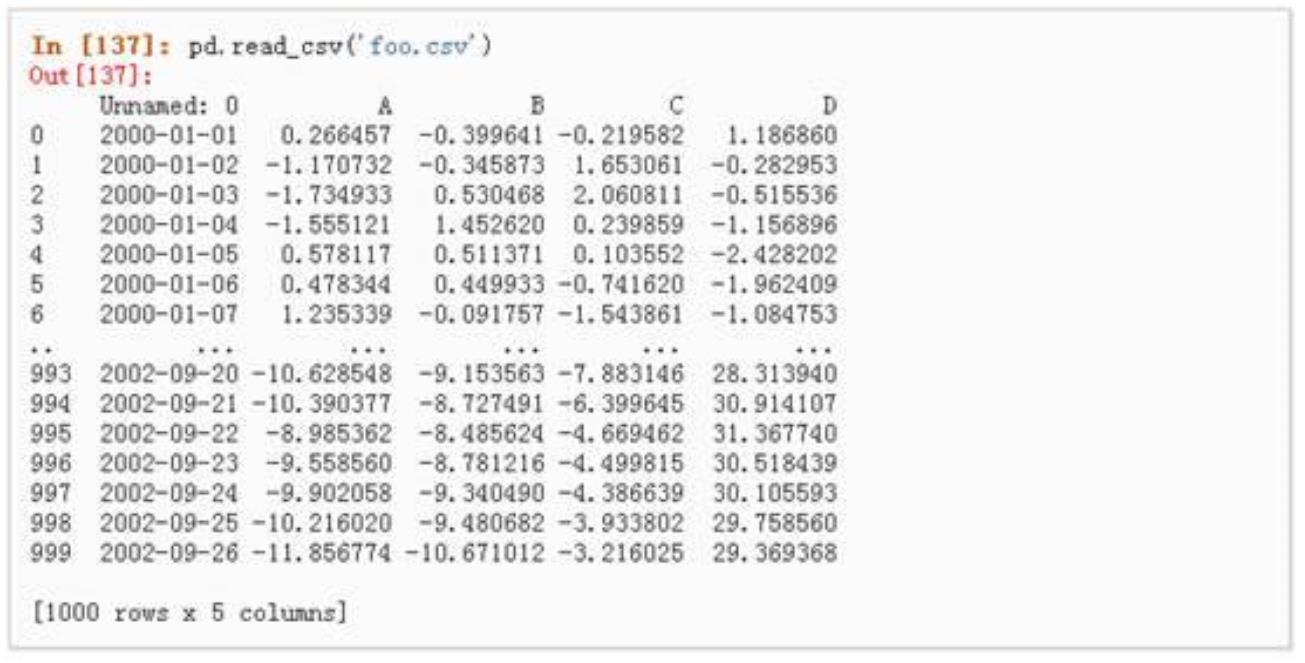

从 HDF5 存储中读取
3
.Excel
写入
从 excel 文件中读取
1
5.5 Python Matplotlib 数据可视化
import matplotlib.pyplot as plt
1
.折线图 plt.plot(X,Y)
plt.xlabel(“X”)
plt.ylabel(“Y”)
plt.title(“title”)
2
3
.散点图 plt.scatter(X,Y)
.直方图 plt.hist(values,bins=15)
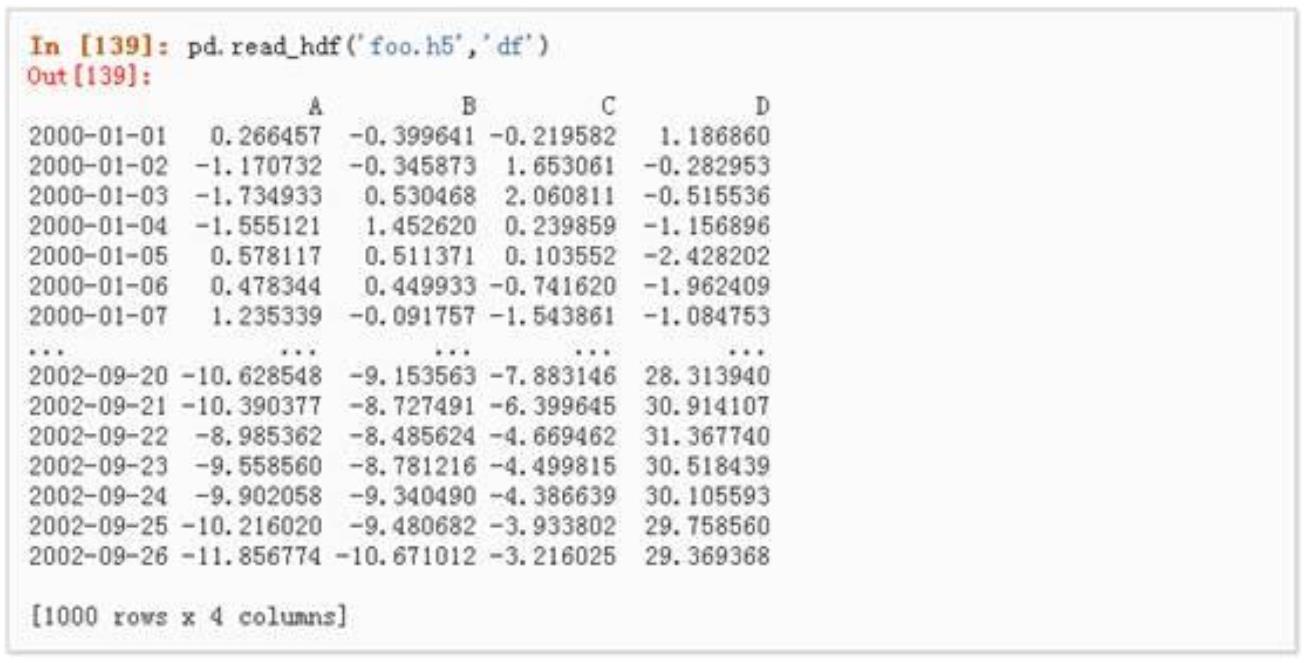

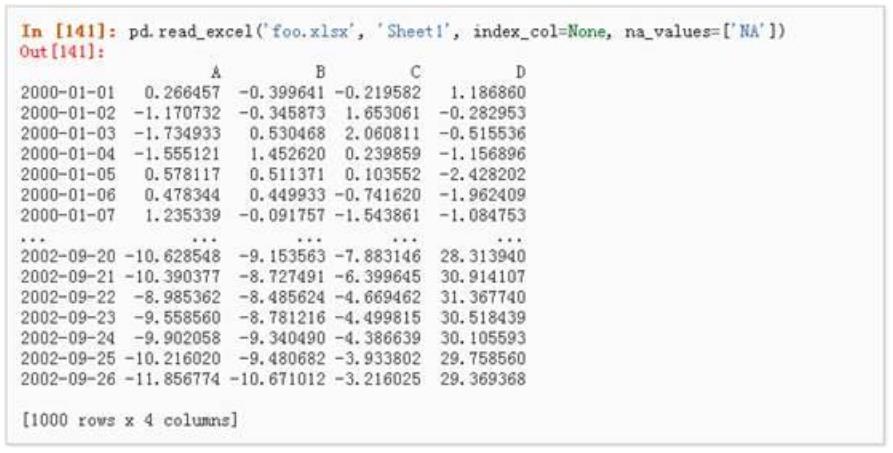
第十六章 Python Scikit-Learn 建模方法
1
1
6.1 sklearn 导论与解读
6.2 sklearn 特征工程(sklearn.preprocessing)
1
1
6.2.1 数据标准化,归一处理
. Standardization, or mean removal and variance scaling
标准化,零均值,单位化方差,Z-score
푥 − 휇
휎
x =
有两种不同的方式实现:
(
1)使用 sklearn.preprocessing.scale()函数,可以直接将给定数据进行标准化。
from sklearn import preprocessing
import numpy as np
X=np.array([[1,-1,2],[2,0,0],[0,1,-1]])
X_scaled=preprocessing.scale(X)
#
#
#
#
#
#
X_scaled
Out[6]:
array([[ 0.
, -1.22474487, 1.33630621],
, -0.26726124],
[-1.22474487, 1.22474487, -1.06904497]])
处理后数据的均值和方差
[ 1.22474487, 0.
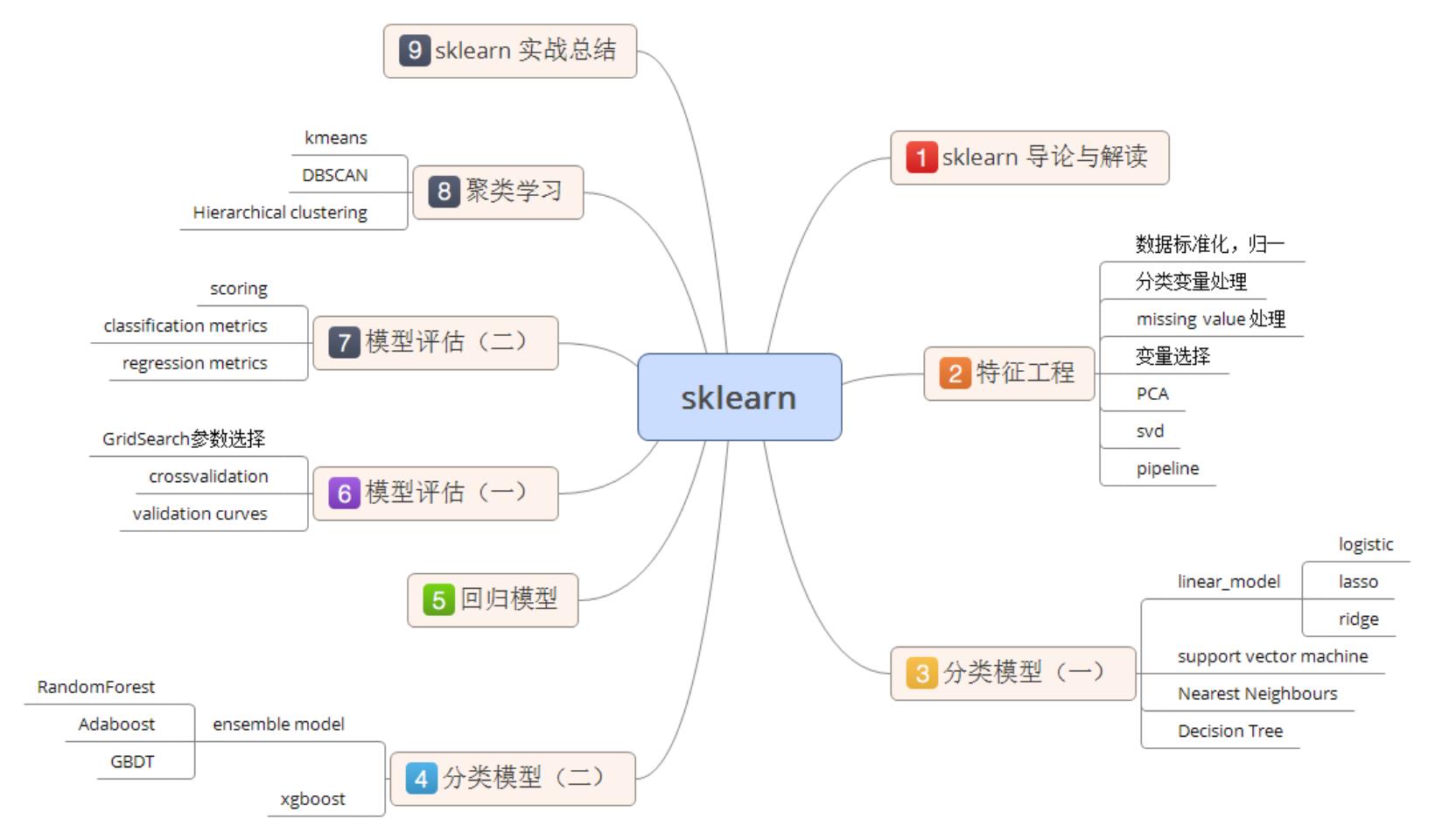


X_scaled.mean(axis=0)
Out[7]: array([ 0., 0., 0.])
X_scaled.std(axis=0)
Out[8]: array([ 1., 1., 1.])
#
#
(
2)使用 sklearn.preprocessing.StandardScaler 类,使用该类的好处在于可以保存训练集中的参数(均
值、方差)直接使用其对象转换测试集数据。
from sklearn.preprocessing import StandardScaler
X_scaler=StandardScaler()
Y_scaler=StandardScaler()
X_train= X_scaler.fit_transform(X_train)
y_train= y_scaler.fit_transform(y_train)
X_test=X_scaler.transform(X_test)
y_test=y_scaler.transform(y_test)
>
>
>> scaler = preprocessing.StandardScaler().fit(X)
>> scaler
StandardScaler(copy=True, with_mean=True, with_std=True)
>> scaler.mean_ 按列求均值
array([ 1. , 0.
>> scaler.scale_
按列求标准差
array([ 0.81649658, 0.81649658, 1.24721913])
>
, 0.33333333])
>
#
可以直接使用训练集对测试集数据进行转换
>
>> scaler.transform(X)
array([[ 0.
, -1.22474487, 1.33630621],
[
[
1.22474487, 0. , -0.26726124],
-1.22474487, 1.22474487, -1.06904497]])
2
. Scaling features to a range (0-1 scaler)将属性缩放到指定范围
通过 preprocessing.MinMaxScaler 类实现。
使用这种方法的目的包括:
1
2
)对于方差非常小的属性可以增强其稳定性。
)维持稀疏矩阵中为 0 的条目。
X_train=np.array([[1.,-1.,2.],[2.,0.,0.],[0.,1.,-1.]])
min_max_scaler=preprocessing.MinMaxScaler()
X_train_minmax=min_max_scaler.fit_transform(X_train)
X_train_minmax
将 X_train中每列最小值设为 0,最大值设为 1,进行 0-1规整化
#
#
#
#
#
#
#
array([[ 0.5
[ 1.
, 0.
, 0.5
, 1.
, 1.
, 0.33333333],
, 0. ]])
],
[ 0.
array([[ 0. ..., -1.22..., 1.33...],
[ 1.22..., 0. ..., -0.26...],
[-1.22..., 1.22..., -1.06...]])
将相同的缩放应用到测试集数据中
X_test=np.array([[-3.,-1.,4.]])




X_test_minmax=min_max_scaler.transform(X_test) 将 X_test中每列值按照 X_train中的规则进行缩放
X_test_minmax
#
Out[34]: array([[-1.5
, 0.
, 1.66666667]])
1
1
6.2.2 类别变量处理
. Binarization ---- 伯努利分布
Feature binarization is the process of thresholding numerical features to get boolean values.
X = [[ 1., -1., 2.],[ 2., 0., 0.],[ 0., 1., -1.]]
binarizer=preprocessing.Binarizer(threshold=1.1).fit(X) #默认 threshold=0.0
binarizer.transform(X)
#
#
#
#
Out[43]:
array([[ 0., 0., 1.],
[ 1., 0., 0.],
[ 0., 0., 0.]])
2
. Encoding categorical features -- a one-of-K or one-hot encoding 哑变量
enc=preprocessing.OneHotEncoder()
enc.fit([[0,0,3],[1,1,0],[0,2,1],[1,0,2]])
#
#
#
Out[45]:
OneHotEncoder(categorical_features='all', dtype=<class 'float'>,
handle_unknown='error', n_values='auto', sparse=True)
enc.transform([[0,1,3]]).toarray()
#
Out[46]: array([[ 1., 0., 0., 1., 0., 0., 0., 0., 1.]])
1
6.2.3 PCA
#
Import Library
from sklearn import decomposition
Create PCA object
pca = decomposition.PCA(n_components=k)
#
#
#
default value of k=min(n_sample,n_features)
Reduced the dimension of training dataset using PCA
train_reduced = pca.fit_transform(train)
Reduce the dimension of test dataset
test_reduced = pca.transform(test)
#





1
6.2.4 Pipeline
1
6.3 基本分类模型(一) classification
1
. 逻辑回归(Logistic Regression)
from sklearn.linear_model import from sklearn.tree import DecisionTreeClassifier
LogisticRegression
2. 决策树(Decision Tree)
model = DecisionTreeClassifier(criterion=’gini’)
# Train the model using the training sets and check score
model.fit(X, y)
Model = LogisticRegression()
Model.fit(X_train, y_train)
Model.score(X_train,y_train)
model.score(X, y)
#
Equation coefficient and Intercept
# Predict output
Print(‘Coefficient’,model.coef_)
Print(‘Intercept’,model.intercept_)
predicted = model.predict(x_test)
#查看每一类别的概率
#
Predict Output
predicted2 = model.predict_proba([[2.,2.]])
with open("iris.dot",'w') as f: #可视化
f= tree.export_graphviz(model, out_file=f)
4. 朴素贝叶斯分类 (Naïve_bayes)
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
Predicted = Model.predict(x_test)
3
. 支持向量机(SVM)
from sklearn import svm
model = suv.svc()
model.fit(X, y)
model.fit(X, y)
model.score()
# Predict Output
#
Predict Output
predicted = model.predict(x_test)
. K 近邻(KNN – K-Nearest Neighbours)
Predicted = model.predict(x_test)
5
from sklearn.neighbours import KNeighboursClassifier
model = KNeighboursClassifier(n_neighbours=6)
model.fit(X, y)
predicted = model.predict(x_test)
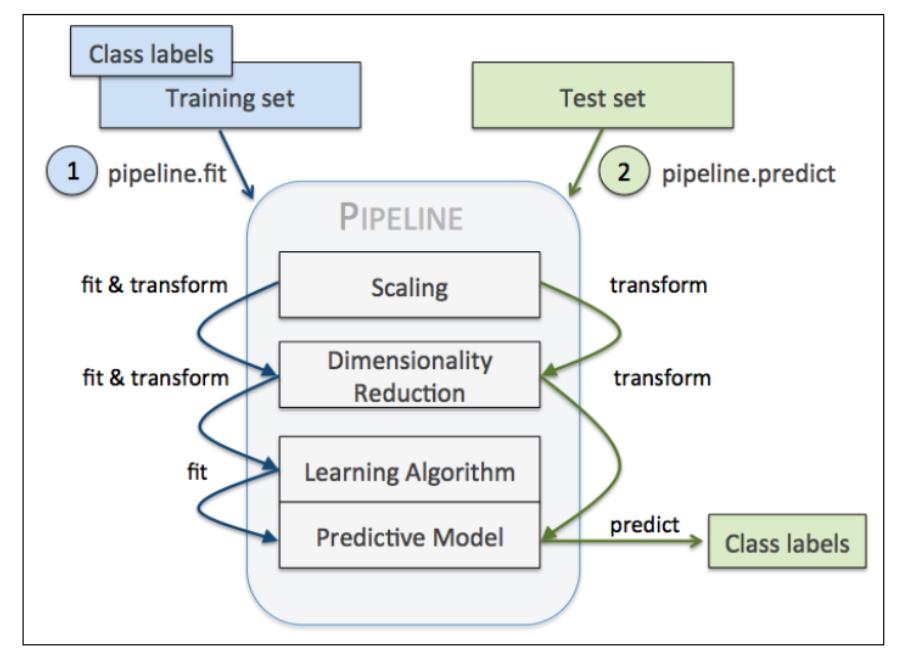
1
6.4 分类模型提升(二)ensemble
1
. 随机森林(Random Forest)
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier()
model.fit(X, y)
predicted = model.predict(x_test)
2
. Gradient Boosting & Adaboost
from sklearn.ensemble import GradientBoostingClassifier
model = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0, max_depth=1,random_state=0)
model.fit(X,y)
predicted = model.predict(x_test)
1
6.5 回归模型
1
.线性回归(Linear Regression)
from sklearn.linear_model import LinearRegression #引入线性回归模块
regressor=LinearRegression() #创建回归容器
regressor.fit(X_train,y_train) #训练
y_predictions=regressor.predict(X_test) #预测
regressor.score(X_test,y_test) #评分
regressor.coef_ #系数
regressor.intercept_ #常数项
1
6.6 模型评估(一)
1
1
6.6.1 cross_validation
.数据拆分为训练集和预测集
from sklearn.cross_validation import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y)
2
.交叉验证
from sklearn.cross_validation import cross_val_score
regressor=LinearRegression()
scores= cross_val_score(regressor,X,y,cv=5) #将数据集分成 5 份
print(scores.mean(),scores)
1
6.6.2 GridSearch 参数选择
#
grid search 模型调优
from sklearn.grid_search import GridSearchCV
from sklearn.svm import SVC
pipe_svc = Pipeline([('scl', StandardScaler()), ('clf', SVC(random_state=1))])


param_range = [0.0001, 0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0]
param_grid = [{'clf__C': param_range, 'clf__kernel': ['linear']}, {'clf__C': param_range,
'
clf__gamma': param_range, 'clf__kernel': ['rbf']}]
gs = GridSearchCV(estimator=pipe_svc, param_grid=param_grid, scoring='accuracy', cv=10,
n_jobs=-1) # cv为 kfold交叉验证中类别数量
gs = gs.fit(X_train, y_train)
print(gs.cv_results_)
print(gs.best_score_)
#
0.978021978022
print(gs.best_params_)
{'clf__C': 0.1, 'clf__kernel': 'linear'}
#
clf= gs.best_estimator_
clf.fit(X_train,y_train)
print('Test accuracy: %.3f' % clf.score(X_test,y_test))
#
Test accuracy: 0.965
1
6.6.3 validation curves
1
. learning curve 学习曲线 – 训练集数量与准确性之间的关系
#
绘制学习曲线
from sklearn.learning_curve import learning_curve
import matplotlib.pyplot as plt
pipe_lr =
Pipeline([('scl',StandardScaler()),('clf',LogisticRegression(penalty='l2',random_state =
0
))])
train_sizes, train_scores, test_scores = learning_curve(estimator=pipe_lr, X=X_train,
y=y_train)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores,axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(train_sizes, train_mean, color='blue',marker='o',markersize=5, label='training
accuracy')
plt.fill_between(train_sizes, train_mean + train_std,train_mean - train_std, alpha=0.15,
color='blue' )
plt.plot(train_sizes, test_mean, color='green', linestyle='--',marker='s',markersize=5,
label='validation accuracy')
plt.fill_between(train_sizes, test_mean + test_std, test_mean - test_std, alpha=0.15,
color='green')
plt.grid()
plt.xlabel('Number of training samples')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.ylim([0.8, 1.0])
plt.show()



从上面的图形中我们可以看出,模型在交叉训练集上表现地很好,但是有点过拟合,因为在两个曲线
之间有一点明显的间隔
2
. validation curve 验证曲线 – 不同的模型参数与准确性之间的关系
#
绘制验证曲线
from sklearn.learning_curve import validation_curve
param_range = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0]
train_scores, test_scores = validation_curve(estimator=pipe_lr, X=X_train, y=y_train,
param_name='clf__C', param_range=param_range, cv=10)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(param_range, train_mean, color='blue', marker='o', markersize=5, label='training
accuracy')
plt.fill_between(param_range, train_mean + train_std, train_mean - train_std, alpha=0.15,
color='blue')
plt.plot(param_range, test_mean, color='green', linestyle='--', marker='s', markersize=5,
label='validation accuracy')
plt.fill_between(param_range, test_mean + test_std, test_mean - test_std, alpha=0.15,
color='green')
plt.grid()
plt.xscale('log')
plt.legend(loc='lower right')
plt.xlabel('Parameter C')
plt.ylabel('Accuracy')
plt.ylim([0.8, 1.0])
plt.show()




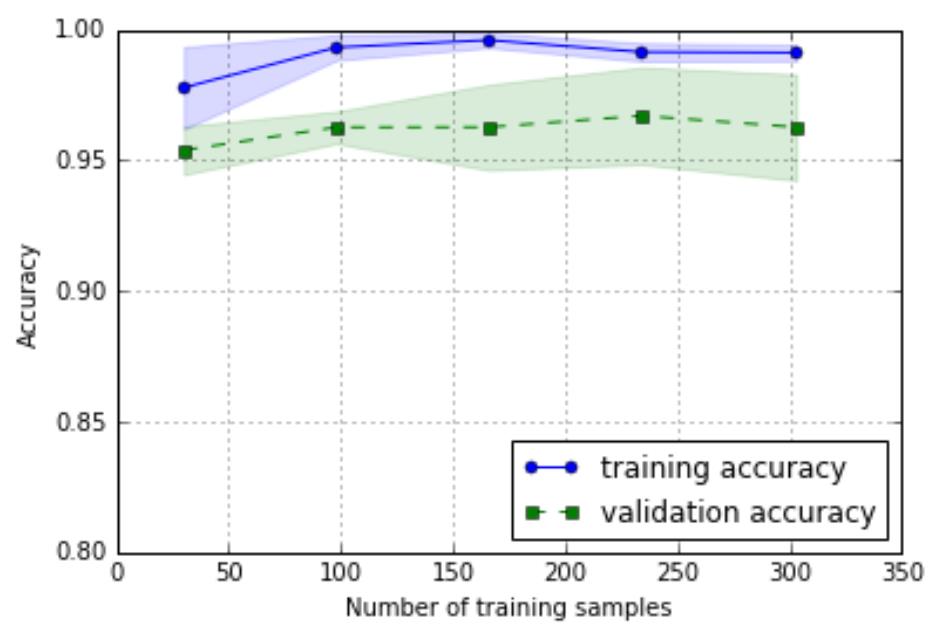
从上图中可以看出,随着参数 C 的增大,模型有点过拟合数据,因为 C 越大,就意味着正则化的强
度越小。然而对于小的参数 C 来说,正则化的强度很大,模型有点欠拟合。从图形中反馈得知,C 在
0
.1 左右是最好的
1
6.7 模型评估(二)
1
6.7.1 Scoring
1
6.7.2 Classification Metrics
1
. 计算混淆矩阵
#
scikit-learn 计算混淆矩阵
from sklearn.metrics import confusion_matrix
pipe_svc.fit(X_train,y_train)
y_pred = pipe_svc.predict(X_test)
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
print(confmat)
#
#
[[71 1]
[ 2 40]]
2
.绘制混淆矩阵
fig,ax= plt.subplots()
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)
for i in range(confmat.shape[0]):
for j in range(confmat.shape[1]):
ax.text(x=j, y=i, s=confmat[i,j],va='center', ha='center')
plt.xlabel('predicted label')
plt.ylabel('true label')
plt.show()


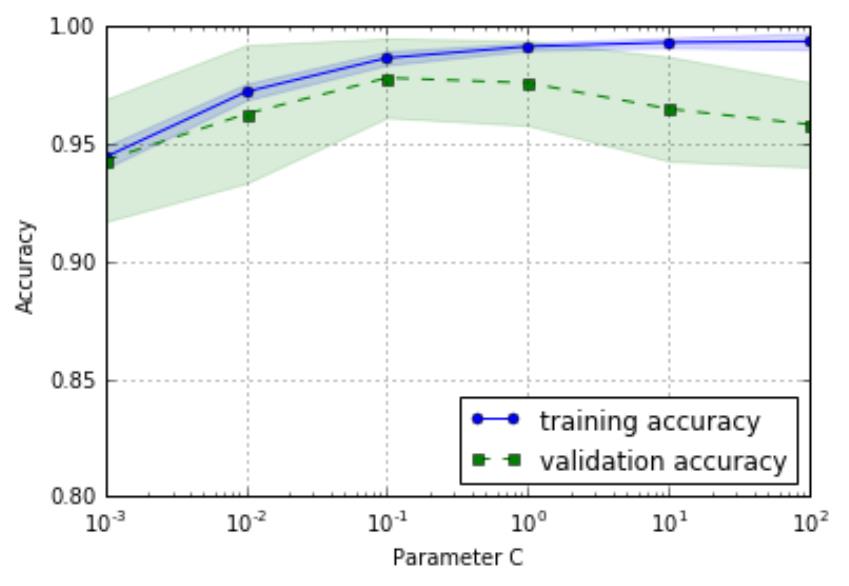
3
. 计算不同的误差评价标准
precision_score, recall_score,F1_score
#
计算不同的误差评价标准。
from sklearn.metrics import precision_score, recall_score,f1_score
precision_score(y_true=y_test,y_pred=y_pred)
#
0.97560975609756095
recall_score(y_true=y_test,y_pred=y_pred)
0.95238095238095233
f1_score(y_true=y_test,y_pred=y_pred)
#
#
0.96385542168674698
4
. 绘制 ROC 曲线
from sklearn.metrics import roc_curve, auc
from scipy import interp
X_train2 = X_train[:, [4,14]]
cv = StratifiedKFold(y_train, n_folds=3, random_state=1)
fig = plt.figure()
mean_tpr=0.0
mean_fpr=np.linspace(0,1,100)
all_tpr = []
#
plot 每个 fold的 ROC曲线,这里 fold的数量为 3,被 StratifiedKFold指定
for i, (train,test) in enumerate(cv):
返回预测的每个类别(这里为 0或 1)的概率
#
probas = pipe_lr.fit(X_train2[train],y_train[train]).predict_proba(X_train2[test])
fpr,tpr,thresholds = roc_curve(y_train[test],probas[:,1],pos_label=1)
mean_tpr += interp(mean_fpr, fpr,tpr) # 线性差值
mean_tpr[0]=0.0
roc_auc=auc(fpr,tpr)
plt.plot(fpr,tpr,linewidth=1,label='ROC fold %d (area = %0.2f)' % (i+1, roc_auc))
#
plot random guessing line
plt.plot([0,1],[0,1],linestyle='--',color=(0.6,0.6,0.6),label='random guessing')
mean_tpr /= len(cv)
mean_tpr[-1] = 1.0



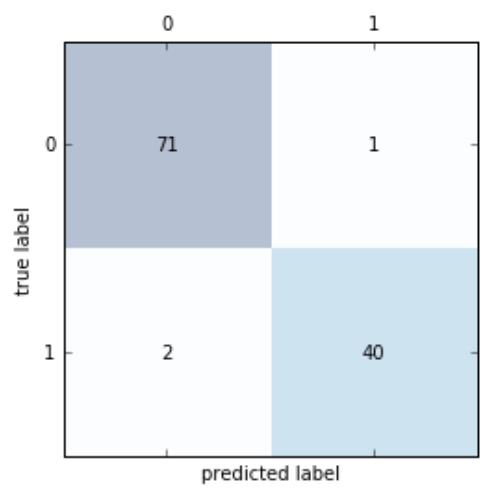
mean_auc = auc(mean_fpr, mean_tpr)
plt.plot(mean_fpr, mean_tpr, 'k--', label='mean ROC (area = %0.2f)' % mean_auc, lw=2)
#
plot perfect performance line
plt.plot([0, 0, 1], [0, 1, 1], lw=2, linestyle=':', color='black', label='perfect
performance')
#
设置 x,y坐标范围
plt.xlim([-0.05,1.05])
plt.ylim([-0.05,1.05])
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.title('Receiver Operator Charateristic')
plt.legend(loc='lower right')
plt.show()
1
6.7.3 Regression Metrics
1
6.8 聚类模型
1
. K-Means
from sklearn.cluster import KMeans
k_means = KMeans(n_clusters=3, random_state=0)
model.fit(X)
predicted = model.predict(x_test)

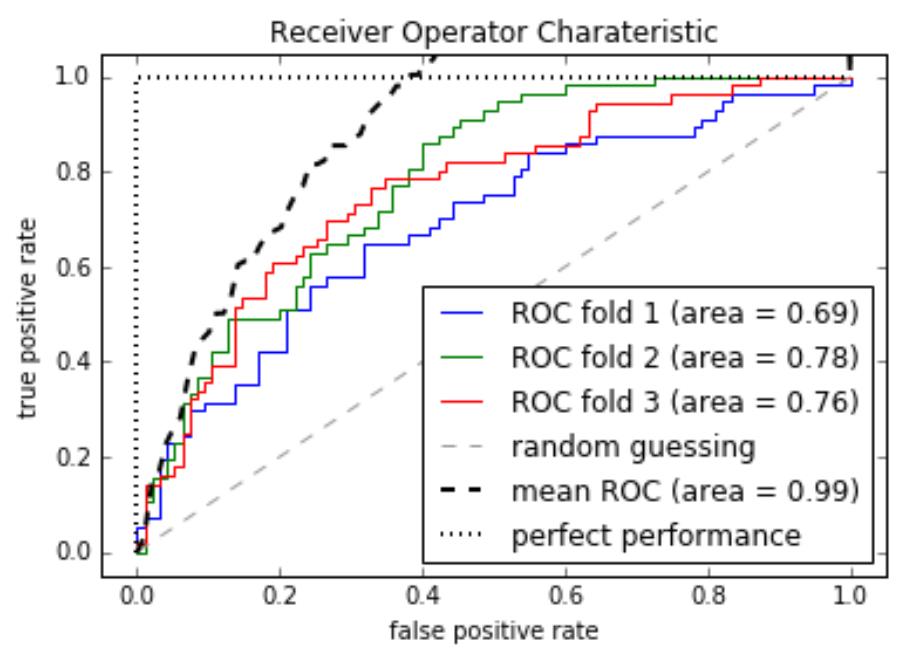
第十七章 Python 进行数据清洗
来源:http://www.ppvke.com/Blog/archives/38206
1
7.1 数据异常类型
1
. 数据错误
错误类型
脏数据或错误数据
数据不正确
数据不一致
数据重复
---- 比如 Age=-2003
---- 比如 ‘0’代表真实的 0,还是缺失值
---- 比如收入单位是万元,利润单位是元
2
. 缺失值
处理原则:
缺失值少于 20%
连续变量使用均值或中位数填补
分类变量不需要填补,单算一类即可,或者用众数填补
缺失值在 20%-80%
填补方法同上
另外每个有缺失值的变量生成一个指示哑变量,参与后续的建模
缺失值在大于 80%
每个有缺失值的变量生成一个指示哑变量,参与后续的建模,原始变量不使用。
•
•
•
•
•
3
. 离群值
1
)单变量离群值处理
绘图
在图中找出离群的异常值,根据情况对其进行删除或者对数据进行变换从而在数值上使其不离群或者
不明显
学生化(标准化)
•用变量除以他们的标准误就可得到学生化数值
建议的临界值:
–
–
2
|SR| >2 ,用于观察值较少的数据集
|SR| >3,用于观察值较多的数据集
)多变量离群值
绘图
在图中找出明显的离群值
聚类法确定离群值

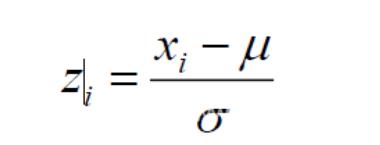
聚类效果评判指标:(群内方差(距离)最小化,群间方差(距离)最大化;这里方差可以理解为一
种距离(欧式距离的平方—欧式距离))
1
7.2 Python 数据清洗案例解读
1
.数据集
Age:年龄
Areas:来自哪里,A/B/C/D 四个地区
ID:患者的唯一识别编号
Package:每天抽几包烟,缺失的为-9,代表不抽烟
SHabit:睡眠习惯,1-早睡早起;2-晚睡早起;3-早睡晚起;
4
-晚睡晚起
2
.删除重复
Data.duplicated() 标记出哪些是重复的
Data.drop_duplicates() 直接将重复删除,默认保
留第一条,传入 take_last=True 则保留最后一个
3
.异常值检测
Data.describe()
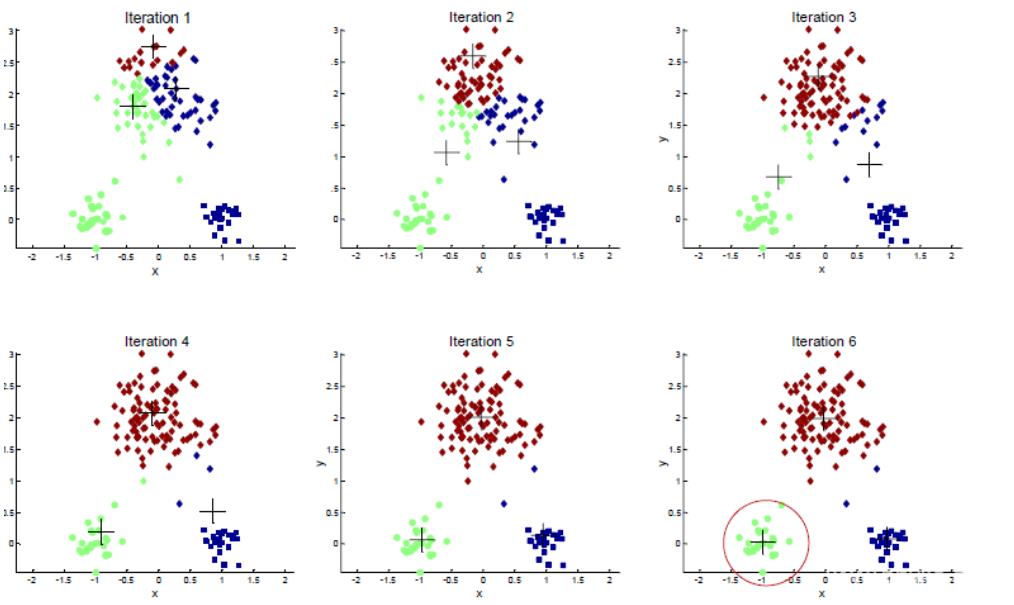

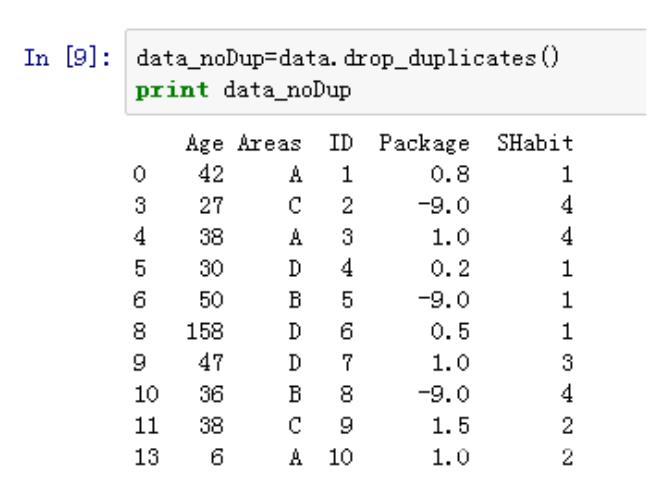
Data[条件]
按条件查看数据
Eg. Print data[data[‘age’]>100]’
Print data[data[‘age’]<10]
4
.替换
两种替换方式:字典或替换关系组成的数组
(
(
1)data.replace([A, B], [A_R, B_R])
2)data.replace({A:A_R, B:B_R})
5
.数据映射
以 Areas 为例,A/B/C 为城市,D 为农村,所以根据 areas 创建新变量 CType:U-城市,R-农村
方法:1)写一个映射字典
areas_to_ctype={‘A’:’U’,’B’:’U’,’C’:’U’,’D’:’R’}
2
)使用 map(映射字典)创建新变量 CType
data_noDup_rep[‘CType’]=data[‘Areas’].map(areas_to_ctype)
6
.数值变量类型化
需求:将年龄 Age 分成四组:
0:30 岁以下,也就是 0 到 30 岁




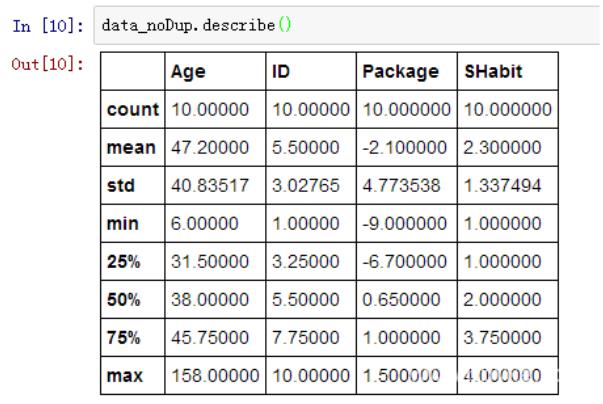
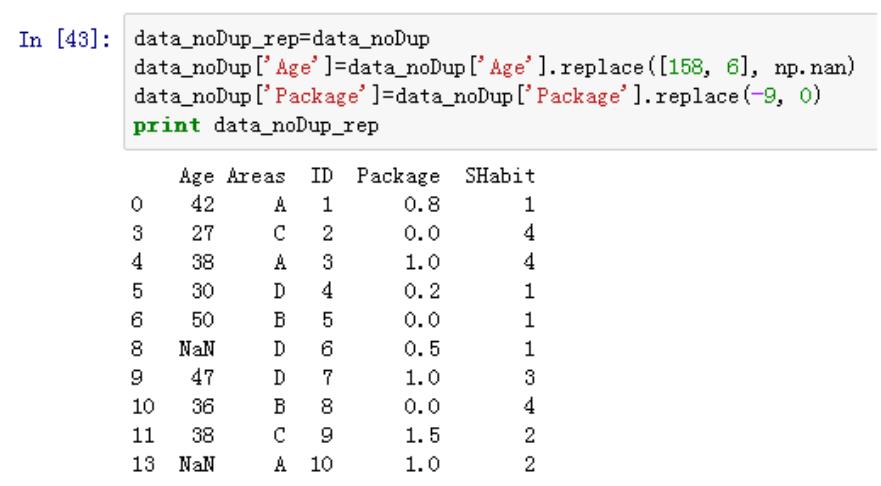
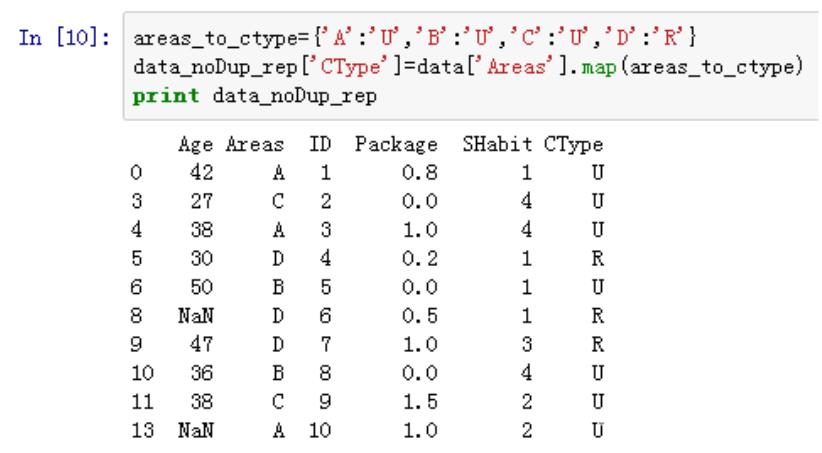
1:30-40 岁
2:40-50 岁
3:50 岁以上,不妨设为 50-100 岁
方法:使用 cut 函数切割
Step1:设置分割点:0,30,40,50,100 : cutPoint=[0,30, 40, 50,80]】
Step2:用 cut(data, cutPoint) 的格式对 age 按照 cutPoint 进行划分
pd.cut(data_noDup_rep[‘Age’],cutPoint)
Step3:将划分后的变量赋给新变量 AgeGroup
data_noDup_rep[‘ageGroup’] =pd.cut(data_noDup_rep[‘Age’],cutPoint)
Step4:设定一个组标签,指定 labels=groupLabel 即可
按照分位数分 n 组: qcut(data, n)
7
.创建哑变量
使用哑变量的两种情况
变量值是无序并列的
多选题
Eg. SHabit(睡眠习惯,1-早睡早起;2-晚睡早起;3-早睡晚起;4-晚睡晚起)
变成:
SHabit_1:是否早睡早起?(0-否,1-是)
SHabit_2:是否晚睡早起?(0-否,1-是)
SHabit_3:是否早睡晚起?(0-否,1-是)
SHabit_4:是否晚睡晚起?(0-否,1-是)
get.dummies( data[‘SHabit’] , prefix=’SHabit’)
数据合并 merge
data_noDup_rep_dum =pd.merge(data_noDup_rep, pd.get_dummies(data_noDup_rep[‘SHabit’],
prefix=’SHabit’ ), right_index=True, left_index=True)
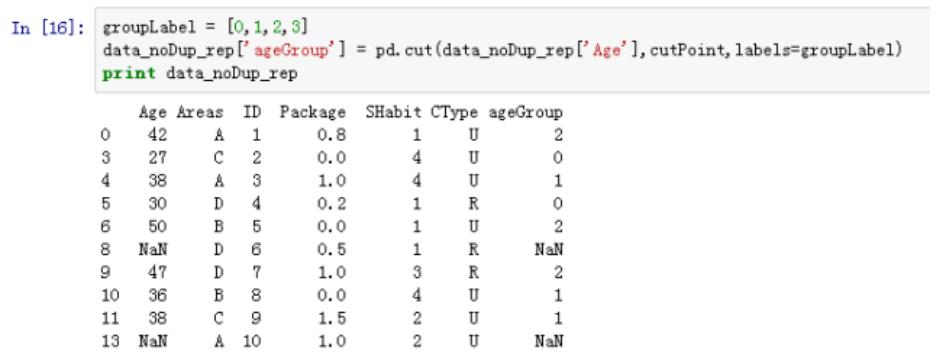
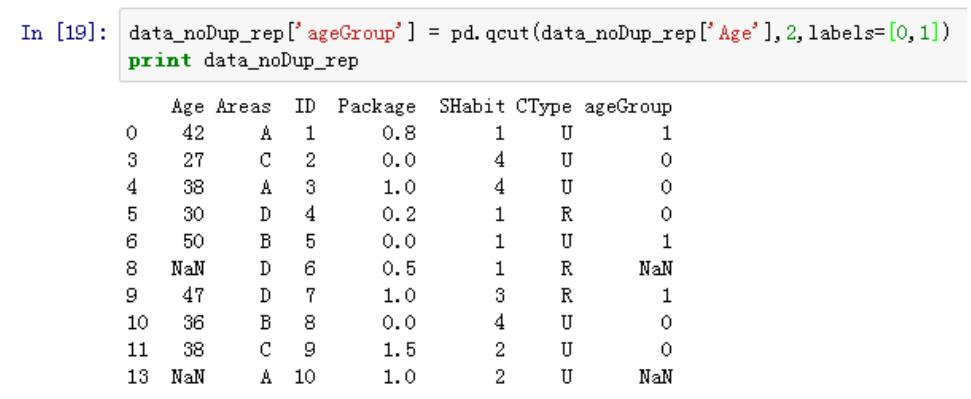
1
7.3 修正数据类型
通过 15.1 获取的数据类型为字符串类型,需要根据实际情况修正
from datetime import datetime as dt
#
#
Takes a date as a string, and returns a Python datetime object.
If there is no date given, returns None
def parse_date(date):
if date == '':
return None
else:
return dt.strptime(date, '%Y-%m-%d')
Takes a string which is either an empty string or represents an integer,
and returns an int or None.
#
#
def parse_maybe_int(i):
if i == '':
return None
else:
return int(i)
#
Clean up the data types in the enrollments table
for enrollment in enrollments:
enrollment['cancel_date'] = parse_date(enrollment['cancel_date'])
enrollment['days_to_cancel'] = parse_maybe_int(enrollment['days_to_cancel'])
enrollment['is_canceled'] = enrollment['is_canceled'] == 'True'
enrollment['is_udacity'] = enrollment['is_udacity'] == 'True'
enrollment['join_date'] = parse_date(enrollment['join_date'])
enrollments[0]
1
7.4 One-Hot Encoding---一位有效编码
One-Hot 编码,又称为一位有效编码,主要是采用 位状态寄存器来对 个状态进行编码,每
个状态都由他独立的寄存器位,并且在任意时候只有一位有效。
在实际的机器学习的应用任务中,特征有时候并不总是连续值,有可能是一些分类值,如性别
可分为“male”和“female”。在机器学习任务中,对于这样的特征,通常我们需要对其进行特征数字
化,如下面的例子:
有如下三个特征属性:
性别:["male","female"]
地区:["Europe","US","Asia"]
浏览器:["Firefox","Chrome","Safari","Internet Explorer"]
对于上述的问题,性别的属性是二维的,同理,地区是三维的,浏览器则是思维的,这样,我们
可以采用 One-Hot 编码的方式对上述的样本“["male","US","Internet Explorer"]”编码,“male”则对应
着[1,0],同理“US”对应着[0,1,0],“Internet Explorer”对应着[0,0,0,1]。则完整的特征数字化的结果
为:[1,0,0,1,0,0,0,0,1]。这样导致的一个结果就是数据会变得非常的稀疏。


from sklearn import preprocessing
enc = preprocessing.OneHotEncoder()
enc.fit([[0,0,3],[1,1,0],[0,2,1],[1,0,2]])
array = enc.transform([[0,1,3]]).toarray()
print array
=
====output=======
[
[ 1. 0. 0. 1. 0. 0. 0. 0. 1.]]
1
7.5 数据特征提取与处理
1
.分类变量特征提取
分类变量通常用读热编码(One-of-K or One-Hot Encoding),通过二进制数来表示每个解释变量的特
征。Scikit-learn 中有 DictVectorizer 类可以用来表示分类特征:
from sklearn.feature_extraction import DictVectorizer
onehot_encoder=DictVectorizer()
instances=[{'city':'New York'},{'city':'San Francisco'},{'city':'Chapel Hill'}]
print(onehot_encoder.fit_transform(instances).toarray())
#
#
#
[[ 0. 1. 0.]
[ 0. 0. 1.]
[ 1. 0. 0.]]
2
.文字特征提取
文字必须转换成可以量化的特征向量,词库模型是文字模型化的最常用方法
from sklearn.feature_extraction.text import CountVectorizer
corpus=['UNC played Duke in basketball','Duke lost the basketball game','I ate a sandwich']
vectorizer=CountVectorizer ()
print(vectorizer.fit_transform(corpus).todense())
print(vectorizer. vocabulary_)
#
#
#
#
[[0 1 1 0 1 0 1 0 0 1]
[0 1 1 1 0 1 0 0 1 0]
[1 0 0 0 0 0 0 1 0 0]]
{'game': 3, 'played': 6, 'the': 8, 'ate': 0, 'lost': 5, 'basketball': 1, 'sandwich': 7, # 'in': 4, 'duke': 2, 'unc': 9}
特征向量降维---停用词过滤,如 a,an,the,助动词 do,be,will 介词 on,around,beneath
CountVectorizer 类可以通过设置 stop_words 参数过滤停用词,默认为英语常用的停用词



第六部分 数据挖掘案例分析
案例一 A Journey through Titanic
https://www.kaggle.com/c/titanic
https://www.kaggle.com/c/titanic/details/getting-started-with-python-ii
.导入数据集
1
import pandas as pd
from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
#
导入数据集
data=pd.read_csv("C:\\Users\\Serna\\Desktop\\Titanic\\train.csv",header=0)
data_test=pd.read_csv("C:\\Users\\Serna\\Desktop\\Titanic\\test.csv",header=0)
2
.查看数据集整体信息
#
查看变量缺失值信息
data.info()
data_test.info()
#
priview data
data_test.head()
data.head()
#
统计信息描述
#查看变量类型
data.dtypes
data.describe()
data_test.describe()
data_test.dtypes



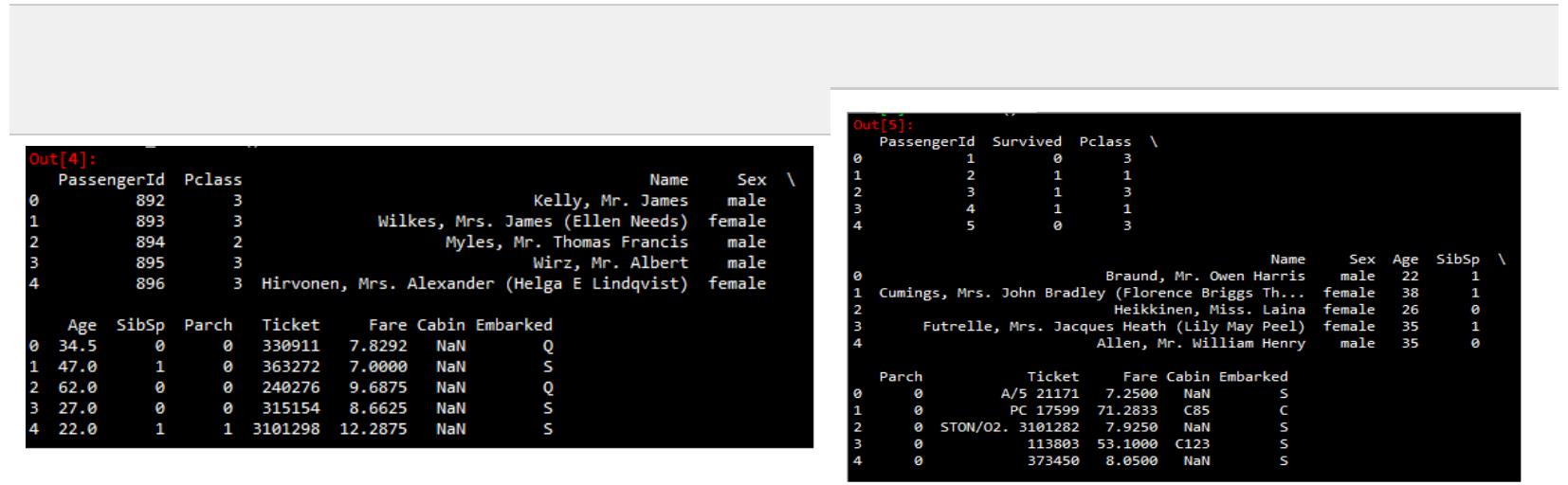

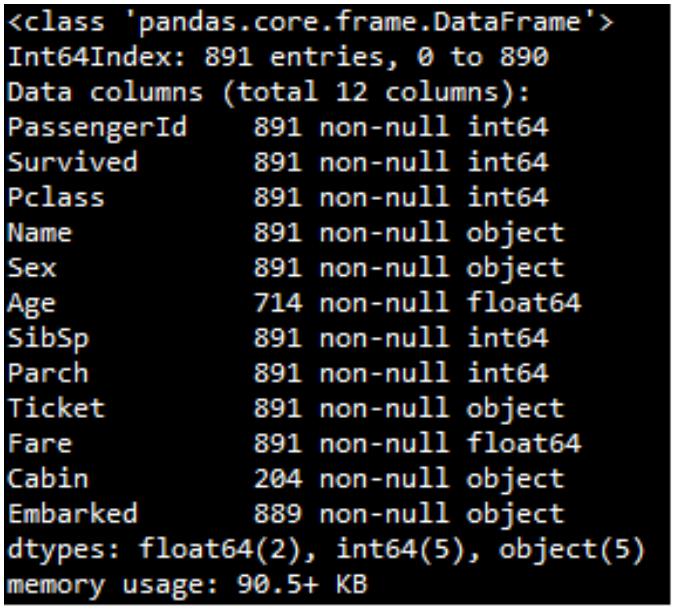
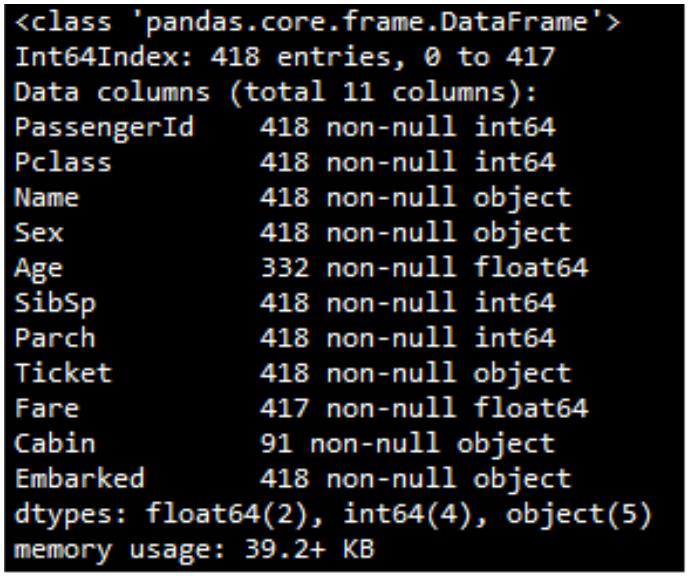
3
.处理各字段信息
1)drop unnecessary columns
(
data=data.drop(['PassengerId','Name','Ticket'],axis=1)
data_test=data_test.drop(['Name','Ticket'],axis=1)
(
2)处理 Sex 字段
data['Gender']=data['Sex'].map({'female':0,'male':1}).astype(int)
data_test['Gender']=data_test['Sex'].map({'female':0,'male':1}).astype(int)
data['Gender'].head()
data_test['Gender'].head()
(
3)处理 Age 字段
#
统计 Age 的平均值,中位数
data['Age'].mean()
data['Age'].median()
#
筛选数据
data[data['Age']>60]
data[data['Age']>60][['Sex','Pclass','Age','Survived']]
data[data['Age'].isnull()][['Sex','Pclass','Age']]
#
绘制直方图
data['Age'].dropna().hist(bins=16,range=(0,80),alpha=.5)
plt.show()
#
=====================处理 Age 字段的缺失值等信息
=================================
=
#
#
Use the age that was typical in each class
根据性别和客舱级别求年龄的平均值
median_ages=np.zeros((2,3))
median_ages_test=np.zeros((2,3))
median_ages
median_ages_test
for i in range(0,2):
for j in range(0,3):
median_ages[i,j]=data[(data['Gender']==i)


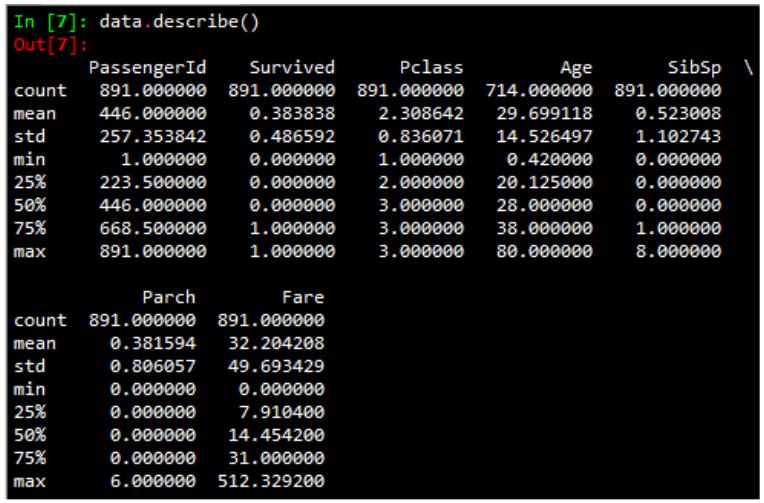
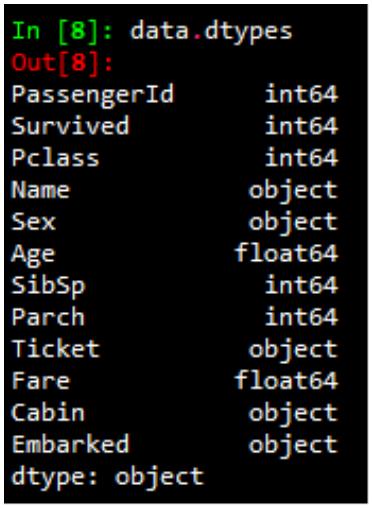
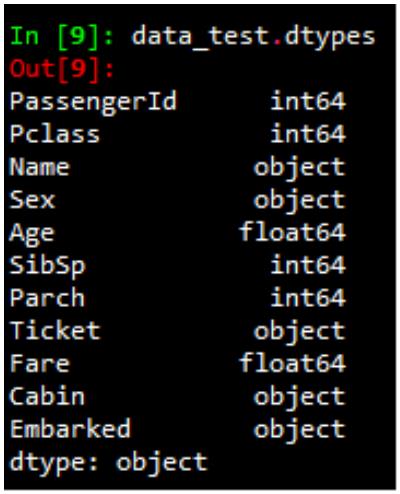
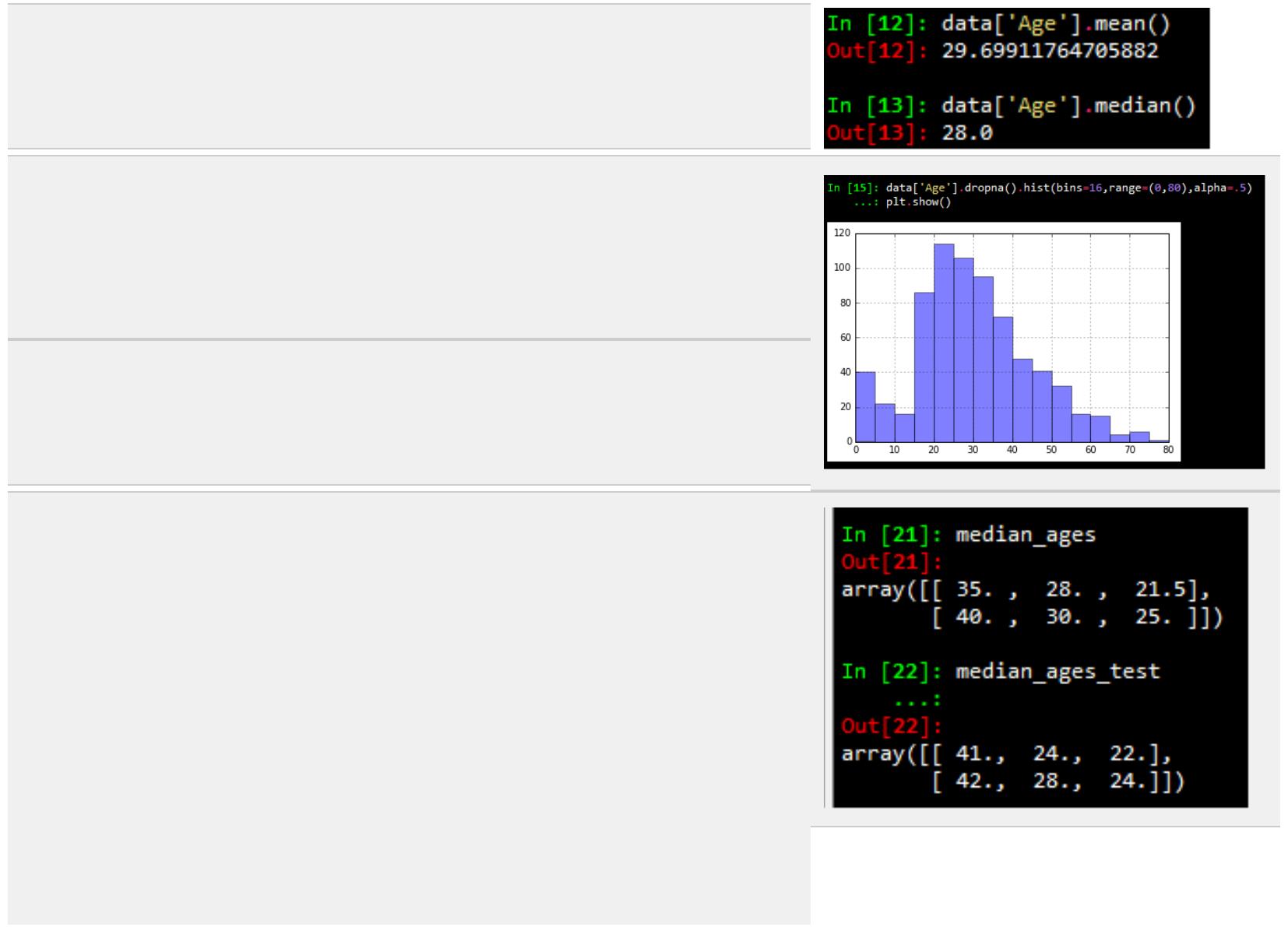
&
&
(data['Pclass']==j+1)]['Age'].dropna().median()
median_ages_test[i,j]=data_test[(data_test['Gender']==i)
(data_test['Pclass']==j+1)]['Age'].dropna().median()
median_ages
median_ages_test
data['AgeFill']=data['Age']
data_test['AgeFill']=data_test['Age']
data.head()
data[data['Age'].isnull()][['Gender','Pclass','Age','AgeFill']].head(10)
#
填充缺失值
for i in range(0,2):
for j in range(0,3):
data.loc[(data.Age.isnull())&(data.Gender==i)&(data.Pclass==j+1),'AgeFill']=median_ages[i,j]
data_test.loc[(data_test.Age.isnull())&(data_test.Gender==i)&(data_test.Pclass==j+1),'AgeFill']=median_ages_test[i,j]
data[data['Age'].isnull()][['Gender','Pclass','Age','AgeFill']].head(10)
data_test[data_test['Age'].isnull()][['Gender','Pclass','Age','AgeFill']].head(10)
#
创建字段,记录 Age 中哪些是原有的,哪些是后加入的
data['AgeIsNull']=pd.isnull(data.Age).astype(int)
data_test['AgeIsNull']=pd.isnull(data_test.Age).astype(int)
data['AgeIsNull'].head()
(
4)Using sex and age for person column
#
#
As we see, children(age < ~16) on aboard seem to have a high chances for Survival.
So, we can classify passengers as males, females, and child
def get_person(passenger):
age,sex=passenger
return 'child' if age<16 else sex
data['Person']=data[['Age','Sex']].apply(get_person,axis=1)
data_test['Person']=data_test[['Age','Sex']].apply(get_person,axis=1)
#
create dummy variables for Person column, & drop Male as it has the lowest average of survived passengers
person_dummies=pd.get_dummies(data['Person'])
person_dummies.columns=['Child','Female','Male']
person_dummies.drop(['Male'],axis=1,inplace=True)
person_dummies_test=pd.get_dummies(data_test['Person'])
person_dummies_test.columns=['Child','Female','Male']
person_dummies_test.drop(['Male'],axis=1,inplace=True)
data=data.join(person_dummies)
data_test=data_test.join(person_dummies)
(
5)处理 Embarked 字段
data['Embarked'].describe() # S,C,Q
data["Embarked"].value_counts()

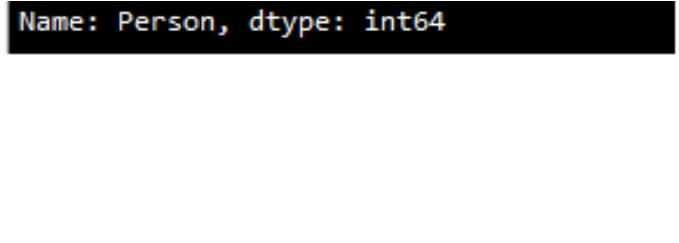
temp1=data["Embarked"].value_counts()
temp1.plot(kind='bar')
plt.show()
#创建 Embarked,Survived 透视图
temp2=data.pivot_table(values="Survived",
index=["Embarked"],aggfunc=lambda x:x.mean())
temp2.plot(kind='bar')
plt.show()
#
#
#
#
#
Either to consider Embarked column in predictions,
and remove "S" dummy variable,
and leave "C" & "Q", since they seem to have a good rate for Survival.
OR, don't create dummy variables for Embarked column, just drop it,
because logically, Embarked doesn't seem to be useful in prediction.
embark_dummies=pd.get_dummies(data['Embarked'])
embark_dummies.drop(['S'],axis=1,inplace=True)
embark_dummies_test=pd.get_dummies(data_test['Embarked'])
embark_dummies_test.drop(['S'],axis=1,inplace=True)
#
原数据集与哑变量合并
data=data.join(embark_dummies)
data_test=data_test.join(embark_dummies_test)
(
6)处理 Fare 字段
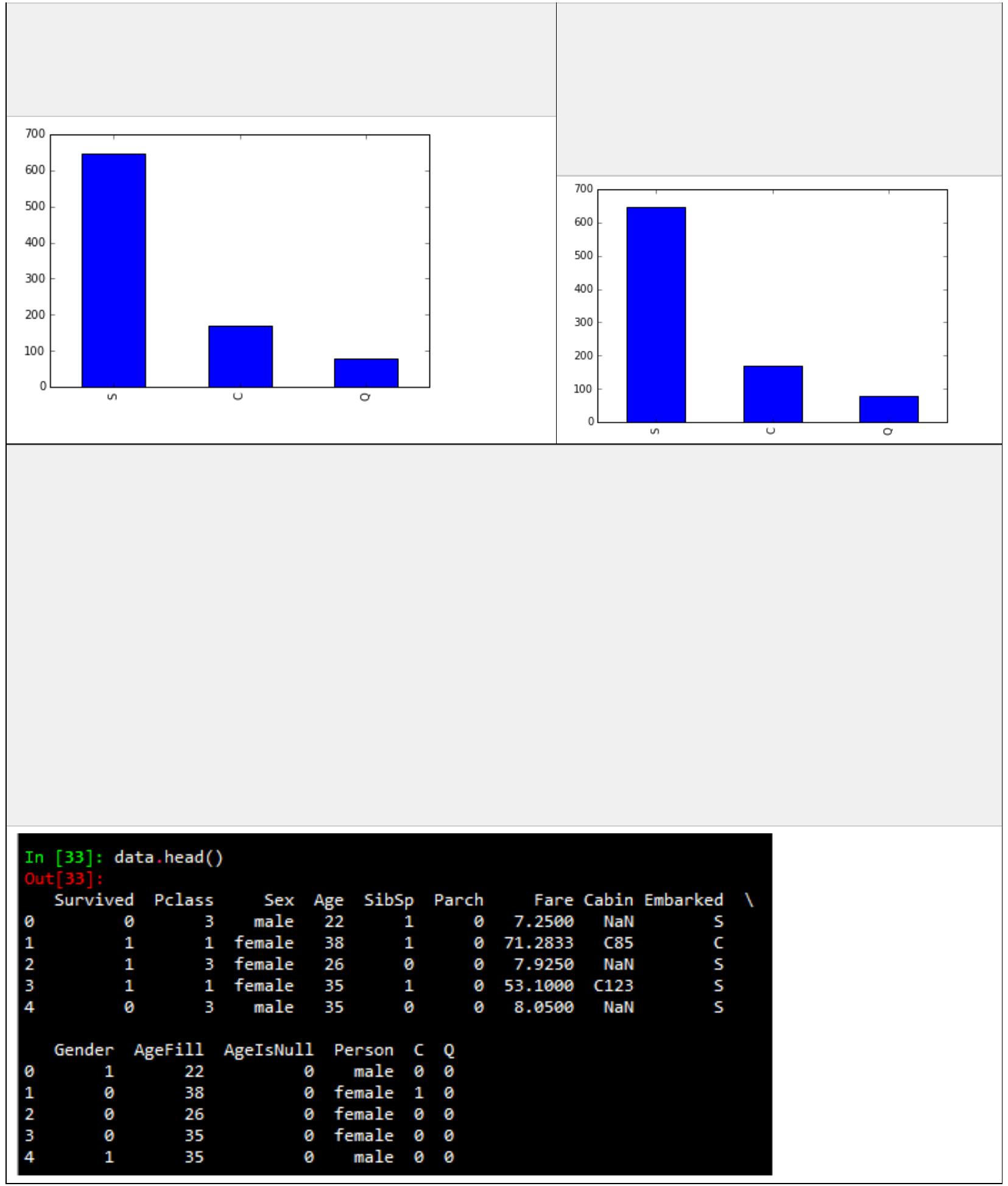
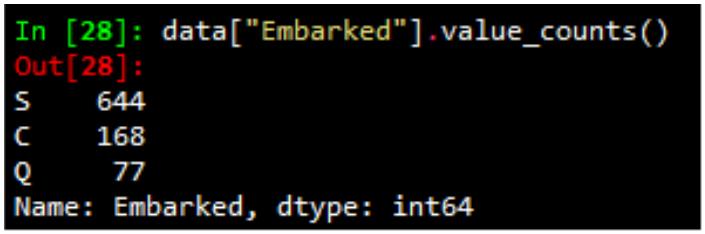
#
# only for data_test, since there is a missing "Fare" values
data_test["Fare"].fillna(data_test["Fare"].median(),inplace=True)
Fare_avg_test=data_test["Fare"].mean()
Fare_std_test=data_test["Fare"].std()
data_test["Fare"]=(data_test["Fare"]-
Fare_avg_test)/Fare_std_test
#
标准化处理
Fare_avg=data["Fare"].mean()
Fare_std=data["Fare"].std()
data["Fare"]=(data["Fare"]-Fare_avg)/Fare_std
data["Fare"].hist(bins=40)
(
7)处理 Family 字段
data['FamilySize']=data['SibSp']+data['Parch']
data_test['FamilySize']=data_test['SibSp']+data_test['Parch']
data['FamilySize'].loc[data['FamilySize']>0]=1
data['FamilySize'].loc[data['FamilySize']==0]=0
data['FamilySize'].value_counts()
(
8)处理 Pclass 字段
temp3=data.pivot_table(values="Survived",index=["Pclass"]
,
aggfunc=lambda x:x.mean())
temp3.plot(kind='bar')
plt.show()
#
create dummy variables for Pclass column, & drop 3rd class as it has the
lowest average of survived passengers
pclass_dummies=pd.get_dummies(data['Pclass'])
pclass_dummies.columns=['class_1','class_2','class_3']
pclass_dummies.drop(['class_3'],axis=1,inplace=True)
pclass_dummies_test=pd.get_dummies(data_test['Pclass'])
pclass_dummies_test.columns=['class_1','class_2','class_3']
pclass_dummies_test.drop(['class_3'],axis=1,inplace=True)
data=data.join(pclass_dummies)
data_test=data_test.join(pclass_dummies_test)
(
9)Drop unimportant columns
data.drop(['Pclass','Sex','Age','SibSp',
'
'
Parch','Cabin','Embarked','Gender','AgeFill',
AgeIsNull','Person'],axis=1,inplace=True)
data=data.dropna()
data_test.drop(['Pclass','Sex','Age','SibSp',
'
'
Parch','Cabin','Embarked','Gender','AgeFill',
AgeIsNull','Person'],axis=1,inplace=True)
data_test=data_test.dropna()




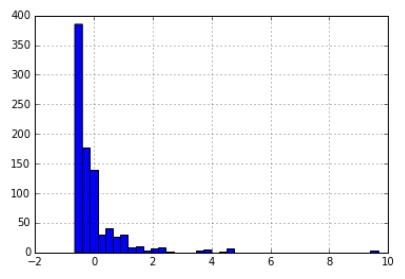
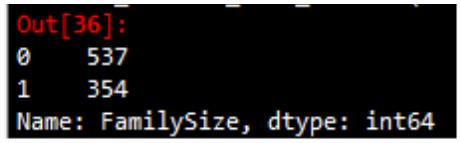
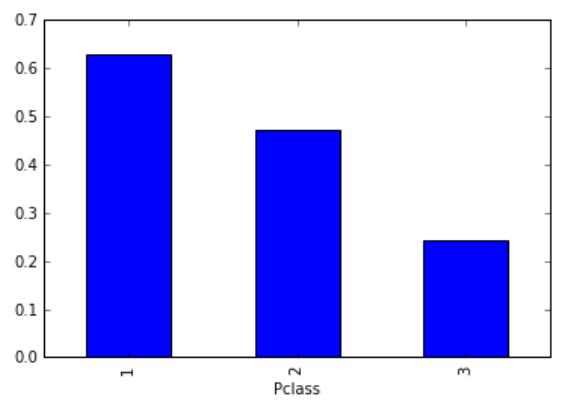
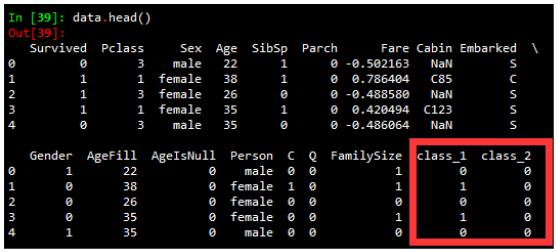
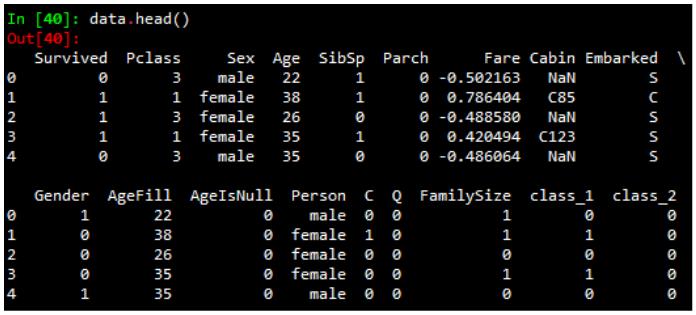
4
.定义训练集与测试集
#
==========================define train and testing sets====================
X_train=data.drop("Survived",axis=1)
Y_train=data["Survived"]
X_test=data_test.drop("PassengerId",axis=1).copy()
5
.建模分析
#
machine learning
# LinearSVC
from sklearn.ensemble import
RandomForestClassifier
svc = LinearSVC()
svc.fit(X_train, Y_train)
from sklearn.linear_model import
LogisticRegression
Y_pred = svc.predict(X_test)
svc.score(X_train, Y_train)
#Out[132]: 0.80359147025813693
#Random Forest
from sklearn.svm import SVC,LinearSVC
from sklearn.neighbors import
KNeighborsClassifier
random_forest=RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train,Y_train)
Y_pred=random_forest.predict(X_test)
random_forest.score(X_train,Y_train)
#Out[133]: 0.92143658810325479
#knn
from sklearn.naive_bayes import
GaussianNB
#
Logistic Regression
logreg=LogisticRegression()
logreg.fit(X_train,Y_train)
Y_pred=logreg.predict(X_test)
logreg.score(X_train,Y_train)
knn=KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train,Y_train)
#
#
Out[130]: 0.80022446689113358
Support Vector Machines
Y_pred=knn.predict(X_test)
knn.score(X_train,Y_train)
#Out[134]: 0.86868686868686873
# Gaussian Naive Bayes
svc = SVC()
svc.fit(X_train, Y_train)
Y_pred = svc.predict(X_test)
svc.score(X_train, Y_train)
gaussian=GaussianNB()
gaussian.fit(X_train,Y_train)
Y_pred=gaussian.predict(X_test)
gaussian.score(X_train,Y_train)
#
Out[131]: 0.81481481481481477
#
Out[137]: 0.75869809203142535
6
.correlation analysis
#
=========================correlation
analysis=====================
get Correlation Coefficient for each feature using Logistic Regression
#
coeff_df=DataFrame(data.columns.delete(0))
coeff_df.columns=['Features']
coeff_df["Coefficient Estimate"] = pd.Series(logreg.coef_[0])
#
preview
coeff_df
submission = pd.DataFrame({
"
"
PassengerId": data_test["PassengerId"],
Survived": Y_pred
}
)
submission.to_csv('titanic.csv', index=False)


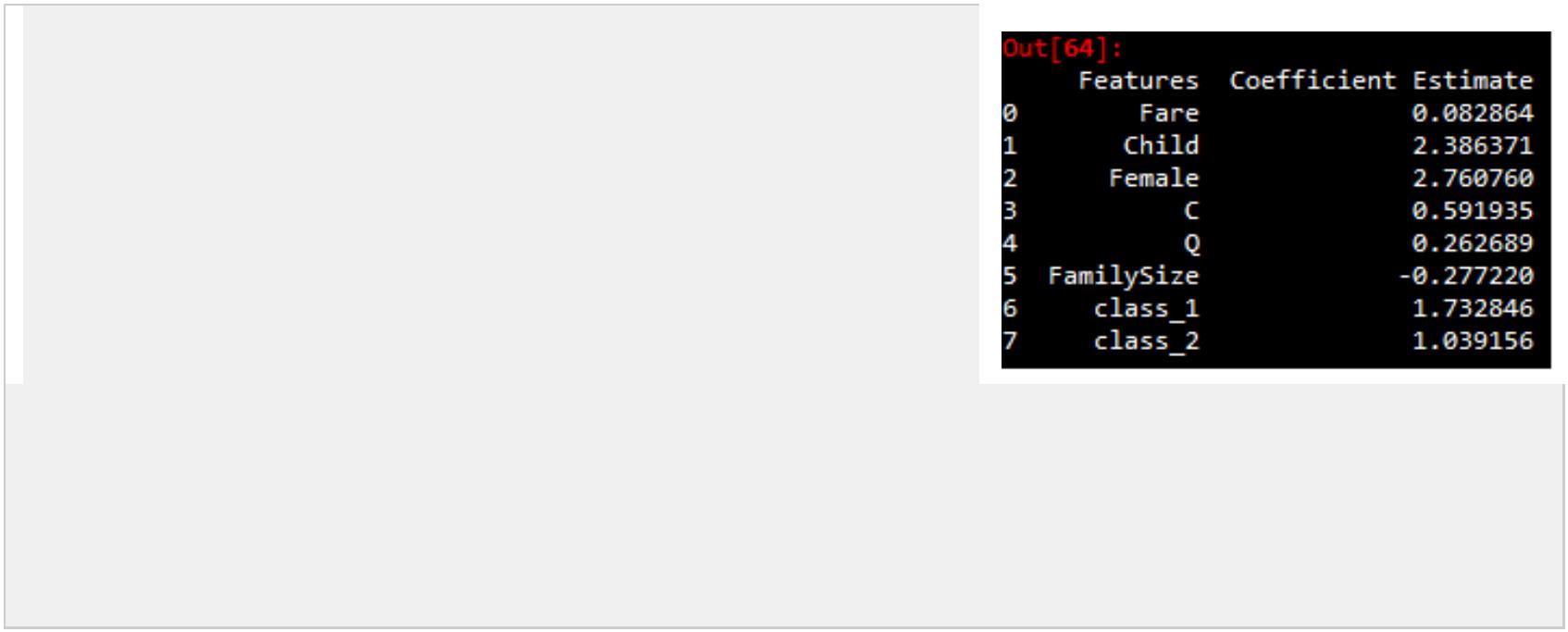
7
.模型评分---以随机森林为例
random_forest.fit(X_train,Y_train)
Y_pred=random_forest.predict(X_test) #预测结果
Y_label=pd.read_csv("C:\\Users\\Allen\\Desktop\\datasets\\titantic\\gendermodel.csv",header=0)['Survived']
#
真实结果
混淆矩阵
#
from sklearn.metrics import confusion_matrix
plt.rcParams[ 'font.sans-serif' ] = [ 'SimHei' ] #用来正常显示中文标签
plt.rcParams[ 'axes.unicode_minus' ] = False #用来正常显示负号
confusion_matrix=confusion_matrix(Y_label,Y_pred)
print(confusion_matrix)
plt.matshow(confusion_matrix)
plt.colorbar()
plt.ylabel(u'实际 Survived')
plt.ylabel(u'预测 Survived')
#
计算精确率和召回率
import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.linear_model.logistic import LogisticRegression
from sklearn.cross_validation import train_test_split, cross_val_score
precisions = cross_val_score(random_forest,X_test,Y_label, cv = 5 , scoring = 'precision' )
print ( u"精确率:" , np.mean( precisions ), precisions )
recalls=cross_val_score(lr,X_test,Y_label,cv=5,scoring='recall')
print ( u'召回率' , np.mean(recalls), recalls)
f1s = cross_val_score(lr,X_test,Y_label, cv = 5 )
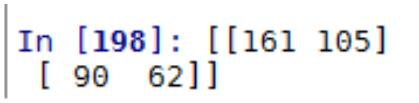
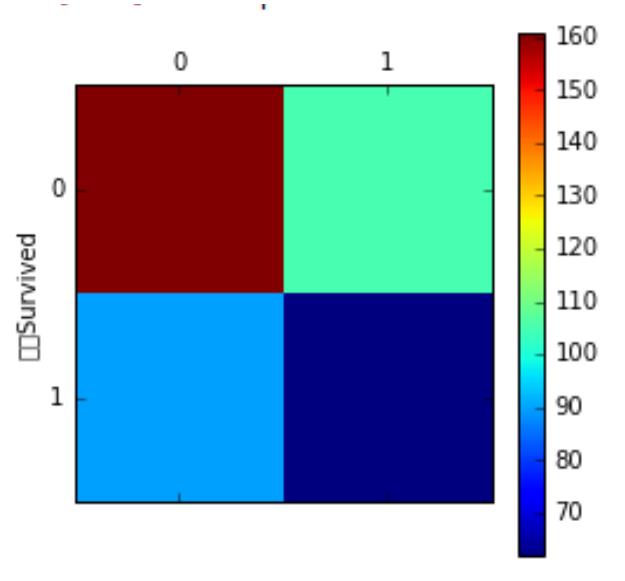
print ( '综合评价指标:' , np.mean(f1s), f1s)
#
ROC 评价指标
from sklearn.metrics import roc_curve, auc
false_positive_rate,recall,thresholds=roc_curve(Y_label,Y_pred)
roc_auc=auc(false_positive_rate,recall)
plt.title("Receiver Operating Characteristic")
plt.plot(false_positive_rate,recall,'b',label='AUC=%0.2f' % roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.0])
plt.ylabel('Recall')
plt.xlabel('Fall-out')
plt.show()
总结:
1
. 查看数据集属性为空情况
titanic_df.info()
print("---------------------------------")
test_df.info()
2
.数据集删除指定列
Data_drop=data.drop([‘列 1’,‘列 2’],axis=1,inplace=True)
.NULL 值填充
3
A[‘列名’].fillna(“填充值”) eg. titanic_df["Embarked"] = titanic_df["Embarked"].fillna("S")
test_df["Fare"].fillna(test_df["Fare"].median(),inplace=True)


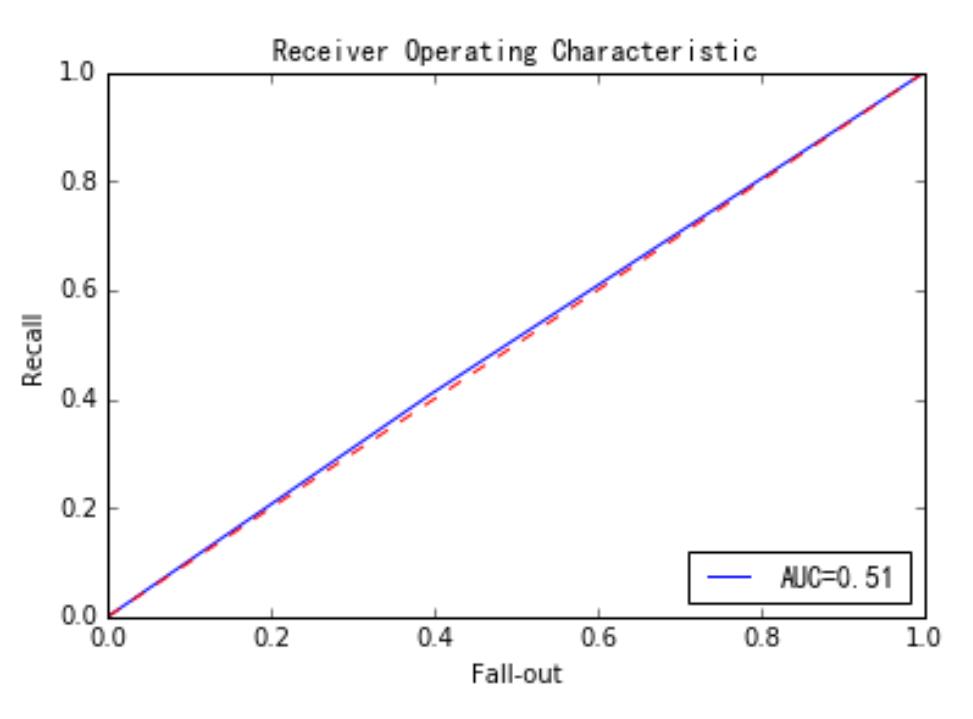
4
.生成哑变量
embark_dummies_titanic=pd.get_dummies(titanic_df['Embarked'])
.添加哑变量
titanic_df=titanic_df.join(embark_dummies_titanic)
.字段类型转换
data[‘列名’]= data[‘列名’].astype(int)
5
6
7
.根据条件筛选列
data_rep=data[‘列名’][条件]
fare_not_survived=titanic_df["Fare"][titanic_df["Survived"]==0]
.求某一列的特征值
8
均值:A[“列名”].mean()
方差:A[“列名”].std()
非空总数:A[“列名”].isnull().sum()
.“年龄”与“性别”字段处理合并处理:分为儿童,成年男,成年女
9
def get_person(passenger):
age,sex=passenger
return 'child' if age<16 else sex
titanic_df['Person']=titanic_df[['Age','Sex']].apply(get_person,axis=1)
test_df['Person']=test_df[['Age','Sex']].apply(get_person,axis=1)
1
0.根据某个字段分组求平均值
字段_new=表 A[[“字段 1”,”字段 2”]].groupby([“字段 1”],as_index=False).mean()
person_perc = titanic_df[["Person", "Survived"]].groupby(['Person'],as_index=False).mean()
案例二 Analysis for airplane-crashes-since-1908
1
.数据集预览
Date
日期
时间
Registration 登记人数
Time
cn/ln
Location 地点
Aboard
登机人数
死亡人数
着陆
Operator 驾驶员
Fatalities
Ground
Summary
Flight#
Route
Type
航班
路线
类型
描述
2
.时间日期格式转化
0
9/17/1908 1908-09-17
data_Analysis['Date']=pd.to_datetime(data['Date'])
提取字段中的年份、月份、日期:
data_Analysis['year']=data_Analysis['Date'].dt.year
data_Analysis['Date']=pd.to_datetime(data_Analysis['Date'])
data_Analysis['Year']=data_Analysis['Date'].dt.year
data_Analysis['Day']=data_Analysis['Date'].map(lambda x:x.day)
data_Analysis['Month']=data_Analysis['Date'].map(lambda x:x.month)
3
.数据分析及可视化
Seaborn API: http://www.stanford.edu/~mwaskom/software/seaborn/tutorial/categorical.html
from matplotlib import pyplot as plt
%
matplotlib inline
import seaborn as sns
(1)查看 Year-Aboard 即每年的平均每次登机人数
(
2)平均每年死亡人数
plt.figure(figsize=(45,10))
sns.barplot('Year','Fatalities',data=data_Analysis)
(
3)每年各事故死亡人数
plt.figure(figsize=(45,10))
sns.stripplot('Year','Fatalities',data=data_Analysis)
(
4)每年事故总数
plt.figure(figsize=(45,10))
sns.countplot(x='Year', data=data_Analysis, palette="Greens_d");
(
5)登机和事故总人数
#
Total Aboard and Fatalities plot - for each year
plt.figure(figsize=(100,10))
Plot1 - background - "total"(top) series
sns.barplot('Year','Aboard',data=data_Analysis,color="blue")
Plot2 - overlay - "bottom" series
#
#
bottom_plot=sns.barplot('Year','Fatalities',data=data_Analysis,color="red")
bottom_plot.set_ylabel("mean(Fatalities) and mean(Aboard)")
bottom_plot.set_xlabel("Year")
(
6)年/月/季节飞机撞击数目
crashes_per_year=Counter(data_Analysis['Year'])
years=list(crashes_per_year.keys())
crashes_year=list(crashes_per_year.values())
crashes_per_day=Counter(data_Analysis['Day'])
days=list(crashes_per_day.keys())
crashes_days=list(crashes_per_day.values())
def get_season(month):
if month >=3 and month <=5:
return 'spring'
elif month>=6 and month <=8:
return 'summer'

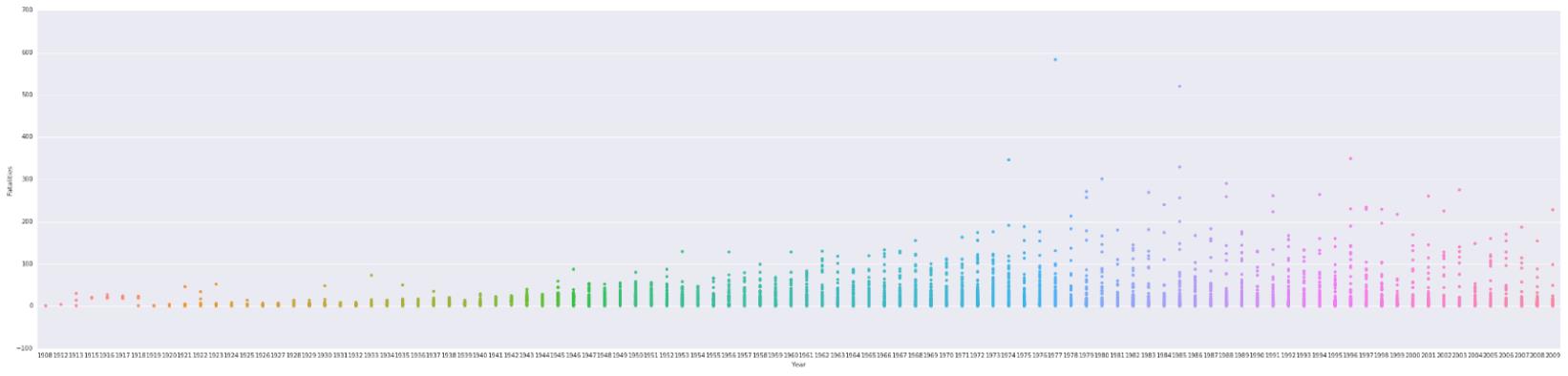
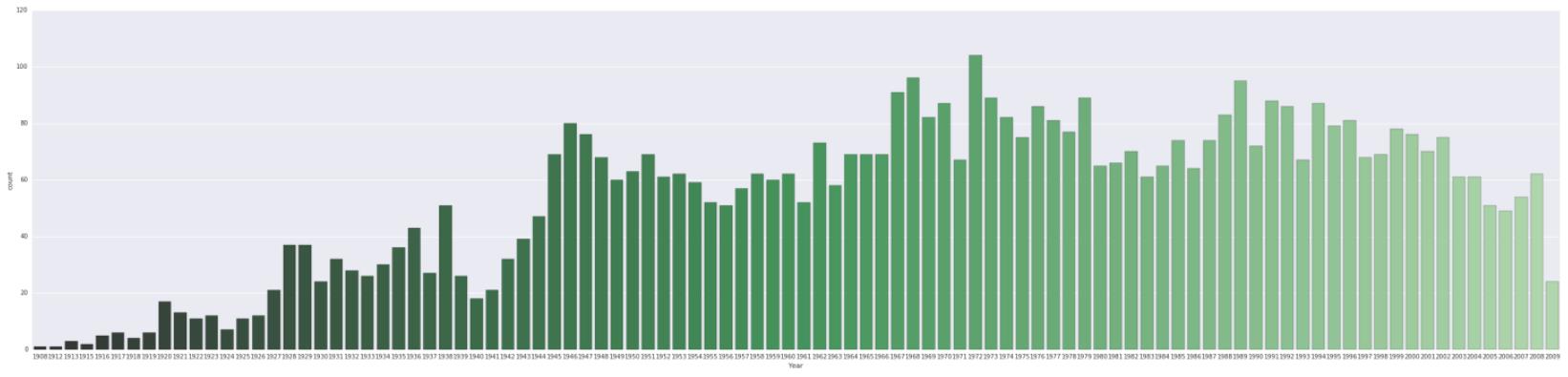
elif month>=9 and month<=11:
return 'autumn'
else:
return 'winter'
data_Analysis['Season']=data_Analysis['Month'].apply(get_season)
crashes_per_season=Counter(data_Analysis['Season'])
seasons=list(crashes_per_season.keys())
crashes_season=list(crashes_per_season.values())
sns.set(style="whitegrid")
sns.set_color_codes("pastel")
fig=plt.figure(figsize=(14,10))
sub1=fig.add_subplot(211)
sns.barplot(x=years,y=crashes_year,color='g',ax=sub1)
sub1.set(ylabel="Crashes",xlabel="Year",title="Plane crashes per year")
plt.setp(sub1.patches,linewidth=0)
plt.setp(sub1.get_xticklabels(),rotation=70,fontsize=9)
sub2=fig.add_subplot(223)
sns.barplot(x=days,y=crashes_days,color='r',ax=sub2)
sub2.set(ylabel="Crashes",xlabel="Day",title="Plane crashes per day")
sub3=fig.add_subplot(224)
sns.barplot(x=seasons,y=crashes_season,color='b',ax=sub3)
texts=sub3.set(ylabel="Crashes",xlabel="Season",title="Plane crashes per season")
plt.tight_layout(w_pad=4,h_pad=3)
(
7)Survived and dead plots
survived=[]
dead=[]
for year in years:
curr_data=data_Analysis[data_Analysis['Year']==year]
survived.append(curr_data['Aboard'].sum() - curr_data['Fatalities'].sum())
dead.append(curr_data['Fatalities'].sum())
f,axes=plt.subplots(2,1,figsize=(14,10))
sns.barplot(x=years,y=survived,color='b',ax=axes[0])
axes[0].set(ylabel="Survived",xlabel="Year",title="Survived per year")



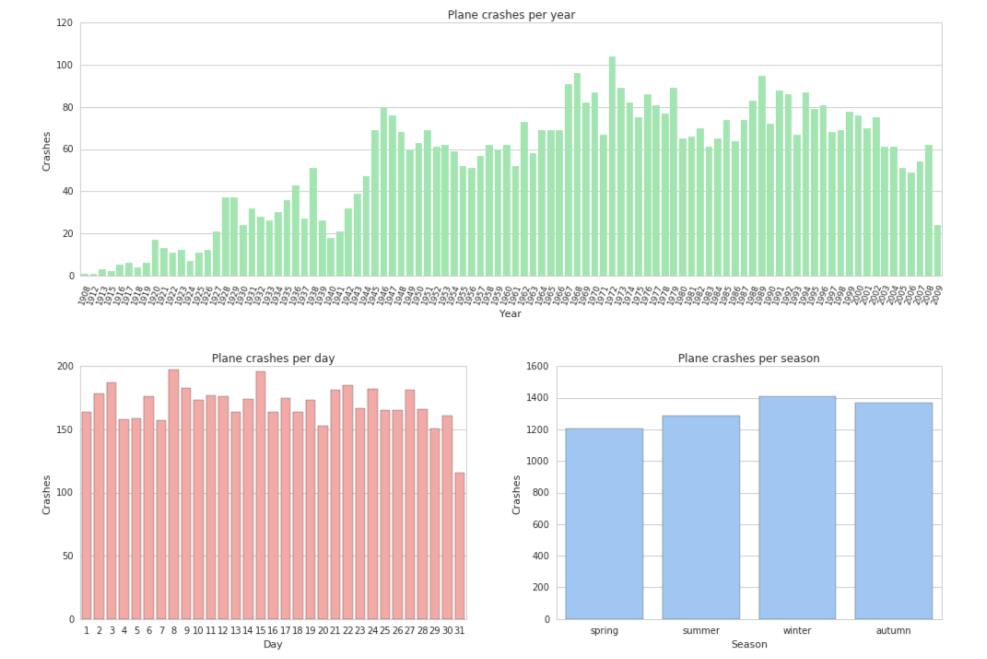
plt.setp(axes[0].patches,linewidth=0)
plt.setp(axes[0].get_xticklabels(),rotation=70,fontsize=9)
sns.barplot(x=years,y=dead,color='r',ax=axes[1])
axes[1].set(ylabel="Fatalities",xlabel="Year",title="Dead per year")
plt.setp(axes[1].patches,linewidth=0)
plt.setp(axes[1].get_xticklabels(),rotation=70,fontsize=9)
plt.tight_layout(w_pad=4,h_pad=3)
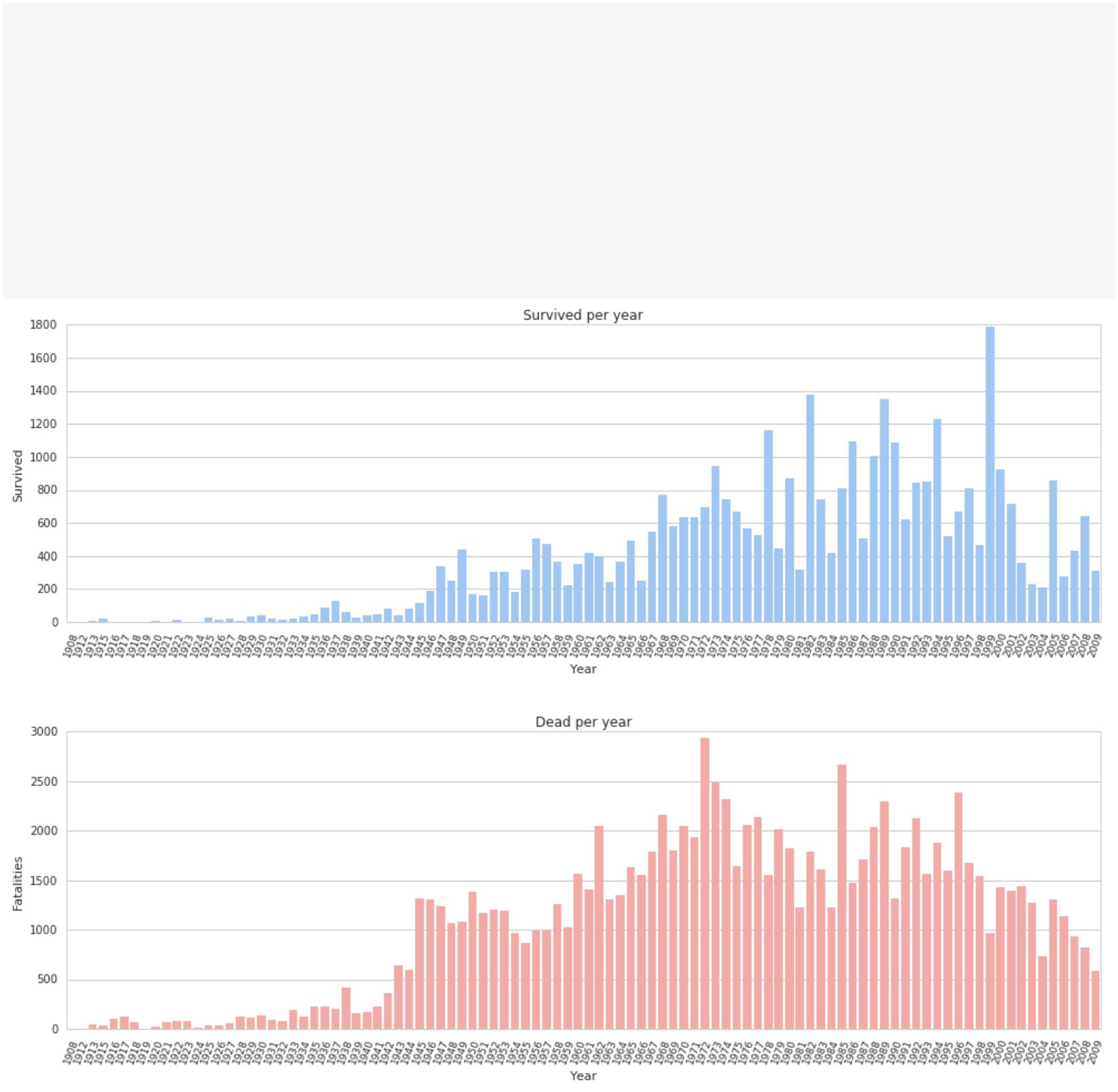
案例三 贷款预测问题
一、查看数据分布等情况
1
.查看数据
2
. 使用 describe()函数来查看数值字段的概要
通过查看数据概要可知,
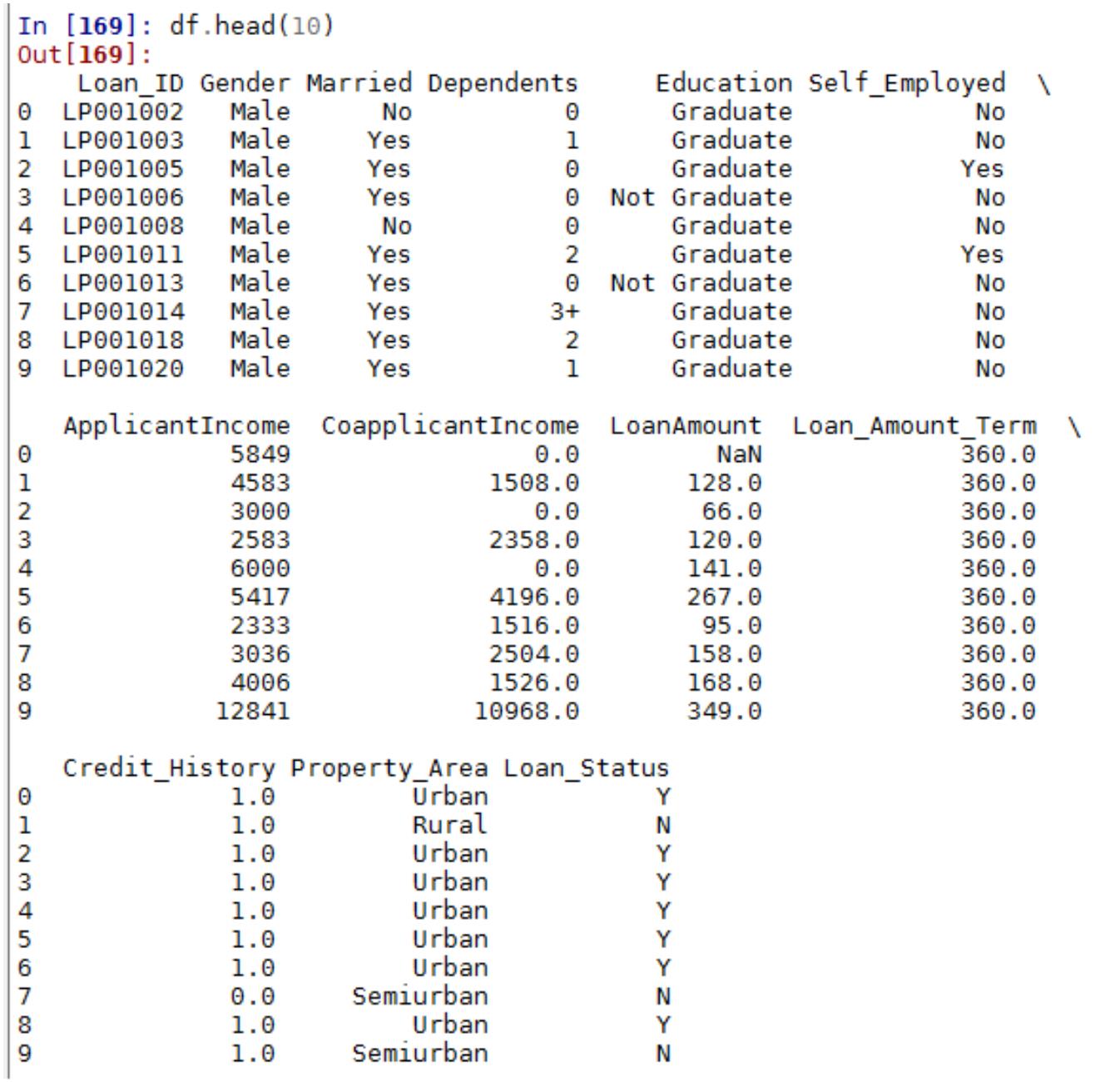
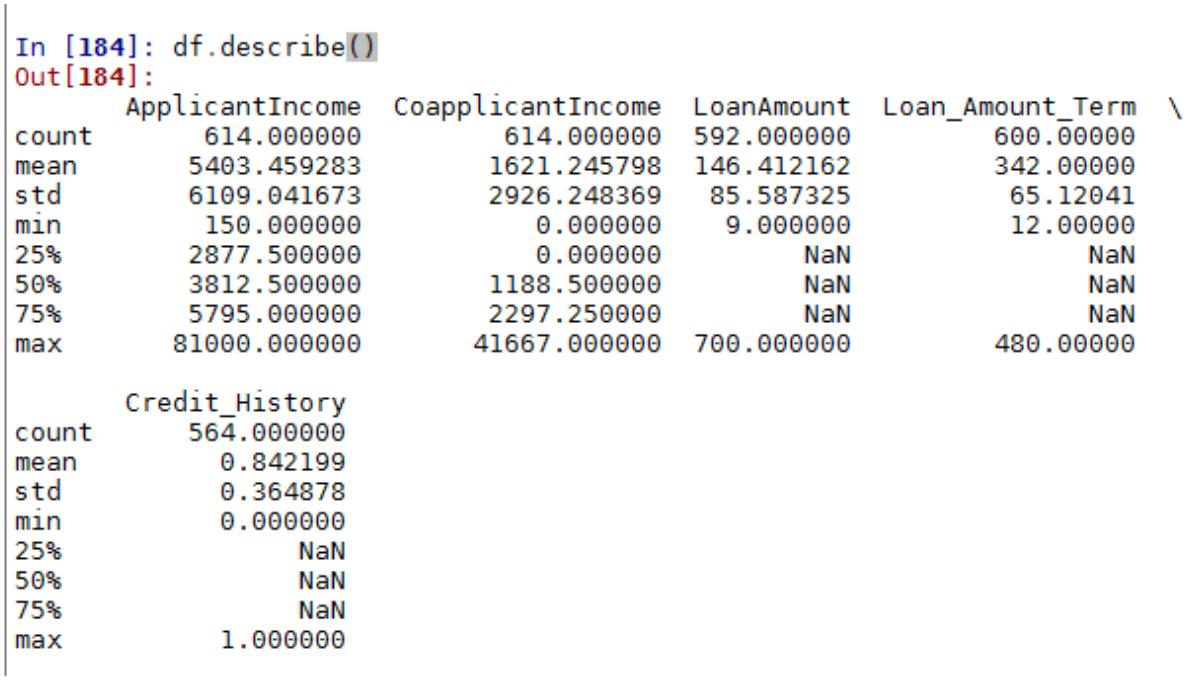
1
2
3
4
3
)LoanAmount 有 (614-592)22 个缺失值
)Loan_Amount_Term 有(614-600)14 个缺失值
)Credit_History 有(614-564)50 个缺失值
)有 84%的申请者有 Credit_History (1—有,0—没有)
.查看 Property_Area 的统计情况
4
.查看 ApplicantIncome 的箱线图
出现了大量的离群值/极值,这可归因于社会上的收入差距。我们可以根据教育水平,性别等分组再查
看箱图。

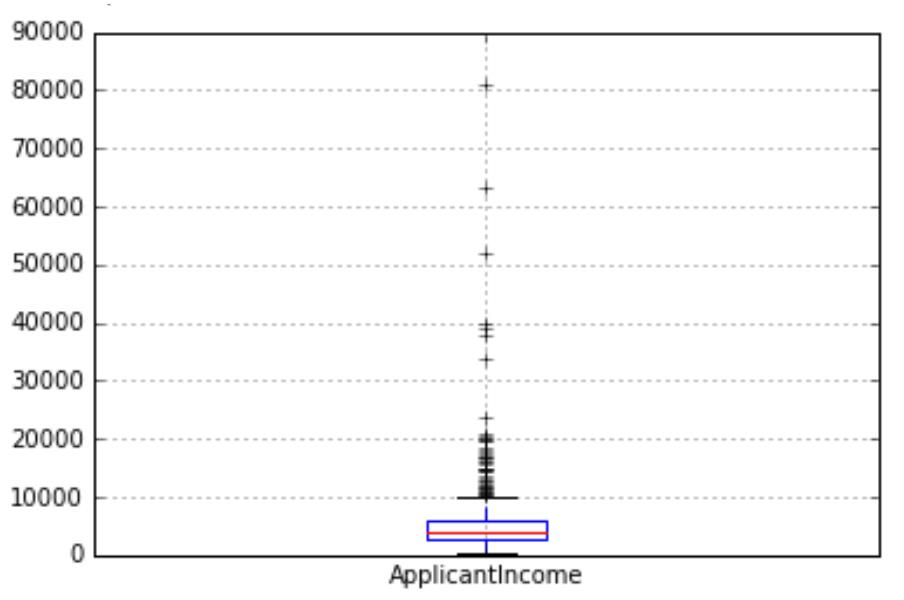
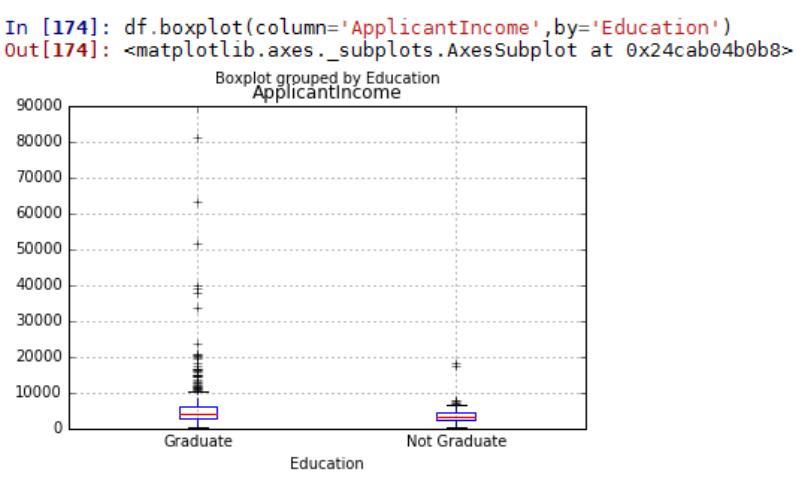
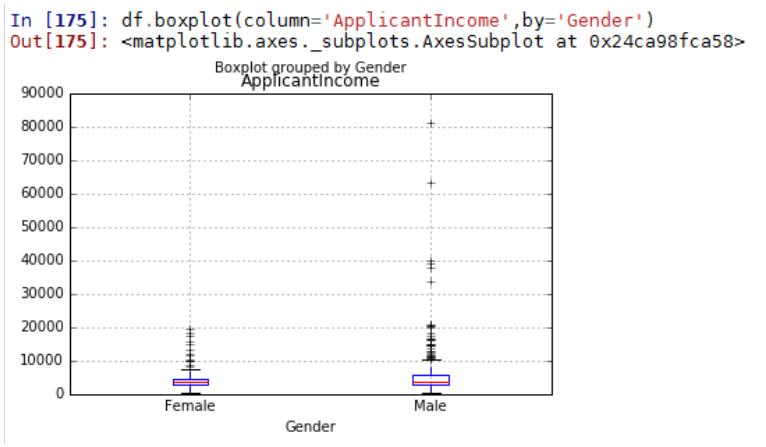
5
.ApplicantIncome 的频率分布直方图
6
.查看不同信用记录的贷款成功率
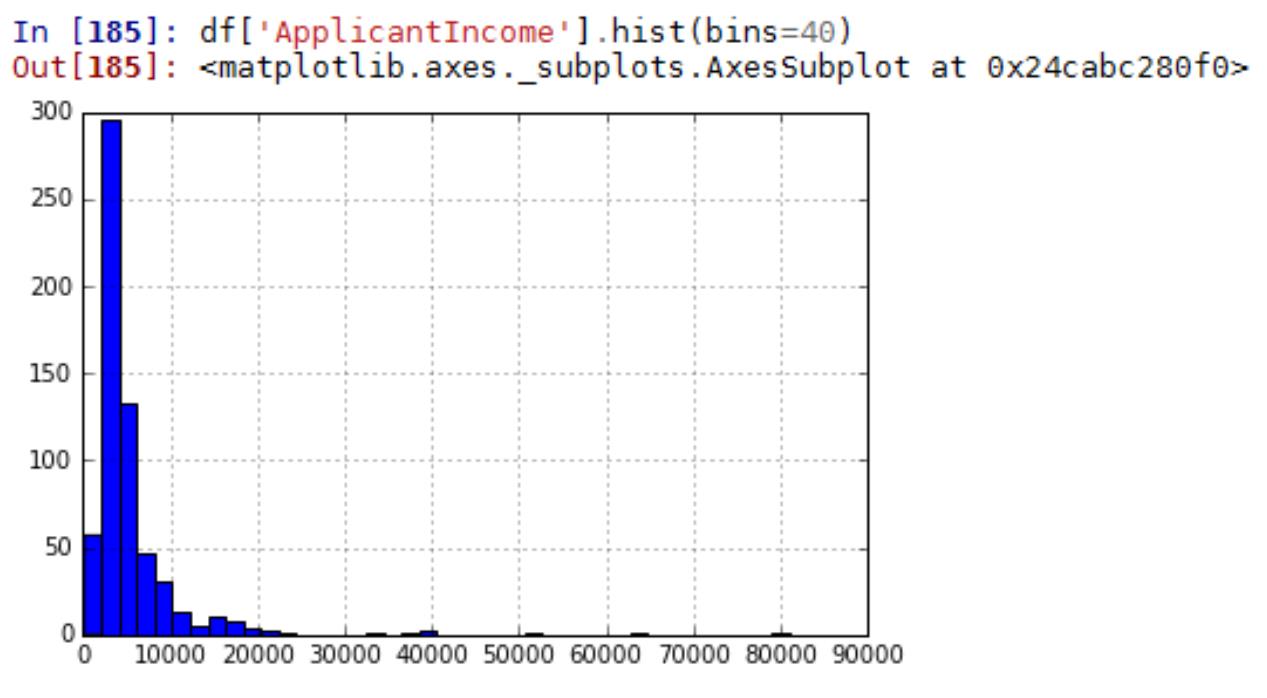


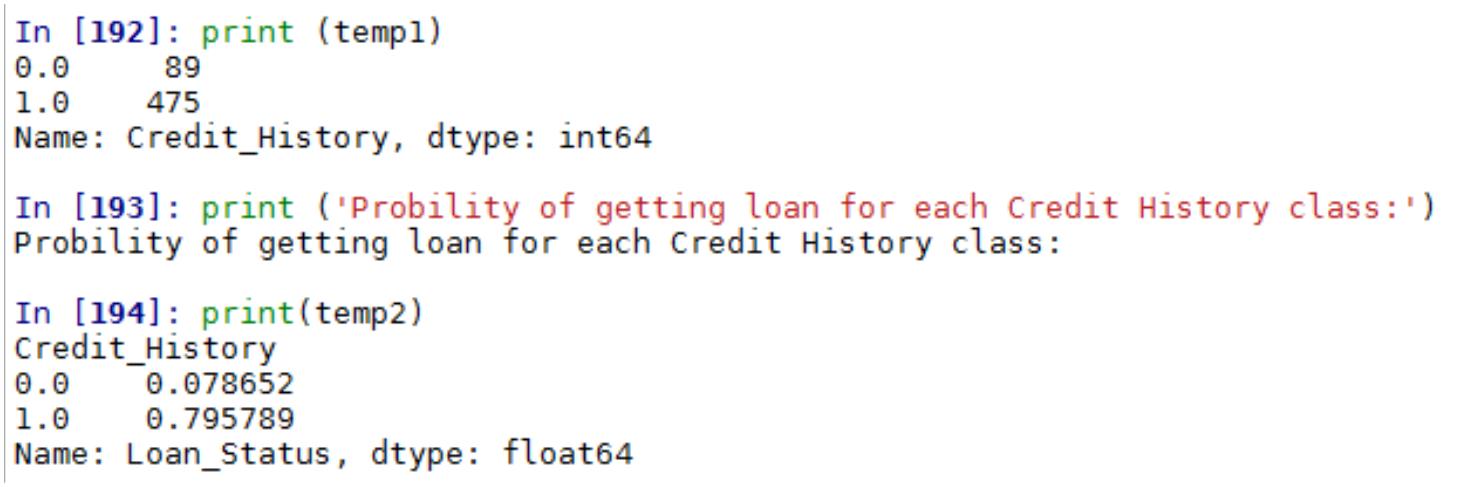
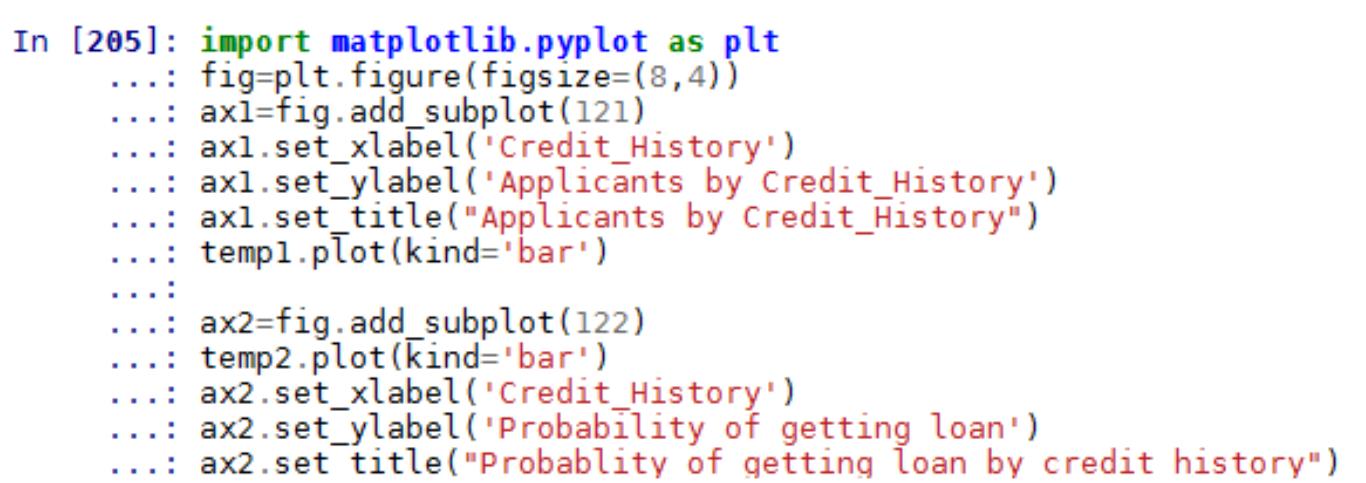
结果表明,如果申请人有一个有效的信用记录,获得贷款的机会远高于没有信用记录的人
在图中加入性别变量
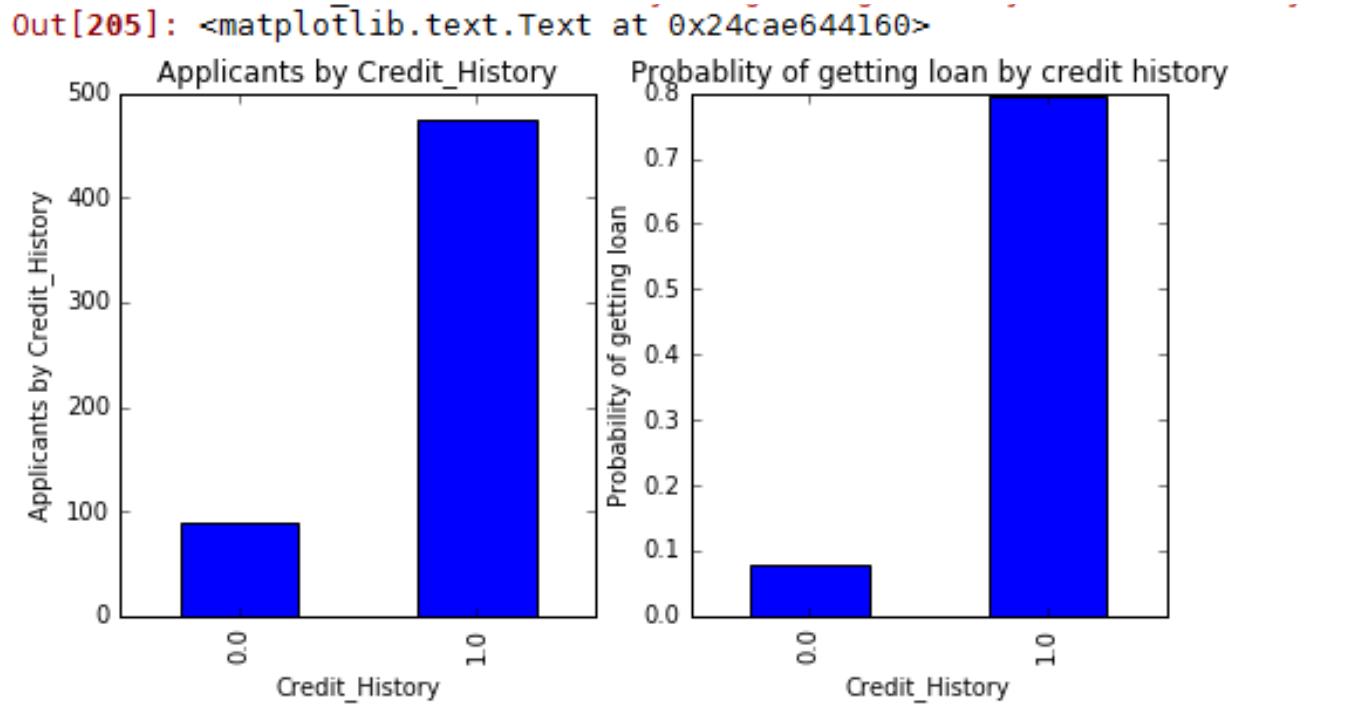
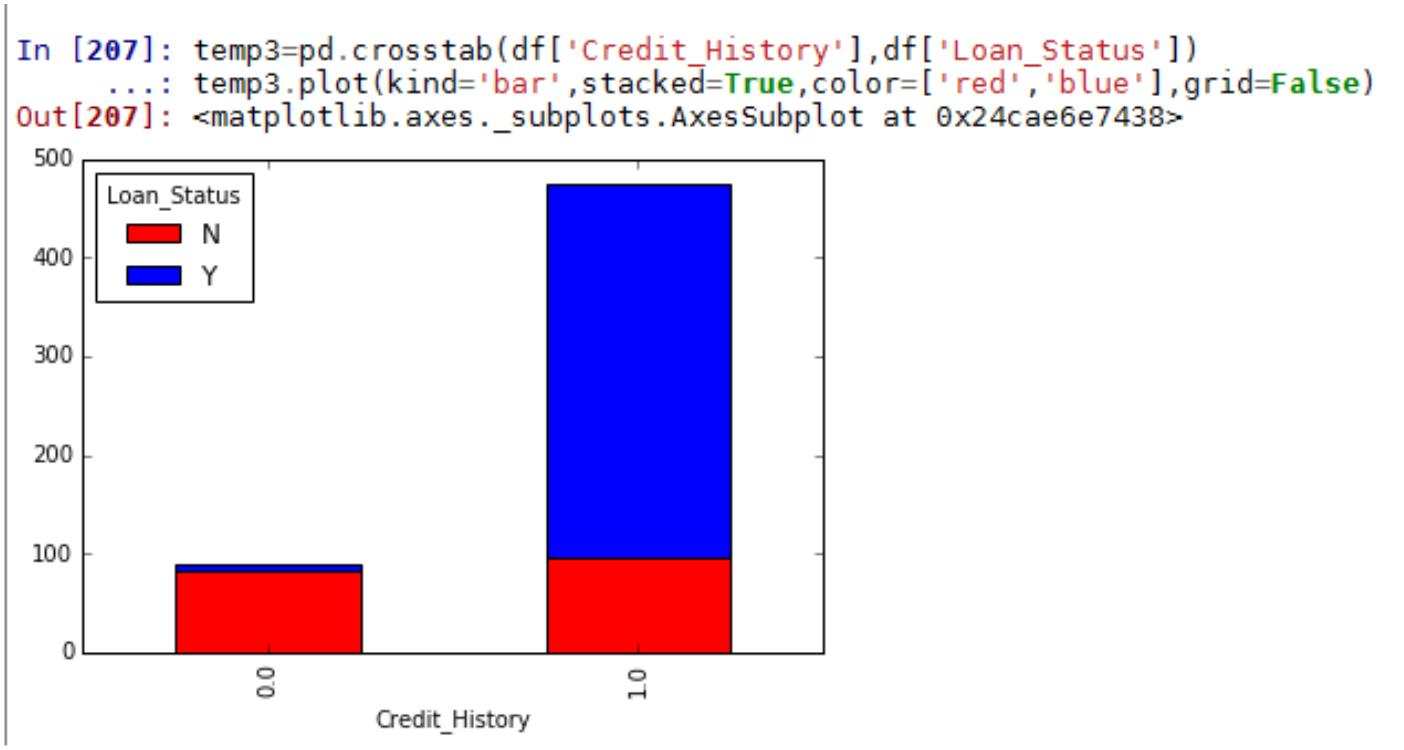
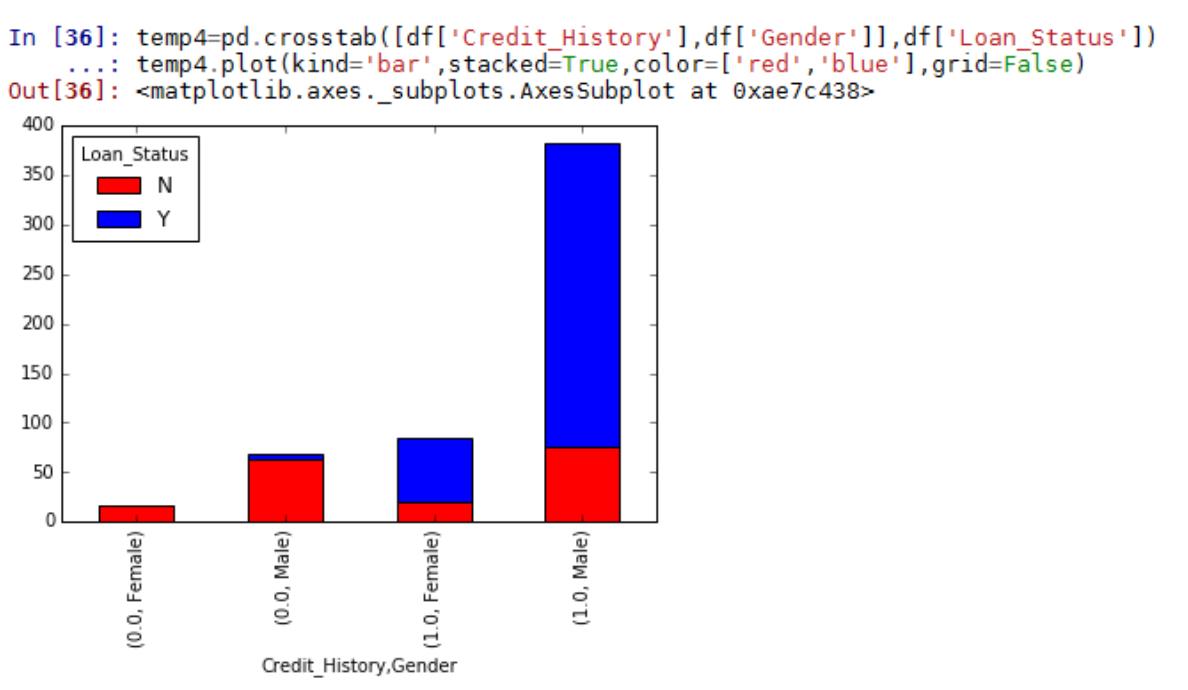
二、数据处理
1
.查看变量中的缺失值
2
.一个人是否受教育与是否自雇人士结合起来,提供一个很好的贷款估计
可以用每一组中贷款金额的中位数的一些变化来估计贷款金额
3.处理 Self_Employed,Credit_History,Loan_Amount_Term 的缺失值
可以看出 86%的值是 NO,故将缺失值估计为“NO”比较可靠
#
处理 Credit_History 的缺失值
df['Credit_History'].value_counts()
df['Credit_History'].fillna(1,inplace=True)
#
处理 Loan_Amount_Term 的缺失值
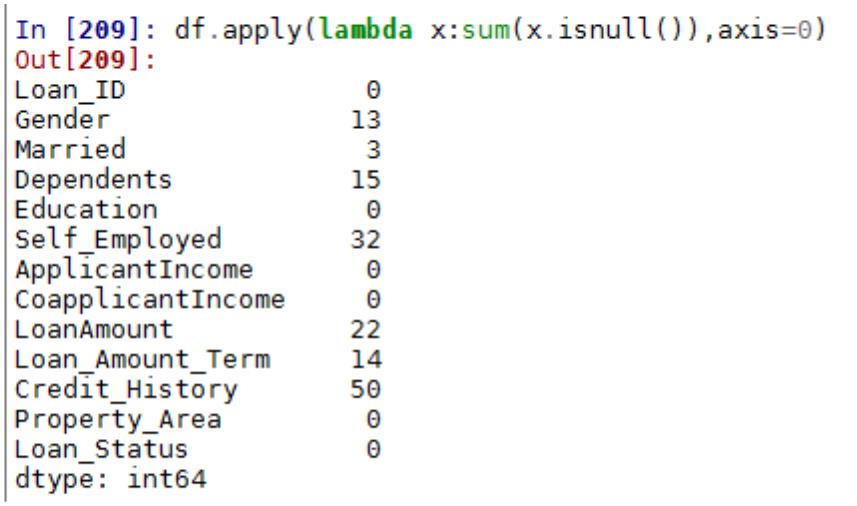
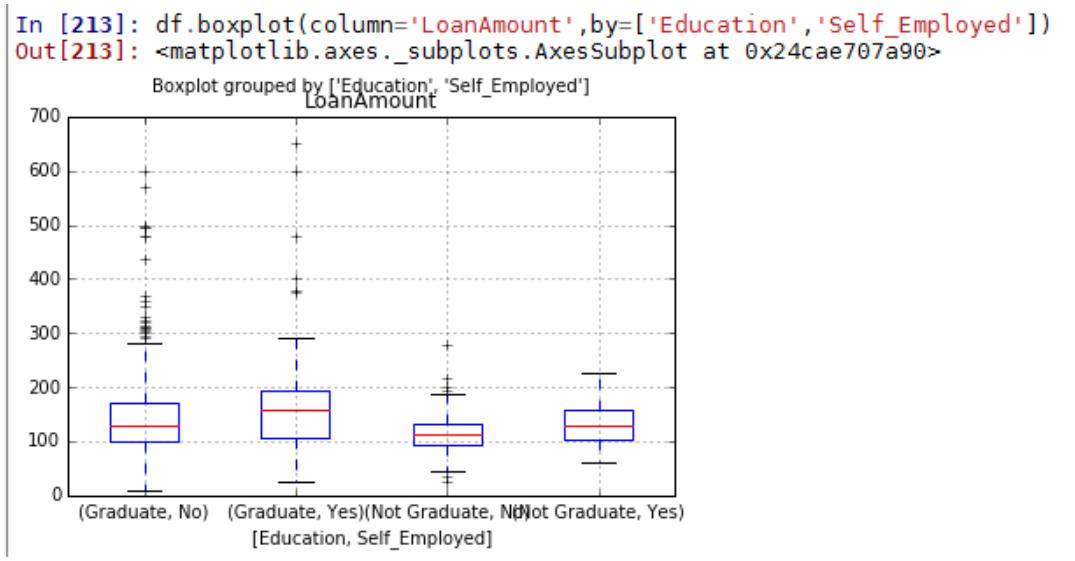
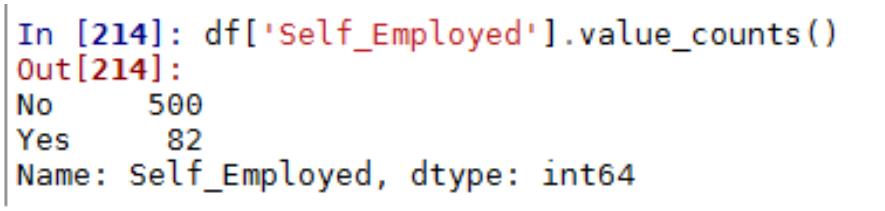
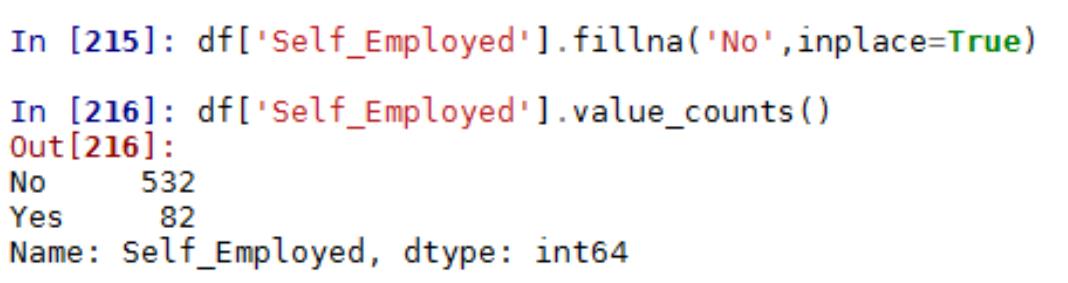
df['Loan_Amount_Term'].describe()data_train['Loan_Amount_Term'].fillna(data_train['Loan_Amount_Ter
m'].isnull().mean(),inplace=True)
df['Loan_Amount_Term'].fillna(df['LoanAmount'].isnull().mean(),inplace=True)
4
.填充 LoanAmount 的缺失值
创建一个数据透视表,提供了我们所有 Education 和 Self_employed 变量的唯一值分组的中位数。定义
一个函数,返回这些单元格的值,并应用它来填充丢失的贷款金额的值。
table=df.pivot_table(values='LoanAmount',index='Self_Employed',columns='Education',aggfunc=np.media
n)
5
.处理 LoanAmount 极端值
6
.ApplicantIncome 将其与 CoapplicantIncome(共同申请者收入)结合起来作为总收入,并采取相同的
对数变换
三、使用 Python 建立数学模型
1
.sklearn 要求所有输入都是数字,我们应该通过编码类别将我们多有的分类变量转换为数值型
from sklearn.preprocessing import LabelEncoder
var_mod=['Gender','Married','Dependents','Education','Self_Employed','Property_Area','Loan_Status']
le=LabelEncoder()

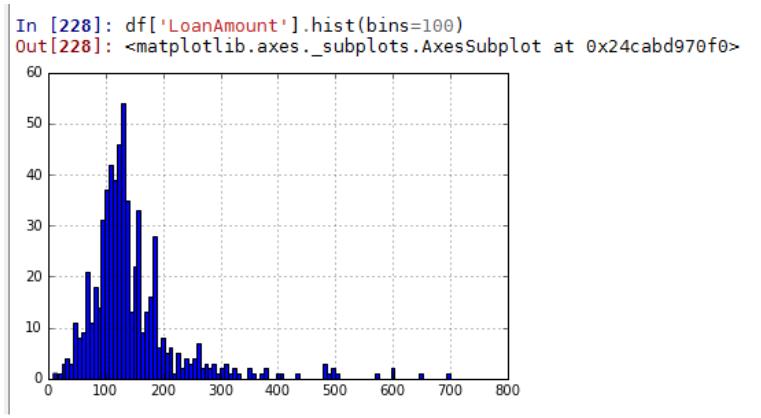

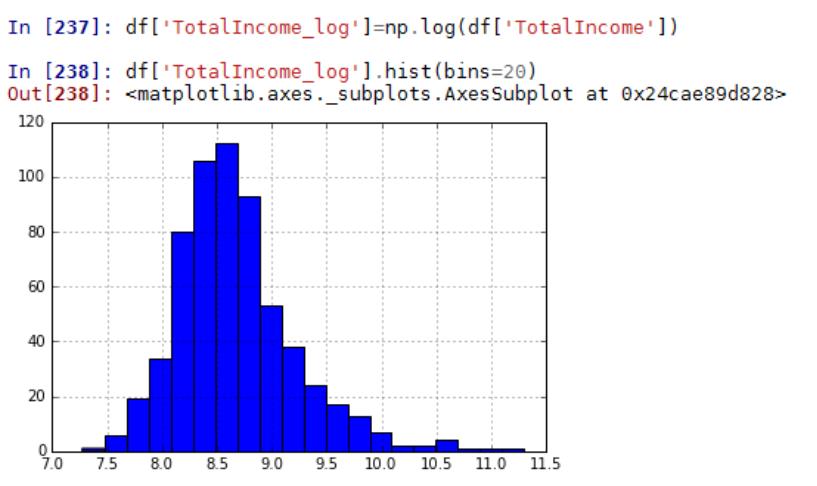
for i in var_mod:
df[i]=le.fit_transform(df[i])
df.dtypes
2
.导入所需的模块,然后定义一个通用的分类函数,它需要一个模型作为输入,并确定准确性度和交
叉验证分数。
#
Import models from scikit-learn module
from sklearn.linear_model import LogisticRegression
from sklearn.cross_validation import KFold #for k-fold cross calidation
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier,export_graphviz
from sklearn import metrics
#
Generic function foe making a classification model and accessing performance
def classification_model(model,data,predictors,outcome):



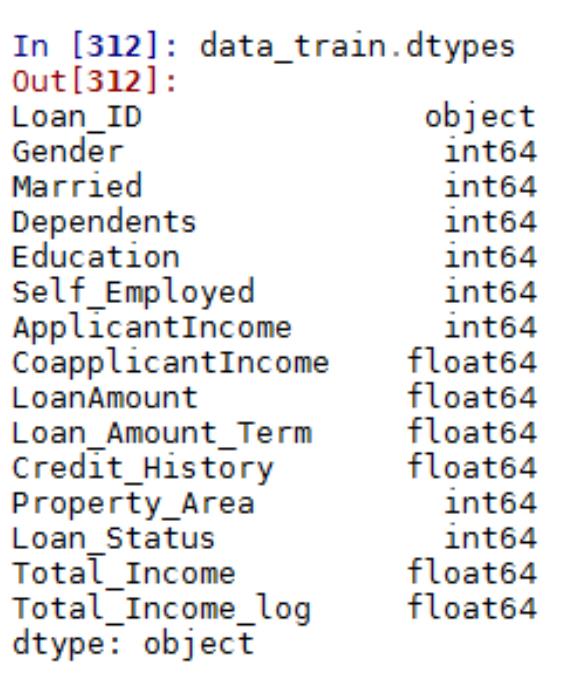
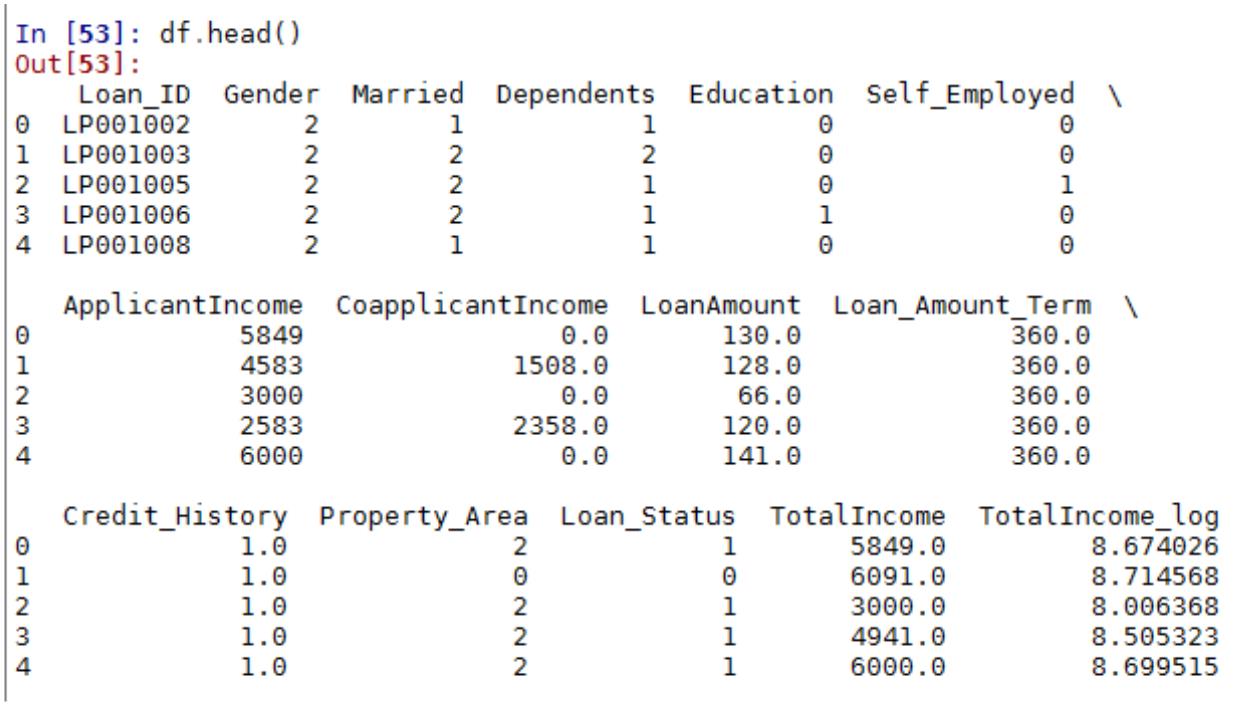
#
Fit the model
model.fit(data[predictors],data[outcome])
make predictions on training set:
predictions=model.predict(data[predictors])
print accuracy
#
#
accuracy=metrics.accuracy_score(predictions,data[outcome])
print ("Accuracy: %s" % "{0:.3%}".format(accuracy))
#
Perform k-fold cross-validation with 5 folds
kf=KFold(data.shape[0],n_folds=5)
error=[]
for train,test in kf:
#
Filter training data
train_predictors=(data[predictors].iloc[train,:])
#
The target we're using to train the algortithm
train_target=data[outcome].iloc[train]
Training the algorithm using the predictors and target
model.fit(train_predictors,train_target)
Record error from each cross-validation run
#
#
error.append(model.score(data[predictors].iloc[test,:],data[outcome].iloc[test]))
print("Cross-Validation Score: %s" % "{0:.3%}".format(np.mean(error)))
#
Fit the model again so that it can be refered outside the function
model.fit(data[predictors],data[outcome])
3
.使用 credit_history 建立我们的第一个模型----逻辑回归
#
逻辑回归
outcome_var='Loan_Status'
model=LogisticRegression()
predictor_var=['Credit_History']
classification_model(model,df,predictor_var,outcome_var)
#
增加变量
predictor_var=['Credit_History','Education','Married','Self_Employed','Property_Area']
classification_model(model,df,predictor_var,outcome_var)
#
决策树
model=DecisionTreeClassifier()
predictor_var=['Credit_History','Gender','Married','Education']
classification_model(model,df,predictor_var,outcome_var)

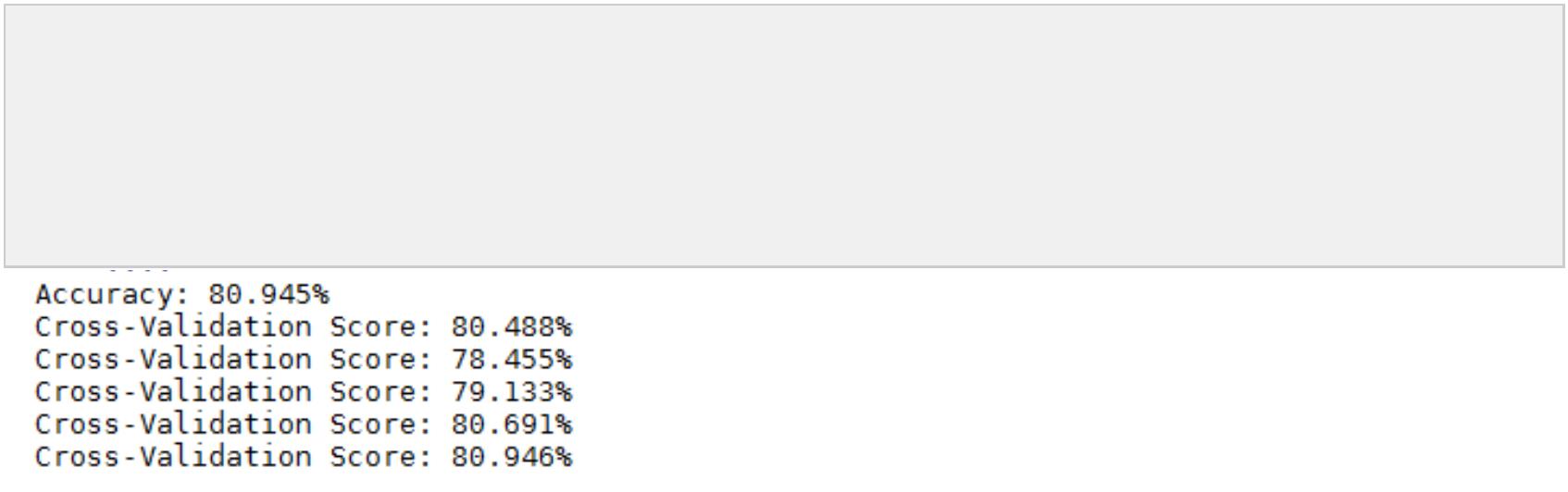



#
随机森林
model=RandomForestClassifier(n_estimators=100)
predictor_var=['Gender','Married','Dependents','Education','Self_Employed',
'
Loan_Amount_Term','Credit_History','Property_Area','TotalIncome_log']
classification_model(model,df,predictor_var,outcome_var)
#
Create a series with feature importances
featimp=pd.Series(model.feature_importances_,index=predictor_var).sort_values(ascending=False)
print featimp
#
使用前 5 个变量来创建模型,此外,修改一点随机森林模型的参数
model=RandomForestClassifier(n_estimators=25,min_samples_split=25,max_depth=7,max_features=1)
predictor_var=['TotalIncome_log','Credit_History','Dependents','Loan_Amount_Term','Property_Area']
classification_model(model,df,predictor_var,outcome_var)



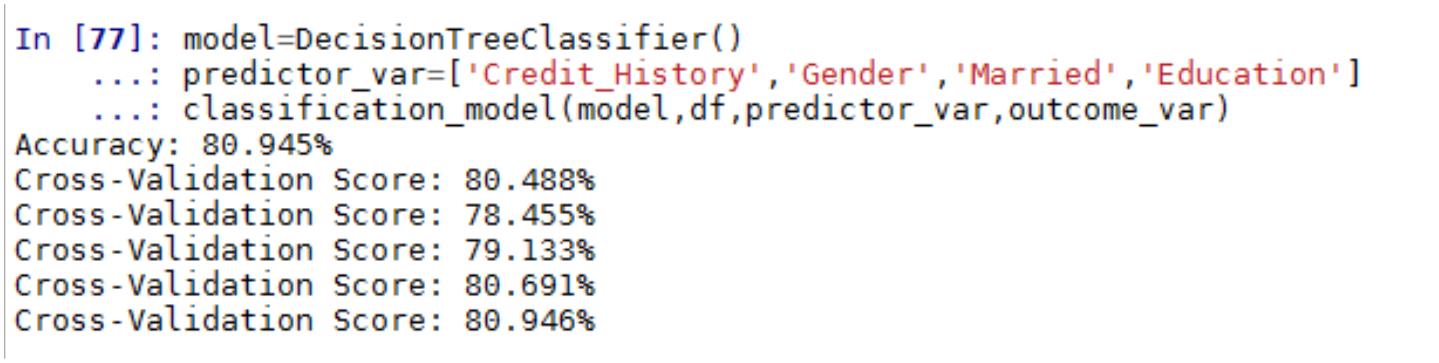
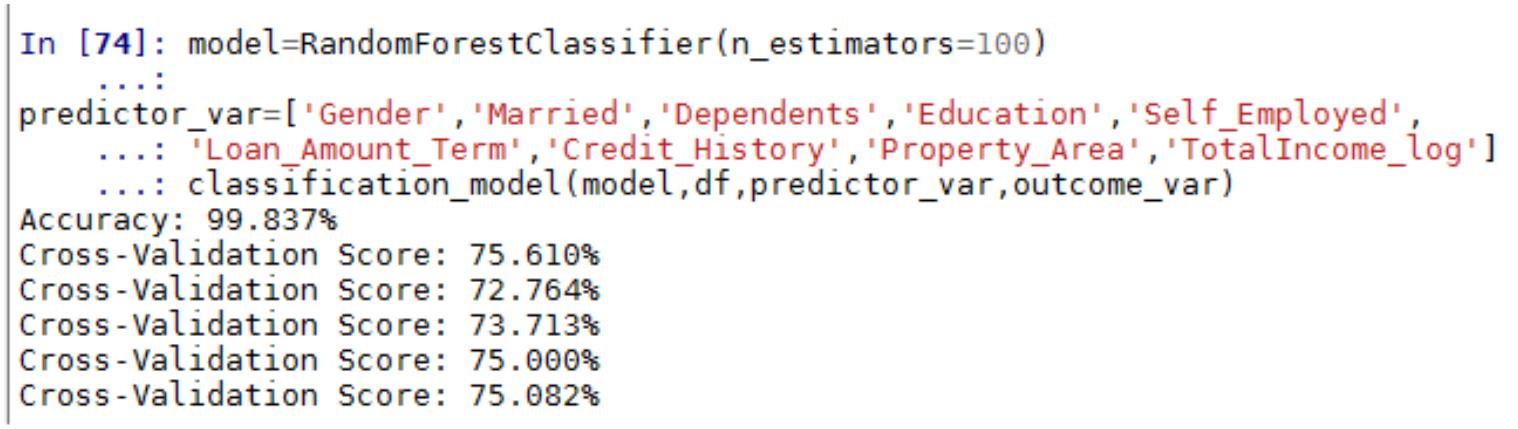
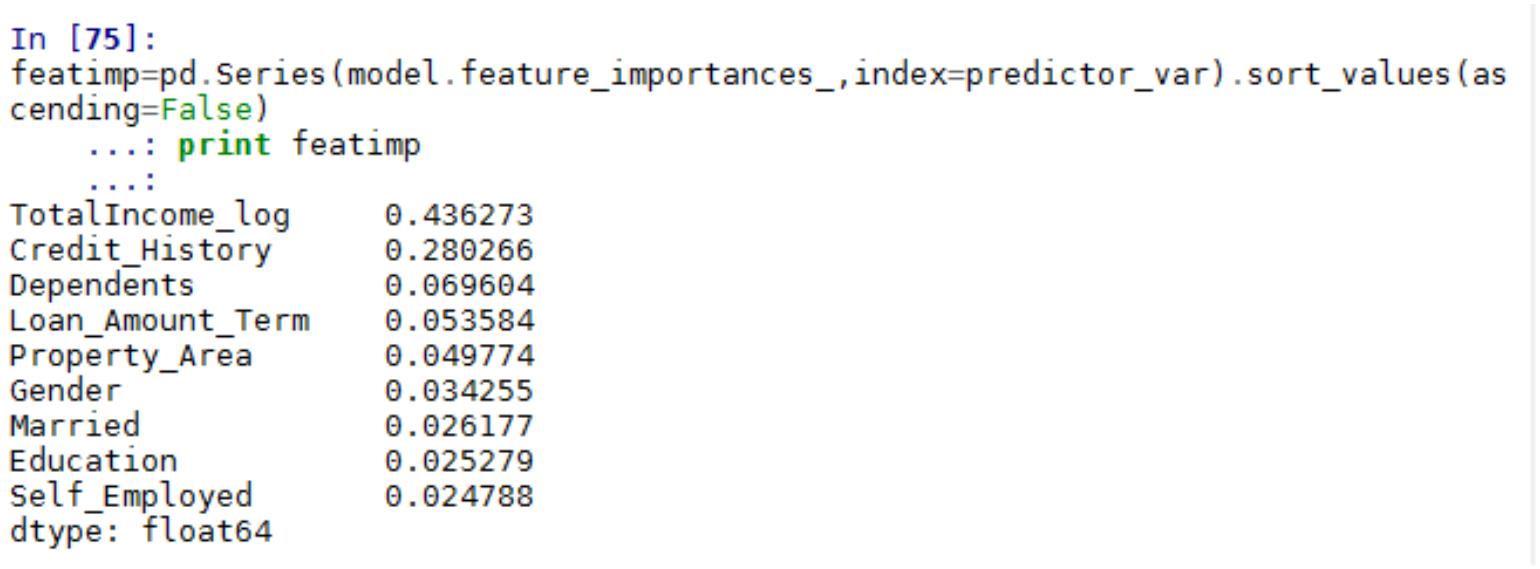
案例四 KNN 算法实现葡萄酒价格模型预测及交叉验证
参考:http://www.jianshu.com/p/48d391dab189
. KNN 算法
用 Numpy 库实现 K-nearest neighbours 回归或分类
kNN 算法的核心思想是如果一个样本在特征空间中的 k 个
1
最相邻的样本中的大多数属于某一个类别,则该样本也属于这
个类别,并具有这个类别上样本的特性。该方法在确定分类决
策上只依据最邻近的一个或者几个样本的类别来决定待分样本
所属的类别。 kNN 方法在类别决策时,只与极少量的相邻样
本有关。由于 kNN 方法主要靠周围有限的邻近的样本,而不
是靠判别类域的方法来确定所属类别的,因此对于类域的交叉
或重叠较多的待分样本集来说,kNN 方法较其他方法更为适
合。
2
.数据
来自《集体智慧编程》给的葡萄酒的价格模型。
#
1.葡萄酒的价格假设由酒的等级与储藏年代共同决定,给定 rating 与 age 之后,就能给出酒的价格
def wineprice(rating,age):
""
"
Input rating & age of wine and Output it's price.
Example:
-
-----
input = [80.,20.] ===> output = 140.0
""
"
peak_age = rating - 50 # year before peak year will be more expensive
price = rating/2.
if age > peak_age:
price = price*(5 -(age-peak_age))
else:
price = price*(5*((age+1)/peak_age))
if price < 0: price=0
return price

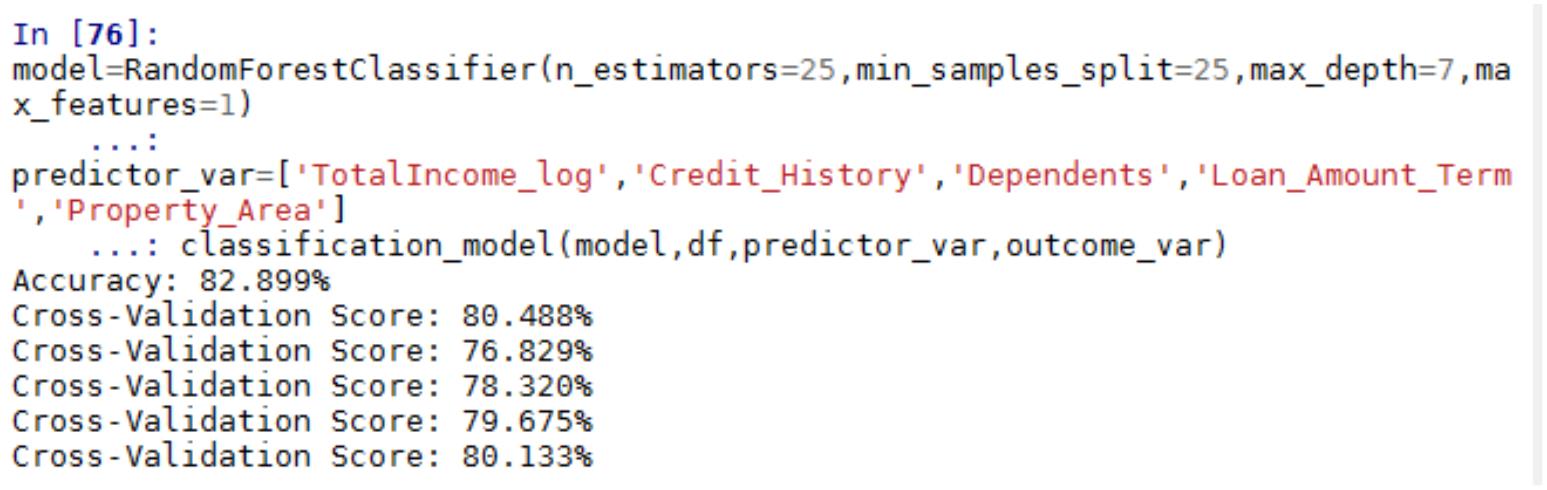
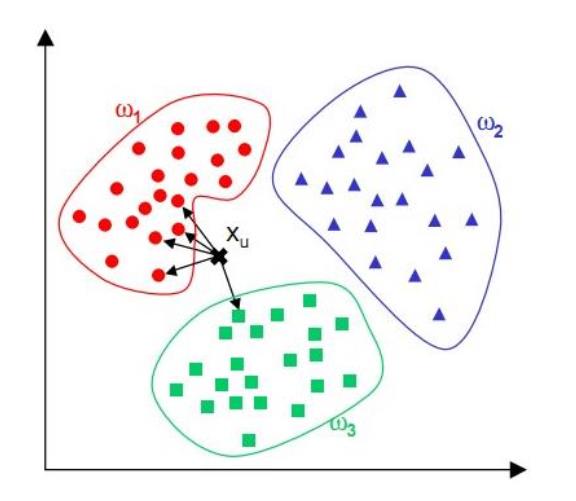
根据上述的价格模型,我们产生 n=500 瓶酒及价格,同时为价格随机加减了 20%来体现随机性,同时
增加预测的难度。注意基本数据都是 numpy 里的 ndarray,为了便于向量化计算,同时又有强大的 broadcast
功能,计算首选。
def wineset(n=500):
"
""
Input wineset size n and return feature array and target array.
Example:
-
-----
n = 3
X = np.array([[80,20],[95,30],[100,15]])
y = np.array([140.0,163.6,80.0])
"
""
X,y = [], []
for i in range(n):
rating = np.random.random()*50 + 50
age = np.random.random()*50
get reference price
price = wineprice(rating,age)
add some noise
#
#
price = price*(np.random.random()*0.4 + 0.8) #[0.8,1.2]
X.append([rating,age])
y.append(price)
return np.array(X), np.array(y)
#
2.相似度,欧式距离
def euclidean(arr1,arr2):
""
"
Input two array and output theie distance list.
Example:
-
-----
arr1 = np.array([[3,20],[2,30],[2,15]])
arr2 = np.array([[2,20],[2,20],[2,20]]) # broadcasted, np.array([2,20]) and [2,20] also work.
d
= np.array([1,20,5])
"
""
ds = np.sum((arr1 - arr2)**2,axis=1)
return np.sqrt(ds)
arr1 = np.array([[3,20],[2,30],[2,15]])
arr2 = np.array([[2,20],[2,20],[2,20]])
euclidean(arr1,arr2)
#
3.给定训练数据 X 和新 sample v,然后返回排序好的距离,以及对应的 index(我们要以此索引近邻们对应的标签值)
def getdistance(X,v):
""
"
Input train data set X and a sample, output the distance between each other with index.
Example:
-
-----
X = np.array([[3,20],[2,30],[2,15]])



v = np.array([2,20]) # to be broadcasted
Output dlist = np.array([1,5,10]), index = np.array([0,2,1])
"
""
dlist = euclidean(X,np.array(v))
index = np.argsort(dlist)
dlist.sort()
#
dlist_with_index = np.stack((dlist,index),axis=1)
return dlist, index
dlist, index = getdistance(X,[80.,20.])
#
4.KNN 算法
def knn(X,y,v,kn=3):
""
"
Input train data and train target, output the average price of new sample.
X = X_train; y = y_train
k: number of neighbors
"
""
dlist,index=getdistance(X,v)
avg=0.0
for i in range(kn):
avg=avg+y[index[i]]
avg=avg/kn
return avg
knn(X,y,[95.0,5.0],kn=3)
wineprice(95.0,5.0)
#
#
#
5.加权 KNN
给更近的邻居分配更大的权重(你离我更近,那我就认为你跟我更相似,就给你分配更大的权重),
而较远的邻居的权重相应地减少,取其加权平均。需要一个能把距离转换为权重的函数,gaussian 函数是一个比
较普遍的选择
def gaussian(dist,sigma=10.0):
"
""Input a distance and return it's weight"""
weight = np.exp(-dist**2/(2*sigma**2))
return weight
x1 = np.arange(0,30,0.1)
y1 = gaussian(x1)
plt.title('gaussian function')
plt.plot(x1,y1);
def knn_weight(X,y,v,kn=3):
dlist, index = getdistance(X,v)
avg = 0.0
total_weight = 0


for i in range(kn):
weight = gaussian(dlist[i])
avg = avg + weight*y[index[i]]
total_weight = total_weight + weight
avg = avg/total_weight
return avg
knn_weight(X,y,[95.0,5.0],kn=3)
#
#
#
6.交叉验证,写一个函数实现交叉验证功能,不能使用 sklearn 库
交叉验证(Cross-Validation): 有时亦称循环估计, 是一种统计学上将数据样本切割成较小子集的实用方法。
于是可以先在一个子集上做分析, 而其它子集则用来做后续对此分析的确认及验证。 一开始的子集被称为训练
集。而其它的子集则被称为验证集或测试集。
#
#
#
交叉验证方法一:Holdout Method(保留)
Holdout method
方法:将原始数据随机分为两组,一组做为训练集,一组做为验证集,利用训练集训练分类器,然后利用验证集验证模
型,记录最后的分类准确率为此 Hold-OutMethod 下分类器的性能指标.。Holdout Method 相对于 K-fold Cross
Validation 又称 Double cross-validation ,或相对 K-CV 称 2-fold cross-validation(2-CV)
#
#
优点:好处的处理简单,只需随机把原始数据分为两组即可
缺点:严格意义来说 Holdout Method 并不能算是 CV,因为这种方法没有达到交叉的思想,由于是随机的将原始数据
分组,所以最后验证集分类准确率的高低与原始数据的分组有很大的关系,所以这种方法得到的结果其实并不具有说
服性.(主要原因是 训练集样本数太少,通常不足以代表母体样本的分布,导致 test 阶段辨识率容易出现明显落
差。此外,2-CV 中一分为二的分子集方法的变异度大,往往无法达到「实验过程必须可以被复制」的要求。)
def my_train_test_split(X,y,train_size=0.95,shuffle=True):
"
""
Input X,y, split them and out put X_train, X_test; y_train, y_test.
Example:
-
-----
X = np.array([[0, 1],[2, 3],[4, 5],[6, 7],[8, 9]])
y = np.array([0, 1, 2, 3, 4])
Then
X_train = np.array([[4, 5],[0, 1],[6, 7]])
X_test = np.array([[2, 3],[8, 9]])
y_train = np.array([2, 0, 3])
y_test = np.array([1, 4])
"
""
order = np.arange(len(y))
if shuffle:
order = np.random.permutation(order)
border = int(train_size*len(y))
X_train, X_test = X[:border], X[border:]
y_train, y_test = y[:border], y[border:]
return X_train, X_test, y_train, y_test
交叉验证方法二:K-fold Cross Validation(k 折叠)
#


#
#
K folds 产生一个迭代器
方法:作为 Holdout Methon 的演进,将原始数据分成 K 组(一般是均分),将每个子集数据分别做一次验证集,其余的
K-1 组子集数据作为训练集,这样会得到 K 个模型,用这 K 个模型最终的验证集的分类准确率的平均数作为此 K-CV
下分类器的性能指标.K 一般大于等于 2,实际操作时一般从 3 开始取,只有在原始数据集合数据量小的时候才会尝试
取 2. 而 K-CV 的实验共需要建立 k 个 models,并计算 k 次 test sets 的平均辨识率。在实作上,k 要够大才能使
各回合中的 训练样本数够多,一般而言 k=10 (作为一个经验参数)算是相当足够了。
#
#
优点:K-CV 可以有效的避免过学习以及欠学习状态的发生,最后得到的结果也比较具有说服性.
缺点:K 值选取上
def my_KFold(n,n_folds=5,shuffe=False):
""
"
K-Folds cross validation iterator.
Provides train/test indices to split data in train test sets. Split dataset
into k consecutive folds (without shuffling by default).
Each fold is then used a validation set once while the k - 1 remaining fold form the training set.
Example:
-
-----
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([1, 2, 3, 4])
kf = KFold(4, n_folds=2)
for train_index, test_index in kf:
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
print("TRAIN:", train_index, "TEST:", test_index)
TRAIN: [2 3] TEST: [0 1]
TRAIN: [0 1] TEST: [2 3]
"
""
idx = np.arange(n)
if shuffe:
idx = np.random.permutation(idx)
fold_sizes = (n // n_folds) * np.ones(n_folds, dtype=np.int) # folds have size n // n_folds
fold_sizes[:n % n_folds] += 1 # The first n % n_folds folds have size n // n_folds + 1
current = 0
for fold_size in fold_sizes:
start, stop = current, current + fold_size
train_index = list(np.concatenate((idx[:start], idx[stop:])))
test_index = list(idx[start:stop])
yield train_index, test_index
current = stop # move one step forward
X1 = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
y1 = np.array([1, 2, 3, 4])
kf = my_KFold(4, n_folds=2)
for train_index, test_index in kf:
X_train, X_test = X1[train_index], X1[test_index]
y_train, y_test = y1[train_index], y1[test_index]
print("TRAIN:", train_index, "TEST:", test_index)
#
#
#
7.KNN 算法交叉验证
评价算法
首先我们用一个函数评价算法,给定训练数据与测试数据,计算平均的计算误差,这是评价算法好坏的重要指标
def test_algo(alg,X_train,X_test,y_train,y_test,kn=3):

error = 0.0
for i in range(len(y_test)):
guess = alg(X_train,y_train,X_test[i],kn=kn)
error += (y_test[i] - guess)**2
return error/len(y_test)
X_train,X_test,y_train,y_test = my_train_test_split(X,y,train_size=0.8)
test_algo(knn,X_train,X_test,y_train,y_test,kn=3)
#
#
交叉验证
得到平均误差,注意这里 KFold 生成器的使用
def my_cross_validate(alg,X,y,n_folds=100,kn=3):
error = 0.0
kf = my_KFold(len(y), n_folds=n_folds)
for train_index, test_index in kf:
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
error += test_algo(alg,X_train,X_test,y_train,y_test,kn=kn)
return error/n_folds
#
选最好的 k 值
errors1, errors2 = [], []
for i in range(20):
error1 = my_cross_validate(knn,X,y,kn=i+1)
error2 = my_cross_validate(knn_weight,X,y,kn=i+1)
errors1.append(error1)
errors2.append(error2)
#
从下图可以看出,模型表现随 k 值的变化呈现一个折现型,
当为 1 时,表现较差;当取 2,3 的时候,
模型表现还不错;但当 k 继续增加的时候,模型表现急剧下
降。
#
#
同时 knn_weight 算法要略优于 knn 算法,有一点点改进。
xs = np.arange(len(errors1)) + 1
plt.plot(xs,errors1,color='c')
plt.plot(xs,errors2,color='r')
plt.xlabel('K')
plt.ylabel('Error')
plt.title('Error vs K');