非监督特征学习

Each of the digits is is represented by a 28x28 grid of pixel intensities, which we will reformat as a vector x(i) with 28*28 = 784 elements. The label is

binary, so y(i)∈{0,1}.

多写了一个 is 。

预备知识（Miscellaneous ）

MATLAB 文件指引（MATLAB Modules ）

注：本文是旧版的作业文件，新版见初学者代码压缩包，但这里旧版的代码仍然可以用来学习。

稀疏自编码器 | sparseae_exercise.zip

checkNumericalGradient.m - 检查 computeNumericalGradient 的计算结果是否正确

computeNumericalGradient.m - 计算函数的数值梯度（待实现）

display_network.m - 可视化自动编码器的图像或滤波器的结果

initializeParameters.m - 随机初始化稀疏自动编码器的权重值

sampleIMAGES.m - 从图像矩阵中采样大小为

的小图（待实现）

sparseAutoencoderCost.m - 计算稀疏自动编码器中代价函数的函数值（即代价）和梯度

train.m - 用来训练和测试稀疏自动编码器的框架

MNIST 数据集使用向导 | mnistHelper .zip

loadMNISTImages.m - 返回包含原始 MNIST 图像的矩阵

loadMNISTLabels.m - 返回包含原始 MNIST 图像标签的矩阵

主成分分析与白化 | pca_exercise.zip

display_network.m - 可视化自动编码器的图像或滤波器的结果

pca_gen.m - 白化练习框架

sampleIMAGESRAW.m - 返回一个

SoftMax 回归 | softmax_exercise.zip

的的原始（未经白化过的）小图像

checkNumericalGradient.m - 检查 computeNumericalGradient 的计算结果是否正确

display_network.m - 可视化自动编码器的图像或滤波器的结果

loadMNISTImages.m - 返回包含原始 MNIST 图像的矩阵

loadMNISTLabels.m - 返回包含原始 MNIST 图像标签的矩阵

softmaxCost.m - 计算 Softmax 目标函数的代价和梯度

softmaxTrain.m - 给定参数下训练一个 Softmax 模型

train.m - 本练习的训练框架

代码风格（Style Guide ）

文件/函数名（File / Function Names ）

函数和文件名应该用小写字母，其中第一个单词一律小写，之后的单词的首字母大写。

变量名（Variable Names ）

变量名应遵从已有的风格惯例。

预备知识推荐（Useful Links ）

Matlab 学习向导

写出高效的 MATLAB 代码 (by Pascal Getreuer)

矩阵微积分参考

矩阵手册

卷积神经网络笔记

推荐读物（UFLDL Recommended Readings ）

如果您正在学习 UFLDL (非监督特征学习与深度学习)，那么您可以考虑下面这份阅读清单。给出这份推荐阅读清单的前提是，我们假设您已经对 CS229 这

门课上的机器学习基础知识（也包括讲座笔记）有所掌握。

基础知识:

CS294A 神经网络/稀疏自编码教程（其中大部分现已在本架教程中，但练习作业仍旧在 CS294A 的课程网站上。）

[

1] Natural Image Statistics book, Hyvarinen et al.

* 这本书很长，您可跳过您熟悉的章节。** 重要章节: 5 (主成分分析与白化; 您可能已有所了解), 6 (稀疏编码), 7 (独立成分分析), 10 (ISA), 11 (TICA),

6 (temporal models).

[

2] Olshausen and Field. Emergence of simple-cell receptive field properties by learning a sparse code for natural images Nature 1996. (稀疏编码)

3] Rajat Raina, Alexis Battle, Honglak Lee, Benjamin Packer and Andrew Y. Ng. 自我学习：从未标记数据中迁移学习. ICML 2007

自动编码器:

[

4] Hinton, G. E. and Salakhutdinov, R. R. 用神经网络对数据降维. Science 2006. 代码在这里.

5] Bengio, Y., Lamblin, P., Popovici, P., Larochelle, H. 神经网络的贪婪逐层训练. NIPS 2006

6] Pascal Vincent, Hugo Larochelle, Yoshua Bengio and Pierre-Antoine Manzagol. 用降噪自编码器提取合成出健壮特征 ICML 2008.

(他们有一个好模型，但然后合理化为一个概率模型。忽略向后合理化的概率模型[Section 4].)

深度学习有效性分析:

[

7] H. Larochelle, D. Erhan, A. Courville, J. Bergstra, and Y. Bengio. 多因素变化下的深层结构问题的实证分析. ICML 2007. (Someone read this and

let us know if this is worth keeping,. [Most model related material already covered by other papers, it seems not many impactful

conclusions can be made from results, but can serve as reading for reinforcement for deep models])

[

8] Dumitru Erhan, Yoshua Bengio, Aaron Courville, Pierre-Antoine Manzagol, Pascal Vincent, and Samy Bengio. 为何非监督的预训练可帮助深度学

习？ JMLR 2010

9] Ian J. Goodfellow, Quoc V. Le, Andrew M. Saxe, Honglak Lee and Andrew Y. Ng. 测量深度网络的不变性. NIPS 2009.

[

径向基网络:

[

10] 径向基网络教程. ** 但请忽略 Theano 代码示例** (有人问我这条是否应该之后移除，虽对了解后来网络来说可能用处不大，但对于了解深度学习还

是有用的。[看来还是留下比较好，对于不知道径向基网络的读者来说是一个很好的介绍，可以复现 Hinton 在 06 年时 Science 上的三通路径向基网络])

卷积网络:

11] 卷积网络教程. 但请忽略 Theano 代码.

[

应用:

计算机视觉 ** [12] Jianchao Yang, Kai Yu, Yihong Gong, Thomas Huang. 基于稀疏编码线性空间金字塔匹配的图像分类, CVPR 2009 ** [13] A.

Torralba, R. Fergus and Y. Weiss. Small codes and large image databases for recognition. CVPR 2008.

语音识别 [14] 基于卷积深度置信网络无监督特征学习的语音识别, Honglak Lee, Y an Largman, Peter Pham and Andrew Y . Ng. In NIPS 2009.

自然语言处理:

15] Yoshua Bengio, Réjean Ducharme, Pascal Vincent and Christian Jauvin, 一个神经概率语言模型. JMLR 2003.

[

16] R. Collobert and J. Weston. 自然语言处理的统一架构：多任务学习的深度神经网络. ICML 2008.

17] Richard Socher, Jeffrey Pennington, Eric Huang, Andrew Y. Ng, and Christopher D. Manning. 半监督递归编码器预测情绪的分布. EMNLP 2011

18] Richard Socher, Eric Huang, Jeffrey Pennington, Andrew Y. Ng, and Christopher D. Manning. 基于动态池化和递归展开自动编码器的释义检测.

NIPS 2011

[

19] Mnih, A. and Hinton, G. E. 统计语言建模新的三种图模型. ICML 2007

高阶内容:

慢特征分析:

20] 基于慢特征分析生成一个复杂细胞的完整特性. Journal of Vision, 2005.

预测稀疏分解

21] Koray Kavukcuoglu, Marc'Aurelio Ranzato, and Yann LeCun, "稀疏编码算法中的快速推理及其在目标识别中的应用", Computational and Biological

Learning Lab, Courant Institute, NYU, 2008.

22] Kevin Jarrett, Koray Kavukcuoglu, Marc'Aurelio Ranzato, and Yann LeCun, "最佳的多阶段目标识别体系结构是什么？", In ICCV 2009

[

均值与协方差联合模型

[

23] M. Ranzato, A. Krizhevsky, G. Hinton. 考虑三路受限玻尔兹曼机模型的自然图像建模. In AISTATS 2010.

24] M. Ranzato, G. Hinton, 基于第三阶受限玻尔兹曼机分解的像素均值和协方差建模. CVPR 2010 (someone and tell us if you need to read the 3-

way RBM paper before the mcRBM one [ 我认为没必要, 实际上 CVPR 论文更易理解.])

[

25] Dahl, G., Ranzato, M., Mohamed, A. and Hinton, G. E. 基于均值协方差的受限玻尔兹曼机的电话语音识别. NIPS 2010.

26] Y. Karklin and M. S. Lewicki, 复杂细胞属性在自然场景中的学习到泛化, Nature, 2008. (someone tell us if this should be here.

Interesting

algorithm + nice visualizations, though maybe slightly hard to understand. [seems a good reminder there are other existing models])

概述

[

27] Yoshua Bengio. 为人工智能学习深度架构. FTML 2009. (该领域更宽视角的描述, 但技术细节无需深究. 当您已经读完该领域的一些文章后就会发现

很好理解.)

实战指导:

[

28] Geoff Hinton. 训练受限玻尔兹曼机的指导. UTML TR 2010–003. 这是一篇实战指导 (如果您尝试实现受限玻尔兹曼机不妨一读，但若不是请跳过因

为这不是一篇教程).

[

29] Y. LeCun, L. Bottou, G. Orr and K. Muller. 高效反向传播. 神经网络: 诀窍, Springer, 1998 如果您尝试实现反向传播; 否这不建议阅读

其它:

[

30] Honglak Lee 的课程

31] 来自 Geoff 的教程

监督学习与优化（Supervised Learning and Optimization

）

线性回归（Linear Regression）

问题描述（Problem Formulation ）

不妨回顾一下知识点，从如何实现线性回归（Linear Regression）开始。这一节的主要思想是知道什么是目标函数（Objective Functions），计算其梯度

（Gradients）以及通过一组参数来优化目标（函数）。这些基本的工具将会构建（在之后的教程中会讲到）复杂的算法。想要更多学习资料的读者可以在参

考监督学习讲座笔记。

在线性回归中，目标是从一个维度输入向量

，去预测目标值。例如，预测房价中表示房子的（美元）价格，

（

是下角标，表示向量

中第个元素）表示房子的第个特征的值，用特征来描述一个房子（如房子的面积，卧室的数目等）。假设现有很多房屋的数据（特征），其中比方说要

表示第个房子的特征，表示为是上角标，表示该房屋样本是数据集里的第个样本），该第个样本的房价表示为。简而言之，我们的目标

的缩写，在这里表示“假说”或“假设函数”），使训练集上的每个样本满足

（

是找到一个表示为

成功找到了像

的函数（

是

。如果

这样的函数，并且使其“看”过了足够多的房屋样本特征和房价，函数

将会是一个很好的房价预测器，即使是在那些它没有“见过”的

房屋特征数据上（也会有好的预测结果）。

为了能找到满足

条件的函数

，首先需要做的是如何表示函数

。在表示该函数形式之初，先选择形如 $ h_{\theta}(x) = \sum

{

j}\theta {j}x{j} = \theta^{\top}x 的线性函数。这里， h{\theta}(x) 表示一组不同\theta

参数的函数家族（称该函数家族为假设空间或假说空间）。在表示完h函数后的任务是找到满足条件： h( x^{(i)})尽可能接近y^{(i)} 下的\theta

参数值。特别地，要找的参数 \theta 是在下面这个函数值最小时的 \theta $ 值：

上面这个函数就是当前问题的“成本函数”或“代价函数”（Cost Function），它测量的是在特定值下，预测值（即

被称为“损失函数”（Loss Function），“惩罚函数”（Penalty Function）或“目标函数”（Objective Function）。

）与

的相差程度。该函数也

函数最小化（Function Minimization

）

现在，要找到函数

处在最小值时，参数的值。实际上，有很多的算法都可以用来找函数的最小值，比方说这里即将提到的以及后面还会讲到一些高

效率且易于自己实现的函数优化算法，比方在后面即将讲到的梯度下降（Gradient descent，注：原英文教程中，该链接无效，这里给出本教程中的一个函

数优化算法——随机梯度下降，Stochastic Gradient Descent的链接）小节中。计算函数最小值通常需要目标函数（Objective Function）

的两个部

分：第一部分是写出计算目标函数

，以计算参数的值。

的代码，第二部分是写出目标函数（Objective Function）

的微分项

Undefined control sequence \triangledown

之后，找到参数的最优值过程的其余部分将由优化算法来处理（回想一下，可微函数

项），是一个指向函数

或增加，以求得函数最小或最大值）。

的梯度

（即微分

Undefined control sequence \triangledown

最陡（下降）增量的方向的矢量——所以，很容易看到优化算法如何在参数上使用这样的一个小变化量（的方法），来减小

（

对于上述

表达式，可通过

和

构成的训练数据集，较容易地在MATLAB里实现计算

来得到参数的值。但还需要计算另一部分，那就是

梯度（项）：

在给定的参数值

后，目标函数（Objective Function）

的微分结果表示为：

练习 1A：线性回归（Exercise 1A: Linear Regression

）

在本次练习中您将会使用MATLAB实现线性回归中的目标函数（Objective Function）和梯度计算（Gradient Copmutation）。

在初学者代码（Starter Code）包中的 ex1/ 目录下，您将会找到 ex1_linreg.m 文件，其包含了一个简单的线性回归（Linear Regression）的实验。该文件

为您提供了大部分较为固定的步骤流程：

. 数据从 housing.data 文件中加载。一个额外的特征值“1”加入到数据集中，（与其对应的）

函数的）截距项存在。

（即向量中的第一个元素）在线性函数中是作为（假设

. 在数据集中的样本顺序是随机排列的，同时数据被分成了训练集和测试集。被用来给学习算法作为输入的特征数据存储在变量 train.X 和 tests.X，被

预测的目标值对每个样本即估计的房价。训练集样本和测试集样本的房价分别存储在 train.y 和 test.y 中。您将会用到训练集寻找最优的参数值来

预测房价，并之后在测试集上检查（该最优参数的）表现。

. 该代码调用 minFunc 优化包。 minFunc 将试图在目标函数的最小值处，找到参数的最优值，目标函数已经在 linear_regression.m 中实现。您的任

务是（在 linear_regression.m 中）实现在参数下目标函数和梯度的计算。

. 在minFunc（包的计算任务）完成后（如训练结束后），训练集和测试集的误差被打印出来。这一部分作为可选任务，您可以在测试集上对预测和实际

价格进行快速的（数据）可视化。

ex1_linreg.m 文件会调用 linear_regression.m 文件，换句话说，在您完成 linear_regression.m 文件里的代码后，您才可执行 ex1_linreg.m 文件（调用

linear_regression.m 文件）。linear_regression.m 文件接收训练数据，训练目标值（房价）以及当前的参数

。

完成本练习的步骤如下：

. 完成 linear_regression.m 文件中的代码，使其可以针对线性回归问题计算早先定义的目标函数

，将计算结果保存至名为的变量中。您完成这

两个步骤可通过循环训练集（数据矩阵

当前更快的版本。

中的列数据）上的样本进行，并且对于每个样本，将其贡献值增加给。将在下一个练习中创建一个比

和

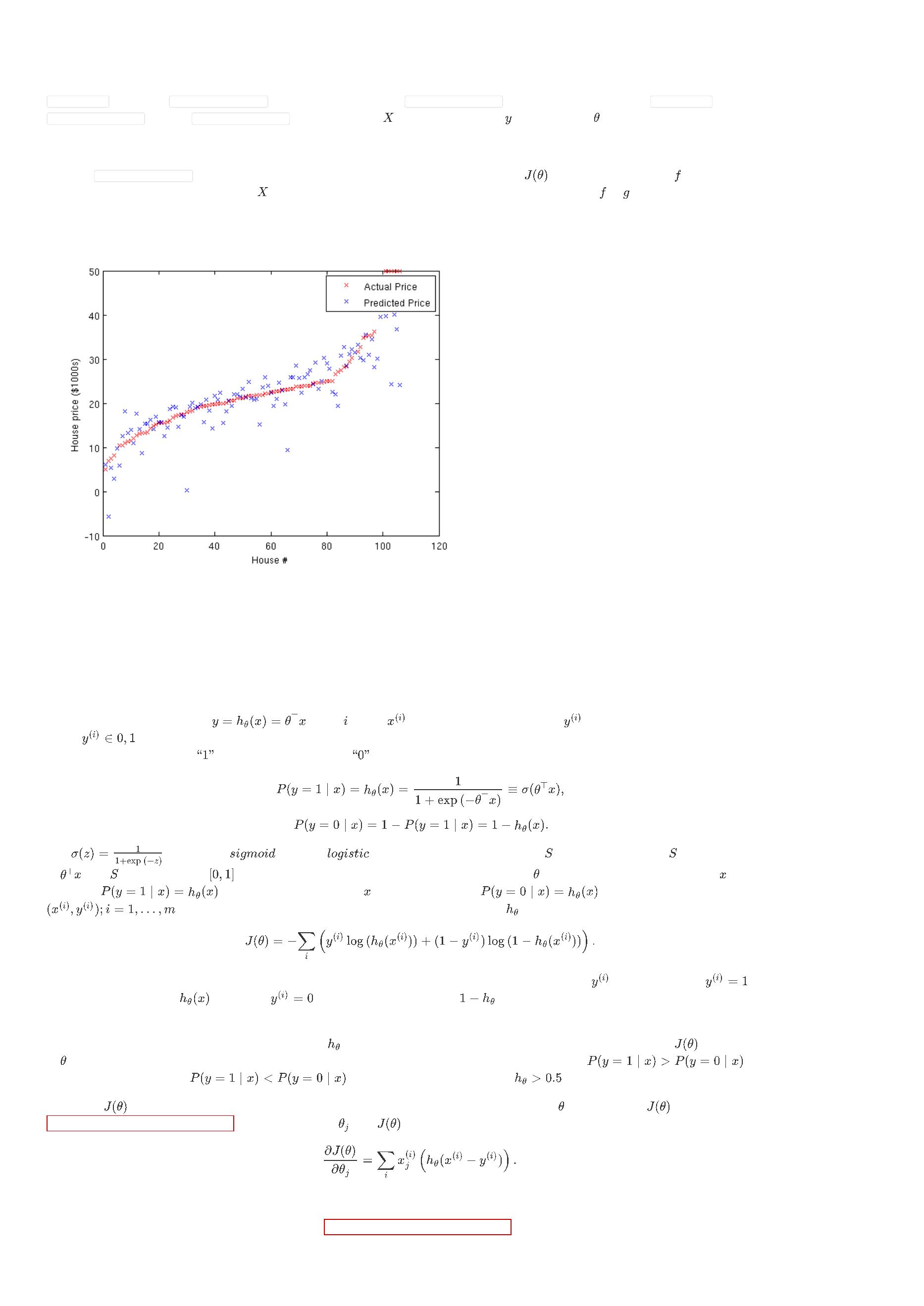
当您成功地完成了练习，绘制的结果图看起来应该像下面这样：

（

您的图看起来可能会略有不同，这取决于随机选择的训练和测试集数据）

特别地，训练集和测试集的均方根（RMS，Root Mean Square）误差值都是介于4.5和5之间。

逻辑斯特回归（Logistic Regression）

在先前的学习中，学习了预测连续数值的方法（如预测房价，房价是连续值而不同于分类问题的离散值），如把输入值（如房屋大小）传给线性的函数。有

时候，反而希望预测离散变量（Discrete Variable），如预测网格中像素强度是代表一个“0”位还是一个“1”位。此时，这便是一个分类问题，逻辑斯特回归

（

Logistic Regression）对于学习这样的（分类）决策来说是一种简单的方法。

在线性回归中，尝试使用线性函数

标签（）预测（问题）的好办法。在逻辑斯特回归（Logistic Regression）中，使用了一个（与先前学到的）不同的假设空间（Hypothesis

Class）来尝试预测样本属于类

来对第个样本

（房屋特征）预测其（可能的）

值（房价）。这显然不是一个解决二值类

的概率，以及与其相对的类

的概率。具体而言，尝试使用如下形式的函数进行学习：

函数

值

通常被称为 “

通过型函数，被“挤”到

” 函数或 “

” （音译：逻辑斯特）函数——它是型函数（因函数图像是形状的），该函数输入

区间上，所以也可将其值看成是概率。我们的目标是找到一个值，使其能满足：当（输入的样本）属于 “1” 类

的概率时，

的值很大；或者反之，当计算属于 “0” 类的概率时，

的值很大。对于一组两类标记

的训练样本，使用下面的成本函数（Cost Function）来评估这个假设

的好坏：

需要注意的是，在上式的加和形式中，对每个训练样本，两项中只有一项是非零的（这取决于样本的真实类别标记

小化成本函数意味着需要使变大，而当时，（正如前文所讲）也想要

是 0 还是 1 ）。当

时，最

变大。对于一个逻辑斯特回归（Logistic Regression）的完整

解释以及成本函数（Cost Function）的推导过程，可以参考 CS229课程之监督学习。

现在，有了评价拟合训练数据的假设（或称为“假设函数”）

好坏的成本函数（Cost Function）。通过学习分类训练数据，最小化

（的方法）来找参

，那么该

数

的最优值。当完成了这一过程，便可对新的测试点通过计算所属“1”类和“0”类最可能的概率，进行分类。如果

样本就将标记为“1”类，否则（）标记为“0”类。其实，这好比检查是否成立。

为了最小化

，可以使用类似线性回归（Linear Regression）的工具。这需要提供一个可以在任意参数值时，可计算出

和（其微分结果的）

Undefined control sequence \triangledown 的函数。在给定参数

时，

的微分结果是：

若写成向量形式，其整个梯度可表示为：

Undefined control sequence \triangledown

除了当前的假设函数

，这里的梯度计算与线性回归基本相同。

练习 1B（Exercise 1B ）

本次练习的初学者代码已经在初学者代码（Starter Code）的 GitHub Rep 中的 ex1/ 目录中。

在本次练习中，您将会实现逻辑斯特回归（Logistic Regression）的目标函数（Objective Function）以及梯度计算（Gradient Computation），并使用您的

代码从 MNIST 数据集中，学习分类数字（“0”或“1”的）图像。如下是列举的一些数字图片样本：

使用 $2828像素规格来表示每个数字图像，将每张数字图像的格式变成有着2828 = 784 个元素的向量x^{(i)}的形式。其类标记是y^{(i)}\in {0,1}$ 两种值中的一

种。

您可以在初学者代码（Starter Code）中的 ex1/ex1b_logreg.m 文件中找到本次的练习。初学者代码（Starter Code）文件里将会给您显示如下任务：

. 调用 ex1_load_mnist.m 文件将 MNIST 训练与测试集数据载入。之后读入像素值到矩阵

中（第个样本的第个像素值就是

），同时

为了标签行向量具有零均值和单位方差，还需对像素强度做一些简单的标准化处理。尽管 MNIST 数据集包含了10个不同的数字（

次练习中，只将读取其中的数字和数字 —— ex1_load_mnist 函数将会为您做（数据载入）这些。

），但在本

. 为了

可以作为截距项（Intercept Term），在代码将中对参数后面追加一行数值

。

. 代码将会调用 minFunc包中的 logistic_regression.m 文件作为目标函数。您的任务是将 logistic_regression.m 文件中的代码补全，并使其返回目标函

数值及其梯度值。

. 在 minFunc包（的计算）完成后，在训练集和测试集上的分类准确率将会打印出来。

（

类似先前的）线性回归中的练习，您将会实现 logistic_regression.m，（该文件中的代码）在所有的训练样本

上进行循环，计算出目标函数

的值。所得到的目标值将会保存在变量中。你也需要计算梯度 Undefined control sequence \triangledown 并将其结果保存至变量中。当你完成

了这些任务，你将可以运行 ex1b_logreg.m 中的代码来训练分类器并测试它（的性能）。

如果您的代码工作正常，您将会发现您的分类器在训练集和测试集上能够达到100％的准确率！实际上，这是一个较简单的分类问题，因为数字

和

本身

看起来就很不相同。在今后的练习中，想要得到像这样完美的结果其实是很困难的。

向量化（Vectorization）

对于如房价数据的小数据量任务，通常使用线性回归，因为代码不需要执行地非常快。尽管您在练习 1A 和 1B 里是建议使用 for 循环的，但对于较大规模的

问题， for 循环的执行效率就比较低了。这是因为在 MATLAB 里，按顺序执行整个样本的循环是缓慢的。为了避免（使用） for 循环，想要重写（这部分）

代码，使其能尽可能地在 MATLAB 里高效地执行向量或矩阵操作（这点同样适用于其他语言，包括 Python，C/C++ —— 要尽可能地重用已经优化过的操

作，这里特指使用向量计算库来优化计算效率）。

下面是一些在 MATLAB 里各种向量化的操作方法。

案例：多矩阵-向量相乘（Example: Many matrix-vector products

）

经常一次计算多个矩阵或矢量的乘积（矩阵乘法）。例如，当对数据集（其中，参数可能是一个二维矩阵或矢量）中的每个样本计算

。要形成一个

包含整个数据集样本的矩阵

本：

，可以将每个输入样本的元素或者向量（按照行或列）

连接起来（更形象地表达是“拼起来”）。这里，每一列是一个样

因此，对于所有的样本

，

可以一次矩阵运算的形式完成所有样本的

计算：

所以，当执行线性回归（Linear Regression）时，可以通过计算

求得所有的

，以避免 for 循环对所有样本的遍历。

案例：标准化向量（Example: normalizing many vectors

）

假设有前文说到的由众多向量

连接形成的矩阵，同时要对所有的

计算

，可以用几个 MATLAB 的矩阵操作来完成。

X_norm = sqrt( sum(X.^2,1) );

Y = bsxfun(@rdivide, X, X_norm);

第一行代码，先对

中的所有元素做平方操作，所有元素再按列相加得到行向量，最终对行向量中的每个元素做开平方根操作。最后得到的是一个

行

列，包含了 $||x(i)||{2}$

bsxfun

Xnorm

rdivide

$X{ji}

x^{(i)}{j}除以在向量X\text{norm}中与其列位置相同的元素，最后得到Y{ji} = X_{ji} / {X\text{norm}}_i = x_j^{(i)}/||x^{(i)}||_2$。bsxfun 可以与几乎所有的二元

操作函数使用（例如，@plus，@ge或@eq），更多详情可以查看 bsxfun 的 MATLAB 文档。

案例：梯度计算的矩阵乘法（Example: matrix multiplication in gradient computations

）

在线性回归的梯度计算中，其形式可概括为：

当有通过单个索引（公式中的）与其它几个固定索引（公式中的）的求和操作时，经常将这个计算改写成矩阵乘法 $[A B]{jk} = \sum_i A{ji} B_{ik}

的形式。即，如果y和\hat{y}是列向量（有y_i \equiv y^{(i)}$），那么可将上面这样的求和模式重新写成下面这样：

因此，由于矩阵的整体计算思想，不需要逐个索引依次计算，实际只需计算

就可以了。在 MATLAB 中的实现如下：

X(j,i) = j'th coordinate of i'th example.

y(i) = i'th value to be predicted; y is a column vector.

theta = vector of parameters

y_hat = theta'*X; % so y_hat(i) = theta' * X(:,i). Note that y_hat is a *row-vector*.

g = X*(y_hat' - y);

进一步优化练习 1A 和 1B（Exercise 1A and 1B Redux ）

返回您练习的 1A 和 1B 代码中，在 ex1a_linreg.m 和 ex1b_logreg.m 文件中，您将发现调用 minFunc 时分别使用的是文件 linear_regression_vec.m 和

logistic_regression_vec.m ，但却是被注释掉的，而不是用 linear_regression.m 和 logistic_regression.m 文件。在本次练习中，请您将

linear_regression_vec.m 和 logistic_regression_vec.m 里的代码以（前文所讲过的）向量化的方式实现并补充完整。将 ex1a_linreg.m 和 ex1b_logreg.m 文

件中的注释取消掉，并比较二者代码的运行时间，检验（现在的代码）是否和先前原本的代码得到的结果是一样的。

调试：梯度检查（Debugging: Gradient Checking）

迄今为止，在 MATLAB 中已经实现了通过计算目标函数的导数来计算梯度的算法（这种求梯度的方法叫做解析解）。在后续章节中，将看到更复杂的模型

（

例如神经网络的反向传播算法）。对于这些模型，梯度的计算会变得难以调试，并难以得到正确结果。有时，代码中的微小错误也可以使模型学习到东

西，尽管表现稍稍不如完全正确的代码。因此，即使代码中微小的错误，也难说对最终结果有不好的影响。在本节中，将描述一种在数值层面（这种求梯度

的方法叫做数值解）上检查你的代码在导数计算部分的正确性。通过用数值解来验证导数求得的梯度结果，可以增加您在代码正确性上的信心。

译者注：_解析解指能够根据题意，得出在一定条件下的能够以数学表达式直接表达出来的的解。而数值解指在题中所给出的条件下难以用数学表达式表

达出来，或者能够表达出来但需要每个给定自变量值下的数字结果，而通过计算（手算或计算机计算）的出来的以表格或图形表示的结果。_数值解一般

是近似结果，它与微分方程的真实结果有偏差（参考：百度知道）。

假设想要最小化带有参数的函数

。在这个例子中，假设有

的导数，即（解析解）。

，

。如果使用 minFunc 或其它优化算法，在此之前已实现了某个

函数的代码，函数

是计算

怎样检查的代码实现是正确的呢？

再来回顾一下导数的数学定义：

因此，对任何特定的参数值，可以用下面这个方法（数值解）检查与导数值（解析解）是否接近:

在实践中，设置

为一小常量，通常设置为

。（

的值域范围尽管很大，但不设置

“非常”小，比如

，因为

这会产生计算机的舍入误差。）

译者注：_舍入误差，由于计算机的字长有限，进行数值计算的过程中，对计算得到的中间结果数据要使用“四舍五入”或其他规则取近似值，因而使计算

过程有误差。这种误差称为舍入误差（参考：百度百科）。

因此，对给定目标函数的导数

解）的正确性

，它计算的是

（即解析解），可以通过下面这个式子从数值角度（即数值解）来验证导数求得的解（即解析

以这两个值彼此的接近程度将取决于。假设

。通常，你会发现的上面这个约等式中的左手边和右手边两个计算出的结果，一致的位

数至少4位（但也经常更多）。

现在，考虑一下参数是一个向量，而非单个实数的情况（为了想要学到的个参数），并且有

。现在，概括了导数检查过程，其中参数

可能是一个向量（如在线性回归和逻辑回归的例子中的）。如果正在通过几个向量或者矩阵来做优化，可以将这些参数“打包”进一个“长”的向量中去。在这

里，可以用同样的方法来检查导数。（这也可以使用现成的优化包来完成）。

假设有目标函数

的导数

的计算并化简出的结果：

；想要检查通过导数算出的梯度

是否输出了正确的导数值（即梯度值）。有

，

其中

是第个基向量（

增加外，参数

是与参数同维度的向量，在

是相同的。同理，

向量中第个位置的元素值为

，其余全部为

）。所以，除了其第个元素被

相减得到的向量。

与

是参数向量在第个位置的元素被

现在，可以从数值上（数值解的角度），对第个参数的梯度

证解析解），以验证解析解的正确性：

进行检查（译者注：检查的是模型参数向量中每一个参数的梯度，从数值解的角度来验

梯度检查代码（Gradient checker code ）

本次练习，将尝试实现上述方法来检查您的线性回归（Linear Regression）和逻辑斯特回归（Logistic Regression）函数的梯度。另外，您也可以使用提供

的 ex1/ grad_check.m 文件（其中带有的参数与 minFunc 类似），对众多随机选择的

做

导数值的检查。

Softmax 回归（Softmax Regression）

介绍（Introduction ）

Softmax 回归（或称为多元逻辑斯特回归），是逻辑斯特回归用来处理多类分类问题的更一般化形式。在逻辑斯特回归中，假定类别标签都是二元的：即

之前曾用这样的一个分类器来做两类的（数字 1 和 0 的）手写数字分类。然而， Softmax 回归可处理 K 个类别的分类问题，其中类别标签

。

不妨再回顾一下逻辑斯特回归，有

个已标记类别的训练集

，假设采取的形式为：

，其中（每个样本的）输入特征是

。在先前的逻辑

斯特回归中，分类设定是两类，所以类标签

其中，模型参数在最小化代价函数时求得：

在 Softmax 回归的设定中，（与前文中两类分类不同）因为重点关注在多类分类，即类别标签可以取

值。因此，训练集样本的类别标签值有。（注意：通常类别标签起始于，而不是）。举个例子，

数字识别任务（译者注： MNIST 是一个手写数字识别库，由 NYU 的 Yann LeCun 等人维护。http://yann.lecun.com/exdb/mnist/ ）中，

即类别总数是个。

个不同的值，而不仅限于（两类分类中的）两个

在

，

给出测试输入，希望假设可以针对同一样本在不同的（其中，

）值下估计概率

的值。也就是说，想要估计类标签取

个

不同的值时的概率。由此，假设将会输出

形式为：

维向量（该向量元素值和为），它给出的是个类别对应的估计概率值。更具体地说，假设

会采取

$$ \begin{align} h_\theta(x) = \begin{bmatrix} P(y = 1 | x; \theta) \ P(y = 2 | x; \theta) \ \vdots \ P(y = K | x; \theta) \end{bmatrix}

frac{1}{ \sum_{j=1}^{K}{\exp(\theta^{(j)\top} x) }}

end{align} $$

这里，

一项。

是模型的参数。需要注意的是，

这一项对分布进行了标准化（

），所以其（最终）会加和为

为方便起见，也写来表示模型的所有参数。当你实现 Softmax 回归时，

行

列的矩阵其实也是一列列所组成的，即

代价函数（Cost Function ）

现在来描述 Softmax 回归的代价函数。在下面的方程中，

值为真的表达式值为假的表达式。例如，

被称为“指示器函数”（ indicator function ，译者注：老版教程中译为“示性函数”），即

，

求出的数值为；而

求出的数值为。代价函数将会是：

Missing or unrecognized delimiter for \left

值得注意的是，逻辑斯特回归的代价函数也可等价地写成如下形式：

Missing or unrecognized delimiter for \left

个不同的类标签的概率值相加外，逻辑斯特回归的代价函数与 Softmax 的代价函数是相似的。需要注意的是，在 Softmax 回归中有：

除了需要将

对于

的最小化（最优化）问题，目前还没有闭式解法（译者注：闭式解法，

，即计算解析解的方法，指无需通过迭代计算而得

到结果的解法）。因此，如往常一样，使用优化算法通过迭代的方式求解。对目标函数求导数（即梯度），其梯度为：

回想

符号的含义。尤其需要注意的是，

本身就是一个向量，所以，其第个元素即

。

，它是关于

的第个元素的偏导数。

有了该导数公式，之后可将其插入到一个优化包中并最小化

Softmax 回归的参数属性（Properties of Softmax regression parameterization

）

Softmax 回归有一个不同寻常的特性，那就是参数冗余（

时，向量中的每个元素就被（其中

）。为解释这个特性，假设有参数向量

，对该向量减去某个固定的向量，此

）替代了。那么此时，假设在计算输入样本的类标签的概率时，就表示为：

换句话说，从参数向量中的每个元素

模型是过参数化的（

中减去一点也不会影响到假设的类别预测！这表明了 Softmax 回归的参数中是有多余的。正式地说， Softmax

，或参数冗余的），这意味着对任何一个拟合数据的假设而言，多种参数取值有可能得到同样的假设

，即从

输入经过不同的模型参数的假设计算从而得到同样的分类预测结果。

进一步说，若成本函数

小化。因此，的最小值时的参数并不唯一。（有趣的是，

或不可逆的，这将会导致在牛顿法的直接实现上遇到数值问题。）

被某组模型参数

最小化，那么对任意的，成本函数也可以被

最

仍是凸的，并且在梯度下降中不会遇到局部最优的问题，但是

矩阵是奇异

注意到，通过设定

参数向量中的最后一个（或该向量中任意其它任意一个）元素

个参数（其中），也可令

，总是可以用

（是全零向量，其元素值均为）代替

，而不会对假设函数有任何影响。因此，可以去掉

，而不影响假设函数的表达能力。实际上，因参数冗余的特性，与其优化全部的

，只优化剩余的

个参数，算法依然能够正常工作。

与逻辑斯特回归的关系（Relationship to Logistic Regression）

在

特例中，一个可以证明的是 Softmax 回归简化为了逻辑斯特回归，表明 Softmax 回归是逻辑斯特回归的一般化形式。更具体地说，当

，

Softmax 回归的假设函数为

$$ \begin{align} h_\theta(x) &=

frac{1}{ \exp(\theta^{(1)\top}x) + \exp( \theta^{(2)\top} x^{(i)} ) }

end{align} $$

利用“假设是过参数化的”（或说“假设的回归参数冗余”）这一特点，设定

$ \begin{align} h(x) &=

frac{1}{ \exp( (\theta^{(1)}-\theta^{(2)})^\top x^{(i)} ) + \exp(\vec{0}^\top x) }

，并且从这两个向量中都减去向量

，得到

end{align} $$

因此，用一个参数向量来表示

，就会发现 Softmax 回归预测其中一个类别的概率为

这与逻辑斯特回归是一致的。

，另一个类别的概率为

，

练习 1C（Exercise 1C ）

针对这一部分练习的初学者代码（Starter code）已经在 GitHub 代码仓库中的 ex1/ 目录下。

在本次练习中，您将会借助

的部分会与先前在练习 1B 中的代码（仅仅是识别数字

的改变可以使您方便地将的值作为矩阵的下标。）

数据集，训练一个用于处理

个数字的分类器。这部分代码除会读取整个

从原本的类到现在的

数据的训练和测试集外，其余

类，即。（标签值

和

）非常类似，并且标签值

这部分代码的表现应该和在练习 1B 中的一样：读取训练和测试数据，同时加入截距项，然后借助 softmax_regression_vec.m 文件调用 minFunc 作为目标函

数。当训练完成后，将会输出手写数字识别问题中，这个类（译者注：对应从个数字）的训练和测试集上的准确率。

到

这

您的任务是实现 softmax_regression_vec.m 文件中计算 softmax 目标函数

的部分，同时将计算结果存储在变量中。

您也务必计算梯度项

列的矩阵（对于

，并将其结果存在变量中。请不要忘记 minFunc 提供了向量参数。初学者代码将会对参数变形为一个

个类这种情况，即）。同时，您也不要忘记了如何将返回的梯度返回成一个向量的方法，即 g=g(:) ；

行

如果有必要得到梯度权，您可以以写一段使用 for 循环的代码开始（请务必使用前面介绍的渐变检查调试策略！）。然而，您也许会发现这个实现的版本速

度太慢，以至于优化不能通过所有的方式（译者注：翻译不确定。“However, you might find that this implementation is too slow to run the optimizer all the

way through.”）。在您得到一个运行较慢梯度权计算的版本后，您可以在进行所有实验前，尝试尽可能地将您的代码进行向量化处理。

下面是几条 MATLAB 的小提示，可能对您实现或者加速代码能起到作用（这些提示可能多少会有用处，但更多地取决于您的实现策略）。

. 假设有一个矩阵

sub2ind来实现：

，想从每行抽出单个元素。其中，从第行抽出的元素，其列值并存在变量

中，是一个行向量。这个转换过程可以用函数

I=sub2ind(size(A), 1:size(A,1), y);

values = A(I);

这段代码将会采用索引对

将会矩阵中位置在

，并计算出矩阵

中在

位置处的一维索引。所以，

将会矩阵

中位置在

处的元素下标，同样，

处的元素下标。

. 当您计算预测类标签概率 $\hat{y}^{(i)}k = \exp(\theta{:,k}^\top x^{(i)}) / (\sum^K_{j=1} \exp(\theta_{:,j}^\top x^{(i)}))$ 时，试着用矩阵乘法以及 bsxfun 来

加速计算。比方说，当是矩阵的形式时，您可以为每个样本及其对应的类使用这样矩阵的形式，来计算乘积（再次强调一下，第

已经从中省略了，也就是说的值被假定为）。

类

检查：偏差和方差（Debugging: Bias and Variance）

到目前为止，已经看到了多种类型的机器学习算法是如何实现的。通常的目标是在新的测试数据上得到尽可能高的预测准确率，来自测试集上的样本是算法

在训练期间未曾见过的。事实证明，训练数据上的准确率有一个上限，该上限是可以在测试数据上预测出来的（有时，在测试数据上的小样本量上能得到较

幸运，更好的效果，但平均来看却倾向于较差的效果）。

从某种意义上说，训练数据是“容易”（学习或者说“容易”拟合），因为模型的参数的训练是基于训练集数据训练得出的，也因该原因，在训练集数据和测试集

数据间的准确率总是有差距。

调试：优化器和目标（Debugging: Optimizers and Objectives）

这一节留下（大坑）待写（译者注：很多年了，该大坑一直没被填上）。

多层神经网络（Multi-Layer Neural Network）

考虑一个监督学习问题，即使用带标签的训练样本

拟合数据。

。神经网络给出一种定义复杂非线性假设的形式

，该形式有参数

，可被用来

说到神经网络，我们从一个最简单的单个神经元的神经网络开始。下面这幅图就表示单个神经元：

该神经元是一个接收

输入的计算单元（其中，有一个输入

是截距项），它会输出

。其中，

称为“激活函数”。本文选择 S 型函数作为激活函数

：

该神经元被定义为一种逻辑斯特回归形式的输入-输出映射。

尽管本文使用的激活函数是型函数，但双曲正切或正切函数也是常见的激活函数可供选择，下面是双曲正切函数：

最近的研表明了一种与众不同的激活函数，校正线性函数（

，译者注：但实际中没人这么说，一般都称为

不同，因为该函数值没有上界，而且不是连续可微的。下面给

）

出

，对于深层神经网络的训练，其效果更好。这种激活函数与型函数和双曲正切函数

激活函数的形式：

下图是型函数，双曲正切函数

以及

函数的图像：

双曲正切函数

是

型函数的一个缩放版本，其输出范围是

，而不是

。

函数是一个线性分段函数，当输入的值小于

表示，而是由参数单独表示。

时，其函数值为

。

需注意的是，与其它地方（ OpenClass ，以及部分 CS229 的课程）不同，截距项的表示没有按照惯例用

最后，说一个在后文有用的恒等式：

导数为），您也可以根据导数的定义对型函数（或双曲函数

，输入值时的梯度是未定义的，但这不会在实际中引起问题，因为在优化过程中，某次迭代的梯度值是基于大量训练样本计算出的梯度的平均。

是一个型函数，其导数为

（若是双曲函数

，则其

）求导。

函数在输入时梯度为，其它取值时

为

神经网络模型（Neural Network model ）

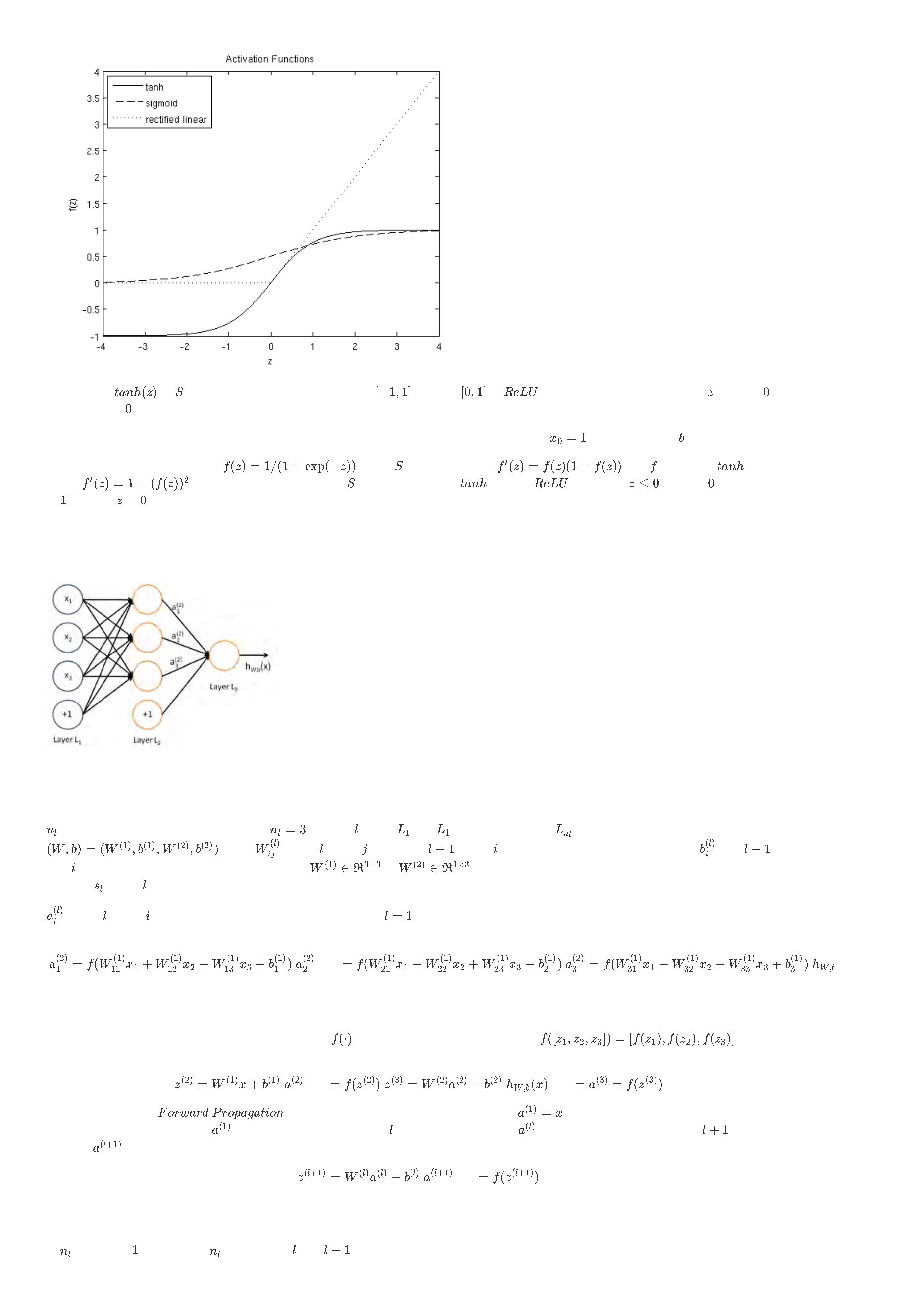
神经网络是通过将众多简单的神经元连接在一起得到的，一个神经元的输出可作为另一神经元的输入。例如，这里有一个小神经网络：

图中，用圆圈表示网络输入。圈里被标为 “+1” 的圆圈称为偏置单元，对应于截距项。网络最左边的那一层称为输入层，而输出层即最右层（在这个例子中，

输出层只有一个节点）。介于最左（输入层）和最右（输出层）的中间层称为隐藏层，称为“隐藏”是因为其值在训练集中无法观察到。该例中的神经网络有 3

个输入单元（不计偏置单元计算在内）， 3 个隐藏单元，和 1 个输出单元。

表示网络的层数；在该例中的神经网络层数

参数

的第个单元的偏置。因此，在我们的例子中，我们有

为 “+1”。表示第层节点单元的数量（不包括偏置单元）。

。第一层表示为

，层

即输入层，输出层用

来表示。神经网络模型的参数是

是第

，

表示第层的第个单元与第

层的第个单元的连接权重。请注意下标的次序，

层

，

。需要注意的是，偏置单元没有与上层的连接，它们输出的值总是

表示第层的第个单元的激活值（也可理解为输出值）。当层数

时，用 $a^{(1)}i = x_i表示第i层的输入。当参数W, b

为确定值时（译者注：即确定了模型的参数），神经网络即定义了一个能输出实数的假设h{W,b}(x)$ 。具体而言，该神经网络表示的计算为：

在后文中，还将用 $z^{(l)}i表示第l层的第i个单元输入的总加权求和，其中包含偏置项（例如，第2层的第i个单元输入的总加权求和值为\textstyle z_i^{(2)} =

sum{j=1}^n W^{(1)}_{ij} x_j + b^{(1)}_i），第l层的第i个单元（译者注：即激活单元的计算或输出值）为a^{(l)}_i = f(z^{(l)}_i)$ 。

需要注意的是，后一种写法更紧凑。具体来说，将激活函数

以把上述方程写成一种更紧凑的形式：

应用到向量中的每一个元素上（例如，

），那么可

这一步称为前向传播（

）。可以写成更一般的情况，回顾一下先前使用

表示输入层的值（译者注：为与下一句对应，

因为输入层没有激活函数，输入层

相当于第一层的输出），那么第层的激活（输出）表示为

，那么写成更一般的形式，计算第

层的激活

（

输出）

表示为：

通过组织原本的参数到矩阵中，可以充分利用矩阵操作进行网络参数的快速计算。

从开始到现在，我们都集中在一开始的神经网络的架构上，但也可以建立其它体系结构（即神经元之间的连接模式），比方包括多个隐藏层。最常见的是一

个层网络，层为输入层，层为输出层，层到层都是密集连接（译者注：即全连接）起来的。此时，计算网络的输出，可以用上述公式中描

述的传播步骤，依次计算所有的激活层，从层

，到层

等等，直到层

。这是一个前馈神经网络（

两个隐含层，以及在输出层有两个输出单元的神经网络：

）的例

子，前馈网络，即没有任何有向环或闭合圈的连通图。

神经网络的输出层可以有多个输出单元。例如，下图是一个有着

和

为训练该网络，需要带类别标签的训练样本

，其中

。若您的预测需要有多个输出，那么就可以使用这种网络架构。（例如，在医学

诊断中的应用，输入特征是向量表示病人的某些特征，需要的输出可能表明不同种疾病（译者注：多个类别）是否存在。）

反向传播算法（Backpropagation Algorithm

）

假设有一组固定的训练集

。可以使用批量梯度下降算法训练网络。当一个训练样本

时，成本函数定义为：

这是一个（半）平方误差函数。给定一组有

个样本的训练集，成本函数定义为：

$$ \begin{align} J(W,b) &= \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} ; \sum_{i=1}^{s_l} ;

sum_{j=1}^{s_{l+1}} \left( W^{(l)}{ji} \right)^2 \ &= \left[ \frac{1}{m} \sum{i=1}^m \left( \frac{1}{2} \left| h_{W,b}(x^{(i)}) - y^{(i)} \right|^2 \right) \right] +

frac{\lambda}{2} \sum_{l=1}^{n_l-1} ; \sum_{i=1}^{s_l} ; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2 \end{align} $$

在

定义中的第一项是均方差项。第二项是一个正则化项（也叫权重衰减项），它会降低权重的大小，并有助于防止过拟合。

（

注：权重衰减通常不用在偏置项），比如在定义中就没有使用权重衰减。一般来说，将权重衰减应用到偏置单元中只会对最终的神经网络

产生很小的影响。如果您在斯坦福选修过 CS229 （机器学习）课程，或者在 YouTube 上看过该课程视频，您也许会认识到这里的权重衰减，其实是课上提

到的贝叶斯正则化方法的变种，在贝叶斯正则化中，高斯先验概率被引入到参数中计算

（极大后验）估计（而不是极大似然估计）。

权重衰减参数用于控制公式中两项的相对重要性。在此重申一下这两个复杂函数的含义：

是针对单个样本计算平方误差得到的代价函数；

而

则是对整体样本的代价函数，它包含权重衰减项。

以上的代价函数通常被用来解决分类和回归问题。在分类问题上，分别用

或

来表示这两个类标签（回顾一下型激活函数的输出值介于

之

间；如果我们之前使用

确保最终其输出值在

双曲正切激活函数，那么激活函数的输出值将会是

上（如果使用双曲正切激活函数，那么输出值在

和

，刚好用来代表两类）。在回归问题上，首先放缩输出值范围，

上）。

优化的目标是最小化把

和

作为参数的函数

。为训练神经网络将会初始化每一个

生成随机值，其中设置为

参数，以及每一个

参数，它们会被初始化为接近

且小的随机值（对于初始化的方法，比方用正态分布

等方法来对参数优化。因为

的效果通常还不错。最后需要注意的是，对参数进行随机初始化是很重要的，而不是把它们的值全部初始化为。如果所有的参数都起始于一个相同的值，

），之后再对目标函数应用如批量梯度下降法（

）

是一个非凸函数，梯度下降有可能使函数值到达局部最优；然而在实际中，梯度下降

那么所有的隐含层单元将会学习到一样的函数值（对于所有的值，

将总是相同的，即对任意输入，有

）。随机初始化

的目的是使对称失效（

）。

梯度下降法中每一次迭代都按照如下公式对参数

和

进行更新：

其中，是学习率，上述公式中一个关键步骤是计算偏导数。现在来讲一下反向传播（

首先讲反向传播是如何计算的，以及针对一个样本

的偏导数：

）算法，它是一种计算偏导数的高效方法。

和

的代价函数

的偏导数。一旦把这些计算

出来了，将会很容易地得到计算所有样本的代价函数

上述两个公式略有不同，因为权重衰减应用在参数

上，而不是参数

。

反向传播算法背后的过程如下：给定一个训练样本

对每层的每个节点计算一个误差项（

，首先前向传递计算整个网络的每层激活，以及假设最终输出的

，该误差项描述的是当前节点对网络输出层误差的贡献度。

。之后反向回传误差，

）

对输出层节点而言，可以直接计算出网络在该节点的输出值（即激活值）和真实目标值的差距，该值就是误差项

那隐单元的误差项呢？对隐含单元来说，基于误差项的加权平均，即把作为输入的节点的误差项的加权平均，来计算

（第

层是输出层）。

，反向传播算法的描述如下：

. 前向传递计算层

直到输出层

的激活函数值。

. 对第

层的第个输出单元，计算该输出单元的误差项 $$ \begin{align} \delta^{(n_l)}_i = \frac{\partial}{\partial z^{(n_l)}i} ;; \frac{1}{2} \left|y - h{W,b}

(x)\right|^2 = - (y_i - a^{(n_l)}_i) \cdot f'(z^{(n_l)}_i) \end{align} $$

. 循环层数。

循环当前层（第层）节点（第个节点），设定

$ \delta^{(l)}i = \left( \sum{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i) $$

. 计算所需部分的偏微分，如下已给出：

$ \begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) &= a^{(l)}j \delta_i^{(l+1)} \ \frac{\partial}{\partial b{i}^{(l)}} J(W,b; x, y) &= \delta_i^{(l+1)}.

end{align} $$

用矩阵或向量的符号标记来重写算法。使用来表示逐个元素的点乘操作（在 Matlab 或 Octave 中，用 .* 表示点乘操作，也称为

乘积）。两

个向量对应元素的点乘是

式：

，逐个元素的点乘表示为

。

和

也都可以应用到向量上，从原本逐个元素的形式改写成等价的形

现在，矩阵形式的反向传播算法描述如下：

. 前馈传播计算第 2 和第 3 层（

）直到输出层

的激活函数值。

. 计算输出层（即第层）与实际值的误差

. 反向循环层数

。

，反向计算各层每个神经元的误差

. 计算所需部分的偏微分，如下已给出：

实现须知：在以上所述的第 2 、第 3 步中，需要计算第层中每个节点的偏导数

。若

是

型激活函数，先前已经将第层的第个节点的

激活函数值存储在了网络中。因此，可以通过先前得出的

可进一步计算反向回传到第层的误差项。

的表达式，计算第层中第个节点的激活函数的偏导数

，从而

现在，便可以描述完整的梯度下降算法了。下面是伪代码，

是一个矩阵（与

同一维度），

是一个向量（与

同一维度）。注意这个

符号，

是一个矩阵，尤其要说明的是，它并不是

乘以

。

，实现一次梯度下降的过程如下：

. 对所有层，设定矩阵或向量中元素值均为

：

，

。

. 使用反向传播计算

. 设定

. 更新参数：

和

。

现在，就可以通过反复迭代上述梯度下降的步骤来训练神经网络，来寻找成本函数

最小值时候的参数值。

神经网络向量化（Neural Network V ectorization ）

注：本章节翻译完全参考旧版 UFLDL 中文教程。

在本节，我们将引入神经网络的向量化版本。在前面关于神经网络介绍的章节中，我们已经给出了一个部分向量化的实现，它在一次输入一个训练样本时是

非常有效率的。下边我们看看如何实现同时处理多个训练样本的算法。具体来讲，我们将把正向传播、反向传播这两个步骤以及稀疏特征集学习扩展为多训

练样本版本。

正向传播（ Forward propagation

）

考虑一个三层网络（一个输入层、一个隐含层、以及一个输出层），并且假定是包含一个单一训练样本

如下：

的列向量。则向量化的正向传播步骤

这对于单一训练样本而言是非常有效的一种实现，但是当我们需要处理

个训练样本时，则需要把如上步骤放入一个 for 循环中。

更具体点来说，参照逻辑回归向量化的例子，我们用 Matlab/Octave 风格变量表示包含输入训练样本的矩阵，

代表第个训练样本。则x正向传播

步骤可如下实现：

非向量化实现

for i=1:m,

z2 = W1 * x(:,i) + b1;

a2 = f(z2);

z3 = W2 * a2 + b2;

h(:,i) = f(z3);

end;

这个 for 循环能否去掉呢？对于很多算法而言，我们使用向量来表示计算过程中的中间结果。例如在前面的非向量化实现中，

用来计算隐层和输出层的激励结果。为了充分利用并行化和高效矩阵运算的优势，我们希望算法能同时处理多个训练样本。让我们先暂时忽略前面公式中的

（把它们设置为），那么可以实现如下:

都是列向量，分别

和

向量化实现 (忽略 b1, b2)

z2 = W1 * x;

a2 = f(z2);

z3 = W2 * a2;

h = f(z3)

在这个实现中，

都是矩阵，每个训练样本对应矩阵的一列。在对多个训练样本实现向量化时常用的设计模式是，虽然前面每个样本对应一个列向

就成了一个的矩阵（

输入到网络中时，它的第列就表示这个输入信号对

量（比如

），但我们可把这些列向量堆叠成一个矩阵以充分享受矩阵运算带来的好处。这样，在这个例子中，

是

网络第二层中的神经元数，

是训练样本个数）。矩阵

的物理含义是，当第个训练样本

隐神经元（网络第二层）的激励结果。

在上面的实现中，我们假定激活函数

接受矩阵形式的输入，并对输入矩阵按列分别施以激活函数。需要注意的是，你在实现

函数，则实现代码如下所示:

的时候要尽量多用

Matlab/Octave 的矩阵操作，并尽量避免使用 for 循环。假定激活函数采用

低效的、非向量化的激活函数实现

function output = unvectorized_f(z)

output = zeros(size(z))

for i=1:size(z,1),

for j=1:size(z,2),

output(i,j) = 1/(1+exp(-z(i,j)));

end;

end

高效的、向量化激活函数实现

function output = vectorized_f(z)

output = 1./(1+exp(-z));

end

% "./" 在Matlab或Octave中表示对矩阵的每个元素分别进行除法操作

最后，我们上面的正向传播向量化实现中忽略了

和

，现在要把他们包含进来，为此我们需要用到 Matlab/Octave 的内建函数 repmat ：

正向传播的向量化实现

z2 = W1 * x + repmat(b1,1,m);

a2 = f(z2);

z3 = W2 * a2 + repmat(b2,1,m);

h = f(z3)

repmat(b1,1,m) 的运算效果是，它把列向量

拷贝

份，然后堆叠成如下矩阵：

这就构成一个

结果还是一个矩阵）的每一列加上

Matlab/Octave 的内建函数，运行起来是相当高效的，远远快过我们自己用 for 循环实现的效果。

的矩阵。它和

相加，就等于是把

矩阵（译者注：这里是训练矩阵而非向量, 所以

代表两个矩阵相乘，

。如果不熟悉的话，可以参考 Matlab/Octave 的帮助文档获取更多信息（输入 “help repmat” )。 repmat 作为

反向传播（Backpropagation

）

现在我们来描述反向传播向量化的思路。在阅读这一节之前，强烈建议各位仔细阅读前面介绍的正向传播的例子代码，确保你已经完全理解。下边我们只会

给出反向传播向量化实现的大致纲要，而由你来完成具体细节的推导（见向量化练习）。

对于监督学习，我们有一个包含

里考虑的是更一般的情况。）

个带类别标号样本的训练集

。（对于自编码网络，我们只需令

即可，但这

假定网络的输出有

维，因而每个样本的类别标号向量就记为

。在我们的 Matlab/Octave 数据结构实现中，把这些输出按列合在一起形成一个

Matlab/Octave 风格变量，其中第

列

就是

。

现在我们要计算梯度项

们可以这样来计算：

和

。对于梯度中的第一项，就像过去在反向传播算法中所描述的那样，对于每个训练样本

，我

在这里表示对两个向量按对应元素相乘的运算（译者注：其结果还是一个向量）。为了描述简单起见，我们这里暂时忽略对参数

正实现反向传播时，还是需要计算关于它们的导数的。

的求导，不过在你真

假定我们已经实现了向量化的正向传播方法，如前面那样计算了矩阵形式的变量

和

，那么反向传播的非向量化版本可如下实现：

gradW1 = zeros(size(W1));

gradW2 = zeros(size(W2));

for i=1:m,

delta3 = -(y(:,i) - h(:,i)) .* fprime(z3(:,i));

delta2 = W2'*delta3(:,i) .* fprime(z2(:,i));

gradW2 = gradW2 + delta3*a2(:,i)';

gradW1 = gradW1 + delta2*a1(:,i)';

end;

在这个实现中，有一个 for 循环。而我们想要一个能同时处理所有样本、且去除这个 for 循环的向量化版本。

为做到这一点，我们先把向量

并且对矩阵的按元素分别执行

不再需要外层的 for 循环）。

和

替换为矩阵，其中每列对应一个训练样本。我们还要实现一个函数 fprime(z) ，该函数接受矩阵形式的输入

。这样，上面 for 循环中的行 Matlab 代码中每行都可单独向量化，以一行新的（向量化的） Matlab 代码替换它

，

（

在向量化练习中，我们要求你自己去推导出这个算法的向量化版本。如果你已经能从上面的描述中了解如何去做，那么我们强烈建议你去实践一下。虽然我

们已经为你准备了反向传播的向量化实现提示，但还是鼓励你在不看提示的情况下自己去推导一下。

稀疏自编码网络（Sparse autoencoder

）

稀疏自编码网络中包含一个额外的稀疏惩罚项，目的是限制神经元的平均激活率，使其接近某个（预设的）目标激活率。其实在对单个训练样本上执行反

向传播时，我们已经考虑了如何计算这个稀疏惩罚项，如下所示：

$$ \begin{align} \delta^{(2)}i = \left( \left( \sum{j=1}^{s_{2}} W^{(2)}_{ji} \delta^{(3)}_j \right) + \beta \left( - \frac{\rho}{\hat\rho_i} + \frac{1-\rho}{1-\hat\rho_i}

right) \right) f'(z^{(2)}_i) . \end{align} $$

在非向量化的实现中，计算代码如下：

稀疏惩罚Delta

sparsity_delta = - rho ./ rho_hat + (1 - rho) ./ (1 - rho_hat);

for i=1:m,

delta2 = (W2'*delta3(:,i) + beta*sparsity_delta).* fprime(z2(:,i));

end;

但在上面的代码中，仍旧含有一个需要在整个训练集上运行的 for 循环，这里

是一个列向量。

作为对照，回想一下在向量化的情况下，

有的训练样本一视同仁。这意味着要向量化实现上面的计算，只需在构造

码，我们只需简单的用 repmat 命令把 sparsity_delta 加到的每一列上即可（译者注：这里原文描述得不是很清楚，看似应加到上面代码中

行等号右边第一项，即上）。

现在应该是一个有

列的矩阵，分别对应着

个训练样本。还要注意，稀疏惩罚项 sparsity_delta 对所

时，往矩阵的每一列上分别加上相同的值即可。因此，要向量化上面的代

监督神经网络（Supervised Neural Networks ）

练习：监督神经网络（Exercise: Supervised Neural Networks）

本次练习中，您将训练一个神经网络分类器，并在 MNIST 数据集上对 10 类的手写数字图像分类。神经网络的输出单元与您在 Softmax 回归练习中创建的

是相同的。仅使用 Softmax 回归的函数去拟合训练集效果并不会很好，其中一个原因是欠拟合（

）。

相比之下，有着更低偏差（）的神经网络应能更好地拟合训练集。在多层神经网络这一节中，网络参数的梯度是使用反向传播算法对所有参数计算平

方误差形式的损失函数（译者注：损失函数，即代价函数）得到的。在本次练习中，需要用到在 Softmax 回归（交叉熵）形式的成本函数，而不是平方误差

形式的代价函数。

神经网络的代价函数与 Softmax 回归的代价函数基本一样。需要注意的是，与从输入数据做预测不同， Softmax 函数把网络

的隐含层的最后一

层作为输入。其损失函数为：

Missing or unrecognized delimiter for \left

神经网络和 Softmax 回归在成本函数上的不同，会导致在对输出层

的误差项上二者计算出的值不同。 Softmax （交叉熵）代价为：

使用这一项，您可以得到计算所有网络参数梯度的完整反向传播算法。

用前文给出的初学者代码，创建神经网络的前向传播代价函数，并计算其梯度。先前，用 minFunc 优化包来做基于梯度的优化。记得您要对梯度计算的结果

进行数值检查。您的实现应该支持多隐含层的神经网络训练。当您在代码实现时，请遵循下面的操作要点：

实现一层隐含层的网络，并做梯度检查。在梯度检查时，您也许会想通过裁剪训练数据的矩阵，来减少输入维度和样本数量。梯度检查时，您可以使用

较小数量的隐单元以减少计算时间。

实现两个隐含层网络的梯度检查。

训练并测试不同的网络架构。您可以实现在一层上有256个隐含单元的隐含层，该结构可以达到在训练集上 100% 的精度。因为有很多参数，所以存在

过拟合的风险。通过对不同的层数，隐含层数，以及权重衰减惩罚值的实验，来进一步理解什么样的架构表现最好。您能找到一个优于您最好的单隐含

层架构的多隐含层网络吗？

（

可选）扩展您的代码使其支持多种非线性隐含单元的选择（型函数，双曲正切

函数和 ReLU 函数）。

监督卷积网络（Supervised Convolutional Neural Network

）

使用卷积进行特征提取（Feature Extraction Using Convolution）

概览（Overview ）

在之前的练习中的图片分辨率都偏低，如手写数字图像。在本节中将会学到一种方法，能够用在实际中更大的图像数据集上。

全连接网络（Fully Connected Networks

）

在稀疏编码器（译者注：后文会讲到，这部分是老版的教程，所以内容跳跃了）中，一种设计选择是先前已经讲到的“全连接”，即所有的隐含层单元与所有

输入单元完全连接起来。在先前练习中使用的是相对较小的图像（例如，在稀疏编码的任务中

像素大小的图像，以及 MNIST 数据集中

像素

大小的图像），这种“全连接”方式的特征学习，虽然在整个图像上的计算是可行的。然而，对于更大图像，如

像素大小的图像的学习来说，由于连

接是全连接的形式来做特征学习，计算代价是很大的——网络大概会有

数量级的输入单元，假设要学习

个特征（译者注：即下一层有

隐含层

单元，该过程是在学习一种基于原始数据的压缩特征表达），那就会有

数量级（译者注：输入层个输入单元与第一个隐含层的

个隐含单元全

连接需要

就有

个参数）的参数需要学习。相较于

像素大小的图像（译者注：假设隐含层也是

个神经元，仅输入层到第一个隐含层需要的参数

倍（译者注：单纯从二者

个，即需要的参数的量级为

），在前向和反向传播的计算上大图像比小图像也会慢大约

相差的参数量级上的比较）。

局部连接网络（Locally Connected Networks

）

该问题的一种简单解决方案是限制隐含单元与输入单元的连接数目，也就是说，隐含单元只允许连接一部分的输入单元（译者注：即隐藏层的神经元与原图

中的一个小图建立连接权重）。具体而言，每个隐藏单元将连接到输入像素中的一个小的连续区域。（对于不同于图像的数据形式，也有一种自然的方式来

选择从输入单元到一个隐含单元需要处理的“连续组”，例如，对于音频，一个隐藏单元可能被连接到一个与之特定时间跨度对应的音频剪辑的输入单元

上。）

局部连接网络的这一想法也借鉴了在生物学上早期视觉系统的观点。具体而言，视觉皮层的神经元有着局部感受区域（即，它们只会对某一位置的刺激做出

反应）。

卷积（Convolutions ）

自然世界中的图像有着“固定不变”的属性（译者注：或称为“静态性”），这也意味这图像的某一部分的数据和另一部分的数据是一样的。这表明，在一张图像

上某部分的特征也可应用到该图片的其它部分，基于这一观点——网络可以使用不同的特征，应用到局部数据一样但不同的位置上。

更确切地说，从一张高分辨率图像上随机地抽样小图片（比方说

学习特征滤波器的权重）应用到这幅图片的其它任何地方。可以把学到的

在同一张图片上获得在每个位置处不同的特征激活值。

大小的图片）做特征学习，将这个完成学习的

大小的特征检测器（译者注：

特征（译者注：滤波器），通过将它们与更大图片“卷”起来的方式，

讲个具体的例子，假设您已经从

大小的图片上做了

大小的抽样的特征学习。再进一步假设，这一特征学习过程是通过有着

个隐含单元

），您将

的自动编码器完成的。为了获得卷积特征（即

大小的图片上每

大小范围的特征，这个

区域是从

会从原图提取

为滤波器）的

大小的小图片，通过您训练的稀疏自动编码器来获取特征激活。这将会产生

大小的卷积特征。

组（译者注：对应这一卷积层的

个神经元或者称

正式地说，给定分辨率大小为

器来进行个特征的学习（译者注：这里特征的学习，即滤波器或神经元权重的学习。是卷积层神经元或滤波器的数目，也是该卷积层输出的通道数），

这个学习过程是通过给出的从可见单元（译者注：原文中是，推测是输入单元，一般来说可见单元既包括输入单元也包括输出单元）到隐含单

的图像

，首先对这些图像进行抽样，抽样出大小为

的小图像

，利用这些小图像通过稀疏自动编码

元的权重

图像的

和偏置

，计算

（译者注：其中，

的三维张量。

（其中，是 S 型函数）。对从大图像抽样出的每个大小为

的小图像

，计算该小

），将这一张大图上的小图计算完，得出这张大图像的

，这个卷积特征是一个

规模为

下一节中，将进一步介绍如何将这些特征“池化”到一起，以获得用于分类的更好特征。

池化（Pooling）

池化：概述（Pooling: Overview ）

在得到卷积特征后，下一步就是用来做分类。理论上，可以用提取到的所有特征训练分类器，分类器可以用如

分类器，但用所有特征的计算量开

销会很大。考虑到每张图像的像素为

，假设已经在

像素大小的输入单元上学习了

个特征（译者注：这里

个特征是指卷积层有

个特征（译者注：

个神经元或滤波器模板）。（原始图像的）每个卷积操作将会产生

这里特征应指神经元或滤波器模板），这样每个样本将会产生长度为

想法是不明智的，这也会使分类器倾向于过拟合。

个元素的输出，因为有

个特征的向量。有着超过三百多万的特征让分类器去学习的

为了解决这个问题，首先回顾一下卷积特征的“固定不变”属性（译者注：即“静态性”），这意味着在一个区域的有效性也可能适用在其它区域。因此，要描述

一个大图像，一个自然的方法是在不同位置处对特征进行汇总统计。例如，一个方法是可以计算在图像中某一区域中一个特定特征的平均值（或最大值）。

这样概括统计出来的数据，其规模（相比使用提取到的所有特征）就低得多，同时也可以改进分类结果（使模型不易过拟合）。这样的聚集操作称为“池

化”，（根据具体的应用而选择池化方法）有时使用“平均池化”或“最大值池化”。

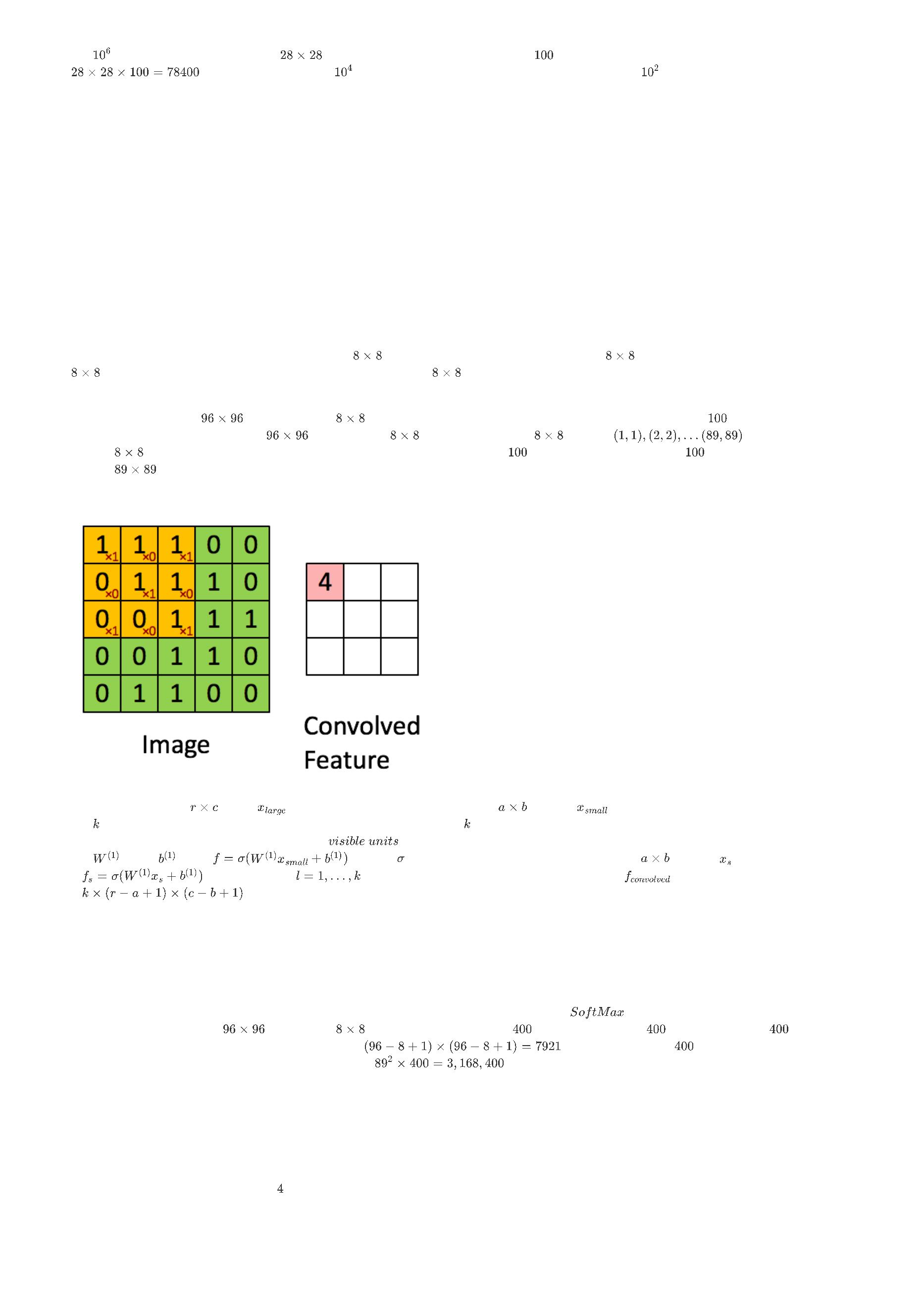
下面这幅图，展示了池化是如何在一幅图像上的个非重叠区域上进行的。

池化的不变性（Pooling for Invariance

）

如果在选择池化区域的时候是选择图像上的连续区域，以及来自相同隐含单元生成的池化特征，那么，这些池化单元将会是“平移不变的”。这意味着哪怕是

小的平移改变，相同（被池化过的）特征也是激活状态（译者注：不确定。“This means that the same (pooled) feature will be active even when the image

undergoes (small) translations.”）。在很多任务中（例如，目标检测，语音识别等）平移不变特性是很必要的，即使图像被平移，但实际上样本（图像）的

标记是一样的。举个例子，如果您正使用

字准确分类。

手写数字图片数据集，并对其进行向左或向右的平移操作，分类器仍能忽视其平移后的位置并对同一数

正式的描述（Formal description ）

正式地说，在获得了卷积特征后，就可以决定池化区域的大小了，比方说可以选择

分辨率的像素规格来对卷积特征进行池化。然后，将卷积特征分

成每块

上。

像素大小的不相交的区域块，并在这些区域块上应用平均（或最大）值特征激活，以获得池化特征。这些池化过的特征便可用在之后的分类

在下一节，将会进一步讲解如何将这些特征“池化”到一起，以得到更好的分类特征。

练习：卷积和池化（Exercise: Convolution and Pooling

）

Convolution and Pooling

In this exercise you will and test convolution and pooling functions. We have provided some starter code. You should write your code at the places

indicated ”YOUR CODE HERE” in the files. For this exercise, you will need to modify cnnConvolve.m and cnnPool.m. Dependencies

The following additional files are required for this exercise:

MNIST helper functions

Starter Code Step 1: Implement and test convolution

In this step, you will implement the convolution function, and test it on a small part of the data set to ensure that you have implemented it correctly. Step 1a:

Implement convolution

Implement convolution, as described in ((Feature Extraction Using Convolution)), in the function cnnConvolve in cnnConvolve.m. Implementing convolution

is somewhat involved, so we will guide you through the process below.

First, we want to compute σ(Wx(r,c)+b) for all valid (r,c) (valid meaning that the entire 8x8 patch is contained within the image; this is as opposed to a full

convolution, which allows the patch to extend outside the image, with the area outside the image assumed to be 0), where W and b are the learned

weights and biases from the input layer to the hidden layer, and x(r,c) is the 8x8 patch with the upper left corner at (r,c). To accomplish this, one naive

method is to loop over all such patches and compute σ(Wx(r,c)+b)

for each of them; while this is fine in theory, it can very slow. Hence, we usually use MATLAB’s built in convolution functions, which are well optimized.

Observe that the convolution above can be broken down into the following three small steps. First, compute Wx(r,c) for all (r,c). Next, add b

to all the computed values. Finally, apply the sigmoid function to the resulting values. This doesn’t seem to buy you anything, since the first step still

requires a loop. However, you can replace the loop in the first step with one of MATLAB’s optimized convolution functions, conv2, speeding up the process

significantly.

However, there are two important points to note in using conv2. First, conv2 performs a 2-D convolution, but you have 4 “dimensions” - image number, filter

(or feature) number, row of image and column of image - that you want to convolve over. Because of this, you will have to convolve each filter separately

for each image, using the row and column of the image as the 2 dimensions you convolve over. This means that you will need two outer loops over the

image number imageNum and filter number filterNum. Inside the two nested for-loops, you will perform a conv2 2-D convolution, using the weight matrix for

the filterNum-th filter and the image matrix for the imageNum-th image.

Second, because of the mathematical definition of convolution, the filter matrix must be “flipped” before passing it to conv2. The following implementation

tip explains the “flipping” of feature matrices when using MATLAB’s convolution functions: Implementation tip: Using conv2 and convn Because the

mathematical definition of convolution involves "flipping" the matrix to convolve with (reversing its rows and its columns), to use MATLAB's convolution

functions, you must first "flip" the weight matrix so that when MATLAB "flips" it according to the mathematical definition the entries will be at the correct

place. For example, suppose you wanted to convolve two matrices image (a large image) and W (the feature) using conv2(image, W), and W is a 3x3

matrix as below: W=⎛⎝⎜147258369⎞⎠⎟ If you use conv2(image, W), MATLAB will first "flip" W, reversing its rows and columns, before convolving W with

image, as below: ⎛⎝⎜147258369⎞⎠⎟−→−flip⎛⎝⎜963852741⎞⎠⎟ If the original layout of W was correct, after flipping, it would be incorrect. For the

layout to be correct after flipping, you will have to flip W before passing it into conv2, so that after MATLAB flips W in conv2, the layout will be correct. For

conv2, this means reversing the rows and columns, which can be done by rotating W 90 degrees twice with rot90 as shown below:

Flip W for use in conv2 W = rot90(W,2);

Next, to each of the convolvedFeatures, you should then add b

the corresponding bias for the filterNum-th filter. Step 1b: Check your convolution

We have provided some code for you to check that you have done the convolution correctly. The code randomly checks the convolved values for a number

of (feature, row, column) tuples by computing the feature activations using randomly generated features and images from the MNIST dataset. Step 2:

Implement and test pooling Step 2a: Implement pooling

Implement pooling in the function cnnPool in cnnPool.m. You should implement mean pooling (i.e., averaging over feature responses) for this part. This

can be done efficiently using the conv2 function as well. The inputs are the responses of each image with each filter computed in the previous step.

Convolve each of these with a matrix of ones followed by a subsampling and averaging. Make sure to use the “valid” border handling convolution. Step 2b:

Check your pooling

We have provided some code for you to check that you have done the pooling correctly. The code runs cnnPool against a test matrix to see if it produces

the expected result.

优化方法：随机梯度下降（Optimization: Stochastic Gradient Descent）

概览（Overview ）

批处理的方法，如有限内存

（例如中的

，使用完整的训练集来计算下一次的参数更新，在每次迭代时往往可以很好地收敛到局部最优解。也有一些现成的实现

函数），因为有很少的超参数需要调整，所以可以直接拿来用。然而一般来说，在实践中计算整个训练集的损失（译

者注：或称为代价）和梯度的过程是非常缓慢的，有时因为数据集太大，无法完全装进主内存，在一台机器上计算更是不可能完成。

批处理优化方法的另一个问题是，没有给一个简单的方法，可以将新的数据进行“在线实时”处理。随机梯度下降（

或者少量的训练样本后，便可沿着目标函数的负梯度（译者注：更新，来寻找局部最优）。在神经网络中的使用是出于运行反向传播会在整个训练集

可以克服这一（译者注：高计算）成本（问题），并加快收敛速度。

）解决了这两个问题，在跑了单个

上进行的高（译者注：计算）成本。

随机梯度下降（Stochastic Gradient Descent

）

标准的梯度下降算法更新目标函数

中的参数（译者注：的过程），如下，

其中，因为是对整个训练集上的代价和梯度的近似，所以上述方程中的期望值

是近似（等于整个训练集）的。随机梯度下降（

）在更新和

计算参数梯度时，由于是使用单个或者少量的训练样本，只是稍稍偏离了期望值。新的更新公式定义如下，

其中，

是训练集中的一个带标记的样本。

中每个参数更新的计算并非使用单个样本，而是关于少量训练样本或者一小批样本。这样做的原因有两个：第一，这降低了参数更新过程

通常来说，

中的方差，使收敛的过程更稳定，第二，这允许在计算中借助深度优化的矩阵运算，可以很好地将成本和梯度的计算矢量化。尽管

的最佳值会

因不同的应用和架构变化，但一个有代表性的大小是

。

在

中的学习率值会比（全量）梯度下降（译者注：这里的全量梯度下降，即

，每次迭代过程中对参数的更新是基于整

个训练集）中的学习率小很多，因为前者在更新过程中的方差更大（译者注：因为并非是在整个训练集上计算参数更新值，少量的训练样本带来的参数更新

并不稳定）。选择合适的学习率和学习率变更策略（即改变学习率的学习速度）是相当困难的。一个标准且在实际中有效的方法，是在迭代开始时就使用一

个足够小的固定学习率，这样固定且小的学习率在首次迭代（迭代，即在训练集上的一次完整遍历）提供了稳定的收敛性，或两次迭代后随着收敛慢下来，

将学习速率降低为原来的一半。

一个更好的方法是在每次迭代后使用一组固定的学习率，并且当紧邻的两次迭代，目标函数变化值小于某个较小的阈值时，就降低学习率。这往往会很好地

收敛于一个局部最优。另一个常用的学习率变化策略，学习率

随着迭代次数变化而变化，其中变量

和

决定了初始时的学习率，并且学习率的开

始减少的过程是独立的。还有更先进的方法，包括基于回溯线搜索的最佳更新寻找（策略）。

最后但重要的一点是，在

中，我们提供给算法的数据（样本的）顺序。如果给（算法）数据是某种有意义的顺序，这可能会使得梯度偏离并导致收敛

性差。一般（为避免该问题）我们都会在训练过程中的每次迭代前，对数据的次序进行“洗牌”（译者注：重新排序）。

动量（Momentum ）

如果目标函数（译者注：可视化）为一个沿着最优方向的长长浅沟，在很多地方有陡峭的墙坡的形式，由于负梯度会沿着一条（当前最）陡峭而不是沿着

（

全局）最低山沟的方向，标准的

将趋于在（局部）窄的峡谷里并来回振荡。深层（网络）结构的目标函数就会有着局部最优，并在这种形式下，标

准的

会导致收敛地很慢，特别是在第一次的陡坡的拉升过程中。动量是一个（推动当前参数）朝目标方向沿着目标浅沟更快（进行参数更新）的一种

方法。下面给出动量的更新过程，

上述方程中，

是当前的速度矢量，它和参数向量有相同的维度。学习率如上所述，在使用动量的时候，因为梯度会较大，所以动量所需要的值就会

比较小，。最后，

确定已经完成的迭代次数，这些迭代次数中梯度纳入当前更新的程度。一般的值设为

，直到初始学习稳定，之后被增加

到

或更高。

卷积神经网络（Convolutional Nerual Network）

概述（Overview ）

卷积神经网络（

）是有一个或多个卷积层（常伴有下采样步骤）并后面跟一个或多个全连接层的标准多层神经网络。卷积神经网络在体系结构的设

计利用了输入图像的二维结构（其它的二维输入还有语音信号等）。

卷积神经网络的实现是借助局部连接和在其之后的绑定权重，其中池化操作有平移不变特征。卷积神经网络的另一个优点在于更容易训练，并且卷积神经网

络的参数虽多但却比相同隐含单元的全连接网络要少。

在本节内容中，我们将会讨论卷积神经网络的架构和用来计算模型中不同参数梯度的反向传播算法。卷积和池化更详细的具体操作见本教程的各自章节。

网络架构（Architecture ）

一个卷积神经网络是由很多个卷积层、后接可选的（一层或多层）下采样层以及后接的全连接层组成的。卷积层的输入是一个规模为

其中（第一个）是图像的高度，第二个是宽度，是图像的通道个数。，例如一个图像的通道数。卷积层有个规模为

的图像，

的滤波器（或称为核），其中小于图片的维度（译者注：图片的高度或宽度），既可以是通道个数，也可能对于不同的滤波器（或称为核）而不

同。

过滤器的规模增加了局部连接的结构（译者注：不是很理解这句话的深层含义：The size of the filters gives rise to the locally connected structure.），原图

被（这种结构）卷积成为规模为

的

个特征图（译者注：这里的“特征图”，即

）。

，是二维的。其中

是一个特征图的

宽度或者高度，原图是正方形，所以这里特征图的边长为

之后，每个（特征）图通常在

小图片值为，例如

的相邻区域进行平均值或最大值下采样（译者注：

手写图片数据集）并通常不超过（对于大图片）。

中的下采样即池化），对于相邻区域的值范围从（对于

在下采样层的之前或之后，（译者注：会对结果）应用一个附加的偏置和型的非线性（译者注：的映射）。

下图描述了卷积神经网络中一个完整的卷积和下采样层。一样颜色的（译者注：神经）单元有着连接权重。

图1：一个卷积神经网络的第一层的池化过程。相同颜色的神经单元有连接权重，不同颜色的神经元表示不同的滤波器（图）（译者注：这里不同颜色的神

经元代表着不同的滤波器或核。对于“RF”，个人理解为感受野（

）的缩写，感受野是视觉系统信息处理的基本结构和功能单元。注

意：滤波器和核是一个意思，滤波器和通道不是一个意思）。

在卷积层后可能有任意个全连接层。在一个标准的多层神经网络中，被密集连接（译者注：即全连接）的这些层是一样的。

反向传播（Back Propagation ）

对于网络中的成本函数

如果第层与第

，

是第

层的误差项，其中

是（译者注：成本函数的）参数，

是带有标签的训练数据。

层是密集连接（译者注：即全连接）的，那么可计算第层的误差项为：

计算第层梯度为：

如果第层是一个卷积和下采样（译者注：即池化）层，那么误差被传播（的过程，可通过如下公式）表示为：

其中，是滤波器（译者注：或称为核，同义）的索引编号，

是激活函数的导数。_上采样操作的误差传播是通过池化层（译者注：即下采样层）与

进到池化层的各神经元（译者注：“进到池化层的各神经元”，即池化层前一层的神经元）计算误差。

举个例子，若做完了平均值池化，然后对（前一层的）池化（神经）单元进行简单的均匀分布（译者注：均匀分布，即

）

上采样。在最大值池化中，即使（上层）输入（译者注：在池化的相邻区域内）的变化很小，（池化）单元会对结果产生扰动（译者注：本句翻译不确

定，"In max pooling the unit which was chosen as the max receives all the error since very small changes in input would perturb the result only through

that unit. "）。

Finally, to calculate the gradient w.r.t to the filter maps, we rely on the border handling convolution operation again and flip the error matrix δ(l)k the same

way we flip the filters in the convolutional layer.

最后，为了计算特征图（即

逆时针旋转，对应

转（译者注：即逆时针旋转

）的梯度，我们再次借助边界来处理卷积运算，并翻转误差矩阵

（译者注：这里的“翻转”，即逆时针旋转

。

中的函数

，

表示对二维矩阵

逆时针旋转次），这个过程与在卷基层翻

）滤波器是一样的。

其中，

是第层的输入，并且有

是输入的图像。操作

是第层的第个输入关于第个滤波器（或称为核）的“有效的”卷积（操

作，译者注：

是误差矩阵）。

练习：卷积神经网络（Excercise: Convolutional Neural Network

）

Overview

In this exercise you will implement a convolutional neural network for digit classification. The architecture of the network will be a convolution and

subsampling layer followed by a densely connected output layer which will feed into the softmax regression and cross entropy objective. You will use mean

pooling for the subsampling layer. You will use the back-propagation algorithm to calculate the gradient with respect to the parameters of the model. Finally

you will train the parameters of the network with stochastic gradient descent and momentum.

We have provided some MATLAB starter code. You should write your code at the places indicated in the files ”YOUR CODE HERE”. You have to complete

the following files: cnnCost.m, minFuncSGD.m. The starter code in cnnTrain.m shows how these functions are used. Dependencies

Convolutional Network starter code

MNIST helper functions

We strongly suggest that you complete the convolution and pooling, multilayer supervised neural network and softmax regression exercises prior to starting

this one. Step 0: Initialize Parameters and Load Data

In this step we initialize the parameters of the convolutional neural network. You will be using 10 filters of dimension 9x9, and a non-overlapping,

contiguous 2x2 pooling region.

We also load the MNIST training data here as well. Step 1: Implement CNN Objective

Implement the CNN cost and gradient computation in this step. Your network will have two layers. The first layer is a convolutional layer followed by mean

pooling and the second layer is a densely connected layer into softmax regression. The cost of the network will be the standard cross entropy between the

predicted probability distribution over 10 digit classes for each image and the ground truth distribution. Step 1a: Forward Propagation

Convolve every image with every filter, then mean pool the responses. This should be similar to the implementation from the convolution and pooling

exercise using MATLAB’s conv2 function. You will need to store the activations after the convolution but before the pooling for efficient back propagation

later.

Following the convolutional layer, we unroll the subsampled filter responses into a 2D matrix with each column representing an image. Using the

activationsPooled matrix, implement a standard softmax layer following the style of the softmax regression exercise. Step 1b: Calculate Cost

Generate the ground truth distribution using MATLAB’s sparse function from the labels given for each image. Using the ground truth distribution, calculate

the cross entropy cost between that and the predicted distribution.

Note at the end of this section we have also provided code to return early after computing predictions from the probability vectors computed above. This

will be useful at test time when we wish make predictions on each image without doing a full back propagation of the network which can be rather costly.

Step 1c: Back Propagation

First compute the error, δd

from the cross entropy cost function w.r.t. the parameters in the densely connected layer. You will then need to propagate this error through the

subsampling and convolutional layer. Use MATLAB’s kron function to upsample the error and propagate through the pooling layer. Implementation tip:

Using kron You can upsample the error from an incoming layer to propagate through a mean-pooling layer quickly using MATLAB's kron function. This

function takes the Kroneckor Tensor Product of two matrices. For example, suppose the pooling region was 2x2 on a 4x4 image. This means that the

incoming error to the pooling layer will be of dimension 2x2 (assuming non-overlapping and contiguous pooling regions). The error must be upsampled

from 2x2 to be 4x4. Since mean pooling is used, each error value contributes equally to the values in the region from which it came in the original 4x4

image. Let the incoming error to the pooling layer be given by delta=(1324) If you use kron(delta, ones(2,2)), MATLAB will take the element by element

product of each element in ones(2,2) with delta, as below: ⎛⎝⎜⎜⎜1133113322442244⎞⎠⎟⎟⎟→kron((1324),(1111)) After the error has been upsampled,

all that's left to be done to propagate through the pooling layer is to divide by the size of the pooling region. A basic implementation is shown below,

Upsample the incoming error using kron delta_pool = (1/poolDim^2) * kron(delta,ones(poolDim));

To propagate error through the convolutional layer, you simply need to multiply the incoming error by the derivative of the activation function as in the usual

back propagation algorithm. Using these errors to compute the gradient w.r.t to each weight is a bit trickier since we have tied weights and thus many

errors contribute to the gradient w.r.t. a single weight. We will discuss this in the next section. Step 1d: Gradient Calculation

Compute the gradient for the densely connected weights and bias, W_d and b_d following the equations presented in multilayer neural networks.

In order to compute the gradient with respect to each of the filters for a single training example (i.e. image) in the convolutional layer, you must first

convolve the error term for that image-filter pair as computed in the previous step with the original training image. Again, use MATLAB’s conv2 function with

the ‘valid’ option to handle borders correctly. Make sure to flip the error matrix for that image-filter pair prior to the convolution as discussed in the simple

convolution exercise. The final gradient for a given filter is the sum over the convolution of all images with the error for that image-filter pair.

The gradient w.r.t to the bias term for each filter in the convolutional layer is simply the sum of all error terms corresponding to the given filter.

Make sure to scale your gradients by the inverse size of the training set if you included this scale in the cost calculation otherwise your code will not pass

the numerical gradient check. Step 2: Gradient Check

Use the computeNumericalGradient function to check the cost and gradient of your convolutional network. We’ve provided a small sample set and toy

network to run the numerical gradient check on.

Once your code passes the gradient check you’re ready to move onto training a real network on the full dataset. Make sure to switch the DEBUG boolean

to false in order not to run the gradient check again. Step 3: Learn Parameters

Using a batch method such as L-BFGS to train a convolutional network of this size even on MNIST, a relatively small dataset, can be computationally slow.

A single iteration of calculating the cost and gradient for the full training set can take several minutes or more. Thus you will use stochastic gradient

descent (SGD) to learn the parameters of the network.

You will use SGD with momentum as described in Stochastic Gradient Descent. Implement the velocity vector and parameter vector update in

minFuncSGD.m.

In this implementation of SGD we use a relatively heuristic method of annealing the learning rate for better convergence as learning slows down. We

simply halve the learning rate after each epoch. As mentioned in Stochastic Gradient Descent, we also randomly shuffle the data before each epoch, which

tends to provide better convergence. Step 4: Test

With the convolutional network and SGD optimizer in hand, you are now ready to test the performance of the model. We’ve provided code at the end of

cnnTrain.m to test the accuracy of your networks predictions on the MNIST test set.

Run the full function cnnTrain.m which will learn the parameters of you convolutional neural network over 3 epochs of the data. This shouldn’t take more

than 20 minutes. After 3 epochs, your networks accuracy on the MNIST test set should be above 96%.

Congratulations, you’ve successfully implemented a Convolutional Neural Network!

自动编码器（Autoencoders ）

注：本文大量参考旧版 UFLDL 中文翻译。

迄今为止，已经讲了神经网络在有监督学习方面的的应用。在有监督学习中，训练样本是有标签的。现在假设有一组无标签的训练样本

，

其中

。自动编码器神经网络（译者注：或称为“自动编码器”）是一个基于反向传播的无监督学习算法，其中设定目标值与输入值相等：

。

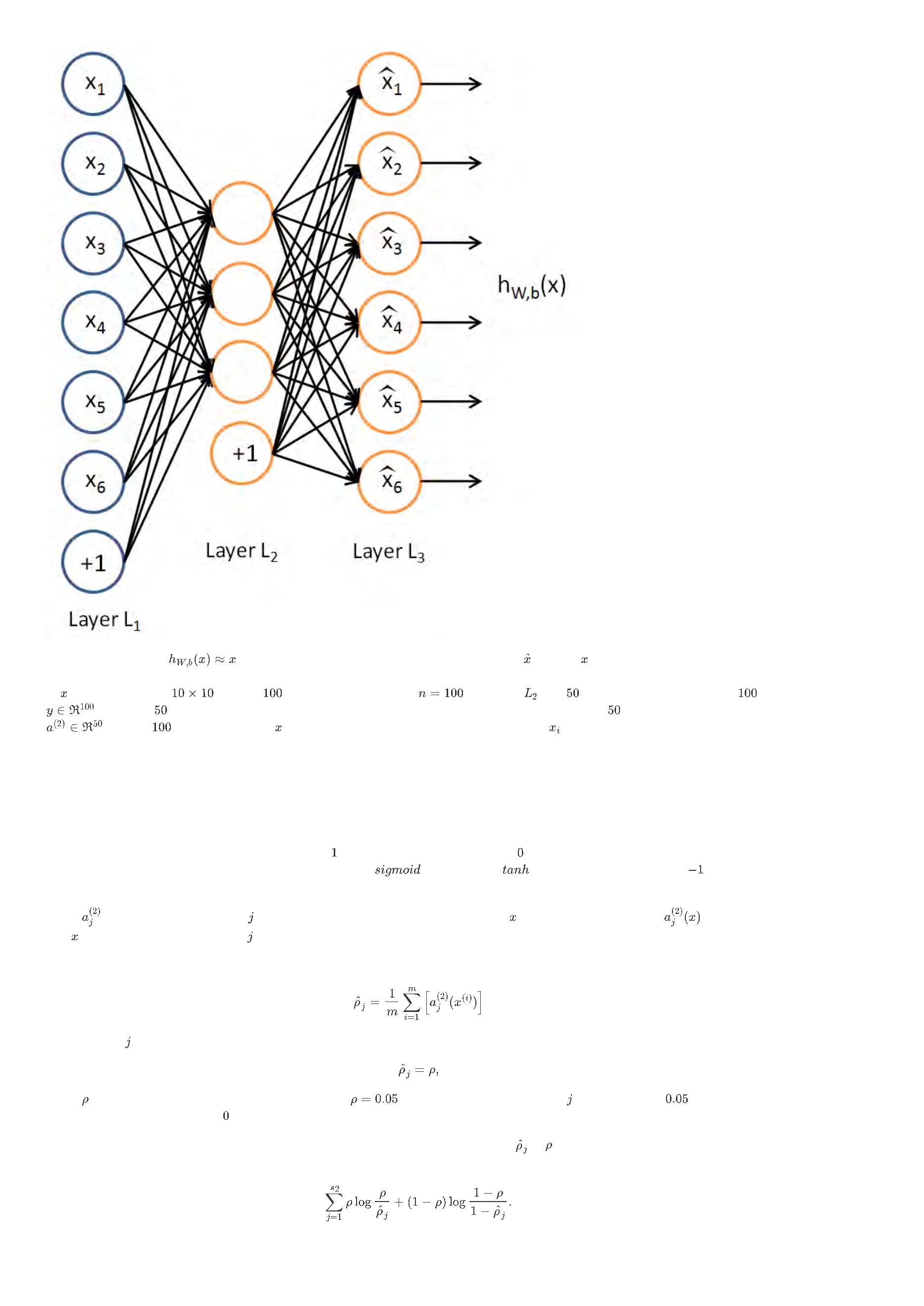
下面是一个自动编码器的示意图：

自动编码器尝试学习一个

义，但是当给自编码神经网络加入某些限制，比如限定隐藏神经元的数量，就可以从输入数据中发现一些有趣的结构。举例来说，假设某个自动编码器的输

是一张分辨率大小为图像（共个像素）的像素灰度值，即，其隐藏层中有个隐藏神经元。注意，输出也是维的

由于只有个隐藏神经元，我们迫使自编码神经网络去学习输入数据的压缩表示，也就是说，它必须从维的隐藏神经元激活度向量

中重构出维的像素灰度值输入。如果网络的输入数据是完全随机的，比如每一个输入都是一个跟其它特征完全无关的独立同分布高

函数。换句话说，它尝试逼近一个恒等函数，从而使得输出接近输入。恒等函数虽然看上去不太有学习的意

入

。

斯随机变量，那么这一压缩表示将会非常难学习。但是如果输入数据中隐含着一些特定的结构，比如某些输入特征是彼此相关的，那么这一算法就可以发现

输入数据中的这些相关性。事实上，这一简单的自动编码器通常可以学习出一个跟主成分分析（PCA）结果非常相似的输入数据的低维表示。

以上论述是基于隐藏神经元数量较小的假设。但即使隐藏神经元的数量较大（可能比输入像素的个数还要多），仍可通过给自动编码器施加一些其他的限制

条件来发现输入数据中有趣的结构。具体来说，如果给隐藏神经元加入稀疏性限制，自动编码器即使在隐藏神经元数量较多的情况下仍然可以发现输入数据

中一些有趣的结构。

稀疏性可以被简单地解释如下。如果当神经元的输出接近于的时候认为它被激活，而输出接近于的时候认为它被抑制，那么使得神经元大部分的时间都

是被抑制的限制则被称作稀疏性限制。这里假设神经元的激活函数是

元是被抑制的。

函数。如果使用

作为激活函数，当神经元输出为

的时，认为神经

来表示在给定输

注意到

表示网络第二层的隐藏神经元的激活值，但该表示方法中并未明确指出哪一个输入带来了这一激活值。所以改用

入为情况下，自动编码器的隐藏神经元的激活值。

进一步，让

表示隐藏神经元的平均活跃度（在训练集上取平均）。可以近似的加入一条限制

其中，是稀疏性参数，通常是一个接近于0的较小的值（比如

件，隐藏神经元的活跃度必须接近于

）。换句话说，想要让隐藏神经元的平均活跃度接近

。为了满足这一条

。

为了实现这一限制，将会在优化目标函数中加入一个额外的惩罚因子，而这一惩罚因子将惩罚那些

跃度保持在较小范围内。惩罚因子的具体形式有很多种合理的选择，我们将会选择以下这一种：

和

有显著不同的情况从而使得隐藏神经元的平均活

这里，

是隐藏层中隐藏神经元的数量，而索引依次代表隐藏层中的每一个神经元。如果您对相对熵（

，也称“信息

增益”）比较熟悉，这一惩罚因子实际上是基于它的。于是惩罚因子也可以被表示为

其中

是一个以为均值和一个以

为均值的两个伯努利随机变量之间的相对熵。相对熵是一种标准的用来测

量两个分布之间差异的方法。（如果您不了解相对熵，不用担心，所有您需要知道的内容都在这份笔记之中。）

伯努利随机分布：一个离散型概率分布，是二项分布的特殊情况。伯努利分布是一种离散分布，有两种可能的结果：表示成功，出现的概率为

，

其中

，

表示失败，出现的概率为

。其分布率为：

Missing or unrecognized delimiter for \left

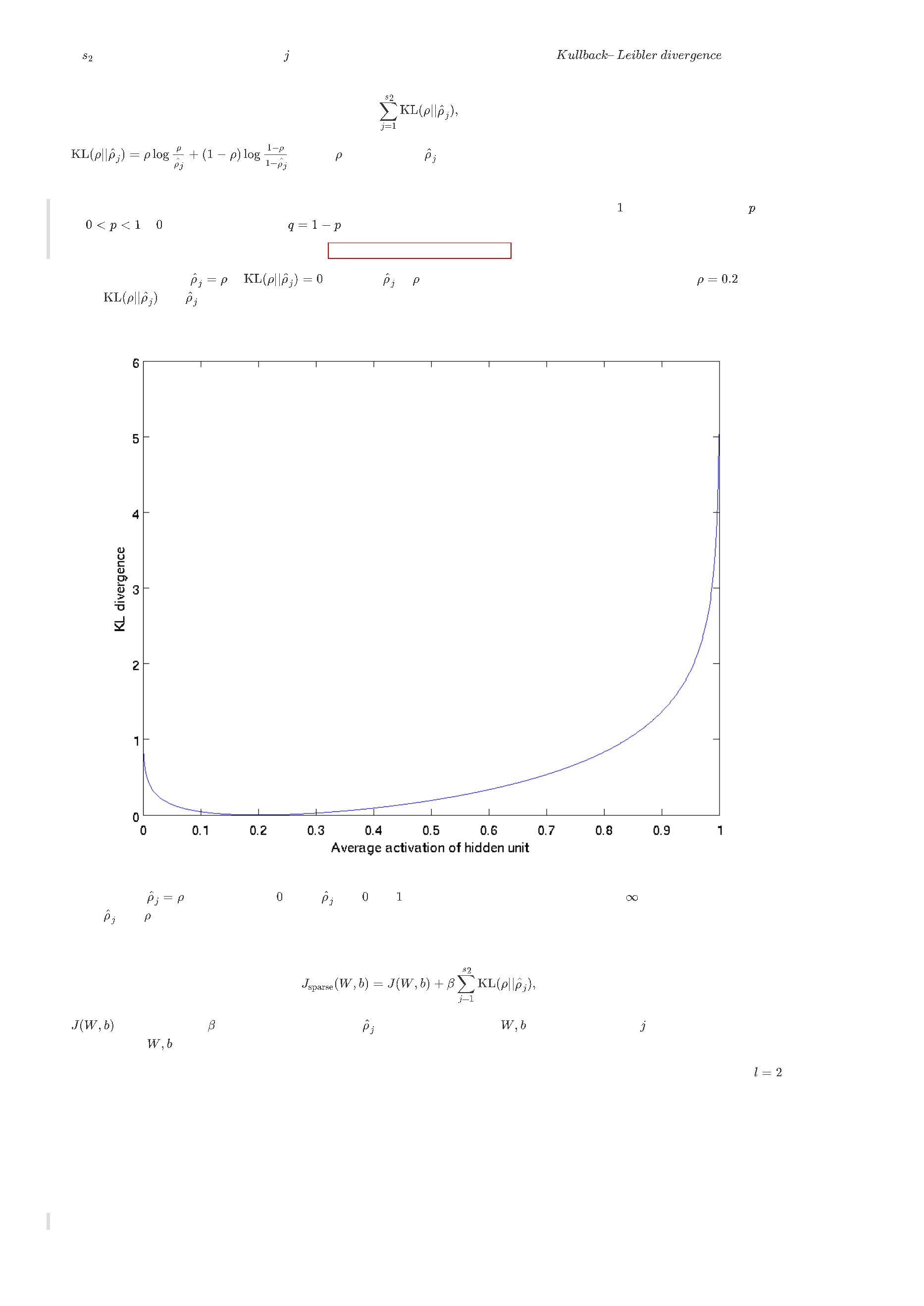
这一惩罚因子有如下性质，当

时

，并且随着

与

之间的差异增大而单调递增。举例来说，在下图中，设定

并且画出

了相对熵值

随着

变化的变化。

可以看出，相对熵在

时达到它的最小值，而当

靠近或者的时候，相对熵则变得非常大（其实是趋向于

）。所以，最小化这一惩罚因

子具有使得

靠近的效果。

现在，总体代价函数可以表示为

其中

如之前所定义，而控制稀疏性惩罚因子的权重。

项则也（间接地）取决于

，因为它是隐藏神经元的平均激活度，而隐藏层神

经元的激活度取决于

。

为了对相对熵进行导数计算，可以使用一个易于实现的技巧，这只需要在您的程序中稍作改动即可。具体来说，前面在后向传播算法中计算第二层（

）更新的时候已经计算了

$ \begin{align} \delta^{(2)}i = \left( \sum{j=1}^{s_{2}} W^{(2)}_{ji} \delta^{(3)}_j \right) f'(z^{(2)}_i), \end{align} $$

现在将其换成

$ \begin{align} \delta^{(2)}i = \left( \left( \sum{j=1}^{s_{2}} W^{(2)}_{ji} \delta^{(3)}_j \right) + \beta \left( - \frac{\rho}{\hat\rho_i} + \frac{1-\rho}{1-\hat\rho_i}

right) \right) f'(z^{(2)}_i). \end{align} $$

译者：怀疑上述公式的稀疏项与前文中描述的不符合，怀疑是否写错了。

就可以了。

有一个需要注意的地方就是需要知道

来计算这一项更新。所以在计算任何神经元的后向传播之前，您需要对所有的训练样本计算一遍前向传播，从而获

取平均激活度。如果您的训练样本可以小到被整个存到内存之中（对于编程作业来说，通常如此），您可以方便地在您所有的样本上计算前向传播并将得到

的激活度存入内存并且计算平均激活度。然后您就可以使用事先计算好的激活度来对所有的训练样本进行后向传播的计算。如果数据量太大，无法全部存入

内存，可以扫过训练样本并计算一次前向传播，然后将获得的结果累积起来并计算平均激活度

（当某一个前向传播的结果中的激活度

被用于计算平

均激活度之后就可以将此结果删除）。然后当完成平均激活度的计算之后，需要重新对每一个训练样本做一次前向传播从而可以对其进行后向传播的

计算。对于后一种情况，对每一个训练样本需要计算两次前向传播，所以在计算上的效率会稍低一些。

证明上面算法能达到梯度下降效果的完整推导过程不再本教程的范围之内。不过如果想要使用经过以上修改的后向传播来实现自编码神经网络，那么就会对

目标函数

做梯度下降。您可以使用梯度验证方法（数值解），验证梯度下降算法（解析解）的正确性。

可视化自动编码器训练结果（Visualizing a T rained Autoencoder

）

训练完（稀疏）自动编码器，我们还想把这自编码器学到的函数可视化出来，好弄明白它到底学到了什么。以在

码器为例。在该自编码器中，每个隐藏单元对如下关于输入的函数进行计算：

图像（即

）上训练自编

$$ \begin{align} a^{(2)}i = f\left(\sum{j=1}^{100} W^{(1)}_{ij} x_j + b^{(1)}_i \right). \end{align} $$

我们将要可视化的函数，就是上面这个以 2D 图像为输入、并由隐藏单元计算出来的函数。它是依赖于参数

是，可看作输入的非线性特征。不过还有个问题：什么样的输入图像可让 $\textstyle a^{(2)}i

得到最大程度的激励？（通俗一点说，隐藏单元\textstyle i要找个什么样的特征？）。这里我们必须给\textstyle x

加约束，否则会得到平凡解（注：平凡解是Ax=0中的零解，即x=0）。若假设输入有范数约束\textstyle ||x||^2 = \sum{i=1}^{100} x_i^2 \leq 1

则可证（请读者自行推导）令隐藏单元\textstyle i得到最大激励的输入应由下面公式计算的像素\textstyle x_j给出（共需计算100个像素，j=1,…,100$ ）：

的（暂时忽略偏置项

）。需要注意的

，

$$ \begin{align} x_j = \frac{W^{(1)}{ij}}{\sqrt{\sum{j=1}^{100} (W^{(1)}_{ij})^2}}. \end{align} $$

当我们用上式算出各像素的值、把它们组成一幅图像、并将图像呈现在我们面前之时，隐藏单元所追寻特征的真正含义也渐渐明朗起来。

译者注：这里可视化是对网络权重进行标准化再可视化，这里是用的方法是不去均值的离差标准化。需要注意的是：不是使用新输入的图像进行可视化

的。

假如我们训练的自编码器有

个隐藏单元，可视化结果就会包含

幅这样的图像——每个隐藏单元都对应一幅图像。审视这

幅图像，我们可以试

着体会这些隐藏单元学出来的整体效果是什么样的。

当我们对稀疏自编码器（

个隐藏单元，在经白化过的

像素的输入上训练）进行上述可视化处理之后，结果如下所示：

注：学习到的特征是从经过“白化”过（ whitened ）的训练图像得到的。白化（ whitening ）是一个预处理步骤，该步骤会让邻近像素变得不相关，移除

输入中的冗余。

上图的每个小方块都给出了一个（带有有界范数的）输入图像，它可使这

了在图像的不同位置和方向进行边缘检测。

个隐藏单元中的某一个获得最大激励。我们可以看到，不同的隐藏单元学会

显而易见，这些特征对物体识别等计算机视觉任务是十分有用的。若将其用于其他输入域（如音频），该算法也可学到对这些输入域有用的表示或特征。

线性解码器（Linear Decoders ）

注：本文参考旧版 UFLDL 中文翻译。

稀疏自编码重述（Sparse Autoencoder Recap

）

稀疏自编码器包含层神经元，分别是输入层、隐含层以及输出层。从前面（神经网络）自编码器描述可知，位于神经网络中的神经元都采用相同的激励函

数。在注解中，我们修改了自编码器定义，使得某些神经元采用不同的激励函数。这样得到的模型更容易应用，而且模型对参数的变化也更为鲁棒。

回想一下，输出层神经元计算公式如下：

其中

是输出。在自编码器中，

，当

近似重构了输入

。

S 型激励函数输出范围是

采用该激励函数时（译注：输出层采用了输出值在

或

的激励函数，那么要使得自编码成立，那

输入层值的范围也是相同才行），就要对输入限制或缩放，使其位于

范围中。一些数据集，比如 MNIST ，能方便将输出缩放到

中，但是很难满

足对输入值的要求。比如， PCA 白化处理的输入并不满足

范围要求，也不清楚是否有最好的办法可以将数据缩放到特定范围中。

线性解码器（Linear Decoder ）

设定

可以很简单的解决上述问题。从形式上来看，就是输出端使用恒等函数

作为激励函数，于是有

。我

们称该特殊的激励函数为线性激励函数（可能称为恒等激励函数更好）。

需要注意，神经网络中隐含层的神经元依然使用 S 型（或者

）激励函数。这样隐含单元的激励公式为

，其中

是 S 型

函数，是输入，

和

分别是隐单元的权重和偏差项。我们仅在输出层中使用线性激励函数。

一个 S 型或

隐含层以及线性输出层构成的自编码器，我们称为线性解码器。

。因为输出是隐单元激励输出的线性函数，改变

在这个线性解码器模型中，

，可以使输出值

大于或者

小于。这使得我们可以用实值输入来训练稀疏自编码器，避免预先缩放样本到给定范围。

随着输出单元的激励函数的改变，这个输出单元梯度也相应变化。回顾之前每一个输出单元误差项定义为：

其中

是所期望的输出，是自编码器的输出，

是激励函数。因为在输出层激励函数为

，这样

，所以上述公式可以简化为

当然，若使用反向传播算法来计算隐含层的误差项时:

因为隐含层采用一个 S 型（或

）的激励函数，在上述公式中，

依然是 S 型（或

）函数的导数。

练习：使用稀疏编码器学习颜色特征（Exercise:Learning color features with Sparse Autoencoders

练习：主成分分析白化（Exercise: PCA Whitening ）

）

练习：实现 2D 数据的主成分分析（Exercise:PCA in 2D ）

练习：主成分分析白化（Exercise: PCA Whitening ）

稀疏编码（Sparse Coding ）

注：本章节翻译完全参考旧版 UFLDL 中文教程。

稀疏编码算法是一种无监督学习方法，它用来寻找一组“超完备”基向量来更高效地表示样本数据。稀疏编码算法的目的就是找到一组基向量

，使得我们能

将输入向量表示为这些基向量的线性组合：

虽然形如主成分分析技术（ PCA ）能使我们方便地找到一组“完备”基向量，但是这里我们想要做的是找到一组“超完备”基向量来表示输入向量

（也

就是说，

）。超完备基的好处是它们能更有效地找出隐含在输入数据内部的结构与模式。然而，对于超完备基来说，系数

不再由输入向量唯一

确定。因此，在稀疏编码算法中，我们另加了一个评判标准“稀疏性”来解决因超完备而导致的退化（ degeneracy ）问题。

这里，我们把“稀疏性”定义为：只有很少的几个非零元素或只有很少的几个远大于零的元素。要求系数

是稀疏的意思就是说：对于一组输入向量，我们只

想有尽可能少的几个系数远大于零。选择使用具有稀疏性的分量来表示我们的输入数据是有原因的，因为绝大多数的感官数据，比如自然图像，可以被表示

成少量基本元素的叠加，在图像中这些基本元素可以是面或者线。同时，比如与初级视觉皮层的类比过程也因此得到了提升。

我们把有

个输入向量的稀疏编码代价函数定义为：

$$ \begin{align} \text{minimize}{a^{(j)}i,\mathbf{\phi}{i}} \sum{j=1}^{m} \left|\left| \mathbf{x}^{(j)} - \sum_{i=1}^k a^{(j)}i \mathbf{\phi}{i}\right|\right|^{2} +

lambda \sum_{i=1}^{k}S(a^{(j)}_i) \end{align} $$

此处

是一个稀疏代价函数，由它来对远大于零的

进行“惩罚”。我们可以把稀疏编码目标函式的第一项解释为一个重构项，这一项迫使稀疏编码算法

能为输入向量提供一个高拟合度的线性表达式，而公式第二项即“稀疏惩罚”项，它使的表达式变得“稀疏”。常量是一个变换量，由它来控制这两项式

子的相对重要性。

虽然“稀疏性”的最直接测度标准是 " " 范式

择是范式代价函数及对数代价函数

，但这是不可微的，而且通常很难进行优化。在实际中，稀疏代价函数

。

的普遍选

此外，很有可能因为减小

或增加

至很大的常量，使得稀疏惩罚变得非常小。为防止此类事件发生，我们将限制

要小于某常量

。包含了限制

条件的稀疏编码代价函数的完整形式如下：

$$ \begin{array} {rc} \text{minimize}{a^{(j)}i,\mathbf{\phi}{i}} & \sum{j=1}^{m} \left|\left| \mathbf{x}^{(j)} - \sum_{i=1}^k a^{(j)}i \mathbf{\phi}{i}\right|\right|^{2} +

lambda \sum_{i=1}^{k}S(a^{(j)}_i) \ \text{subject to} & \left|\left|\mathbf{\phi}_i\right|\right|^2 \leq C, \forall i = 1,...,k \ \end{array} $$

概率解释 [基于1996年Olshausen 与Field 的理论]

到目前为止，我们所考虑的稀疏编码，是为了寻找到一个稀疏的、超完备基向量集，来覆盖我们的输入数据空间。现在换一种方式，我们可以从概率的角度

出发，将稀疏编码算法当作一种“生成模型”。

我们将自然图像建模问题看成是一种线性叠加，叠加元素包括个独立的源特征

以及加性噪声

：

我们的目标是找到一组特征基向量，它使得图像的分布函数

尽可能地近似于输入数据的经验分布函数 $P^(\mathbf{x})

。

一种实现方式是，最小化P^(\mathbf{x})与P(\mathbf{x}\mid\mathbf{\phi})之间的KL散度，此KL$ 散度表示如下：

$$ \begin{align} D(P^(\mathbf{x})||P(\mathbf{x}\mid\mathbf{\phi})) = \int P^(\mathbf{x}) \log \left(\frac{P^*(\mathbf{x})}

{

P(\mathbf{x}\mid\mathbf{\phi})}\right)d\mathbf{x} \end{align} $$

因为无论我们如何选择，经验分布函数

则有下式：

都是常量，也就是说我们只需要最大化对数似然函数

。假设是具有方差

的高斯白噪音，

$$ \begin{align} P(\mathbf{x} \mid \mathbf{a}, \mathbf{\phi}) = \frac{1}{Z} \exp\left(- \frac{(\mathbf{x}-\sum^{k}{i=1} a_i \mathbf{\phi}{i})^2}{2\sigma^2}\right)

end{align} $$

为了确定分布

，我们需要指定先验分布

。假定我们的特征变量是独立的，我们就可以将先验概率分解为：

此时，我们将“稀疏”假设加入进来——假设任何一幅图像都是由相对较少的一些源特征组合起来的。因此，我们希望 a_i 的概率分布在零值附近是凸起的，而

且峰值很高。一个方便的参数化先验分布就是：

这里

是决定先验分布的形状的函数。

后，我们就可以写出在由定义的模型之下的数据的概率分布：

当定义了

和

那么，我们的问题就简化为寻找：

这里

表示的是输入数据的期望值。

不幸的是，通过对的积分计算

通常是难以实现的。虽然如此，我们注意到如果

的分布（对于相应的）足够陡峭的话，我们就可以

用

的最大值来估算以上积分。估算方法如下：

$$ \begin{align} \mathbf{\phi}^{*'}=\text{argmax}{\mathbf{\phi}} < \max{\mathbf{a}} \log(P(\mathbf{x} \mid \mathbf{\phi})) > \end{align} $$

跟之前一样，我们可以通过减小

生。

或增大来增加概率的估算值（因为

在零值附近陡升）。因此我们要对特征向量加一个限制以防止这种情况发

最后，我们可以定义一种线性生成模型的能量函数，从而将原先的代价函数重新表述为：

$$ \begin{array} {rl} E\left( \mathbf{x} , \mathbf{a} \mid \mathbf{\phi} \right) & := -\log \left( P(\mathbf{x}\mid \mathbf{\phi},\mathbf{a}\right)P(\mathbf{a})) \ &=

sum_{j=1}^{m} \left|\left| \mathbf{x}^{(j)} - \sum_{i=1}^k a^{(j)}i \mathbf{\phi}{i}\right|\right|^{2} + \lambda \sum_{i=1}^{k}S(a^{(j)}_i) \end{array} $$

其中

，并且关系不大的常量已被隐藏起来。因为最大化对数似然函数等同于最小化能量函数，我们就可以将原先的优化问题重新表述为：

$$ \begin{align} \mathbf{\phi}^{},\mathbf{a}^{}=\text{argmin}{\mathbf{\phi},\mathbf{a}} \sum{j=1}^{m} \left|\left| \mathbf{x}^{(j)} - \sum_{i=1}^k a^{(j)}i

mathbf{\phi}{i}\right|\right|^{2} + \lambda \sum_{i=1}^{k}S(a^{(j)}_i) \end{align} $$

使用概率理论来分析，我们可以发现，选择

惩罚和

惩罚作为函数

，分别对应于使用了拉普拉斯概率

和柯西

先验概率

。

学习算法

使用稀疏编码算法学习基向量集的方法，是由两个独立的优化过程组合起来的。第一个是逐个使用训练样本来优化系数

本对基向量进行优化。

，第二个是一次性处理多个样

如果使用

范式作为稀疏惩罚函数，对

的学习过程就简化为求解由

范式正则化的最小二乘法问题，这个问题函数在域

内为凸，已经有很多

技术方法来解决这个问题（诸如 CVX 之类的凸优化软件可以用来解决

正则化的最小二乘法问题）。如果是可微的，比如是对数惩罚函数，则可以

采用基于梯度算法的方法，如共轭梯度法。

用

范式约束来学习基向量，同样可以简化为一个带有二次约束的最小二乘问题，其问题函数在域内也为凸。标准的凸优化软件（如 CVX ）或其它迭

代方法就可以用来求解，虽然已经有了更有效的方法，比如求解拉格朗日对偶函数（ Lagrange dual ）。

根据前面的的描述，稀疏编码是有一个明显的局限性的，这就是即使已经学习得到一组基向量，如果为了对新的数据样本进行“编码”，我们必须再次执行优

化过程来得到所需的系数。这个显著的“实时”消耗意味着，即使是在测试中，实现稀疏编码也需要高昂的计算成本，尤其是与典型的前馈结构算法相比。

稀疏自编码符号一览表（Sparse Autoencoder Notation Summary

）

注：本章节翻译完全参考旧版 UFLDL 中文教程。

下面是我们在推导稀疏自编码（ sparse autoencoder ）时使用的符号一览表：

符号

含义

训练样本的输入特征，

输出值/目标值. 这里可以是向量. 在 autoencoder 中，

第

个训练样本

输入为时的假设输出，其中包含参数

该输出应当与目标值具有相同的维数.

连接第

第

层

单元和第

单元的偏置项. 也可以看作是连接第层偏置单元和第

组合展开为一个长的列向量而得到.

层

单元的参数.

层

单元的参数.

参数向量. 可以认为该向量是通过将参数

网络中第

层

单元的激活（输出）值.

另外，由于

层是输入层，所以

激活函数. 本文中我们使用

第

层

单元所有输入的加权和. 因此有

学习率

层的单元数目（不包含偏置单元）.

第

网络中的层数. 通常

权重衰减系数.

层是输入层，

层是输出层.

对于一个 autoencoder ，该符号表示其输出值；亦即输入值的重构值. 与

稀疏值，可以用它指定我们所需的稀疏程度.

含义相同.

（

sparse autoencoder 中）隐藏单元的平均激活值.

sparse autoencoder 目标函数中）稀疏值惩罚项的权重.

稀疏编码自编码表达（Sparse Coding: Autoencoder Interpretation

）

注：本文参考旧版 UFLDL 中文翻译。

. 稀疏编码（Sparse coding ）

稀疏编码是一种模拟哺乳动物视觉系统主视皮层 V1 区简单细胞感受野的人工神经网络方法。该方法具有空间的局部性、方向性和频域的带通性，是一

种自适应的图像统计方法。

稀疏自编码算法，试着学习得到一组权重参数

非常有用。

以及相应的截距，通过这些参数可以得到稀疏特征向量

，这些特征向量对于重构输入样本

[STL_SparseAE](./images/240px-STL_SparseAE.png)

稀疏编码可以看作是稀疏自编码方法的一个变形，该方法试图直接学习数据的特征集。利用与此特征集相应的基向量

征空间转换到样本数据的空间，这样就可以用学习得到的（译者注：所在的样本空间的）特征集重构样本数据

，将学习得到的特征集从特

。

确切地说，在稀疏编码算法中，有样本数据供特征学习。特别是，学习一个用于表示样本数据的稀疏特征集，和一个将特征集从特征空间转换到样

本数据空间的基向量

，可以构建如下目标函数：

其中，

是

的

范数，等价于

。

范数即大家熟知的欧几里得范数，

范数是向量元素的绝对值之和。

上式第一部分

是利用基向量

将特征集重构为样本数据（译者注：的空间时与原样本间）所产生的误差，第二部分

为稀疏性惩罚项

（

sparsity penalty term ），用于保证特征集的稀疏性。

但是，如目标函数所示，它（译者注：即第一项的

是重构出的与同空间的样本数据，的关系是此消彼长），（译者注：

值。因此，需要为中每项增加额外约束。问题变为：

范数）的约束性并不强――按常数比例缩放

的同时再按这个常数的倒数缩放（译者注：因为

与

过大）结果不会改变误差大小，却会减少稀疏代价项（即

）的

遗憾的是，因为目标函数并不是一个凸函数（译者注：两个变量

优化问题。但是，在给定的情况下，最小化求解是凸的。同理，给定最小化

分别求解。实践表明，这一策略取得的效果非常好。

和

存在乘积项，此外

有约束限制

求解

），所以不能用梯度方法解决这个

也是凸的。这表明，可以通过交替固定

和

但是，以上表达式带来了另一个难题：不能用简单的梯度方法来实现约束条件

。在实际问题中，此约束条件被削弱成一个（译者注：旧版译

文此处有错）“权重衰变”（ "weight decay" ）项（译者注：前文 [多层神经网络](../监督神经网络（Supervised Neural Networks）/多层神经网络（Multi-

Layer Neural Networks）.md) 一节中出现过权重衰减，即目标函数

中的正则化项

）以保证

的每一项值够

小。这样我们就得到一个新的目标函数：

注意上式中的第三项

，等价于

，是

中各项的平方和。

这一目标函数带来了最后一个问题，即

范数在点处不可微影响了梯度方法的应用。尽管可以通过其他非梯度下降方法避开这一问题，但是本文通过使

用近似值“平滑”

范数的方法解决此难题。使用代替，对范数进行平滑，其中是“平滑参数”（ "smoothing parameter" ）或者“稀疏参

数”（ "sparsity parameter" ）。

绝对值函数

在

处不可微的原因：

因为

时

，其在

处的左导数

；

时

，其在

处的右导数

。即函数

在

处的

左右导数都存在但不相等，故在

处的导数不存在，即不可导。也就是所谓的不可微。

如果平滑参数远大于（译者注：这里没有特指样本数据，下面紧接着所讲的目标函数中的

导，其平方根近似于。在下文提及拓扑稀疏编码时，“平滑”会派上用场。

相当于这里的），则

的值将由平滑参数

主

因此，最终的目标函数是：

其中，稀疏惩罚项由原本的

经平滑变为

。

是

的简写。

该目标函数可以通过以下过程迭代优化：

. 随机初始化基向量

. 重复以下步骤直至收敛：

. 根据上一步给定的基向量

. 根据上一步得到的特征集，求解能够最小化

，求解能够最小化

的

观察修改后的目标函数

，给定特征集的条件下，目标函数可以简化为

是一个常数。这里是简化后已忽略特征集的目标函数）。

（译者注：因为特征集

的

范式不

是基向量

的函数，所以

简化后的目标函数是一个关于

的简单二次多项式，因此对

求导是很容易的。对其求导的一种快捷方法是矩阵微积分（ [这里](../预备知识

的条件下，目标函数却不具备这样的求

（

Miscellaneous ）/预备知识推荐（Useful Links）.md) 给出了矩阵运算相关的内容）。遗憾的是，在给定基向量

导方法，因此目标函数的最小化步骤只能用梯度下降或其他类似的最优化方法。

目标函数

不具备矩阵微积分的求导方法。其中，

是给定的基向量，是特征集矩阵，是唯一的变量。

理论上，通过上述迭代方法求解目标函数的最优化问题最终得到的特征集与通过稀疏自编码学习得到的特征集是差不多的。但是实际上，为了获得更好的

算法收敛性需要使用一些小技巧，后面的 [练习：稀疏编码（Exercise:Sparse Coding）](../无监督学习（Unsupervised Learning）/练习：稀疏编码

（

Exercise:Sparse Coding）.md) 小节会详细介绍这些技巧。用梯度下降方法求解目标函数也略需技巧，另外使用矩阵运算或反向传播算法则有助于解决此

类问题。

. 拓扑稀疏编码（Topographic sparse coding

）

通过稀疏编码，我们能够得到一组用于表示样本数据的特征集。不过，让我们来找些灵感，我们希望学习得到一组有某种“秩序”的特征集。举个例子，视觉

特征，如前面所提到的，大脑皮层 V1 区神经元能够按特定的方向对边缘进行检测，同时，这些神经元（在生理上）被组织成超柱（ hypercolumns ），在超

柱中，相邻神经元以相似的方向对边缘进行检测，一个神经元检测水平边缘，其相邻神经元检测到的边缘就稍微偏离水平方向，沿着超柱，神经元就可以检

测到与水平方向相差更大的边缘了。

超柱（ hypercolumns ）由感受野相同的各种特征检测功能柱组合而成，是简单知觉的基本结构与功能单位。

感受野是视网膜上的一定区域，当它受到刺激时，能激活视觉系统与这个区域有联系的各层神经细胞的活动。

功能柱是具有相同感受野并具有相同功能的视皮层神经元，在垂直于皮层表面的方向上呈柱状分布，只对某一种视觉特征发生反应，从而形成了

该种视觉特征的基本功能单位。

受该例子的启发，我们希望学习到的特征也具有这样 “ 拓扑秩序” 的性质。这对于要学习的特征意味着什么呢？直观的讲，如果“ 相邻” 的特征是“ 相似” 的，就

意味着如果某个特征被激活，那么与之相邻的特征也将随之被激活。

具体而言，假设将特征（随意地）组织成一个方阵。我们就希望矩阵中相邻的特征是相似的。实现这一点的方法是将相邻特征按经过平滑的

行分组，如果按方阵对特征矩阵分组，则用代替

是部分重合的，因此从第行第列开始的区域是一个分组，从第行第列开始的

成环绕，就好像这个矩阵是个环形曲面，所以每个特征都以同样的次数进行了分组。于是，将经过平滑的所有分组的

其中）值之和代替经过平滑的惩罚值，得到新的目标函数如下：

范式惩罚进

，其分组通常

区域是另一个分组，以此类推。最终，这样的分组会形

惩罚（译者注：即

范数，

，

稀疏惩罚项由原本的

经平滑变为

，这里经过分组变为

。

实际上，“分组”可以通过“分组矩阵”

完成，分组矩阵

的第行标识了哪些特征被分到第组中，即如果第组包含特征

则

。通过分组矩阵

实现分组使得梯度的计算更加直观，使用此分组矩阵，目标函数被重写为：

其中，可以令

，则

等价于

。

该目标函数能够使用之前部分提到的迭代方法（译者注：梯度下降或其他类似的最优化方法）进行求解。拓扑稀疏编码得到的特征与稀疏编码得到的类似，

只是拓扑稀疏编码得到的特征是以某种方式有“ 秩序” 排列的。

. 稀疏编码实践（Sparse coding in practice

）

如上所述，虽然稀疏编码背后的理论十分简单，但是要写出准确无误的实现代码并能快速又恰到好处地收敛到最优值，则需要一定的技巧。

回顾一下之前提到的简单迭代算法：

. 随机初始化基向量

. 重复以下步骤直至收敛到最优值：

. 根据上一步给定的基向量，求解能够最小化

. 根据上一步得到的特征集，求解能够最小化

的特征集

的基向量

这样信手拈来地执行这个算法，即使得到了结果，结果也并不会令人满意。以下是两种更快更优化的收敛技巧：

. 将样本分批为“小批量”（ mini-batches ，即少量样本的样本集合，不是指将一个样本切分）

. 良好的特征集初始值

.1 将样本分批为“ 小批量” （Batching examples into mini-batches

）

如果一次性在大规模数据集（如

个小图像样本）上执行简单的迭代算法，每次迭代都要花很长时间，算法要花很长时间才能达到收敛结果。为了提

高收敛速度，可以选择在小批量（少数样本数据）上运行该算法。每次迭代的时候，不是在所有的

法”指的是更新参数），而是使用小批量（译者注：即个图像中的少数图像），即从

个图像上执行该算法（译者注：这里“执行该算

个图像样本中随机选出

个样本，在这 batchsize 为

个图像样本的迷你块（ mini-batch ）上执行这个算法（译者注：即做参数更新）。

这样就可以达到一石二鸟的目的：第一，提高了每次迭代的速度，因为现在每次迭代只在

它提高了收敛的速度。

幅图像样本上执行而不是

个；第二，也是更重要的，

梯度下降（ Gradient Descent ）的三种形式

. 全批量梯度下降（ Full-Batch Gradient Descent）：基于全部样本做参数更新。参数更新最准确，参数更新计算耗时；

. 随机梯度下降（ Stochastic Gradient Descent ）：基于一个样本做参数更新，参数更新最不准确（每次参数更新，参数的变化量方差大），参数

更新最快；

. 小批量梯度下降（ Mini-Batch Gradient Descent ）：基于一定数量（某个固定 batchsize 值）的样本做参数更新，通过控制 batchsize 对参数更新

的准确性和更新时间进行一定平衡。

现在一般情况下所说的随机梯度下降，指的是小批量梯度下降。

这样做的好处：其一，利用矩阵运算的形式简化计算的同时，也可以用矩阵运算库加快代码运算速度；其二，相比每次单一样本做参数更新要更准确，

同时也比全量样本做更新要快（即通过控制 batchsize ，可对参数更新的准确性和更新时间进行一定程度的平衡）。

iteration 和 epoch 的区别

iteration 指一次参数更新。这一次参数更新可以基于全量（全量梯度下降）、一个样本（随机梯度下降）或小批量（小批量梯度下降）的样本。 epoch

指参数的更新遍历一次完整的训练数据集。这其中可能包含很多次参数更新（ iteration ）。

.2 良好的初始值（Good initialization of

）

另一个能获得更快速更优化收敛的重要技巧是：在给定基向量

的条件下，根据目标函数使用梯度下降（或其他方法）求解特征集之前找到良好的特征

的最优值前已找到一个最佳矩阵，不然每次迭代过程中随机初始化值会导致很差的收敛效果。下面给出一个

矩阵的初始值。实际上，除非在优化

初始化的较好方法：

. 令特征集矩阵

. 规范化，令

每一列），除以其在

（

是小批量样本的矩阵表示）

。

表示第个样本的第个特征，

表示基向量

中的第个基向量。即，用特征集矩阵中的每个特征（

的

中对应基向量的范数（模）。

无疑，这样的初始化有助于算法的改进，因为上述的第一步希望找到满足

的矩阵；第二步对作规范化处理是为了保持较小的稀疏惩罚值。这

也表明，只采用上述步骤的某一步而不是两步对做初始化处理将严重影响算法性能。

为什么这样的初始化能改进算法的详细解释

.3 实践算法（The practical algorithm

）

有了以上两种技巧，稀疏编码算法修改如下：

. 随机初始化基向量

. 重复以下步骤直至收敛

. 随机选取一个小批量规模（ batchsize ）为

. 初始化特征集矩阵（如前文所述）。即，首先令特征集矩阵

. 根据上一步给定的基向量，求解能够最小化的特征集矩阵

. 根据上一步得到的特征集矩阵，求解能够最小化的基向量

的小批量样本

；再规范化，令

通过上述方法，可以相对快速地得到局部最优解。

练习：稀疏编码（Exercise:Sparse Coding ）

独立成分分析（Independent Component Analysis

）

注：本章节翻译完全参考旧版 UFLDL 中文教程。

. 概述（Introduction ）

试着回想一下，在介绍稀疏编码算法时我们想为样本数据学习得到一个超完备基（ over-complete basis ）。具体来说，这意味着用稀疏编码学习得到的基向

量之间不一定线性独立。

尽管在某些情况下这已经满足需要，但有时我们仍然希望得到的是一组线性独立基。独立成分分析算法（ ICA ）正实现了这一点。而且，在 ICA 中，我们希

望学习到的基不仅要线性独立，而且还是一组标准正交基。（一组标准正交基

需要满足条件：

（如果

）或者

（

如果））

与稀疏编码算法类似，独立成分分析也有一个简单的数学形式。给定数据，我们希望学习得到一组基向量――以列向量形式构成的矩阵

，其满足以下

特点：首先，与稀疏编码一样，特征是稀疏的；其次，基是标准正交的（注意，在稀疏编码中，矩阵用于将特征映射到原始数据，而在独立成分分析

中，矩阵

由于

工作的方向相反，是将原始数据映射到特征）。这样我们得到以下目标函数：

实际上是描述样本数据的特征，这个目标函数等价于在稀疏编码中特征的稀疏惩罚项。加入标准正交性约束后，独立成分分析相当于求解如下

优化问题：

与深度学习中的通常情况一样，这个问题没有简单的解析解，而且更糟糕的是，由于标准正交性约束，使得用梯度下降方法来求解该问题变得更加困难――

每次梯度下降迭代之后，必须将新的基映射回正交基空间中（以此保证正交性约束）。

实践中，在最优化目标函数的同时施加正交性约束（如下一节的正交 ICA 中讲到的）是可行的，但是速度慢。在标准正交基是不可或缺的情况下，标准正交

ICA的使用会受到一些限制。（译者注：原文给的超链接无法打开）

. 标准正交ICA（Orthonormal ICA ）

标准正交 ICA 的目标函数是：

通过观察可知，约束

隐含着另外两个约束：

第一，因为要学习到一组标准正交基，所以基向量的个数必须小于输入数据的维度。具体来说，这意味着不能像通常在稀疏编码中所做的那样来学习得到超

完备基（ over-complete bases ）。

第二，数据必须经过无正则 ZCA 白化（也即，设为）。（为什么必须这样做？见 TODO ）

因此，在优化标准正交 ICA 目标函数之前，必须确保数据被白化过，并且学习的是一组不完备基（ under-complete basis ）。

然后，为了优化目标函数，我们可以使用梯度下降法，在梯度下降的每一步中增加投影步骤，以满足标准正交约束。过程如下：

重复以下步骤直到完成： 1.

，

其中

是满足

的矩阵空间

在实际中，学习速率是可变的，使用一个线搜索算法来加速梯度。投影步骤通过设置

（ TODO ：解释为什么这就象 ZCA 白化）.

来完成，这实际上可以看成就是 ZCA 白化

. 拓扑ICA（Topographic ICA ）

与稀疏编码算法类似，加上一个拓扑代价项，独立成分分析法可以修改成具有拓扑性质的算法。

独立成分分析重建（ RICA ）

. 独立成分分析概述（ ICA Summary

）

独立成分分析（ ICA ）允许我们使用下面的公式来生成经白化后（译者注：白化是一个数据预处理步骤，用于降低数据冗余）数据的稀疏表示：

其中，

是权重矩阵，是输入。在独立成分分析中，权重矩阵保持正交约束时，我们最小化隐藏层数据的

惩罚项（即

范数）

。正交约束

的存在确保了特征数据的不相关。换句话说，白化过的数据经正交变换仍然是白化的数据。

正交的含义正交最早出现于三维空间中的向量分析。在三维向量空间中，两个向量的内积如果是零，那么就说这两个向量是正交的。换句话说，两

个向量正交意味着它们是相互垂直的。若向量正交，则记为。对于一般的希尔伯特空间，也有内积的概念，所以人们也可以按照上面

的方式定义正交的概念。特别的，我们有维欧氏空间中的正交概念，这是最直接的推广。和正交有关的数学概念非常多，比如正交矩阵，正交补

空间，施密特正交化法，最小二乘法等等。另外在此补充正交函数系的定义：在三角函数系中任何不同的两个函数的乘积在区间上的积分等

，则称这样的三角函数组成的体系叫正交函数系。

与

于

独立成分分析中的正交约束带存在缺点，也就是说，随着输入的特征数据的增多，优化也因这个硬约束（正交约束）愈加困难，导致训练时间延长。那如

何加速呢？如果数据维度大到不能白化，怎么办？记住！如果输入数据，那么白化矩阵的大小就是维度的。

. 独立成分分析重建（ RICA ）

正因如此，有一种称为 “重建独立成分分析”（Reconstrunction ICA，RICA）的算法，就是基于独立成分分析算法克服了这一缺点，以柔性重建惩罚替代独立

成分分析的正交约束。

为了有助于理解该算法，当特征是不完备的，可以得到一个完美重建。要实现这一点，需要限制

。当特征非过完备、数据已经白化、趋向于

无穷大时，从 RICA 恢复到 ICA 也是可能的；在这一点上，完美重建变成一种硬约束。既然在目标函数中有重建的惩罚项，且没有硬约束，那么我们就能提

高过完备特征的比例。但当我们使用过完备基时，结果还是合理的嘛？为了能解释这个问题，我们转向另一个常见的模型上——稀疏自编码。

过完备（over-complete ）表示信号的矩阵的列数大于行数，现有的向量远远多于应有的基的个数，这些向量构成的矩阵过完备了。也就是拥有的向

量对于表示整个空间的性质来说已经完全冗余了。

为了更好理解转移到一个过完备案例中，我们重新回顾一下稀疏自编码，其目标函数如下：

自编码器有着不同的变化，但为了连续性的缘故，此公式使用了

RICA）唯一的区别是 sigmoid 的非线性。从自编码器的视角来观察重建惩罚项，可以看出重建惩罚起着退化控制的作用；也就是说，重建惩罚允许最稀疏

的数据表示，这一过程是通过确保滤波矩阵不学重复或冗余的特征进行的。

稀疏惩罚，同时有一个对应的重建矩阵

。这个稀疏编码和独立成分分析重建

（

因此我们可以将过完备例子中的 RICA 看成是带了

稀疏性约束且没有非线性的稀疏自编码器。这使得独立成分分析重建（RICA）超过过完备基并可以像

稀疏自编码器一样使用反向传播进行优化。独立成分分析重建（RICA）对非白化数据上也展现出了更鲁棒的特性，这再一次体现了与自编码器行为上的相

似。

练习：RICA（Exercise: RICA ）

数据预处理（Data Preprocessing ）

注：本章节翻译完全参考旧版 UFLDL 中文教程。

. 概要（Overview ）

数据预处理在众多深度学习算法中都起着重要作用，实际情况中，将数据做归一化和白化处理后，很多算法能够发挥最佳效果。然而除非对这些算法有丰富

的使用经验，否则预处理的精确参数并非显而易见。在本节中，希望能够揭开预处理方法的神秘面纱，同时为预处理数据提供技巧（和标准流程）。

提示：当开始处理数据时，首先要要观察数据并获知其特性。本部分将介绍一些通用技术，在实际中应该针对具体数据选择合适的预处理技术。例如一

种标准的预处理方法是对每一个数据点都减去它的均值（也被称为移除直流分量，局部均值消减，消减归一化），这一方法对诸如自然图像这类数据是

有效的，但对非平稳的数据则不然。

. 数据归一化（Data Normalization ）

数据预处理中，标准的第一步是数据归一化。虽然这里有一系列可行的方法，但是这一步（数据归一化）通常是根据数据的具体情况而明确选择的。特征归

一化常用的方法包含如下几种：

简单缩放

逐样本均值消减（也称为移除直流分量）

特征标准化（使数据集中所有特征都具有零均值和单位方差）

.1 简单缩放（Simple Rescaling ）

在简单缩放中，我们的目的是通过对数据的每一个维度的值进行重新调节（这些维度可能是相互独立的），使得最终的数据向量落在

间内（根据数据情况而定）。这对后续的处理十分重要，因为很多_默认参数（如 PCA 白化中的）都假定数据已被缩放到合理区间。

或

的区

例如，在处理自然图像时，我们获得的像素值在

区间中，常用的处理是将这些像素值除以

，使它们缩放到

中。

.2 逐样本均值消减（Per-example mean subtraction

）

如果您的数据是_平稳的（即数据每一个维度的统计都服从相同分布），那么您可以考虑在每个样本上减去数据的统计平均值（逐样本计算）。（这个均值是

基于当前这幅图像的）

例如，对于图像，这种归一化可以移除图像的平均亮度值（ intensity ，亮度或像素强度值）。很多情况下我们对图像的像素值并不感兴趣，而更多地

关注其内容，这时对每个数据点移除像素的均值是有意义的。

注意：虽然该方法广泛地应用于图像，但在处理彩色图像时需要格外小心，具体来说，是因为不同色彩通道中的像素并不都存在平稳特性。

.3 特征标准化（Feature Standardization

）

特征标准化指的是（独立地）使得数据的每一个维度具有零均值和单位方差。这是归一化中最常见的方法并被广泛地使用（例如，在使用支持向量机时，特

征标准化常被建议用作预处理的一部分）。在实际应用中，特征标准化的具体做法是：首先计算每一个维度上数据的均值（使用全体数据计算），之后在每

一个维度上都减去该均值。下一步便是在数据的每一维度上除以该维度上数据的标准差。

例如，处理音频数据时，常用 [Mel 倒频系数](http://en.wikipedia.org/wiki/Mel-frequency_cepstrum MFCCs) 来表征数据。然而 MFCC 特征的第一个分

量（表示直流分量）数值太大，常常会掩盖其它分量。这种情况下，为了平衡各个分量的影响，通常对特征的每个分量独立地使用标准化处理。

梅尔频率倒谱系数（ MFCCs ， Mel Frequency Cepstral Coefficents ）是一种在自动语音和说话人识别中广泛使用的特征。它是在 1980 年由 Davis

和 Mermelstein 提出。从那时起，在语音识别领域， MFCCs 在人工特征方面可谓是鹤立鸡群，一枝独秀，从未被超越啊（至于说 Deep Learning 的特

征学习那是后话了）。参考：语音信号处理之（四）梅尔频率倒谱系数（MFCC）

. PCA/ZCA白化（PCA/ZCA Whitening ）

在做完简单的归一化后，白化通常会被用来作为接下来的预处理步骤，它会使算法工作得更好。实际上许多深度学习算法都依赖于白化来获得好的特征。

在进行 PCA/ZCA 白化时，首先使特征零均值化是很有必要的，这保证了

。特别地，这一步需要在计算协方差矩阵前完成（唯一例外的情

况是已经进行了逐样本均值消减，并且数据在各维度上或像素上是平稳的）。

接下来在 PCA/ZCA 白化中我们需要选择合适的

（回忆一下，这是规则化项，对数据有低通滤波作用）。选取合适的值对特征学习起着很

大作用，下面讨论在两种不同场合下如何选取

：

）

.1 基于重构的模型（Reconstruction Based Models

在基于重构的模型中（包括自编码器，稀疏编码，受限玻尔兹曼机，k-均值），经常倾向于选取合适的

通常认为数据中的高频分量是噪声，低通滤波的作用就是尽可能抑制这些噪声，同时保留有用的信息。在 PCA 等方法中，假设数据的信息主要分布在方差

较高的方向，方差较低的方向是噪声（即高频分量），因此后文中的选择与特征值有关）。

以使得白化达到低通滤波的效果。（译注：

一种检验

是否合适的方法是用该值对数据进行 ZCA 白化，然后对白化前后的数据进行可视化。如果

值过低，白化后的数据会显得噪声很

大；相反，如果

值过高，白化后的数据与原始数据相比就过于模糊。一种直观上得到

大小的方法是以图形方式画出数据的特征值，如下

图的例子所示，您可以看到一条"长尾"，它对应于数据中的高频噪声部分。您需要选取合适的

说，选取的应大于大多数较小的、反映数据中噪声的特征值。

，使其能够在很大程度上过滤掉这条"长尾"，也就是

[ZCA_Eigenvalues_Plot.png](./images/ZCA_Eigenvalues_Plot.png)

在基于重构的模型中，损失函数有一项是用于惩罚那些与原始输入数据差异较大的重构结果（译注：以自动编码机为例，要求输入数据经过编码和解码之后

还能尽可能地还原输入数据）。如果太小，白化后的数据中就会包含很多噪声，而模型要拟合这些噪声，以达到很好的重构结果。因此，对于基于

重构的模型来说，对原始数据进行低通滤波就显得非常重要。

提示：如果数据已被缩放到合理范围（如

），可以从

或

开始调节

。

.2 基于正交化ICA的模型（ICA-based Models (with orthogonalization)

对基于正交化 ICA 的模型来说，保证输入数据尽可能地白化（即协方差矩阵为单位矩阵）非常重要。这是因为：这类模型需要对学习到的特征做正交化，以

解除不同维度之间的相关性（详细内容请参考独立成分分析| ICA 一节）。因此在这种情况下，要足够小（比如）。

）

提示：也可以在 PCA 白化过程中同时降低数据的维度。这是一个很好的主意，因为这样可以大大提升算法的速度（减少了运算量和参数数目）。确定

要保留的主成分数目有一个经验法则：即所保留的成分的总方差达到总样本方差的以上（详细内容请参考 [主成分分析 | PCA ](./主成分分析白化

PCA Whitening）.md) 一节中成分数量的选择）。

（

注意: 在使用分类框架时，我们应该只基于训练集上的数据计算 PCA/ZCA 白化矩阵。需要保存以下两个参数留待测试集合使用： a. 用于零均值化数据

的平均值向量； b. 白化矩阵。测试集需要采用这两组保存的参数来进行相同的预处理。

. 大图像（Large Images ）

对于大图像，采用基于 PCA/ZCA 的白化方法是不切实际的，因为协方差矩阵太大。在这些情况下我们退而使用 1/f 白化方法（更多内容后续再讲）。

. 标准流程（Standard Pipelines ）

在这一部分中，我们将介绍几种在一些数据集上有良好表现的预处理标准流程.

.1 自然灰度图像（Natural Grey-scale Images

）

灰度图像具有平稳特性，我们通常在第一步对每个数据样本分别做均值消减（即减去直流分量），然后采用 PCA/ZCA 白化处理，其中的

要足够大

以达到低通滤波的效果。

.2 彩色图像（Color Images ）

对于彩色图像，色彩通道间并不存在平稳特性。因此我们通常首先对数据进行特征缩放（使像素值位于

区间），然后使用足够大的

来做

PCA/ZCA。注意在进行 PCA 变换前需要对特征进行分量均值归零化。

.3 音频 (MFCC/频谱图)（Audio (MFCC/Spectrograms)

）

对于音频数据（ MFCC 和频谱图），每一维度的取值范围（方差）不同。例如 MFCC 的第一分量是直流分量，通常其幅度远大于其他分量，尤其当特征中

包含时域导数（ temporal derivatives ）时（这是音频处理中的常用方法）更是如此。因此，对这类数据的预处理通常从简单的数据标准化开始（即使得数据

的每一维度均值为零、方差为），然后进行 PCA/ZCA 白化（使用合适的

）。

.4 MNIST 手写数字（MNIST Handwritten Digits

）

MNIST 数据集的像素值在

区间中。我们首先将其缩放到

区间。实际上，进行逐样本均值消去也有助于特征学习。

注：也可选择以对 MNIST 进行 PCA/ZCA 白化，但这在实践中不常用。

中英文对照

中文

英文

normalization

归一化

白化

whitening

直流分量

局部均值消减

消减归一化

缩放

DC component

local mean subtraction

sparse autoencoder

rescaling

逐样本均值消减

特征标准化

平稳

per-example mean subtraction

feature standardization

stationary

Mel 倒频系数

零均值化

低通滤波

基于重构的模型

自编码器

稀疏编码

受限Boltzman机

k-均值

MFCC

zero-mean

low-pass filtering

reconstruction based models

autoencoders

sparse coding

RBMs

k-Means

长尾

long tail

损失函数

正交化

loss function

orthogonalization

用反向传导思想求导（Deriving gradients using the backpropagation idea

）

注：本章节翻译参考旧版 UFLDL 中文教程。

译者注：本文更多的是一种思想，应用反向传播算法更新参数的思想，用在一般的函数的求导问题上。不仅看起来清晰，理解起来也透彻。这也从侧面

体现神经网络可以表示复杂函数的能力，反之亦然。

. 简介（Introduction ）

在 [多层神经网络-反向传导算法](./监督神经网络（Supervised Neural Networks）/多层神经网络（Multi-Layer Neural Networks）.md) 一节中，介绍了在稀

疏自编码器中用反向传导算法来求梯度的方法。事实证明，反向传导算法与矩阵运算相结合的方法，对于计算复杂矩阵函数（从矩阵到实数的函数，或用符

号表示为：从

）的梯度是十分强大和直观的。

首先，回顾一下反向传导的思想，为了更适合目的，将其稍作修改呈现于下：

. 对第

层（最后一层）中的每一个输出单元，令

其中，

是“目标函数”（稍后解释）。对

. 对第层中的每个节点，令 $$ \delta^{(l)}i = \left( \sum{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) \bullet \frac{\partial}{\partial z^{(l)}_i} f^{(l)}

(z^{(l)}_i) $$

. 计算需要的偏导数

符号简要说明：

符号

说明

是神经网络的层数

第

是

层神经元的个数

层第个节点到第

层第个节点的权重

是第层第个单元（即节点）的输入

是第层第个节点的激励

是矩阵的 Hadamard 积或逐个元素乘积，对

矩阵

和

，它们的乘积是

矩阵

，即

是第层中各单元的激励函数

Hadamard 乘积

矩阵

的 Hadamard 乘积定义为二者对应位置的乘积。设相同维度的矩阵（

则二者的 Hadamard 乘积为

矩阵均为

关于

行

列），其中，

，

假设有一个函数

，

以矩阵

为参数生成一个实数。我们希望用反向传导思想计算

的梯度，即

。大致思路是将函数

看成一个多层

神经网络，并使用反向传导思想求梯度。

为了实现这个想法，取目标函数为

，当计算最后一层神经元的输出时，会产生值

以及网络中任意一个权重的导数。

。对于中间层，将选择激励函数

。

稍后会看到使用这种方法，可以很容易计算出对于输入

. 示例（Examples ）

为了阐述如何使用反向传导思想计算关于输入的导数，在示例 1 ，示例 2 中用 [稀疏编码](./稀疏编码（Sparse Coding）.md) 章节中的两个函数。在示例 3

中，使用独立成分分析一节中的一个函数来说明使用此思想计算关于权重的偏导的方法，以及在这种特殊情况下，如何处理相互捆绑或重复的权重。

.1 示例1：稀疏编码中权重矩阵的目标函数（Example 1: Objective for weight matrix in sparse coding

）

回顾一下 [稀疏编码自编码表达](./稀疏编码自编码表达（Sparse Coding: Autoencoder Interpretation）.md) ，当给定特征集矩阵时，权重矩阵

（译者

注：在该章节中，

为基向量）的目标函数为：

的梯度，即

我们希望求

对于基向量

。因为目标函数是两个含

的式子之和，所以它的梯度是每个式子的梯度之和。第二项的梯度很容易

求，因此我们只考虑第一项的梯度。

第一项，，可以看成一个用特征集矩阵做输入的神经网络的实例，通过四步进行计算，文字以及图形描述如下：

. 把

. 将第二层的激励减，第二层使用了单位激励函数。

. 通过单位权重将结果不变地传到第三层。在第三层使用平方函数作为激励函数。

. 将第三层的所有激励相加。

作为第一层到第二层的权重。

[Backpropagation Method Example 1.png](./images/400px-Backpropagation_Method_Example_1.png)

该网络的权重和激励函数如下表所示：

层

权重

激励函数

（单位函数）

（单位向量）

为了使

一旦将

，可令

。

看成神经网络，梯度

激励函数的导数

就很容易求了——使用反向传导得到：

层

Delta

该层输入

层

激励函数的导数

Delta

该层输入

因此

译者注：从形式看，是从第一层（

）开始逐层向上使用

替换 delta ，直到最后一层，将

替换为最后一层的输入。然后再化简得到其最简

形式（示例 2 和 3 与此类似）。

.2 示例2：稀疏编码中的经过平滑的L1稀疏惩罚项（Example 2: Smoothed topographic L1 sparsity penalty in sparse coding

）

回顾 [稀疏编码自编码表达](./稀疏编码自编码表达（Sparse Coding: Autoencoder Interpretation）.md) 一节中对特征集矩阵经过平滑的

稀疏惩罚项：

其中

是分组矩阵，是特征集矩阵，是一个常数。

一般称为“平滑参数”（ "smoothing parameter" ）或者“稀疏参数”（ "sparsity parameter" ）。其存在是用来解决目标函数的

可微问题（该问题影响了梯度方法的应用）。尽管可以通过其他非梯度下降方法避开这一问题，但是本文通过使用近似值“平滑”

决此难题。

范数在点处不

范数的方法解

稀疏编码目标函数的一种形式是：

其中，稀疏惩罚项由原本的

经平滑变为

。

是

的简写。

分组矩阵

。“分组”可以通过“分组矩阵”

完成，分组矩阵

的第行标识了哪些特征被分到第组中，即如果第组包含特征

则

。

通过分组矩阵实现分组使得梯度的计算更加直观。 **拓扑稀疏编码得到的特征与稀疏编码得到的类似，只是拓扑稀疏编码得到的特征是以某种

方式有“秩序”排列的。**这个“秩序”就提现在分组矩阵

上。

我们希望求得

[Backpropagation Method Example 2.png](./images/600px-Backpropagation_Method_Example_2.png)

该网络的权重和激励函数如下表所示：

。像上面那样，把这一项看做一个神经网络的实例：

层

权重

激励函数

（单位向量）

为使

，可令

。

一旦把

看做一个神经网络，梯度

激励函数的导数

变得很容易计算——使用反向传导得到：

层

Delta

该层输入

因此

.3 示例3：ICA重建代价（Example 3: ICA reconstruction cost

）

回顾独立成分分析（ ICA ）一节重建代价一项：

，其中

是权重矩阵，是输入。

我们希望计算

——对于权重矩阵

的导数，而不是像前两例中对于输入的导数。不过我们仍然用类似的方法处理，把该项看做

一个神经网络的实例：

[Backpropagation Method Example 3.png](./images/400px-Backpropagation_Method_Example_3.png)

该网络的权重和激励函数如下表所示：

层

权重

激励函数

（单位向量）

为使

既然可将

，可令

看做神经网络，那么就能计算出梯度

。

。然而，现在面临的难题是

在网络中出现了两次。幸运的是，可以证明如果

在网络中出现

多次，那么对于

的梯度是对网络中每个

实例的梯度的简单相加（您需要自己给出对这一事实的严格证明来说服自己）。知道这一点后，首先将计算

delta ：

层| 激励函数的导数

| 该层输入 | |:-:|:-:|:-:| |4|

| |1|

| |3|

| |2|

（

在网络中出现了两次）为计算对于

：

的梯度，首先计算对网络中每个

实例的梯度。

对于

：

最后进行求和，得到对于

的最终梯度，注意需要对

梯度进行转置，来得到关于

的梯度（原谅我在这里稍稍滥用了符号）：

自我学习（Self-Taught Learning ）

自我学习（Self Taught Learning ）

注：本章节翻译完全参考旧版 UFLDL 中文教程。

. 综述（Overview ）

如果已经有一个足够强大的机器学习算法，为了获得更好的性能，最靠谱的方法之一是给这个算法以更多的数据。机器学习界甚至有个说法：“有时候胜出者

并非有最好的算法，而是有更多的数据。”

人们总是尝试获取更多的已标注数据，但是这样做成本往往很高。例如研究人员已经花了相当的精力在使用类似 AMT（ Amazon Mechanical Turk ，译者

注：一个众包模式的任务平台，研究人员将未标注的数据发布成任务并支付一定费用让别人对数据做标注）这样的工具上，以期获取更大的训练数据集。相

比大量研究人员通过手工方式构建特征，用众包的方式让多人手工标数据是一个进步，但是我们可以做得更好。

具体的说，如果算法能够从未标注数据中学习，那么我们就可以轻易地获取大量无标注数据，并从中学习。自学习和无监督特征学习就是这种的算法。尽管

一个单一的未标注样本蕴含的信息比一个已标注的样本要少，但是如果能获取大量无标注数据（比如从互联网上下载随机的、无标注的图像、音频剪辑或者

是文本），并且算法能够有效的利用它们，那么相比大规模的手工构建特征和标数据，算法将会取得更好的性能。

在自学习和无监督特征学习问题上，可以给算法以大量的未标注数据，学习出较好的特征描述。在尝试解决一个具体的分类问题时，可以基于这些学习出的

特征描述和任意的（可能比较少的）已标注数据，使用有监督学习方法完成分类。

在一些拥有大量未标注数据和少量的已标注数据的场景中，上述思想可能是最有效的。即使在只有已标注数据的情况下（这时我们通常忽略训练数据的类标

号进行特征学习），以上想法也能得到很好的结果。

. 特征学习（Learning features ）

我们已经了解到如何使用一个自编码器（ autoencoder ）从无标注数据中学习特征。具体来说，假定有一个无标注的训练数据集

标代表“不带类标”）。现在用它们训练一个稀疏自编码器（可能需要首先对这些数据做白化或其它适当的预处理）。

（下

[STL_SparseAE](./images/STL_SparseAE.png)

利用训练得到的模型参数

，给定任意的输入数据，可以计算隐藏单元的激活量（ activations ）。如前所述，相比原始输入

来说，可能是一个更好的特征描述。下图的神经网络描述了特征（激活量）的计算。

[STL_SparseAE_Features](./images/STL_SparseAE_Features.png)

这实际上就是之前得到的稀疏自编码器，在这里去掉了最后一层（译者注：解码部分）。

假定有样本数量为

的已标注训练集

（下标表示“带类标”），我们可以为输入数据找到更好的特征描述。例

。接下来，可以直接使用来代替原始数据（“替代表示”， Replacement

来代替原始数据（“级联表示”， Concatenation Representation ）。

如，可以将输入到稀疏自编码器，得到隐藏单元激活量

Representation ）。也可以合二为一，使用新的向量

两种特征表示方法，在这里可能用“特征转换”更合适

替代表示（ Replacement Representation ）：使用转移（或激活）函数映射的原样本得到的新特征

或称为，代替原样本作为特

征；

级联表示（ Concatenation Representation ）：使用经转移（或激活）函数映射后的特征

和原样本特征拼接起来得到的新特征

，

代替原样本作为特征。

经过变换后，训练集就变成

使用替换还是将二者合并）。在实践中，将

或者是

合并通常表现的更好。但是考虑到内存和计算的成本，也可以使用替换操作。

（取决于

和

可以基于这样的特征训练一个有监督学习算法（例如支持向量机、逻辑斯特回归等），最终得到一个判别函数对值进行预测。预测过程如下：给定一个测

试样本

，重复之前的过程，将其送入稀疏自编码器，得到

。然后将

（或者

）送入支持向量机或逻辑斯特回归的分类器中，得

到预测值。

. 数据预处理（On pre-processing the data

）

译者注：在将数据送入稀疏编码器前，我们可能已经对数据做了预处理操作，在这之后的训练和测试，也需要对数据做同样的预处理操作（比方需要将

预处理中使用的参数保留起来，供后面训练和测试的时候使用，保证预处理的过程是一样的）。

在特征学习阶段，我们在未标注训练集

上学习，这一过程中可能计算了各种数据预处理参数。例如计算数据均值并且对数据做均值标

（又或者使用 PCA 白化或 ZCA 白化）。

准化（ mean normalization ）；或者对原始数据做主成分分析（ PCA ），然后将原始数据表示为

这样的话，有必要将这些参数保存起来，并且在后面的训练和测试阶段使用同样的参数，以保证数据进入稀疏自编码神经网络之前经过了同样的变换。例

如，如果对未标注数据集进行 PCA 预处理，就必须将得到的矩阵保存起来，并且应用到有标注训练集和测试集上；而不能使用有标注训练集重新估计出

一个不同的矩阵（也不能重新计算均值并做均值标准化），否则的话可能得到一个完全不一致的数据预处理操作，导致进入自编码器的数据分布迥异于训

练自编码器时的数据分布。

. 无监督特征学习的术语（On the terminology of unsupervised feature learning

）

有两种常见的无监督特征学习方式，区别在于您有什么样的未标注数据。自学习（ self-taught learning ）是其中更为一般的、更强大的学习方式，它不要

求未标注数据

二者的区别。

和已标注数据

来自同样的分布。另外一种带限制性的方式也被称为半监督学习，它要求

和

服从同样的分布。下面通过例子解释

假定有一个计算机视觉方面的任务，目标是区分汽车和摩托车图像；也即训练样本里面要么是汽车的图像，要么是摩托车的图像。哪里可以获取大量的未标

注数据呢？最简单的方式可能是从互联网上下载一些随机的图像数据集，在这些数据上训练出一个稀疏自编码器，从中得到有用的特征。这个例子里，未标

注数据完全来自于一个和已标注数据不同的分布（未标注数据集中，或许其中一些图像包含汽车或者摩托车，但是不是所有的图像都如此）。这种情形被称

为自学习（译者注：含有杂质图像）。

相反，如果有大量的未标注图像数据，要么是汽车图像，要么是摩托车图像，仅仅是缺失了类标号（没有标注每张图片不是汽车就是摩托车）。也可以用这

些未标注数据来学习特征。这种方式，即要求未标注样本和带标注样本服从相同的分布，有时候被称为半监督学习。在实践中，常常无法找到满足这种要求

的未标注数据（到哪里找到一个每张图像不是汽车就是摩托车，只是丢失了类标号的图像数据库？）因此，自学习在无标注数据集的特征学习中应用更广。

深度网络概览（Deep Networks: Overview ）

注：本章节翻译参考旧版 UFLDL 中文教程。

. 概述（Overview ）

在之前的章节中，您已经构建了一个包括输入层、隐藏层以及输出层的三层神经网络。虽然该网络对于 MNIST 手写数字数据库非常有效，但是它还是一个

非常“浅”的网络。这里的“浅”指的是特征（隐藏层的激活值）只使用一层计算单元（一层的隐藏层）来得到的。

在本节中，将开始讨论深度神经网络，即含有多个隐藏层的神经网络。通过引入深度网络，我们可以计算更多复杂的输入特征。因为每一个隐藏层可以对上

一层的输出进行非线性变换，因此深度神经网络拥有比“浅层”网络更加优异的表达能力（例如可以学习到更加复杂的函数关系）。

值得注意的是，当训练深度网络的时候，每一层隐层应该使用非线性的激活函数

。这是因为多层的线性函数组合在一起本质上也只有线性函数的表达

能力（例如，将多个线性方程组合在一起仅仅产生另一个线性方程）。因此，在激活函数是线性的情况下，相比于单隐藏层神经网络，包含多隐藏层的深度

网络并没有增加表达能力。

. 深度网络的优势（Advantages of deep networks

）

为什么要使用深度网络呢？使用深度网络最主要的优势在于，它能以更加紧凑简洁的方式来表达比浅层网络大得多的函数集合。正式点说，我们可以找到一

些函数，这些函数可以用层网络简洁地表达出来（这里的简洁是指隐层单元的数目只需与输入单元数目呈多项式关系）。但是对于一个只有

络而言，除非它使用与输入单元数目呈指数关系的隐层单元数目，否则不能简洁表达这些函数。

层的网

输入单元个数和隐含单元个数的关系

举一个简单的例子，比如我们打算构建一个布尔网络来计算个输入比特的奇偶校验码（或者进行异或运算）。假设网络中的每一个节点都可以进行逻

辑“或”运算（或者“与非”运算），亦或者逻辑“与”运算。如果我们拥有一个仅仅由一个输入层、一个隐层以及一个输出层构成的网络，那么该奇偶校验函数所

需要的节点数目与输入层的规模呈指数关系。但是，如果我们构建一个更深点的网络，那么这个网络的规模就可做到仅仅是的多项式函数。

输入单元个数和隐含层层数的关系

当处理对象是图像时，我们能够使用深度网络学习到“部分-整体”的分解关系。例如，第一层可以学习如何将图像中的像素组合在一起来检测边缘（正如我们

在前面的练习中做的那样）。第二层可以将边缘组合起来检测更长的轮廓或者简单的“目标的部件”。在更深的层次上，可以将这些轮廓进一步组合起来以检

测更为复杂的特征。

最后要提的一点是，大脑皮层同样是分多层进行计算的。例如视觉图像在人脑中是分多个阶段进行处理的，首先是进入大脑皮层的 “V1” 区，然后紧跟着进入

大脑皮层 “V2” 区，以此类推。

. 训练深度网络的困难（Difficulty of training deep architectures

）

虽然几十年前人们就发现了深度网络在理论上的简洁性和较强的表达能力，但是直到最近，研究者们也没有在训练深度网络方面取得多少进步。问题原因在

于研究者们主要使用的学习算法是：首先随机初始化深度网络的权重，然后使用有监督的目标函数在有标签的训练集 $\textstyle \left{ \left( x_{l}^{\left( 1

right)},{{y}^{\left( 1 \right)}} \right),...,\left( x_{l}^{\left( {{m}{l}} \right)},{{y}^{\left( {{m}{l}} \right)}} \right) \right}$ 上进行训练。例如通过使用梯度下降法来降低训

练误差。然而，这种方法通常不是十分奏效。这其中有如下几方面原因：

.1 数据获取问题（Availability of data

）

使用上面提到的方法，我们需要依赖于有标签的数据才能进行训练。然而有标签的数据通常是稀缺的，因此对于许多问题，我们很难获得足够多的样本来拟

合一个复杂模型的参数。例如，考虑到深度网络具有强大的表达能力，在不充足的数据上进行训练将会导致过拟合。

.2 局部极值问题（Local optima ）

使用监督学习方法来对浅层网络（只有一个隐藏层）进行训练通常能够使参数收敛到合理的范围内。但是当用这种方法来训练深度网络的时候，并不能取得

很好的效果。特别的，使用监督学习方法训练神经网络时，通常会涉及到求解一个高度非凸的优化问题（例如最小化训练误差

其中参数是要优化的参数。对深度网络而言，这种非凸优化问题的搜索区域中充斥着大量“坏”的局部极值（译者注：这里的“坏”可以理解为与全局最小值

相差很大），因而使用梯度下降法（或者像共轭梯度下降法， L-BFGS 等方法）效果并不好。

，

.3 梯度弥散问题（Diffusion of gradients

）

梯度下降法（以及相关的 L-BFGS 算法等）在使用随机初始化权重的深度网络上效果不好的技术原因是：梯度会变得非常小。具体而言，当使用反向传播方

法计算导数的时候，随着网络的深度的增加，反向传播的梯度（从输出层到网络的最初几层）的幅度值会急剧地减小。结果就造成了整体的损失函数相对于

最初几层的权重的导数非常小。这样，当使用梯度下降法的时候，最初几层的权重变化非常缓慢，以至于它们不能够从样本中进行有效的学习。这种问题通

常被称为“梯度的弥散”.

与梯度弥散问题紧密相关的问题是：当神经网络中的最后几层含有足够数量神经元的时候，可能单独这几层就足以对有标签数据进行建模，而不用最初几层

的帮助（译者注：相当于层数冗余）。因此，对所有层都使用随机初始化的方法训练得到的整个网络的性能将会与训练得到的浅层网络（仅由深度网络的最

后几层组成的浅层网络）的性能相似。

. 逐层贪婪训练方法（Greedy layer-wise training

）

那么，我们应该如何训练深度网络呢？逐层贪婪训练方法是取得一定成功的一种方法。我们会在后面的章节中详细阐述这种方法的细节。简单来说，逐层贪

婪算法的主要思路是每次只训练网络中的一层，即我们首先训练一个只含一个隐藏层的网络，仅当这层网络训练结束之后才开始训练一个有两个隐藏层的网

络，以此类推。在每一步中，我们把已经训练好的前

层（译者注：的网络权重）固定，然后增加第层（也就是将我们已经训练好的前

的输

出作为输入）。每一层的训练可以是有监督的（例如，将每一步的分类误差作为目标函数），但更通常使用无监督方法（译者注：例如自动编码器，在前面

的章节中已经给出细节）。这些各层单独训练所得到的权重被用来初始化最终（或者说全部）的深度网络的权重，然后对整个网络进行“微调”（即把所有层

放在一起来优化有标签训练集上的训练误差）。

逐层贪婪的训练方法取得成功要归功于以下几方面：

.1 数据获取（Availability of data

虽然获取有标签数据的代价是昂贵的，但获取大量的无标签数据是容易的。自学习方法（ self-taught learning ）的潜力在于它能通过使用大量的无标签数据

来学习到更好的模型。具体而言，该方法使用无标签数据来学习得到所有层（不包括用于预测标签的最终分类层）的最佳初始权重。相比纯监督学习

方法，这种自学习方法能够利用多得多的数据，并且能够学习和发现数据中存在的模式。因此该方法通常能够提高分类器的性能。

）

.2 更好的局部极值（ Better local optima

）

当用无标签数据训练完网络后，相比于随机初始化而言，各层初始权重会位于参数空间中较好的位置上。然后我们可以从这些位置出发进一步微调权重。从

经验上来说，以这些位置为起点开始梯度下降更有可能收敛到比较好的局部极值点，这是因为无标签数据已经提供了大量输入数据中包含的模式的先验信

息。

在下一节中，我们将会具体阐述如何进行逐层贪婪训练。

无监督学习（Unsupervised Learning ）

栈式自编码算法（Stacked Autoencoders ）

注：本章节翻译参考旧版 UFLDL 中文教程。

. 概述（Overview ）

逐层贪婪训练法依次训练网络的每一层，进而预训练整个深度神经网络。在本节中，我们将会学习如何将自编码器“栈化”到逐层贪婪训练法中，从而预训练

或者说初始化）深度神经网络的权重。

（

栈式自编码神经网络是一个由多层稀疏自编码器组成的神经网络，其前一层自编码器的输出作为其后一层自编码器的输入。对于一个层栈式自编码神经网

络，我们沿用自编码器一章的各种符号，假定用表示第个（译者注：个人认为这里应该是第层）自编码器对应的

参数，那么该栈式自编码神经网络的编码过程就是，按照从前向后的顺序执行每一层自编码器的编码步骤：

同理，栈式神经网络的解码过程就是，按照从后向前的顺序执行每一层自编码器的解码步骤：

其中，

通过将

是最深层隐藏单元的激活值，其包含了我们感兴趣的信息，这个向量也是对输入值的更高阶的表示。

作为 SoftMax 分类器的输入特征，可以将栈式自编码神经网络中学到的特征用于分类问题。

. 训练（Training ）

一种比较好的获取栈式自编码神经网络参数的方法是采用逐层贪婪训练法进行训练。即先利用原始输入来训练网络的第一层，得到其参数

然后网络第一层将原始输入转化成为由隐藏单元激活值组成的向量（假设该向量为），接着把作为第二层的输入，继

；最后，对后面的各层采用同样的策略，即将前层的输出作为下一层输入的方式依次训练。

；

续训练得到第二层的参数

对于上述训练方式，在训练每一层参数的时候，会固定其它各层参数保持不变。所以，如果想得到更好的结果，在上述预训练过程完成之后，可以通过反向

传播算法同时调整所有层的参数以改善结果，这个过程一般被称作“微调（ fine-tuning ）”。

实际上，使用逐层贪婪训练方法将参数训练到快要收敛时，应该使用微调。反之，如果直接在随机化的初始权重上使用微调，那么会得到不好的结果，因为

参数会收敛到局部最优。

如果你只对以分类为目的的微调感兴趣，那么惯用的做法是丢掉栈式自编码网络的“解码”层，直接把最后一个隐藏层的

进行分类，这样，分类器（ SoftMax ）的分类错误的梯度值就可以直接反向传播给编码层了。

作为特征输入到 SoftMax 分类器

. 具体实例（Concrete example ）

让我们来看个具体的例子，假设你想要训练一个包含两个隐含层的栈式自编码网络，用来进行 MNIST 手写数字分类（这将会是你的下一个练习）。首先，

你需要用原始输入训练第一个自编码器，它能够学习得到原始输入的一阶特征表示（如下图所示）。

[Stacked SparseAE Features1.png](./images/400px-Stacked_SparseAE_Features1.png)

这里的“一阶特征”就是输入时的特征（输入层），“二阶特征”是网络第二层（第一个隐含层）的特征。

接着，你需要把原始数据输入到上述训练好的稀疏自编码器中，对于每一个输入

，都可以得到它对应的一阶特征表示

。然后你再用这些一阶特

征作为另一个稀疏自编码器的输入，使用它们来学习二阶特征。（如下图所示）

[Stacked SparseAE Features2.png](./images/400px-Stacked_SparseAE_Features2.png)

同样，再把一阶特征输入到刚训练好的第二层稀疏自编码器中，得到每个

对应的二阶特征激活值

。接下来，你可以把这些二阶特征作为

SoftMax 分类器的输入，训练得到一个能将二阶特征映射到数字标签（译者注：样本类型）的模型。

[Stacked Softmax Classifier.png](./images/400px-Stacked_Softmax_Classifier.png)

如下图所示，最终，你可以将这三层结合起来构建一个包含两个隐藏层和一个最终 SoftMax 分类器层的栈式自编码网络，这个网络能够如你所愿地对

MNIST 数字进行分类。

[Stacked Combined.png](./images/500px-Stacked_Combined.png)

. 讨论（Discussion ）

栈式自编码神经网络具有强大的表达能力及深度神经网络的所有优点。

更进一步，它通常能够获取到输入的“层次型分组”或者“部分-整体分解”结构。为了弄清这一点，回顾一下，自编码器倾向于学习得到能更好地表示输入数据

的特征。因此，栈式自编码神经网络的第一层会学习得到原始输入的一阶特征（比如图片里的边缘），第二层会学习得到二阶特征，该特征对应一阶特征里

包含的一些模式（比如在构成轮廓或者角点时，什么样的边缘会共现）。栈式自编码神经网络的更高层还会学到更高阶的特征。

举个例子，如果网络的输入数据是图像，网络的第一层会学习如何去识别边，第二层一般会学习如何去组合边，从而构成轮廓、角等。更高层会学习如何去

组合更形象且有意义的特征。例如，如果输入数据集包含人脸图像，更高层会学习如何识别或组合眼睛、鼻子、嘴等人脸器官。

微调多层自编码算法（Fine-tuning Stacked AEs ）

注：本章节翻译参考旧版 UFLDL 中文教程。

. 介绍（Introduction ）

微调（ Fine-tunning ）是深度学习中的常用策略，可以大幅提升一个栈式自编码神经网络的性能表现。从更高的视角来讲，微调将栈式自编码神经网络的所

有层视为一个模型，这样在每次迭代中，网络中所有的权重值都可以被优化。

. 一般策略（General Strategy ）

幸运的是，实施微调栈式自编码神经网络所需的工具都已齐备！为了在每次迭代中计算所有层的梯度，我们需要使用稀疏自动编码一节中讨论的反向传播算

法。因为反向传播算法可以延伸应用到任意多层，所以事实上，该算法对任意多层的栈式自编码神经网络都适用。

. 使用反向传播法进行微调（Finetuning with Backpropagation

）

为方便读者，以下我们简要描述如何实施反向传播算法：

. 进行一次前馈传递，对

层、

层直到输出层

，使用前向传播步骤中定义的公式计算各层上的激活值（激励响应）。

. 对输出层（第层），令

符号说明

：

输出层（第

层）误差

：对输出层函数的导数，传入上一层输出的结果

：输出层目标函数关于所求参数

和

的偏导数

当使用 SoftMax 分类器时， SoftMax 层满足：

，其中为输入数据对应的类别标签，

为条件概率向量。 3. 对

令

符号说明

：

第

层与第

层间的网络权重参数

：误差从输出层经反向传播到第层的误差

. 计算所需的偏导数：

注：我们可以认为输出层 SoftMax 分类器是附加上的一层，但是其求导过程需要单独处理。具体地说，网络“最后一层”的特征会进入 SoftMax 分类器。

所以，第二步中的导数由

量）。

计算，其中

（其中，为输入数据对应的类别标签，

为条件概率向

机器学习梯度下降矩阵乘法神经网络模型监督学习

「喜欢这篇文章，您的关注和赞赏是给作者最好的鼓励」

关注作者

非监督特征学习

评论