什么是算法
百度百科:
算法是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。
个人理解:
算法就是根据一定的条件,对一些数据计算,得到目标结果。
好的算法
我们从两个维度上去判断一个算法是否是一个好的算法,时间和空间,我们一般认为花最少的时间、使用最小的内存空间实现同一目标的算法是好的算法。我们把对时间和空间的计算被称作:
时间复杂度
空间复杂度
时间复杂度
算法的时间复杂度是一个函数,用来描述算法的运行时间,一般使用大O符号表示,所以一个算法的时间复杂度我们可以说是O(f(n)),f(n)我们这里表示算法需要执行的次数,n代表数据规模。下面我们通过几个例子介绍相同需求下的不同算法的时间复杂度。
图1
图2

从上面两张图我们可以看出,同样是求相同数据规模的和,随着数据规模n的增加,第一个算法比第二个算法的执行次数大大增加,相应的第一个算法比第二个算法的时间复杂度也是大大增加的。所以上图中,图一的总执行次数是O(2n+3),图二的总执行次数是O(3)。
图3

从图3来说,我们可以通过数学的方式计算出,总执行次数为O(1+1+n+(n+1)*n/2+(n+1)*n/2)=O(n²+2n+2)。
但是我们分析一个算法的时间复杂度,侧重的是随着数据规模的增大 ,算法增长的规律,而不是研究一个算法到底执行了多少次数。所以我们在这里引出函数渐进增长的概念:
给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,函数f(n)总是比g(n)大,我们就说f(n)的增长渐进快于g(n)。
下面我们假定几个算法的总执行次数如下图所示:

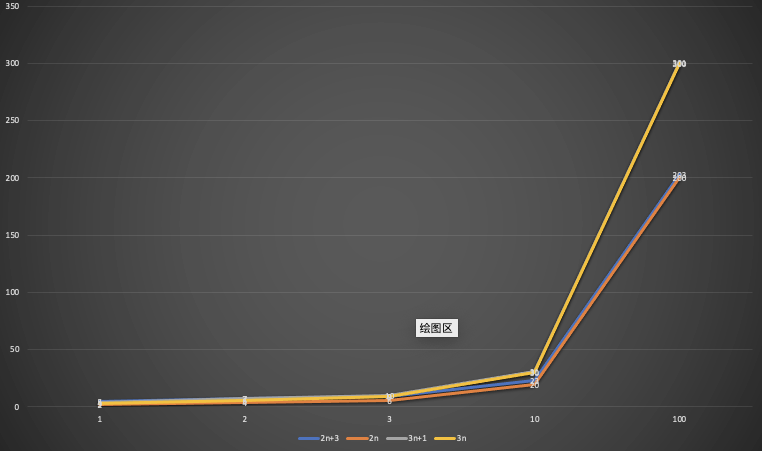
从上述折线图我们可以看出,随着数据规模n的增加,A1和A2,B1和B2算法的折线图逐渐重叠在一起,所以我们可以得出下面这个结论:
随着数据规模的增大,算法的常数操作可以忽略不计。

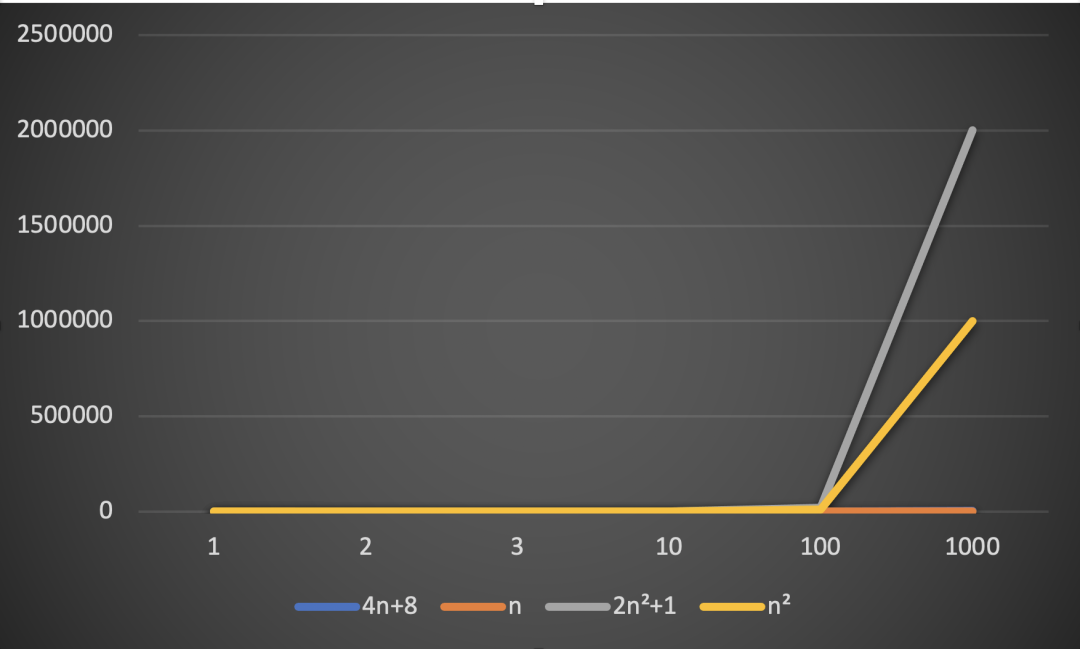
从上述折线图我们可以看出,随着数据规模n的增加,C1和C2近乎重叠,再比较C系列算法和D系列算法,可以看到随着n的增大,即使不考虑n²前的常数,D系列执行次数也是远远超过C系列算法的。所以我们可以得出下面这个结论:
随着数据规模的增大,与最高次项相乘的常数可以忽略。

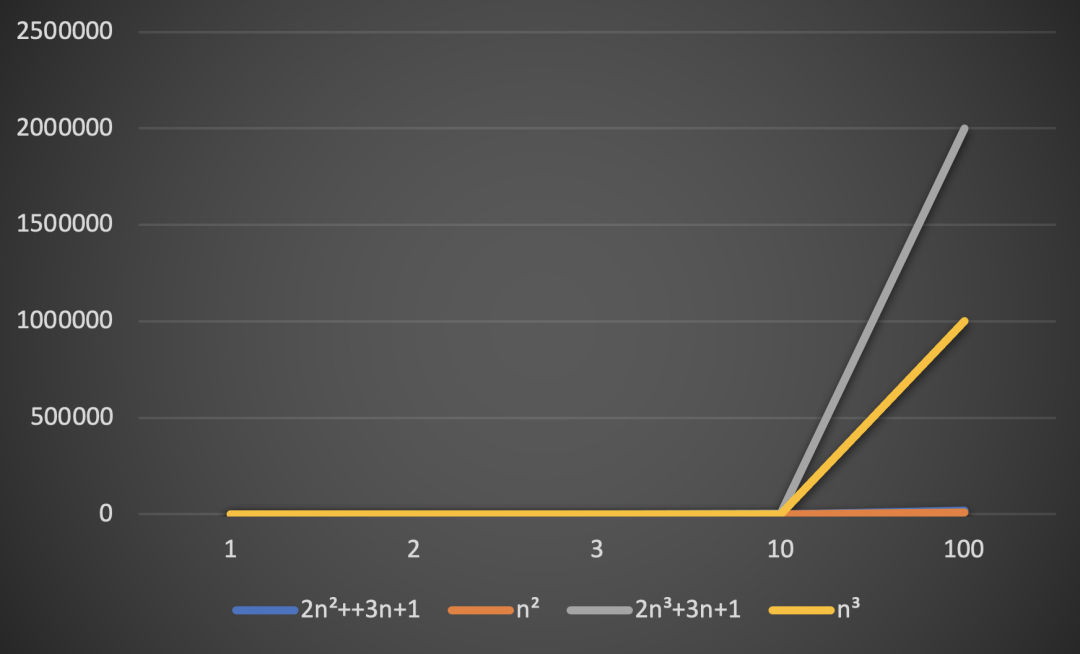
从上述折线图我们可以看出去,E2和F2当n大于10之后,F2的执行次数远远的超过了E2的执行次数。
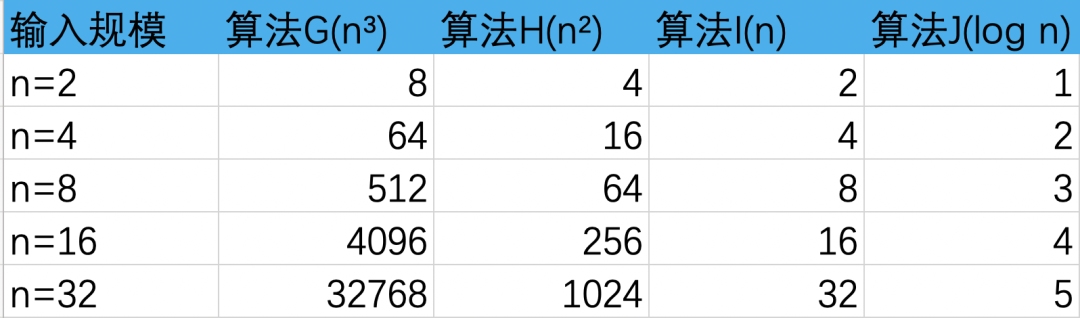
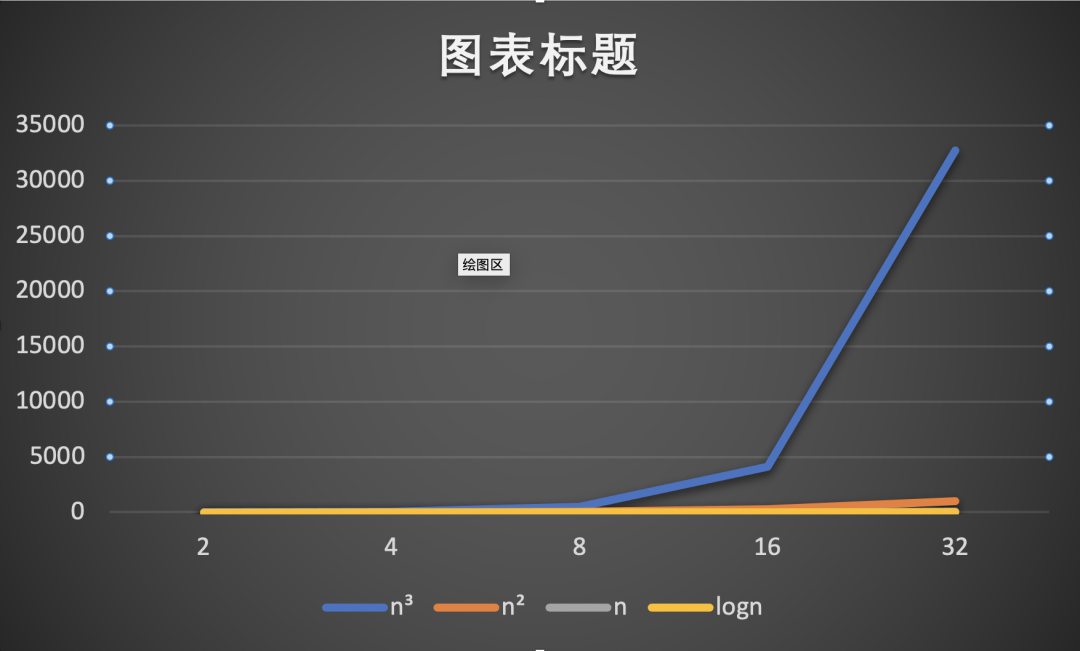
从上述两个折线图,我们可以得出算法中n的次幂越小,执行效率越高。
综上所述,我们可以得出算法随着数据规模n的增大,有下面这些规则:
算法中的函数常数可以忽略。
算法中的最高次幂的常数因子可以忽略。
算法中最高次幂越小,算法的执行效率越高。
而我们常常使用大O表示法来表示一个算法的时间复杂度,基于对上面几个算法函数渐进增长的分析,推到一个算法的时间复杂度可以有下面这些规则参考:
计算运行次数的函数中的所有加法常数用1来代替。
在修改后的函数中,只保留最高项。
如果最高项存在,且最高项的常数因子不为1,则去除这个常数因子。
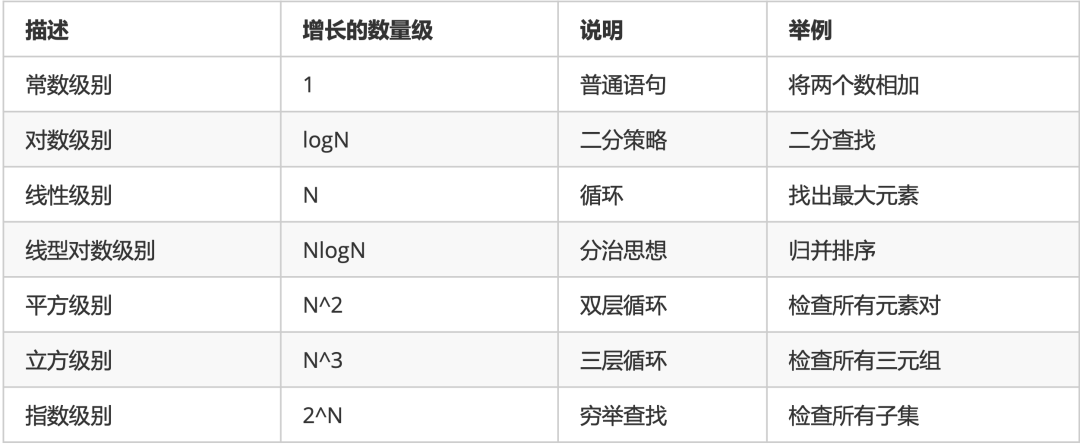
我们常见的算法复杂度有下面这些,O(1)、O(logn)、O(n)、O(nlogn)、O(n²)、O(n³)。
这里说一下logn,一般情况下,我们说的都是以2为底的对数函数,但是在推导时间复杂度的逻辑上,可以是2、3、4(任何数字为底都可以)。
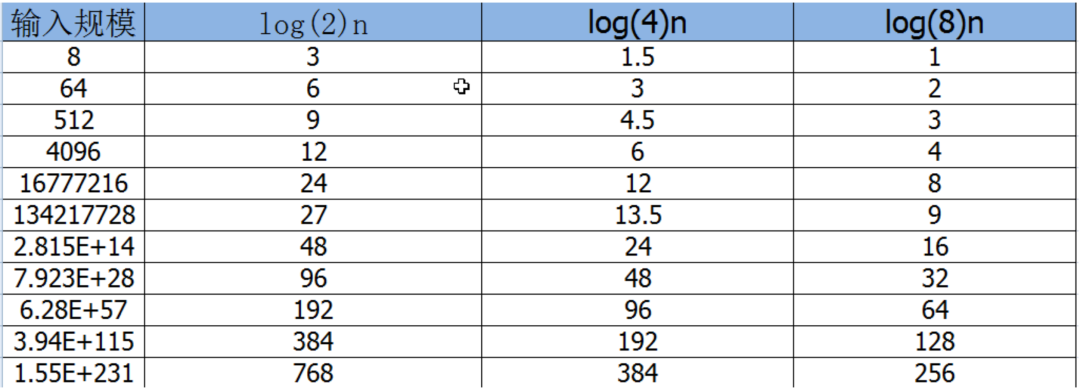
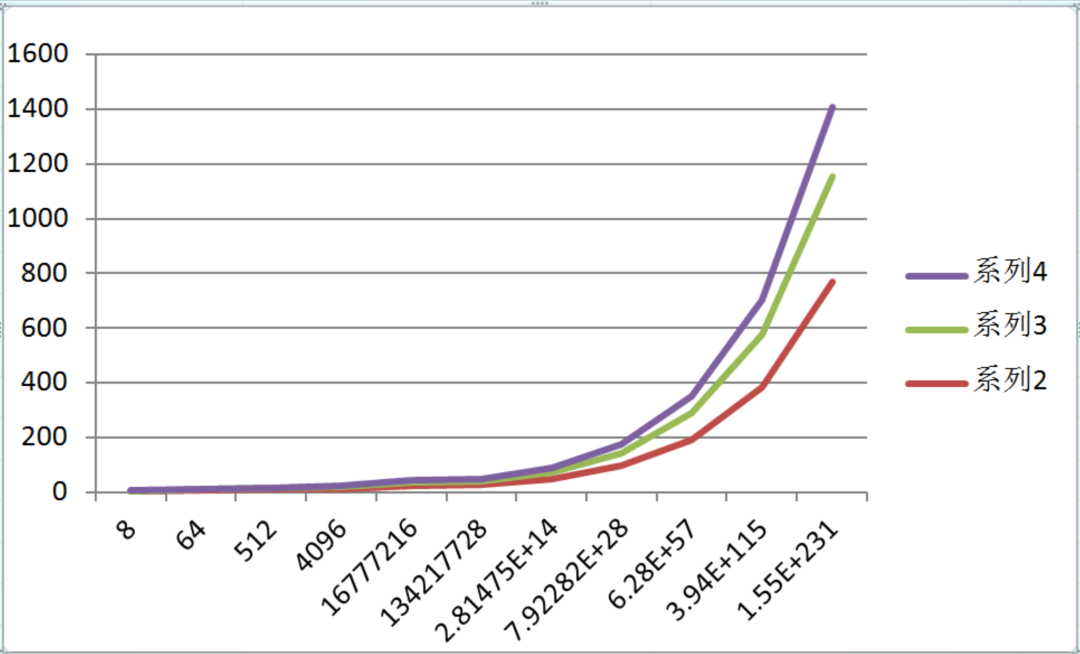
从上面我们可以看到,对于对数函数,无论以几为底,他们的增长趋势都是趋近一致的,所以我们在推导对数函数的时间复杂度时,可以忽略底数。
上面那些常见的时间复杂度的大小依次为:
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³)
我们总结一下上面那些时间复杂度常常出现的应用场景。