图论中,强连通图指每一个顶点皆可以经由该图上的边抵达其他的每一个点的有向图。意即对于此图上每一个点对(Va,Vb),皆存在路径Va→Vb以及Vb→Va。「强连通分量」则是指一张有向图G的极大强连通子图G'。如果将每一个强连通分量缩成一个点,则原图G将会变成一张有向无环图。一张图被称为有向无环图当且仅当此图不具有点集合数量大于一的强连通分量,因为有向环即是一个强连通分量,而且任何的强连通分量皆具有至少一个有向环。如图所示,图中有三个强连通分量:
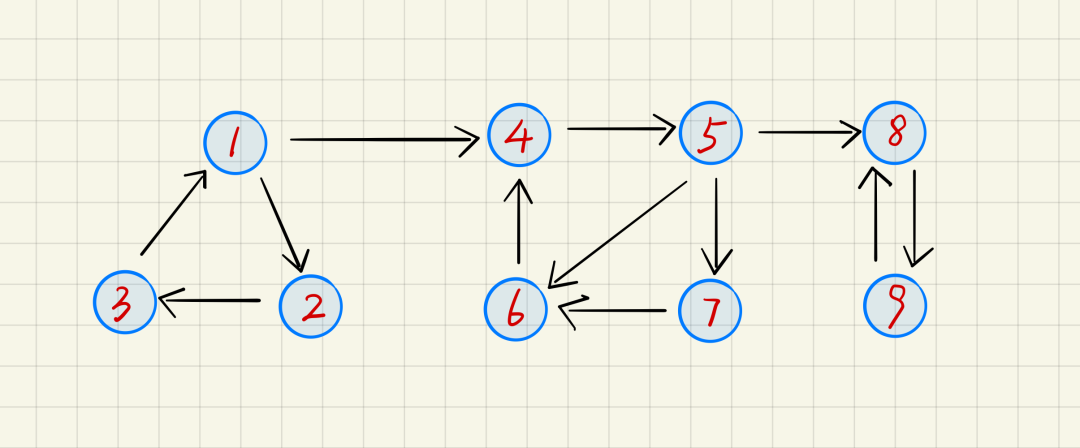
{1,2,3} {4,5,6,7} {8,9}
第一节 寻找强连通分量的有效算法
1.1Kosaraju算法
1.1.1 算法步骤
step1:对原图进行DFS,记录顶点的后序遍历序列(入栈) step2:每次选择栈顶的顶点(出栈),对反向图进行DFS,标记能够遍历到的顶点,这些顶点构成一个强连通分量。 如果还有顶点没有标记,继续step2,否则算法结束
1.1.2 算法原理
反图与原图的强连通分量是相同的 若原图能从分量1走到分量2,则反图不能从分量1走到分量2
1.1.3 代码
下面的代码中,默认每个节点是可以自联通的。存储图的数据结构为邻接表。目的是有的小伙伴的图的id可能是不连续的,这样剩下了节点映射的操作。为了方便,在代码中手动建图,如果读者需要,可以在txt中编辑好图,读入文件的时候建图。
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Stack;
public class Kosaraju {
public List<List<Integer>> getScc(HashMap<Integer, LinkedList<Integer>> map,HashMap<Integer, LinkedList<Integer>> revmap){
List<List<Integer>> result = new LinkedList<>();
Stack<Integer> stack = new Stack<>();
//声明一个节点遍历状态数组,记录节点是否被遍历过,由于节点id是大于0的,故visited中的0进行空置(就是不使用)
boolean[] visited = new boolean[map.size()+1];
//对原图进行DFS
for (int id:map.keySet()) {
if(!visited[id]) {
visited[id] = true;
dfs1(map,id,visited,stack);
}
}
//将节点遍历状态重置
visited = new boolean[map.size()+1];
while(!stack.isEmpty()){
//每次选择栈的顶点出栈,对反向图进行DFS
int num = stack.pop();
if(!visited[num]){
visited[num] = true;
List<Integer> trace = dfs2(revmap,num,visited,new LinkedList<Integer>(){{add(num);}});
result.add(trace);
}
}
return result;
}
public void dfs1(HashMap<Integer, LinkedList<Integer>> map, int id ,boolean[] visited,Stack<Integer> stack){
if(map.get(id) == null) return ;
//记录后续遍历的序列(入栈操作)
for(int num : map.get(id)){
if(!visited[num]){
visited[num] = true;
dfs1(map,num,visited,stack);
}
}
stack.add(id);
}
public List<Integer> dfs2(HashMap<Integer, LinkedList<Integer>> revmap, int id ,boolean[] visited, LinkedList<Integer> trace){
if(revmap.get(id) == null) return trace;
for(int num : revmap.get(id)){
if(!visited[num]){
visited[num] = true;
trace.add(num);
dfs2(revmap,num,visited,trace);
}
}
return trace;
}
public static void main(String[] args) {
//建立例子中的正向图
HashMap<Integer,LinkedList<Integer>> map = new HashMap<>();
map.put(1,new LinkedList<Integer>(){{add(2);add(4);add(1);}});
map.put(2,new LinkedList<Integer>(){{add(3);}});
map.put(3,new LinkedList<Integer>(){{add(1);}});
map.put(4,new LinkedList<Integer>(){{add(5);}});
map.put(5,new LinkedList<Integer>(){{add(6);add(7);add(8);}});
map.put(6,new LinkedList<Integer>(){{add(4);}});
map.put(7,new LinkedList<Integer>(){{add(6);}});
map.put(8,new LinkedList<Integer>(){{add(9);}});
map.put(9,new LinkedList<Integer>(){{add(8);}});
//建立例子中的反向图
HashMap<Integer,LinkedList<Integer>> revmap = new HashMap<>();
revmap.put(1,new LinkedList<Integer>(){{add(3);}});
revmap.put(2,new LinkedList<Integer>(){{add(1);}});
revmap.put(3,new LinkedList<Integer>(){{add(2);}});
revmap.put(4,new LinkedList<Integer>(){{add(1);add(6);}});
revmap.put(5,new LinkedList<Integer>(){{add(4);}});
revmap.put(6,new LinkedList<Integer>(){{add(5);add(7);}});
revmap.put(7,new LinkedList<Integer>(){{add(5);}});
revmap.put(8,new LinkedList<Integer>(){{add(5);add(9);}});
revmap.put(9,new LinkedList<Integer>(){{add(8);}});
Kosaraju demo = new Kosaraju();
List<List<Integer>> result = demo.getScc(map,revmap);
}
}
1.2 Tarjan算法
Tarjan算法是基于对图的深度优先搜索的算法,每个强连通分量为搜索树种的一颗子树。搜索时,把的当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否是一个强连通分量。
Tarjan算法可以通过一次深度遍历,找到强连通分量。Tarjan包含以下几种数据结构:
标记数组Dfn[]:记录点的访问次序 标记数组Low[]:动态改小点的访问次序 栈数组Stack[]:顶点入栈,分量出栈
1.2.1 Tarjan算法的伪代码描述
DFS(u){
1.记录:Dfn[u] = Low[u] = ++num;
入栈:Stack[++t] = u;
for(对 u 的邻接点v){
//如果v没有被访问过
if(Dfn[v] == 0){//如果v没有被访问过
2.调用:DFS(v);
3.回溯时改小;
Low[u] = min(Low[u],Low[v]);
}
else if(v在栈中){//说明u,v已经构成了环
4.有环时改小:
Low[u] = Low[v];
}
if(Dfn[u] == Low[u]){//如果u是分量的根
5.输出分量
u与u之后访问的点出栈
}
}
}
下面是原版论文中Tarjan算法的伪代码流程:

(原版论文中Tarjan算法伪代码流程)
1.2.2 代码
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Stack;
public class Tarjan {
public List<List<Integer>> getScc(HashMap<Integer, LinkedList<Integer>> map){
List<List<Integer>> result = new LinkedList<>();
HashMap<Integer,Integer> dfn = new HashMap<>();
HashMap<Integer,Integer> low = new HashMap<>();
Stack<Integer> stack = new Stack<>();
for (int num: map.keySet()) {
if(!dfn.containsKey(num)){
tarjanDfs(map,num,dfn,low,stack,result);
}
}
return result;
}
static int time = 1;
public void tarjanDfs(HashMap<Integer, LinkedList<Integer>> map, int num,
HashMap<Integer,Integer> dfn, HashMap<Integer,Integer> low,
Stack<Integer> stack,List<List<Integer>> result){
time++;
dfn.put(num,time);
low.put(num,time);
stack.add(num);
for(int id:map.get(num)){
if(!dfn.containsKey(id)){
tarjanDfs(map,id,dfn,low,stack,result);
//回溯的时候需要改小
low.put(num, Math.min(low.get(num),low.get(id)));
}
else if(stack.contains(id)) low.put(num,low.get(id));
if(dfn.get(num) == low.get(num) && stack.contains(id)){
//输出分量
LinkedList<Integer> trace = new LinkedList<>();
int temp;
do {
temp = stack.pop();
trace.add(temp);
}while(temp != num);
result.add(trace);
}
}
}
public static void main(String[] args) {
//建立例子中的正向图
HashMap<Integer,LinkedList<Integer>> map = new HashMap<>();
map.put(1,new LinkedList<Integer>(){{add(2);add(4);}});
map.put(2,new LinkedList<Integer>(){{add(3);}});
map.put(3,new LinkedList<Integer>(){{add(1);}});
map.put(4,new LinkedList<Integer>(){{add(5);}});
map.put(5,new LinkedList<Integer>(){{add(6);add(7);add(8);}});
map.put(6,new LinkedList<Integer>(){{add(4);}});
map.put(7,new LinkedList<Integer>(){{add(6);}});
map.put(8,new LinkedList<Integer>(){{add(9);}});
map.put(9,new LinkedList<Integer>(){{add(8);}});
Tarjan demo = new Tarjan();
List<List<Integer>> result = demo.getScc(map);
System.out.println();
}
}
往期回顾
欢迎大家关注微信公众号:哦呦明知山有虎

文章转载自哦呦明知山有虎,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






