该算法是我在 2014 年写的,2016年开始申请专利(中国专利和美国专利),2021年专利才申请下来。
该算法(与专利)不属于字节跳动并购 Terark 中的资产。
该算法已经于 2024年6月23日 开源:topling-ark,具体代码:pinyin_build.cpp。
该算法与 Topling 的主营业务数据库(MyTopling)没啥关系,不过我们的数据库其底层索引与存储引擎也用到了我们实现的更基础的自动机算法。
(一)背景
当搜索词中有错别字时,搜索引擎会尝试纠错,其中一种方案是通过相似拼音纠错:搜索引擎把这些字还原成拼音,用一个拼音相同的已知的搜索词代替。
这是一种众所周知的纠错策略,但是,当输错的字是多音字,特别是有多个这样的错误输入时,所有的搜索引擎都尽量绕开这个问题,或者仅使用最常用的那些音去纠错。 因为要考虑所有可能的拼音组合,在极端情况下会导致指数爆炸! 例如美团的实现(枚举多音字全排列)。
这里的纠错指通过还原拼音进行纠错,基本假定是:
- 用户输入的错别字,仅仅错在汉字字符,该汉字字符对应的拼音是正确的
- 对于多音字,用户输入的错别字的多个拼音至少有一个与期望的正确的字的多个拼音中的一个相同;或者说,就是两者的交集不为空
- 拼音可以只有声母匹配,忽略韵母
现存的解决方案是用 Trie 树,或者 hash table 来实现。这其中最大的问题是多音字引起的组合爆炸,我们的方法解决了这个组合爆炸问题。
以柙脯柙脯优惠卷为例,下面是我们的算法演示:
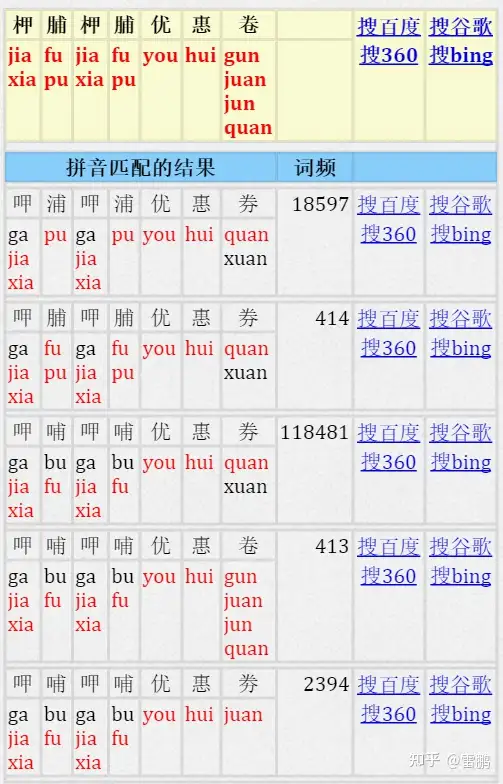
相当于正则表达式 : (jia|xia)(fu|pu)(jia|xia) (fu|pu)(you)(hui)(gun|juan|jun|quan)
如果允许只匹配声母,该正则表达式就更复杂(粗体是仅匹配声母的正则表达式):(jia|xia)(fu|pu)(jia|xia)(fu|pu)(you)(hui)(gun|juan|jun|quan)|(j|x)(f|p)(j|x)(f|p)(y)(h)(g|j|q)
其它单元格中的内容也类似,红色表示匹配。
(二)传统方法
我们的demo页面中没有显示只考虑声母,忽略韵母的条目,在下面这个列表中加上。
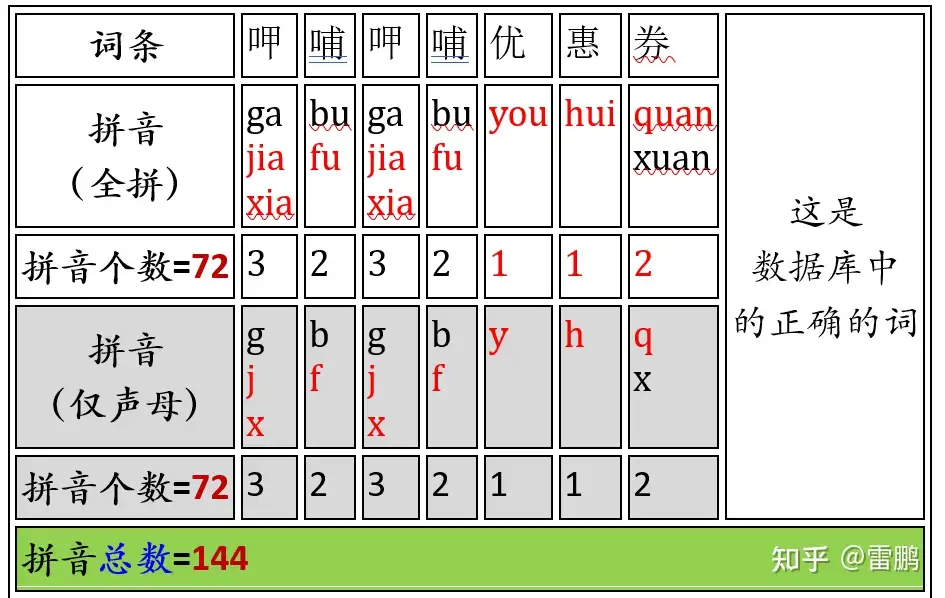
使用传统方法,要把上面这些拼音的排列组合都建索引,仅对呷哺呷哺优惠券这一个词,就有 144 个索引条目。所以传统方法都尽量规避这个问题,而不是面对并解决这个问题,比如采用这样一些策略:
- 使用更小的多音字字典(我们这个 demo 中使用的是能找到的最全的一个多音字字典)
- 对忽略韵母的情况,使用另外一个数据库
- 已知短语中某个词的正确读音时,就不再进行多音字扩展
- 使用概率算法,直接忽略概率低于某一个阈值的音
- 对每个词条,设定一个最大扩展数目的限制
- 其它等等……
(三)我们的算法
我们的算法相当于先创建了一个 Key 为正则表达式(DFA),Value为 词+词频 的数据库。用户的输入也被转化成一个正则表达式(DFA),用这个正则表达式去搜索数据库,得到相应的匹配,这个搜索过程实际上是一个DFA求交操作,DFA求交操作可以快速执行。
3.1 创建 DFA 数据库
这其中最关键的一点是数据库的创建,这个数据库实际上是一个DFA,直接创建这个DataBaseDFA,就要对几百万个正则表达式(DFA)求并,这个求并操作有些类似于NFA转化DFA的幂集构造法,非常有可能(几乎肯定会)造成状态爆炸。
我们的算法可以非常高效地将这个DFA创建出来,该算法中实际上包含了至少三个算法:
- 创建拼音DFA,除了前述仅匹配声母的功能,还有其它功能:
- 如果已知了某个包含了多音字的词的正确读音,就不再对该词进行多音字扩展,只使用这个正确读音,比如,银行的正确读音为 yinhang,那么 yinxing 就不考虑了
- 同一个短语中,组成这种已知读音的词可能有重叠,所有的重叠都需要考虑
- 把每个词的 拼音—词 DFA,加入一个 tempFulldfa,其中拼音是前述的正则表达式对应的 DFA
- 将 tempFulldfa 转化为目标 DataBaseDFA
其中 1,2 都是非常有挑战的算法,3 比较简单。
3.2 使用 DFA 求交进行搜索
已有算法
对多个DFA求交是一个已经很成熟并且存在了几十年的算法。利用DFA求交进行(编辑距离)纠错也已经是一个成熟算法。在这些算法中,只有key的概念,而无value,并且,他们只有用来搜索的key是dfa,数据库中的key仍然是字符串本身。
这种已有的利用DFA求交进行搜索的算法,是用 keyDFA 和 DataBaseDFA 求交,产生一个新的DFA,再使用深度优先遍历去枚举新DFA能表达的所有字符串。与我们的算法不同。
相关链接:http://www.tuicool.com/articles/QRFn63
我们的算法
我们的算法是搜索的 key 和数据库中的 key 都是 DFA,并且,这个 key 是字符串的一种变换,value 是原字符串本身(或原字符串ID)。这样的搜索,还没有找到其它人提出的类似方法。
3.3 我们的算法有更多潜在应用
- 输入法:直接拿用户输入作为 key 在 DataBaseDFA 上搜索即可,比纠错更简单
- 语音识别中可能也会有这样的问题,我们需要找语言识别方面的专家来确认这一点
- 人工智能中,决策树算法的优化等等
(四)关于算法专利的问题
纯算法无法申请专利,但是算法的具体应用可以申请专利。应尽量扩大该算法的专利应用范围。
(五)DFA 数据库创建算法详述
该算法的灵感来源于Paper: Incremental Construction of Minimal Acyclic Finite-State Automata
该Paper(以下简称ICoMAFSA)第4章中描述的算法可以动态地将一个字符串(Item)加入一个DataBaseDFA中,并同时保持该 DataBaseDFA 最小化。
以下文字中用 RegEx 表示 正则表达式。
该算法的核心思想是通过在 key value 之间加入一个分隔符,然后利用 DFA 实现映射,详细内容可参考我的博文 把自动机用作 Key-Value 存储 中提到的 map2。
在创建出来的 DataBaseDFA中,key 的数量可以是 value 数量的几百倍甚至几千倍(有多个不同的key对应相同的value),但只会占用很少的空间。
另外,虽然在该算法中key的数量只是很大数量的有限个,但是该算法可以推广到无限数量的key(只要 KeyDFA中有环即可,该算法中的 KeyDFA 是拼音DFA,没有环,所以有限)。
图例和背景知识:一个字符串可以看作是一个线性DFA(以字符串 hello 为例)
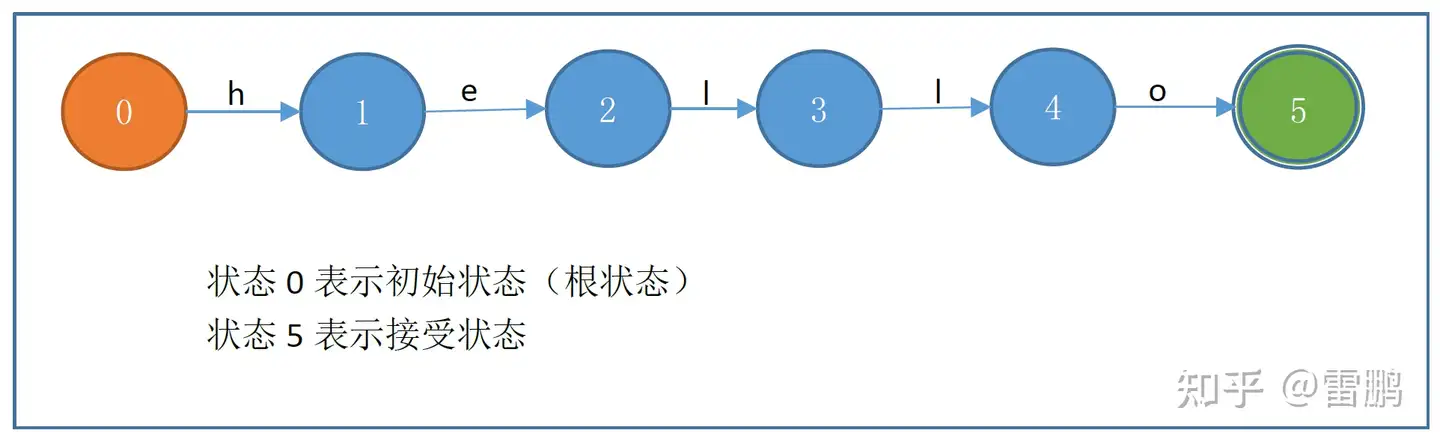
5.1 创建拼音 DFA
虽然是以 RegEx 为例进行说明,但是创建拼音 DFA 并不是先创建 RegEx,再编译成 DFA,而是实现专门为创建这种拼音DFA的算法。
该算法先从输入词条的拼音创建一个 DAG 形状的 NFA,然后将该 NFA 转化为 DFA。在创建 NFA 的过程中,对每个有拼音的不同子串,使用 ICoMAFSA 的算法创建包含多个 key 的 DFA,然后再将这些小 DFA 用 ε-转移 连接起来。
下面以呷哺呷哺优惠券为例,呷哺呷哺优惠券是保存在 DataBaseDFA 中的,不同于前面的错误输入柙脯柙脯优惠卷(和它的正则表达式)。
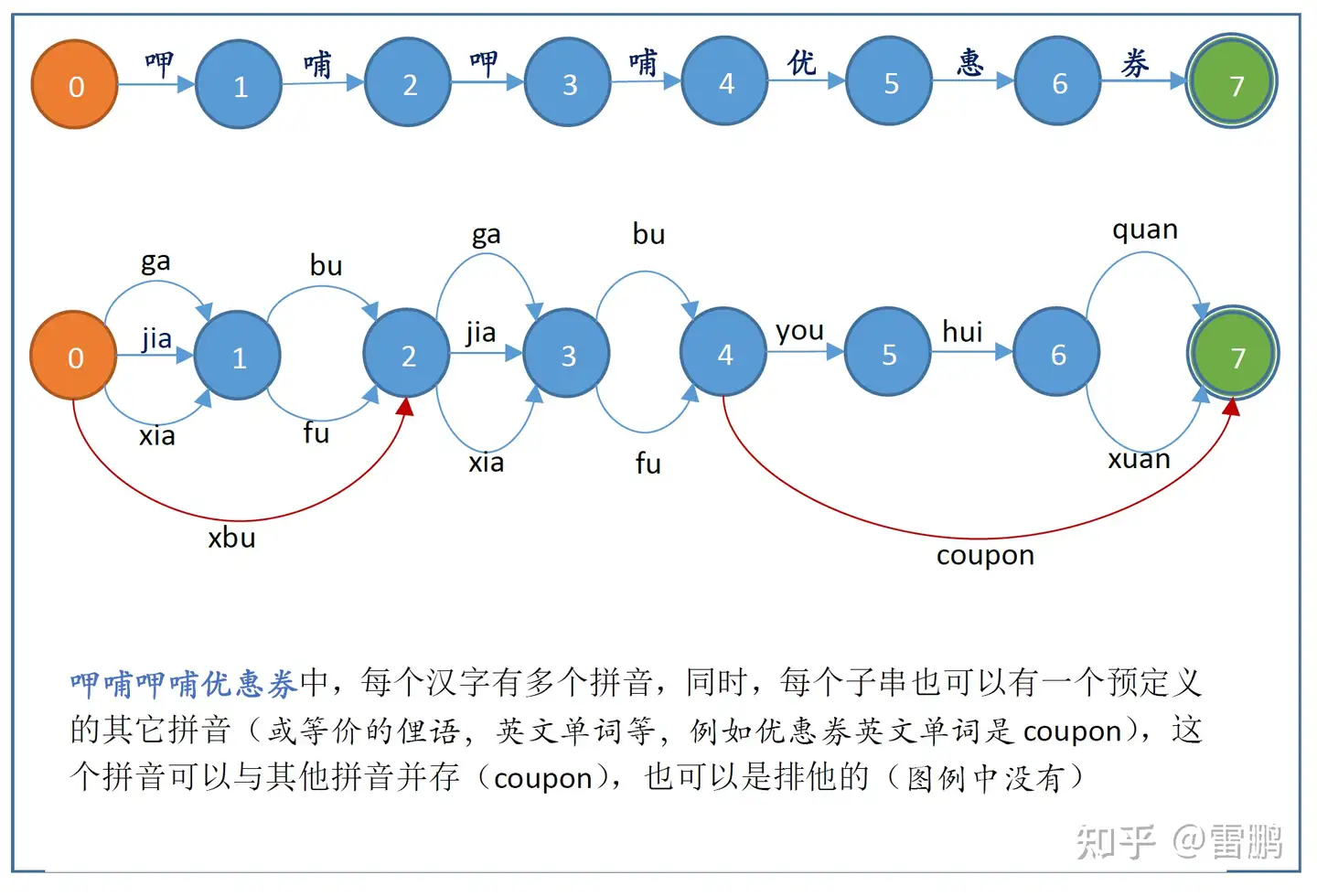
5.2 创建 tempFulldfa
tempFulldfa 是一个 DataBaseDFA。
我的拼音 DFA 创建算法中,可以将一个有唯一字符串前缀的 ItemDFA 加入 DataBaseDFA 中。以呷哺呷哺优惠券为例,这个 ItemDFA 可以用 RegEx 表示(去除了词频):
呷哺呷哺优惠券 \t (jia|xia)(fu|pu)(jia|xia)(fu|pu)(you)(hui)(quan|xuan)
其中 呷哺呷哺优惠券 \t在 DataBaseDFA 中是一个唯一字符串前缀(词库中的一个词加上分隔符),后面(SuffixDFA)是个简化的 RegEx(因为该 RegEx 实际上还可以再加上仅声母的拼音……)。
该算法的关键之处在于:在 add_SuffixDFA 中,以拓扑逆序将 SuffixDFA 中的状态逐个加入 DataBaseDFA (加入的同时消除等价状态)。在拼音的例子中,SuffixDFA 永远是一个 DAG(有向无环图),从而可以保证加入SuffixDFA 之后得到的新的 DataBaseDFA 必然是最小化的。
ICoMAFSA 中的 add_SuffixString 以逆序逐个加入 SuffixString 中的各个字符(对应的 Target DFA State)。如果把一个字符串看作是一个线性 DFA,其逆序本质上就是 String DFA 的拓扑逆序。从而,理论上就可以把它看成是 General ADFA 的特殊情况。
在该算法中,也可以用整数ID代替原始词条(呷哺呷哺优惠券)本身,这样需要在另外一个地方保存ID和原始词条的映射关系,会复杂一些但更灵活更有扩展性。
因为拓扑逆序实际上就是 DAG 的后序遍历顺序,该算法对非 DAG 也可以 work,因为同样是后序遍历,但是对非 DAG 无法保证每次加入 SuffixDFA 之后得到的新 tempFulldfa 是最小化的(需要严格证明)。
Reverse DFA (翻转DFA)
把上面的tempFulldfa作为DataBaseDFA并没有什么用处,因为它只能用词条去搜索相应的SuffixDFA,但我们是要用拼音去搜索相应的词条。
因为DFA是从root开始搜索,所以,我们只需要把tempFulldfa 翻转一下就可以了。因为要翻转,所以,在以增量方式创建tempFulldfa时,需要把tempFulldfa的每个输入先翻转,上面的示例翻转之后就是:
券惠优哺呷哺呷 \t (naux|nauq)(iuh)(uoy)(uf|up)(aij|aix)(uf|up)(aij|aix)
因为每个汉字是多个字节,翻转汉字实际上需要把所有的字节都反过来,按字节反过来之后就是乱码了,示例中以汉字为单位翻转只是为了便于理解。
以这样的翻转方式创建好tempFulldfa之后,再将tempFulldfa翻转回去,就得到了我们需要的DataBaseDFA:key是拼音DFA,value是原始词条(或ID),示例如下:
(jia|xia)(fu|pu)(jia|xia)(fu|pu)(you)(hui)(quan|xuan) \t呷哺呷哺优惠券
理论上,Dfa Reverse操作的时间和空间复杂度都是,其中n是DFA的状态数,DataBaseDFA的状态数动辄就是几个亿,甚至几十亿,这是完全不可忍受的!幸运的是,虽然没有理论在理论上进行证明,实际上对上面的tempFulldfa进行reverse,时间和空间复杂度都是 O(n)(需要严格证明)。
(六)代码:以拓扑逆序加入 SuffixDFA
void append_adfa_topological(size_t len, state_id_t root2) {
assert(stack.empty());
//
// append reverse topological order on path
stack.push_back(root2);
R.resize_indegree(au->total_states());
// now indegree serve as 'color' flag for DFS
while (!stack.empty()) {
state_id_t parent = stack.back();
switch (R.indegree(parent)) {
case 0:
R.indegree_set(parent, 1);
au->for_each_dest_rev(parent,
[&](state_id_t child) {
switch (R.indegree(child)) {
case 0:
stack.push_back(child);
break;
case 1: // back edge
if (child == parent)
throw std::logic_error("add_suffix_adfa: found a self-loop");
else
throw std::logic_error("add_suffix_adfa: found a back-loop");
break;
case 2:
break;
default:
assert(0);
break;
}
});
break;
case 1:
R.indegree_set(parent, 2);
path.push_back(parent); // on_finish
// fall through:
case 2:
stack.pop_back();
break;
default:
assert(0);
break;
}
}
assert(path.back() == root2);
//
// compute_reverse_adfa_and_indegree:
//
// now path[len+1...end) is in reverse topological order
inv_nfa.index.reserve(path.size()-(len+1)+1);
inv_nfa.index.erase_all();
for (size_t j = len+1, n = path.size(); j < n; ++j)
inv_nfa.index.unchecked_push_back({path[j], 0});
inv_nfa.index.unchecked_push_back({nil_state+0, 0});
std::sort(inv_nfa.index.begin(), inv_nfa.index.end()
, CompareIndexEntry());
size_t trans_num = 0;
R.indegree_set(root2, 1);
for (size_t j = len+1, n = path.size(); j < n; ++j)
R.indegree_set(path[j], 0);
for (size_t j = len+1, n = path.size(); j < n; ++j) {
au->for_each_dest(path[j], [&](state_id_t child) {
R.indegree_inc(child);
auto p = inv_nfa.lower_bound(child);
assert(p < inv_nfa.index.end()-1 && p->state == child);
p[1].offset++;
trans_num++;
});
}
tmp_idx.resize_no_init(inv_nfa.index.size());
tmp_idx[0] = 0;
for (size_t j = 1; j < inv_nfa.index.size(); ++j)
tmp_idx[j] = inv_nfa.index[j].offset += inv_nfa.index[j-1].offset;
inv_nfa.data.resize_no_init(trans_num);
for (size_t j = len+1, n = path.size(); j < n; ++j) {
state_id_t parent = path[j];
au->for_each_move(parent,
[&,parent](state_id_t child, auchar_t ch) {
auto p = inv_nfa.lower_bound(child);
assert(p < inv_nfa.index.end()-1 && p->state == child);
auto& idx = tmp_idx[p - inv_nfa.index.begin()];
inv_nfa.data[idx++] = CharTarget<state_id_t>(ch, parent);
});
}
for (size_t j = len+1, n = path.size(); j < n; ++j) {
state_id_t& child = path[j];
std::pair<size_t, bool> ib = R.find_or_add(child);
if (!ib.second) { // existed an equivalent state
state_id_t EqState = ib.first;
if (EqState == child)
break;
auto p = inv_nfa.lower_bound(child);
assert(p < inv_nfa.index.end()-1 && p->state == child);
for (size_t k = p[0].offset; k < p[1].offset; ++k) {
auto ct = inv_nfa.data[k]; // inverse transition to parent
au->set_move(ct.target, EqState, ct.ch); // modify parent
}
au->del_state(child);
R.indegree_set(child, 0); // reset indegree of deleted state
R.indegree_inc(child = EqState);
}
}
}
(七)伪代码:用DFA求交算法匹配拼音KeyDFA和DataBaseDFA
(伪代码,不是严格的 C++ 代码,主要为了易于理解)
dfa_intersection_search(KeyDFA, DataBaseDFA) {
// a queue which add new elements at tail
// and can search by key = pair<StateID, StateID>
// the first StateID of key identify states of KeyDFA
// the second StateID of key identify states of DataBaseDFA
// qset[nth] access the nth added element
// the qset never delete elements
qset = new bfs_queue_set<pair<StateID, StateID> >();
// new qset is empty, the first add will always success
qset.add_element(pair(KeyDFA.root, DataBaseDFA.root));
matched_states = {};
// This is an implicit BFS (Breath First Search)
// bfshead is the pointer(element index) for qset
// qset.size() will increase when new elements are added
for (bfshead = 0; bfshead < qset.size(); ++bfshead) {
pair(state1, state2) = qset[bfshead];
if (KeyDFA.is_final(state1)) {
// Delim is a special char, such as '\t'
// Delim will not in any where except between PinYin and HanZi
target = DataBaseDFA.target_of(state2, Delem);
if (target != nil) {
matched_states.add_element();
}
}
// children_of return children in label_char order
children1 = KeyDFA.children_of(state1);
children2 = DataBaseDFA.children_of(state2);
children = {};
// compute intersection on label_char
for (i = 0, j = 0; i < children1.size() && j < children2.size; ) {
if (children1[i].label_char < children2[j].label_char) {
++i;
}
else if (children1[i].label_char > children2[j].label_char) {
++j;
}
else { // label_char matched
target1 = children1[i].target;
target2 = children2[j].target;
// qset.size() will increased if add_element success
// add_element fails if pair(target1, target2) already
// exists in qset
qset.add_element(pair(target1, target2));
++i; ++j;
}
}
}
for_each(state in matched_states) {
for_each(string in DataBaseDFA.right_lange(state)) {
output(string);
}
}
}
(八)专利证书








