(一)背景
学过编译原理的同学都知道 DFA 有穷自动机,DFA 包含:
- 状态集合 Q
- 终止状态集合 F,F 是 Q 的一个子集
- 字母表 Σ
- 状态转移函数 Q×Σ→Q:
DFA 可以简单地分成两类:① 接受有限个字符序列; ② 接受无限个字符序列。其中 ① 必然有环, ② 必然无环。
对于无环的 ②,可以再分为两种:Ⓐ 树形的(Trie 树),每个状态仅有一个父状态;Ⓑ 非树形的,至少有一个状态有多个父状态。
Trie 树想必大家都很熟悉,特别是双数组 Trie 树,几乎是自然语言处理、文本匹配……的标准工具。
虽然 Topling 的关系数据库 MyTopling 和 存储引擎 ToplingDB 表面上与 DFA 自动机无关,但是其索引压缩算法和 Value 压缩算法都是来源于自动机算法的助力。
(二)DFA 等价与最小化
《编译原理》教科书会大略地讲解有穷自动机。《自动机原理》教科书会更深入地讲解各种自动机,有些会略微提一下 DFA 的最小化。但是都不会详细深入地讲解 DFA 最小化的各种算法、原理,我们在此进行一点补充。
DFA 的状态转移函数定义了 DFA 的形状,形状不同的 DFA 有可能是等价的(接受相同的语言/字符序列)。
等价但形状不同的 DFA,状态数最少的那个,称为最小的 DFA,最小的等价的 DFA 形状必然相同,非最小的状态数相同的等价的 DFA 形状有可能不同。“形状相同”更正式的说法是“同构”。
可以把一个 DFA “最小化”为与它等价的那个 DFA,存在多种 DFA 的“最小化”算法。时间复杂度最低的通用的 DFA 最小化算法是 Hopcroft 算法,不管有环的还是无环的都可以用 Hopcroft 算法来最小化。
不管是哪种 DFA 最小化算法,都依赖于“状态等价”这个性质,状态等价指的是:
如果两个状态的所有转移函数
可以看到,这个定义是递归的,如果 DFA 中没有环,可以直接按这个定义来高效地计算等价状态,这是自底向上的。
如果有环,直接按这个定义计算等价状态就会陷入无限递归,Hopcroft 算法(Topling 的开源实现)使用 Partition refinement 来高效地计算等价状态,是自顶向下的,可以处理这种情况。这类算法是通用的,有环的没环的都可以用,所以性能比不上自底向上专用于无环DFA的算法。
(三)自底向上的算法
自底向上的算法比较简单,比如对于 Trie 树,所有的叶节点都是等价的,可以合并为一个,知道了叶节点等价之后,开始计算叶节点的父节点,又计算出一批等价的状态集合,如此循环反复,就得到了最小化的 DFA。根据这个描述,此算法是 Offline 的,把 Trie 树转化为等价的 DFA,当然,这个算法也可以工作在不是 Trie 树的无环 DFA 上,Topling 高效地实现了这个算法(已开源)。
论文 ICoMAFSA 描述了一个增量的无环 DFA 构建算法,可以增量地向一个 DFA 插入一个个字符串,并提供了一个参考实现,Topling 以更高效的方式实现了该算法,比参考实现的内存消耗小 20 多倍,同时速度也快 20 多倍。这个算法的关键在于,将状态等价的定义转化为代码实现,在 Topling 的实现中,状态使用数组来表达,状态 ID 就是数组索引/下标,状态等价逻辑上是个 HashSet<uint, HashAndEqualFunc>,其中的关键就是 HashAndEqualFunc 的实现,它持有一个指向 DFA 的指针,Hash 和 Equal 作为 DFA 的成员函数:C++ 代码比较复杂(为了性能),但主要逻辑是简单的(C++ 伪代码):
uint DFA::StateHash(uint s) const {
uint h = 1234567; // magic number for init hash
ForEachDelta([&h](SigmaChar c, uint t) {
h = HashCombine(h, c);
h = HashCombine(h, t);
});
return HashCombine(h, IsFinal(s) ? 1 : 0);
}
bool DFA::StateEqual(uint s1, uint s2) const {
if (IsFinal(s1) != IsFinal(s2)) return false;
vector<pair<SigmaChar, uint> >
v1 = GetAllDelta(s1),
v2 = GetAllDelta(s2);
return v1 == v2; // v1.size == v2.size && contents are all equal
}
而这个 HashSet 的实现非常微妙,我们可以不用保存作为 Hash Key 的 uint,而是让这个 key 直接作为 HashSet 中冲突链数组的索引/下标,这样 HashSet 就只需要保存 Hash 索引依赖的最小信息(bucket 与冲突链)。
这里又引入一个 Array Based Hash Table 的概念,就是将 HashTable 的 所有 KeyValue 放入数组,以 vector 的形式存储,用数组索引代替 HashTable 的结点指针, 详见 gold_hash_map 相关内容。
我们的 DFA 实现对内存用量和性能进行了高度优化,与这种 HashSet 一起,实现了内存消耗与性能的双重优化。
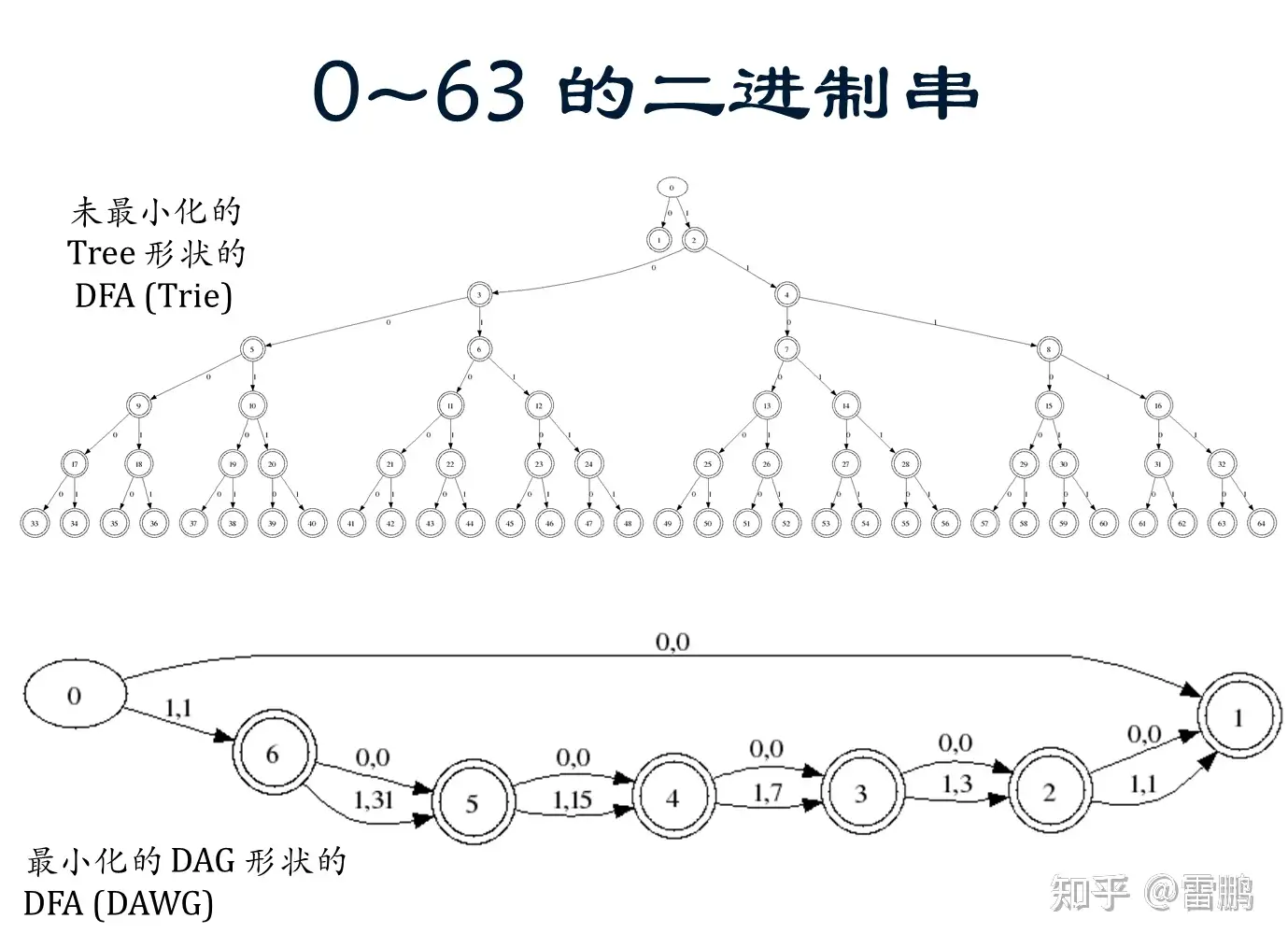
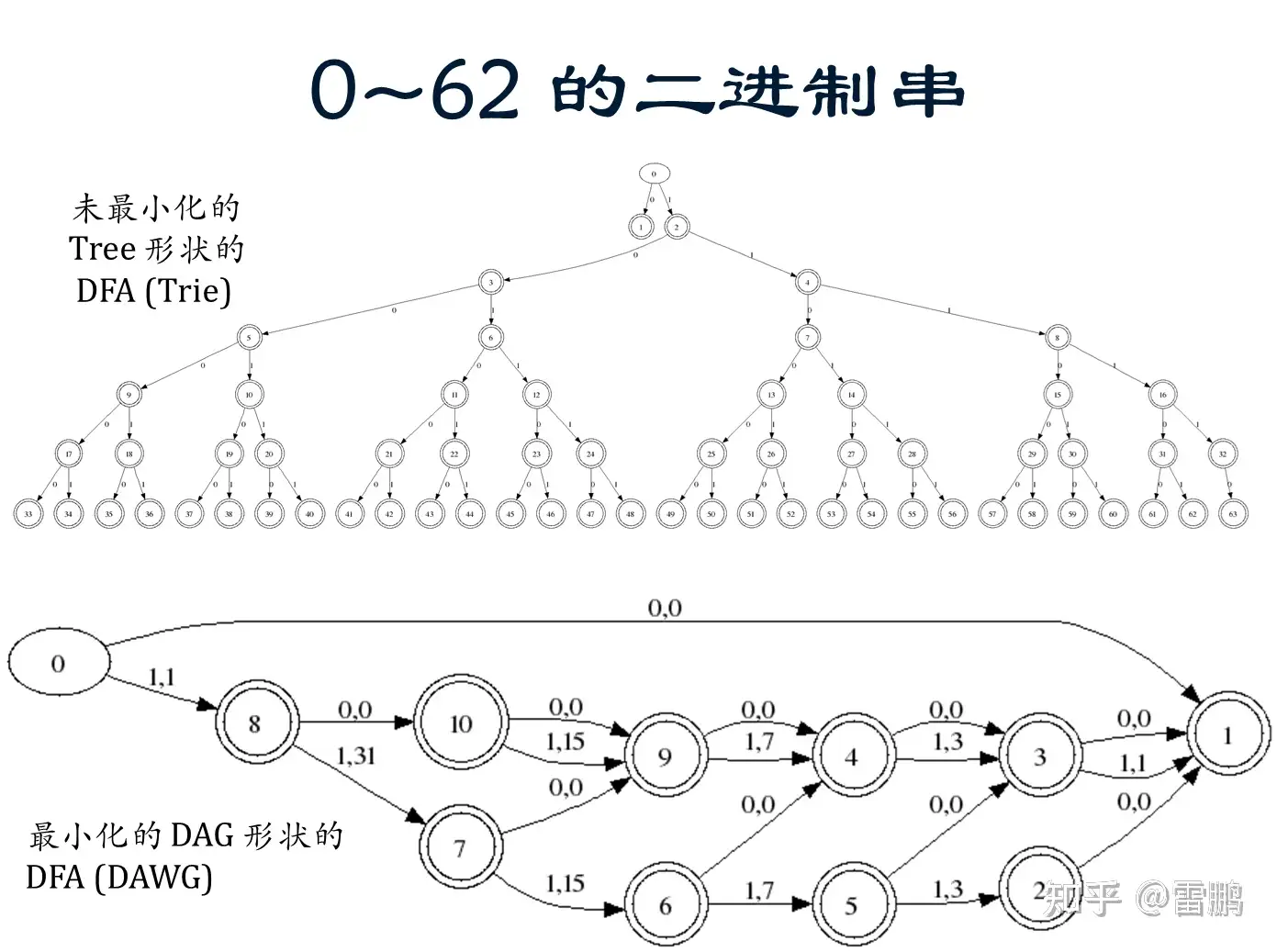
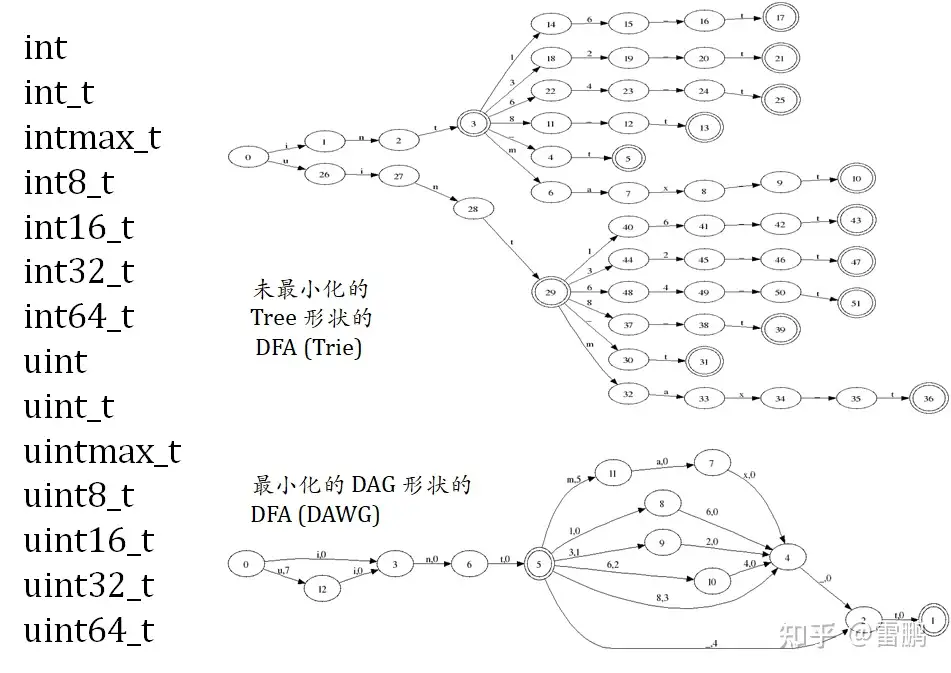
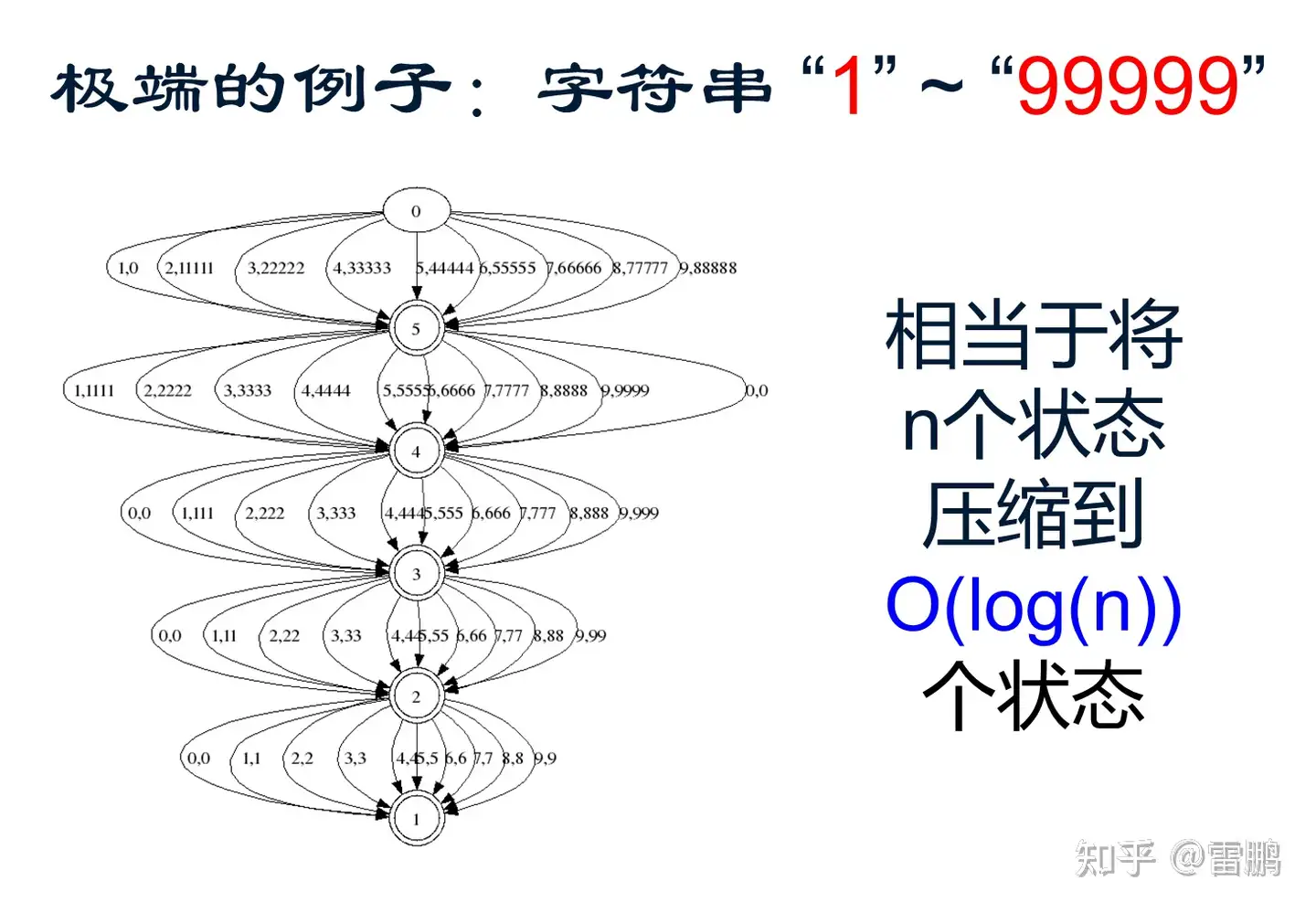
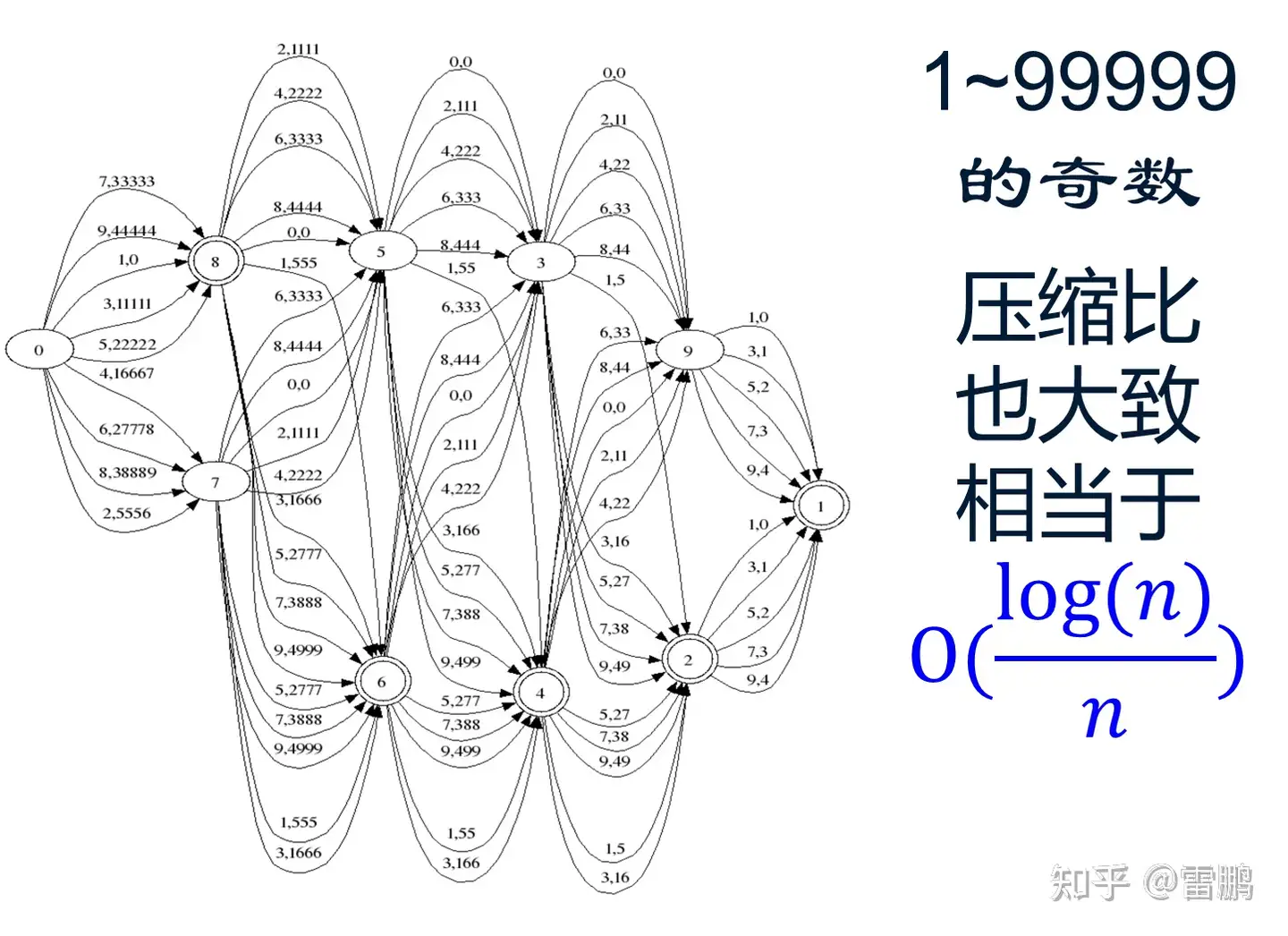
(五)DFA 最小化的例子
0~63 的二进制串的最小化 DFA 比 0~62 的更小,更多例子(正则表达的DFA,点击其中链接)。
【完】






