1. 数据结构
1.1 逻辑结构
集合 : 数据结构中的元素除了"同属一个集合的关系"之外 , 别无其他关系
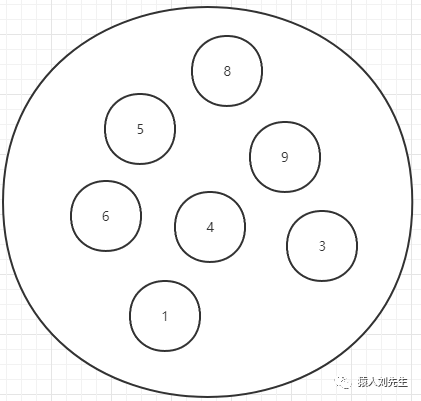
线性结构 : 数据结构中的元素存在一对一的关系
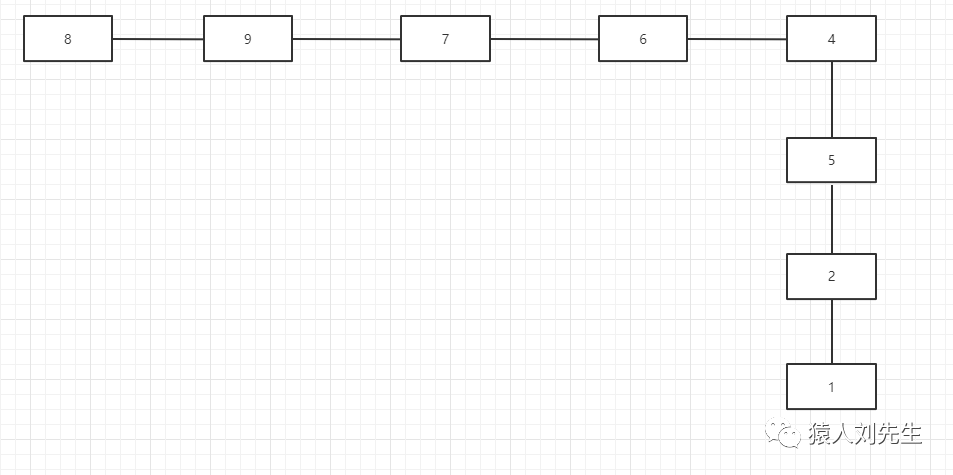
树形结构 : 数据结构中的元素存在一对多的相互关系
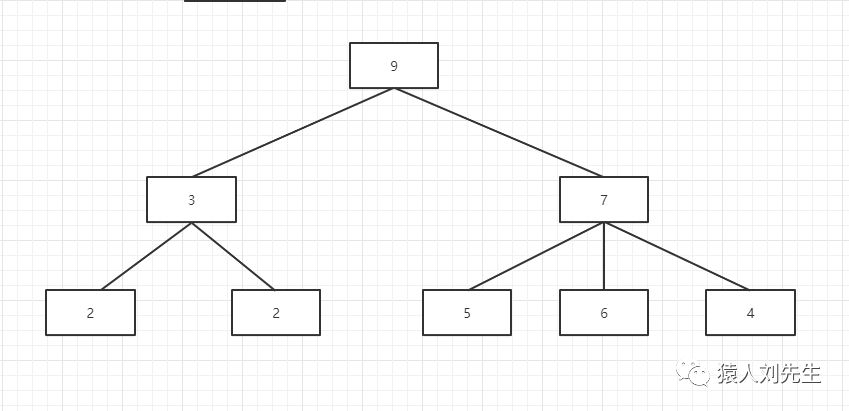
圆形结构 : 数据结构中的元素存在多对多的相互关系
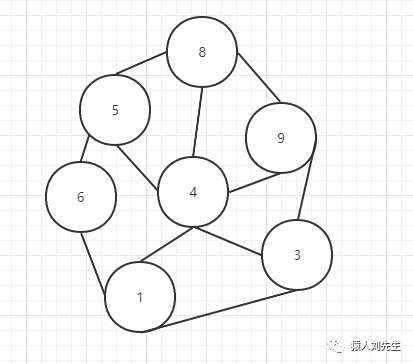
1.2 物理结构
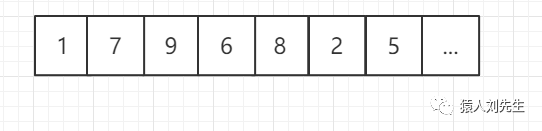
顺序存储结构 : 是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的
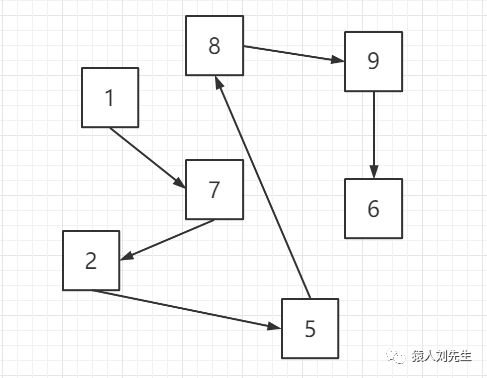
链式存储结构 : 是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的 数据元素的存储关系并不能反映其逻辑关系,因此需要用一个指针存放数据元素的地址,这样通过地址就可以找到相关联数据元素的位置 , 显然,链式存储就灵活多了,数据存在哪里不重要,只要有一个指针存放了相应的地址就能找到白了
1.3 数组
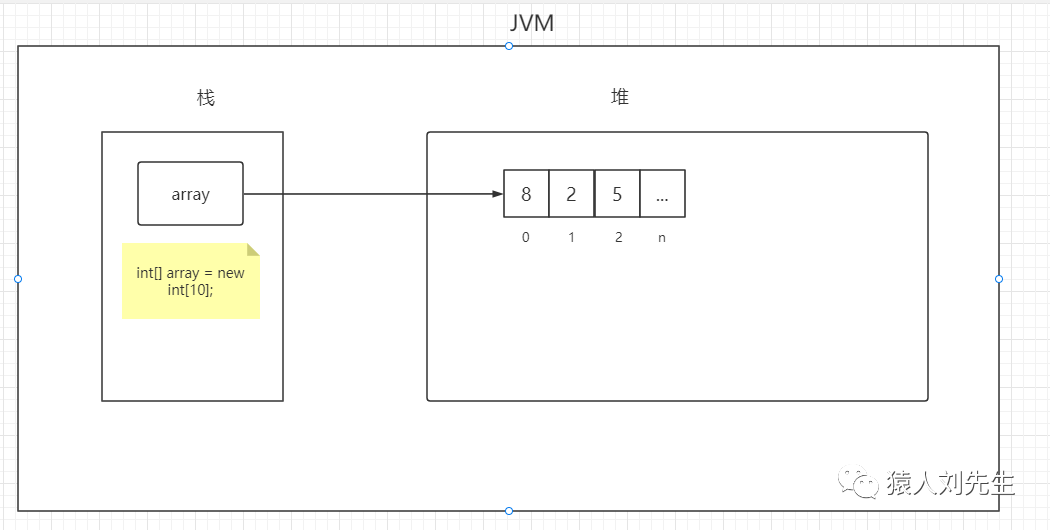
数组支持随机访问,根据下标随机访问的时间复杂度为O(1) 数组排好序的前提下 , 使用二分查找的情况 , 数组的时间复杂度为O(logn) 数组在顺序查找的情况下 , 需要遍历每一个元素 , 直到相等 , 然后返回 , 所以时间复杂度是O(N)
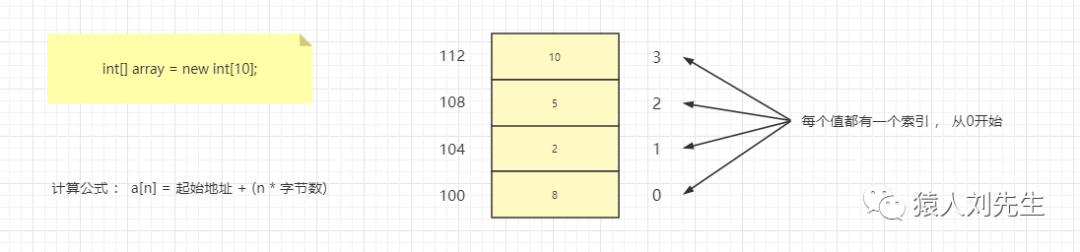
如果使用尾插法 , 时间复杂度为O(1) , 因为不涉及其他元素的移动 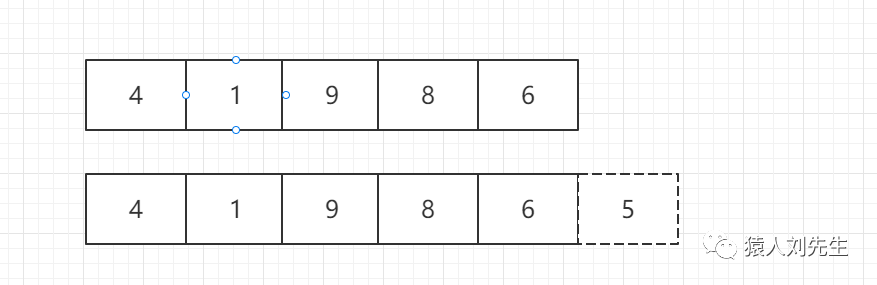
如果使用头插法 , 时间复杂度为O(N) , 因为数组的每一个元素都要向后移动 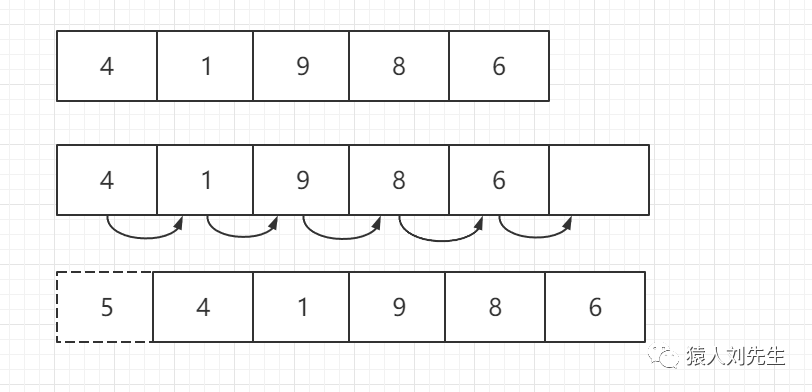
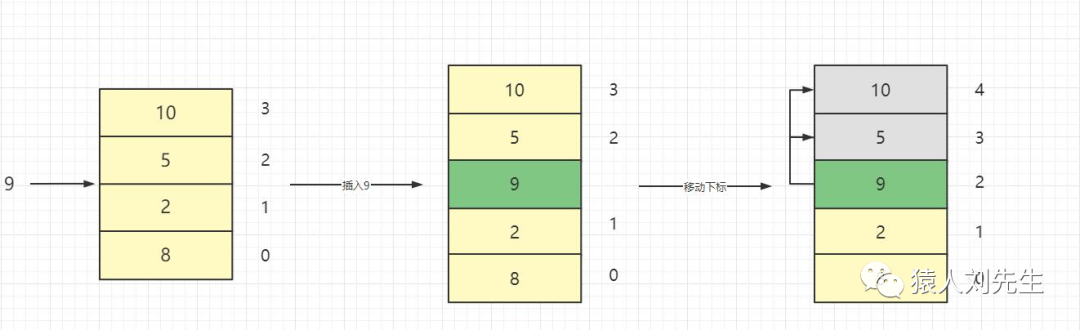
如果在中间插入 , 时间复杂度也是O(N) , 因为插入位置后面的元素也需要向后移动
如果使用头删法 , 时间复杂度为O(N) , 因为其它元素要向前移动一位 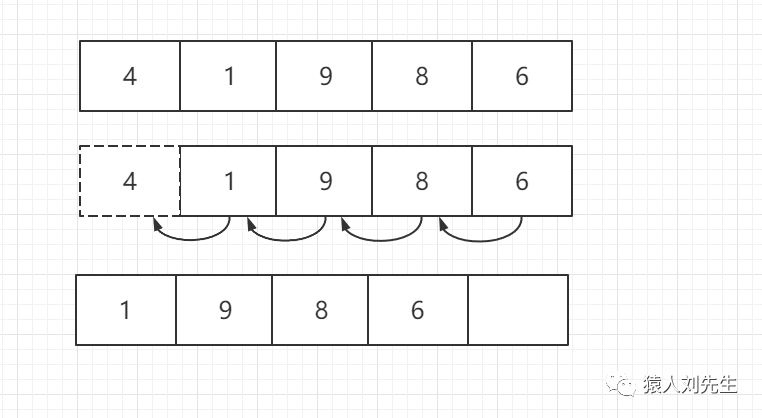
如果使用尾删法 , 时间复杂为O(1) , 不涉及到其它元素的移动 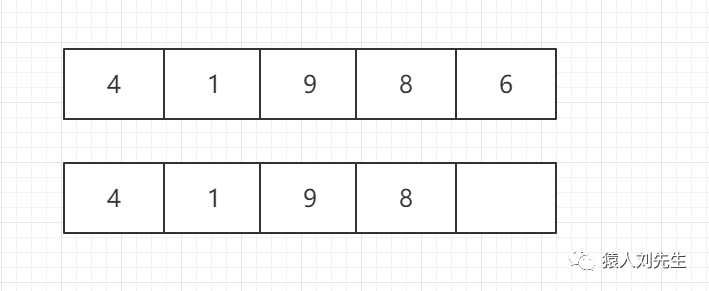
如果在中间删除 , 时间复杂度也为O(N) , 因为删除位置之后的元素要向前移动一位
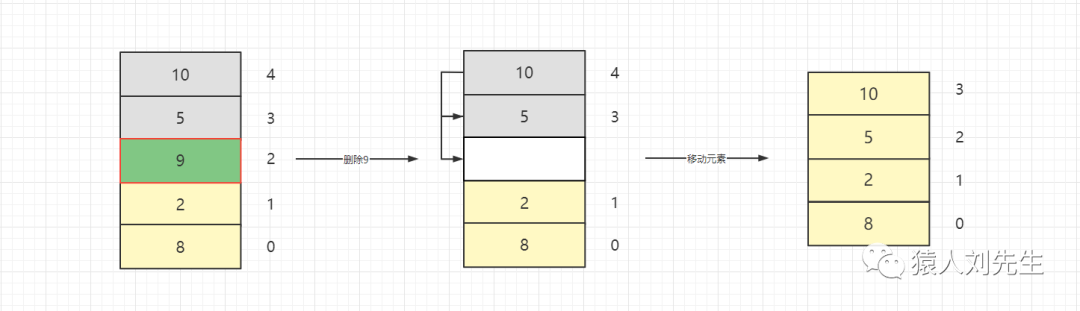
动态数组头插时间复杂度O(N) , 因为会涉及到其他元素向后移动或者是扩容 动态数组尾插时间复杂度如果不扩容 , 那么是O(1) , 如果需要扩容的话 , 那么就是O(N) 动态数组中间插入 , 时间复杂度O(N) , 因为会涉及其它元素的移动或者是数组的扩容
动态数组头删时间复杂度 : O(N) . 因为会涉及其他元素向前移动或者是缩容的情况 动态数组尾删时间复杂度 , 如果考虑缩容 , 那么时间复杂度为O(N) , 否则的话时间复杂度为O(1) 动态数组中间删除时间复杂度为O(N) , 因为会涉及到其他元素向前移动或者是缩容
动态数组查询的情况和常态数组是相同的
步骤如下:
判断容量是否够用,也就是size + 1 <= elements.length;elements表示旧数组
创建一个新的数组newElements,容量为elements的1.5倍(使用位运算效率更高);
将elements中的元素挪到newElements中;
将element指针指向newElements;
1.4.5 动态数组的缩容
步骤如下:
判断容量是否够用,也就是size 大于elements容量的一半时,或者容量小于DEFAULIT_CAPACITY默认容量10时,没必要进行缩容操作;
创建一个新的数组newElements,容量为elements的1/2(使用位运算效率更高);
将elements中的元素挪到newElements中;
将element指针指向newElements;
链表站在物理结构来说属于链式结构 , 而站在逻辑结构来说也属于线性结构 , 链表包含单链表,双向链表,循环链表等等。相对于线性表,添加,删除操作非常方便,因为不用移动大量的结点,只需要修改对应的前后结点指针即可,既然是链表,结点除了基本信息也要加入下一结点指针,方便计算机在内存中查找 , 我们通常把存放基本信息的域成为数据域 , 存放直接后继位置的域成为指针域 , 这两部分组成的数据元素的存储映象 , 称为结点 , 第一个结点称为头结点也叫哑元结点 , 第二个结点才属于真正的第一结点 , 而头结点的数据域可以不存放任何东西 , 也可以存放链表的长度等一些公共的信息
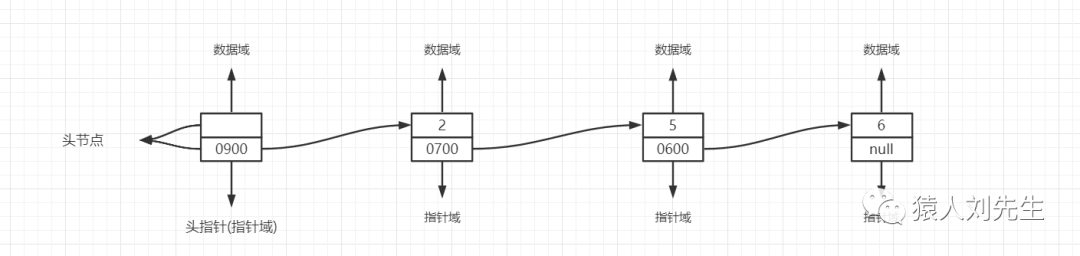
单链表中包含多个节点 , 每一个结点都有一个指向后继元素的next(下一个)指针 , 最后一个结点的next指针值为null , 表示该链表的结束


1.5.3 双向链表

1.5.4 单链表增加和删除
单链表头插
* 修改新结点的next指针 , 使其指向当前的表头结点

* 更改表头指针的值 , 使其指向新节点(之前的表头指针指向的是15 , 修改后指向为新数据的)

单链表尾插


单链表中间插入
*新节点的next指针指向位置结点的下一个节点
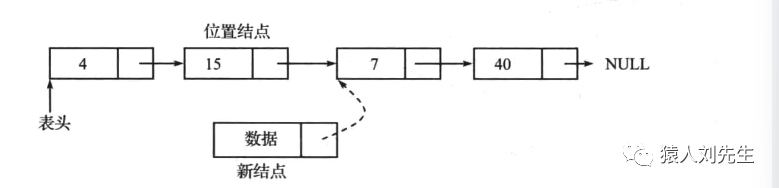
* 位置结点的next指针指向新节点
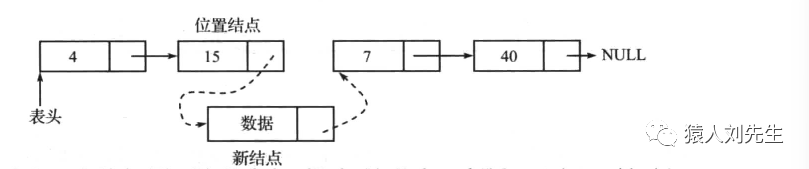
如果使用的是头插法 , 则时间复杂度为O(1) , 否则的话时间复杂度为O(N) , 而不管哪种方式插入空间复杂度为O(1)
单链表的头删
*创建一个临时节点 , 它指向表头指针所指的节点

* 修改表头指针的值 , 使其指向下一个结点 ,并移除临时结点(删除前 , 表头指针指向15 , 删除后 , 表头指针指向7)

单链表的尾删


移除表尾结点的

单链表的中间删除

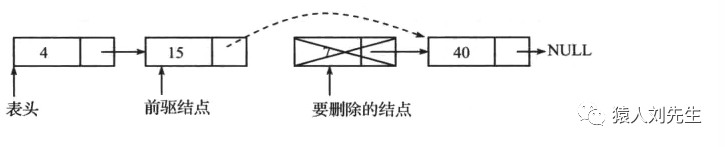
如果使用的是头删法 , 则时间复杂度为O(1) , 否则的话时间复杂度为O(N) , 而不管哪种方式插入空间复杂度为O(1)
1.5.5 双向链表增加和删除
双向链表头插

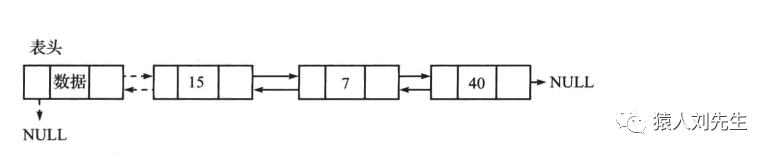
在这种情况下需要遍历到链表的最后 , 然后插入新结点


需要遍历链表 , 知道位置结点 , 然后插入新元素
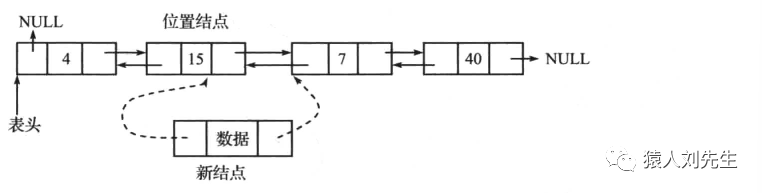
*位置结点的后继结点的前驱指针指向新结点,位置结点的后继结点指向新结点
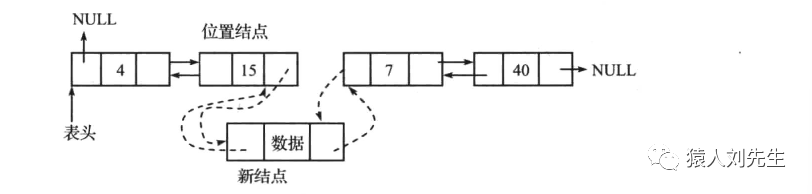
如果使用的是头插法 , 则时间复杂度为O(1) , 否则的话时间复杂度为O(N) , 而不管哪种方式插入空间复杂度为O(1)
双向链表头删
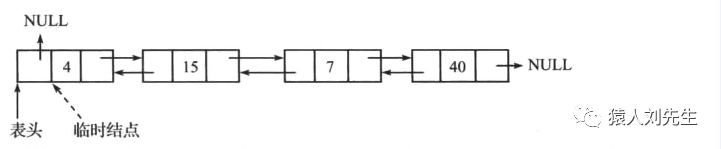

这种情况的处理比删除双向链表的第一个结点要复杂一些,因为要找到表尾结点的前驱结点。需要3步来实现



在这种情况下,被删除的结点总是位于两个结点之间,因此表头和表尾的值不需要更新。该删除操作可通过两步实现

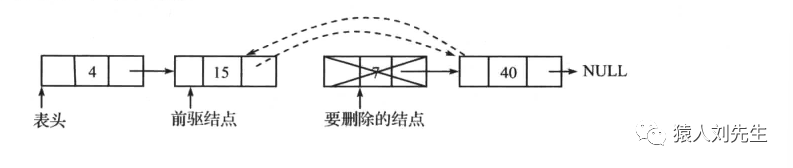
如果使用的是头删法 , 则时间复杂度为O(1) , 否则的话时间复杂度为O(N) , 而不管哪种方式插入空间复杂度为O(1)
1.5.6 循环链表增加和删除
循环链表头插
 * 更新新结点的next指针为表头结点,然后遍历循环链表直至表尾。即插入位置应为循环链表中下一个结点是表头结点的结点位置(该结点是表头的前驱结点)
* 更新新结点的next指针为表头结点,然后遍历循环链表直至表尾。即插入位置应为循环链表中下一个结点是表头结点的结点位置(该结点是表头的前驱结点)
* 更新表头的前驱结点的next 指针指向新结点,得到如下图所示的循环链表

* 设置新结点为表头结点

循环链表尾插

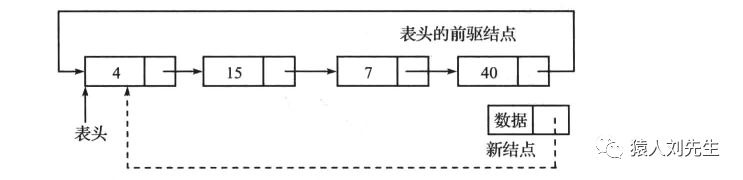
* 更新表头的前驱结点的next 指针指向新结点,得到如下图所示的循环链表

时间复杂度为O(N) , 用于扫描长度为N的链表 , 空间复杂度为O(1)
循环链表头删

* 创建一个指向表头结点的临时结点。更新表尾结点的next指针,使其指向第一个结点的后继结点
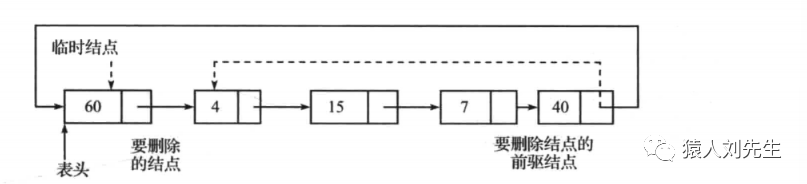
* 修改表头指针的值,使其指向后继结点。移除临时结点

循环链表尾插
为了删除循环链表中的最后一个结点,需要遍历循环链表到倒数第二个结点。该结点将成为新的表尾结点,其next指针将指向链表的第一个结点。以下图的链表为例。为了删除最后一个结点40,首先遍历链表到结点7,再将结点7的next 指针指向结点60,并将这个结点重命名为表尾。

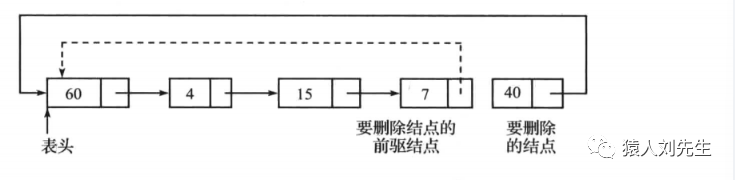
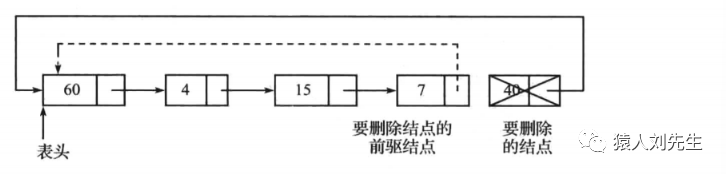
时间复杂度为O(N) , 用于扫描长度为N的链表 , 空间复杂度为O(1)
小结 :
单链表/双向链表头插/头删时间复杂度 : O(1)
单链表/双向链表中间插入/删除时间复杂度 : O(N)
循环链表插入/删除时间复杂度 : O(N)
单链表/双向链表/循环链表获取数据时间复杂度 : O(N)
数组头插/头删时间复杂度 : O(N)
数组尾删/尾插时间复杂度 : O(1)
数组中间插入/删除时间复杂度 : O(N)
数组/动态数组根据下标随机访问时间复杂度 : O(1)
数组/动态数组二分查找时间复杂度 : O(logn)
数组/动态数组顺序查找时间复杂度 : O(N)
动态数组头插/头删时间复杂度 : O(N)
动态数组尾插/尾删时间复杂度 : 不扩容 : O(1) , 扩容 :O(N)
动态数组中间插入/删除时间复杂度 : O(N)






