Redis篇 - 我真的学过HyperLogLog

logerJava 2021-07-15

854

前言

为什么集合写的好好的，突然要来写 Redis 呢 ?

一切的原因都要从今天的需求说起，今天接了一个需求，目标是做一个推广页的 UV (统计访客, 每天只记录同一个访客一次) 统计，因为前段时间刚刚看过老钱写的《Redis深度历险》 HyperLogLog 篇依旧历历在目，一样是统计 UV 的场景，我就直接提出用 HyperLogLog 去处理这个问题，然后被领导问为什么要用 HyperLogLog 好在哪的时候卡壳了，emmm ... 本来想凭借我这广阔的技术海无形装逼，这特么不尴尬了。

于是我痛定思痛，决定对照着看过的本博客和书籍复习一波 HyperLogLog，连夜肝了一篇 HyperLogLog 也相当于读书笔记，准备明天分享给你们分享，有实战代码哦👍

HyperLogLog 与基数统计

HyperLogLog 是最早由 Flajolet 及其同事在 2007 年提出的一种估算基数的近似最优算法，具体定义可以参考维基百科：https://en.jinzhao.wiki/wiki/HyperLogLog

所谓基数统计可以理解为用来统计一个集合中不重复的元素，也就是我们今天要讲解 HyperLogLog 的原因

业务场景分析

领导的需求是：统计每个网页的访客数量, 每个用户只记录一次

我们来捋顺一下思路, 可能你会想出如下几种方案：

Plan A : 数据库里建张表，没有一个表解决不了的问题，如果有那么就建两张表 .
Plan B : 建立一个 Set 集合, 存储当天访问过此页面的所有用户 id .
Plan C : bitmap，类似用户签到的解决方案，依据年月做 key , 日期作为偏移量 .

我们来分析一下这几种方案，首先数据库解决是不可能了，甭说做每个月的 UV 统计分析了, 一天的访问量存起来空间就占了太多了; 那么为每个页面设置一个 Set 怎么样呢 ? 依旧是访问量的问题，如果访问量很高 Set 的集合会非常大，集合一大去重的时候就 ... 你懂的，所以 Set 也不行; 那么 bitmap 呢 ? bitmap 的一个元素可以对应到 bit 数组中的一位，使用 bitmap 确实很节省内存，可是在大数据量的场景下，依旧需要很多内存，并不适用。

三个计划全部拉闸，怎么办呢？哎，拉闸就对了，不拉闸怎么讲我们今天要说的 HyperLogLog 呢？

概率算法

HyperLogLog 采取概率算法，所谓概率算法就是通过一定的概率统计方法预估基数值，而概率算法并不直接存储数据集合本身，这种方法可以极大的节省内存，并保证误差在一定范围内，HyperLogLog 在标准误差（0.81%）的前提下能够统计 2^64 个数据!

Redis 中的 HyperLogLog 原理

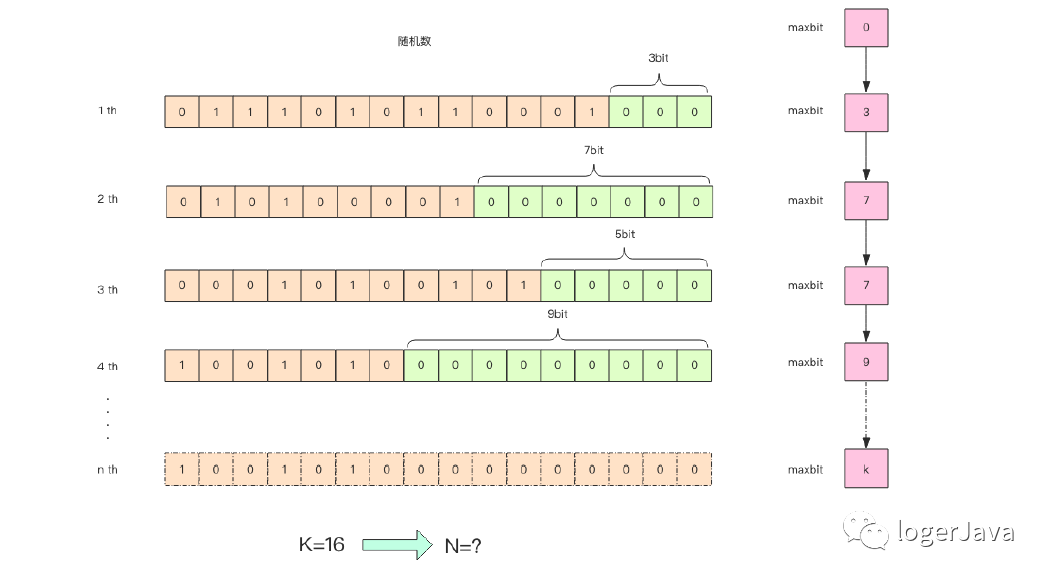
这张图的意思是，给定一系列的随机整数，我们记录下低位连续零位的最大长度K，这个参数就是图中的 maxbit，通过这个K值可以估算出随机数的数量 N，下面我们编写一段代码，观察 N 和 K 的关系

public class PfTest {
static class BitKeeper {
private int maxbits;
public void random() {
long value = ThreadLocalRandom.current().nextLong(2L << 32);
int bits = lowZeros(value);
if (bits > this.maxbits) {
this.maxbits = bits;
          }
      }
private int lowZeros(long value) {
int i = 1;
for (; i < 32; i++) {
if (value >> i << i != value) {
break;
              }
          }
return i - 1;
      }
  }
static class Experiment {
private int n;
private BitKeeper bitKeeper;
public Experiment(int n) {
this.n = n;
this.bitKeeper = new BitKeeper();
      }
public void work() {
for (int i = 0; i < n; i++) {
this.bitKeeper.random();
          }
      }
public void debug() {
           System.out.printf("%d %.2f %d\n", this.n, Math.log(this.n) / Math.log(2), this.bitKeeper.maxbits);
      }
  }
public static void main(String[] args) {
for (int i = 1000; i < 100000; i += 100) {
           Experiment experiment = new Experiment(i);
           experiment.work();
           experiment.debug();
      }
  }
}

输出结果很多，截取一部分，输出结果如下：

1000 9.97 13
1100 10.10 15
1200 10.23 14
1300 10.34 11
1400 10.45 11
1500 10.55 12
1600 10.64 8
1700 10.73 10
1800 10.81 12
1900 10.89 10
2000 10.97 14
2100 11.04 9
2200 11.10 13
2300 11.17 11
2400 11.23 9

我们可以看到，K 和 N 的对数之间确实存在着线性相关性：N ≈ 2K

如果 N 介于 2k 和 2k+1 之间，用这种方式估计的值都等于 2k，这明显是不合理的，所以我们可以使用多个 BitKeeper 进行加权估计，就可以得到一个比较准确的值了：

public class PfTest {
static class BitKeeper {
private int maxbits;
public void random() {
long value = ThreadLocalRandom.current().nextLong(2L << 32);
int bits = lowZeros(value);
if (bits > this.maxbits) {
this.maxbits = bits;
          }
      }
private int lowZeros(long value) {
int i = 1;
for (; i < 32; i++) {
if (value >> i << i != value) {
break;
              }
          }
return i - 1;
      }
  }
static class Experiment {
private int n;
private int k;
private BitKeeper[] keepers;
public Experiment(int n) {
this(n, 1024);
      }
public Experiment(int n, int k) {
this.n = n;
this.k = k;
this.keepers = new BitKeeper[k];
for (int i = 0; i < k; i++) {
this.keepers[i] = new BitKeeper();
          }
      }
public void work() {
for (int i = 0; i < this.n; i++) {
long m = ThreadLocalRandom.current().nextLong(1L << 32);
               BitKeeper keeper = keepers[(int) (((m & 0xfff0000) >> 16) % keepers.length)];
               keeper.random();
          }
      }
public double estimate() {
double sumbitsInverse = 0.0;
for (BitKeeper keeper : keepers) {
               sumbitsInverse += 1.0 / (float) keeper.maxbits;
          }
double avgBits = (float) keepers.length / sumbitsInverse;
return Math.pow(2, avgBits) * this.k;
      }
  }
public static void main(String[] args) {
for (int i = 100000; i < 1000000; i += 100000) {
           Experiment exp = new Experiment(i);
           exp.work();
double est = exp.estimate();
           System.out.printf("%d %.2f %.2f\n", i, est, Math.abs(est - i) / i);
      }
  }
}

我在搜寻网上博客解释时，有一个老哥的解释比较生动形象，我们这里也采用他的解释方法：

这个过程有点类似于选秀节目里面的打分，一堆专业评委打分，但是有一些评委因为自己特别喜欢所以给高了，一些评委又打低了，所以一般都要屏蔽最高分和最低分，然后再计算平均值，这样得出来的分数就差不多是公平公正的了。

在计算平均值的时候，采用了调和平均数，也就是倒数的平均值，它能有效地平滑离群值的影响

avg = (3 + 4 + 5 + 104) / 4 = 29
avg = 4 / (1/3 + 1/4 + 1/5 + 1/104) = 5.044

我们观察输出结果，误差率百分比控制在个位数：

100000 93786.03   0.06
200000 192010.26 0.04
300000 295451.43 0.02
400000 394595.83 0.01
500000 502096.02 0.00
600000 644347.82 0.07
700000 752617.39 0.08
800000 840280.38 0.05
900000 898276.74 0.00

真实的 HyperLogLog 要比上面的示例代码更加复杂一些，也更加精确一些。上面这个算法在随机次数很少的情况下会出现除零错误，因为 maxbit = 0
是不可以求倒数的。

关于 HyperLogLog 大家也可以进入这个网站实际操作一下，理解的更快：http://content.research.neustar.biz/blog/hll.html

实战

我们先来看一下 RedisTemplate 操作 HyperLogLog 的方法：

// 将指定的元素添加到HyperLogLog中，可以添加多个元素
public void pfAdd(String key, String... value) {
       redisTemplate.opsForHyperLogLog().add(key, value);
  }
// 返回给定HyperLogLog的基数估算值。当一次统计多个HyperLogLog时(通过key实现时间窗口统计user:web1:2020061600、user:web1:2020061601)，需要对多个HyperLogLog结构进行比较，并将并集的结果放入一个临时的HyperLogLog，性能不高，谨慎使用
public Long pfCount(String... key) {
return redisTemplate.opsForHyperLogLog().size(key);
  }
// 将多个HyperLogLog进行合并，将并集的结果放入一个指定的HyperLogLog中
public void pfMerge(String destKey, String... sourceKey) {
       redisTemplate.opsForHyperLogLog().union(destKey, sourceKey);
  }

loger来写一段代码，看一下 HyperLogLog 到底怎么来统计 UV ：

public class RedisTest {
@Autowired
private RedisTemplate redisTemplate;
public void addUV(String id, LocalDate localDate){
String redisKey = String.format("single:%s", localDate);
       redisTemplate.opsForHyperLogLog().add(redisKey, id);
  }
// 统计指定日期范围内的uv
public long calculateUV(LocalDate start, LocalDate end) {
// 整理该日期范围内的key
       List<String> keyList = new ArrayList<>();
while (!start.isAfter(end)) {
String key = String.format("single:%s", start);
           keyList.add(key);
           start = start.plusDays(1);
      }
// 合并这些日期内的数据
String redisKey = String.format("interval:%s:%S", start, end);
       redisTemplate.opsForHyperLogLog().union(redisKey, keyList.toArray());
// 返回统计后的结果
return redisTemplate.opsForHyperLogLog().size(redisKey);
  }
}

感兴趣的小伙伴建议自己写到 idea 里面试一下

参考资料

[HyperLogLog算法原文] HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm

http://algo.inria.fr/flajolet/Publications/FlFuGaMe07.pdf

[Rdis作者博客] Redis new data structure: the HyperLogLog

http://antirez.com/news/75

[Reids—神奇的HyperLoglog解决统计问题] - 我没有三颗心脏、敖丙

https://mp.weixin.qq.com/s/9dtGe3d_mbbxW5FpVPDNow

《Redis深度历险-核心原理与实践应用》 - 钱文品/ 著

扫描二维码关注更多技术分享

redis

文章转载自logerJava，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

Redis篇 - 我真的学过HyperLogLog

评论