点击关注公众号,干货第一时间送达
这是一道纯coding 的题目,
考查诸位的代码能力,
不过,你需要先想出来怎么做,
想出来就好做。
想不出来?
那就多看看小编的文章,多练习练习即可。
题目来自力扣:

一道 "困难" 的题目
原题链接:
https://leetcode.cn/problems/perfect-rectangle/description/
一、屏幕前的吴彦祖和刘亦菲们,请听题

抽象,太抽象了。。。
举个例子:
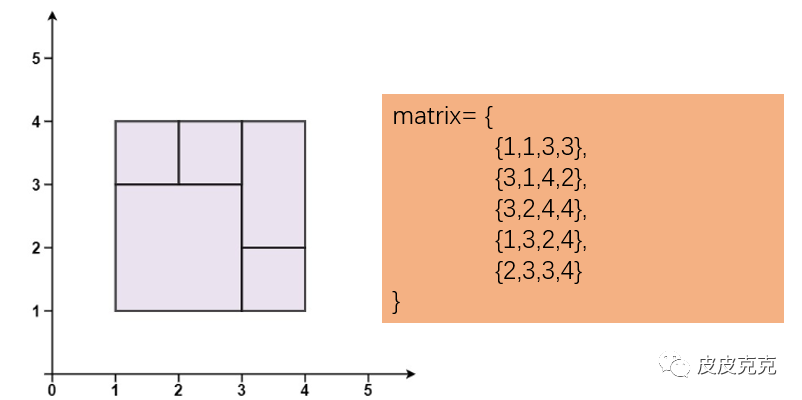
如上图,是可以组成完美矩形的情况。
来个不行的:
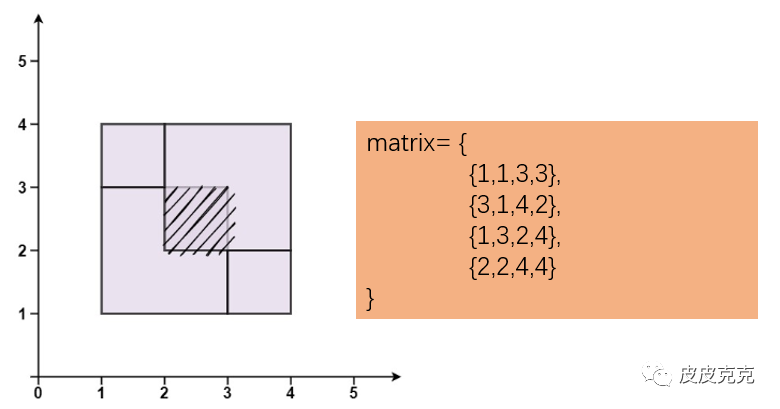
懂了吧?
懂了题意,想想咋解题呢。
二、解题
其实,要组成完美矩阵,
需要两个条件:
(1)小矩形的面积之和 = 大矩形的面积
(2)小矩形的四个顶点,除了组成大矩形的四个顶点外,其他顶点都出现2次:
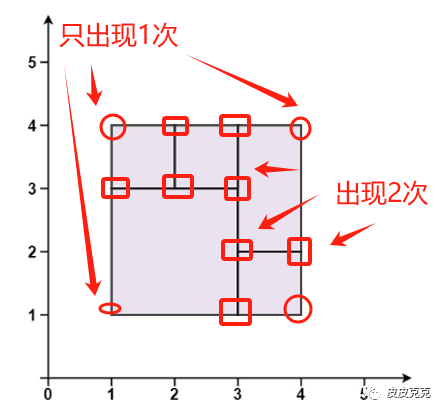
明白了这两个条件,就好写代码了。
面积的累加和,可以通过变量累加得到:

完美矩形的四个顶点,可以通过 set 去重获得:
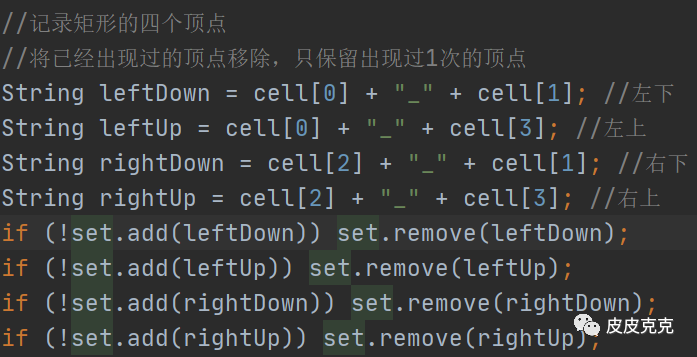
看看代码。
完整代码:
public class CodingDemo_03 {
/**
* 完美矩形
* @param rectangles
* @return
*/
public boolean isRectangleCover(int[][] rectangles) {
if (rectangles == null || rectangles[0] == null){
return false;
}
//1, 记录每个矩形的四个顶点,找出最左、右、上、下的四个点坐标
int mostLeft = Integer.MAX_VALUE;
int mostRight = Integer.MIN_VALUE;
int mostUp = Integer.MIN_VALUE;
int mostDown = Integer.MAX_VALUE;
//用于记录矩形面积
int area = 0;
//用于记录矩形的顶点,因为如果要组成完美矩形,大矩形除了四个顶点外,其他
//顶点都出现了2次
Set<String> set = new HashSet<>();
//2, 开始尝试每个小矩形
for (int[] cell : rectangles) {
mostLeft = Math.min(mostLeft, cell[0]);
mostDown = Math.min(mostDown, cell[1]);
mostRight = Math.max(mostRight, cell[2]);
mostUp = Math.max(mostUp, cell[3]);
//矩形面积累加
area += (cell[2] - cell[0]) * (cell[3] - cell[1]);
//记录矩形的四个顶点
//将已经出现过的顶点移除,只保留出现过1次的顶点
String leftDown = cell[0] + "_" + cell[1]; //左下
String leftUp = cell[0] + "_" + cell[3]; //左上
String rightDown = cell[2] + "_" + cell[1]; //右下
String rightUp = cell[2] + "_" + cell[3]; //右上
if (!set.add(leftDown)) set.remove(leftDown);
if (!set.add(leftUp)) set.remove(leftUp);
if (!set.add(rightDown)) set.remove(rightDown);
if (!set.add(rightUp)) set.remove(rightUp);
}
//记录完每个小矩形后,判断是否能够组成完美矩形
//先判断set中最后剩下的点,是否是小矩形中最左、右、上、下的四个点
if (!set.contains(mostLeft+"_"+mostDown) ||
!set.contains(mostLeft+"_"+mostUp) ||
!set.contains(mostRight+"_"+mostDown) ||
!set.contains(mostRight+"_"+mostUp) ||
set.size() != 4){
return false;
}
//最后再判断小矩形面积之和,是否等于大矩形面积
return area == (mostRight-mostLeft) * (mostUp-mostDown);
}
}
去力扣试试:

文章转载自皮皮克克,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






