这是一道 "矩阵" 类型的题目,
在企业面试中,出题率不高:
可是,不代表不出
正是因为这样,"矩阵" 类型的题目,
不多,
但是,个个经典!
能掌握精髓,便可走遍天下。
不像动态规划,必须要多刷
今天的题目,来自力扣:

原题链接:
https://leetcode.cn/problems/largest-1-bordered-square/description/
一、屏幕前的吴彦祖和刘亦菲们,请听题

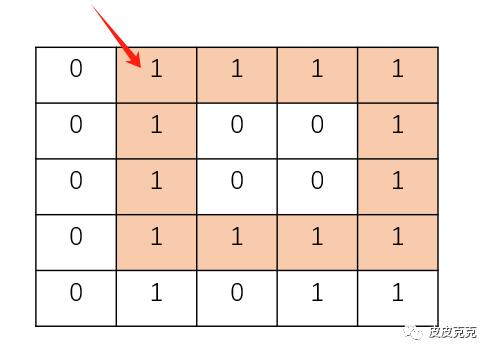
举个例子:
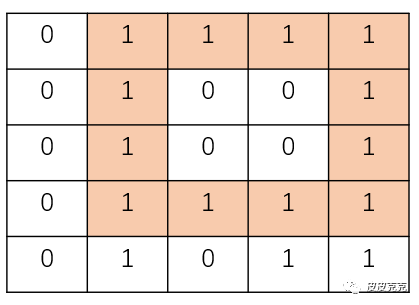
如上图中,以 1 为边界的正方形,边长为 4,共有4*4=16个元素。
屏幕前聪明的你,
会怎么去求呢?
这题可以用动态规划,但是小编要考大家纯code能力,
不用动态规划,
怎么写代码?
二、解题
可以借助辅助矩阵,也就是 预处理矩阵。
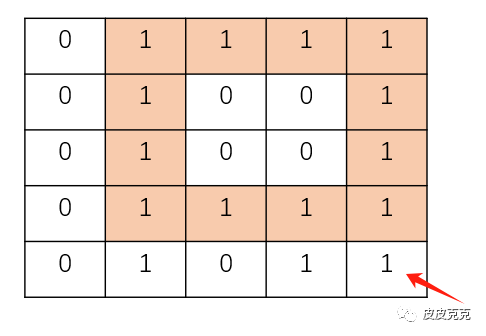
想求矩阵中边界全是1的正方形子矩阵,
显然,需要定位点:
如上图,如果咱们能求出该点向右和向下,同时能够有多少个连续的1,
是不是就可以知道最大的正方形边长了?
连续的1的个数,怎么求?
可以通过倒推。
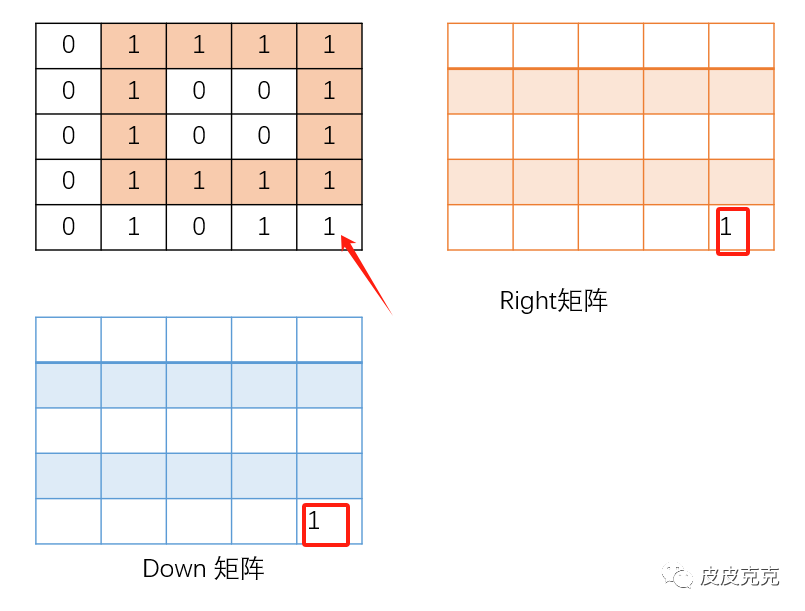
(1)先定位到矩阵右下角,判断是否是1
利用辅助矩阵 right[][],down[][] 记录
right[][] 表示某个坐标(x,y) 向右,有多少个连续的1
down[][] 表示某个坐标(x,y) 向下,有多少个连续的1
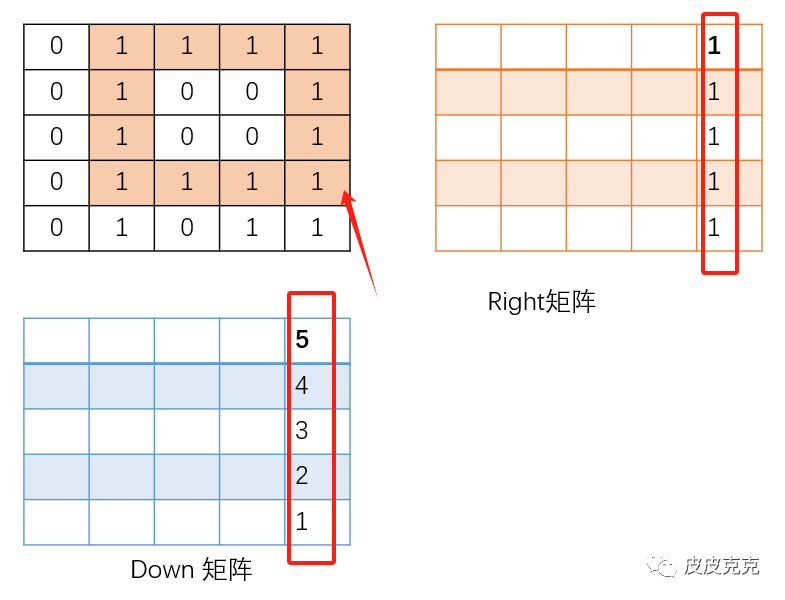
(2)先倒推最后一列,从下往上倒推
根据right矩阵的性质,
最后一列是没有右侧元素的,所以right的值,只依赖于原矩阵grid 对应的点是否是1。
根据down矩阵的性质,down[i][j] 是依赖于下面相邻格子的值 down[i+1][j] +1
(3)再倒推最后一行,从右往左倒推
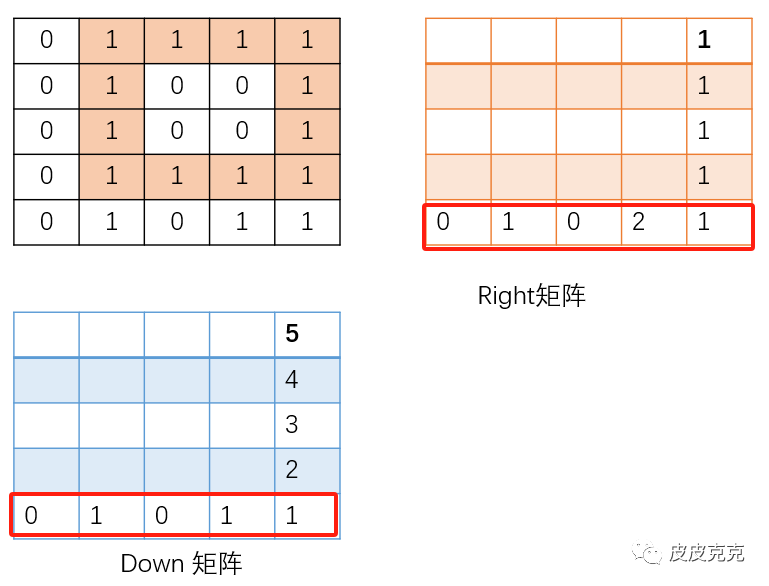
(4)最后,推导中间的位置
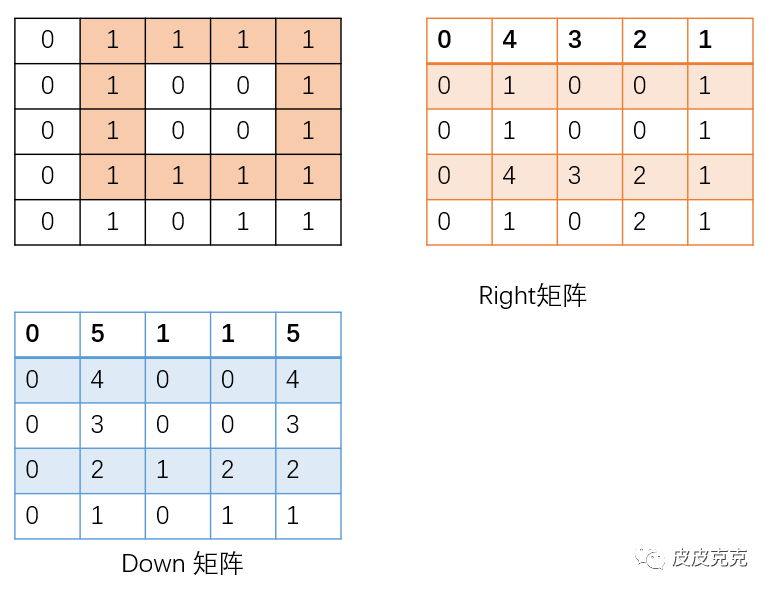
这样,辅助矩阵推导完毕,
原矩阵中,最大的正方形,可能有哪些?
根据正方形边长,从两个辅助矩阵求即可。
比如,原矩阵grid 边长是5,我们先判断是否有边长为5的正方形。
从 (0,0) 出发,判断right[][] 矩阵点右侧是否有连续的1的个数 >= 5的
发现没有,所以不可能存在边长为5的正方形。
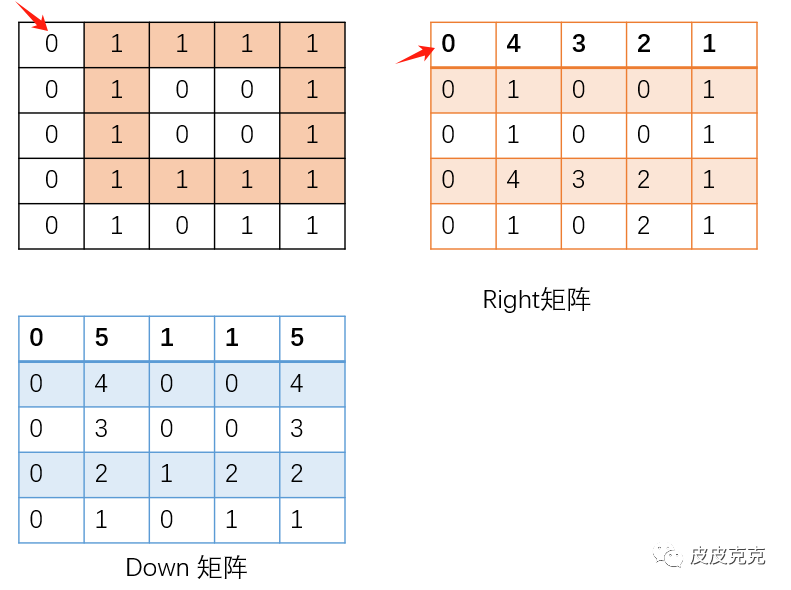
边长为4的正方形呢?
可以找到一个点,向右有连续的4个1:
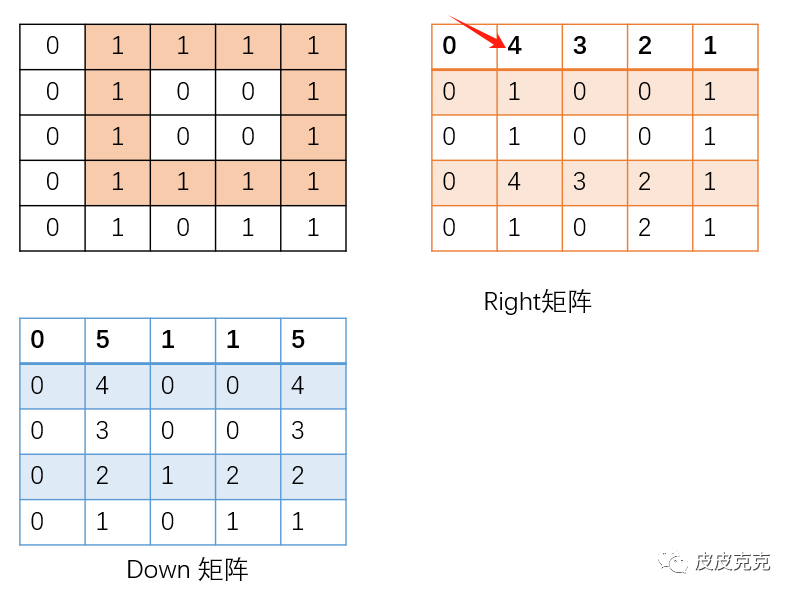
然后,指针下移4位,发现这个点,向右也有连续的4个1:
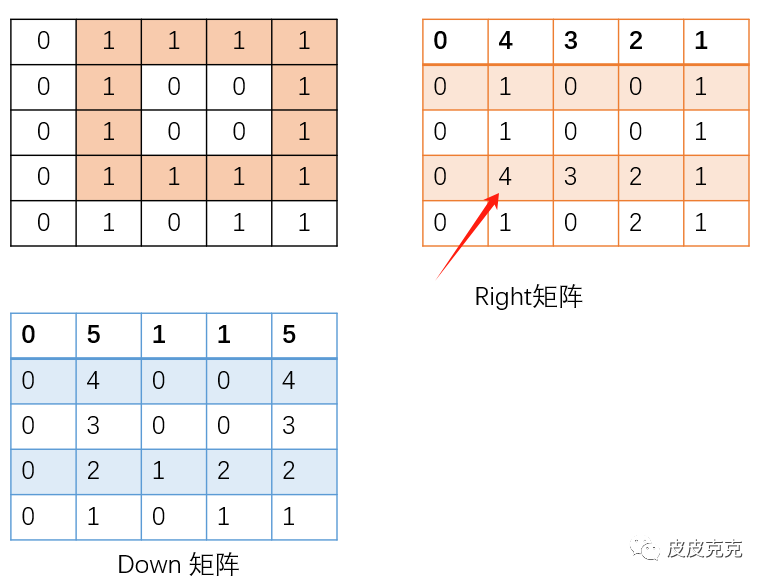
再判断down矩阵即可。
看看代码。
完整代码:
public class CodingDemo_03 {
/**
* 最大的以1为边界的正方形
* @param grid
* @return
*/
public int largest1BorderedSquare(int[][] grid) {
int M = grid.length;
int N = grid[0].length;
//1,创建辅助矩阵
int[][] right = new int[M][N];
int[][] down = new int[M][N];
//2,填充辅助矩阵
setBoard(grid, right, down);
//3, 判断最大正方形
for (int size = Math.min(M,N); size != 0; size--) {
if (hasBoard(size, right, down)){
return size*size; //返回这个正方形的面积
}
}
return 0;
}
//通过辅助矩阵,判断是否存在边长为size的正方形
private static boolean hasBoard(int size, int[][] right, int[][] down){
for (int i = 0; i != right.length -size+1; i++) {
for (int j = 0; j != right[0].length -size+1; j++) {
//判断向右,和向下,连续的1,是否够数
// i+size-1 和 j+size-1
// 是从子矩阵左上角,跳转到左下角
// 和从子矩阵左上角,跳转到右上角
if (right[i][j] >= size && down[i][j] >= size
&& right[i+size-1][j] >= size && down[i][j+size-1] >= size){
return true;
}
}
}
return false;
}
private static void setBoard(int[][] grid, int[][] right, int[][] down){
int M = grid.length;
int N = grid[0].length;
//1,先判断矩阵右下角
if (grid[M-1][N-1] == 1){
right[M-1][N-1] = 1;
down[M-1][N-1] = 1;
}
//2, 从矩阵右下角,倒推最后一列
for (int row = M-2; row >= 0; row--) {
//因为此时是最后一列,right矩阵是没有右侧依赖的,所以只依赖grid
//而down,则是依赖于下方的相邻格子
if (grid[row][N-1] == 1){
right[row][N-1] = 1;
down[row][N-1] = down[row+1][N-1] + 1;
}
}
//3, 从矩阵右下角,倒推最后一行
for (int col = N-2; col >= 0; col--) {
//同理
if (grid[M-1][col] == 1){
right[M-1][col] = right[M-1][col+1] + 1;
down[M-1][col] = 1;
}
}
//4,倒推中间节点
for (int row = M-2; row >= 0; row--) {
for (int col = N-2 ; col >= 0; col--) {
if (grid[row][col] == 1){
right[row][col] = right[row][col+1] +1;
down[row][col] = down[row+1][col] +1;
}
}
}
}
}
去力扣试试: