点击关注公众号,干货第一时间送达
见证奇迹的时刻。
不,
谜底揭晓的时刻,来了!
上篇文章:数据结构和算法【24】戳气球
针对戳气球这题,给诸位留了个问题,
因为上篇文章给出的暴力递归算法,
超时了!
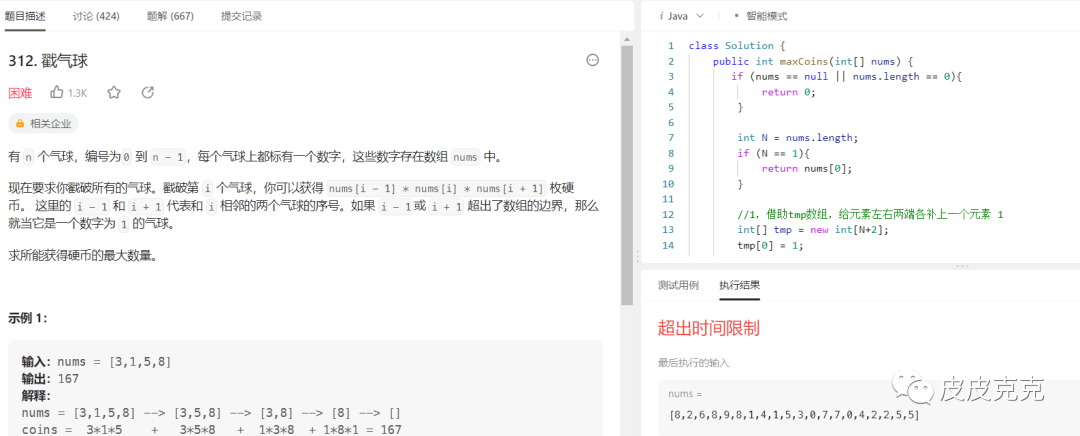
优化方案,此刻来袭!
(友情提示:关于暴力递归方法求解戳气球问题,感兴趣的小伙伴请翻看上篇文章:数据结构和算法【24】戳气球)
再看一遍题目:

一、优化方案
暴力递归的方法,只有两个变量:
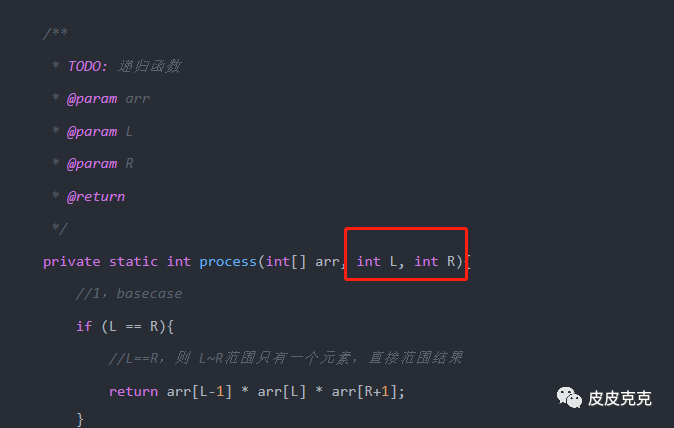
这两个参数,表示咱们尝试的范围,范围是 0 ~ arr.lenght-1。
那咱们就,
用暴力递归,改出动态规划表。
(假设给定数组 arr = {4,2,3,5,1,6}, 为了避免边界计算问题,咱们在数组左右两端分别加上元素1,形成新数组 arr = {1,4,2,3,5,1,6,1})
(1)构建dp[][] 动态规划表
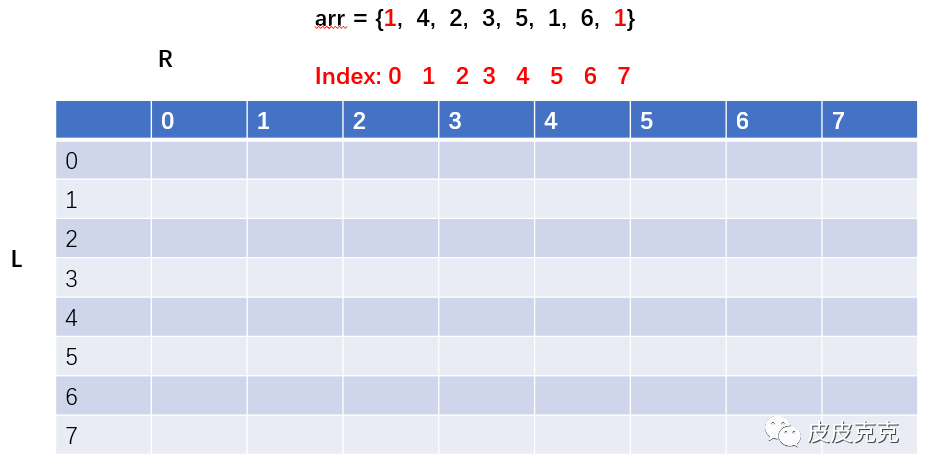
(2)因为arr 左右两端是我们新加的辅助元素,不会在尝试范围内,所以填上x
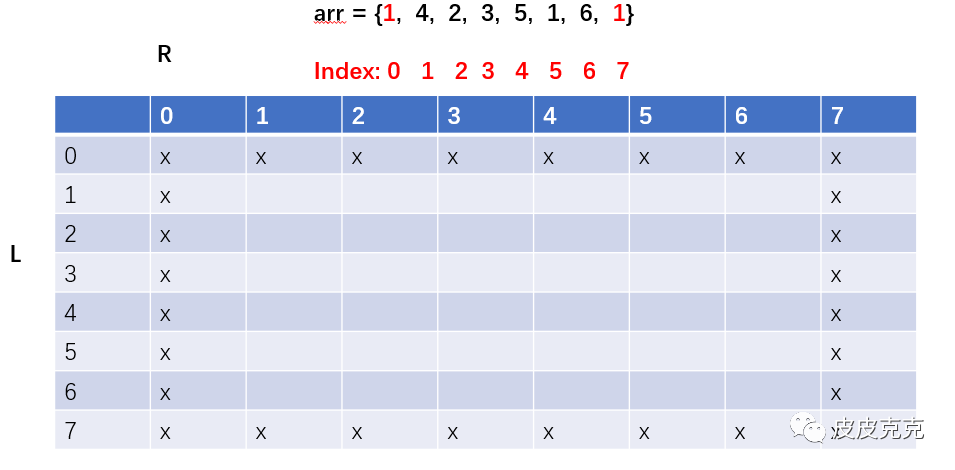
(3)因为在 L ~ R 范围尝试,所以 L 不可能大于R,对应的格子填上x
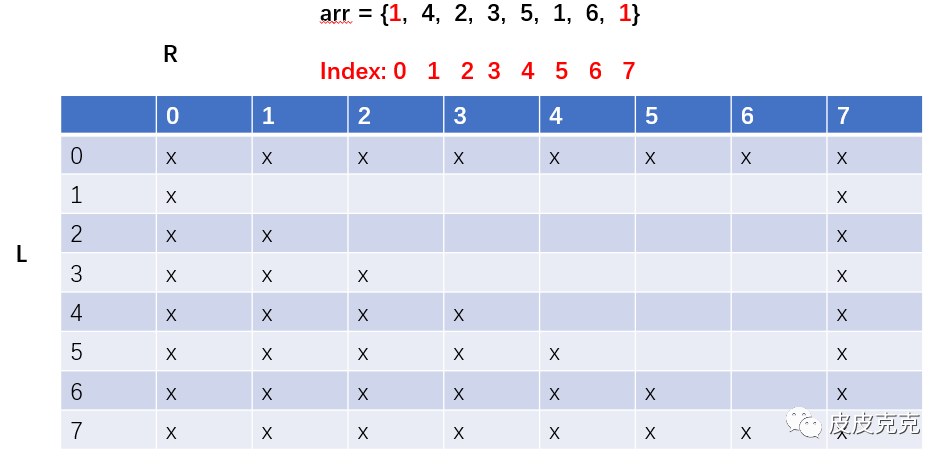
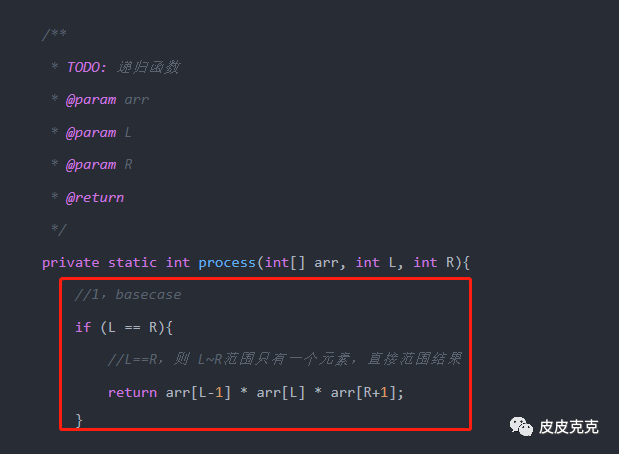
(4)查看暴力递归方法里面的 basecase,对应位置填上可以直接计算的值

(5)我们最终需要求的就是格子 dp[1][6]
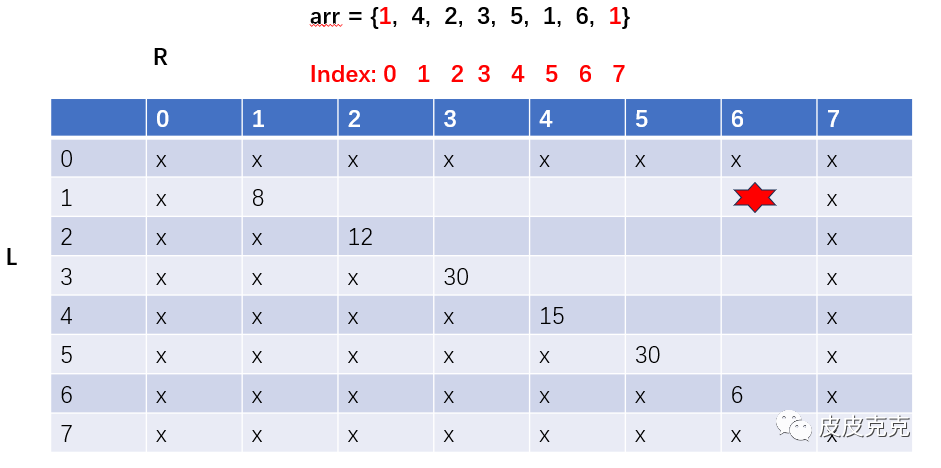
(6)参考暴力递归方法,可以发现规律
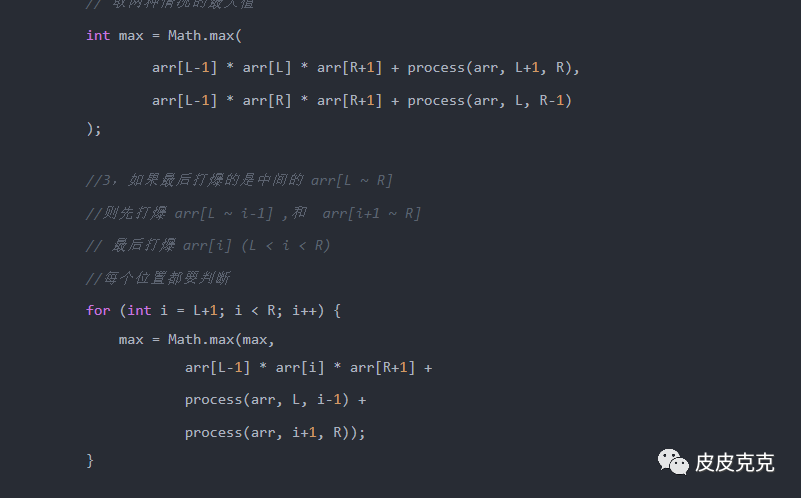
当前位置dp[i][j] 依赖哪些位置?
最终答案要求dp[1][6],不妨倒推。
求process(1,6) 时,
会先求出:
process(2,6) -> 最后打爆arr[1] 时候,依赖A:

process(1,5) -> 最后打爆 arr[6],依赖 B:
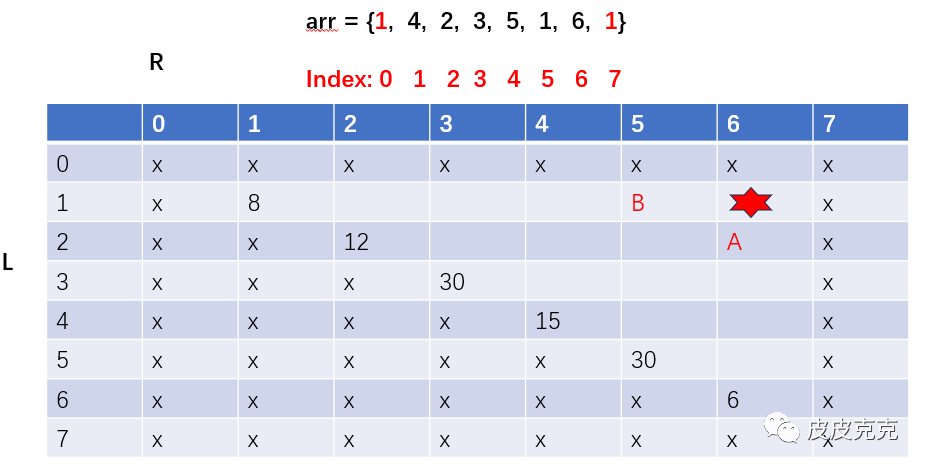
process(1,1) -> 最后打爆arr[2],依赖 C:
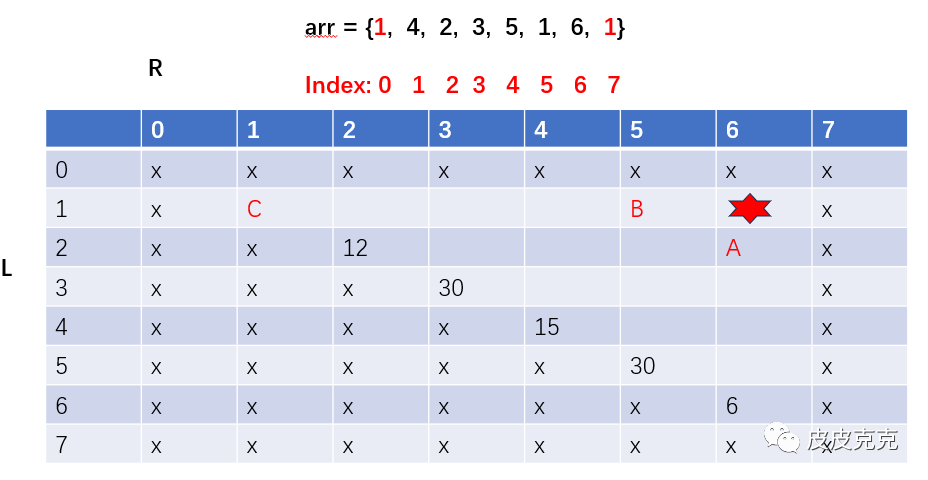
process(3,6) -> 最后打爆arr[2],依赖D:
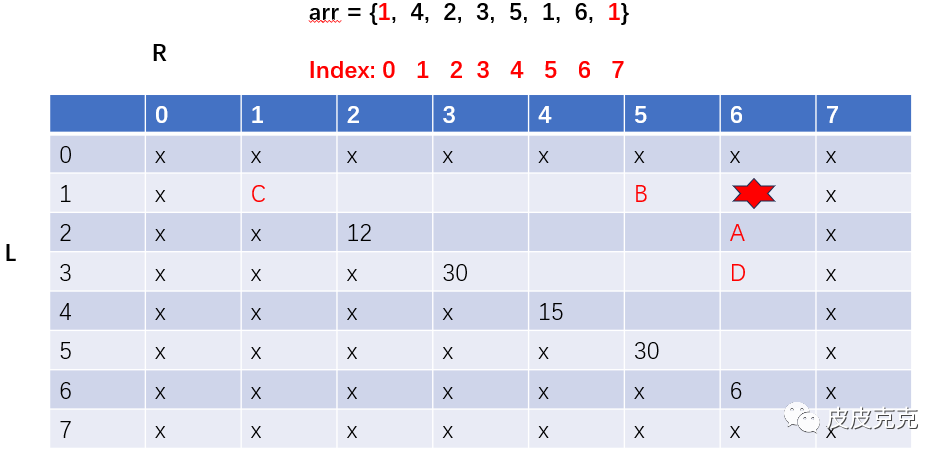
依此类推,会发现dp[1][6] 只依赖同行和同列:
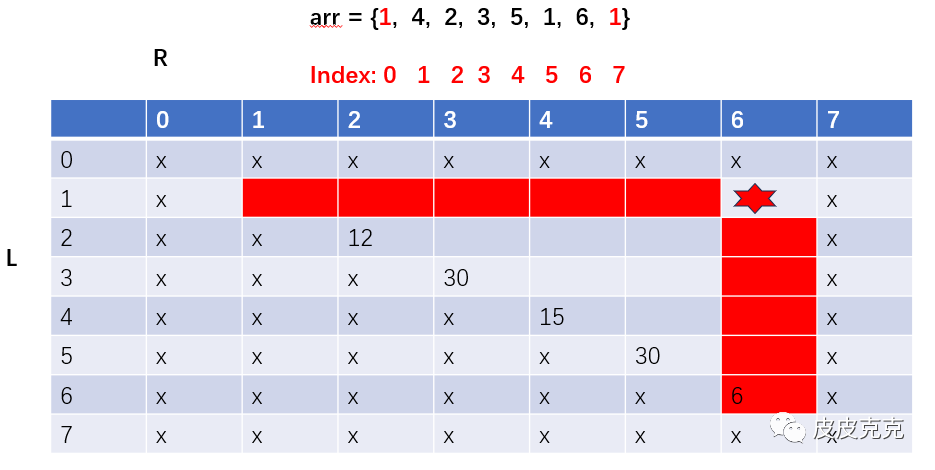
其他位置呢?
也是如此。
看看代码
完整代码:
public class CodingDemo {
/**
* TODO: 戳气球II
* @param nums
* @return
*/
private static int maxCoins2(int[] nums) {
if (nums == null || nums.length == 0){
return 0;
}
if (nums.length == 1){
return nums[0];
}
int N = nums.length;
//1,创建辅助数组
//辅助数组左右两端补1,中间复制原数组
int[] tmp = new int[N+2];
tmp[0] = 1;
tmp[N+1] = 1;
for (int i = 0; i < N; i++) {
tmp[i+1] = nums[i];
}
//2,创建dp表
int[][] dp = new int[N+2][N+2];
//填对角线
for (int i = 1; i <= N; i++) {
dp[i][i] = tmp[i-1] * tmp[i] * tmp[i+1];
}
//3,从下往上,从左往右,填充dp
for (int L = N; L >= 1 ; L--) {
for (int R = L+1; R <= N; R++) {
//3.1 最后打爆L气球
int finalL = tmp[L-1] * tmp[L] * tmp[R+1] + dp[L+1][R];
//3.2 最后打爆R气球
int finalR = tmp[L-1] * tmp[R] * tmp[R+1] + dp[L][R-1];
//3.3 取较大的
dp[L][R] = Math.max(finalL, finalR);
//3.4 如果最后打爆的是 L ~ R 中间的,需要依次遍历
for (int i = L+1; i < R; i++) {
dp[L][R] = Math.max(dp[L][R],
tmp[L-1] * tmp[i] * tmp[R+1] + dp[L][i-1] + dp[i+1][R]);
}
}
}
return dp[1][N];
}
public static void main(String[] args) {
int[] arr = {3,1,5,8};
System.out.println(maxCoins2(arr));
}
}
输出:
D:\java\bin\java.exe
167
再试试力扣:
搞定!

文章转载自皮皮克克,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






