点击关注公众号,干货第一时间送达
"想梦想仗剑走天涯,看一看世界的繁华......."
不不不,
小时候的梦想是,能拿着一把玩具枪,随便乱打
这不,来了!
一、各位,请听题

原题来自力扣:
https://leetcode.cn/problems/burst-balloons/
姑且想象成,用玩具枪,打爆气球
满足儿时的愿望 。
。
举个栗子:

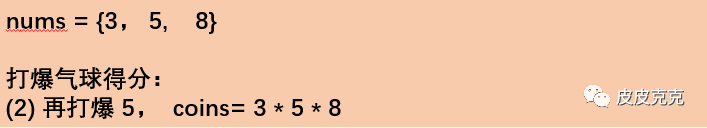


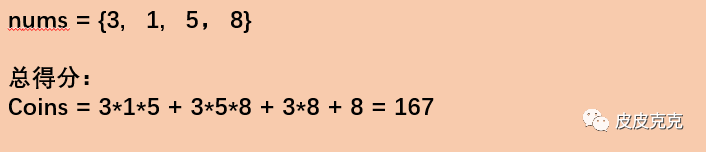
题意都清楚否?
怎么解呢?
二、解题
给定数据arr[],表示每个气球对应的分数。
那我们就在这个数组范围内做尝试。
arr[L ~ R] ,(0 <= L <= R <= N-1)
我们假设在选择打爆 L ~ R 范围内的气球时,范围外的气球都还存在!
那么我们选择打爆 L ~ R 范围的气球,就有三种情况:
(1)最后打爆的是 L 气球,也就是最左边的一个气球:
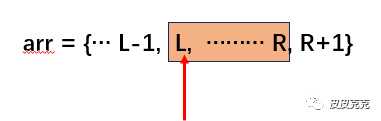
那么得分就是:打爆 arr[L-1],打爆arr[R+1],打爆 arr[L+1 ~ R],最后打爆 arr[L],即 arr[L-1] * arr[L] * arr[R+1] + p(L+1, R)
( p(L+1, R) 是递归函数,表示需要打爆 L+1 ~ R 范围的气球的最高得分)
(2)最后打爆的是 R气球,也就是最右边的气球:
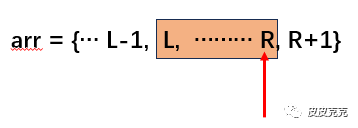
那么得分就是:打爆 arr[L-1],打爆arr[R+1],打爆 arr[L ~ R-1],最后打爆 arr[R],即 arr[L-1] * arr[R] * arr[R+1] + p(L, R-1)
(3)最后打爆的是 L ~ R气球,也就是中间的气球:
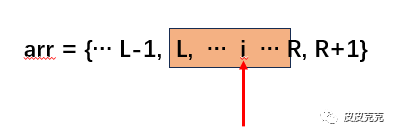
很显然,得分是:打爆 arr[L-1],打爆 arr[R+1],然后在 L ~ R 范围遍历尝试。
怎么尝试?
问的好!
L ~ R 范围任意一点 i,可以划分为 L ~ i-1 , i , i+1 ~ R 三部分,i 是定值,另外两部分利用递归调用即可。
代码怎么写?
按照上面分析的逻辑,实现即可,
为了避免边界的问题,可以在数组两端各加上一个 1,方便计算:
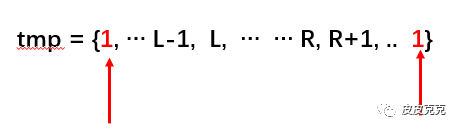
看看下面的完整代码。
完整代码:
public class CodingDemo {
/**
* TODO: 戳气球
* @param nums
* @return
*/
private static int maxCoins(int[] nums) {
if (nums == null || nums.length == 0){
return 0;
}
int N = nums.length;
if (N == 1){
return nums[0];
}
//1,借助tmp数组,给元素左右两端各补上一个元素 1
int[] tmp = new int[N+2];
tmp[0] = 1;
tmp[N+1] = 1;
//2, 把原数组值 复制到 tmp: 1 ~ N 位置
for (int i = 0; i < N; i++) {
tmp[i+1] = nums[i];
}
//3, 然后从 tmp 的 1 ~ N-1 递归判断,可以避免边界问题
return process(tmp, 1, N);
}
/**
* TODO: 递归函数
* @param arr
* @param L
* @param R
* @return
*/
private static int process(int[] arr, int L, int R){
//1,basecase
if (L == R){
//L==R,则 L~R范围只有一个元素,直接范围结果
return arr[L-1] * arr[L] * arr[R+1];
}
//2,在 L~R范围内,
//先判断最后打爆两边的气球,最大分数
//2.1 最后打爆 arr[L] 气球,则分数是 arr[L-1] * arr[L] * arr[R+1]
// 此情况下,中间的 arr[L+1 ~ R] 是要先打爆的,递归判断
// 2.2 最后打爆 arr[R] 气球,则分数是 arr[L-1] * arr[R] * arr[R+1]
// 此情况下,中间的 arr[L ~ R-1] 是要先打爆的,递归判断
// 取两种情况的最大值
int max = Math.max(
arr[L-1] * arr[L] * arr[R+1] + process(arr, L+1, R),
arr[L-1] * arr[R] * arr[R+1] + process(arr, L, R-1)
);
//3,如果最后打爆的是中间的 arr[L ~ R]
//则先打爆 arr[L ~ i-1] ,和 arr[i+1 ~ R]
// 最后打爆 arr[i] (L < i < R)
//每个位置都要判断
for (int i = L+1; i < R; i++) {
max = Math.max(max,
arr[L-1] * arr[i] * arr[R+1] +
process(arr, L, i-1) +
process(arr, i+1, R));
}
//4,返回结果
return max;
}
public static void main(String[] args) {
int[] arr = {3,1,5,8};
System.out.println(maxCoins(arr));
}
}
输出:
D:\java\bin\java.exe
167
完事了?
还没有。
这种暴力递归的方式,在力扣上,超时了
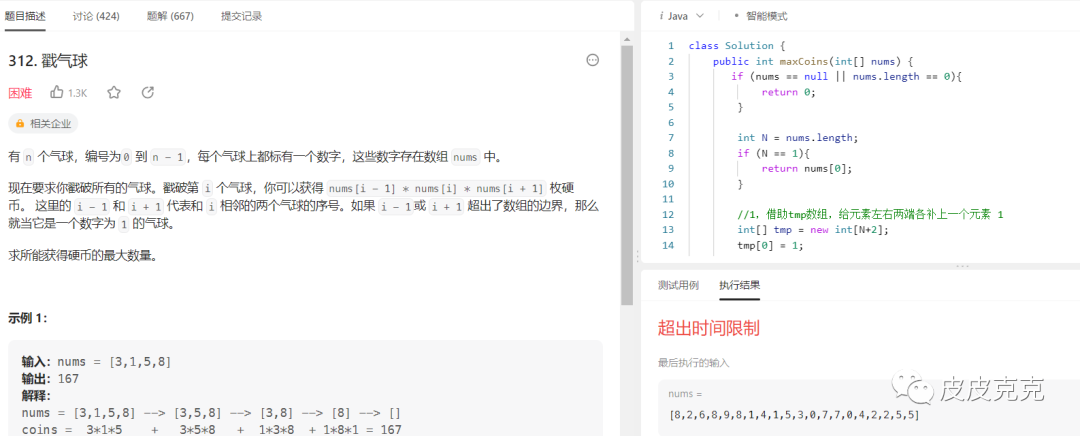
如何优化?
下篇文章,咱们揭晓。







