点击关注公众号,干货第一时间送达
介绍一种经典的树!
完全二叉树。
百度百科上面给的定义是:
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树
第一次看这个,
我没懂
只能说中华文化博大精深,在下才疏学浅
不过,我们可以简化+转换。
满二叉树,应该都懂吧!
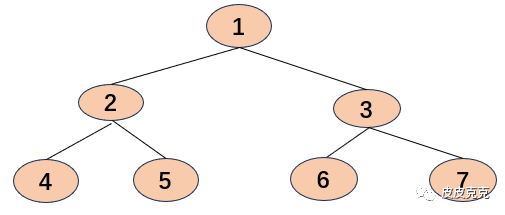
每个节点都有左孩子和右孩子。
但是,如果有节点只有一个孩子呢?
像这种:
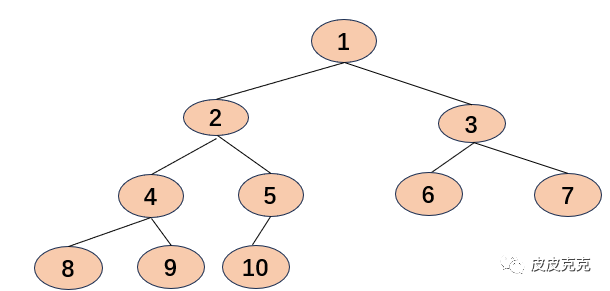
是完全二叉树。
而这种就不是完全二叉树:
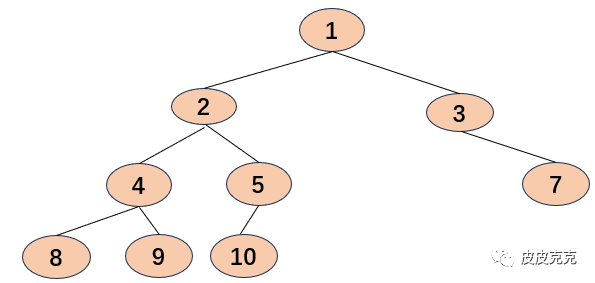
懂了没?
完全二叉树的判断:
层序遍历二叉树
1>如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树;
2>如果遇到一个结点,左孩子不为空,右孩子为空;或者左右孩子都为空,且则该节点之后的队列中的结点都为叶子节点,该树才是完全二叉树,否则就不是完全二叉树
含义都整明白了吧,
看看代码。
完整代码:
public class CodingDemo {
private static class TreeNode{
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
/**
* TODO: 判断是否是完全二叉树
* @param root
* @return
*/
private static boolean isCBT(TreeNode root){
if (root == null){
return true;
}
//1,剩下的节点是否必须是叶子节点
boolean leaf = false;
//2,队列
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.add(root);
//3,开始层序遍历
while (!queue.isEmpty()){
//3.1 弹出当前节点
TreeNode curNode = queue.poll();
//3.2 如果出现节点有右孩子,但是没有左孩子,则不是完全二叉树
// 如果出现节点有左孩子,但是没有右孩子,则后续的节点必须是叶子节点
if ( (leaf && (curNode.left != null || curNode.right != null)) ||
(curNode.left == null && curNode.right != null)
) {
return false;
}
//3.3
if (curNode.left != null){
queue.add(curNode.left);
}
if (curNode.right != null){
queue.add(curNode.right);
} else {
// 如果出现节点有左孩子,但是没有右孩子,则层序遍历的后续节点,必须是叶子节点
leaf = true;
}
}
return true;
}
public static void main(String[] args) {
TreeNode node1 = new TreeNode(1);
node1.left = new TreeNode(2);
node1.left.left = new TreeNode(4);
node1.left.left.left = new TreeNode(8);
node1.left.left.right = new TreeNode(9);
node1.left.right = new TreeNode(5);
node1.left.right.left = new TreeNode(10);
node1.left.right.right = new TreeNode(11);
node1.right = new TreeNode(3);
node1.right.left = new TreeNode(6);
node1.right.left.left = new TreeNode(12);
node1.right.right = new TreeNode(7);
System.out.println(isCBT(node1));
}
}
输出:
D:\java\bin\java.exe
true

文章转载自皮皮克克,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






