点击关注公众号,干货第一时间送达
今天来点不一样的!
一、各位,请听题

题意要是没懂的话,看下面的示意图。
示意图:
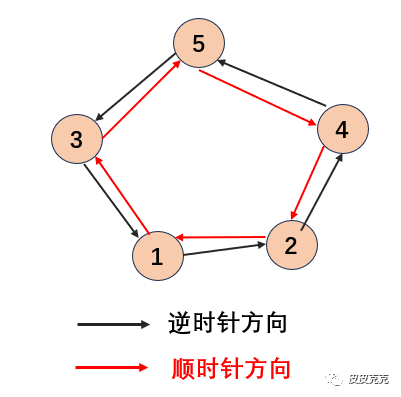
(1)相邻的山峰有 {1,2}、{2,4}、{4,5}、{3,5}、{1,3} 这些山峰相互可见
(2)山峰3,沿着逆时针,经过1,2两座山峰,因为1,2山峰都比3低,所以可以经过然后到达山峰4。即表示山峰3在逆时针方向上可以看到山峰4;相反,山峰4在顺时针方向可以看到山峰3。
但是山峰3沿着顺时钟方向呢? 下一个是山峰5,是过不去的,挡住了后面的视线,所以顺时针方向山峰3和山峰4不可见。
这就是题意了。
怎么求?
小编我刚开始看的时候也是一脸懵,
无从下手啊!
小编曾有一瞬间,想用穷举法穷举出来答案
可是,如果山峰很多呢?
让你穷举
二、解题
用单调栈!
(之前的文章:数据结构和算法【7】单调栈 2 有详细介绍单调栈,可以点击翻看一下)
我们可以先遍历给定数组arr,数组肯定有最大值,并且最大值可能不止一个,我们任意选取一个即可。
然后开始沿着一个方向上,找下一个山峰,如果下一个山峰的高度小于当前山峰,我们就把下一个山峰记录到栈中;如果下一个山峰的高度大于当前山峰,我们就弹出栈顶山峰。
重点来了!
弹出的山峰,离它最近且比它大的山峰,是不是就是下一个山峰?
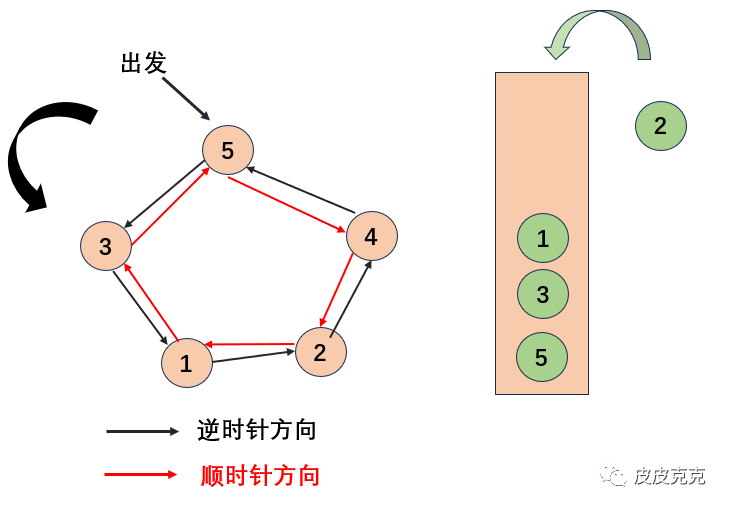
此时,会弹出山峰1,压入山峰2,而对于山峰1来说,它可见的只有山峰2和山峰3,山峰2是当前遍历的元素,山峰3是栈顶元素,都是直接可得的。
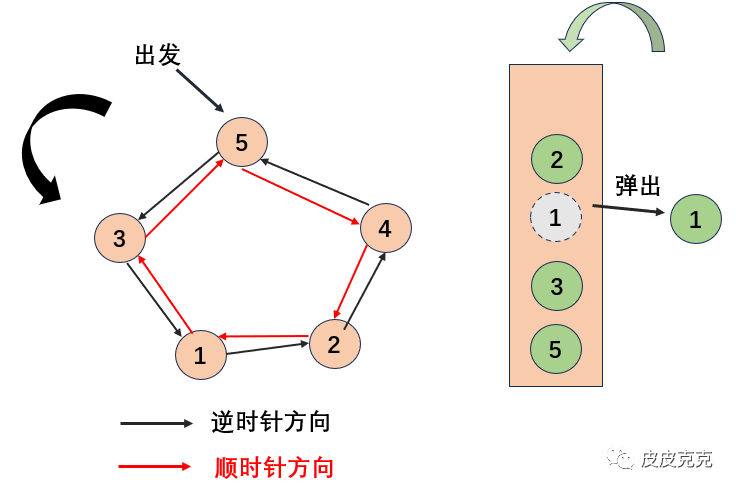
最后清算栈即可,单调栈方法的详解在之前的文章:数据结构和算法【7】单调栈 2里有的,这里不再赘述。
对于本题,我们再加一个变量,用来记录山峰出现的次数,因为可能有山峰高度一样。
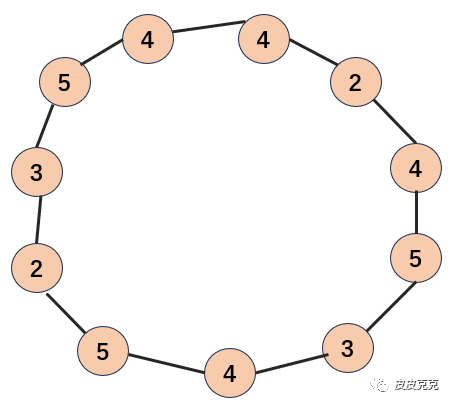
比如下面这个 :
:

如果有山峰高度一样,这些山峰内部是相互可见。
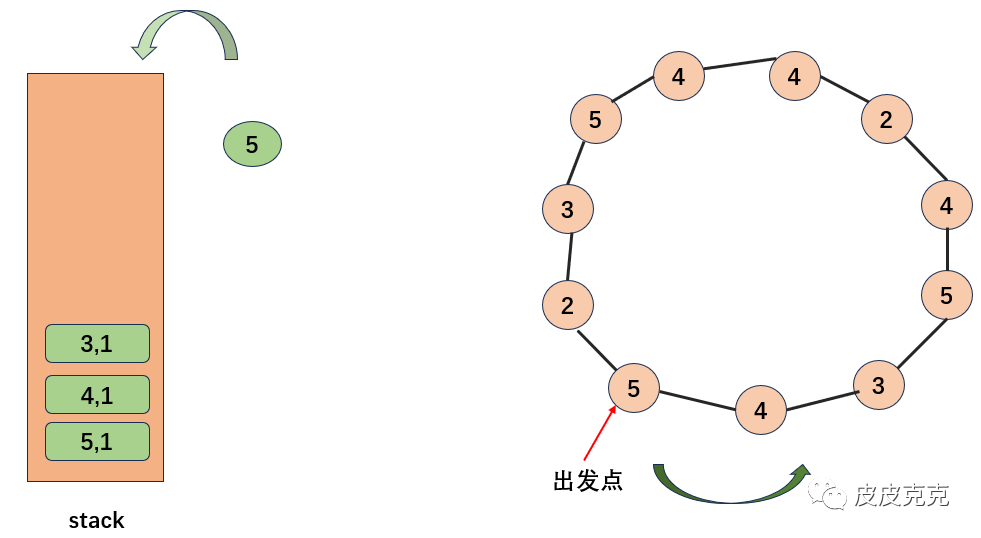
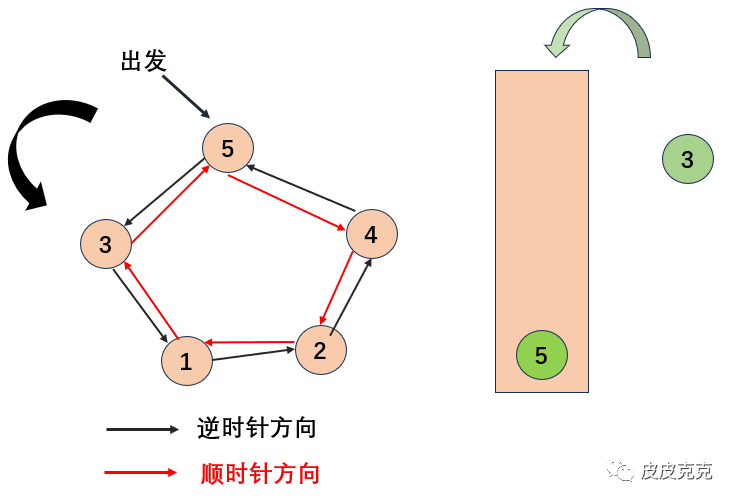
此时,弹出山峰3,山峰3可见的,只有当前的山峰5,和栈顶的山峰4。再弹出山峰4,山峰4可见的,只有当前的山峰5,和栈顶的山峰5。然后山峰5,次数加1。
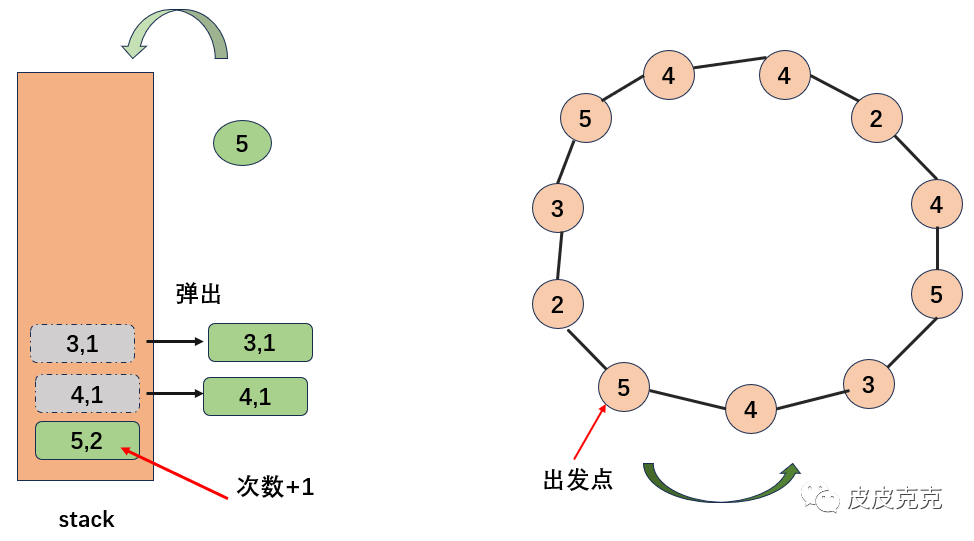
但是!如果弹出的时候,弹出山峰的次数不是1呢?
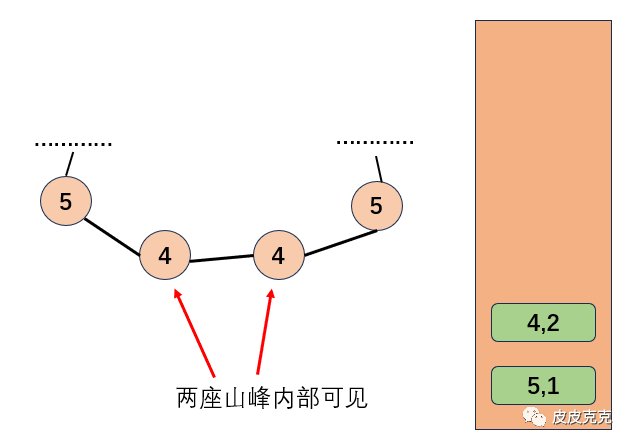
两座山峰4相互可见,出现次数一共是2,两座山峰4相互可见,也可以看见外部的,则总数是:2*2 + C(2,2) = 5对。
如果是3座山峰4呢? 2*3 + C(2,3) = 9对。
最后,清算栈的时候注意分3个阶段,代码里面有注释。
去看看吧。
完整代码:
public class CodingDemo {
/**
* TODO: 计算可见山峰对数
* @param arr
* @return
*/
private static int getVisibleMount(int[] arr){
if (arr == null || arr.length < 2){
return 0;
}
//1,找到任意最大值节点
int N = arr.length;
int maxIndex = 0;
for (int i = 0; i < N; i++) {
maxIndex = arr[maxIndex] < arr[i] ? i : maxIndex;
}
//2, 创建栈,先把找到的最大值节点存入
Stack<Record> stack = new Stack<Record>();
stack.push(new Record(arr[maxIndex]));
//3, 从最大值节点,开始逆时针旋转到下一个节点
int index = getNextIndex(maxIndex, N);
int res = 0;//结果值
//4, 开始遍历
while (index != maxIndex){
//4.1 比较遍历的节点,和栈顶val大小
while (stack.peek().val < arr[index]){
//弹出栈顶,获取这个元素出现的次数
//通过排列组合计算可见山峰对数
int k = stack.pop().times;
res += 2*k + combine(k);
}
//4.2 如果当前元素等于栈顶val,则栈顶times加1,否则新建记录Record
if (stack.peek().val == arr[index]){
stack.peek().times++;
} else {
stack.push(new Record(arr[index]));
}
//4.3 继续下一个遍历
index = getNextIndex(index, N);
}
//5,开始清算栈
//5.1 第1阶段,
while (stack.size() > 2){
int k = stack.pop().times;
//栈顶元素顺时针,逆时钟分别可以预见较高的山峰,然后栈顶元素val内部相互可见
res += 2*k + combine(k);
}
//5.2 第2阶段,需要判断弹出栈顶后,栈中剩下的山峰出现了几次,
// 如果是1次,则表示从顺时钟和逆时针看到是同一个山峰,则取 k
// 如果不是1次,则表示从顺时针和逆时针看到的不是同一个山峰,取 2*k
if (stack.size() == 2){
int k = stack.pop().times;
res += combine(k) + (stack.peek().times == 1 ? k : 2*k);
}
//5.3 阶段3,处理栈最后一个元素
res += combine(stack.pop().times);
return res;
}
//排列组合公式C(x,n) 的简化
private static int combine(int k){
return k == 1 ? 0 : (k * (k-1)/2);
}
//获取当前i位置节点的下一个位置,因为是环,需要考虑超出数组边界的情况
private static int getNextIndex(int i, int size){
return i < (size-1) ? (i+1) : 0;
}
private static class Record{
int val;
int times;
public Record(int val) {
this.val = val;
this.times = 1;
}
}
public static void main(String[] args) {
// int[] arr = {5,4,3,5,4,2,4,4,5,3,2};
int[] arr = {3,1,2,4,5};
System.out.println(getVisibleMount(arr));
}
}
输出:
D:\java\bin\java.exe
7







