点击关注公众号,干货第一时间送达
各位,请听题:

解题:
毫无疑问,经典汉诺塔问题的解法是递归,各位肯定都会。
但是,该题目要求不能使用递归,且左侧柱子的盘子不能直接移动到右侧柱子,必须经过中间,那么就有点意思了。
我们可以采用栈!
大盘子不能压在小盘子上面,可以通过栈的单调性来解决,每当前面的栈弹出盘子 pop,准备压到当前栈顶时候,需要先判断pop 和当前栈顶head的大小关系,只有小于的时候才允许执行。
且从左侧移动到右侧,必须经过中间,那么我们将移动拆分成4步:
LeftToMid,MidToLeft,MidToRight,RightToMid
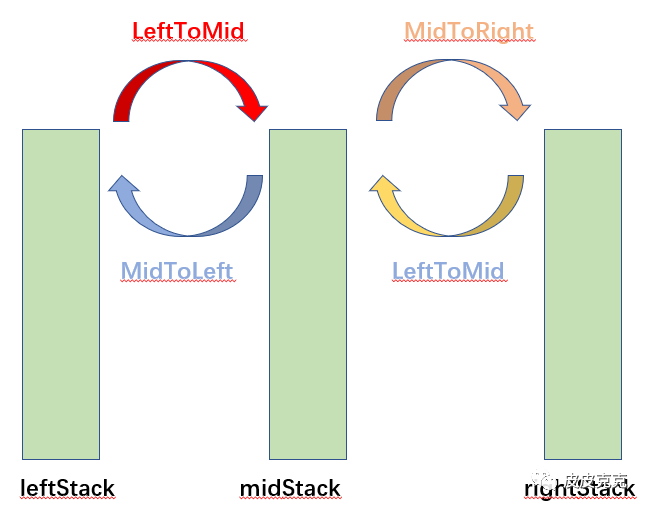
这里,还需要再介绍一个原则:相邻不可逆
例如:LeftToMid 和 MidToLeft 是相逆的;
MidToRight 和 RightToMid 是相逆的;
想达到最优步骤,如果上一步是 LeftToMid,那么当前这一步就肯定不能是 MidToLeft,因为这样毫无意义!
那么就要求我们在程序执行过程中,需要遵循相邻不可逆性。
通俗的讲,就是上一步和当前这一步不能相逆。
此外!
而我们定义的操作有4种:LeftToMid,MidToLeft,MidToRight,RightToMid
在最优步数程序执行中,4个动作只有1个不违法上述原则,其他3个动作均违规。
证明:
最开始盘子肯定放在左侧柱子,第一步动作是 LeftToMid,后面的每一步都有前一步操作。
1)假设前一步是 LeftToMid:
a. 根据大盘不能压小盘原则,LeftToMid 肯定不能重复发生
b. 根据相邻不可逆原则,MidToLeft 肯定不能发生
c. 根据 大盘不能压小盘原则,MidToRight 和 RightToMid 只有一个合规
2)假设前一步是 MidToLeft:
a. 根据大盘不能压小盘原则,MidToLeft 不能重复发生
b. 根据相邻不可逆原则,LeftToMid 不能发生
c. 根据大盘不能压小盘原则,MidToRigth 和 RightToMid 只有一个合格
同理,其他步骤也是如此,每次走,4种选择只有一张合规。那么根据这个性质,判断所有步骤,记录合规的步骤,即可。
为了大家方便学习交流,小编把递归和非递归使用栈的的代码都直接附上。
一、递归方法代码
public class CodingDemo {
public static void hanoi2(int num){
p(num, "LEFT", "MID","RIGHT");
}
public static void p(int num, String left, String mid, String right){
if (num == 1){
System.out.println(left + " to " + right);
return;
}
p(num-1, left, mid, right);
System.out.println(left + " to "+ right);
p(num-1, mid, right, left);
}
public static void main(String[] args) {
hanoi2(3);
}
}
输出:
D:\java\bin\java.exe
LEFT to RIGHT
LEFT to RIGHT
MID to LEFT
LEFT to RIGHT
MID to LEFT
MID to LEFT
RIGHT to MID
二、非递归使用栈方法代码
public class CodingDemo {
/**
* TODO:用栈实现汉诺塔
* @param num
* @return
*/
public static int hanoi(int num){
//1,创建三个栈,分别表示左 中 右 三个柱子
Stack<Integer> leftStack = new Stack<Integer>();
Stack<Integer> midStack = new Stack<Integer>();
Stack<Integer> rightStack = new Stack<Integer>();
//2,栈顶压入最大值,用于初始
leftStack.push(Integer.MAX_VALUE);
midStack.push(Integer.MAX_VALUE);
rightStack.push(Integer.MAX_VALUE);
//3,初始化左柱子
// 盘子最开始是全部从从上到下按照从小到大的顺序放在左柱子的
for (int i = num; i > 0; i--) {
leftStack.push(i);
}
//4,开始移动
int step = 0;//移动次数
Action[] moveRecord = { Action.No };//初始移动
while (rightStack.size() != num+1){//终止条件是右柱子上面的盘的个数等于num
step += move(moveRecord, Action.MidToLeft, Action.LeftToMid, leftStack, midStack,
"LEFT","MID");
step += move(moveRecord, Action.LeftToMid, Action.MidToLeft, midStack, leftStack,
"MID","LEFT");
step += move(moveRecord, Action.RightToMid, Action.MidToRight, midStack, rightStack,
"MID","RIGHT");
step += move(moveRecord, Action.MidToRight, Action.RightToMid, rightStack, midStack,
"RIGHT", "MID");
}
return step;
}
/**
* 汉诺塔移动
* @param moveRecord 盘子移动记录,moveRecord[0] 记录了上一步是怎么移动的
* @param preAction 上一步如果移动
* @param nowAction 当前这一步如何移动
* @param fromStack 盘子从哪个柱子来
* @param toStack 盘子要到哪个柱子去
* @param from 来时柱子字符串表示, 用于打印
* @param to 去时柱子字符串表示。 用于打印
* @return
*/
public static int move(Action[] moveRecord, Action preAction, Action nowAction,
Stack<Integer> fromStack, Stack<Integer> toStack,
String from, String to){
if (moveRecord[0] != preAction && fromStack.peek() < toStack.peek()){
toStack.push(fromStack.pop());//移动
System.out.println("Move: 【"+toStack.peek() + "】 from "+ from + " to " + to);
moveRecord[0] = nowAction;//记录这一步,为下一步提供[0]判断
return 1; //表示当前移动有效,是一步
}
return 0;//表示当前移动无效,这一步不算
}
public enum Action{
No, LeftToMid, MidToLeft, MidToRight, RightToMid
}
public static void main(String[] args) {
System.out.println(hanoi(3));
}
}
输出:
D:\java\bin\java.exe
Move: 【1】 from LEFT to MID
Move: 【1】 from MID to RIGHT
Move: 【2】 from LEFT to MID
Move: 【1】 from RIGHT to MID
Move: 【1】 from MID to LEFT
Move: 【2】 from MID to RIGHT
Move: 【1】 from LEFT to MID
Move: 【1】 from MID to RIGHT
Move: 【3】 from LEFT to MID
Move: 【1】 from RIGHT to MID
Move: 【1】 from MID to LEFT
Move: 【2】 from RIGHT to MID
Move: 【1】 from LEFT to MID
Move: 【1】 from MID to RIGHT
Move: 【2】 from MID to LEFT
Move: 【1】 from RIGHT to MID
Move: 【1】 from MID to LEFT
Move: 【3】 from MID to RIGHT
Move: 【1】 from LEFT to MID
Move: 【1】 from MID to RIGHT
Move: 【2】 from LEFT to MID
Move: 【1】 from RIGHT to MID
Move: 【1】 from MID to LEFT
Move: 【2】 from MID to RIGHT
Move: 【1】 from LEFT to MID
Move: 【1】 from MID to RIGHT
26
Process finished with exit code 0







