点击关注公众号,干货第一时间送达
这是一道力扣标注为 "困难" 的题:
算是这一类题型中的经典。
学会了,你就更牛掰了。
其实,
小编之前的文章:数据结构和算法【9】最大子矩阵的大小
和这题非常类似
ok,话不多说,咱们看看这道题。
力扣原题链接:
https://leetcode.cn/problems/largest-rectangle-in-histogram/description/
一、各位,请听题

举个例子:
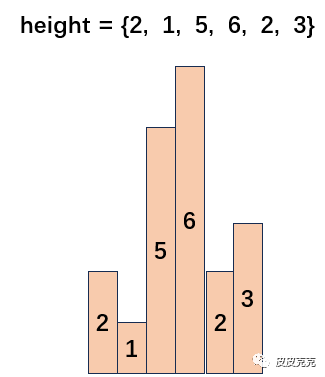
这个柱状图中,最大矩形是哪部分呢?
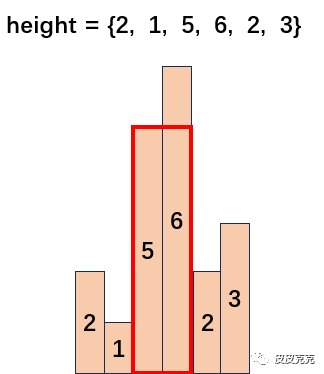
就是红框的这部分,这个矩形面积就是 area = 2*5 = 10。
怎么求解呢?
有了解过 单调栈 吗?
没有的话,
可以翻看一下小编之前的文章:数据结构和算法【7】单调栈 2
这类题的解法就是利用单调栈。
二、解题
矩形的面积,是 底 * 高,
底,就是多少个柱子;
而高,取决于有多少柱子的高度可以相等,
也就是取决于最小高度的柱子。
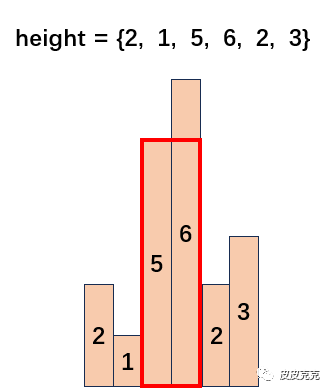
就像上面,红色框的矩形,高度是由 5柱子决定的,而不是6柱子。
如果我们可以计算出,每个柱子向左和向右能够延伸多远,这个延伸距离就是底,
再乘 高,就是矩形的面积了。
延伸距离取决于什么?
取决于每个柱子,左右两侧,小于这个柱子的最近的柱子。
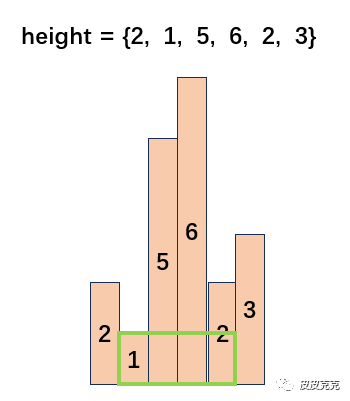
比如柱子5,左侧比5小且最近的是1,右侧比5小且最近的是2
这分别是左右两侧的边界,边界不取,取边界里面的值。
也就是 (1, 2) ,矩形面积就是柱子5和柱子6公共的部分,也是最大的矩形面积部分
然后,计算每根柱子能延伸的距离,求出最大面积即可。
这个过程,利用的就是单调栈。
对单调栈不熟悉的吴彦祖和刘亦菲们,
建议翻看一下小编之前的文章:数据结构和算法【7】单调栈 2 里面有详细介绍。
看看代码。
完整代码:
public class CodingDemo {
/**
* TODO: 柱状图中最大的矩形
* @param heights
* @return
*/
private static int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0){
return 0;
}
//结果值
int res = 0;
//1, 创建栈,
Stack<Integer> stack = new Stack<Integer>();
//2,遍历高度数组
for (int i = 0; i < heights.length; i++) {
while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
//2,1 弹出栈顶
int pop = stack.pop();
//2.2 此时的栈顶
int top = stack.isEmpty() ? -1 : stack.peek();
//2.3 计算延伸面积
int area = heights[pop] * (i - top -1);
//2.4 取最大值
res = Math.max(res, area);
}
//把当前i,压入栈顶
stack.push(i);
}
//3,清空栈
while (!stack.isEmpty()){
//相同的步骤
int pop = stack.pop();
int top = stack.isEmpty() ? -1 : stack.peek();
int area = heights[pop] * (heights.length - top - 1);
res = Math.max(res, area);
}
return res;
}
public static void main(String[] args) {
int[] arr = {2,1,5,6,2,3};
System.out.println(largestRectangleArea(arr));
}
}
输出:
D:\java\bin\java.exe
10
去力扣试试:

文章转载自皮皮克克,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






