摘要:随着技术的进步和社会化大生产的发展,出现了许多可靠、寿命长、长期在线使用或多种操作状态交替的复杂工程设备系统。一旦发生小型局部故障,可能会导致灾难性后果。因此,预测设备的剩余使用寿命是一个重要的工程问题。对于设备的剩余寿命预测,应用一维布尔双参数分布模型和对偶威布尔分布模型来描述设备的寿命特性,并使用模拟退火算法来估计设备寿命威布尔分布的未知参数。实验结果证明了该方法的有效性和准确性。
1、介绍
据不完全统计,全球机械事故约占事故总数的1/3。每年因机械产品安全而造成的人员伤亡和财产损失都在增加。特别是对于连续不间断运行的设备,必须确保其部件,特别是关键部件的高可靠性。当系统由于关键部件的损坏而损坏,导致系统无法工作时,除了高昂的维护成本外,还会因设备停止工作而带来间接损失。
基于物理模型的预测方法基于降解过程中材料物理行为的数学模型来估计剩余使用寿命。不同的物理故障机制对应于不同的物理模型。
基于知识的预测方法基于现有的技术知识和各种推理方法来预测设备的故障时间。这种方法不需要预先对设备的寿命进行特定的建模。主要的应用方法是模糊逻辑和专家系统。
基于数据驱动的设备故障预测建立在不同的统计模型理论之上。通过对设备历史故障数据和现有观测数据的剩余寿命预测,经典的预测方法有深度神经网络和灰色理论模型、马尔可夫链模型等。
基于统计经验的数学模型是通过大量的设备寿命测试来获得产品的失效数据。然后,根据统计分析的标准,选择合适的寿命统计分布模型来拟合故障数据,从而获得产品寿命的特征分布。与其他三种方法相比,基于统计经验的数学模型需要最少的先验信息,基于类似事件的概率分布,如指数、威布尔分布和正态分布。
在正常情况下,结构更复杂的机电设备的寿命分布函数与电子产品的寿命分布相似,大多服从指数分布。然而,实践证明,只有少数复杂机电产品服从指数分布,大多数产品服从威布尔分布。通过对威布尔分布的研究,指数分布只是一种特殊的形式。目前,威布尔分布广泛应用于机械制造、生命科学和航空航天领域。
2、问题描述
将Et设置为武器装备组件在t时刻的损伤因子。Et是一个综合指标,它考虑了武器部件的损坏状态、结构的重要性、维护成本等。
其中,Et 0表示武器部件完好无损。EE ft(E f可由专家根据工程经验给出,假设E f 7.0)表示武器装备部件的使用寿命终止。Et 1代表武器装备被完全摧毁。
在某型武器装备管理中,有必要定期测试其关键部件的综合性能指标。两次连续测试之间的间隔为15天。当综合性能指标达到故障阈值时,部件的寿命结束,必须更换。对现役武器装备部件剩余寿命分布的预测对于后期采取有效的维修保养措施非常实用。
在对某一部件寿命的实际调查中,记录了该设备240个全寿命部件的测试数据。分析该类设备关键部件的寿命分布规律,并对其可靠性进行分析。
3、模型的建立与解决方案
A.关键部件寿命数据的趋势观察
如图1所示,本文首先观察了240种关键成分从使用开始到使用寿命结束的分布趋势。在使用之初,关键部件的寿命测试数据相对稳定。在60-80次测试间隔(间隔15天)后,寿命测试数据开始显著上升。
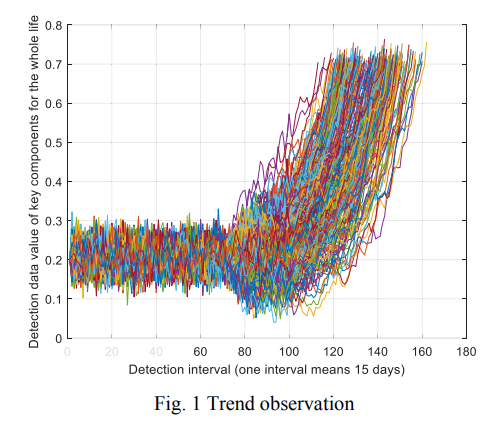
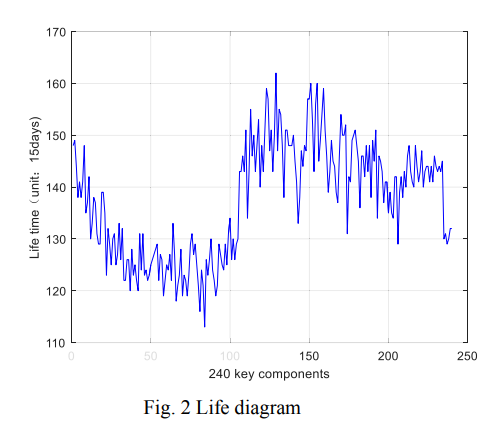
如图2所示,我们绘制了240个关键部件的使用寿命。观察近似的寿命分布,很难直观地给出寿命的分布。因此,我们计算了关键成分累积时间的经验分布函数。
1) 总失效时间的经验分布函数
定义:当关键部件的综合性能指标达到失效阈值E f 7.0时,该部件结束其寿命。在这一点上,它可以表示为一个失败的组件。
假设i表示第i个时间间隔。其中,i表示162个时间间隔,每个时间间隔相隔15天。
假设每个时间间隔内发生故障的关键部件的数量为。i n那么,在累积时间内发生故障关键部件的编号为:

因此,关键部件的累积失效概率为:

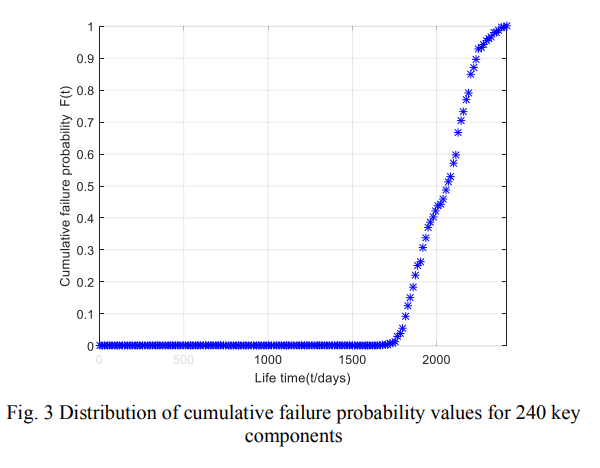
从图3中可以看出,关键部件累计失效时间的分布函数先呈稳定趋势,经过一定时间后呈上升趋势。根据数理统计[17],正态分布、对数正态分布和指数分布的分布函数都是可能的,而威布尔分布的分布功能在故障诊断的寿命中尤为突出,指数分布可视为威布尔分布中的特殊形式,因此假设这一关键分量的数据服从威布尔分布
B.一维布尔模型的建立与求解
1) 一维布尔双参数分布模型
累积概率分布函数为:
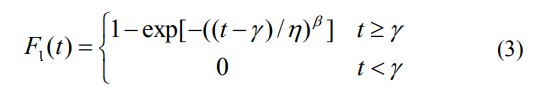
其中η表示标度参数,η>0;β表示形状参数,β>0;γ表示位置参数,γ≥0。
相应的密度函数为:
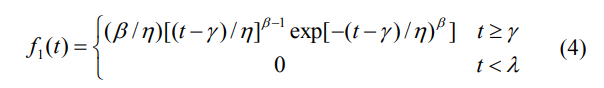
在实际应用中,通常假设t=0时的分量无效,即η>0。
从而可以将三参数威布尔分布简化为两参数威布尔分配,即:
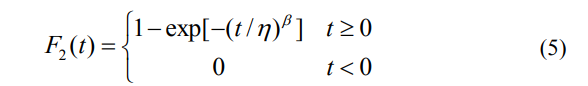
相应的密度函数为:
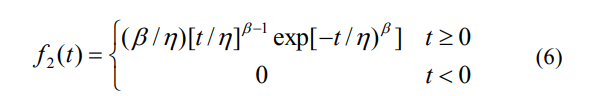
2) 一维布尔双参数分布模型的求解
这里,使用模拟退火算法来优化240个关键部件的累积故障概率值的分布。
模拟退火算法源自统计热物理,模拟在熔融状态下将物体缓慢冷却到结晶状态的物理过程。它是一种通用的概率算法,避免了陷入局部最优和对初始值依赖性不强的特点。它在生命科学和地理探测领域获得了应用方法。
具体步骤如下:
步骤1:初始化:
设当前温度T=T0,即开始退火的初始温度。随机生成初始解x0,并计算相应的目标函数值E(x0)。
步骤2:设T等于冷却计划的下一个值Ti
步骤3:在当前解决方案xi的基础上生成新的解决方案xj。并计算相应的目标函数值E(xj),得到△E=E(xj)-E(xi)。
步骤4:如果△E>0,则接受新的解xj作为新的解;如果△E<0,则通过概率exp(-△E/Ti)(Metropolis准则)接受新的解xj,Ti是当前温度。
步骤5:在温度Ti下,重复Lk扰动和接受过程(Lk为马尔可夫链的长度),即执行步骤3和步骤4。
步骤6:判断温度T是否等于Tf。若相等,则终止算法;否则,请转至步骤2并继续。
基于单向布尔分布模型,采用模拟退火算法求解两个未知参数问题。一个序列被视为一个解决方案。每个解对应于一个目标函数值,并与实际值进行误差测试。经过两次交换,三次交换并继续生成新的解来搜索解空间,然后我们就可以找到最优参数解。
单向布尔分布的模拟模型参数通过模拟退火优化算法求解:η=2109.3, β=13482.8
因此,拟合了最佳单向布尔模型函数:
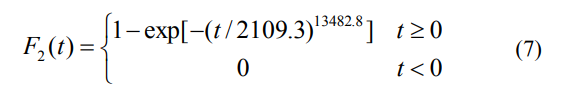
240个关键部件的累积寿命概率和拟合值如图4所示:
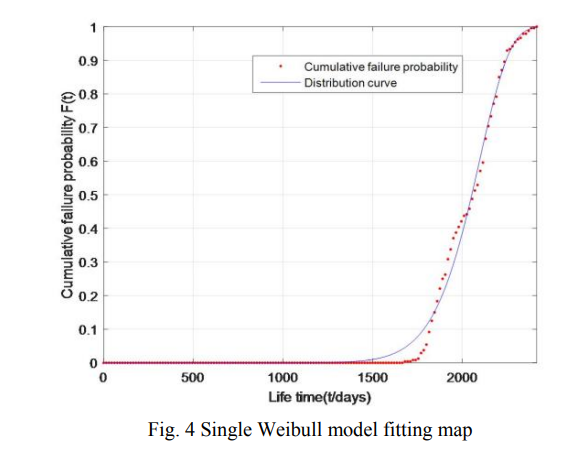
如图4所示,本文优化了240个关键部件的累积失效概率值分布,并找到了单向布尔分布模型。发现拟合效果不是很好。变换后的无效数据点与拟合曲线之间存在较大的间隙。故障数据的散点图具有拐点,方程(3-5)所示的威布尔分布是没有任何拐点的曲线。因此,如果用它来拟合具有拐点的故障数据,会在拐点处产生较大的误差,不利于进一步分析部件故障原因和故障机理。
由于收集的数据来自实际加工现场,因此数据相对可靠。那么故障数据曲线的拐点意味着检测到的故障数据包含不同的故障特征。分布曲线不能完全用平滑曲线来表示,而应该用由两条或多条简单分布曲线组成的复杂模型来表示。典型的复杂模型有竞争风险模型、并行模型和混合模型。
因此,本文对模型进行了相应的改进,建立了对偶威布尔模型.
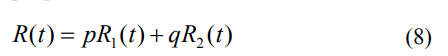
其中t≥0,0≤p≤1,p+q=1。
R1(t)和R2(t)是简单的两参数威布尔分布,其为:
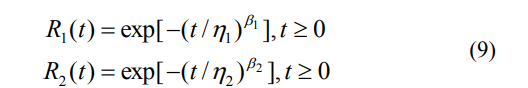
此时的双威布尔分布模型为:
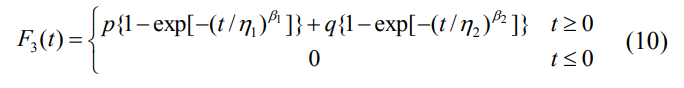
其中,β1、β2为形状参数;η1、η2为标度参数
此时,仍然使用模拟退火优化算法来解决问题并修改相应的优化目标函数: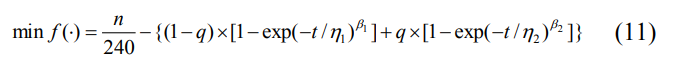
二维布尔分布的拟合模型参数通过模拟退火优化算法求解: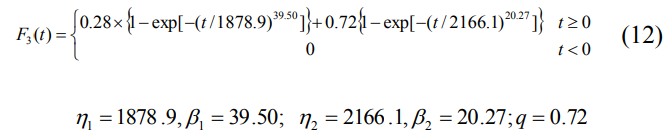
因此,拟合了最佳的双布尔模型函数:
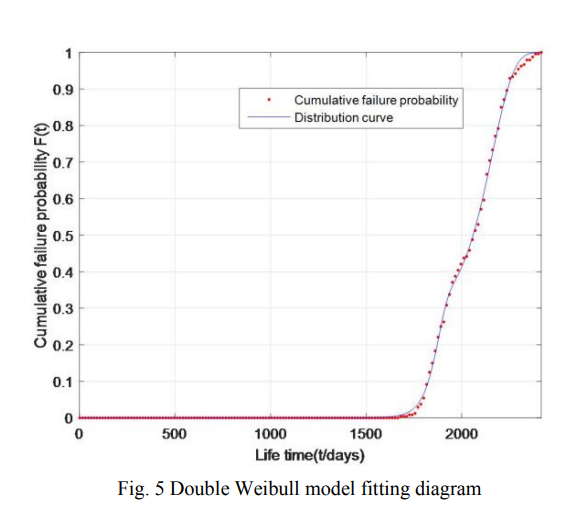
图5总结了240个关键部件的累积寿命概率和拟合值。
从图4和图5可以清楚地看出,双威布尔分布模型的拟合效果优于单布尔分布模型。
D.拟合优度测试
为了进一步验证分布模型的可靠性,本文基于误差平方和计算样本数据的观测值与拟合模型的计算值之间的差值。
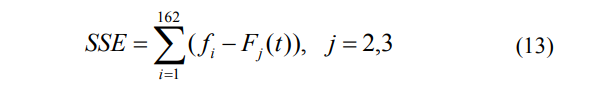
其中F2(t)表示单个Weibul分布;
F3(t)表示双威布尔分布。
f=1,2,3,……,162表示关键部件的累计失效概率。
使用Matlab求解单威布尔和双威布尔模型的误差之和,如下表1所示。

如表1所示,进一步验证了改进后的模型:对偶威布尔分布模型的优越性。
5、结论
与指数分布相比,单威布尔分布和双威布尔分布更能真实地反映武器装备系统的寿命特征。对于实例分析的武器装备部件,使用双威布尔分布来描述系统的使用寿命,以便维修人员能够合理安排维修计划,并提前采取更换策略,以确保设备的可用性。本文采用模拟退火算法对设备威布尔分布的未知参数进行估计,为预测设备系统的剩余寿命奠定了基础。结果表明,该方法接近构件的实际剩余寿命,也表明了该方法的有效性。






