大家好，今天很高兴能够在这里跟大家分享一下我们在几何深度图学习（Geometric Deep Graph Learning）方面的工作。

1. 图计算模型优势及发展基础模型的挑战

大语言模型这几年来很火，大家都试着用大语言模型来做各种应用。在此背景下图模型是否还有用？事实上，图模型有它自己的优势，比如图模型可以抓到实体之间的关系。用大语言模型就很难做到这一点，因为大语言模型不太了解图的构造或者多跳推理，因此，大语言模型不能够取代图模型。举个例子来说，在推荐场景，图模型可以用协同过滤来发现用户之间的共同喜好，而大语言模型就很难做到。

图模型有继续存在的价值，那我们也要问，图模型能否发展出一个通用的基础模型？
大语言模型优势是经过训练，可以应用到各个不同的方面，不只是总结，还可以用于问答、翻译等等。但图模型基本上每一种应用都需要训练一个不同的模型。在图模型方面，能否做一个通用的基础模型？实际上有困难，因为不同的应用，图的构造是非常不同的。但如果只聚焦在一个应用方面，比如推荐场景，是可以实现跨市场和跨领域的商品推荐这样的泛化能力。所以要思考的第一个问题：当前基于图神经网络（ GNN）的图模型解决方案是否足够强大，能够作为图基础模型的基座呢？

以推荐领域为例。使用图模型来做基础的推荐模型，首先可以跨区域通用。比如一个公司，在北美的市场上建立了一个推荐模型，需要到其他市场推广，把北美训练的图模型找一些参数来做模型调优，就可以用在不同地域市场并且都有相当好的效果。

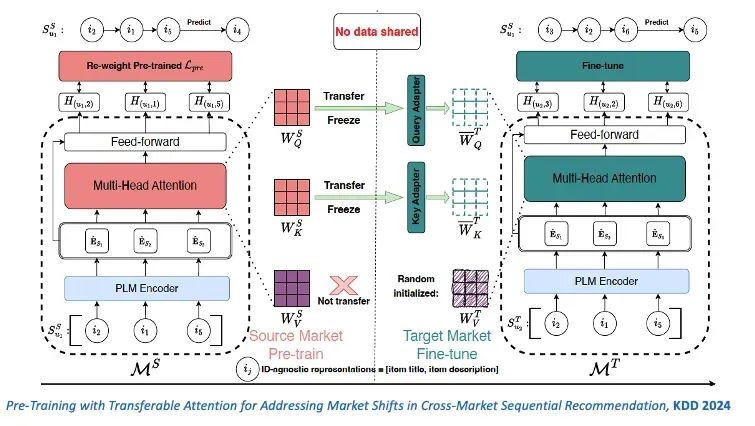
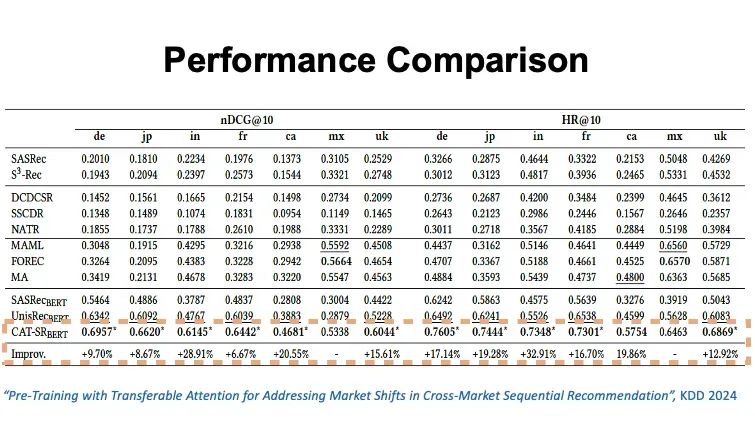
同时，推荐模型可以跨领域应用，例如从音乐推荐转向电子产品推荐，尽管推荐的物品不同，但用户是具有共性的。当然这也比较具有挑战。为此，在进行模型调优时，需要利用语言模型给出特定的指令，来根据不同产品的特性来调优。例如，我们在音乐领域训练了一个模型，再给它指令如何去训练针对电子产品领域的模型，最终也取得了不错的效果。由此可见，在某些特定领域里面，我们是有可能训练出一个基础模型的。

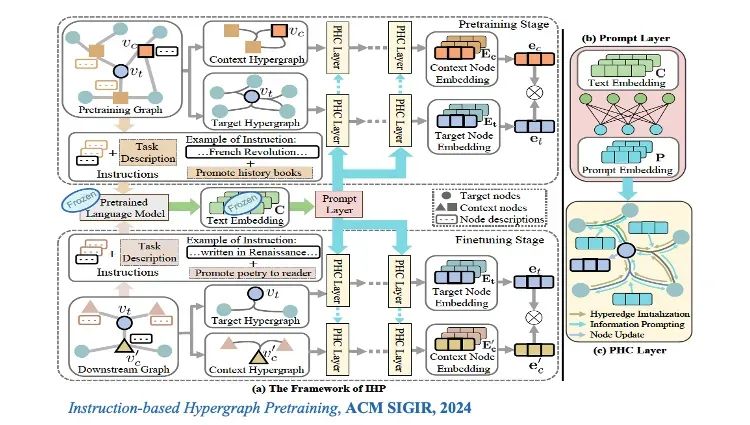
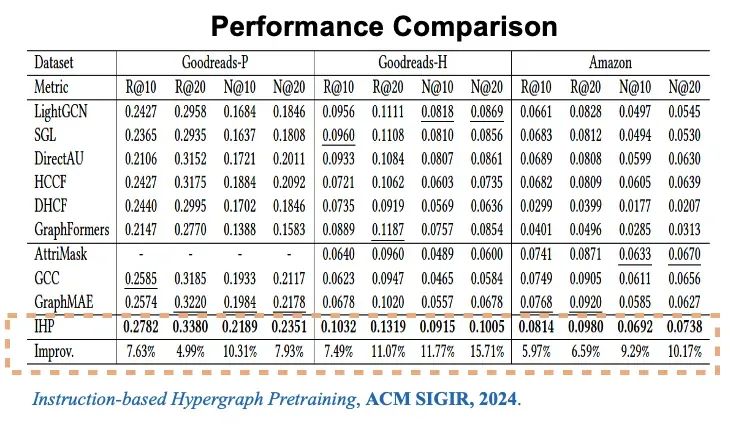
但如果进行通用训练，比如将训练的社交网络模型应用于知识图谱或生物领域，可能不太行得通，问题出在哪里呢？

基本上，图是一个非欧氏空间的空间构造。然而，解决图的问题时，大家都在使用图神经网络（GNN)。尽管图神经网络有各种变化，但无论如何变化，它们仍然在进行节点聚合。然而，这些方法主要是在欧氏空间（欧几里得空间）内进行，而忽略了图作为非欧氏空间的特性。

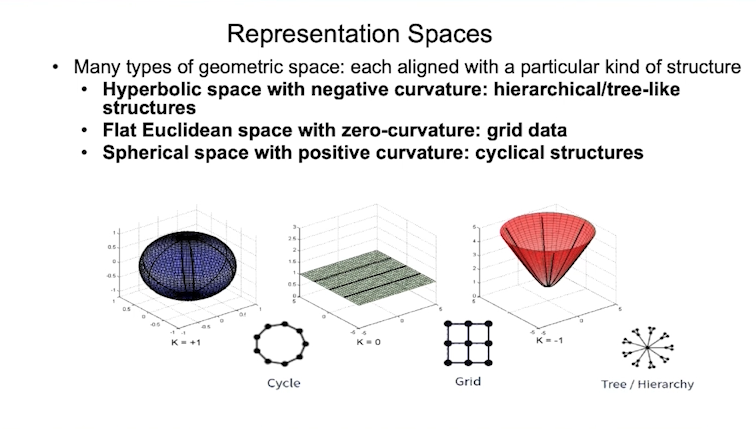
我们需要仔细考虑图的结构，比如在图中可能有分层结构或类似树状的结构。那么我们如何评估一个图有多像一棵“树”呢？事实上，这里有一个变量叫做δ——超曲率。如果δ的值较小，则表示其接近树状结构或层次性结构；较大则表示它有可能更趋于自由结构。我们看树形结构，它的δ值是零；在超几何空间中，它的δ范围也很小；然而在欧氏空间中，这个δ范围则非常大，几乎无穷大。像DBLP、Twitter这样的图，它们的δ值都非常小，基本上表明它们具有一定层次的结构。由此可见，与欧氏空间相比，双曲空间（Hyperbolic space）更符合这种分层结构。如果一个图是循环结构（Cyclical structure），那么我们可以用超球空间（Hyperspherical space）来表示它。总的来说，基本上存在着3种不同的空间：

• 双曲空间（Hyperbolic space），曲率为负数，可以代表分层/树形结构；（图右侧红色）

• 欧氏空间（Euclidean space），曲率为零，适合表示网格结构；（图中间绿色）

• 球面空间（Spherical space），曲率为正数，用于表示循环结构。（图左侧蓝色）

4.混合曲率空间提供图基础模型研究新方向

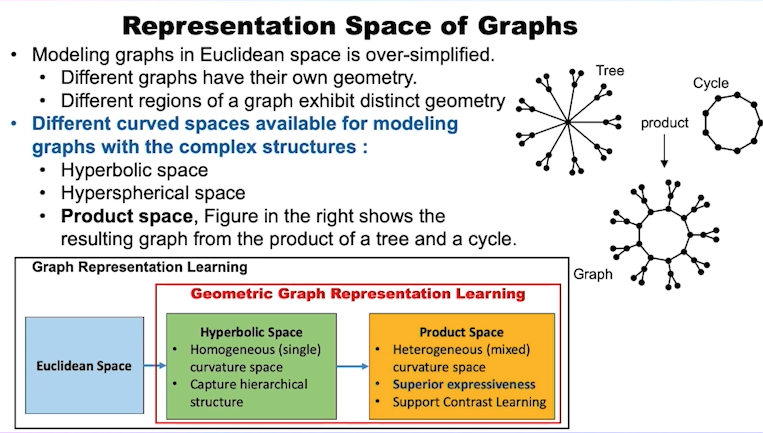
不同的图具有不同的结构，有的接近树状结构，有的接近循环。实际上，即使是在同一个图上，不同部分的结构也可能不同。因此，仅用单一的空间来表示可能不够理想，可以使用乘积空间来表示，以增加灵活性。例如把一个双曲空间（Hyperbolic space）做乘积。虽然双曲空间可以有效捕获层级结构，但它存在单一曲率的限制，如果用乘积空间来表示，就可以得到混合的曲率空间，这样不仅可以得到更好的表达，还能进行对比学习。这样，就可以在每个组成部分空间中计算距离，并将它们结合起来。总体来说，乘积空间（product space）为比较和学习图的不同部分提供了更好的框架。

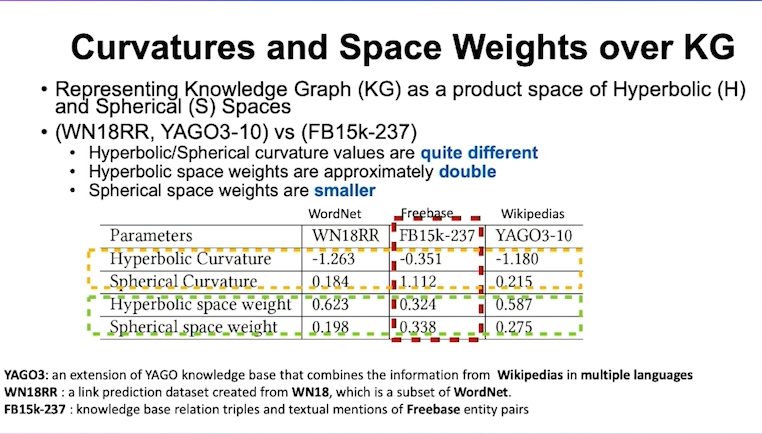
以知识图谱为例，尽管知识图谱看似相似，但实际上它们之间存在差异。例如，Freebase、WordNet和Wikipedia这三个不同的知识图谱，如果我们把这些图解构为双取空间和球面空间的乘积的话，Freebase与WordNet和Wikipedia是不同的。因为Freebase的双曲曲率小很多，但其球面曲率值较大，它的权重也不同。这表明，在构建基础图模型时，将WordNet转移到Wikipedia的可能性较高，而转移到Freebase的成功率较低，因为与Freebase的图构造不同。

对于任意的图，如CiteSeer（一个图书文献搜索引擎） 或机场的航线图，通过将其分解为多个空间的乘积，可以发现它们之间的结构差异。例如，机场航线图在双曲空间中的曲率比CiteSeer大得多，这表明其结构层次更深。

因此，使用混合曲率空间来表示这些图，提供了一种量化表示图结构的方法，这为构建图的基础模型提供了一个新的方向。

5.混合曲率空间具有显著优势及效果

无需外部标签

传统的图神经网络训练需要依赖于有标签的数据。然而，在混合曲率空间中，我们可以利用不同的曲率空间作为多个视图，通过对比学习来训练模型，而无需数据标注。这种方法称为自监督学习（self-supervised learning），它允许模型通过观察数据之间的相似性来学习，而不需要依赖于预先定义的标签。

拆解图聚类，得到曲率

通过将图按不同的组成空间拆分，分解为更多的空间，并在这些空间上进行对比学习，可以显著提高模型的精度。每个空间都有不同的曲率，这有助于我们更好地理解和处理数据。即使不使用标签，这种方法也比在欧氏空间中进行有监督学习或自监督学习的效果要好，可以更精确地捕捉数据的结构和关系。

使用黎曼曲率判断图聚类边界

在混合曲率空间中，优势在于节点间的连接可以通过不同的曲率来表示。在传统的欧几里得空间中，两个节点要么连接（值为1），要么不连接（值为0）。而在混合曲率模型中，连接两个节点的边可以通过一个正数或负数来表示。正数意味着节点之间非常接近，应该被归为同一组；而负数则表示它们应该分开。这个特性有助于我们确定簇边界（determine the cluster boundary）

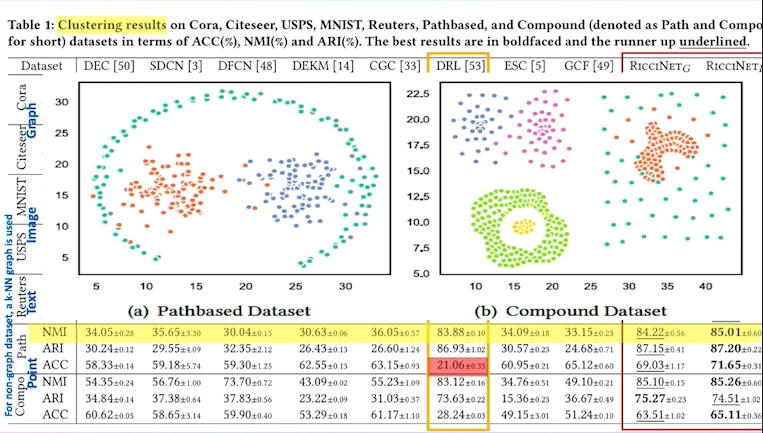
以一个复杂结构为例，我们可以通过分析一个形态不规则的图聚类，来说明如何利用黎曼曲率来识别图聚类的边界位置。例如，在一个具有三个聚类（红、蓝、绿点）的复杂结构中，传统的聚类方法难以解决，因为很难把边界画出来。通过在混合曲率空间操作，每个边都有一个曲率，就能够把黎曼流（Ricci flow）画出来。

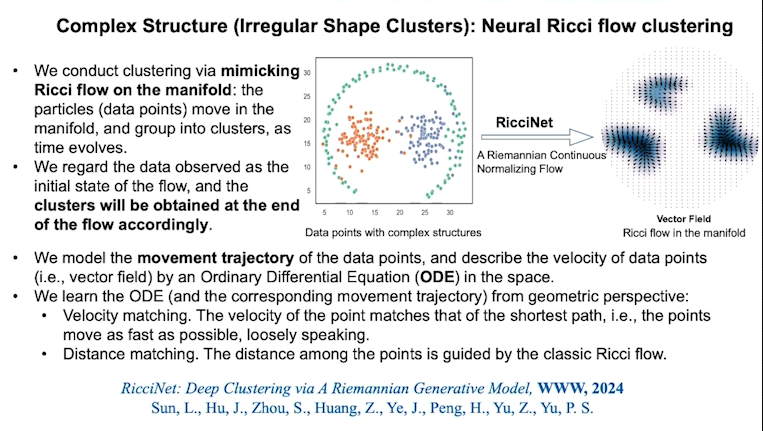
通过在混合曲率空间中定义图，可以解决传统的聚类方法难以处理的复杂问题。这种方法可以推广到图像数据（image data）、文本数据（text data）和点数据（point data），是一种很通用的解决方案。我们的结果显示，RicciNet比传统方法有显著优势。之所以能够取得这么好的效果，是因为我们的策略并不是单纯寻找边界，而是在构建一个黎曼流。之所以能够取得这么好的效果，是因为我们的策略并不是单纯寻找边界，而是在构建一个黎曼流。

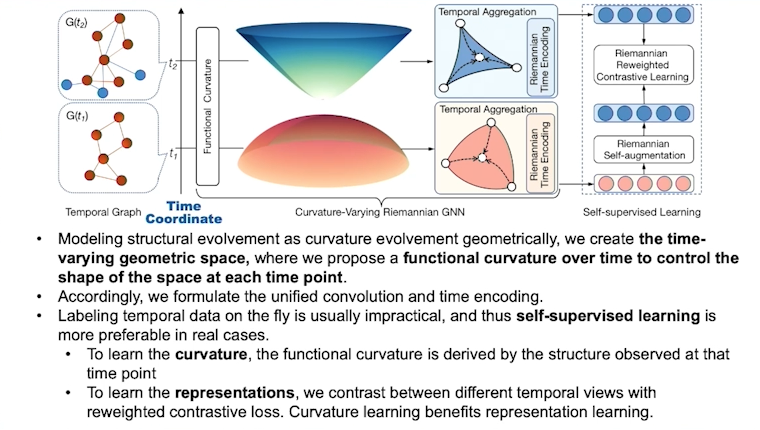
几何深度图学习可以捕捉动态图的变化

现实生活中，图的点边会随着时间不断变化。对于不断变化的图，如社交网络图，我们需要捕捉节点嵌入的变化以及曲率的变化。

在学习随时间变化的图时，可以使用对比学习（contrastive learning）的方法。通过将早期图的快照用于预测当前图的构早，可以提升链接预测和节点分类的效果，但在欧氏空间面临着嵌入空间和曲率的差异这一挑战。这是离线的做法。

此外也可以使用持续图学习（continual graph learning）的方法。从传统的欧氏空间拓展到非欧氏空间，采用自监督学习（self-supervised learning），同时要解决遗忘问题。为此，采用教师-学生模型，其中学生模型学习当前曲率，教师模型则整合历史信息，来做对比学习。最终，实验结果显示该方法在节点分类任务中表现优秀。

以推荐场景为例，采用混合曲率空间方法

我们可以利用混合曲率空间来进行推荐系统的构建。在推荐系统中，我们主要有两种节点：用户（user）和商品（item）。然而，在混合曲率空间中，用户与商品之间的图结构是不同的。商品之间的连接通过知识图谱建立，因此形成了一种层次结构；而用户之间的连接则源于社交网络，构成了一个循环结构。因此，用户和商品的表示分别位于不同的几何空间中。如果我们能够理顺这两者之间的关系，就可以有效地进行推荐，实际的推荐结果也显示出不错的效果。

6.总结

今天我们讨论了图模型是否可以作为基础模型。前面提到，对于一个特定领域可能是可以成功的，但在完全不同的领域则可能面临挑战。然而，如果我们将图映射到非欧几里得空间，并转换为混合曲率空间，这将为我们提供描述不同图构造的新方式，这就给了我们希望可以将其发展为基础模型。

虽然当前的大语言模型非常强大，但它并无法取代图模型。因此，我们面临的挑战是如何将大语言模型与图模型结合起来。

👇完整视频回放