机器学习之线性代数：线性空间的基与维数

在n维线性空间内，有时我们会关心至少需要多少个向量能够生成整个n维线性空间。梳理前面学过的知识，我们能够了解到n个不同的标准单位向量会生成整个n维线性空间。

假设集合V是三维线性空间的向量集：

V集包含三维空间内的三个标准单位向量，V的线性生成集会充满整个三维空间。下图是V的部分线性生成集。

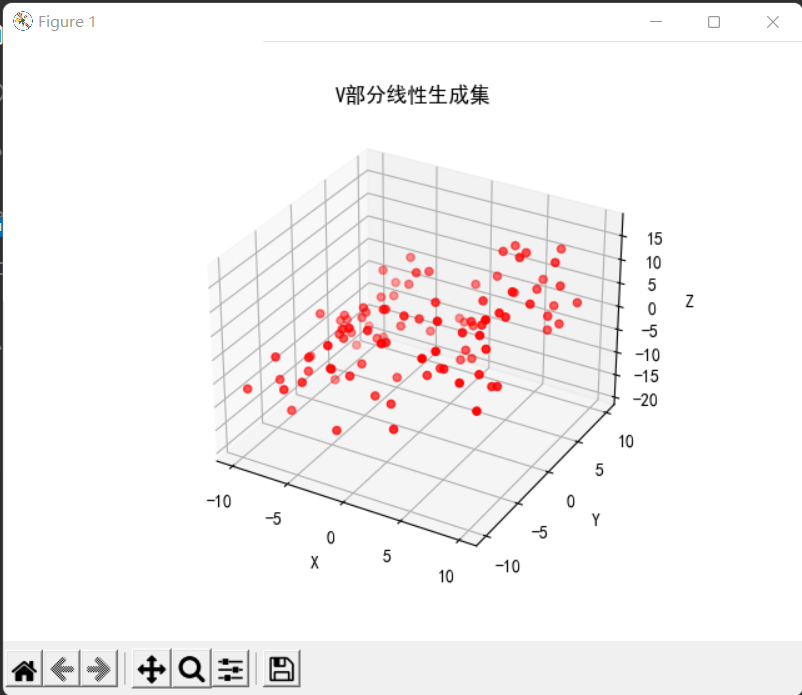
从图中可以看出，V的线性生成集充斥在三维空间内。

Python绘图代码：

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d
import random
  
# 线性生成集函数
def linear_set(V,num):
    # 线性生成集
    SUBV = []
    for i in range(num):
        x = random.randint(-10,10)
        y = random.randint(-10,10)
        z = random.randint(-10,10)
        s = x * V[0] + y*V[1] + z*V[2]
        SUBV.append(s)
    return SUBV
  
# 设置中文字体
plt.rcParams['font.sans-serif']=['SimHei']
# 设置正常显示负号
plt.rcParams['axes.unicode_minus']=False
# F空间向量集V
V = np.array([[1,0,1],[0,1,0],[0,0,1]])
# 向量集V部分线性生成集
SV = linear_set(V,100)
# 创建3D子图
ax = plt.subplot(projection = '3d')
x,y,z = zip(*SV)
# 设置图形标题  
ax.set_title('V部分线性生成集')  
ax.scatter(x, y, z, c = 'r')
# 设置x坐标轴  
ax.set_xlabel('X')  
# 设置y坐标轴
ax.set_ylabel('Y')  
# 设置z坐标轴
ax.set_zlabel('Z')  
plt.show()

若去掉V集任意一个向量，V的线性生成集不会充斥在三维空间内，它的线性生成集会充斥在三维空间的一个平面。

例如：

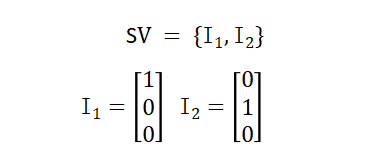
SV集包含三维空间内的两个标准单位向量，SV的线性生成集是三维空间的一个平面，该平面是z为0的xOy面。下图是SV的部分线性生成集。

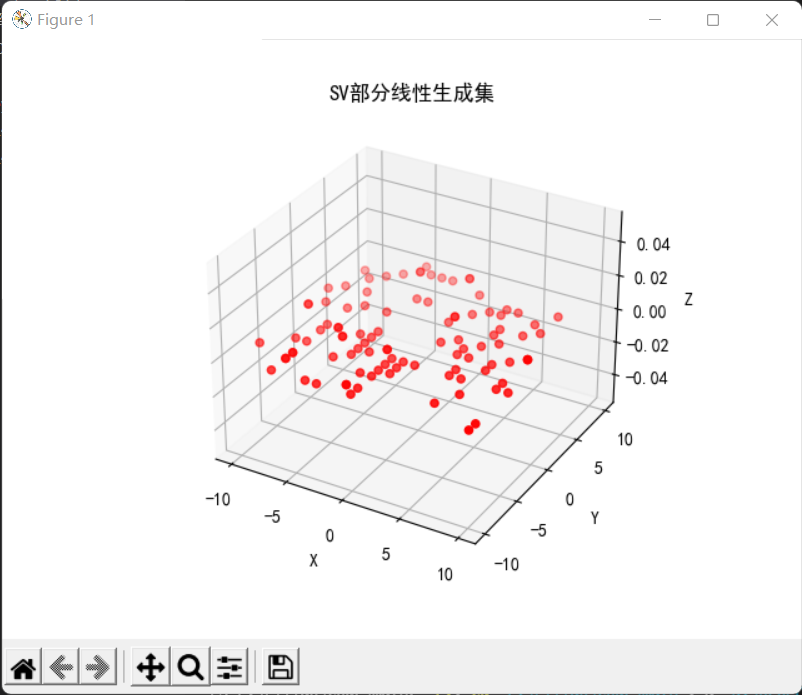
在三维空间内，若V集线性无关且生成整个三维空间，则称V集为三维空间的一组有限基，V集内的向量个数为该空间的维数，该空间的维数为三维。

SV集的线性生成集为三维空间的xOy面，且SV集线性无关，它构成三维空间的子空间xOy面，SV集为xOy面的一组有限基，该空间的维数为二维。

下面给出线性空间即的定义：

设S为线性空间V中有限个元素组成的集合，若S线性无关且生成V，则称S为V的一组有限基，若线性空间V仅包含0或有一组有限基，则称它为有限维空间，否则称它为无限维空间。

若V是一个有限维线性空间，那么V的所有有限基包含的元素个数都相同。

基是生成线性空间V所需要的最小向量组，向量组中的向量都是线性无关的，任意一个向量都不能被向量组中其它向量的线性组合表示。

若S集

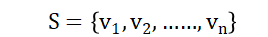
线性无关，S生成了空间E，S就叫做空间E的一组基。

V集

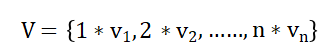
也是空间E的一组基，V集的向量由S集的向量乘以纯量得出。虽然S和V是空间E不相同的一组基，但S和V本质上没什么不同，V集是S集的伸缩。

下面给出线性空间维数的定义：

若线性空间V有一组包含n个元素的基，那么我们称整数n为空间V的维数，若空间仅包含0元素，则该空间的维数为0。