今天分享的是中科大发布的一篇工作。
题目是Logic-of-Thought: Injecting Logic into Contexts for Full Reasoning in Large Language Models.
思维逻辑:为大型语言模型注入逻辑以实现全面推理
文章链接: https://arxiv.org/pdf/2409.17539

摘要
为了解决这个问题,近期有研究提出了Logic-of-Thought (LoT)方法,通过引入命题逻辑来生成扩展的逻辑信息,并将其作为额外的提示信息与原始输入结合,从而增强模型的推理能力。与现有的提示方法兼容,LoT方法可以与Chain-of-Thought等现有技术无缝结合,进一步提升模型的推理表现。
实验结果显示,LoT方法在多个逻辑推理任务中都取得了显著进展。例如,LoT在ReClor数据集上提升了Chain-of-Thought的表现4.35%;在LogiQA上,LoT让Chain-of-Thought with Self-Consistency的表现提高了5%;在ProofWriter数据集上,LoT提高了Tree-of-Thoughts的表现8%。
通过Logic-of-Thought提示方法,研究人员成功增强了LLM的逻辑推理能力,为复杂问题的处理提供了新的思路和技术支持。
主要方法
1. 命题(Propositions)
命题是指那些具有明确真值特征的声明性句子,并且命题不能同时为真和为假。在逻辑推理中,命题是构建逻辑表达式的基本元素。文中使用大写字母(如A、B、C)来表示具体的命题,举例来说,“你有键盘打字技能”就是一个命题;而小写字母(如p、q、r)则用来表示任何命题。
2. 连接词(Connectives)
连接词是作用于命题的运算符,它们可以对单一命题进行操作,或者将多个命题连接起来,形成新的逻辑表达式。常用的连接词包括:
¬:表示取反操作,意为“非”或“否定”。例如,¬p表示“p的否定”。
→:表示蕴含,即如果前一个命题为真,则后一个命题为真(“如果p,则q”)。例如,p → q表示“p是q的充分条件”。
∧:表示合取,即只有当两个命题都为真时,整个表达式才为真。例如,p ∧ q表示“p和q都为真”。
3. 逻辑推理法则(Logical reasoning laws)
逻辑推理法则是两个逻辑表达式之间推导关系的定义。常用的符号包括:
⇒:表示某个逻辑表达式可以推导出另一个逻辑表达式。
⇔:表示两个逻辑表达式可以互相推导。
文章中提到三条基本的逻辑推理法则:
双重否定法则(Double Negation Law):¬¬p ⇔ p,表示两次取反等于原命题本身。例如,“非非p”与p是等价的。 对换法则(Contraposition Law):(p → q) ⇔ (¬q → ¬p),表示“如果p蕴含q”,则等价于“非q蕴含非p”。 传递法则(Transitive Law):(p → q) ∧ (q → r) ⇒ (p → r),表示如果p蕴含q,且q蕴含r,那么p也必然蕴含r。
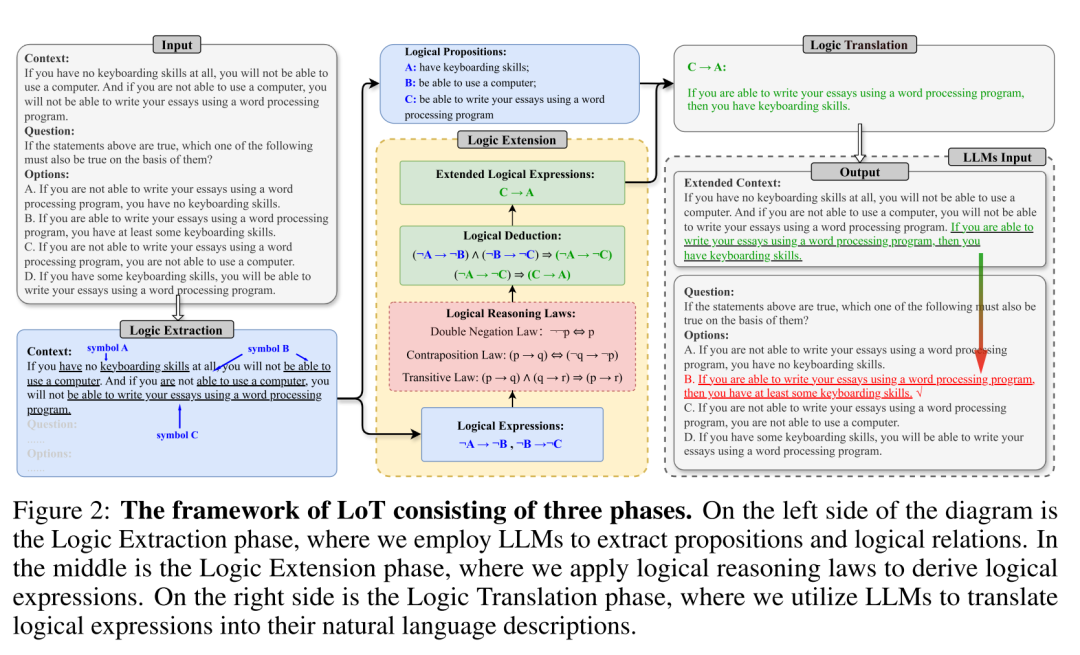
LoT方法主要分为以下三个阶段:
1. 逻辑提取阶段(Logic Extraction)
首先,LoT方法指示LLM从输入文本中挑选出包含条件推理关系的句子,提取出具有逻辑含义的语句集合。接着,模型会识别和标记文本中的命题符号,并根据命题之间的逻辑关系,使用符号(如否定符号“¬”或蕴含符号“→”)进行表示。例如,模型从不同的句子中提取出“能够使用计算机”这一相同意思的描述,并将其统一表示为符号B。通过进一步分析,得到新的逻辑表达式¬A → ¬B。
2. 逻辑扩展阶段(Logic Extension)
在逻辑扩展阶段,LoT利用Python程序结合基本的逻辑推理法则(如传递法则和对换法则),对提取出的逻辑表达式进行推导和扩展。例如,通过推导,¬A → ¬B和¬B → ¬C可以推导出新的表达式C → A。这一阶段的目的是通过逻辑推理,生成更复杂的逻辑关系,为后续阶段提供更加丰富的信息。
3. 逻辑翻译阶段(Logic Translation)
最后,LoT方法将扩展后的逻辑表达式转化为自然语言描述,并将这些描述与原始输入结合,形成一个增强的输入提示。这一过程通过将命题符号(如C和A)与其自然语言描述(例如“能够使用文字处理程序写作业”和“具备键盘打字技能”)相结合,避免了信息丢失,同时增强了输入的逻辑信息。例如,逻辑表达式C → A被翻译为“如果具备键盘打字技能,那么能够使用文字处理程序写作业”,并作为新的提示信息加入原始输入中。
通过这三个阶段,LoT方法不仅提升了语言模型的逻辑推理能力,还有效避免了信息丢失,为模型提供了更准确、更丰富的推理支持。
逻辑推理框架实例解析
1. 原始输入
背景信息(Context):
“如果你没有键盘技能,你将无法使用电脑。”
“并且如果你不能使用电脑,你就不能用文字处理程序写论文。”
问题(Question):
“如果上述陈述为真,以下哪一项也必须为真?”
选项(Options):
A. 如果你不能用文字处理程序写论文,那么你没有键盘技能。
B. 如果你能用文字处理程序写论文,那么你至少有一些键盘技能。
C. 如果你不能用文字处理程序写论文,那么你不能使用电脑。
D. 如果你有一些键盘技能,你就能用文字处理程序写论文。
2. 逻辑提取
在逻辑提取阶段,我们使用LLM从给定的背景信息中提取出核心命题和它们之间的逻辑联系。具体步骤如下:
提取命题:
命题1:如果你没有键盘技能(记作P),你将无法使用电脑(记作Q)。即 。 命题2:如果你不能使用电脑(Q),你就不能用文字处理程序写论文(记作R)。即 。 符号化表示:
3. 逻辑扩展
逆否命题: 根据命题1 ,其逆否命题为 。 根据命题2 ,其逆否命题为 。 连锁推理: 将 和 结合起来,可以得到 。 即:如果你不能用文字处理程序写论文(),那么你没有键盘技能()。 等价转换: 的等价形式为 。 即:如果你有键盘技能(P),那么你可以用文字处理程序写论文(R)。 逆否命题: 的逆否命题为 。 即:如果你不能用文字处理程序写论文(),那么你没有键盘技能()。 最终结论: 从 可以推出。 即:如果你能用文字处理程序写论文(R),那么你至少有一些键盘技能(P)。
4. 逻辑翻译
翻译结论: 对应选项:
总结
当前的LoT方法支持的连接词和逻辑推理法则还比较有限。如果要增加更多的连接词和推理法则,就意味着在逻辑提取和翻译阶段,提示设计会变得更加复杂,同时逻辑推导的难度也会增加。






