二分查找（面试总结）

• 二分查找算法介绍

• 二分查找算法历史

• 算法实现中的问题

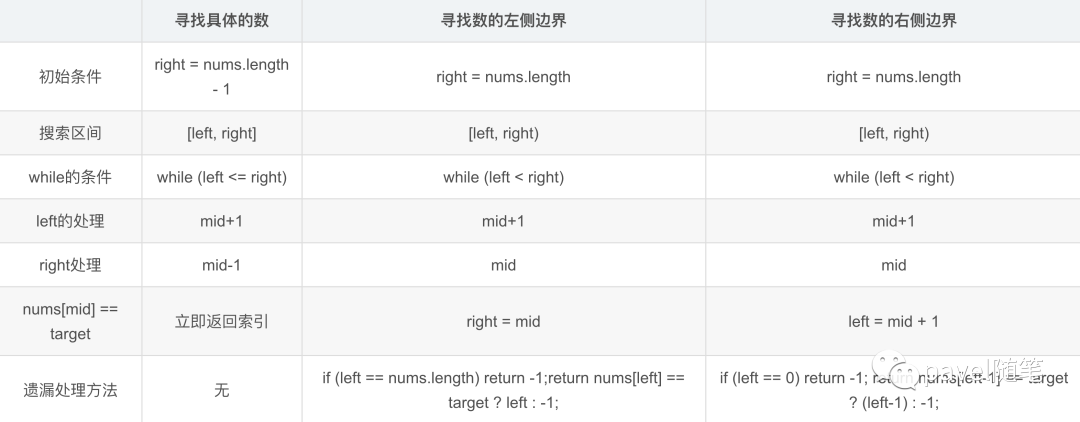
• 实现细节讨论（面试遇见的不同情况）

  1）寻找集合中具体某个元素

         2）寻找集合中元素的左边界

         3）寻找集合中元素的右边界

• 总结

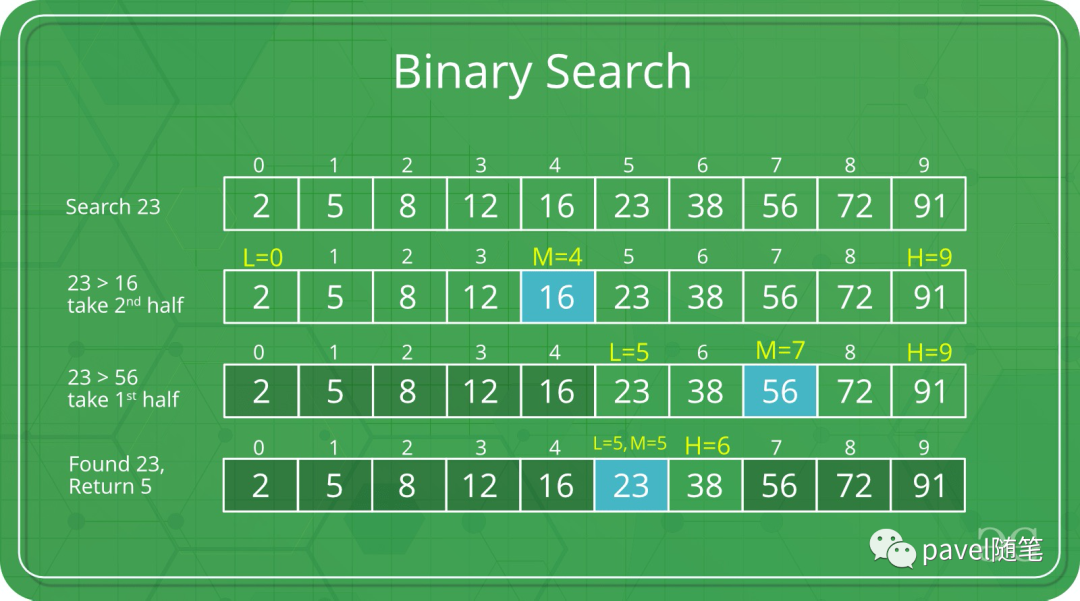
二分查找算法历史

在1946年，约翰·莫奇利在摩尔学院讲座上第一次提出二分搜索的概念。1957年，威廉·皮特逊发表了第一个应用插值搜索的算法。在此时，每个发表的二分搜索算法只对长度为2的幂减一的数组有用。直到1960年，德里克·亨利·莱默发表了一个对于所有长度的数组都适用的算法。1962年，赫尔曼·博滕布鲁赫发表了一个用ALGOL 60写的二分搜索，将判断相等的步骤放到算法末尾。虽然将平均迭代次数增加一，但是每次迭代中的比较次数减少了1次。均匀二分搜索则是史丹佛大学的A. K.钱德拉在1971年发明的。1986年，伯纳德·查泽尔和列奥尼达斯·吉巴斯引入了分散层叠来解决计算几何中大量存在的搜索问题。

维基百科

实现中的问题

当乔恩·本特利将二分搜索问题布置给专业编程课的学生时，百分之90的学生在花费数小时后还是无法给出正确的解答，主要因为这些错误程序在面对边界值的时候无法运行，或返回错误结果。1988年开展的一项研究显示，20本教科书里只有5本正确实现了二分搜索。不仅如此，本特利自己1986年出版的《编程珠玑》一书中的二分搜索算法存在整数溢出的问题，二十多年来无人发现。Java语言的库所实现的二分搜索算法中同样的溢出问题存在了九年多才被修复。

维基百科

尽管二分查找的基本思想相对简单，但细节可以令人难以招架，本文针对这些边界问题行了相关总结。普通算法实现伪代码：

public int binarySearch (int[] nums, int target) {
    int left = 0;
    int rigt = ...;
    while (left ... rigt) {
        int mid = (left + rigt) / 2;
        if (nums[mid] == target) {
            return mid;
        }else if (nums[mid] < target) {
            left = ...;
        }else if (nums[mid] > target) {
            rigt = ...;
        }
    }
    return -1;
}

...代表需考虑的细节位置，如：while循环中的不等号是否应该带等号，left是否应该加一，right是否应该减一等。小技巧：计算 mid 时需要技巧防止溢出同时加快运算速度。建议写成: mid = start + ((end - start) >> 1)。

代码实现：

public int binarySearch (int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    while(left <= right) {
        int mid = start + ((end - start) >> 1);
        if(nums[mid] == target)
            return mid;
        else if (nums[mid] < target)
            left = mid + 1;
        else if (nums[mid] > target)
            right = mid - 1;
    }
    return -1;
}

上述代码中：为什么 while 循环的条件中是 <=，而不是 < ？

因为初始化 right 的赋值是 nums.length - 1，即最后一个元素的索引，而不是 nums.length。

while(left <= right)的终止条件是 left == right + 1，写成区间的形式就是 [right + 1, right]，或者带个具体的数字进去 [3, 2]，可见这时候搜索区间为空，因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的，直接返回 -1 即可。

while(left < right)的终止条件是 left == right，写成区间的形式就是 [right, right]，或者带个具体的数字进去 [2, 2]，这时候搜索区间非空，还有一个数 2，但此时 while 循环终止了。也就是说，**索引 2 没有被搜索**，如果这时候直接返回 -1 就可能出现错误。

非要用 while(left < right) 也可以，只需加上以下代码：

while(left < right) {
    // ...
}
//最后加一个遗漏检查
return nums[left] == target ? left : -1;

代码实现：

public int binarySearch (int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0;
    int right = nums.length; 
    while (left < right) { 
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; 
        }
    }
    return left;
}

 上述代码中：为什么 while(left < right) 而不是 <= ?

因为初始化 right = nums.length 而不是 nums.length - 1 。因此每次循环的是 [left, right) 左闭右开。while(left < right) 终止的条件是 left == right，此时搜索区间 [left, left) 恰巧为空，所以可以正确终止。

为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？

函数的返回值（即 left 变量的值）取值区间是闭区间 [0, nums.length]，所以我们简单添加两行代码就能在正确的时候 return -1。

while (left < right) {
    //...
}
//跳出left值只能为0 或者  nums.length
// target 比所有数都大，即 nums.length
if (left == nums.length) return -1;
// 类似之前算法的处理方式
return nums[left] == target ? left : -1;

为什么该算法能够搜索左侧边界？

找到 target 时不要立即返回，而是缩小区间右边界 right，在区间 [left, mid) 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。 可以看到当mid为target或者大于target的操作，其实是一样的，都是right=mid，所以最后返回的left，其实是数组中，大于等于target的元素的第一个位置。

代码实现：

public int binarySearch (int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0;
    int right = nums.length;
    while (left < right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            left = mid + 1; 
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; 
}

如果 nums 中不存在 target 这个值，怎么办？

while 循环结束时，nums[left] 一定不等于 target 了，而 nums[left - 1]可能是target。类似前面的左侧边界搜索，因为 while 的终止条件是 left == right，就是说 left 的取值范围是 [0, nums.length]，所以可以添加两行代码，正确地返回 -1。

while (left < right) {
    // ...
}
if (left == 0) return -1;
return nums[left-1] == target ? (left-1) : -1;