今天为大家分享一篇SIGMOD 2024年的向量检索论文:
SeRF: Segment Graph for Range-Filtering Approximate Nearest Neighbor Search
SeRF:支持范围过滤最近邻检索的分段图索引
论文作者来自美国Rutgers大学,新西兰Auckland大学和阿里巴巴。
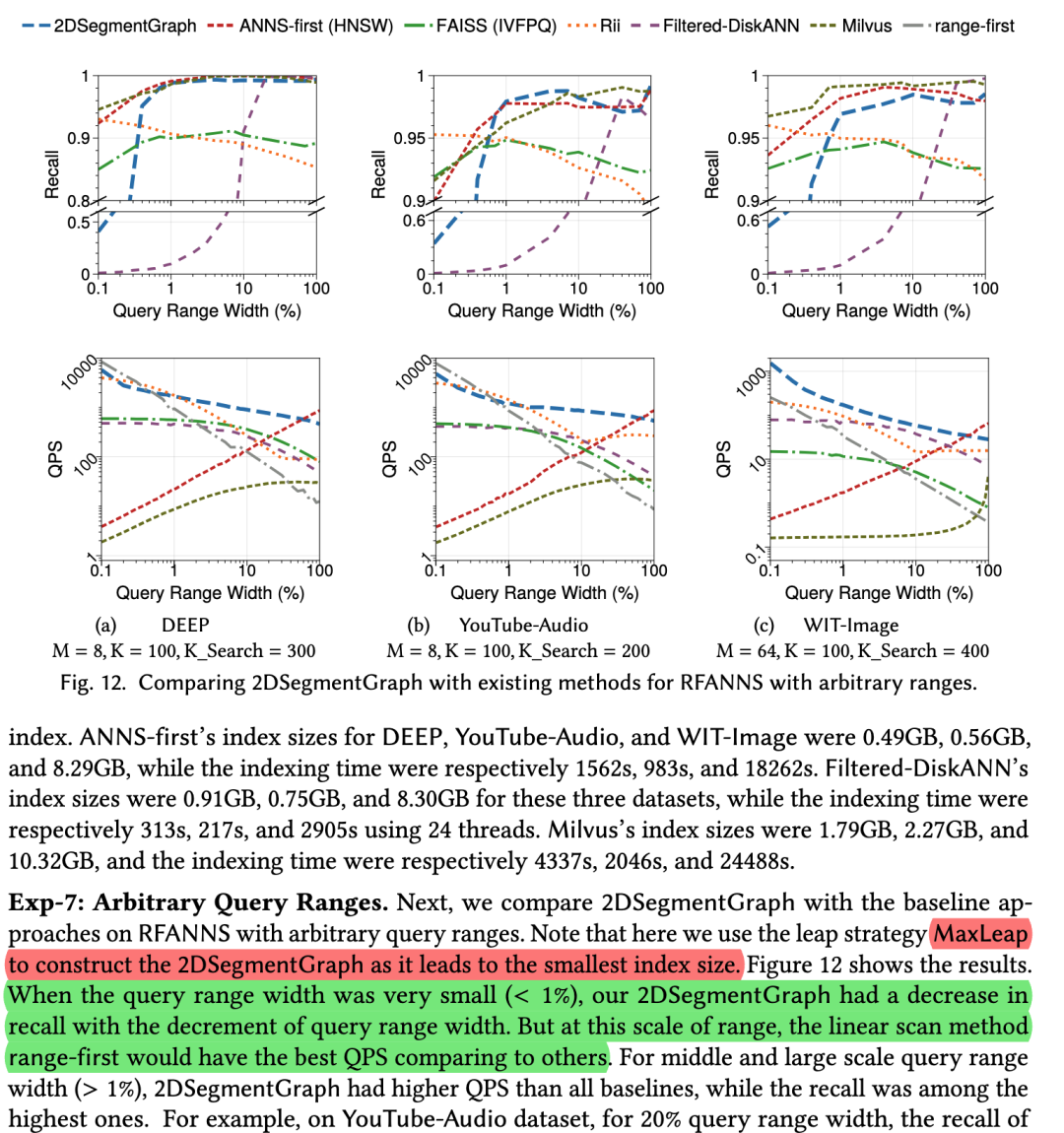
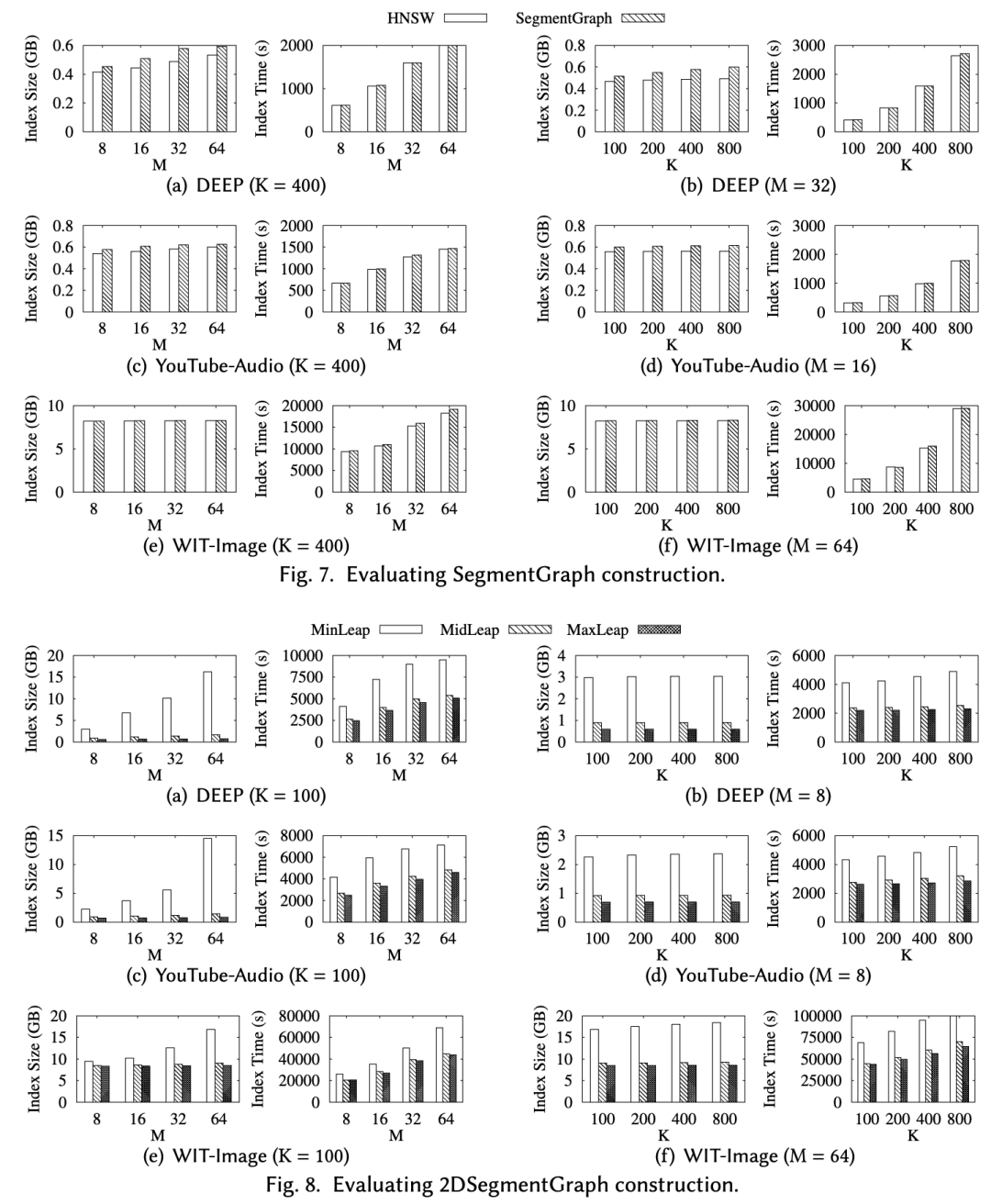
论文地址:https://dl.acm.org/doi/pdf/10.1145/3639324代码地址:https://github.com/rutgers-db/SeRF在向量相似性索引中支持标量的范围查询是非常重要的功能。比如查询“根据用户偏好,推荐距离其2公里以内的餐厅”,其中距离是硬性的标量范围,而根据偏好的搜索则是向量的近邻检索。实现这一功能很困难,如果首先使用向量索引返回近邻结果,再做标量筛选,则需要返回过量近邻结果以保证筛选后最终返回足量结果;如果首先使用标量筛选,在筛选过后又没有向量索引可以支持高效相似性搜索,在选择率高时尤其低效。本论文提出的方法SeRF专注在后一种策略,重点解决在任意范围查询之后如何提供相似性索引的问题。暴力的方法是为所有可能的范围都预先建立一个索引,但显然时空上均不可行。SeRF提供了一种压缩策略,可以将这些索引全部压缩至一个图中,在查询时激活部分边进行查询。从结果来看,除去选择率特别低的情况,SeRF均能对目前已有方法(IVFPQ、Milvus、HNSW-ANNS-first)作出有效提升,但在索引大小和构建时间方面有所牺牲。
在SeRF中,数据按照标量值排序;查询时首先使用标量索引(排序数组二分查找)找出符合范围查询条件的数据下标(连续的一段数据子集),然后在向量索引(图索引)中查询。图索引的构建顺序(点插入顺序)也和标量值排序保持一致。
我们首先考虑半范围查询,即符合标量范围的数据下标为[1,z]的查询(在SQL中表现为property<z'而非x'<property<y')。我们从下标1开始,建n个图(n为数据集大小),第i个图仅包含[1,i]下标的数据子集,命名为,,...,,这样对于查询[1,z],我们直接使用进行查询即可。接下来考虑如何压缩这n个结构高度相似的图。注意到在不断插入新点的过程中,老点的邻居也会更新,可能会插入一条指向新点的边,也可能在裁边时裁掉某些边,因此我们可以在这个过程中记录每条边的“寿命”,即插入时间和删除时间。在查询时(包括构建时的查询)我们只关注时间满足要求的边而忽视其它的。注意这里的时间实际上指的是标量的值。这样一个结构被称为分段图。
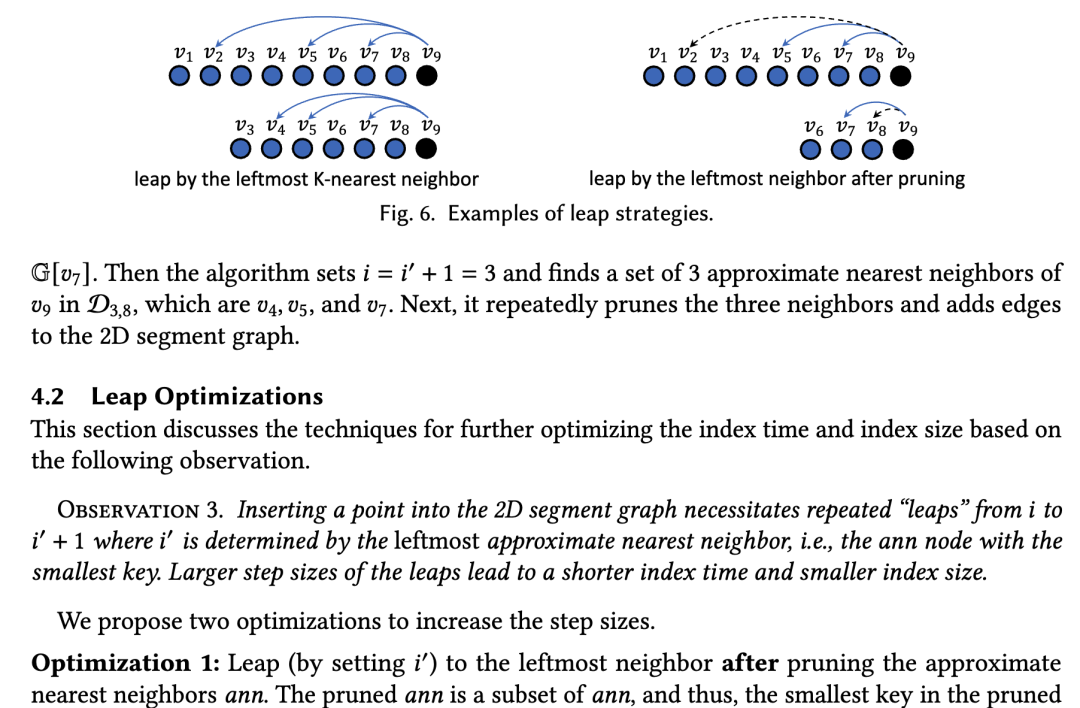
上述压缩算法解决了半范围查询的问题,但要解决全范围的查询,则又要建立n个分段图,每个分段图负责一个开始下标。为压缩着n个分段图,SeRF再次为每条边再加上一个寿命,表示这条边在哪些连续的分段图中存活。注意到相邻的分段图会非常相似,它们之间的区别仅有一个起点而已。为了简化构建,在全范围查询中,SeRF甚至取消了裁边过程,一条边一旦加入,则不会被删除。构建SeRF时通过两层循环构建,外层顺序遍历每一个点进行插入,内层则从1开始遍历,内层代表范围起点,外层代表范围终点,每次迭代尝试在该范围内插入边。SeRF进一步提出一些优化策略,使得内层的迭代可以每次步进更大,但可能牺牲一些精度,不能保证无损压缩。
本文提出一个基于压缩图的支持任意范围标量查询的向量索引SeRF。作者从压缩这一角度入手设计算法,结构清楚,论证扎实,在大部分情况下均能对现有算法作出性能提升。但在索引构建时间和内存大小方面仍有一定的提升空间。SeRF与同年提出的ACORN相比,设计上具有相似性,ACORN启发式地通过二跳邻居以复原在数据子集下的图结构,SeRF通过为边赋属性在查询时判断激活以复原子结构。此外,二者都放弃了裁边策略以尽量保留原始结构。不同的是,SeRF有一定保证能基本复原出对应结构,算法上更加严谨;而ACORN对原始结构的复原受查询选择率影响较大。有关ACORN的介绍,可以参考之前的推送:https://mp.weixin.qq.com/s/cZ_oAPtw_szeJ2E4QYDM5Q
[1] SIGMOD'24 ACORN:Efficient Indexing of Billion-Scale Datasets of Deep Descriptors
(https://dl.acm.org/doi/pdf/10.1145/3654923)
王泽宇复旦大学与巴黎西岱大学联合培养博士生,研究领域为高维数据(向量、序列等)管理和分析。以第一作者在SIGMOD,VLDB,VLDBJ,TKDE等数据库领域会议/期刊发表多篇论文,并担任审稿人。
个人主页:https://zeyuwang.top/
谷歌学术:https://scholar.google.com.hk/citations?hl=zh-CN&user=XXGhABIAAAAJ
技术博客:https://www.jianshu.com/u/d015902c6d09