背景
OpenGauss的堆表数据和索引数据都以页面(Block)为单位存储,默认大小为8KB。以堆表为例,在写入一个元组数据(Tuple)之前,需要快速找到具有足够空闲空间的页面,并将数据写入,并且由于堆表不是和索引聚簇表一样有序排列,所以写入页面的位置没有限制。当然,如果当前系统中所有页面都没有足够空间,那么此时则需要新建一个空页面。
由于数据库场景本身非常强调性能,因此上述场景中其实隐含了一些额外的性能需求:
1.快速并且准确地找到满足所需空闲空间的页面;
2.快速判断当前系统中没有足够空间,需要新建空页面。
FSM(Free Space Map),也就是空闲空间映射,就是为了应对上述需求。顾名思义,FSM需要做到:调用者提供所需空间后,快速返回满足条件的页面地址,或是告诉调用者系统中目前无满足条件页面。
整体上,FSM通过逻辑上的树形结构来维护空闲空间信息,在树形结构中,每一个节点存储其所有子节点中最大的空闲空间,查询和更新信息的时间复杂度都为O(log n)。其中,叶子节点和非叶子节点的存储结构相同,只不过前者管理数据页面,后者管理下层FSM页面。一张表对应一个FSM文件,FSM文件名为表文件名_fsm。
FSM叶子节点
前文提到,FSM通过树形结构维护空闲空间,而其中的节点也是一个页面大小(默认8KB),其结构如下:

其中PageHeaderData结构与普通页面一致,但是大部分字段无用,空闲空间存储在FSMPageData结构中,该结构中1个数据页面的空闲程度可以用1个字节来表示。以8K页面大小为例,该字节取值与页面空闲空间的映射关系如下:
| 取值 | 空闲空间大小 |
|---|---|
| 1 | 0~32字节 |
| 2 | 33~64字节 |
| … | … |
| 254 | 8097~8128字节 |
| 255 | 8129~8191字节 |
大部分数值表示32个字节的范围,边界值1和255略有不同。这部分映射的逻辑在函数fsm_space_needed_to_cat中。
单个FSMPageData中,数据页的信息是一颗逻辑上的完全二叉树(注意这里是前文提到的树形结构中的单个节点内的结构),叶子节点代表数据页面的空闲程度,非叶子节点代表其子节点的最大空闲程度(便于空闲空间搜索)。为了节省空间,其用一个数组表示,完全二叉树中节点和数组下标一一映射:
0
/ \
1 2
/ \ / \
3 4 5 6
/ \ / \ / \ / \
7 8 9 10 11 12 13 14
FSMPageData具体定义如下:
typedef struct {
int fp_next_slot; // 指向下一个开始查找的页面的叶子节点序号, 查找空闲空间时(fsm_search_avail)时会涉及
uint8 fp_nodes[FLEXIBLE_ARRAY_MEMBER]; // 每个字节代表一个页面的空闲程度(或是其子节点的最大空闲程度),数组大小为NodesPerPage
} FSMPageData;
#define NodesPerPage (BLCKSZ - MAXALIGN(SizeOfPageHeaderData) - offsetof(FSMPageData, fp_nodes)) // 单个页面能存储的空闲空间节点个数
#define NonLeafNodesPerPage (BLCKSZ / 2 - 1) // 单个FSM页面中,最大非叶子节点个数
#define LeafNodesPerPage (NodesPerPage - NonLeafNodesPerPage) // 单个FSM页面中,最大叶子节点个数
数组长度为NodesPerPage,叶子节点也就是对应的真实数据页面为LeafNodesPerPage个,以8K页面为例,一个FSMPageData可以表示约4000个页面的空闲程度。实际场景中,一个FSM叶子节点内二叉树存储的值可能如下,每个节点存储下层节点中最大的页面空闲空间映射值:
254
/ \
20 254
/ \ / \
3 20 5 254
/ \ / \ / \ / \
3 1 1 20 3 5 254 10
| | ... | |
data page n n+1 ... n+6 n+7
FSM非叶子节点
FSM非叶子节点存储的数据结构和叶子节点一致,其含义基本一致,不过其内部叶子节点不再指向真实的数据页面,而是指向另一个FSM Page。整体树形结构默认为3层,如下图所示:
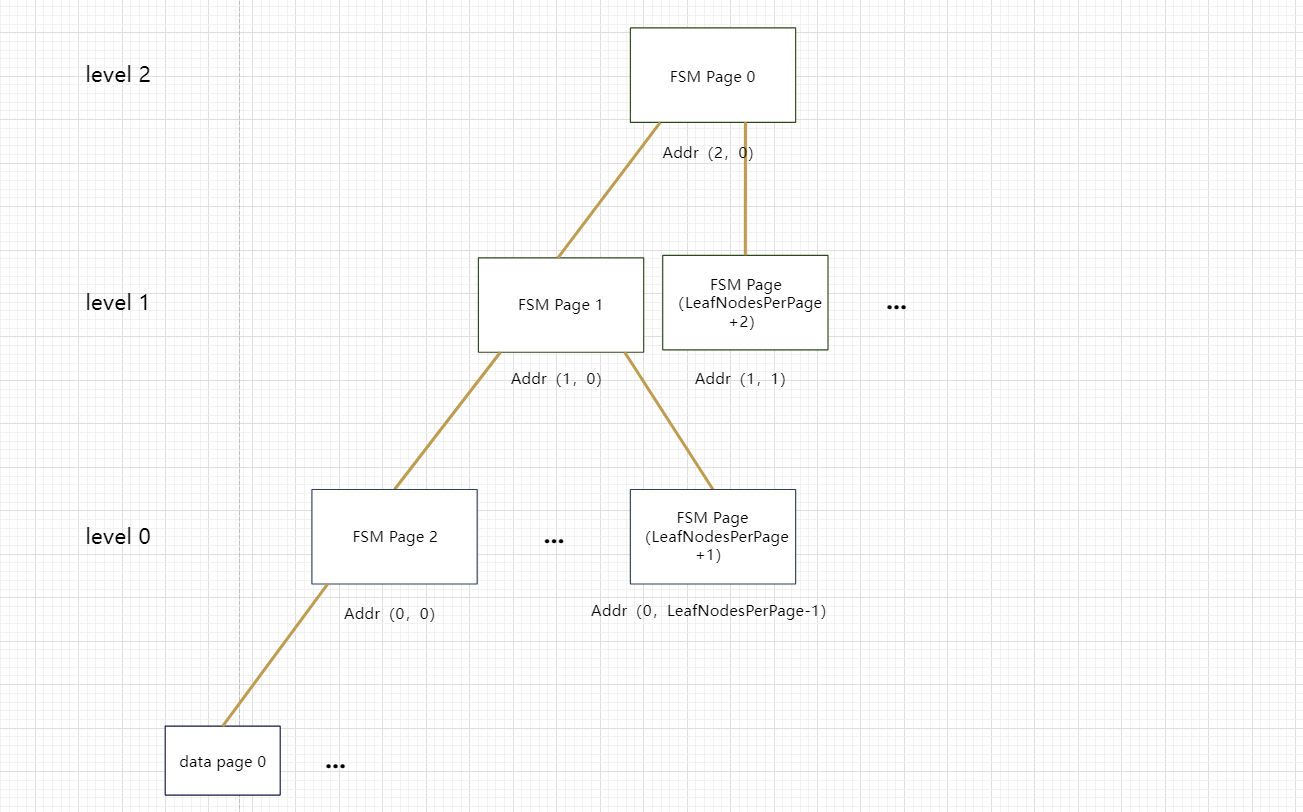
这里每个节点对应一个FSM Page,其中第0层就是上文提到的叶子节点,可以存储约4000个页面(32MB)的空闲空间信息,3层树状结构理论上可以管理4000*4000*32M(约512TB)空闲空间,对于单表容量最大32TB的OpenGauss来说完全够足够了。
每个节点通过level和level内编号的逻辑地址唯一标识,比如根节点的地址为add(2,0)。相应地,FSM页面的逻辑地址,唯一对应一个物理地址,也就是FSM文件中该block的序号,如根节点的物理地址为0,也就是FSM文件的第0个页面。FSM页面的物理地址增长顺序对应上图中FSM树状结构的深度优先遍历顺序,比如上图中,若当前FSM文件中最后一个页面的序号为LeafNodesPerPage+1, 逻辑地址为Addr(0,LeafNodesPerPage-1),且此时FSM文件需要继续扩展一个页面,则下一个页面LeafNodesPerPage+2的逻辑地址为Addr(1,1),基于这种规则,新增FSM页面只需要向右扩展树形结构,不涉及页面分裂。
数据页面序号和FSM叶子节点序号按顺序对应,逻辑地址Addr(0,0)的FSM页面管理0到LeafNodesPerPage-1的数据页面,依此类推。
FSM逻辑地址数据结构FSMAddress:
typedef struct
{
int level; // 所在的层数
int logpageno; // 该层的第几个节点
} FSMAddress;
其和物理地址BlockNumber的映射关系见函数fsm_logical_to_physical:
BlockNumber fsm_logical_to_physical(const FSMAddress& addr)
{
BlockNumber pages;
int leafno;
int l;
leafno = addr.logpageno; // 同一层内序号
for (l = 0; l < addr.level; l++)
leafno *= SlotsPerFSMPage; // 在树状结构中,叶子节点层有leafno+1个节点在物理顺序上比addr对应节点小
pages = 0;
for (l = 0; l < FSM_TREE_DEPTH; l++) {
pages += (BlockNumber)leafno + 1;
leafno /= SlotsPerFSMPage;
} // 假设节点为叶子节点,把每一层比addr对应节点靠前的节点都加起来
pages -= (BlockNumber)addr.level; // 如果节点非叶子节点(level不为0)则上面去掉步骤多加的个数,比如节点level为1,那循环里多做了一次 pages += 0 + 1
return pages - 1; // 页号起始值为0,所以-1
}
空闲空间查找
FSM页面内空闲空间查找
一个FSM页面管理约4000个数据页面的空间,其空闲空间查找接口函数为fsm_search_avail,具体代码如下:
// buf为FSM页面buffer,minvalue为1到255的所需空间映射值,advancenext为true则下次查找位置向后移一个页面, 是否持有buffer的排他锁
int fsm_search_avail(Buffer buf, uint8 minvalue, bool advancenext, bool exclusive_lock_held)
{
Page page = BufferGetPage(buf);
FSMPage fsmpage = (FSMPage)PageGetContents(page); // 即前文介绍的FSMPageData
int nodeno; // 完全二叉树数组下标
int target; // 本次搜索的node起始位置
uint16 slot; // 叶子节点层序号,即nodeno - NonLeafNodesPerPage
restart:
if (fsmpage->fp_nodes[0] < minvalue)
return -1; // 如果根节点映射值小于预期值,说明这个FSM页面管理的数据空间里没有符合条件的数据页,直接返回-1
target = fsmpage->fp_next_slot; // 上次调用fsm_search_avail时设置的此次搜索起始点,受advancenext影响,若其为true,则fp_next_slot为上次搜索结果的右兄弟。这样做的好处是相对避免多个线程间争用同一个数据页面。
if (target < 0 || (unsigned int)(target) >= LeafNodesPerPage)
target = 0; // 如果值fp_next_slot无效则此次搜索从头开始
target += NonLeafNodesPerPage; // fp_next_slot为叶子节点序号,对应的完全二叉树下标要加NonLeafNodesPerPage
nodeno = target;
while (nodeno > 0) {
if (fsmpage->fp_nodes[nodeno] >= minvalue)
break; // 当前数据页有足够空间则返回
nodeno = parentof(rightneighbor(nodeno)); // 否则从当前叶子节点的右兄弟的父亲节点开始搜索,注意rightneighbor如果已经在最右点则不会移动
} // 这里我们可以看到其搜索路径始终往右兄弟和父亲节点的方式,如果碰到最右边则只向上找父亲节点,搜索范围基本上是一个每次向右扩大一倍的三角形,所以时间复杂度是logN。这个循环结束后,我们找到了一个符合条件的节点,而这个节点有不小的概率是非叶子节点。
while (nodeno < NonLeafNodesPerPage) { // 从当前节点向下层找符合条件的孩子,直到叶子节点,和上面步骤不同,这里左孩子优先,所以整体上所有节点被搜索到的概率比较均匀。
int childnodeno = leftchild(nodeno);
if ((unsigned int)(childnodeno) < NodesPerPage && fsmpage->fp_nodes[childnodeno] >= minvalue) {
nodeno = childnodeno;
continue;
}
childnodeno++; /* point to right child */
if ((unsigned int)(childnodeno) < NodesPerPage && fsmpage->fp_nodes[childnodeno] >= minvalue) {
nodeno = childnodeno;
} else { // 这里单个FSM页面内,叶子节点和非叶子节点不一致了,说明页面损坏。
RelFileNode rnode;
ForkNumber forknum;
BlockNumber blknum;
BufferGetTag(buf, &rnode, &forknum, &blknum);
ereport(DEBUG1,
(errmsg("fixing corrupt FSM block %u, relation %u/%u/%u",
blknum,
rnode.spcNode,
rnode.dbNode,
rnode.relNode)));
/* make sure we hold an exclusive lock */
if (!exclusive_lock_held) {
LockBuffer(buf, BUFFER_LOCK_UNLOCK);
LockBuffer(buf, BUFFER_LOCK_EXCLUSIVE);
exclusive_lock_held = true;
}
fsm_rebuild_page(page); // 通过叶子节点值重建整个FSM Page
if (IsSegmentFileNode(rnode)) {
PageSetLSN(page, GetXLogInsertRecPtr());
MarkBufferDirty(buf);
} else {
MarkBufferDirtyHint(buf, false);
} // 将这个FSM页面置脏,和数据页面一样等待pageWriter刷到磁盘
goto restart; // 重新查找
}
}
slot = nodeno - NonLeafNodesPerPage; // 数组下标改为数据页序号(slot号)
fsmpage->fp_next_slot = slot + (advancenext ? 1 : 0); // fp_next_slot = slot + 1让别的线程尽量使用别的数据页,减少冲突
return slot;
}
堆表和索引空闲空间查找
上面我们介绍了一个FSM页内的数据查找,对于堆表的空闲空间搜索,查询入口为GetPageWithFreeSpace,其逻辑多了整个FSM树状结构的搜索
BlockNumber GetPageWithFreeSpace(Relation rel, Size spaceNeeded)
{
uint8 min_cat = fsm_space_needed_to_cat(spaceNeeded); // 需要的空间映射为1到255的值
return fsm_search(rel, min_cat); // 从FSM树状结构查找返回数据页号
}
static BlockNumber fsm_search(Relation rel, uint8 min_cat)
{
int restarts = 0;
FSMAddress addr = g_fsm_root_address; // addr (2, 0) 第二层第0个节点,也就是根节点
gstrace_entry(GS_TRC_ID_fsm_search);
for (;;) {
int slot;
Buffer buf;
uint8 max_avail = 0; // 存储搜索过程中页面的最大空闲空间
buf = fsm_readbuf(rel, addr, false); // 读取FSM页面
/* Search within the page */
if (BufferIsValid(buf)) {
LockBuffer(buf, BUFFER_LOCK_SHARE);
slot = fsm_search_avail(buf, min_cat, (addr.level == FSM_BOTTOM_LEVEL), false); // FSM页面内搜索slot
if (slot == -1)
max_avail = fsm_get_max_avail(BufferGetPage(buf)); // 如果FSM buffer有效,但时不满足min_cat,则先把它的max_avail记录,后续更新
UnlockReleaseBuffer(buf);
} else
slot = -1; // buffer无效
if (slot != -1) { // 找到符合条件的slot了
if (addr.level == FSM_BOTTOM_LEVEL) { // 如果当前FSM节点为叶子节点,那slot对应数据页面,计算数据页面block号后返回
return fsm_get_heap_blk(addr, (uint16)slot);
}
addr = fsm_get_child(addr, (uint16)slot); // 当前FSM节点非叶子节点,则addr更新为对应下层FSM页面,下一次循环继续调用fsm_search_avail查找
} else if (addr.level == FSM_ROOT_LEVEL) { // 如果没找到有效slot,并且当前节点为根节点,那么说明当前表或者索引内没有符合条件的页面,返回InvalidBlockNumber
return InvalidBlockNumber;
} else { // 没搜到符合的,但是不是根节点,那么可能时搜到的父亲节点和子节点不统一,搜错了路径,可以更新fsm信息,而后继续从根节点开始搜索。
uint16 parentslot;
FSMAddress parent;
parent = fsm_get_parent(addr, &parentslot); // 找父亲节点
fsm_set_and_search(rel, parent, parentslot, max_avail, 0); // 更新父亲节点对应的slot值
if (restarts++ > 10000) { // 重新搜索超过10000次则放弃,实际情况应该不会走到这个分支
return InvalidBlockNumber;
}
addr = g_fsm_root_address;
}
}
}
对于堆表数据来说,要写入数据时,都会找FSM获取符合条件的页面,而在索引空间中,略有不同。因为索引数据其本身就是一个有序的树状搜索结构,对于新加入的数据,key值就已经决定了它需要插入到哪个位置。因此索引只会在页面分裂时向FSM索要空页面,得到页面后,后续插入逻辑由其自己控制。
FSM更新
FSM信息需要不断更新,其主要的接口为fsm_set_and_search。但基于代价考虑,FSM的更新在大部分场景下都不是实时的,比如像页面插入一行数据,不会立即更新其对应的FSM slot。FSM主要在3个场景下更新:1.上文提到的堆表空闲空间查找的过程中,对不符合条件的页面,会顺带更新 2.新增或者合并数据页面时会更新FSM 3.auto vacuum
fsm_set_and_search主要代码如下:
// rel为数据表,addr为FSM页面的逻辑地址,slot为页面中要更新的位置,newValue为新的空闲空间映射值,minValue只在search为true时用到,此时这个函数会额外执行fsm_search_avail并返回
static int fsm_set_and_search(Relation rel, const FSMAddress &addr, uint16 slot, uint8 newValue, uint8 minValue,
bool search)
{
Buffer buf;
Page page;
int newslot = -1;
buf = fsm_readbuf(rel, addr, true);
LockBuffer(buf, BUFFER_LOCK_EXCLUSIVE); // 因为要更新buffer内容所以加排他锁
page = BufferGetPage(buf);
if (fsm_set_avail(page, slot, newValue)) {
MarkBufferDirtyHint(buf, false);
} // 如果fsm_set_avail更新FSM页面的slot取值成功,则把这个FSM页面放入脏页队列
if (minValue != 0 && search) {
newslot = fsm_search_avail(buf, minValue, addr.level == FSM_BOTTOM_LEVEL, true);
} // 查找空闲空间
UnlockReleaseBuffer(buf);
return newslot;
}
bool fsm_set_avail(Page page, int slot, uint8 value)
{
int nodeno = NonLeafNodesPerPage + slot; // slot时叶子节点编号,加NonLeafNodesPerPage得到数组编号
FSMPage fsmpage = (FSMPage)PageGetContents(page);
uint8 oldvalue;
Assert((unsigned int)(slot) < LeafNodesPerPage);
oldvalue = fsmpage->fp_nodes[nodeno];
if (oldvalue == value && value <= fsmpage->fp_nodes[0])
return false; // 如果新老值没变化,则返回false,表示未做修改
fsmpage->fp_nodes[nodeno] = value;
/*
* Propagate up, until we hit the root or a node that doesn't need to be
* updated.
*/
do {
uint8 newvalue = 0;
int lchild;
int rchild;
nodeno = parentof(nodeno);
lchild = leftchild(nodeno);
rchild = lchild + 1;
newvalue = fsmpage->fp_nodes[lchild];
if ((unsigned int)(rchild) < NodesPerPage)
newvalue = Max(newvalue, fsmpage->fp_nodes[rchild]);
oldvalue = fsmpage->fp_nodes[nodeno];
if (oldvalue == newvalue)
break;
fsmpage->fp_nodes[nodeno] = newvalue;
} while (nodeno > 0); // 自下而上更新这个FSM页面内的非叶子节点值
/*
* sanity check: if the new value is (still) higher than the value at the
* top, the tree is corrupt. If so, rebuild.
*/
if (value > fsmpage->fp_nodes[0])
fsm_rebuild_page(page); // 如果更新到最后发现本次更新的值还是大于根节点,那说明这个页面损坏了,调用fsm_rebuild_page,根据叶子节点更新所有非叶子节点。
return true;
}
bool fsm_rebuild_page(Page page)
{
FSMPage fsmpage = (FSMPage)PageGetContents(page);
bool changed = false;
int nodeno;
// 从最后一个非叶子节点开始,将其值更新为当前左右孩子的最大值
for (nodeno = NonLeafNodesPerPage - 1; nodeno >= 0; nodeno--) {
const int lchild = leftchild(nodeno);
int rchild = lchild + 1;
uint8 newvalue = 0;
/* The first few nodes we examine might have zero or one child. */
if ((unsigned int)(lchild) < NodesPerPage)
newvalue = fsmpage->fp_nodes[lchild];
if ((unsigned int)(rchild) < NodesPerPage)
newvalue = Max(newvalue, fsmpage->fp_nodes[rchild]);
if (fsmpage->fp_nodes[nodeno] != newvalue) {
fsmpage->fp_nodes[nodeno] = newvalue;
changed = true;
}
}
return changed;
}






