1. 抽象向量空间
1.1 向量和函数
函数和向量其实分享相同的性质:
适用于加和运算
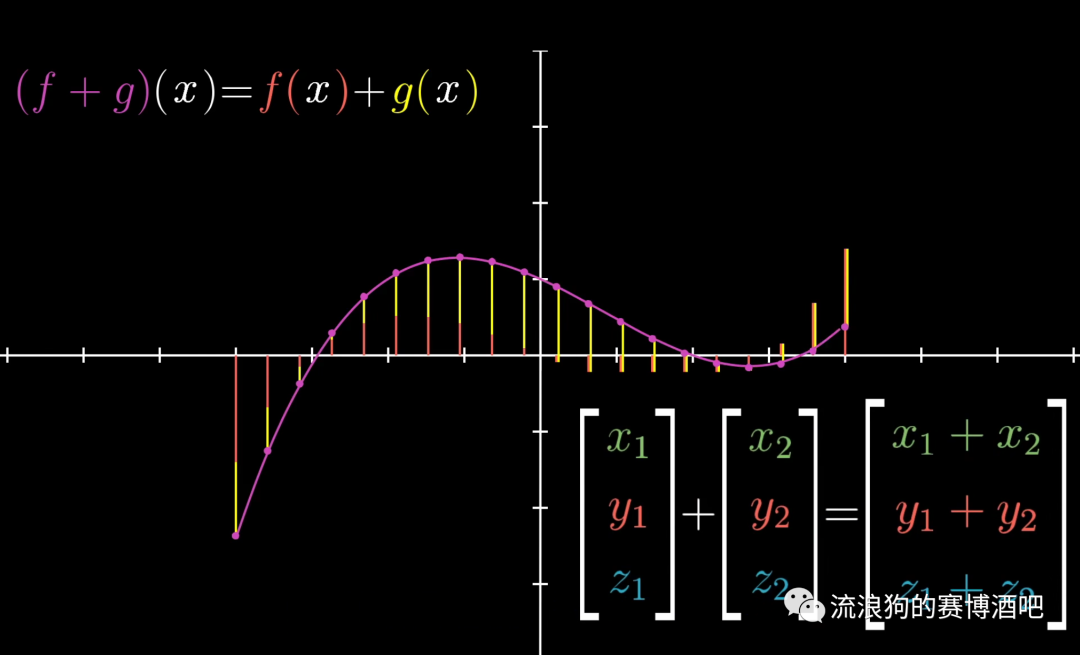
image-20211125124951002 适用于数乘运算
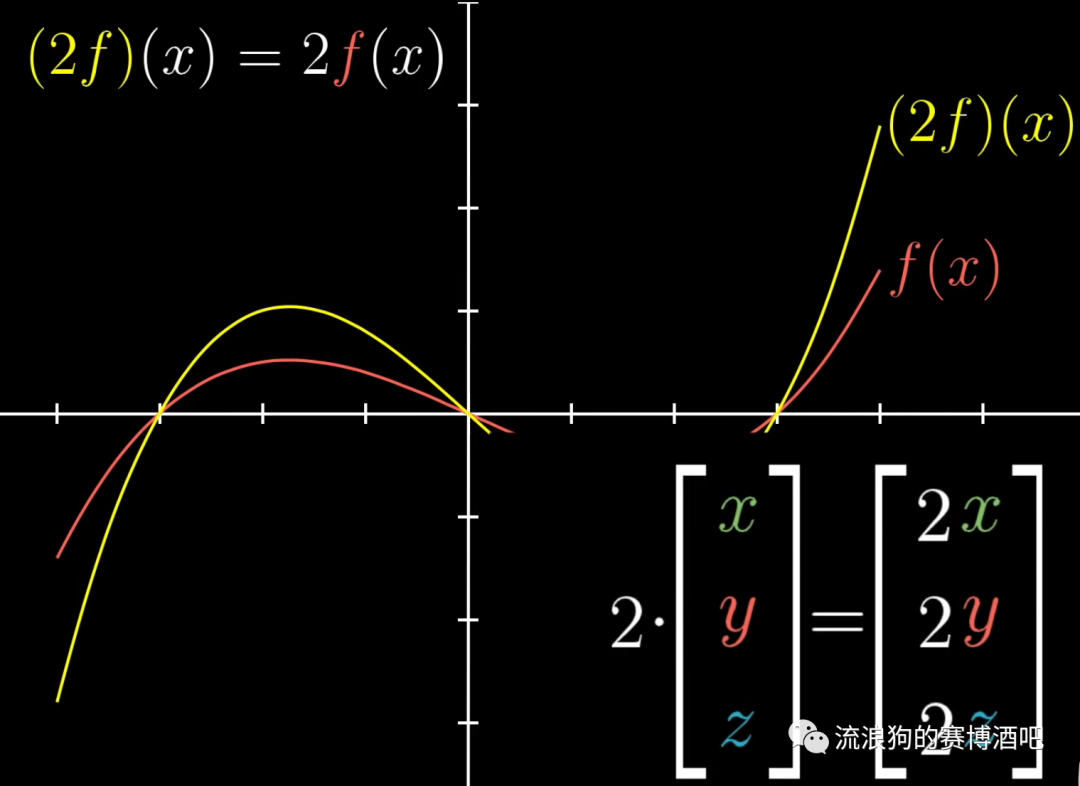
image-20211125125157980
1.2 函数的线性运算
我们已知向量的线性变换,需要变换后的向量依然满足下列两条性质:
可加性: 成比例:(一阶齐次):
那么怎样的函数变换可以被称为线性运算呢?
有一个常见的例子就是求导,因为求导具有可加性和成比例性:
求导的可加性:
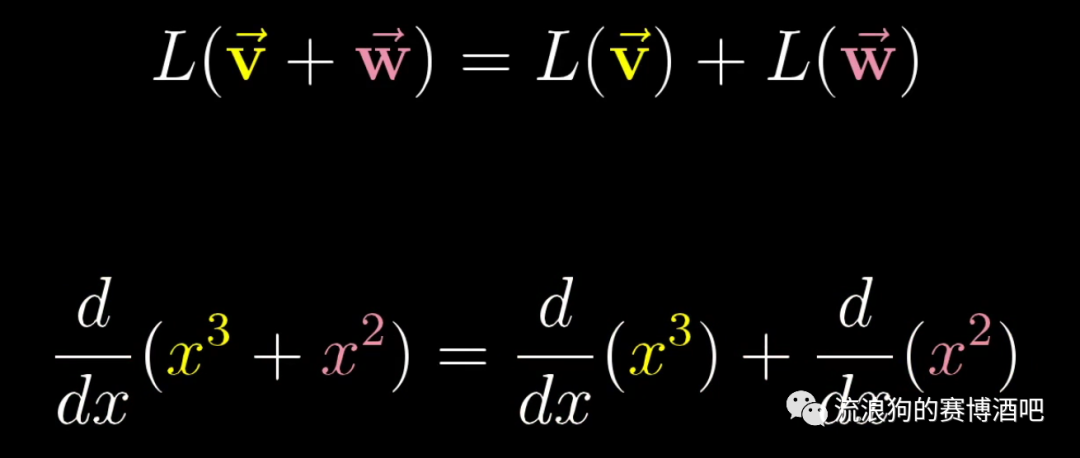
image-20211125130345639 求导的成比例性:
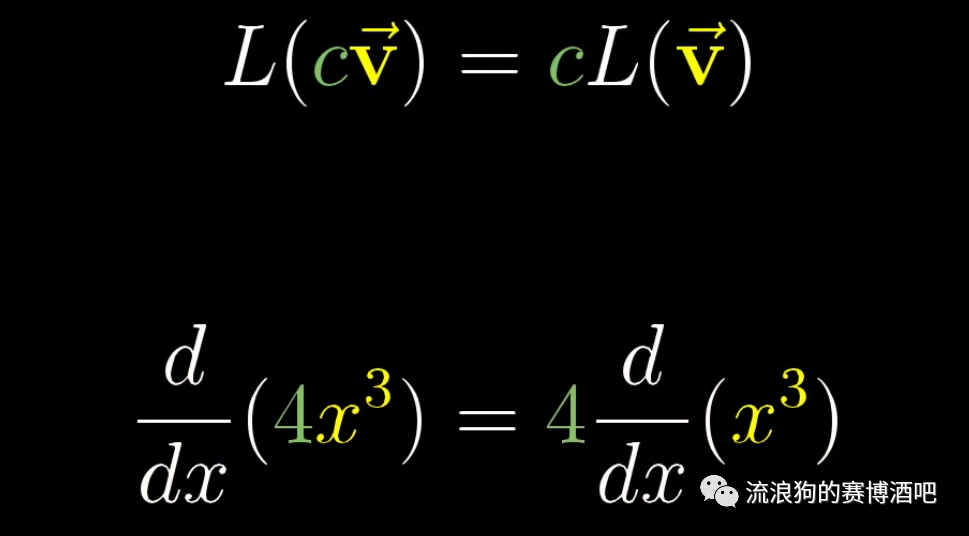
image-20211125130410815
因此,求导过程和线性变换之间应该是可以类比的。
1.3 用矩阵描述求导过程
首先,我们把求导对象限制在多项式空间中,但并不限制多项式的最高次数。这意味着,这个多项式空间有无穷维。
由于多项式的表达形式已经是线性组合形式,所以我们直接取的不同次幂作为基函数(basis function)。在这里,基函数与空间中的基向量的作用是一样的。

由于多项式是每个基函数乘以它的系数,所以可以被写成向量的形式,其每个基向量的标量就是每个基函数的系数。并且其形式通常表现为一串有限长的自然数后面跟着无限个0。
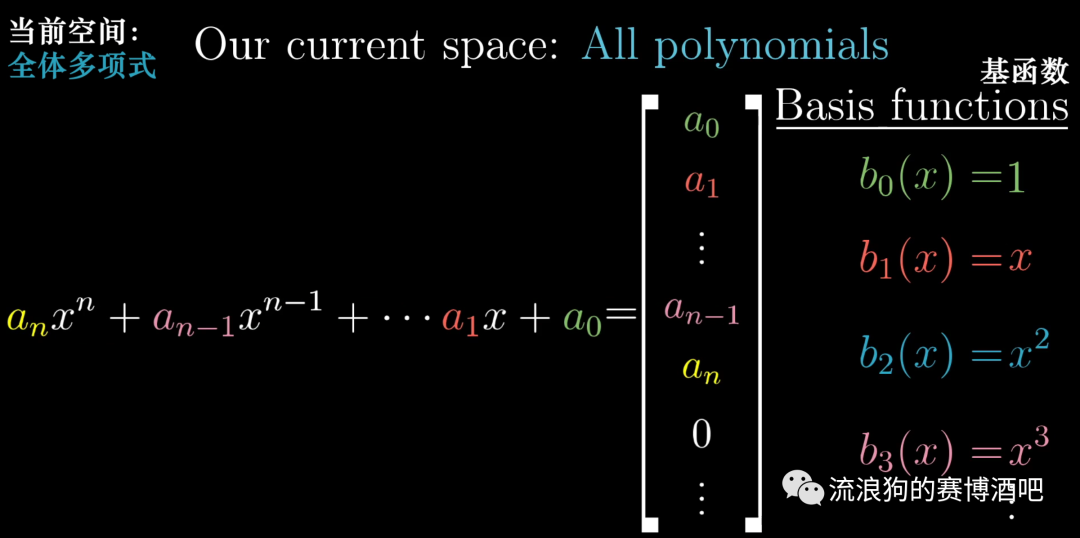
而求导过程,可以被描述为一个矩阵,其对角是从(0,1)开始的升序自然数列。

因此求任一多项式的导数,就可以描述为上述向量与上述矩阵的乘积。
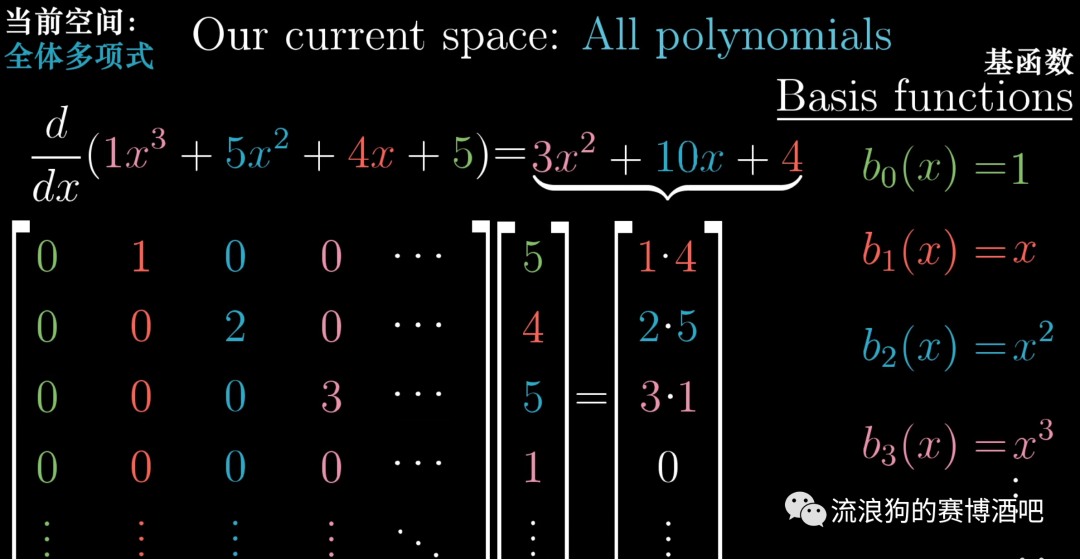
1.4 向量空间
不仅仅是求导。其他函数计算过程只要是满足线性条件,都可以使用线性代数中的概念,只是名称可能会发生一些改变,例如

并且不仅限于函数,只要我们处理的对象集具有合理的数乘和相加概念,线性代数中向量的相应概念都应该能运用到这个对象上。而这些类似向量的对象,其构成的集合被称为向量空间。
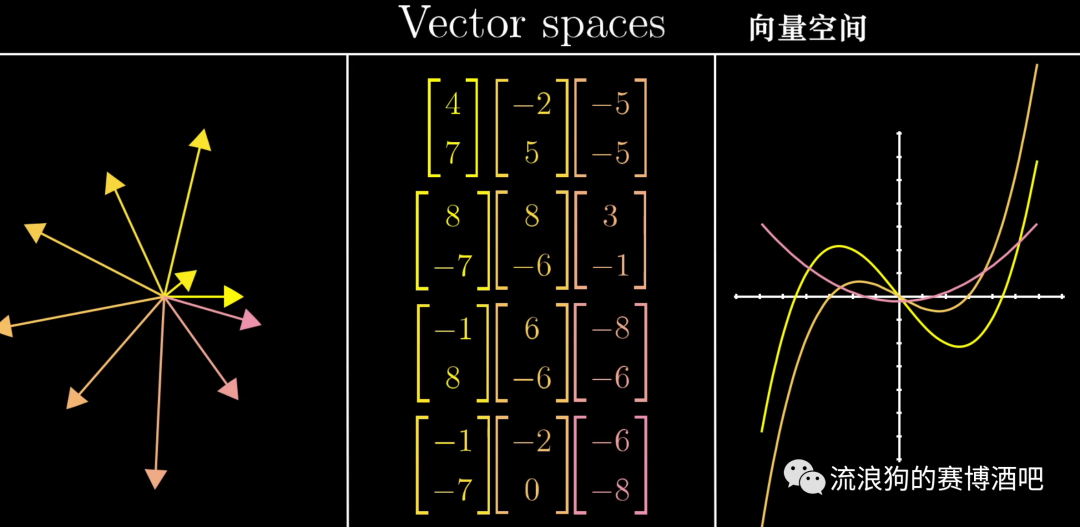
但如何判断这个向量空间是否满足使用线性代数结论的条件呢?方法是看这个向量空间是否满足以下8条公理(axioms)。而向量的具体形式其实并不重要。

现代快刷系列笔记部分到此结束,以后有用到的其他相关知识再补充。
重申, 以上笔记均来自3b1b的课程视频:线性代数的本质https://www.bilibili.com/video/BV1ys411472E?p=1
以下为全文字笔记链接:

文章转载自流浪狗的赛博酒吧,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






