随着移动互联网的快速发展,共享单车系统在近年来得到了广泛的应用和普及。基于固定站点的共享单车系统已经引起了学术界和工业界的广泛关注,研究重点主要集中在单车租赁需求预测、单车调度等方面。相比之下,关于共享单车骑行者路由算法的研究相对较少。一个路由方案通常涉及两个站点,指示骑行者在哪个地点租借和归还单车。现有的路由研究大多针对单个骑行者,但在高峰时段,多个骑行者同时发出路由请求,这一问题尚未得到充分的探讨。本次为大家带来数据库领域顶级期刊TKDE 2023的文章《Centralized Routing for Bike-Sharing Systems》。共享单车作为共享经济的典型产物,近年来迅速普及并受到广泛关注,特别是在解决“最后一公里”出行问题方面,成为通勤者的便利选择。目前,共享单车系统主要有两种类型:基于站点的系统和无桩系统。基于站点的系统通过在多个位置设置自行车架(桩),并在电子控制下进行管理,骑行者可以在一个站点租借自行车,并在另一个站点归还。无桩系统则不依赖固定站点,骑行者可通过移动应用解锁并在任何合适位置停车。本文主要聚焦于基于站点的共享单车系统。在基于站点的系统中,骑行者面临的核心问题是如何选择取车和还车的站点,以尽量减少步行距离。为此,现有研究通常通过历史数据预测站点的自行车和车位的可用性。然而,这些研究多忽视了高峰时段多个骑行者同时发起路由请求的情况。虽然可以逐个解决骑行者的路由问题,但这种单个骑行者的短期视角难以提供全局最优解。前期处理的骑行者可能会占用某些自行车或车位,导致后续骑行者无法获取所需资源。因此,仅依靠个别最优解并不能确保全局最优,尤其是在资源有限的情况下。目前,关于共享单车集中路由问题的研究仍较为缺乏。该问题的挑战在于站点上自行车和车位的有限数量,多个骑行者可能争夺同一站点的资源,导致无法同时满足所有骑行者的需求。因此,需要在解决资源冲突的同时,优化骑行者的整体出行时间。因此本文研究了共享单车骑行者的集中路由问题,并证明了该问题是NP-hard的。本文将其表述为整数线性规划模型,并提出了一种舍入算法和基于贪心策略的路由算法为共享单车系统的优化提供新的解决方案。在现有研究中,整数线性规划(ILP)方法已被用于解决kDM问题(k-dimensional matching),因此本文首先证明共享单车骑行者路由问题可以等价地表述为一个整数线性规划问题,通过对其线性规划(LP)松弛解进行舍入,设计了一种ILP的近似求解方法,即LPround: • 排名构建(第1至第7行):这一部分算法首先为每个骑行者初始化一个默认的步行路径,然后通过线性规划求解每个骑行者的取车和还车站点建议。接着,去掉不可能的路径(如没有车或车位的站点),最后按路径的优先级进行排序,保留最有可能满足需求的路径。• 按排名进行舍入(第7至第15行):这一步,算法按照之前排序的优先级,逐一决定哪些路径可以被选为最终的取车或还车站点。对于每条路径,算法检查是否有足够的资源(如自行车或车位)来满足骑行者的需求。如果有,就将这条路径选入最终方案,并更新站点的资源状态;如果没有,就跳过这条路径,继续考虑其他可能的路径。时间成本分析:LP舍入方法的时间复杂度并未明确给出,因为本文使用了单纯形算法来求解该问题,而单纯形算法的时间复杂度仍然未知。然而,可以明确的是,pool(存放<i, j1, j2>三元组的池)的大小与程序中的变量数量相关,而变量数量又与解空间的大小正相关。变量数量众多导致了一个相当大的搜索空间,因此LP方法的时间成本也较大。 贪心启发式方法已广泛应用于求解组合优化问题,并取得了较好的表现。因此本文提出了一种基于贪心策略的路由算法,该算法通过贪心选择为骑行者分配最优路由计划。如算法2所示,贪心算法分为两个步骤:• 初始化(第1至第11行):在第1至第4行,算法为每个请求初始化路由计划,默认将骑行者从起点直接步行到终点。在第6至第11行,对于每个由请求和两个站点组成的可能三元组,计算相应的出行时间,并将其作为候选路由计划加入pool,前提是其出行时间小于步行的时间。• 贪心式站点分配(第12至第20行):当pool不为空时,贪心算法不断从pool中选择节省骑行时间最多的三元组(即相对于步行来说节省的时间最大)。每次选择一个三元组后,贪心算法通过将sj1和sj2分别分配给pi*.sj1和pi*.sj2来更新ri的路由计划。由于ri已经被分配了站点,贪心算法会将包含ri的所有三元组从pool中移除。接着,算法将sj1和sj2的自行车和车位数量各自减少1。如果减去后的bj1为0,表示sj1站点的自行车已经被借完,贪心算法会移除所有包含sj1作为取车站点的三元组。同样,dj2在第19行也会按照类似的方式进行检查。时间复杂度分析:初始化阶段的时间复杂度为 O(mn2),其中m为请求数量,n为车站数量,主要由第6至第11行遍历三元组的操作决定。每次while循环的执行时间复杂度为 O(mn2)。由于最多有m个请求需要路由,因此while循环的时间复杂度为 O(m2n2)。总体贪心算法的时间复杂度为O(m2n2)。本文提出了一种基于排序的遍历方法,通过剪枝三元组来加速pool的计算。一种简单的实现方法是遍历所有可能的三元组 R×S×S,这会导致总共测试mn2个三元组。本文通过剪枝不可能的三元组来优化计算成本,即排除那些总出行时间大于步行时间的三元组。对于某个特定的骑行者ri,本文首先将各车站到骑行者起点和终点的步行时间按升序排序,这样得到两个排序列表,分别表示从起点和终点出发到各个车站的步行时间,记作 和
和 。接着从列表开始,依次检查和测试
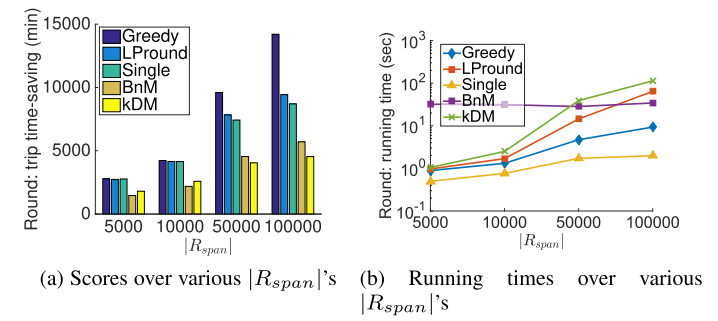
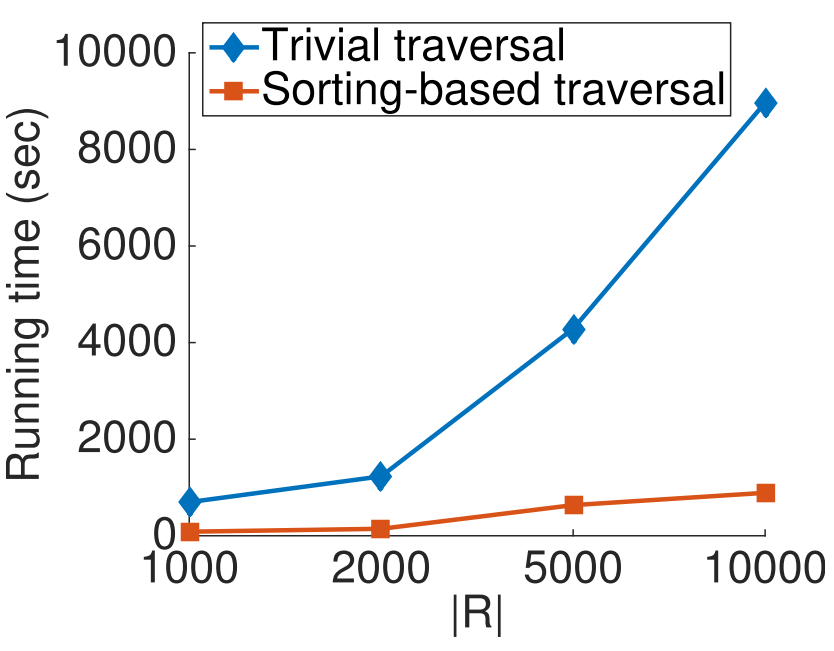
。接着从列表开始,依次检查和测试  中的元素,直到找到某个车站满足以下条件:数据集. 论文使用了三个真实数据集GeoLife、T-drive、AIS以及一个合成数据集Brinkhoff。实验使用了Citi Bike在纽约曼哈顿部署的自行车站点数据,共有411个站点。对于步行速度和骑行速度,分别用vw和vb表示,默认值设定为5 km/h和20 km/h。对比方法. 本文将提出的贪心算法(Greedy)和LP舍入方法(LPround)与三个基准方法进行比较:Single[1]、kDM[2]和BnM[3]。Computing pool:本文首先调查了使用简单遍历方法和基于排序的遍历方法(算法3)计算池所需的时间,结果如图1所示。结果明显,基于排序的遍历方法比简单遍历更高效,得益于其剪枝策略。此外,简单遍历的运行时间随着请求数量的增加呈指数增长。相比之下,基于排序的遍历方法的运行时间增长保持平稳。即使请求数量达到1万,其计算时间也仅为数百秒,仍然非常高效。LP-Based Methods:对于两种线性规划舍入方法——LPround和kDM,本文通过调整z来控制程序中的变量数量,如图2所示。 如图2a所示,LPround的得分明显高于kDM。如前所述,将kDM应用于实验任务时,得到的线性程序中的变量数量是LPround的
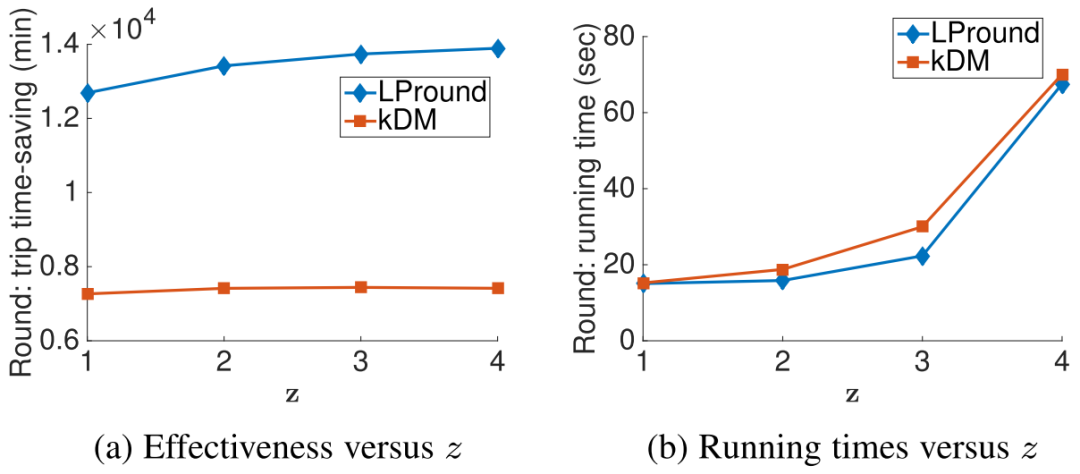
中的元素,直到找到某个车站满足以下条件:数据集. 论文使用了三个真实数据集GeoLife、T-drive、AIS以及一个合成数据集Brinkhoff。实验使用了Citi Bike在纽约曼哈顿部署的自行车站点数据,共有411个站点。对于步行速度和骑行速度,分别用vw和vb表示,默认值设定为5 km/h和20 km/h。对比方法. 本文将提出的贪心算法(Greedy)和LP舍入方法(LPround)与三个基准方法进行比较:Single[1]、kDM[2]和BnM[3]。Computing pool:本文首先调查了使用简单遍历方法和基于排序的遍历方法(算法3)计算池所需的时间,结果如图1所示。结果明显,基于排序的遍历方法比简单遍历更高效,得益于其剪枝策略。此外,简单遍历的运行时间随着请求数量的增加呈指数增长。相比之下,基于排序的遍历方法的运行时间增长保持平稳。即使请求数量达到1万,其计算时间也仅为数百秒,仍然非常高效。LP-Based Methods:对于两种线性规划舍入方法——LPround和kDM,本文通过调整z来控制程序中的变量数量,如图2所示。 如图2a所示,LPround的得分明显高于kDM。如前所述,将kDM应用于实验任务时,得到的线性程序中的变量数量是LPround的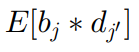 倍。这意味着kDM的线性程序更加复杂,在程序无法在迭代次数限制内最优求解时,导致其解决质量较差。程序复杂度也解释了kDM在时间效率上的较低表现,如图2b所示。Real Trips:如图3所示,方法在节省时间上的排名仅受∣Rspan∣的影响。针对相同的∣Rspan∣,各方法在真实行程中的时间节省要小于合成的行程。这是因为与合成行程相比,真实行程的距离通常较短,尤其是合成行程的起点和终点是随机生成的,往往距离较远。这些较短的旅行减少了使用自行车节省大量时间的可能性。实际上,这些非通勤的短途行程并不以节省时间为目标,因此不属于本文问题的关注范围。出于相同的原因,当∣Rspan∣较小时,产生的显著通勤行程较少,这时很难区分Greedy、LPround和SINGLE的效果。当∣Rspan∣较大时,与合成出行结果相比,Greedy依然能比LPround节省更多时间。这也是由于短途行程的影响。较短的旅行距离使得骑行方案较少,导致池的大小变小。较小的池意味着解空间较小,这时简单的Greedy方法表现较好。在运行时间上,Greedy仍然足够高效,仅比SINGLE稍慢。本文研究了共享单车系统中的路由问题。与现有研究不同,本文考虑了多个出行请求在车站有限的自行车和车位资源下的竞争。本文对该问题进行了形式化建模,并提出了其对应的线性规划表达式。研究结果表明,该问题是NP难题,因此,本文提出了两种近似算法来解决该问题:LP舍入算法和基于贪心策略的算法。LP舍入算法将问题转化为整数线性规划,而贪心算法则按照三元组得分的降序进行选择。通过大量实验,结果表明,贪心算法在效率和效果上都表现良好。而LP舍入算法则在处理大量通勤出行请求时具有更强的竞争力,但其运行时间较长。[1] Gast N, Massonnet G, Reijsbergen D, et al. Probabilistic forecasts of bike-sharing systems for journey planning[C]//Proceedings of the 24th ACM international on conference on information and knowledge management. 2015: 703-712.[2] Chan Y H, Lau L C. On linear and semidefinite programming relaxations for hypergraph matching[J]. Mathematical programming, 2012, 135(1): 123-148.[3] Munkres J. Algorithms for the assignment and transportation problems[J]. Journal of the society for industrial and applied mathematics, 1957, 5(1): 32-38.
倍。这意味着kDM的线性程序更加复杂,在程序无法在迭代次数限制内最优求解时,导致其解决质量较差。程序复杂度也解释了kDM在时间效率上的较低表现,如图2b所示。Real Trips:如图3所示,方法在节省时间上的排名仅受∣Rspan∣的影响。针对相同的∣Rspan∣,各方法在真实行程中的时间节省要小于合成的行程。这是因为与合成行程相比,真实行程的距离通常较短,尤其是合成行程的起点和终点是随机生成的,往往距离较远。这些较短的旅行减少了使用自行车节省大量时间的可能性。实际上,这些非通勤的短途行程并不以节省时间为目标,因此不属于本文问题的关注范围。出于相同的原因,当∣Rspan∣较小时,产生的显著通勤行程较少,这时很难区分Greedy、LPround和SINGLE的效果。当∣Rspan∣较大时,与合成出行结果相比,Greedy依然能比LPround节省更多时间。这也是由于短途行程的影响。较短的旅行距离使得骑行方案较少,导致池的大小变小。较小的池意味着解空间较小,这时简单的Greedy方法表现较好。在运行时间上,Greedy仍然足够高效,仅比SINGLE稍慢。本文研究了共享单车系统中的路由问题。与现有研究不同,本文考虑了多个出行请求在车站有限的自行车和车位资源下的竞争。本文对该问题进行了形式化建模,并提出了其对应的线性规划表达式。研究结果表明,该问题是NP难题,因此,本文提出了两种近似算法来解决该问题:LP舍入算法和基于贪心策略的算法。LP舍入算法将问题转化为整数线性规划,而贪心算法则按照三元组得分的降序进行选择。通过大量实验,结果表明,贪心算法在效率和效果上都表现良好。而LP舍入算法则在处理大量通勤出行请求时具有更强的竞争力,但其运行时间较长。[1] Gast N, Massonnet G, Reijsbergen D, et al. Probabilistic forecasts of bike-sharing systems for journey planning[C]//Proceedings of the 24th ACM international on conference on information and knowledge management. 2015: 703-712.[2] Chan Y H, Lau L C. On linear and semidefinite programming relaxations for hypergraph matching[J]. Mathematical programming, 2012, 135(1): 123-148.[3] Munkres J. Algorithms for the assignment and transportation problems[J]. Journal of the society for industrial and applied mathematics, 1957, 5(1): 32-38.
李佳俊 重庆大学计算机技术专业2023级硕士生,重庆大学Start Lab成员。主要研究方向:时空数据挖掘 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有3~5名研究生名额,欢迎计算机、GIS等相关专业的学生报考!
图文|李佳俊
校稿|何 翔
编辑|朱明辉
审核|李瑞远
审核|杨广超



 和
和 。接着从列表开始,依次检查和测试
。接着从列表开始,依次检查和测试  中的元素,直到找到某个车站满足以下条件:
中的元素,直到找到某个车站满足以下条件: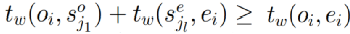

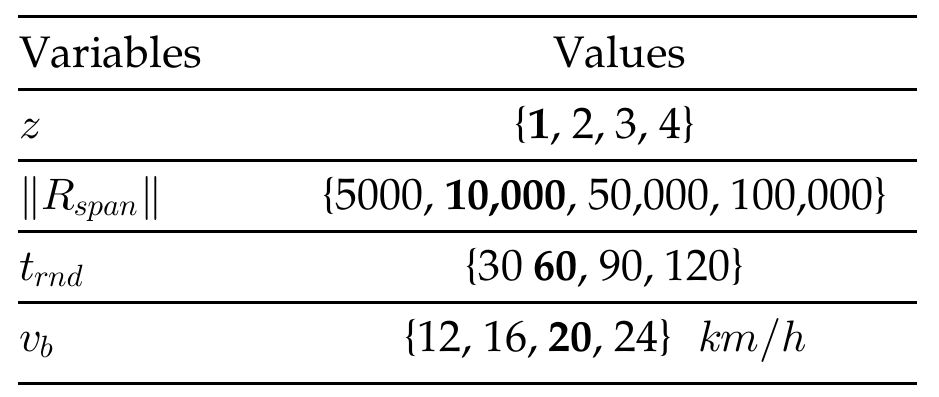
 倍。这意味着kDM的线性程序更加复杂,在程序无法在迭代次数限制内最优求解时,导致其解决质量较差。程序复杂度也解释了kDM在时间效率上的较低表现,如图2b所示。
倍。这意味着kDM的线性程序更加复杂,在程序无法在迭代次数限制内最优求解时,导致其解决质量较差。程序复杂度也解释了kDM在时间效率上的较低表现,如图2b所示。