在许多基于轨迹数据的应用中,轨迹简化已经成为一项重要任务。虽然针对这项任务提出了许多方法,但它们都存在各种问题,包括(1)不是全局优化整个轨迹数据库的简化效果,(2)大多数方法假设所有轨迹具有相同的压缩率,但实际不同轨迹具有不同的采样率或复杂度,(3)非查询驱动。本次为大家带来数据库领域顶级会议ICDE的论文《Collectively
Simplifying Trajectories in a Database: A Query Accuracy Driven Approach》
随着GPS设备、智能手机等移动计算和地理定位技术的进步,空间中各种运动物体(如人、车辆)产生了大量的轨迹数据,这些数据被收集并服务于各种应用,例如挖掘热门路线或识别乘车候选者。由于存储和查询海量轨迹数据的成本很高,因此引入了轨迹简化技术,旨在减少轨迹的大小,从而减少存储并加快查询速度,同时保留尽可能多的信息。轨迹简化旨在从轨迹中删除点以节省存储成本并加快查询速度,其理念在于删除携带不重要信息的点。然而,现有的研究方向大多为“基于误差驱动的轨迹简化”(EDTS),没有针对于简化轨迹的查询准确性进行优化。此外,现有的简化技术是局部性质的,基于每条轨迹操作。基于此,论文提出了基于查询准确性的轨迹简化问题(QDTS),给定轨迹数据库D和一个存储预算W,查询驱动的轨迹简化旨在找到一个简化后的轨迹数据库D',使得在D和D'上的查询结果之间的差异最小化。对于QDTS问题存在三个挑战:挑战1:面对不同采样率或不同复杂度的轨迹如何实现个性化的压缩率?挑战2:如何直接优化简化数据库的查询准确性?挑战3:如何设计高效的算法来处理大规模的轨迹数据,并确保简化过程具有良好的扩展性。因此,论文提出了一种基于多智能体强化学习的解决方案RL4QDTS,它避免了现有方法的上述问题。论文的主要贡献如下:- 提出了QDTS问题,旨在给定的存储预算内找到一个简化的轨迹数据库,尽量保持简化数据库上的查询准确性,这是对轨迹简化领域的首次系统研究。
- 开发了一种基于多智能体强化学习的解决方案RL4QDTS,它与轨迹数据的索引相结合,协同简化轨迹数据库,旨在优化简化数据库上的查询准确性,提高效率,展示了RL4QDTS的目标与QDTS问题的目标是一致的。
- 在四个真实轨迹数据集上进行了实验,结果表明,在两种适应性、四种误差度量以及不同存储预算下,针对五种查询操作,RL4QDTS始终优于现有的EDTS解决方案。例如,对于范围查询,其改进达到了35%,对于两种kNN查询分别为41%和28%,对于相似度查询为35%,对于聚类为40%,均优于最佳基线方法。
RL4QDTS算法从最简化的数据库开始,其中每个原始轨迹 T 的简化轨迹 T' 仅包含 T 的第一个和最后一个点。然后,它迭代地将原始点引入简化的数据库,直到预算耗尽。为了提高效率,它在轨迹数据库上构建了一个八叉树。每当需要选择一个点时,它首先在八叉树中选择一个立方体,然后在该立方体中选择一个点。八叉树将二维空间和一维时间空间递归地分割为 8 个子空间,称为立方体。这本质上是两个决策任务的顺序过程,具体来说,RL4QDTS 使用Agent-Cube来遍历八叉树以找到一个立方体,然后,使用Agent-Point来选择立方体中要插入简化数据库的点。这两个决策过程被建模为马尔科夫决策过程(MDP),并被设计为智能体协作地优化简化数据库上的查询准确性。考虑选择立方体的任务,Agent-Cube通过自顶向下地遍历八叉树来选择一个立方体,从根节点开始。每次它访问一个节点时,它都会决定是否停止。如果停止,意味着选择了该节点的立方体;否则,它会决定访问8个子节点中的哪一个节点,MDP涉及状态,动作和奖励。a. 状态(State):论文用sc表示Agent-Cube的MDP中的一个状态,用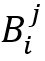 表示一个立方体,位于第i层并对应于其父节点的第j个节点。对于
表示一个立方体,位于第i层并对应于其父节点的第j个节点。对于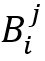 ,使用落入其中的轨迹数量
,使用落入其中的轨迹数量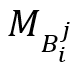 和查询数量
和查询数量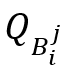 来捕捉数据和查询的分布情况,如下所示:
来捕捉数据和查询的分布情况,如下所示: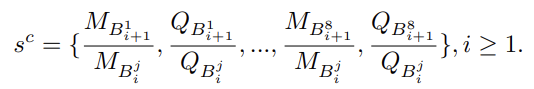
为了避免数据规模问题,状态的值通过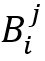 中的轨迹和查询总数进行归一化。
中的轨迹和查询总数进行归一化。b. 动作(Actions):论文用ac表示MDP的一个动作,当访问立方体为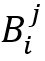 时,定义了两种可能的动作类型:(1)继续访问8个节点之一,(2)停止遍历并将当前立方体返回给Agent-Point以选择立方体内的点。动作ac通过ac=k (1≤k≤9)进行定义,其中ac=1至8表示继续访问立方体的子节点,ac=9表示停止遍历。
时,定义了两种可能的动作类型:(1)继续访问8个节点之一,(2)停止遍历并将当前立方体返回给Agent-Point以选择立方体内的点。动作ac通过ac=k (1≤k≤9)进行定义,其中ac=1至8表示继续访问立方体的子节点,ac=9表示停止遍历。
c. 奖励(Rewards):当动作是(1)时,由于尚未向简化数据库中插入点,奖励不能被立即观察到。当动作是(2)时,简化数据库将被更新,并且可以获取一些奖励信号(例如,通过比较在原始数据库和简化数据库上的查询准确性来获取这些信号)。总之,Agent-Cube最终会选择一个立方体供Agent-Point选择,并获得一定的奖励信号。他们合作学习查询感知策略,因此Agent-Cube和Agent-Point共享相同的奖励。
2.3 Agent-Point:选择点的MDP
论文将Agent-Cube选择的立方体记为B,定义Agent-Point在B内选择要引入到数据库中的点的MDP。
a. 状态(State):令sp表示Agent-Point的MDP的状态,用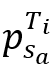 和
和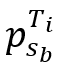 分别表示轨迹Ti中立方体内的首尾点。对于满足sa≤sj ≤sb的每个点
分别表示轨迹Ti中立方体内的首尾点。对于满足sa≤sj ≤sb的每个点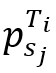 ,定义一对值
,定义一对值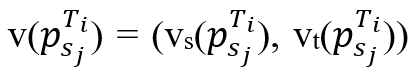 .其中
.其中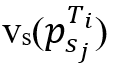 等于
等于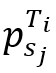 与同步点之间的“空间”距离,
与同步点之间的“空间”距离,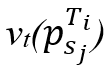 等于
等于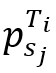 与其在轨迹Ti上相邻两点间线段上最接近点之间的时间差。然后,在每个轨迹Ti的所有点中,找到具有最大vs值的点
与其在轨迹Ti上相邻两点间线段上最接近点之间的时间差。然后,在每个轨迹Ti的所有点中,找到具有最大vs值的点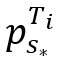 ,其中s*为索引,即
,其中s*为索引,即
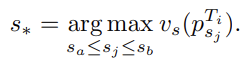
最后,状态sp定义为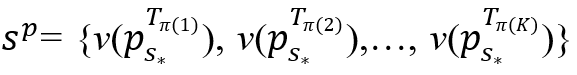 ,其中π表示T1,T2,…,
,其中π表示T1,T2,…,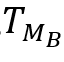 的排列顺序,使得
的排列顺序,使得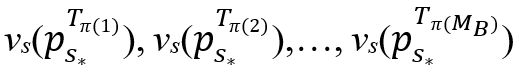 按降序排列。K(K≤MB)是一个可根据经验调节的参数,用来控制状态空间的大小。
按降序排列。K(K≤MB)是一个可根据经验调节的参数,用来控制状态空间的大小。
b. 动作(Actions):动作的设计与sp保持一致,动作定义如下:ap = k (1 ≤ k ≤K),其中ap表示将点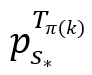 插入到D‘。
插入到D‘。
c. 奖励(Rewards):选择在插入∆个点后执行查询以实现累积效应,在状态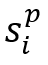 和
和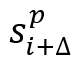 分别考虑简化数据库D’和D’’,定义奖励R如下:
分别考虑简化数据库D’和D’’,定义奖励R如下:
R = diff(Q(D),Q(D’)) - diff(Q(D), Q(D’’))其中diff(Q(D), Q(D’))衡量了在D和D‘上查询结果的差异,让奖励R在从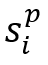 到
到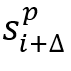 的所有相关转换中共享,以及在此过程中涉及的Agent-Cube的转换。累计奖励的计算公式如下:
的所有相关转换中共享,以及在此过程中涉及的Agent-Cube的转换。累计奖励的计算公式如下: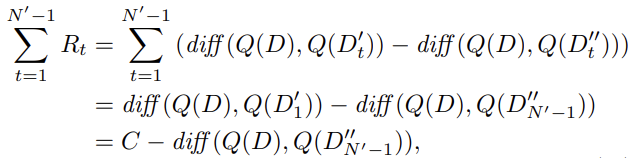
其中Dt‘(Dt’’)表示执行动作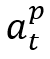 之前(之后)处于状态
之前(之后)处于状态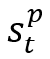 的简化数据库,将初始项diff(Q(D), Q(D1’))视为常数C,并且在该状态下尚未插入点,即MDP的目标是最小化
的简化数据库,将初始项diff(Q(D), Q(D1’))视为常数C,并且在该状态下尚未插入点,即MDP的目标是最小化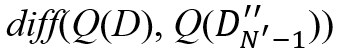 。
。
2.4 DQN(Deep Q-Network)的策略学习
MDP的核心问题是找到一个最优策略,该策略指导智能体在特定状态下选择动作,从而使累积奖励最大化。考虑上述MDP是连续的,采用DQN来学习Agent-Cube和Agent-Point的策略。具体来说,采用具有重放记忆的深度Q学习来学习策略,对Agent-Cube表示为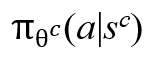 ,对Agent-Point表示为
,对Agent-Point表示为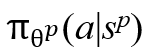 。该策略通过DQN在给定状态sc或sp中采用动作a,其参数由
。该策略通过DQN在给定状态sc或sp中采用动作a,其参数由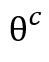 或
或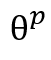 表示。
表示。
如算法1所示,首先为原始轨迹数据库D构建八叉树(第2行),然后将每条轨迹的第一个和最后一个点插入简化轨迹数据库D'(第3 - 5行),剩余的预算W-2M在第6~9行中利用。首先调用Agent-Cube选择一个立方体B,然后将立方体传递给Agent-Point更新D',这个过程一直持续到预算耗尽,最终返回包含W个点的D'(第10行)。
在算法2中,Agent-Cube首先初始化索引h和l来表示立方体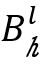 (第2行),为了对立方体采样,用上述公式构造状态
(第2行),为了对立方体采样,用上述公式构造状态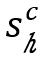 (第四行),并使用策略
(第四行),并使用策略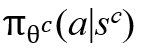 对动作
对动作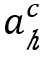 进行采样(第5行)。如果
进行采样(第5行)。如果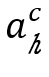 = 9或者探索达到树的最后一级,则中断并返回当前立方体B(第6~8行);否则,通过h←h+1和l←
= 9或者探索达到树的最后一级,则中断并返回当前立方体B(第6~8行);否则,通过h←h+1和l←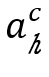 更新索引并探索下一个立方体
更新索引并探索下一个立方体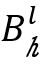 (第9~12行)。
(第9~12行)。
在算法3中,Agent-Point首先以一个立方体B作为输入,计算出每条轨迹Tj的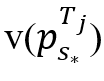 的值,其中1 ≤ j ≤ MB(第2行)。然后,它使用一个最大优先队列来维护这些值的降序排列π(第3行)。接下来,通过上述公式来构造一个状态sp(第4行),并使用策略
的值,其中1 ≤ j ≤ MB(第2行)。然后,它使用一个最大优先队列来维护这些值的降序排列π(第3行)。接下来,通过上述公式来构造一个状态sp(第4行),并使用策略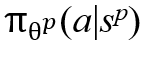 对其采样,其中sp作为输入(第5行)。令ap = k (1 ≤ k≤ K)表示采样动作,通过将点
对其采样,其中sp作为输入(第5行)。令ap = k (1 ≤ k≤ K)表示采样动作,通过将点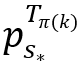 插入到D‘来执行该动作(第6行)。
插入到D‘来执行该动作(第6行)。
图1是RL4QDTS的一个运行示例,为了方便演示,忽略时间维度,使用四叉树。输入D = <T1,T2,T3>,存储预算W = 7,两个范围查询Q1,Q2。基于D,有Q1(D) = <T2>,Q2(D) = <T2,T3>,记录树节点中的轨迹数(MB)和查询数(QB)。(1)将每条轨迹的首尾点插入D‘,剩余预算1(即7-2*3)。(2)Agent-Cube从节点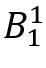 开始构造其状态,观察4个子节点,采取探索节点
开始构造其状态,观察4个子节点,采取探索节点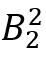 的动作。(3)在
的动作。(3)在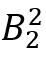 处采取探索节点
处采取探索节点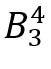 的动作。(4)在
的动作。(4)在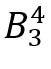 处,Agent-Cube接收到
处,Agent-Cube接收到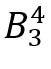 提供给Agent-Point的动作。(5)Agent-Point在
提供给Agent-Point的动作。(5)Agent-Point在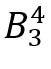 处构造状态,并采取将点p5插入到D‘的动作。(6)最后,因为耗尽预算,算法中断并返回D’,输出与查询D相同的结果。
处构造状态,并采取将点p5插入到D‘的动作。(6)最后,因为耗尽预算,算法中断并返回D’,输出与查询D相同的结果。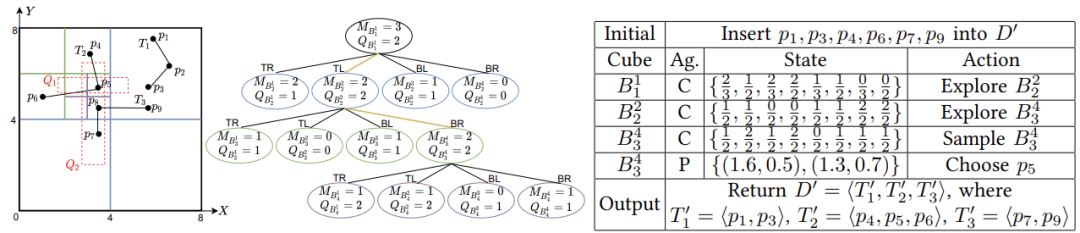
时间复杂度:RL4QDTS算法的时间复杂度为O(N+ W(n + log MB)),其中N、W、n和MB分别表示D中点的总数、存储预算、输入轨迹中点的最大数量,以及数据立方体中轨迹的最大数量。具体来说,构建D上的八叉树需要O(N)的时间,其中最大树深度E是一个小常数。处理剩余的W - 2M个点的部分主导了复杂度,包括:(1)通过Agent-Cube选择立方体的复杂度为O(1),它探索八叉树的有界级别;(2)通过Agent-Point计算值的复杂度为O(n);(3) 使用复杂度为O(logMB)的最小优先队列进行维护;(4) 假设K是一个小常数,通过Agent-Point构造状态、采样动作和插入点的复杂度为O(1)。数据集:实验在Geolife、T-Drive、Chengdu和OSM四个真实世界的轨迹数据集上进行。Geolife包含了182个用户五年的轨迹数据,T-Drive包含了来自北京的10,357辆出租车一周内的轨迹数据,Chengdu包含了滴滴出行发布的7天的出租车轨迹数据,OSM用于测试可扩展性,包含了由OpenStreetMap社区发布的30亿个点的轨迹数据。基线:实验将Top-Dowm、Bottom-up、RLTS+和Span-Search这四种方法作为基线方法进行比较,其中Span-Search只对应一种误差度量DAD并且只进行“E”(E:逐个简化每条轨迹)调整,其余方法对应误差度量SED、PED、DAD和SAD以及一种调整(“E”和“W”,W:将数据库作为整体,同时简化所有轨迹)。参数设置:Agent-Cube和Agent-Point分别采用两层的前馈神经网络来实现,他们的第一层都有25个神经元,tanh作为激活函数,第二层Agent-Cube有9个神经元,Agent-Point有K个神经元,K设置为2,对应于线性函数的动作空间。基于经验结果,参数S和E分别设置为9和12。在训练过程中,我们随机抽样了6,000至48,000条轨迹数据,分为12个数据库进行训练。每个数据库生成了五个episode来训练策略,并在训练过程中选择具有最佳性能的模型。使用Adam随机梯度下降算法进行模型训练,初始学习率为0.01。范围查询用于构建状态和获取奖励,设置∆=
50,每50个点插入时执行100个查询,以评估模型性能。 实验对比了五种查询任务在三种查询分布下的算法有效性,确定了在数据、高斯和真实分布下各个查询任务的最佳表现算法。如图2、图3和图4所示,结果表明RL4QDTS算法提供更高质量的查询结果,在不同压缩率、查询任务、生成分布和真实数据集上均优于现有的基于误差驱动的方法。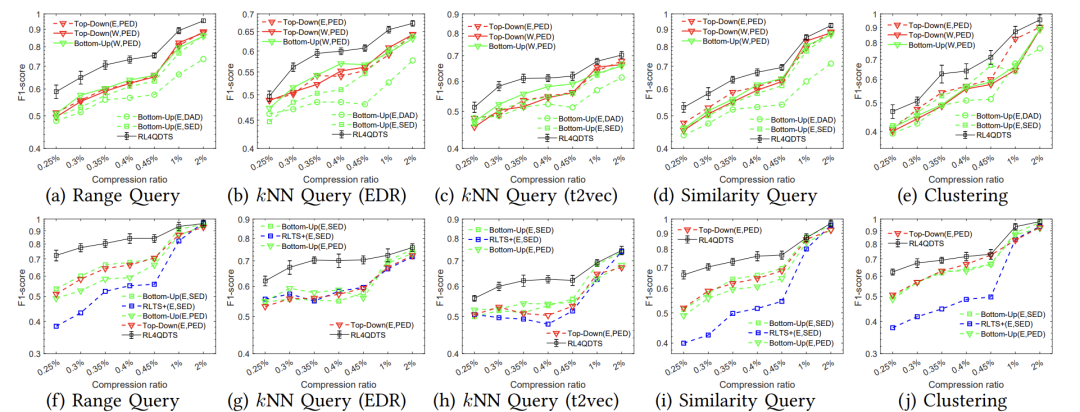
(数据分布(a)-(e)和高斯分布(f)-(j))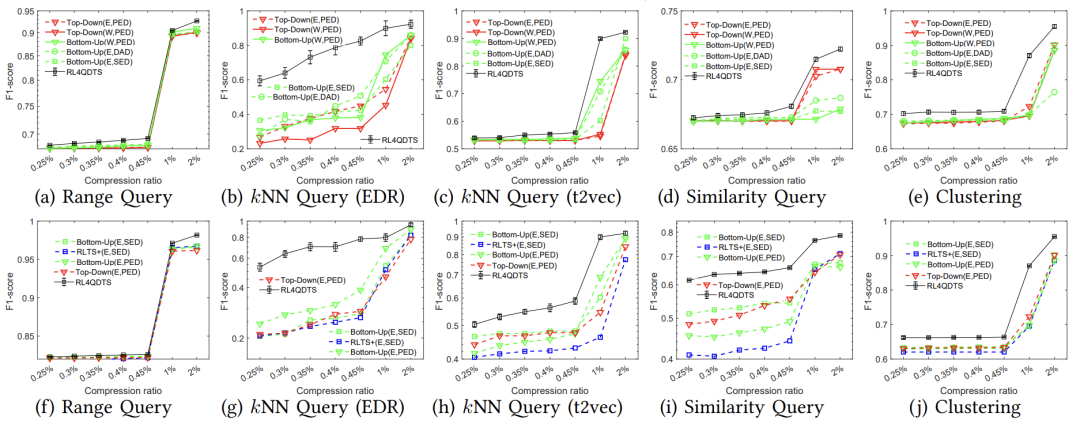
(数据分布(a)-(e)和高斯分布(f)-(j))
图4在Chengdu上与基线的有效性比较(真实分布(a)-(e))变形研究:如图5所示,论文运行了100个范围查询,以SED度量原始轨迹与简化轨迹之间的变形程度,结果显示RL4QDTS算法的SED始终低于选择的基线方法,表明RL4QDTS算法是一种查询感知的解决方案。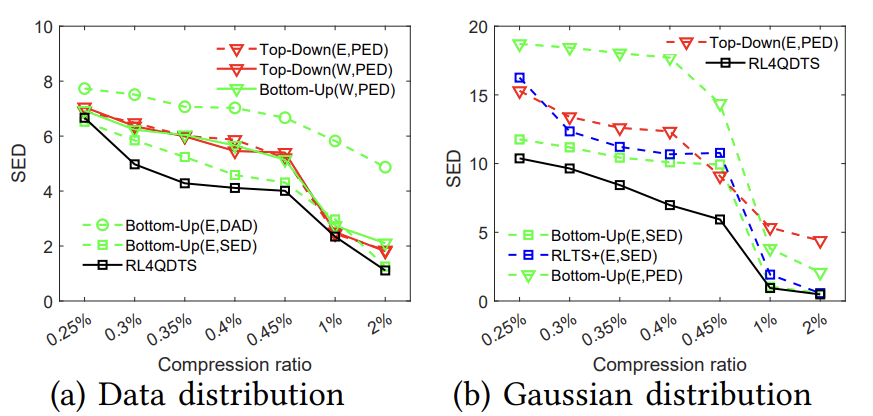
效率评估:论文进一步研究了预算大小W从0.25% * N到2% * N的影响,其中N固定为1亿个点。图6显示了在Geolife上的运行时间,RL4QDTS算法比Top-Down的适应性慢,但比Bottom-Up的适应性快至少两倍。随着W的增加,因为它通过Agent-Point基于立方体内的部分轨迹计算值,而Top-Down的适应性是基于整个轨迹计算值的,所以RL4QDTS变得比Top-Down的适应性更快。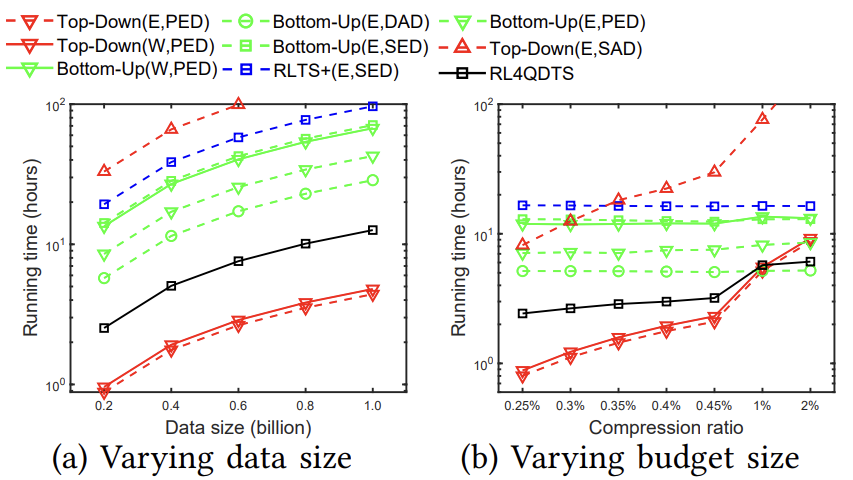
可转移性测试:论文在两种情境下测试了RL4QDTS的转移性能。首先在Geolife上使用高斯分布的范围查询(µ =
0.5,σ =
0.25)来训练RL4QDTS,并评估其在µ(0.5~0.9)和 σ(0.25~0.85)变化的范围查询中的有效性(见图7(a)和(b))。其次,使用相同的模型在高斯分布上训练后,论文测试了其对Zipf分布的范围查询的有效性,该分布具有不同的指数参数a(从4~8),以评估在显著的分布变化下的转移性能(见图7(c))。RL4QDTS在所有µ和σ设置下始终优于基线(见图7(a)和(b))。在图7(c)中,尽管查询分布发生了显著变化,但RL4QDTS的表现仍然相当不错甚至更好,这证明了它的稳健性,图7(d)-(g)中可视化了分布变化。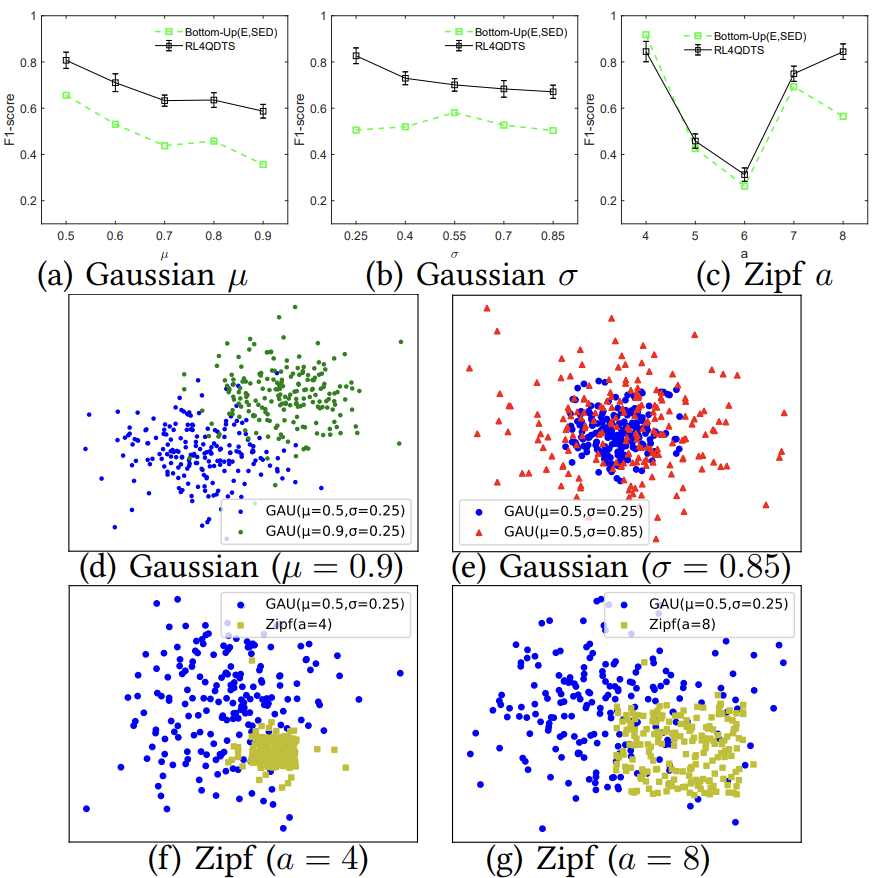
四.总结
论文引入了基于查询准确性的轨迹简化问题,旨在最小化原始数据库和简化数据库上查询结果之间的差异。论文提出了一种基于多智能体强化学习的解决方案RL4QDTS,两个智能体协同工作,共同简化数据库中的轨迹,同时优化查询准确性。论文对真实世界的轨迹数据集进行了广泛的实验,结果表明RL4QDTS算法在各种查询处理操作中始终优于现有的EDTS算法。
重庆大学时空实验室(Spatio-TemporalArt Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!

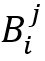 表示一个立方体,位于第i层并对应于其父节点的第j个节点。对于
表示一个立方体,位于第i层并对应于其父节点的第j个节点。对于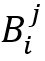 ,使用落入其中的轨迹数量
,使用落入其中的轨迹数量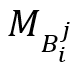 和查询数量
和查询数量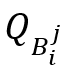 来捕捉数据和查询的分布情况,如下所示:
来捕捉数据和查询的分布情况,如下所示: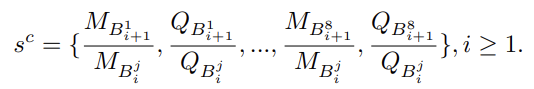
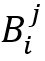 中的轨迹和查询总数进行归一化。
中的轨迹和查询总数进行归一化。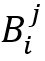 时,定义了两种可能的动作类型:(1)继续访问8个节点之一,(2)停止遍历并将当前立方体返回给Agent-Point以选择立方体内的点。动作ac通过ac=k (1≤k≤9)进行定义,其中ac=1至8表示继续访问立方体的子节点,ac=9表示停止遍历。
时,定义了两种可能的动作类型:(1)继续访问8个节点之一,(2)停止遍历并将当前立方体返回给Agent-Point以选择立方体内的点。动作ac通过ac=k (1≤k≤9)进行定义,其中ac=1至8表示继续访问立方体的子节点,ac=9表示停止遍历。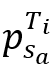 和
和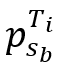 分别表示轨迹Ti中立方体内的首尾点。对于满足sa≤sj ≤sb的每个点
分别表示轨迹Ti中立方体内的首尾点。对于满足sa≤sj ≤sb的每个点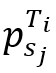 ,定义一对值
,定义一对值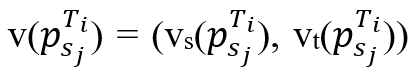 .其中
.其中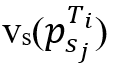 等于
等于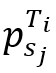 与同步点之间的“空间”距离,
与同步点之间的“空间”距离,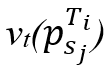 等于
等于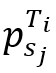 与其在轨迹Ti上相邻两点间线段上最接近点之间的时间差。然后,在每个轨迹Ti的所有点中,找到具有最大vs值的点
与其在轨迹Ti上相邻两点间线段上最接近点之间的时间差。然后,在每个轨迹Ti的所有点中,找到具有最大vs值的点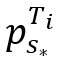 ,其中s*为索引,即
,其中s*为索引,即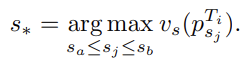
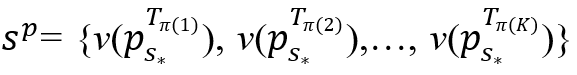 ,其中π表示T1,T2,…,
,其中π表示T1,T2,…,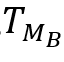 的排列顺序,使得
的排列顺序,使得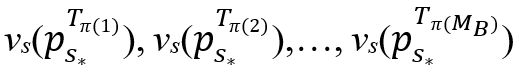 按降序排列。K(K≤MB)是一个可根据经验调节的参数,用来控制状态空间的大小。
按降序排列。K(K≤MB)是一个可根据经验调节的参数,用来控制状态空间的大小。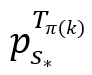 插入到D‘。
插入到D‘。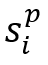 和
和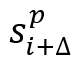 分别考虑简化数据库D’和D’’,定义奖励R如下:
分别考虑简化数据库D’和D’’,定义奖励R如下: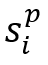 到
到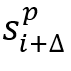 的所有相关转换中共享,以及在此过程中涉及的Agent-Cube的转换。累计奖励的计算公式如下:
的所有相关转换中共享,以及在此过程中涉及的Agent-Cube的转换。累计奖励的计算公式如下: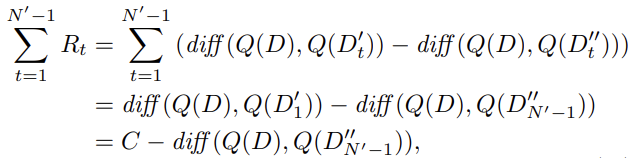
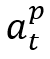 之前(之后)处于状态
之前(之后)处于状态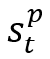 的简化数据库,将初始项diff(Q(D), Q(D1’))视为常数C,并且在该状态下尚未插入点,即MDP的目标是最小化
的简化数据库,将初始项diff(Q(D), Q(D1’))视为常数C,并且在该状态下尚未插入点,即MDP的目标是最小化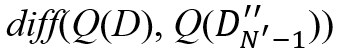 。
。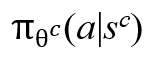 ,对Agent-Point表示为
,对Agent-Point表示为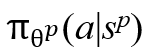 。该策略通过DQN在给定状态sc或sp中采用动作a,其参数由
。该策略通过DQN在给定状态sc或sp中采用动作a,其参数由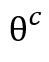 或
或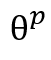 表示。
表示。
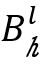 (第2行),为了对立方体采样,用上述公式构造状态
(第2行),为了对立方体采样,用上述公式构造状态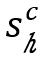 (第四行),并使用策略
(第四行),并使用策略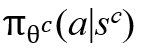 对动作
对动作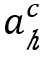 进行采样(第5行)。如果
进行采样(第5行)。如果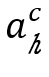 = 9或者探索达到树的最后一级,则中断并返回当前立方体B(第6~8行);否则,通过h←h+1和l←
= 9或者探索达到树的最后一级,则中断并返回当前立方体B(第6~8行);否则,通过h←h+1和l←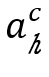 更新索引并探索下一个立方体
更新索引并探索下一个立方体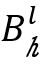 (第9~12行)。
(第9~12行)。
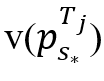 的值,其中1 ≤ j ≤ MB(第2行)。然后,它使用一个最大优先队列来维护这些值的降序排列π(第3行)。接下来,通过上述公式来构造一个状态sp(第4行),并使用策略
的值,其中1 ≤ j ≤ MB(第2行)。然后,它使用一个最大优先队列来维护这些值的降序排列π(第3行)。接下来,通过上述公式来构造一个状态sp(第4行),并使用策略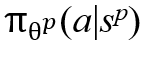 对其采样,其中sp作为输入(第5行)。令ap = k (1 ≤ k≤ K)表示采样动作,通过将点
对其采样,其中sp作为输入(第5行)。令ap = k (1 ≤ k≤ K)表示采样动作,通过将点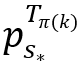 插入到D‘来执行该动作(第6行)。
插入到D‘来执行该动作(第6行)。
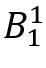 开始构造其状态,观察4个子节点,采取探索节点
开始构造其状态,观察4个子节点,采取探索节点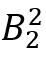 的动作。(3)在
的动作。(3)在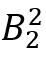 处采取探索节点
处采取探索节点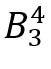 的动作。(4)在
的动作。(4)在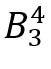 处,Agent-Cube接收到
处,Agent-Cube接收到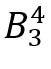 提供给Agent-Point的动作。(5)Agent-Point在
提供给Agent-Point的动作。(5)Agent-Point在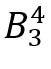 处构造状态,并采取将点p5插入到D‘的动作。(6)最后,因为耗尽预算,算法中断并返回D’,输出与查询D相同的结果。
处构造状态,并采取将点p5插入到D‘的动作。(6)最后,因为耗尽预算,算法中断并返回D’,输出与查询D相同的结果。














