用机器学习(ML)模型取代经典的B-Tree等索引结构可以在某些类型的查询方面提高效率,但现存方法需要替换数据库已部署的索引和查询处理算法,因而存在一定障碍。那应当如何解决这个问题呢?本次为大家带来数据库领域顶级会议SIGMOD的论文:《The RLR-Tree: A Reinforcement Learning Based
R-Tree for Spatial Data》
针对空间数据的学习索引通常将数据集中的空间数据点映射到一个统一的秩空间(如使用空间填充曲线),然后学习该数据集的累积分布函数CDF,将搜索键映射到数据对象列表中的秩。尽管这些学习索引在提高处理某些类型查询的效率方面取得了成功,但它们仍然有各种限制:(1) 现有的学习索引只能处理点对象,而不能处理其他类型的空间对象。(2) 部分方法不考虑KNN查询或空间连接查询这种重要的空间查询,而另一些不返回准确的查询结果。(3) 一些基于学习的空间数据索引不考虑更新,而另一些需要经常重新训练他们的模型。此外,它们需要替换空间数据库系统目前使用的索引结构和查询处理算法,这使得它们难以部署在当前的数据库系统中。论文使用机器学习(ML)技术构建一个数据驱动R-Tree以提供更高的查询效率。具体来说,论文为构建和更新R-Tree的两个关键操作构建ML模型,这两个操作目前都依赖于手工制作的启发式规则。论文提出的方法有几个显著的特点:(1) 基于学习的索引可以处理任何空间对象,如矩形对象。(2) R-Tree结构没有被修改,因此目前部署的所有查询处理算法都将仍然适用,这使当前数据库更容易部署基于学习的索引。(3) 基于学习的索引返回准确的查询结果。(4) 基于学习的索引是为动态环境设计的,可以随时处理更新。(1) 训练机器学习(ML)模型以在R-Tree的构建和更新中取代启发式规则,以在更新频繁且批量加载不可行的动态环境中提高其查询效率。(2) 论文将“选择子树”和“分割”操作模型建模为两个MDPs(Markov
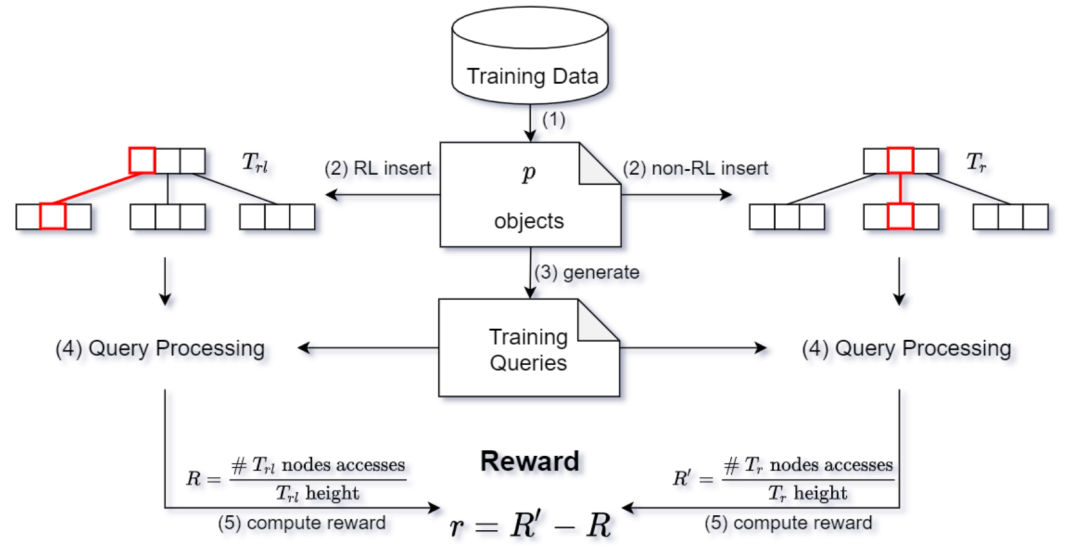
decision processes),并仔细设计了它们的状态、动作和奖励信号。(3) 论文设计了一个有效和高效的学习过程来学习好的策略解决MDPs。学习过程使论文能够用一个小数据集训练RL模型而构建一个针对超过1亿个空间对象的R-Tree。R-Tree是平衡树,用于索引多维对象,每个节点包含m到M个条目。非叶节点条目包括子节点引用及其最小边界矩形(MBR),叶节点则包含对象引用和对象的MBR。查询不与MBR相交则不会与R-Tree对象相交。R-Tree的构建和更新依赖于“选择子树”和“分割”操作:插入对象时,从根节点通过“选择子树”迭代决定插入哪个子树,直至叶节点,超过M条目的叶节点将通过“分割”操作分组成两个节点。该过程可能向上传播,需要在父节点中添加新节点引用。R-Tree的查询性能在很大程度上取决于R-Tree的构建和更新方式,并且研究者已经提出了许多不同的R-Tree变体。R-Tree变体大多采用手工制作的“选择子树”和“分割”策略,没有一种策略可以在所有场景下构建和更新具有主导查询性能的R-Tree。基于此,论文的目标是使用Reinforcement
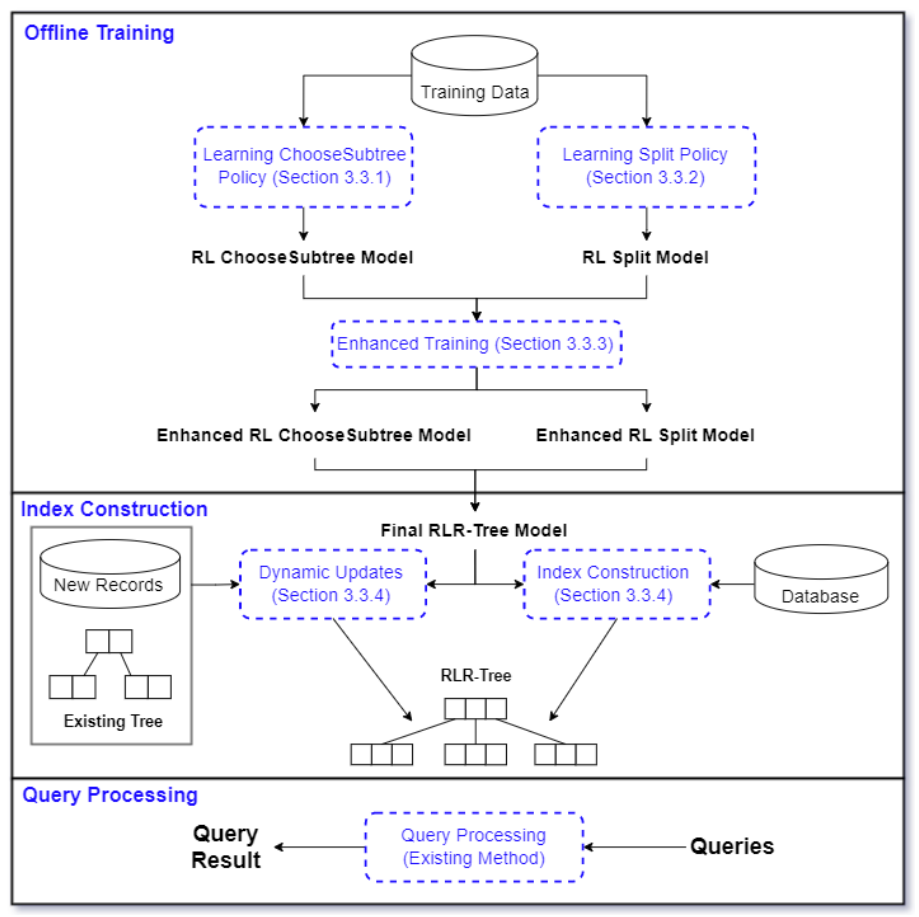
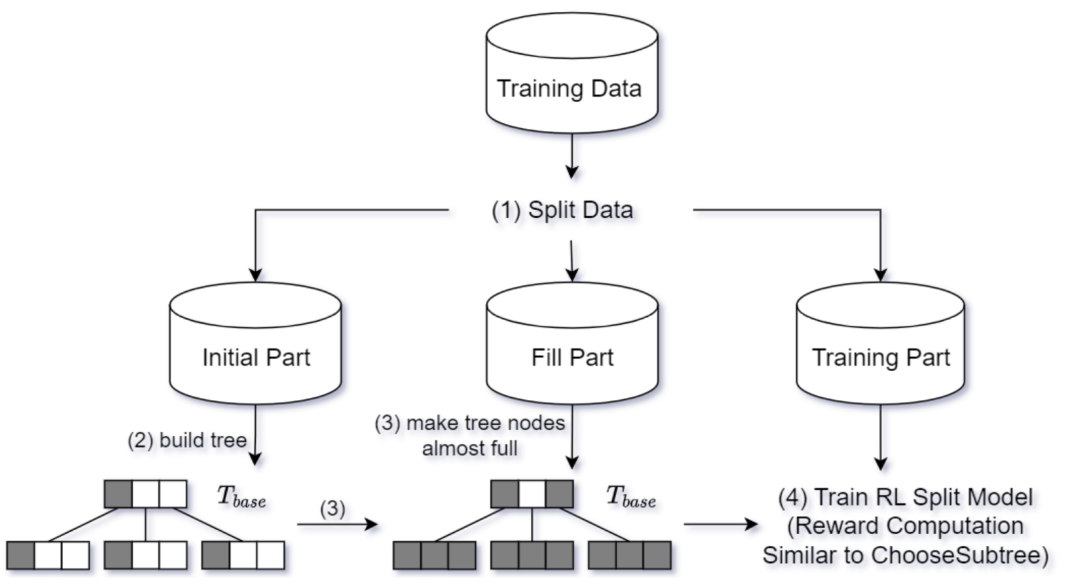
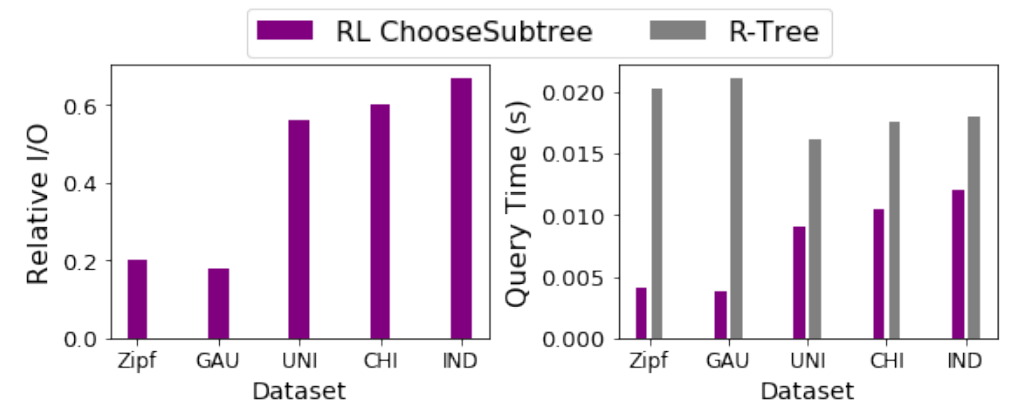
Learning(RL)模型来为“选择子树”和“分割”进行决策。这个新的索引被称为RLR-Tree。插入新对象到R-Tree是结合两个顺序决策过程:自顶向下的“选择子树”和自底向上的节点“分割”。强化学习(RL)适合处理这类顺序决策问题,故论文通过将插入过程建模为两个马尔可夫决策过程(MDPs),使用RL来优化这两个操作的策略。图1展示了使用RL构建和更新RLR-Tree的方法,并说明如何用它回答空间查询。通过小数据集进行离线训练,训练出的模型能够集成到R-Tree构建中,适用于处理动态更新。此外,RLR-Tree能够使用任何为R-Tree设计的查询处理算法来处理空间查询。要将新对象插入到R-Tree中,需要从根开始进行自上而向下的遍历,并在每个节点中决定将新对象插入哪个子节点。如果要用RL来选择一个子树,论文将这个问题表示为一个MDP。一个MDP由四个组成部分组成,即状态(States)、动作(Actions)、转移(Transitions)和奖励(Rewards)。1) MDP的状态空间:状态是描述决策过程中可能所处环境或情境的一个集合。论文认为状态来自于其子节点将被选择以插入对象的树节点。当决定将新对象插入哪个子节点时,必须考虑如果分别把新对象添加进每个子节点后会发生什么变化。捕获子节点𝑁变化的特征包括:(1)ΔArea(N, o),将新对象𝑜添加到𝑁中,𝑁的MBR面积增长。(2)ΔPeri(N, o),加入𝑜后𝑁的MBR的周长增长。(3)ΔOvlp(N, o),插入𝑜后𝑁和其他子节点重叠的增长。(4)OR(N),条目数与容量之比,代表节点的占有率。论文只使用一小部分子节点来定义状态。因为大多数子节点都不适合插入新对象的,插入新对象可能会大大增加它们的MBR,RL代理将不考虑它们来表示一个状态。状态表示设计如下:首先以面积递增的顺序检索top-𝑘子节点。然后,对于每个检索到的子节点计算上述四个特征。之后将𝑘个子节点的特征连接起来,得到一个4𝑘维的向量来表示一个状态。𝑘是一个需要根据经验来设置的参数。2) MDP的动作空间:动作是决策者在特定状态下可以选择的行为集合。论文提出了一种通过对RL代理进行训练来决定直接插入新对象的子节点的新思想。为了使动作空间和状态表示一致,论文定义了动作空间A = {1,…,𝑘},其中动作𝑎=𝑖意味着RL代理选择第𝑖个子节点来插入新对象。3) MDP转移:在“选择子树”操作过程中,给定一个状态(R-Tree中的节点)和一个操作(将新对象插入到子节点),RL代理将转换到子节点。如果子节点是叶节点,则代理将达到最终状态。4) MDP奖励:奖励是决策过程中从一个状态转移到另一状态的即时回报,用于评估动作的效果。论文目标是构建更新高效查询处理的R-Tree,故奖励需反映查询性能提升。论文奖励信号的思想是:保持一个具有固定的“选择子树”和“分割”策略的参考树。参考树可以是任何现有的R-Tree变体。奖励信号的计算是基于使用参考树和RLR-Tree处理随机查询的成本差距计算的。具体来说,奖励信号的设计如下:(1) 维护一个RLR-Tree,它使用RL来选择子树,并采用指定的“分割”策略。(2) 维护一个参考树,它采用了预先指定的“选择子树”策略和与RLR-Tree相同的“分割”策略。(3) 将参考树与RLR-Tree同步,从而使它们具有相同的树结构。(4) 给定𝑝个新对象{𝑜1,……,𝑜𝑝},将它们插入到参考树和RLRTree中,然后生成预定义大小的𝑝个范围查询。(5) 𝑝个范围查询同时使用参考树和RLR-Tree进行处理,计算归一化的节点访问率,并将其定义为#acc_nodes/Tree_height,是用于回答在树高上的范围查询的访问节点数。设𝑅和𝑅’分别为RLR-Tree和参考树的节点访问率,计算𝑟=𝑅'−𝑅 作为奖励信号。𝑟越高,RLR-Tree需要访问的处理范围查询的节点就比参考树越少。(6) 在插入𝑝对象时遇到的所有转移都共享相同的奖励𝑟。(1) 初始化网络:首先创建主网络Q(s, a, θ)和目标网络Q(s, a, θ-),并且给它们赋予相同的随机权重。(2) 重置回放内存:在每个epoch开始重置回放内存,这是用来存储过去的行动、状态和奖励的地方。(3) 对象插入树:对于每个对象,首先将它插入到参考树中,然后在RLR-Tree上执行从上到下的遍历。(4) 选择动作:在遍历的每一层都计算当前的状态表示,并使用𝜖-贪心策略基于𝑄值来选择动作,直到达到终点状态(叶节点)。(5) 存储转换:在叶节点插入新对象,并使用与参考树相同的“分割”策略来保证没有节点溢出。这些转换会被存储起来。(6) 生成查询:同时会生成一个以当前对象为中心的预定义大小的范围查询,并将这个查询添加到查询集合中。(7) 计算奖励:如图2所示,当所有对象都被插入后,根据查询集合中的查询来计算奖励。所有在插入过程中遇到的转移都会分享相同的奖励,并被推送到回放内存中。(8) 更新网络:然后从回放内存中随机抽取一批转换记录,并使用它们来更新主网络的参数。自上而下的遍历以一个叶节点结束。如果叶节点溢出,它将被分割为两个节点,分割操作可以向上传播。1) MDP的状态空间:论文避免了考虑过多可能的分割方式。首先,将节点中的条目按每个维度的投影值进行排序。然后对于每个排序后的序列,考虑在第𝑖个元素处进行分割(𝑚 ≤ 𝑖 ≤ 𝑀 + 1−𝑚),其中前𝑖个条目分配给第一组,剩下的分配给第二组。之后进一步排除那些导致两个节点重叠的分割方式。从剩余的分割中按总面积升序选择前𝑘个分割。对于每个选定的分割,考虑四个特征:由分割创建的两个节点的面积和周长。将所有𝑘个分割的特征连接起来,生成一个4𝑘维的向量来表示状态。2) MDP的动作空间:将动作空间定义为A = {1,……,𝑘},其中𝑘是用于表示状态的分割数。动作𝑎=𝑖意味着采用第𝑖个分割。3) MDP转移:在分割中,给定一个状态(R-Tree中的一个节点)和一个操作(一次分割),代理将转换到表示该节点父节点的状态。如果节点没有溢出,则为终止态。4) MDP奖励信号:维护一个定期与RLR-Tree同步的参考树,使用节点访问率的差异作为两棵树处理训练查询作为奖励信号。RLR-Tree采用了与参考树相同的“选择子树”策略,并使用RL代理来决定如何分割一个溢出的节点。只有在节点溢出时,才会调用“分割”操作。论文首先构建一个树,其中大多数节点都已满,这样就可以经常遇到节点分割。论文生成了不同大小的R-Trees,并使用通过在数据集中插入剩余的对象所引起的转移来进行训练。具体的训练过程如下:(1) 训练周期:在每个训练周期中,重复进行𝑝𝑎𝑟𝑡𝑠−1次迭代来训练代理。(2) 构建基础R-Tree(𝑇𝑏𝑎𝑠𝑒):在第𝑖次迭代中,使用训练数据集的前𝑖𝑝𝑎𝑟𝑡𝑠部分来构建一个基础基础R-Tree(𝑇𝑏𝑎𝑠𝑒)。剩余的数据被分成两部分:一部分是填充部分,包含不会导致𝑇𝑏𝑎𝑠𝑒节点溢出的对象;另一部分是训练部分,包含其余对象。填充部分的对象被插入𝑇𝑏𝑎𝑠𝑒,而训练部分的对象将用于后续触发分割进行训练。(3) 预训练准备:如图三所示这一步骤确保了𝑇𝑏𝑎𝑠𝑒中的大多数节点都将被填满。(4) 开始训练:一旦𝑇𝑏𝑎𝑠𝑒构建完成,就开始使用训练部分的对象进行训练。首先,同步𝑇𝑟和𝑇𝑟𝑙与𝑇𝑏𝑎𝑠𝑒,确保它们具有相同的结构并且几乎被填满。(5) 插入和分裂:对于训练部分中的每个对象,直接使用预定的“选择子树”和“分割”策略将其插入参考树𝑇𝑟。RLR-Tree使用与参考树相同的“选择子树”策略达到叶节点𝑁。如果𝑁溢出,则生成一个以该对象为中心的预定义大小的范围查询,并添加到查询集𝑅𝑄中,然后迭代分割𝑁并向上移动到其父节点,直到𝑁不再溢出。(6) 状态表示与动作选择:对于每个节点𝑁,计算状态表示,并使用𝜖贪心策略根据它们的𝑄值选择一个动作。这些转移被存储起来。(7) 计算奖励:处理完𝑝个对象后,使用𝑅𝑄中的查询计算奖励。处理这些对象时遇到的转移共享相同的奖励。(8) 更新网络:从回放内存中随机抽取一批转移,并使用它来更新主网络的参数。目标网络的参数定期与主网络同步。一种简单的方法是分别训练RL“选择子树”和RL“分割”,然后使用学习到的策略来构建一个RLR-Tree。然而,论文期望这两个代理能够相互帮助,以实现更好的性能。因此论文提出了一个增强的训练过程来交替训练两个代理。即在奇数epoch训练“选择子树”的RL代理,而“分割”的代理被固定为RLR-Tree的“分割”策略。在偶数epoch训练“分割”的代理,而“选择子树”的代理被固定为RLR-Tree的“选择子树”策略。论文将学习到的“选择子树”和“分割”的模型加入到R-Tree的插入算法中,构建RLR-Tree如下。对于要插入的每个对象,在自顶向下遍历中迭代计算节点的状态表示,并使用“选择子树”的模型选择对应于最大𝑄值动作的子树,直到对象插入叶节点。当一个节点溢出时,计算它的状态表示,并使用为”分割“训练的模型来选择与𝑄值最大的动作对应的分割。对于动态更新,可以使用训练过的模型将新的数据记录插入到现有的树中。实验结果表明,即使没有经常进行再训练,训练后的模型也不会出现显著的性能下降。论文利用了三个合成数据集和两个大型真实数据集,进行了实验评估。评估通过为每种查询大小随机生成1000个范围查询进行,查询范围从整个区域的0.005%到0.5%不等。所有用于训练和测试的查询均为单独生成,确保它们不重复。实验比较了包括R-Tree(参考树)、R*-Tree(改进查询性能的R-Tree变种)、RR*-Tree(对动态环境查询有最佳性能的R-Tree变体)、LISA(唯一一个基于磁盘的学习索引,支持精确范围和KNN查询)以及STR(展示所有数据可用时打包R-Tree的性能)等基线。评估标准包括运行时间和I/O成本。图4展示了五个数据集上RL“选择子树”策略的平均相对I/O成本,显示其在所有数据集上均优于R-Tree。尽管训练集大小仅为10万,训练后模型也能有效适用于更大数据集。此外,图4也展示了RL“选择子树”的查询处理时间,其与R-Tree的时间比值与相对I/O成本在五个数据集上保持一致。为了评估RL”分割“的性能,图5报告了在五个数据集上的结果。RL Split在所有5个数据集上都取得了显著的改进,并始终优于R-Tree。图5还报告了RL Split的查询处理时间。类似于RL“选择子树”,I/O成本和查询时间显示一致的结果。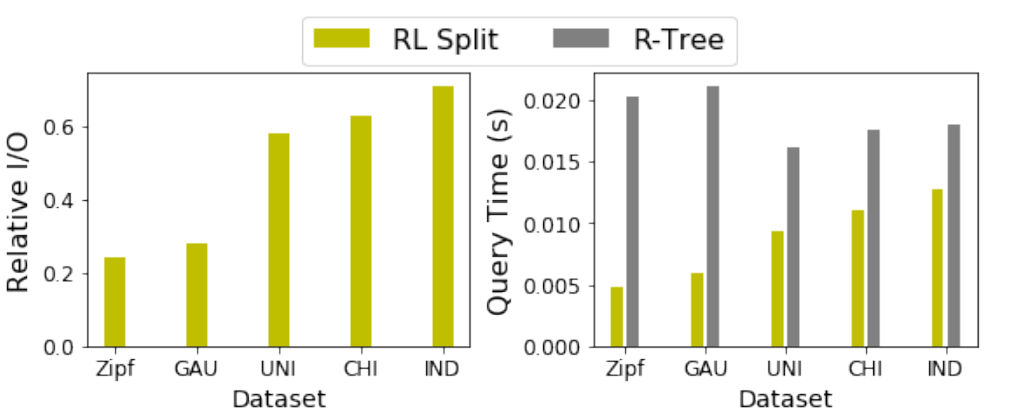
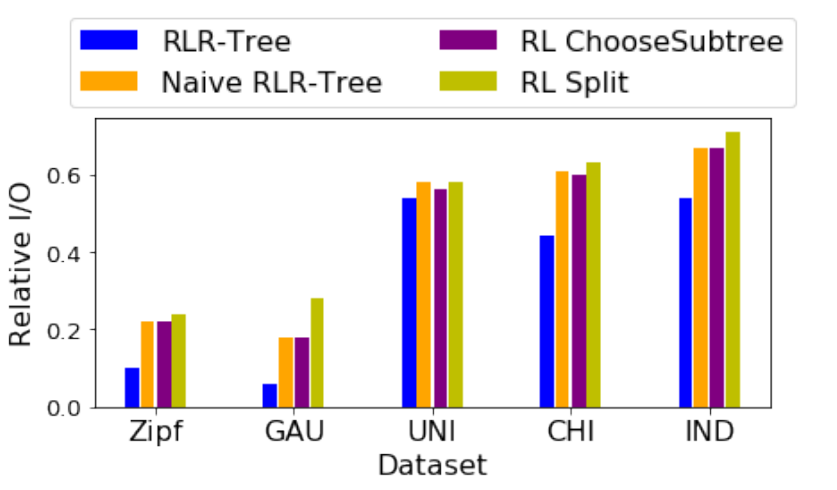
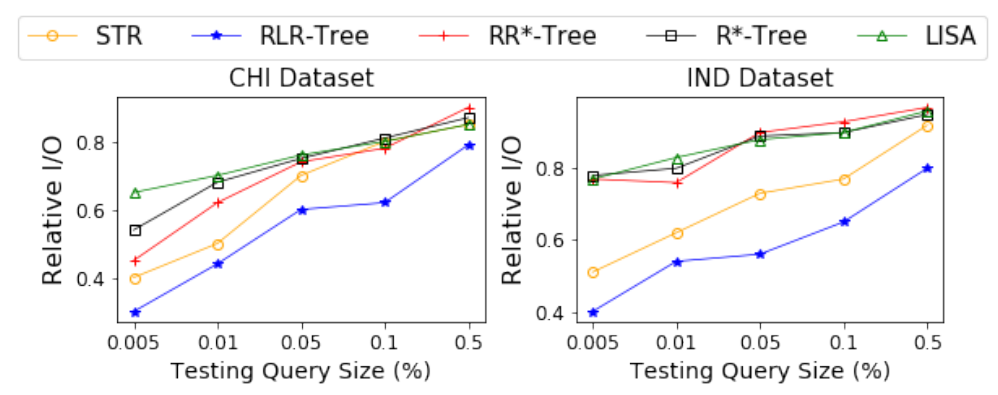
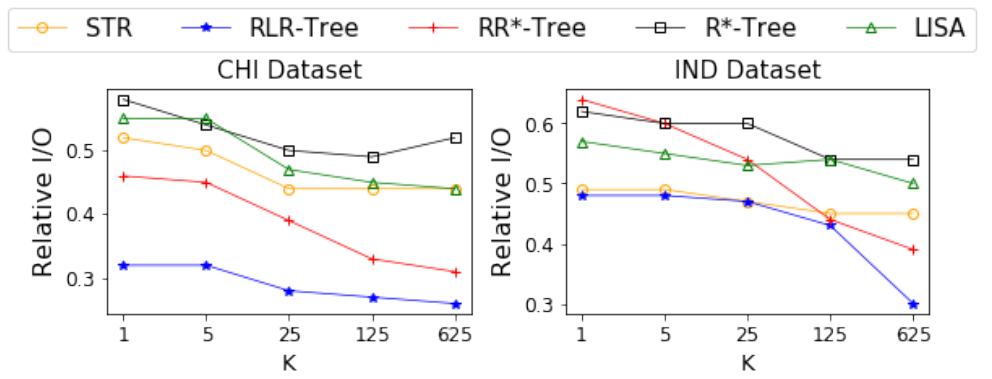
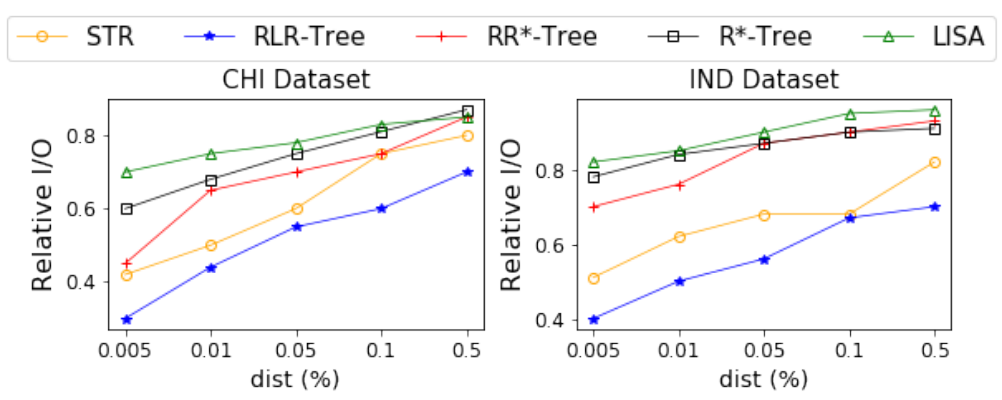
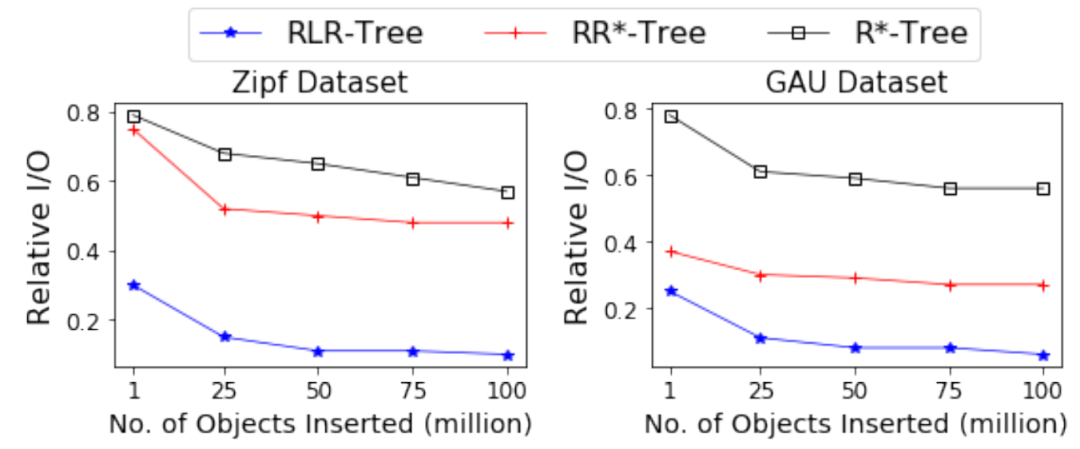
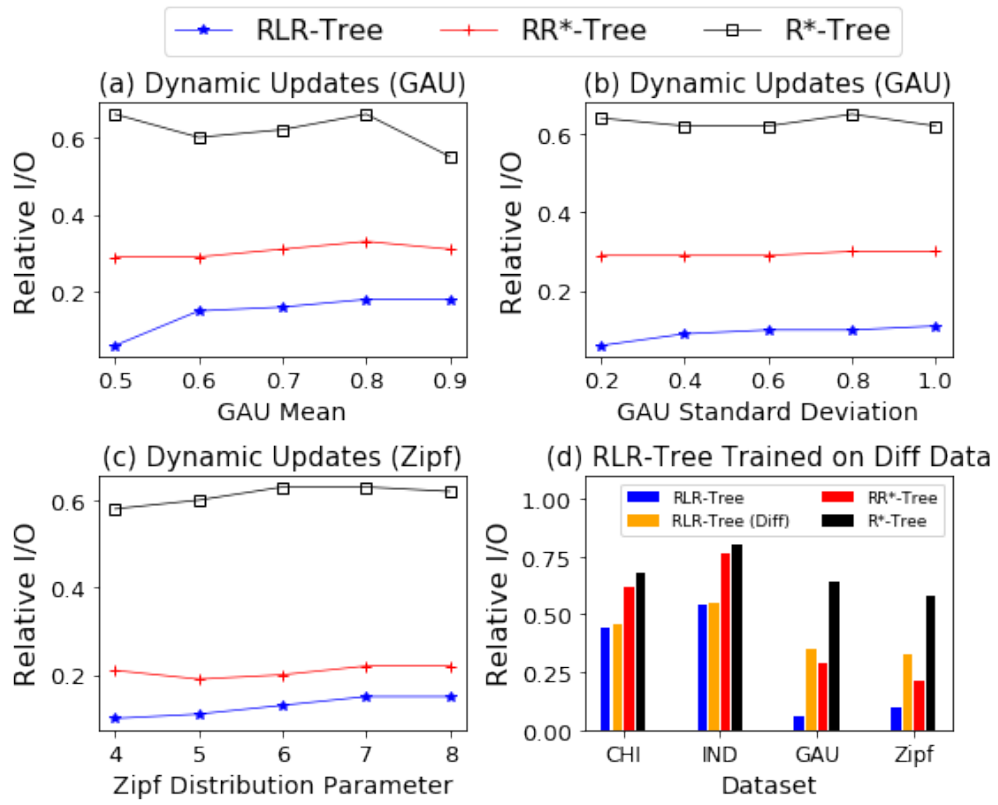
这组实验是为了评估RLR-Tree的性能,它是由一个组合的RL“选择子树”和RL”分割“模型构建的。1) 增强训练过程:论文首先比较了RL“选择子树”、RL”分割“、朴素RLR-Tree(直接使用RL“选择子树”和RL分割得到的),以及使用增强训练过程得到的RLR-Tree的相对I/O成本上的性能。如图6所示,通过应用增强训练过程,RLR-Tree在所有数据集上的性能最好。与朴素的RLR-Tree相比,增强的训练过程在查询性能方面提高了高达66.7%。图6 朴素RLR-Tree和RLR-Tree的RL“选择子树”、RL“分割”2) 范围查询。论文使用不同大小的范围查询来评估RLR-Tree在两个真实数据集上的查询性能,如图7所示,首先,RLR-Tree始终优于基线,表现比R*-Tree、RR*-Tree、LISA和STR分别高出48.7%、48%、53.8%和25.0%。其次,随着查询范围的减小,RLR-Tree相对于基线的优势变得越来越显著。3) KNN查询:在实验中,论文考虑了不同的K值,即K∈ {1, 5, 25, 125, 625}。对于每个K值,随机在数据空间中生成了1,000个均匀分布的查询点。实验结果显示,RLR-Tree在两个真实数据集上对所有K值的查询均优于所有基线方法。其次,RLR-Tree相对于R-Tree的查询性能随着K值的增大而提高。4) 空间连接查询:论文在两个真实数据集上进行了RLR-Tree处理空间连接查询性能的实验评估。空间连接查询返回一组对象对 (𝑞𝑜, 𝑑𝑜),其中𝑞𝑜属于查询集合𝑄𝑆,𝑑𝑜属于数据集𝐷𝑆,并且𝑞𝑜与𝑑𝑜之间的欧氏距离小于给定的阈值𝑑𝑖𝑠𝑡。实验中,阈值𝑑𝑖𝑠𝑡为(0.005%,0.01%,0.05%,0.1%,0.5%),每个𝑑𝑖𝑠𝑡值对应1000个随机查询点。实验结果显示,RLR-Tree在所有的𝑑𝑖𝑠𝑡值下都一致地优于基线方法,尤其是在较小的𝑑𝑖𝑠𝑡值时,其优势更为显著。实验评估了RLR-Tree在动态环境中处理更新时的性能。1) 不更改数据分布的更新:论文首先分别用两个数据集训练并构建了两个规模为10万的RLR-Tree。然后,使用相应的训练模型将高达1亿个同分布的数据对象插入到各自的树中。实验结果显示,RLR-Tree在整个过程中显著优于基线方法。随着更多数据对象的插入,模型的性能表现有所提升。这一发现强调了RLR-Tree在处理动态环境中数据更新,且数据分布不变时的强大性能和适应能力。2) 具有数据分布变化的更新:实验首先使用两个数据集分别训练并构建了两个规模为100,000的RLR-Trees。然后插入同数据集不同分布的对象,并报告了1,000个随机查询的平均相对I/O成本。实验结果如图11所示,即便在数据分布发生变化的情况下,且没有重新训练强化学习(RL)模型,RLR-Tree仍然一致地优于基线方法,尽管性能有轻微的下降。论文提出了一种基于RL的方法来构造一个更好的R-Tree,即RLR-Tree。实验结果表明,RLR-Tree在范围查询、KNN查询和空间连接查询方面始终优于R-Tree。RLR-Tree在更大的数据集上具有特别显著的性能,并且能够在数据分布的某些变化中处理动态更新。| 重庆大学计算机科学与技术专业2020级本科生,重庆大学Start Lab成员。主要研究方向:时空数据管理 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!