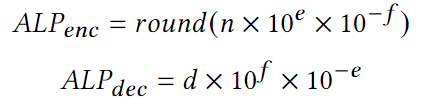浮点数据的无损压缩有别于整数压缩,因为浮点数并不能精确地表示大多数真实值,往往导致计算过程中引入舍入误差。这些误差限制了现有轻量级压缩方案的使用,而最近提出的压缩方案的(解)压缩速度又有待提高。本次为大家带来数据库领域顶级会议SIGMOD 2023的论文《ALP: Adaptive Lossless floating-Point Compression》。
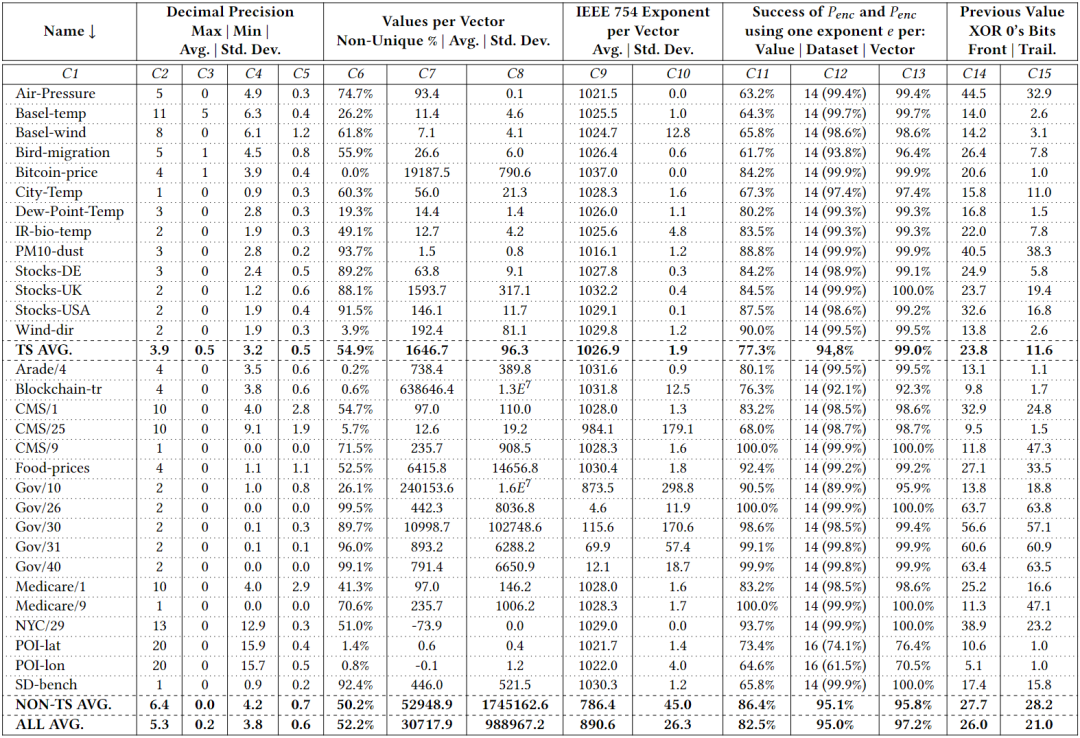
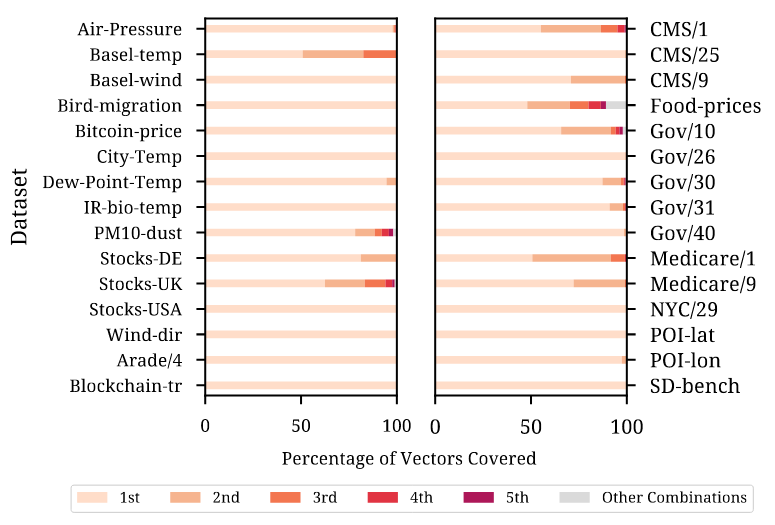
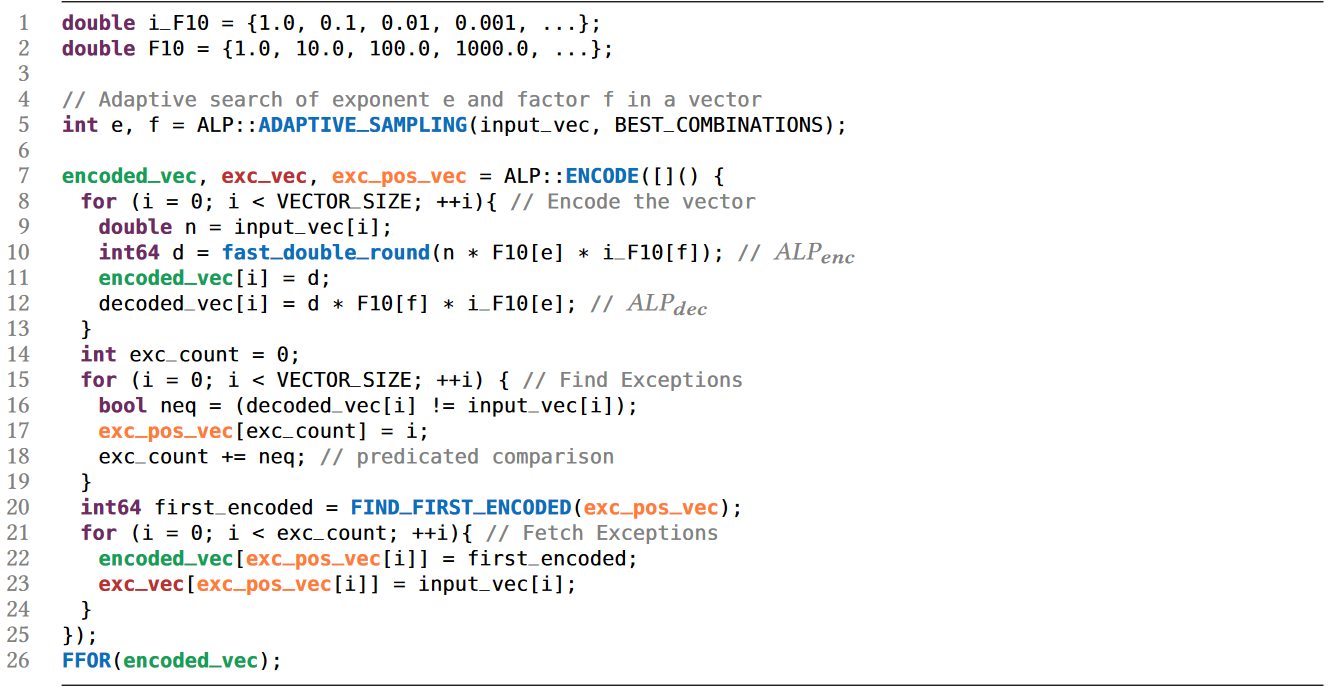
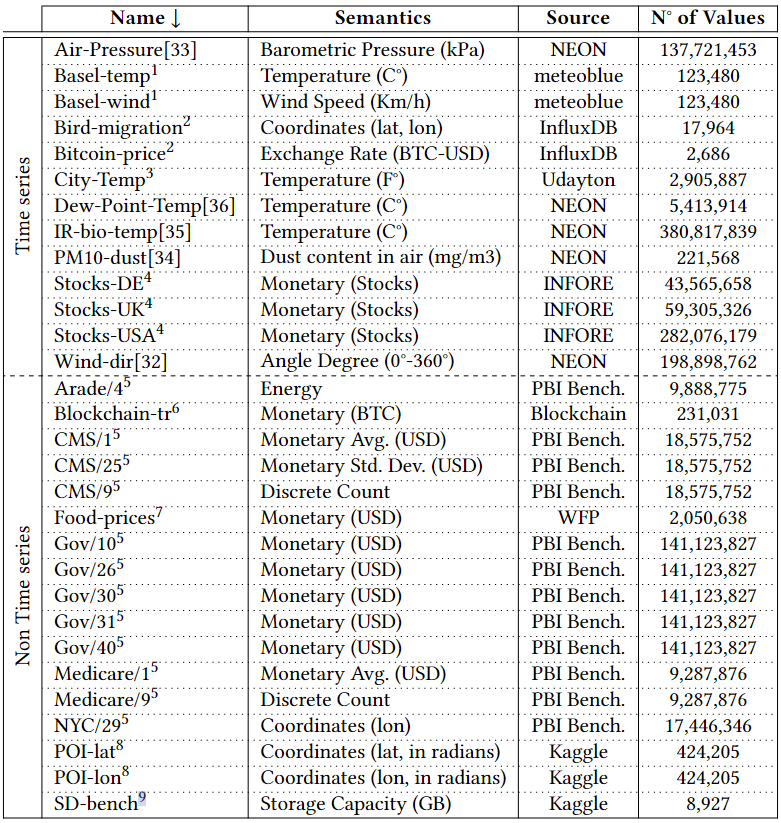
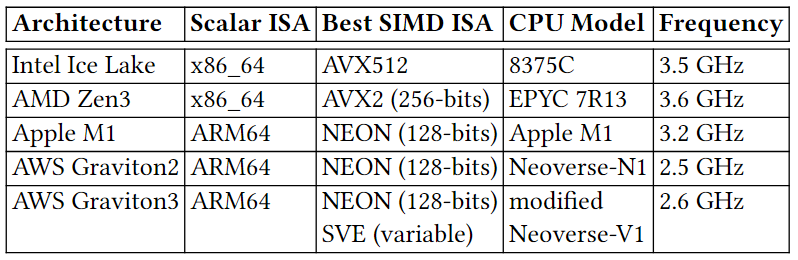
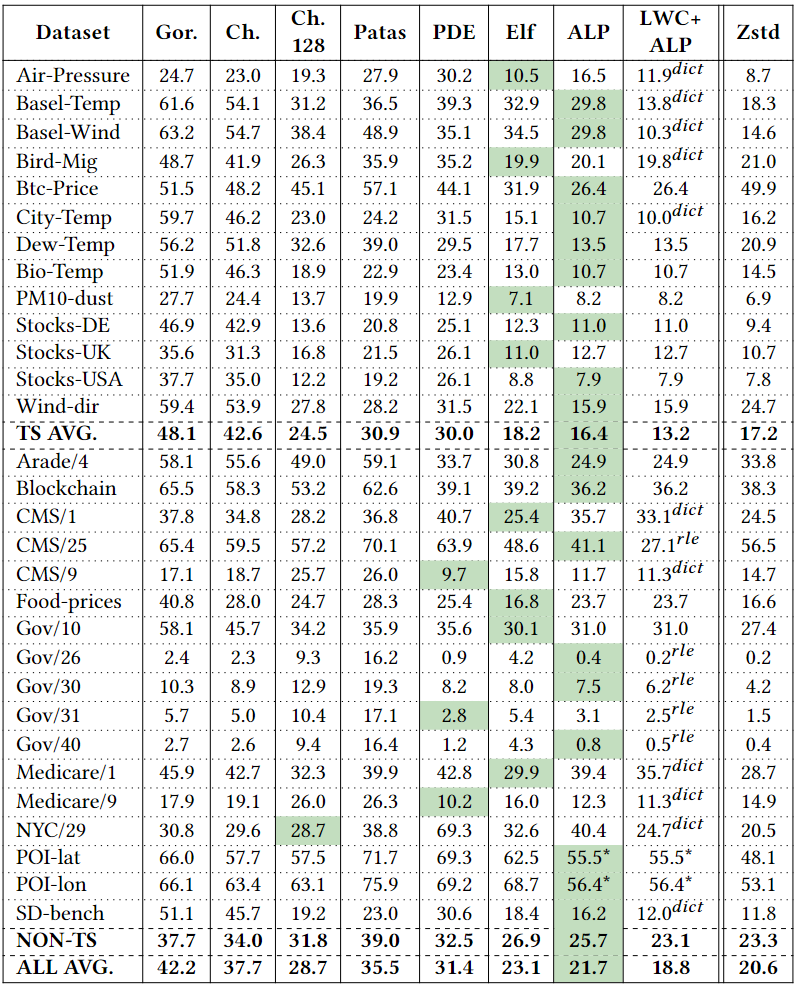
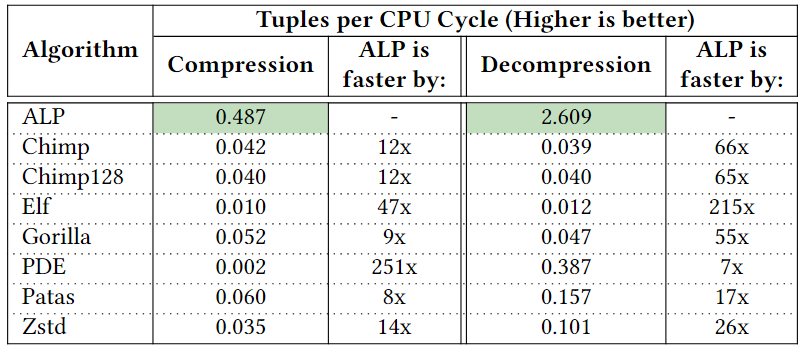
如今,分析数据系统和大数据格式等都采用柱状压缩存储,存储采用的压缩方法可分为通用压缩和轻量级压缩。轻量级压缩,也称“编码”,主要是利用列的类型和域的知识进行压缩,常见的有参考系编码Frame Of Reference (FOR),增量编码Delta Encode,字典编码Dictionary Encode和游程编码Run Length Encode(RLE)等。然而,对于IEEE 754双精度浮点数,加法等计算往往会引入舍入误差,这使得Delta和FOR编码无法被用于编码原始浮点数据。对于通用压缩算法,大数据格式中常用的有gzip、Zstd、Snappy和LZ4。然而,其缺点是:在(解)压缩中往往比轻量级编码慢;往往会强制对大数据块进行解压缩。为应对上述问题,出现了一系列新的浮点编码:Gorilla、Chimp、PseudoDecimals (PDE)、Patas和Elf等。其中一个常见的想法是对数据流使用异或运算符,得益于使用异或运算可在位模式级别组合两个浮点值,在不引入舍入误差的情况下提供与加法类似的功能。上述新提出的轻量编码虽然能够避免通用算法的一些缺点,但它们的(解)压缩速度(或压缩率)并不比通用算法快多少,即仍然不够轻量级。为此,作者对常用浮点数据集进行了研究分析,并提出了一种新的自适应无损压缩算法ALP。 作者将双精度浮点数转换为整数,再利用整数的轻量编码来实现压缩,本质上是以PDE为代表的基于十进制编码的改进版本。以浮点数n = 8.0605为例,可将小数点向右移动e位,直到没有小数(此处即e = 4)。该过程可表示为:Penc = round(n× 10e),其中舍入操作是由于其中一个乘数是双精度浮点类型,所以需要将结果舍入以得到整数。随后,可以认为已经将一个64位双精度浮点数转换为一个32位整数d = 80605(即Penc)和一个表示小数点挪动位数的32位整数e = 4。相应的,在解压时应有Pdec = d × 10-e,但是在这个过程中可能丢失了原始精确。根据IEEE 754,double型8.0605的实际表示是8.0604999999999999933209。但是,Pdec的实际运算结果为8.0605000000000011084,这是由于在Pdec中乘以10-e时引入了误差。10−4实际不能被double型精确表示为0.0001,而是0.000100000000000000002082。而在e ≤ 21的情况下,10e有精确的双精度表示,所以在计算过程中Penc并不存在这个问题。通过对常用数据集的分析,作者指出利用Penc和Pdec进行成功编码和解码主要依赖于两个因素:(i) 指数e的实际精度;(ii) 浮点数n的可见精度,并提出了两点发现: 参照表1可见,更高的指数e(如14和16)占主导地位,在所有数据集中拥有平均95%的成功编码率。这是由于更高的指数e能够使得Pdec中的逆因子10-e更精确。例如,用双精度浮点数表示的10-14等于1.00000000000000007771E−15,因此计算结果Pdec更为准确。然而,更高的指数e也会导致更大的Penc,以至于需要使用int64存储,不利于压缩。如表1所示,在大多数数据集中,指数e = 14可使得利用Penc和Pdec将浮点数表示为整数的成功率最高。这是因为10-14的双精度浮点数值和实际值之间的差异很小,对Pdec的结果影响也很小。然而,对于平均可见精度超过14的数据集(如POI-lat、POI-lon),当双精度浮点数n的数量级加上其可见小数精度的和达到16时,由于IEEE 754双精度的52位整数表示位宽的限制,Penc很容易失败。具体来说,Penc的计算过程在舍入之前,得到的整数d还是一个双精度浮点数。然而,double只能精确表示−253 ~ 253之间的整数。一旦超出该范围,在253和254之间,只有偶数整数可以精确表示为double型;在254和255之间,只能存在4的倍数,以此类推。因此,如果一个双精度浮点数乘法运算的结果大于253,将自动舍入。这解释了POI-lat和POI-lon的成功编码率相对较低的原因,以及10𝑒只有在e ≤ 21时有才精确的双精度浮点数表示形式的原因。 通过对每个向量统一使用一个指数e,Penc和Pdec编码有可能达到近100%的成功率。而目前最先进的基于十进制编码(区别于使用异或操作的基于二进制的编码方式)的方法PDE,是将指数e嵌入到每个值中。因此,通过利用这点,可以有效提高压缩率。如上所述,高指数e在将双精度浮点数存储为整数的编码过程中获得了更高的成功率。然而使用14这样的高指数会导致浮点数被编码为64位的长整数。具体来说,当对低精度的数据集使用高指数e时,编码结果会是一个包含大量尾随零的64位长整数(例如:当n ≈ 37.3且e = 14时,Penc = 3730000000000000)。为此,作者提出可用缩减因子 f 的额外乘法切除这些尾部的零,从而得到一个更小的整数。因此,Penc和Pdec的重新定义如下:一个可能的隐患是缩减因子 f 可能会导致新的舍入误差。然而,由 f 引入的误差可以忽略不计,实际上并不会造成影响。在现有的ALP编码过程中,需要执行额外的嵌套暴力搜索以找到最佳的指数e和因子 f 的组合(这里作者将最佳组合定义为能够使得𝐴𝐿𝑃𝑒𝑛𝑐成功编码并产生最小的整数d的组合)。于是,可知该最佳组合的搜索空间为253个e, f 组合(假设f ≤ e且0 ≥ e ≤ 21)。 然而,实际上同一向量中的大多数值都可以通过使用一个统一的指数进行编码。此外,各向量在十进制精度和变化幅度方面表现出较低的方差。因此,作者认为上述搜索空间实际上可以大大减少,并且应该在基于向量的基础上进行。为了证实这一点,作者计算了各数据集中每个向量的最佳组合。图1显示,在大多数数据集中5个e, f 组合足以涵盖数据集中所有向量中的最佳组合。对于一些数据集,如Basel-wind、Bird-migration等,甚至只需要一个组合。对于同一向量中的数据,其指数位以及尾数的前几位往往具有较低的方差,即,它们往往具有相似的前导位。当浮点数的数量级加上其十进制精度超过16时,通常不可能用上述ALP过程将一个双精度浮点数编码为整数,而必须处理超过52位的整数,这样的数据不是很可压缩。因此,作者提出在遇到这样的数据时,自适应地切换到不同的编码策略,以向量化的方式利用前导位相似的规律,对低方差的部分使用轻量级的整数编码进行压缩(如RLE)。ALP是一种用于压缩双精度浮点数据的自适应无损编码,其压缩是建立在上文提到的ALPenc过程之上的。在编码过程中,ALP必须验证ALPenc和ALPdec是否能安全地还原原来的双精度浮点数n,若不能则将该双精度浮点数n视为异常情况。算法1给出了ALP编码的伪代码,下文描述了其技术细节:ALP对同一向量内的所有双精度浮点数使用一个指数e和因子 f 组合。由上文可知这种方法需要能够使用较高的指数e,因此,ALP将编码后产生的整数限制为int64而非int32类型。此外,ALP引入了因子f,从而减少了整数尾随零的位数。在与因子 f 相乘后,得到的整数会再次变小,然后对同一向量内的所有值使用相同的位数进行紧凑的位打包。由于指数、因子和位宽这些参数每个向量只存储一次,因此它们不会占用太多空间。SIMD指令集不支持舍入操作。ALP用fast_double_round取代了round函数,利用了双精度浮点数最多只能存储52位的精确整数的限制。具体来说,fast_double_round通过加减以下数字来进行舍入:sweetn = 251 + 252,即将双精度浮点数取到不允许有小数部分的范围内(在252和253之间),从而“自动”进行舍入。例如,为舍入一个双精度浮点数n,fast_double_round函数将会执行:nrounded = cast < int64 > ( n + sweetn – sweetn),这种方法只涉及到加减法,因此适用于SIMD。 当出现异常值时,ALP在 encoded_vec 中存储辅助值(即算法1中第20行first_encoded)。这个辅助值是算法1中FIND_FIRST_ENCODED函数获得的第一个成功编码值d。接着,算法存储异常值原值及其出现的位置以供后续解压,这种方式能够有效的避免控制结构(if-then-else)的使用,从而提高解压缩效率。ALP编码本身并不会压缩数据,而是使用轻量级整数压缩方法FFOR来进一步编码。FFOR将位(解)打包的实现与FOR编码和解码过程融合到一个执行这两个过程的内核中,在减法和位填充循环之间节省了一个SIMD存储和加载指令,从而提高了性能。论文为找到各向量的最佳 e 和 f 组合设计了一种两级采样机制,具体如下:第一级采样,ALP从一个行组的n个等距向量中抽样m个等距值。这里行组定义为w个大小为v的连续向量的集合。因此,从第一次采样中获得的值的总数为m × n。而对于每个向量ni,算法在整个搜索空间上执行暴力搜索以找到最佳e、f 组合。这个过程产生了n个组合(每个向量一个),但只保留出现次数最多的k种。第二级采样(算法1的第5行)从一个向量中采样s个等距值。然后,尝试从k种组合中找到在当前的最佳组合。为了进一步优化搜索,算法实现了一种贪婪的提前退出策略:如果两个连续的组合k’i +1和k’i+2的性能差于或等于组合k’i的性能则停止搜索,并选择k’i组合对整个向量进行编码。算法2给出了ALP解压缩过程的伪代码。ALP首先从每个向量的头文件中读取用于编码的唯一指数e和因子f组合。然后,ALP需要反转FFOR整数编码以恢复每个值。对于编码为异常的值,则直接从异常段读取,同时读取它们在原始向量上的位置,以便正确地进行补丁修复。在第一级采样期间,检测行组中的双精度浮点数是否适用于ALP压缩。为应对不适用的情况,作者提出了ALPrd(ALP for real double)算法,利用其数据的靠前位较为相似的特点进行压缩。算法3展示了ALPrd的压缩与解压缩过程:ALPrd根据行组中数据的前64 - p位较为相似,后p位变动较大的特点,对前者建立歪斜字典进行压缩,后者则使用位打包。这里的异常指字典中没有的值,这些值及其对应位置分别以16位的值直接存储在异常数组中。采样后,算法考虑大小为2b且b ≤ 3的字典,并用样本中最频繁的值来填充这些字典,然后选择能够满足异常值占比不超过10%的最小的字典大小b,若均无法满足则使用b = 3。接着将字典编码按b位进行位包,并将字典对应的实际值存储为16位值。解压为上述过程的逆过程,解码高位部分的歪斜字典并与读取的低位部分进行拼接即可。作者针对当下具有代表性的时序和非时序数据集进行了实验对比,这些数据集在语义上有很大的差异。 如表2所示,14个数据集包含代表货币价值的双精度浮点数,其中4个表示坐标,2个以双精度存储的离散计数,1个计算机存储容量。此外,其他10个数据集涵盖了各种科学度量。根据图1,各数据集中组合的最大数量k设置为5。每个行组的向量数量w固定为100(模拟通常的现代OLAP引擎行组大小)。每个向量v的大小固定为1024(以适应CPU缓存)。在第一级采样中,每个行组m中采样的向量数设置为8,每个向量n采样的值数设置为32。最后,在第二级采样级别上,每个向量s采样的值的数量设置为32。论文选择将ALP与Gorilla, Chimp, Chimp128, Patas, PDE, Elf以及Zstd进行对比。其中,ALP, Gorilla, Chimp, Chimp128, Patas和PDE是用C++实现的,Elf是用Java实现的,Zstd是Facebook的C实现版本,并被配置为默认的压缩级别。 论文在不同的硬件架构(如表3所示)上对ALP算法运行速度进行了测试,并使用了自动向量化、标量化和SIMDized代码多种方式。表4显示了所有方法在各数据集上的压缩率情况,其中性能最好的方法被用绿色进行了标记。ALP在压缩率方面明显优于其他浮点编码方案。ALP较PDE相比,压缩效果平均提高了31%。与Gorilla、Patas、Chimp和Chimp128相比,ALP分别提高了约49%、39%、43%和24%。压缩率方面Elf与ALP旗鼓相当。论文以一个算法在一个CPU时钟周期内能够压缩的元组的数量来衡量速度,并在Ice Lake硬件架构下进行了(解)压缩速度测试,测试结果如下:测试结果显示出ALP算法的(解)压缩运行速度表现出色,优于其他竞争对手。论文提出了一种高效的自适应无损浮点数据压缩算法ALP,如果双精度浮点数起源于十进制,则将其无损编码为整数;否则仅对双精度浮点数的前导位进行向量压缩(ALPrd)。此外,作者借助自动向量化、FastLanes库提供的构建块,以及一个高效的两阶段采样算法对ALP算法进行了加速。最后,论文通过实验证明了ALP算法在压缩率以及(解)压缩速度上均表现出色。
徐小龙 重庆大学计算机科学与技术专业2020级本科生,重庆大学Start Lab成员。主要研究方向:时空数据压缩 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!