Sketch是一个极好的概率数据结构,它通过维护一个摘要来记录数据流近似统计数据。如何保持它的线性性质是在压缩时需要考虑的一个重要的因素。本文带来的是发表在国际顶级会议SIGMOD 2023的论文《TreeSensing: Linearly Compressing Sketches with Flexibility》提出了在保持sketch线性性质的同时进行灵活压缩的方法。现在各种数据流吞吐量极大,通常采用Sketch数据结构来进行统计查询。Sketch广泛应用于数据库、数据挖掘、网络中执行各种任务例如top-k查询,分布式数据分析,加速机器学习等。线性性质是sketch的一个重要性质,在分布式场景中,每个节点使用本地数据构建一个sketch,并且定期将其发送给中央分析器中,由于sketch具有线性性质,在中央分器中可以直接将收到的多个sketch进行聚合,用聚合后的sketch回答查询,而不是查询每一个sketch。本文研究了sketch进行压缩后如何继续保持这种线性性质。一个sketch压缩算法C(·),C(Si)是压缩后的sketch
Si,保持线性性质的压缩算法满足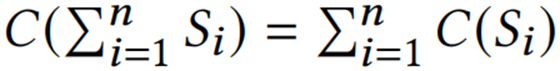 ,有以下两点可以说明压缩算法保持其线性性质的重要性:1)在一个有n个节点和一个中央分析器发分布式分析场景中,每一个周期内每个节点Ni构建一个局部sketch Si,将其压缩为C(Si),并将C(Si)发送到中央分析器中,中心分析器希望将每个局部sketch聚合在一起并使用聚合后的sketch进行全局分析任务。如果压缩算法那保持线性属性,就可以首先对收到的压缩后的局部sketch进行聚合,
,有以下两点可以说明压缩算法保持其线性性质的重要性:1)在一个有n个节点和一个中央分析器发分布式分析场景中,每一个周期内每个节点Ni构建一个局部sketch Si,将其压缩为C(Si),并将C(Si)发送到中央分析器中,中心分析器希望将每个局部sketch聚合在一起并使用聚合后的sketch进行全局分析任务。如果压缩算法那保持线性属性,就可以首先对收到的压缩后的局部sketch进行聚合,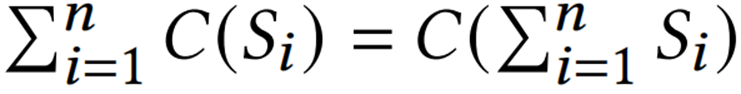 最后执行一次恢复操作,这样可以只执行一次恢复操作,否则的话需要对每个C(Si)进行恢复后在进行聚合。2)线性属性问题的另一个场景是安全聚合,这是联邦学习和云计算中的一个关键主题。例如在联邦学习中,n个worker在一个聚合器中协同训练一个模型,训练时,每个worker使用其局部数据计算梯度Gi,为了保证安全性,worker会引入随机噪声εi,所有worker的噪声满足
最后执行一次恢复操作,这样可以只执行一次恢复操作,否则的话需要对每个C(Si)进行恢复后在进行聚合。2)线性属性问题的另一个场景是安全聚合,这是联邦学习和云计算中的一个关键主题。例如在联邦学习中,n个worker在一个聚合器中协同训练一个模型,训练时,每个worker使用其局部数据计算梯度Gi,为了保证安全性,worker会引入随机噪声εi,所有worker的噪声满足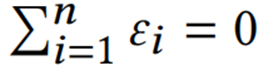 。因此,全局的梯度
。因此,全局的梯度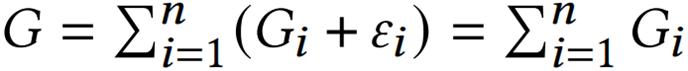 ,广播梯度会是一个十分占用资源的操作,所以对其进行压缩是有利可图的。在保证线性性质的情况下,聚合器可以直接聚合接收到数据
,广播梯度会是一个十分占用资源的操作,所以对其进行压缩是有利可图的。在保证线性性质的情况下,聚合器可以直接聚合接收到数据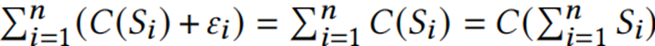 ,并且向每个worker进行广播。否则无法聚合压缩后的数据。本文提出了树传感TreeSensing,是一个精确高效灵活的框架来线性压缩sketch。首先将S分为两个部分:一个小sketch Ṡ,只包含计数值小的计数器;一个大sketch
,并且向每个worker进行广播。否则无法聚合压缩后的数据。本文提出了树传感TreeSensing,是一个精确高效灵活的框架来线性压缩sketch。首先将S分为两个部分:一个小sketch Ṡ,只包含计数值小的计数器;一个大sketch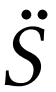 ,只包含计数器值大的计数器。满足S =Ṡ +
,只包含计数器值大的计数器。满足S =Ṡ + 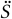 。例如,S =[1, 89, 2, 3, 1],将其拆分成Ṡ = [1, 0, 2, 3, 1]和
。例如,S =[1, 89, 2, 3, 1],将其拆分成Ṡ = [1, 0, 2, 3, 1]和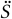 = [0, 89, 0, 0, 0]。接下来本文提出两个技术来针对这两种sketch进行压缩处理。第一个是针对小sketch的压缩TreeEncoding,第二个是针对大sketch的压缩SketchSensing。文章发现,实际应用中,绝大多数的sketch是高度倾斜的,即大多数计数器值都很小,只有一小部分值较大,如果都统一成32bits来存储每个计数显然会浪费很大的空间。因此本文提出的针对小sketch的TreeEncoding用更小的位数的计数器(例如4bits)。此外虽然可以使用TreeEncoding对整个sketch进行编码,但是不适合较大数值的计数器,而且在许多应用程序中只利用较大数值的计数器,(例如分布式ML)。文章发现由大计数器组成的sketch是一个稀疏数组,所以很适合采用压缩感知技术,因此文章提出了SketchSensing采用压缩感知以一种几乎无损的方式压缩大sketch。如图1所示,先用一个阈值把sketch中的数组
= [0, 89, 0, 0, 0]。接下来本文提出两个技术来针对这两种sketch进行压缩处理。第一个是针对小sketch的压缩TreeEncoding,第二个是针对大sketch的压缩SketchSensing。文章发现,实际应用中,绝大多数的sketch是高度倾斜的,即大多数计数器值都很小,只有一小部分值较大,如果都统一成32bits来存储每个计数显然会浪费很大的空间。因此本文提出的针对小sketch的TreeEncoding用更小的位数的计数器(例如4bits)。此外虽然可以使用TreeEncoding对整个sketch进行编码,但是不适合较大数值的计数器,而且在许多应用程序中只利用较大数值的计数器,(例如分布式ML)。文章发现由大计数器组成的sketch是一个稀疏数组,所以很适合采用压缩感知技术,因此文章提出了SketchSensing采用压缩感知以一种几乎无损的方式压缩大sketch。如图1所示,先用一个阈值把sketch中的数组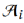 分离成小数组
分离成小数组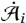 和大数组
和大数组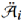 ,其中小数组只包含数值小的计数器值,大数组只包含计数器值较大的数值,其余位置置为零。强调一下,算法是一个几乎可以完全恢复的有损压缩算法。TreeEncoding使用一个称为层次结构树的结构来紧凑地记录小数组。层次结构树将小型计数器(例如4bits)组织成一个树的形状。一旦计数器溢出,它就会通过扩展到更高层中的计数器来自动扩大其大小,并将相应1bits溢出指示器设置为true。本文提出了一种名为ShiftBfEncoder 的技术来进一步压缩溢出指示器。实践中层次结构树仅需要两到三层就可以获得良好的性能。数据结构:如图2所示,一个层次结构树由l层组成:L1, …Ll,两个相邻层以一下方式关联,Li中的ki个相邻的计数器与Li+1相关联。此外每个计数器Li[j]使用一个1bit的指示器来记录是否溢出。压缩过程:首先构造一个空的层次结构树,第一层插入小数组的值,如果发生溢出,就将溢出的计数器置为
,其中小数组只包含数值小的计数器值,大数组只包含计数器值较大的数值,其余位置置为零。强调一下,算法是一个几乎可以完全恢复的有损压缩算法。TreeEncoding使用一个称为层次结构树的结构来紧凑地记录小数组。层次结构树将小型计数器(例如4bits)组织成一个树的形状。一旦计数器溢出,它就会通过扩展到更高层中的计数器来自动扩大其大小,并将相应1bits溢出指示器设置为true。本文提出了一种名为ShiftBfEncoder 的技术来进一步压缩溢出指示器。实践中层次结构树仅需要两到三层就可以获得良好的性能。数据结构:如图2所示,一个层次结构树由l层组成:L1, …Ll,两个相邻层以一下方式关联,Li中的ki个相邻的计数器与Li+1相关联。此外每个计数器Li[j]使用一个1bit的指示器来记录是否溢出。压缩过程:首先构造一个空的层次结构树,第一层插入小数组的值,如果发生溢出,就将溢出的计数器置为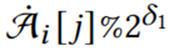 ,溢出指示器置为1并且增加其父计数器
,溢出指示器置为1并且增加其父计数器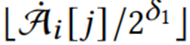 。父计数器通过汇总其溢出的值来合并其子计数器,这是一个有损的进程。恢复过程:为了以最大的努力恢复一个小数组(使用整个层次结构树),首先构建一个辅助的层次结构树。辅助层次树与压缩的层次树具有相同的形状,但每个计数器包含32bits。首先将辅助层次结构树的𝑙𝑡ℎ层设置为𝐿𝑙,即𝐿'𝑙=𝐿𝑙。接着逐层恢复𝐿'𝑙-1利用溢出指示器,如果是true则L‘i[j] = L'i[j]
+L'i+1[⌊j/ki⌋] × 2δi。讨论:TreeEncoding不能保证精确恢复,但在良好的参数选择下,可以实现几乎无损恢复。对于每个父计数器,如果它只记录一个子计数器的溢出值,则我们将其定义为纯计数器。可以看到,只有当所有的父计数器都是纯的时,TreeEncoding才能实现精确的恢复。这是因为每个非纯计数器都通过汇总子计数器的溢出值来合并它们,这是一个有损的过程。对于2层层次树(𝑙= 2),可以修改合并方法,使所有溢出值中取最大值,以减少误差。[可选]ShiftBfEncoder 优化。为了更进一步压缩溢出指示器,文章提出了ShiftBfEncoder。文章注意到,只有一小部分计数器会溢出,所以溢出指示器是非常稀疏的。如图3所示。首先将该指示器分成许多连续的组,每个组包含𝑥位(在示例中𝑥=4)。对于每个组,将其散列到ShiftBfEncoder中的𝛾位置,(在示例中𝛾=2)。如图3所示,为了对一个组0100进行编码,定位它的两个散列位置0010和0000,并对它们执行按位或操作:0100|0010 = 0110和0100|0000 = 0100。请注意,ShiftBfEncoder存在由散列碰撞引起的假阳性错误:考虑一个真值为0000的给定组,如果其两个散列位置的值分别为1010和1000,则其恢复值将为1010和1000=1000,其中在第一位出现错误。我们可以通过添加更多的散列来减少这个错误,但这将减少ShiftBfEncoder的稀疏性,降低总体精度。因此,文章建议对较高层的组使用更多的散列,而对较低层的组使用更少的散列。压缩过程:如图4所示,为了压缩大计数器数组
。父计数器通过汇总其溢出的值来合并其子计数器,这是一个有损的进程。恢复过程:为了以最大的努力恢复一个小数组(使用整个层次结构树),首先构建一个辅助的层次结构树。辅助层次树与压缩的层次树具有相同的形状,但每个计数器包含32bits。首先将辅助层次结构树的𝑙𝑡ℎ层设置为𝐿𝑙,即𝐿'𝑙=𝐿𝑙。接着逐层恢复𝐿'𝑙-1利用溢出指示器,如果是true则L‘i[j] = L'i[j]
+L'i+1[⌊j/ki⌋] × 2δi。讨论:TreeEncoding不能保证精确恢复,但在良好的参数选择下,可以实现几乎无损恢复。对于每个父计数器,如果它只记录一个子计数器的溢出值,则我们将其定义为纯计数器。可以看到,只有当所有的父计数器都是纯的时,TreeEncoding才能实现精确的恢复。这是因为每个非纯计数器都通过汇总子计数器的溢出值来合并它们,这是一个有损的过程。对于2层层次树(𝑙= 2),可以修改合并方法,使所有溢出值中取最大值,以减少误差。[可选]ShiftBfEncoder 优化。为了更进一步压缩溢出指示器,文章提出了ShiftBfEncoder。文章注意到,只有一小部分计数器会溢出,所以溢出指示器是非常稀疏的。如图3所示。首先将该指示器分成许多连续的组,每个组包含𝑥位(在示例中𝑥=4)。对于每个组,将其散列到ShiftBfEncoder中的𝛾位置,(在示例中𝛾=2)。如图3所示,为了对一个组0100进行编码,定位它的两个散列位置0010和0000,并对它们执行按位或操作:0100|0010 = 0110和0100|0000 = 0100。请注意,ShiftBfEncoder存在由散列碰撞引起的假阳性错误:考虑一个真值为0000的给定组,如果其两个散列位置的值分别为1010和1000,则其恢复值将为1010和1000=1000,其中在第一位出现错误。我们可以通过添加更多的散列来减少这个错误,但这将减少ShiftBfEncoder的稀疏性,降低总体精度。因此,文章建议对较高层的组使用更多的散列,而对较低层的组使用更少的散列。压缩过程:如图4所示,为了压缩大计数器数组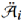 ,首先将所有计数器轮入到一个预定义参数𝑟(称为舍入参数)的倍数。例如,如果是𝑟=4,则一个值为69的计数器将被四舍五入为68。这个过程减少了原始数组的信息。接下来,将
,首先将所有计数器轮入到一个预定义参数𝑟(称为舍入参数)的倍数。例如,如果是𝑟=4,则一个值为69的计数器将被四舍五入为68。这个过程减少了原始数组的信息。接下来,将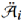 均匀地分割成𝑓片段(称为原始片段),每个片段都有𝑚=𝑤/𝑓个计数器。文章从一个随机种子中生成压缩感知中的感知矩阵𝜙。给定一个预定义的压缩比率λ,每个𝜙大小为m×m‘,其中m’
= m/λ。最后通过将每个原始片段乘以𝜙,将𝑓个原始片段压缩成𝑓个更小的片段(称为传感片段)。恢复:为了恢复一个大的阵列,我们首先从感知片段和感知矩阵中解码每个原始片段。这可以通过解决一个𝐿1优化问题来实现。压缩感知保证了原始片段在足够稀疏的情况下可以完全恢复。最后,文章将解码后的片段组装成一个完整的数组。近似恢复:SketchSensing的恢复过程是灵活的。可以只使用部分感知片段来近似地恢复一个sketch。由𝑑个不完整数组组成的近似恢复的sketch也可以回答查询:对于每个查询,它将访问𝑑个列计数器,其中一些可能会缺少。文章将缺失计数器的值视为无效,并在其他有效计数器中报告最小值。只要其中一个散列计数器有效,恢复的sketch就可以报告一个有效的结果。文章在CPU平台和FPGA平台上分别进行实验。实验使用的三种层次结构树如图表1所示数据集:CAIDA:由CAIDA 2018在骨干链路上收集的IP路径数据集。本文使用了两个不同大小的路径数据,一个包含约3000万条的小型1分钟路径,和一个包含约1.5G条的大型1小时路径。2)Criteo:一个包含约4500万份广告记录的在线广告点击数据流。3)Zipf:文章使用Web波动,根据Zipf分布生成不同偏度的多个数据集,每个数据集有32M条数据。评价指标:1)平均相对误差(ARE):
均匀地分割成𝑓片段(称为原始片段),每个片段都有𝑚=𝑤/𝑓个计数器。文章从一个随机种子中生成压缩感知中的感知矩阵𝜙。给定一个预定义的压缩比率λ,每个𝜙大小为m×m‘,其中m’
= m/λ。最后通过将每个原始片段乘以𝜙,将𝑓个原始片段压缩成𝑓个更小的片段(称为传感片段)。恢复:为了恢复一个大的阵列,我们首先从感知片段和感知矩阵中解码每个原始片段。这可以通过解决一个𝐿1优化问题来实现。压缩感知保证了原始片段在足够稀疏的情况下可以完全恢复。最后,文章将解码后的片段组装成一个完整的数组。近似恢复:SketchSensing的恢复过程是灵活的。可以只使用部分感知片段来近似地恢复一个sketch。由𝑑个不完整数组组成的近似恢复的sketch也可以回答查询:对于每个查询,它将访问𝑑个列计数器,其中一些可能会缺少。文章将缺失计数器的值视为无效,并在其他有效计数器中报告最小值。只要其中一个散列计数器有效,恢复的sketch就可以报告一个有效的结果。文章在CPU平台和FPGA平台上分别进行实验。实验使用的三种层次结构树如图表1所示数据集:CAIDA:由CAIDA 2018在骨干链路上收集的IP路径数据集。本文使用了两个不同大小的路径数据,一个包含约3000万条的小型1分钟路径,和一个包含约1.5G条的大型1小时路径。2)Criteo:一个包含约4500万份广告记录的在线广告点击数据流。3)Zipf:文章使用Web波动,根据Zipf分布生成不同偏度的多个数据集,每个数据集有32M条数据。评价指标:1)平均相对误差(ARE):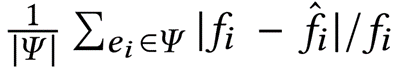 𝑓𝑖为项目𝑒𝑖的真实频率,表示估计的频率,𝛹为查询集。对于Top-𝑘查询,𝛹由top-𝑘频繁项(默认为𝑘=500)组成。对于Full ARE,𝛹包含所有项。2)压缩错误(CE):
𝑓𝑖为项目𝑒𝑖的真实频率,表示估计的频率,𝛹为查询集。对于Top-𝑘查询,𝛹由top-𝑘频繁项(默认为𝑘=500)组成。对于Full ARE,𝛹包含所有项。2)压缩错误(CE):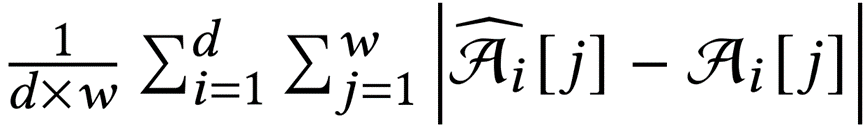 其中
其中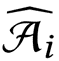 是第i个恢复的sketch。3)损失:对于分类(使用逻辑回归),文章使用交叉熵。
是第i个恢复的sketch。3)损失:对于分类(使用逻辑回归),文章使用交叉熵。
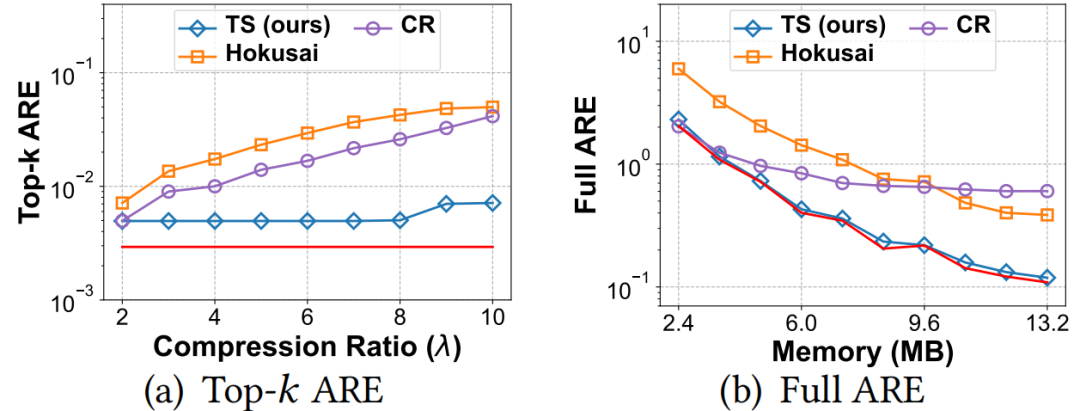
图5 比较top-𝑘的ARE(红线表示未压缩sketch的ARE)。
Sketch的Top-k
ARE。文章在五种计数器CM、CU、CMM、CML、CSM上与Hokusai,Elastic,Cluster-Reduce(CR)进行比较。如图5所示可以发现物种sketch在top-k场景下,TreeSensing与无压缩的sketch 的ARE几乎相同,可以说明文中提出的算法可以近乎无损的进行恢复。
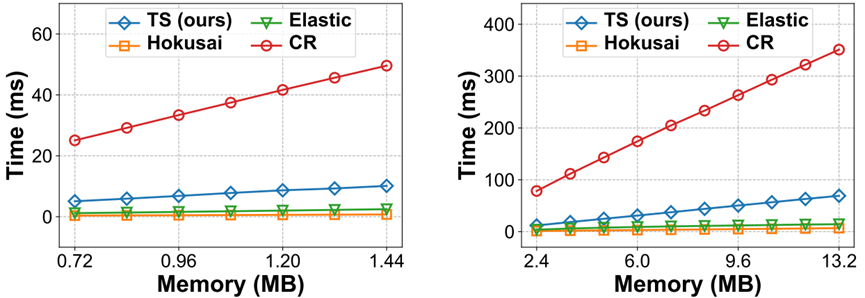
图6 Full ARE的比较(红线表示未压缩sketch的ARE)。
Sketch的Full
ARE。根据图6可以发现,对于所有的五个sketch,TreeSensing的Full
ARE几乎与未压缩的sketch相同,这意味着TreeSensing实现了几乎无损的恢复。此外,我们可以看到,TreeSensing在所有五种sketch上总是优于其他算法。sketch的计数精度:根据图7可以看出与非压缩sketch相比,TreeSensing的top-𝑘ARE略高,Full ARE几乎相同。我们可以看到,TreeSensing在top-𝑘ARE和Full ARE上都明显优于其他算法。具体来说,TreeSensing算法比其他算法实现了小8.2×的top-𝑘ARE和小6.4×的Full
ARE。图7 Sketch计数的精度比较(红线表示未压缩sketch的ARE)。图8 压缩效率的比较(红线表示未压缩sketch的ARE)。压缩效率:可以发现TreeSensing比Cluster-Reduce减少快3∼6倍,但比Hokusai 和Elastic。在图8(a)中,只使用了SketchSensing。可以看到,要压缩一个1.44MB的sketch,TreeSensing、Hokusai、Elastic和CR分别需要10.0 ms、0.7
ms、2.4 ms和50.0 ms。在图8(b)中,我们同时使用了TreeEncoding和SketchSensing。可以看到,要压缩一个13.2MB的sketch,TreeSensing、Hokusai、Elastic和CR分别需要69.1 ms、6.7
ms、17.0 ms和353.1 ms。本文提出了一种精确、高效、灵活的线性压缩sketch的TreeSensing框架。在TreeSensing技术中,我们首先将原始sketch分成两个部分sketch,然后用两个关键技术,即TreeEncoding和SketchSensing,压缩这两个部分sketch。并且对TreeSensing进行了理论分析。实验结果表明,TreeSensing的性能明显优于现有的解决方案。| 重庆大学计算机科学与技术专业硕士一年级在读学生,重庆大学START团队成员。 | 
|
时空艺术团队(START,Spatio-Temporal Art)来自重庆大学时空实验室,旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!

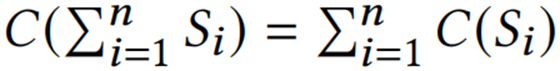 ,有以下两点可以说明压缩算法保持其线性性质的重要性:1)在一个有n个节点和一个中央分析器发分布式分析场景中,每一个周期内每个节点Ni构建一个局部sketch Si,将其压缩为C(Si),并将C(Si)发送到中央分析器中,中心分析器希望将每个局部sketch聚合在一起并使用聚合后的sketch进行全局分析任务。如果压缩算法那保持线性属性,就可以首先对收到的压缩后的局部sketch进行聚合,
,有以下两点可以说明压缩算法保持其线性性质的重要性:1)在一个有n个节点和一个中央分析器发分布式分析场景中,每一个周期内每个节点Ni构建一个局部sketch Si,将其压缩为C(Si),并将C(Si)发送到中央分析器中,中心分析器希望将每个局部sketch聚合在一起并使用聚合后的sketch进行全局分析任务。如果压缩算法那保持线性属性,就可以首先对收到的压缩后的局部sketch进行聚合,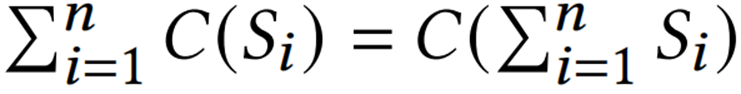 最后执行一次恢复操作,这样可以只执行一次恢复操作,否则的话需要对每个C(Si)进行恢复后在进行聚合。2)线性属性问题的另一个场景是安全聚合,这是联邦学习和云计算中的一个关键主题。例如在联邦学习中,n个worker在一个聚合器中协同训练一个模型,训练时,每个worker使用其局部数据计算梯度Gi,为了保证安全性,worker会引入随机噪声εi,所有worker的噪声满足
最后执行一次恢复操作,这样可以只执行一次恢复操作,否则的话需要对每个C(Si)进行恢复后在进行聚合。2)线性属性问题的另一个场景是安全聚合,这是联邦学习和云计算中的一个关键主题。例如在联邦学习中,n个worker在一个聚合器中协同训练一个模型,训练时,每个worker使用其局部数据计算梯度Gi,为了保证安全性,worker会引入随机噪声εi,所有worker的噪声满足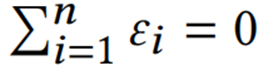 。因此,全局的梯度
。因此,全局的梯度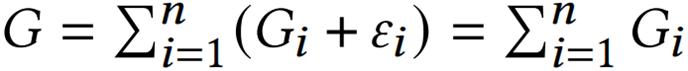 ,广播梯度会是一个十分占用资源的操作,所以对其进行压缩是有利可图的。在保证线性性质的情况下,聚合器可以直接聚合接收到数据
,广播梯度会是一个十分占用资源的操作,所以对其进行压缩是有利可图的。在保证线性性质的情况下,聚合器可以直接聚合接收到数据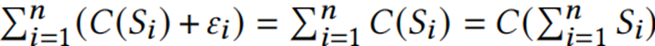 ,并且向每个worker进行广播。否则无法聚合压缩后的数据。
,并且向每个worker进行广播。否则无法聚合压缩后的数据。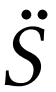 ,只包含计数器值大的计数器。满足S =Ṡ +
,只包含计数器值大的计数器。满足S =Ṡ + 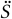 。例如,S =[1, 89, 2, 3, 1],将其拆分成Ṡ = [1, 0, 2, 3, 1]和
。例如,S =[1, 89, 2, 3, 1],将其拆分成Ṡ = [1, 0, 2, 3, 1]和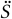 = [0, 89, 0, 0, 0]。接下来本文提出两个技术来针对这两种sketch进行压缩处理。第一个是针对小sketch的压缩TreeEncoding,第二个是针对大sketch的压缩SketchSensing。
= [0, 89, 0, 0, 0]。接下来本文提出两个技术来针对这两种sketch进行压缩处理。第一个是针对小sketch的压缩TreeEncoding,第二个是针对大sketch的压缩SketchSensing。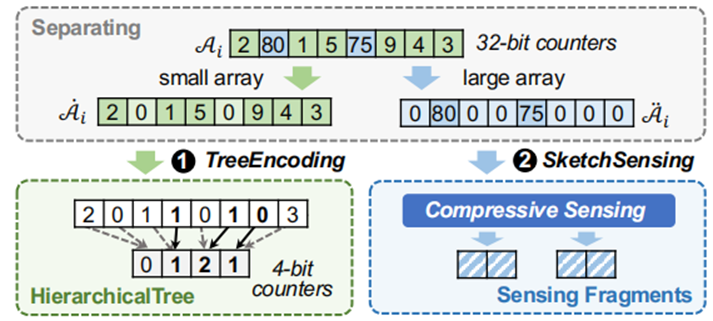
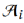 分离成小数组
分离成小数组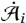 和大数组
和大数组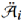 ,其中小数组只包含数值小的计数器值,大数组只包含计数器值较大的数值,其余位置置为零。强调一下,算法是一个几乎可以完全恢复的有损压缩算法。
,其中小数组只包含数值小的计数器值,大数组只包含计数器值较大的数值,其余位置置为零。强调一下,算法是一个几乎可以完全恢复的有损压缩算法。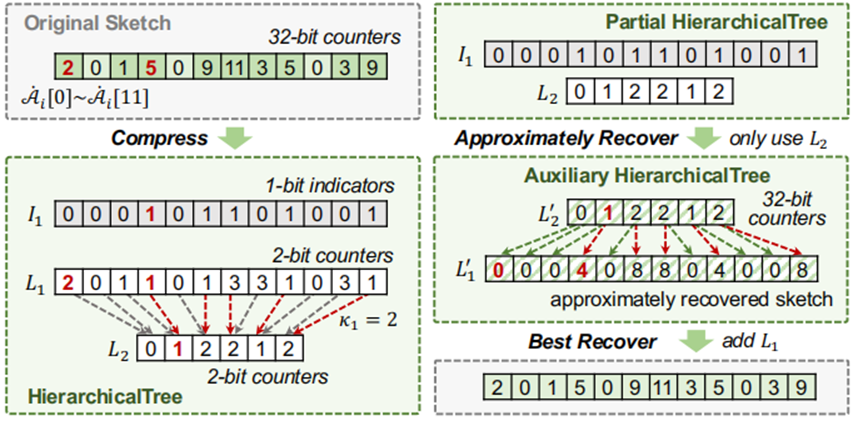
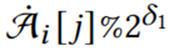 ,溢出指示器置为1并且增加其父计数器
,溢出指示器置为1并且增加其父计数器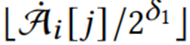 。父计数器通过汇总其溢出的值来合并其子计数器,这是一个有损的进程。
。父计数器通过汇总其溢出的值来合并其子计数器,这是一个有损的进程。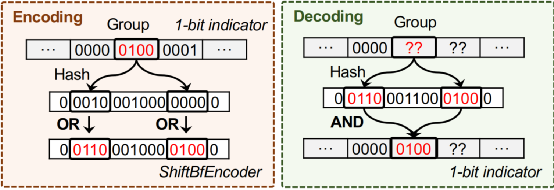
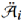 ,首先将所有计数器轮入到一个预定义参数𝑟(称为舍入参数)的倍数。例如,如果是𝑟=4,则一个值为69的计数器将被四舍五入为68。这个过程减少了原始数组的信息。接下来,将
,首先将所有计数器轮入到一个预定义参数𝑟(称为舍入参数)的倍数。例如,如果是𝑟=4,则一个值为69的计数器将被四舍五入为68。这个过程减少了原始数组的信息。接下来,将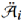 均匀地分割成𝑓片段(称为原始片段),每个片段都有𝑚=𝑤/𝑓个计数器。文章从一个随机种子中生成压缩感知中的感知矩阵𝜙。给定一个预定义的压缩比率λ,每个𝜙大小为m×m‘,其中m’
= m/λ。最后通过将每个原始片段乘以𝜙,将𝑓个原始片段压缩成𝑓个更小的片段(称为传感片段)。
均匀地分割成𝑓片段(称为原始片段),每个片段都有𝑚=𝑤/𝑓个计数器。文章从一个随机种子中生成压缩感知中的感知矩阵𝜙。给定一个预定义的压缩比率λ,每个𝜙大小为m×m‘,其中m’
= m/λ。最后通过将每个原始片段乘以𝜙,将𝑓个原始片段压缩成𝑓个更小的片段(称为传感片段)。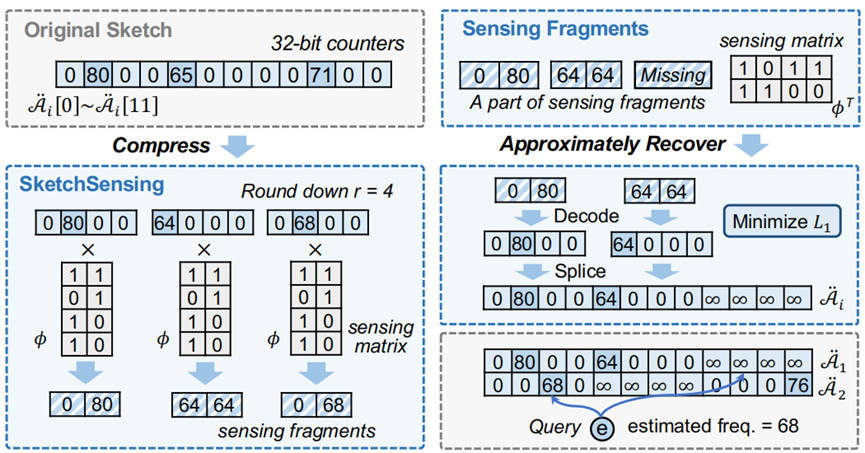

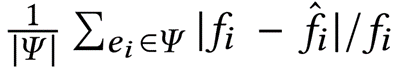 𝑓𝑖为项目𝑒𝑖的真实频率,表示估计的频率,𝛹为查询集。对于Top-𝑘查询,𝛹由top-𝑘频繁项(默认为𝑘=500)组成。对于Full ARE,𝛹包含所有项。2)压缩错误(CE):
𝑓𝑖为项目𝑒𝑖的真实频率,表示估计的频率,𝛹为查询集。对于Top-𝑘查询,𝛹由top-𝑘频繁项(默认为𝑘=500)组成。对于Full ARE,𝛹包含所有项。2)压缩错误(CE):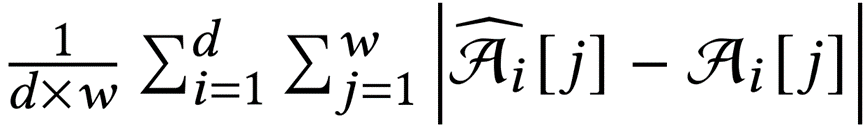 其中
其中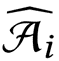 是第i个恢复的sketch。3)损失:对于分类(使用逻辑回归),文章使用交叉熵。
是第i个恢复的sketch。3)损失:对于分类(使用逻辑回归),文章使用交叉熵。