轨迹的相似性计算是捕捉物体运动的轨迹的应用之一。传统上,轨迹相似度通过非学习度量(如Hausdorff)进行量化,直接作用于轨迹上。最近的研究利用深度学习将轨迹映射到多维向量,即embeddings。本次为大家带来数据库领域顶级会议VLDB 2024的文章《Trajectory Similarity Measurement: An Efficiency Perspective》,从效率视角出发,分析了非学习型方法和基于学习的方法的时间复杂性。
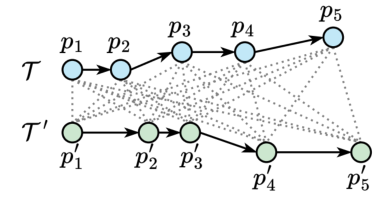
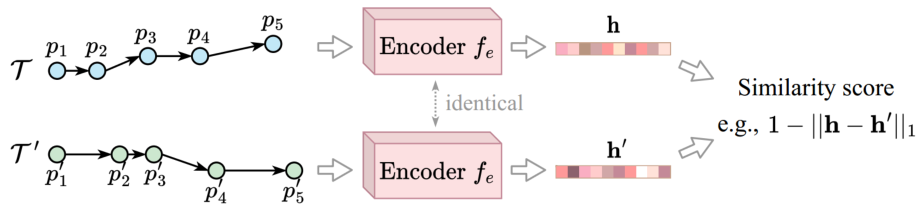
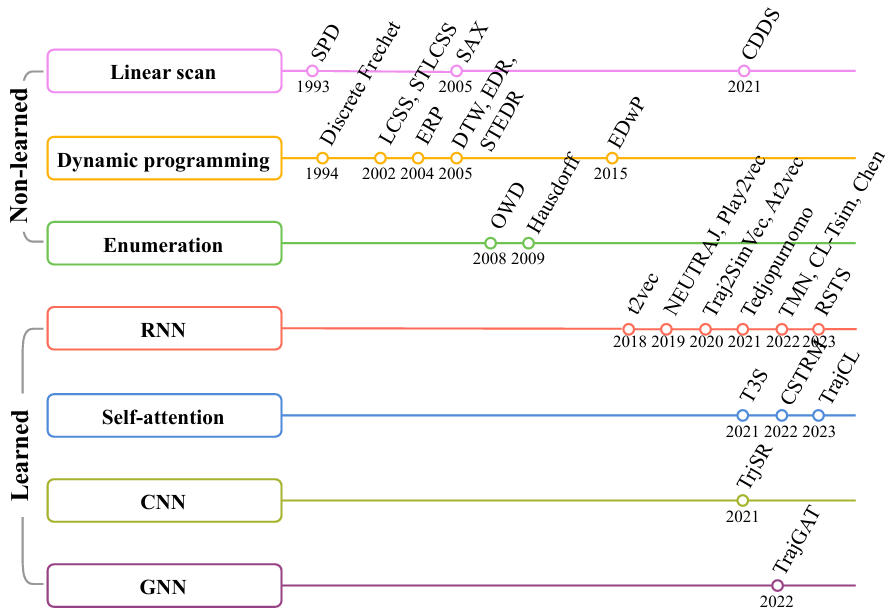
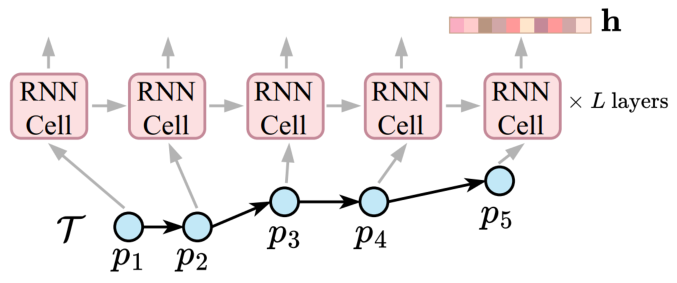
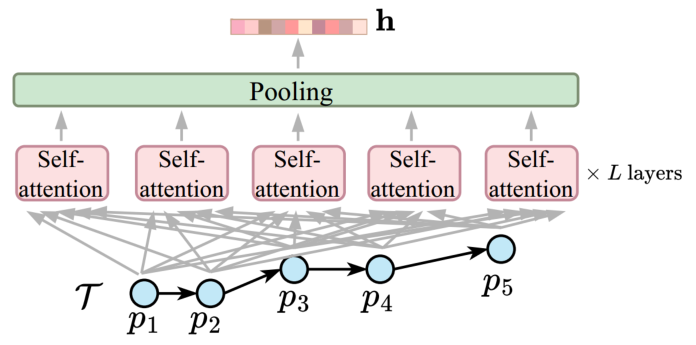
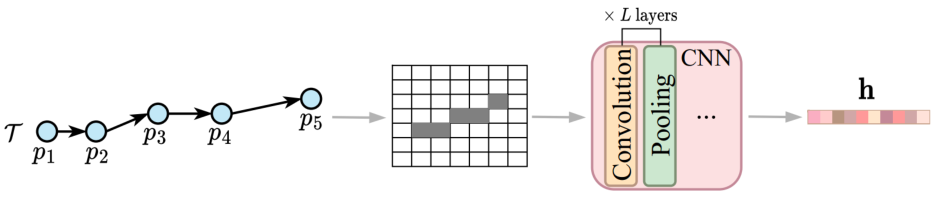
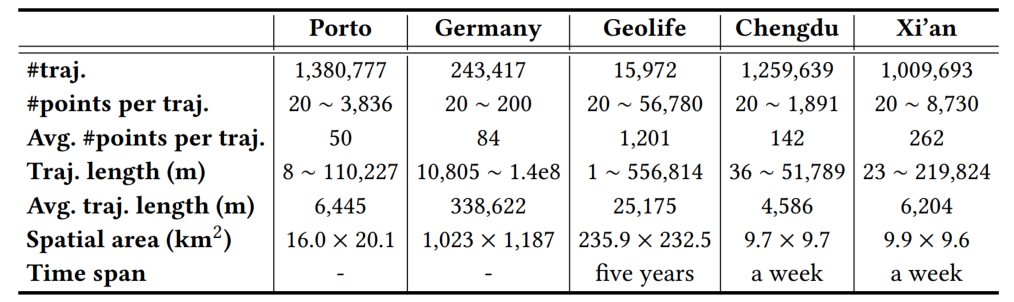
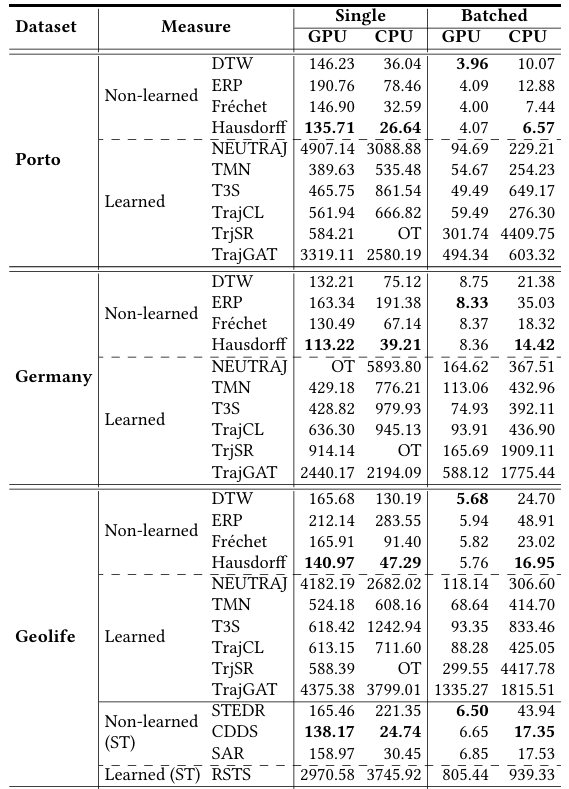
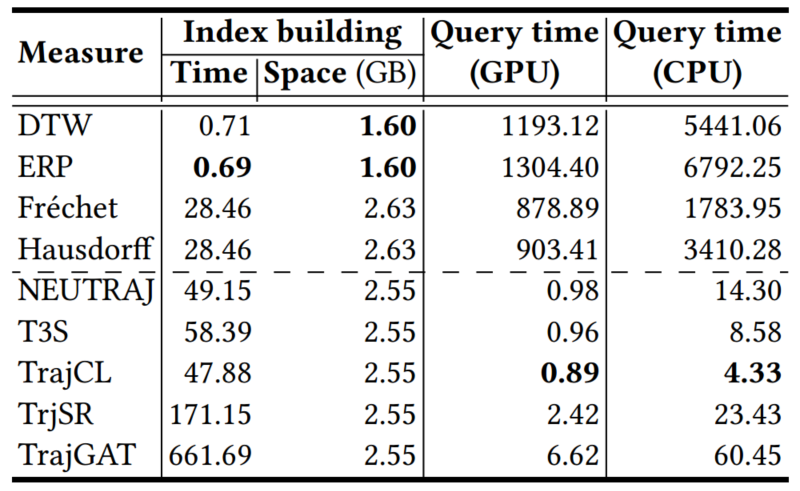
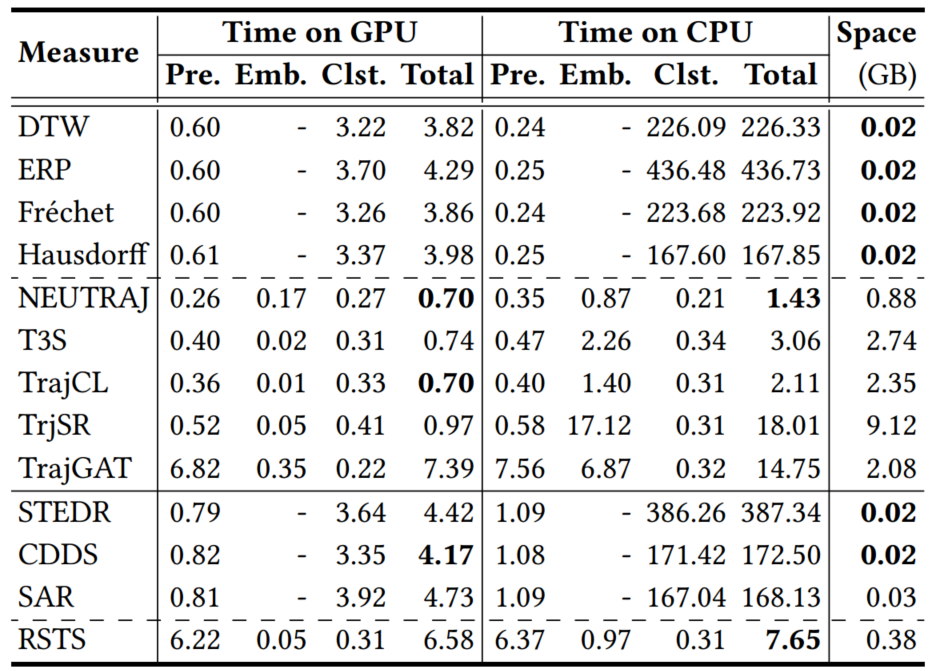
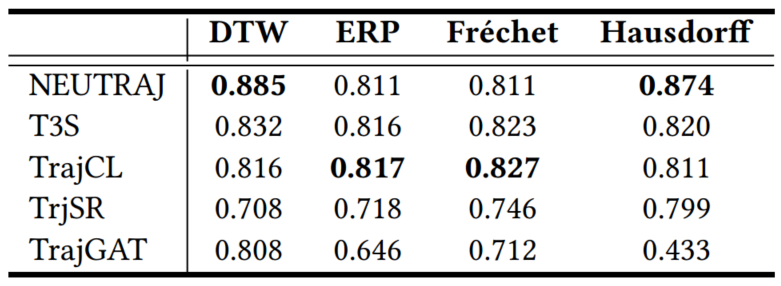
由于轨迹中编码了丰富的位置和运动信息以及许多应用设置,不存在单一的通用轨迹相似性度量。轨迹相似性度量可以大致分为两类:非学习型度量和学习型度量。早期的研究主要集中在非学习型度量上,通过匹配两个轨迹之间的点以捕获相似性(见图1)。例如,Hausdorff计算了点匹配,以最小化两个轨迹之间点到轨迹的距离总和。上述非学习型度量在要检查的轨迹点的数量上具有二次的时间复杂度。图1 非学习型度量的计算(虚线表示点对点的距离计算)学习型度量主要利用深度学习来提高计算效率。通常遵循以下步骤:(1)将轨迹编码为向量,称为轨迹嵌入(trajectory embeddings),(2)计算轨迹嵌入之间的向量距离(例如,曼哈顿距离)作为轨迹距离(见图2)。例如,t2vec、NEUTRAJ和TMN使用递归神经网络,而T3S和TrajCL使用自注意模型。 在学习型度量中,一些方法(如NEUTRAJ和T3S)“学习”逼近现有的非学习测度(如Hausdorff),即训练信号是由非学习测度提供的实际轨迹相似性。这种方法牺牲精度以换取更高的计算效率。另一系列的学习型度量方法(如t2vec和TrajCL)不仅提高了效率,而且提高了度量效果。这种方法通常使用自监督学习技术,直接从未标记的轨迹中学习鲁棒度量,而不依赖于任何非学习型度量。一旦经过训练,它们通常具有更好的效果,特别是在应用于低质量轨迹时。然而,作者观察到学习型度量的时间复杂度并不一定低于非学习型度量的时间复杂度。例如,T3S[和TrajCL在轨迹点数量上也具有二次的时间复杂度。由此提出了两个问题:(1)学习型度量是否比非学习型度量具有更好的计算时间和空间效率?(2)在给定训练时间限制的情况下,例如,由于应用需求不同,所学习的度量在准确性方面如何相互比较?论文通过对轨迹相似度量的有效性以及在训练时间约束下学习到的度量的准确性进行综合实验,为这些问题提供了初步答案。接下来介绍空间/时空轨迹相似性度量的现有研究,包括非学习和学习型轨迹相似性度量,以及轨迹查询,包括轨迹相似性查询和轨迹聚类。图3总结了论文关注的基于欧几里得空间的代表性度量。非学习型度量通常采用点匹配的方式,根据不同的计算方法分为3类:(i)基于线性扫描,(ii)基于动态规划和(iii)基于枚举。基于线性扫描的度量方法只对两个轨迹进行一次扫描。假设每个轨迹有n个点,这些度量需要O(n)时间来计算,并且需要Θ(1)空间来存储部分相似性结果,不包括保存轨迹的O(1)空间。例如,Sum-of-Pair Distance(SPD)简单地将两个轨迹上的点按照点的顺序进行匹配,并对成对点的距离求和。SPD假设轨迹具有相同数量点。Close-Distance Duration Similarity(CDDS)进一步考虑了时间维度,当两个轨迹上的点都在给定的空间距离阈值内时,对时间跨度进行求和作为相似度。 基于线性扫描的度量可能得到次优点匹配,从而导致错误的轨迹相似值。为了解决这个问题,提出了基于动态规划(DP)的方法。如图1所示,这些度量在O(n2)时间内用DP增量地检查所有点对,使用Θ(n)空间来存储中间相似度(距离)值。例如,Dynamic Time Warping(DTW)是为时间序列分析(如语音识别)而设计的,通过使用欧几里得距离函数扩展到轨迹,利用其多对一的点匹配特性来处理具有不同移动速度或采样率的轨迹。DTW计算两个轨迹之间的一组点对齐,以最小化点对点距离之和。且DTW不需要相同长度的轨迹。Discrete Fréchet也允许多对一的点匹配,返回任何匹配点对之间的最大距离。这些方法直接计算所有成对的点距离,并将它们聚合形成轨迹相似性(见图1)。它们需要O(n2)的时间和O(1)的空间,因为不需要存储中间结果。例如,Hausdorff是为图像匹配而设计的,它计算的是点到轨迹的最大距离。一个小的Hausdorff距离意味着两条轨迹形成了紧密的匹配。根据设计目的可以分为两类:(i)通过监督学习学习和近似现有的非学习型度量,使用一些非学习型度量来提供监督信号;(ii)学习独立于任何非学习型度量的潜在相似性测度。对于后一类,使用自监督学习来学习轨迹嵌入(embeddings)。两个轨迹之间的相似性是基于它们的嵌入计算的,例如,使用L1距离。这些方法的核心组件是轨迹编码器,以轨迹作为输入,输出嵌入。编码器在学习型度量中起着核心作用。由于轨迹是序列,RNNs形成了一个天然的轨迹编码器。通过考虑历史状态(即来自前几个点的聚合信息)和当前状态(即要编码的当前点)来循环地编码每个轨迹点。当RNN终止时,最终的输出状态需要来自轨迹上所有点的聚合信息,这些信息被用作轨迹嵌入,即图4中的h。基于RNN的度量(使用长短期记忆LSTM或门控制循环单元GRU)至少需要Ω(nd 2)时间来编码一个轨迹,因为它们需要计算n个状态的隐藏表示(对于轨迹上的n个点),而每个隐藏表示需要Θ(d 2)时间来计算。这里的d是嵌入维度。基于RNN的度量需要Ω(d 2)空间存储模型参数,以及另一个Ω(d)空间用于存储中间结果。例如,t2vec通过引入空间接近感知损失函数来适应GRU,当模型在空间接近轨迹上产生较大的相似性预测误差时,该函数会对模型进行惩罚。多头自注意力(简称“自注意力”)是一种较新的序列模型,可以解决RNNs中的遗忘问题。它学习输入序列中每两个元素之间隐藏的相关性(见图5)。对轨迹进行编码需要花费Ω(n2d)时间。虽然这似乎比RNN所花费的时间要高,但自注意模型可能比GPU上运行得比RNNs快得多。基于自注意的度量需要Ω(d2+nd+n2)空间,其中模型参数(即权重矩阵)占用Ω(d2)空间,计算注意力系数的中间结果占用Ω(nd+n2)空间。 CNN模型广泛应用于图像表示学习,通过叠加卷积核和池化层来捕获图像特征。要将轨迹转换为固定大小的图像,需要创建一个与包围轨迹的数据空间相对应的空白图像。然后,将轨迹点映射到图像的像素,其中像素值表示映射到像素的点的数量(见图6)。TrjSR是唯一的基于CNN的模型。通过从低分辨率轨道图像重建超分辨率轨道图像来训练。TrjSR用Ω(mk2nkc)时间编码一个轨迹,其中k是卷积核的边长,nk是核的数量,c是通道大小,d是像素的数量。同时TrjSR需要Ω(k2nkc+mc)的空间。基于CNN的一个问题是,它们丢失了轨迹点的序列信息,同时不能区分向相反方向的两条轨迹。GNNs是为图嵌入而设计的。在GNN层中,每个节点接收和聚合来自其邻居的节点嵌入(聚合)。然后,将聚合后的信息与节点的嵌入相结合,形成更新后的嵌入(组合)。 TrajGAT是唯一基于GNN的度量(见图7)。TrajGAT构建的多级四叉树将空间划分为不同大小的单元,以帮助创建具有多粒度轨迹视图的图。为了从轨迹构造图,TrajGAT查询四叉树中的每个轨迹点,并将遍历路径上的树节点作为图节点添加到图中。添加的树节点之间的边保留为图边。为了编码一个轨迹图,TrajGAT需要Ω(nned)时间,其中ne是图中每个节点的邻居数,空间则为Ω(d2+nd+nne)。(1)数据集。论文使用5个真实世界的轨迹数据集,并丢弃少于20个点的短轨迹来预处理数据集。表1总结了预处理后的数据集统计信息。(2)对比方法。图8列出了测试的相似性度量,其中“ST”指的是考虑空间距离和时间差异的度量。(3)环境。所有实验都在一个虚拟机上运行,该虚拟机具有8核Intel Xeon 4214 CPU (2.2 GHz), 128GB RAM和NVIDIA V100 GPU (5120个FP32内核和16GB VRAM)。论文重复每个实验五次,取平均结果。此处仅展现部分实验结果分析,更多实验设置、结果详见原论文。表2显示了在线完成所有计算(包括轨迹嵌入)时的运行时间。总的来说,当非学习型度量在相同的计算单元上在线运行时,运行时间比学习型度量要少。在GPU上进行批处理计算时,即使学习型方法被认为是最好的,非学习型方法也至少要快一个数量级。具体从表中可以看出:(1)非学习型度量和学习型度量在GPU上的批处理计算时间最少。(2)当计算每对轨迹之间的相似性时,非学习测度更倾向于CPU,而学习测度更倾向于GPU。(3)在非学习型度量中,基于枚举的Hausdorff由于其计算规则简单,总体上是最快的(不包括时空测度)。(4)在学习到的度量中,基于注意力的T3S和TrajCL在时间上的响应速度更快,其中T3S的响应速度较慢,因为它还使用了RNN。 表2 轨迹相似度计算的运行时间(粗体为最佳结果,仅截取部分数据集)论文报告了查询效率和准确性的结果。这两个方面的结果共同指导了针对不同应用场景的学习型度量的选择。根据以往文献,论文使用命中率(HR@50)来衡量学习型度量的准确性。此外,论文还报告了指数构建的成本。表6显示了索引构建和查询处理的运行时间。索引构建时间包括构建索引的时间和计算数据轨迹嵌入的时间(对于学习型度量)。同样,学习型度量的查询时间包括计算查询轨迹嵌入的时间(因为查询轨迹可能在线到达)。总的来说,学习型度量在索引构建上花费了更多的时间,以实现更快的查询处理速度。 论文遵循常用的轨迹聚类范式。对于非学习型度量,使用k- medoids算法对原始轨迹进行聚类。对于学习型度量,在嵌入上使用k- medoids。默认数据集由来自数据集的1000个随机采样轨迹组成,其中轨迹上的点数在20到200之间。集群个数默认为10。基于学习型度量的轨迹聚类也是基于非学习型度量的轨迹聚类的近似。论文使用rand指数(RI)来评估聚类精度。表4和表5展现了总体结果。总的来说,学习型度量比非学习型度量更快,但它们会占用更多的内存空间,结果也不准确。论文重新审视了非学习和学习型轨迹相似性度量,并全面研究了它们的效率。学习型度量在轨迹嵌入可以预先计算的情况下,确实优于非学习的度量。然而,当近似非学习型度量时,这些学习型度量的准确性不足。在学习型度量中,自注意力模型训练速度最快,且提供了最高的准确性。非学习型度量不需要预先计算,更适合一次性相似性计算。| 重庆大学计算机技术专业2023级硕士生,重庆大学Start Lab团队成员。 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有3~5名研究生名额,欢迎计算机、GIS等相关专业的学生报考!
图文|朱明辉
校稿|李佳俊
编辑|朱明辉
审核|李瑞远
审核|杨广超