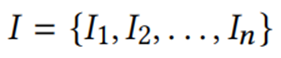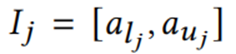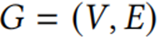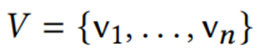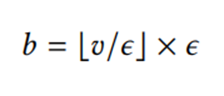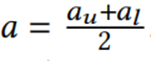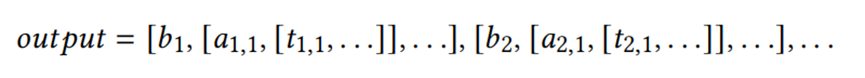在保证最大误差的前提下使用一系列线段来近似一系列带时间戳的数据点是一个基本的数据压缩问题,称为分段线性近似(PLA)。如何在保证最大精度损失和减少空间存储之间进行权衡是该算法需要解决的问题。为此,今天为大家带来PVLDB 2023的论文《Sim-Piece: Highly Accurate Piecewise Linear Approximation through Similar Segment Merging》,它通过找到可以将这些线段组织成的最小组数来优化表示PLA线段的存储要求,以便联合表示它们,显著改善了存储和运算时间之间的平衡。

分段线性近似(PLA)是一种基本的数据压缩问题,使用一系列线段表示时间序列测量值,同时将近似误差保持在预定的可接受阈值内。一些算法与空间效率和精度损失之间的权衡有关,即存储空间的节省随着误差阈值的增加而增加。PLA技术已被证明能够有效地支持存储大量历史时间序列数据,同时还能解决许多数据分析任务,比如检测季节性和预测,而不会牺牲效率。根据所选的最大误差阈值,PLA方法可以大幅减少时间序列数据的大小,实现的压缩率远远超出了最先进的无损压缩算法的能力。然而,在许多应用中,收集到的数据存在一定程度的不精确度。例如,传感器温度测量通常具有0.1−0.5度的精度。对于这样的应用,希望使用相对于值范围的严格误差阈值,以便在不牺牲保真度的情况下减小数据大小。不幸的是,PLA方法的优点在这种情况下并不明显,而无损压缩技术可以节省更多的空间,如图1所示。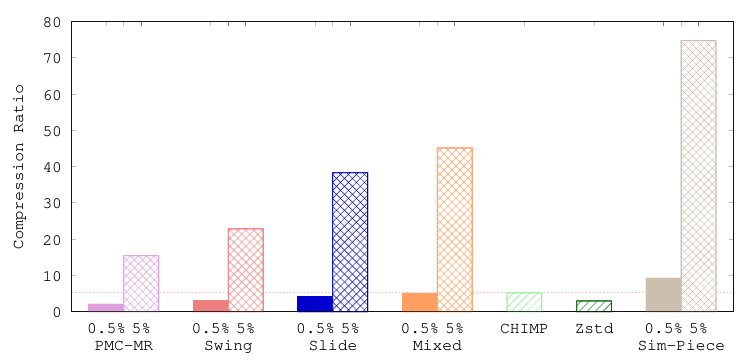
图1 四种有损PLA方法对两种误差阈值的压缩率比较论文旨在利用PLA生成的线段之间的相似性。如图1所示,对于相同的误差界限,Sim‑Piece大大扩展了有损近似的空间节省。此外,Sim‑Piece提出了有损压缩表示,即使在可接受的误差阈值非常小的情况下,也能提供令人印象深刻的空间节省。当考虑线段时,Sim‑Piece将其起点固定为原始值内的量化值。然后,通过维持一对斜率(即满足所需近似保证的极上斜率和极下斜率)将后续数据点添加到线段,直到某个点落在它们之间的区域之外。由于两个斜率之间的任何一条线都可以近似线段的数据点,论文可以找到具有相交候选线集的线段组并将它们联合表示,以减少总体空间需求,如图2所示。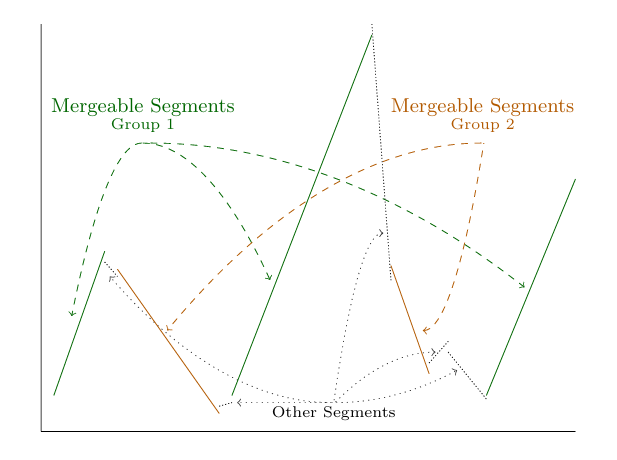
PLA分割的关键是确定结点的位置和类型。有些方法在结点处强制执行连续性条件(连接结点),有些方法允许不连续性(不相交结点),还有一些技术实际上同时考虑了两者。结点处的连续性要求增加了问题的复杂性。i)调整起始结的值
ii)对于给定的最大误差阈值,读取现有值并计算允许近似线的上下坡度
iii)在联合结的情况下,修剪段的最后一点,使其本质上不相交的
如果新加入的点不位于两个斜率之间,则触发一个新的段的建立,否则利用角度不断该段段的上下斜率的值,如图3所示。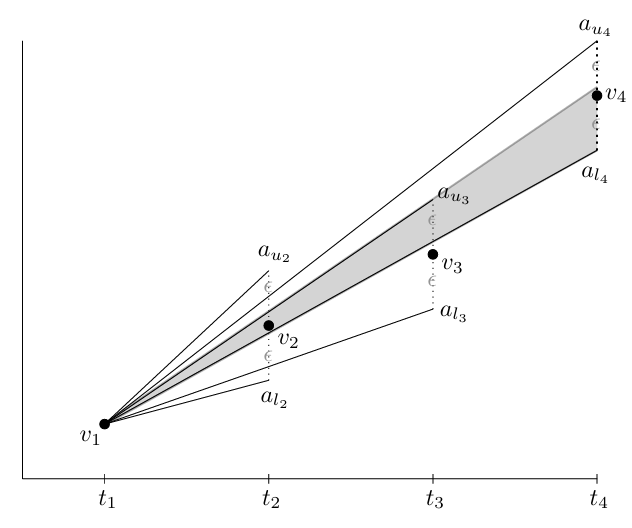
图3中斜坡角度形成的灰色区域说明了可以用来描述的所有候选线。在定义的精度范围内,可以得出用斜率值间隔来捕捉在灰色区域内所有可能的线。当然,不同段的间隔经常会相交,使得可以做到共同代表它们。I是一组线段,其中Ij代表其中第j个线段的斜率的区间。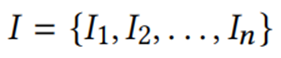
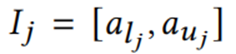
现在生成一个图G,其中顶点区间V中的每个vj代表一个Ij。当且仅当Ii和Ij相交时顶点vi和vj之间有一条边。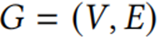
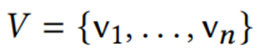
单纯顶点:如果一个顶点的邻居形成一个圈,即它的邻居都通过边相互连接,则称为单纯顶点。一个完美的消除方案:在有序的v1-vn中,vi是单纯顶点。当且仅当存在一个完美消除方案时,一个图是一个区间图。感兴趣的是在误差阈值ε内提供近似。因此不需要考虑所有不同的原始值。相反,可以对一个值V应用如下所示的一个量化函数,从而得到一个量化的值b。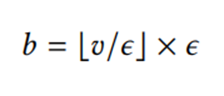

算法1
通过算法1提取得到区间,然后目标是找到每个量化值的最佳间隔组。图4a描述了共享一个共同的起点的五个间隔的角度。观察到,由这些间隔形成的角度可能会重叠,因此,存在可能代表多个间隔的候选线。更具体地说,目标是提出最小的数量的相交间隔组。问题描述:将I划分为不相交集,使每个集合中的所有区间相交,分区数最小化。在图4b中,将图4a中的候选线集绘制为斜率间隔,从而使重叠区域更加明显。使用图4c中的区间图可以更清楚地表示不同区间之间的交叉点。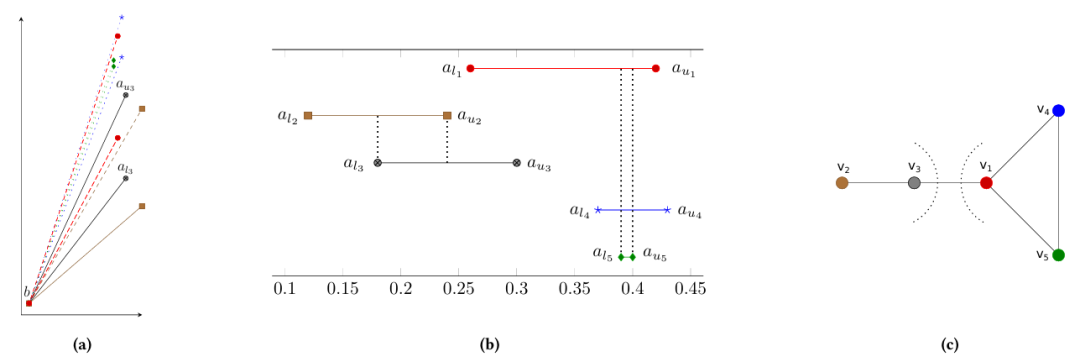
图4 五个线段的候选线集,由每个线段的最大和最小可能坡度(4a)、各自的区间集(4b)和各自的区间图(4c)描述
所以目标就是解决“不相交完全连接集或小团的最小覆盖”问题。该问题已经研究完备,具体算法如下算法2所示,具体解决方法与解释可以从原文中更好地得到,这里不加赘述。

算法2
算法2的输出是一组列表,包括量化值b、上下界au和al,以及组合间隔的起始时间戳。由于可以使用由上界和下界定义的区域内的任何线,所以选择使用该区域中间的线。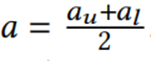
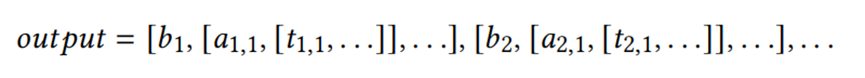
对时间序列中的每个数据点的处理需要一个恒定的内存量,并且产生的间隔数不能超过n,因此需要O(n)空间。此外,随着算法2合并间隔,所需的空间只能逐步减小。因此,空间复杂度是O(n)。关于端到端处理的时间复杂度,算法1为O(n)时间,因为它是按顺序处理输入值的。现在假设算法1产生的间隔数为k。在运行时间的最坏情况下,所有的间隔都可以放在同一批中,算法2的排序步骤将以O(klogk)时间计算。在实践中,输入段根据它们的起点分散在多个b值之间,从而导致更快地执行。扫描和合并已排序的列表需要O(k)时间。使用英特尔®酷睿™i7-10510U的电脑上进行了实验,最大睿频为4.90GHz,8MBL3缓存,总共16GB DDR3 2133MHz RAM。数据集由来自两个来源的8个时间序列组成。如下表所示: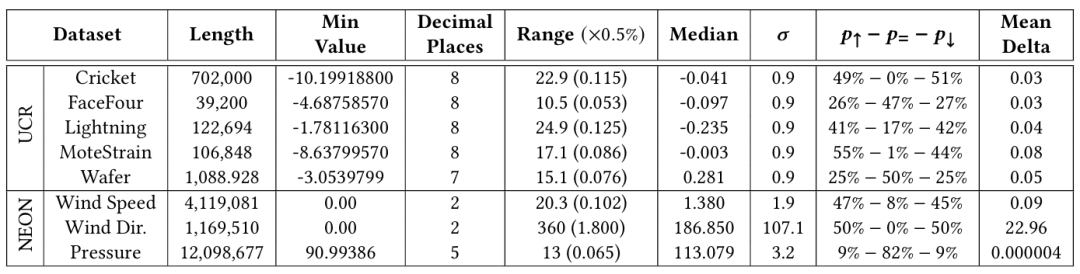
4.3 压缩比比较
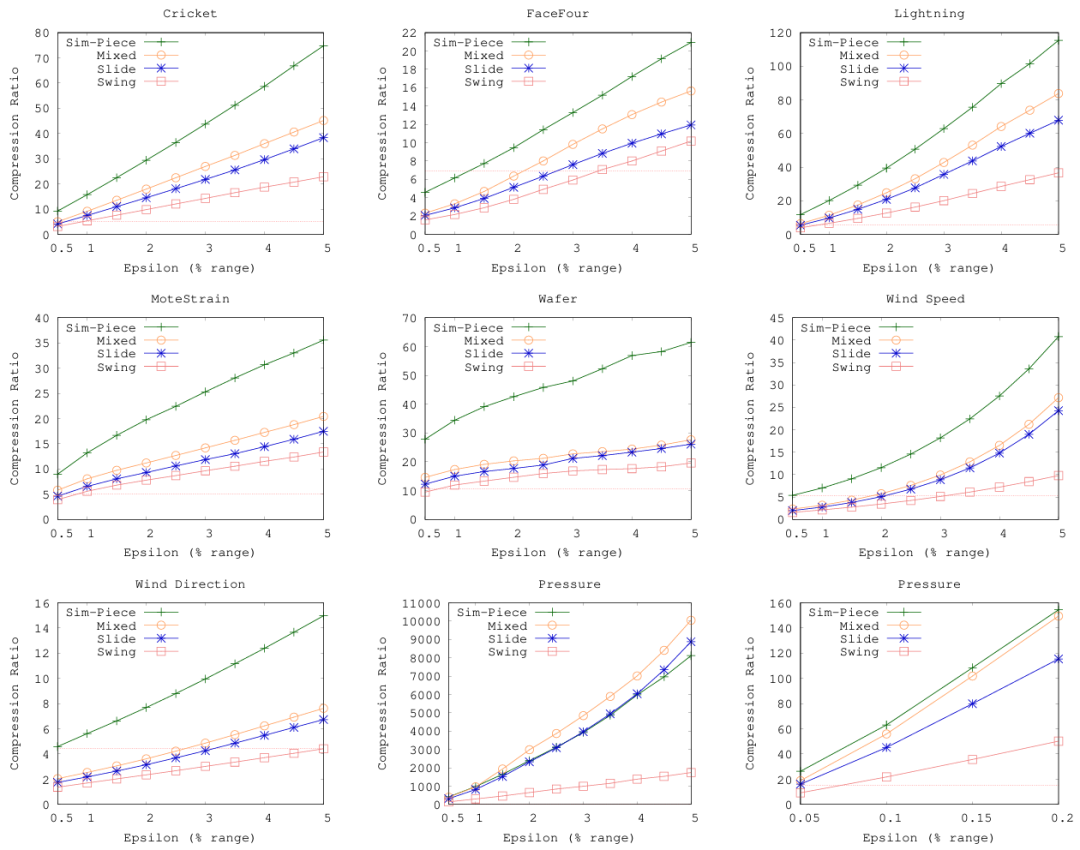
在图5中可以看到,Sim-Piece显然是最节省空间的算法,提供的压缩比远远优于第二好的方法。
i)实际的平均绝对误差(MAE)
ii)近似的均方根误差(RMSE)。
表2 5%压缩率下的MAEr,MAE和RMSE
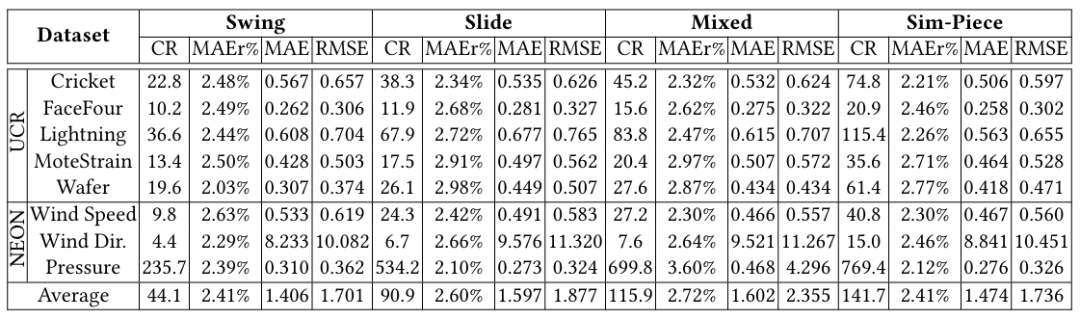
与其他技术相比,Sim-Piece提供了第二好的平均MAE和RMSE值。然而需要考虑到,平均而言,Sim-Piece实现的压缩比是Swing的3.2倍以上。为了更好地了解每个算法获得的精度,在图6中绘制了不同方法获得的其近似的MAE的压缩比。注意到,对于相同的MAE(x轴值),Sim-Piece实现了显著提高的压缩。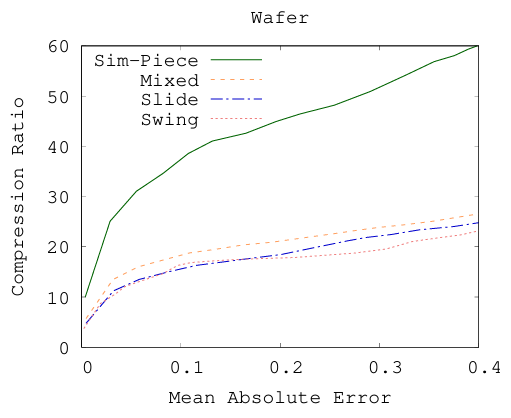
图6 每种PLA技术所实现的近似值的MAE下的压缩率Sim-Piece在早期的大误差值方法中保持了其优势,大约占整个范围的30%。因此,Sim-Piece不仅在需要高精度时提高了空间效率,而且当误差阈值较大时,它也优于早期的方法。对于大于数据集范围的30%的大误差值,只有少数的PLA段是由基于角度的PLA产生的,这导致合并相似段的机会更少。因此,其余算法表现得更好。然而,但在这种设置下,准确性显然很低。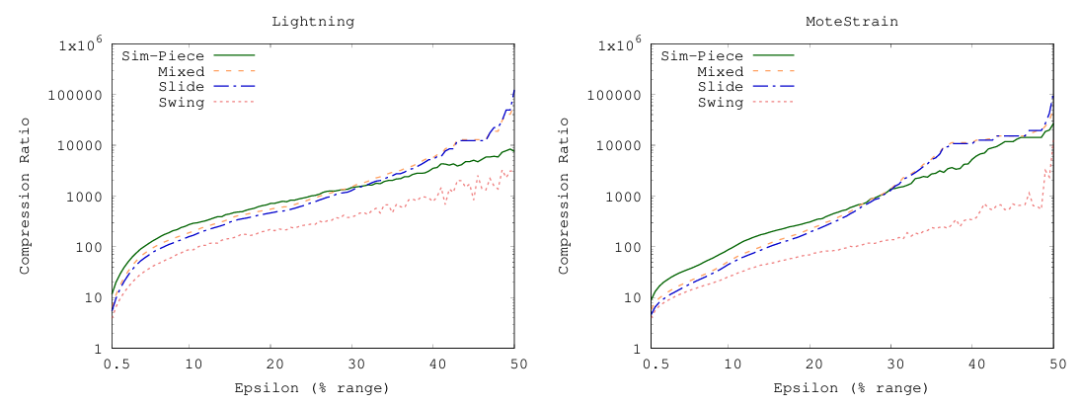
除上述实验外,还对单调性模拟,季节性,通用压缩性等进行了比较,都取得了不错的性能。模拟块对分段的起点应用量化函数,以便得到有限数量的离散起点值。提出的值的数量取决于误差阈值以及输入信号所显示的单调性。下一个实验调查了后者对模拟性能的影响。生成一个遵循类随机游走模型的合成信号。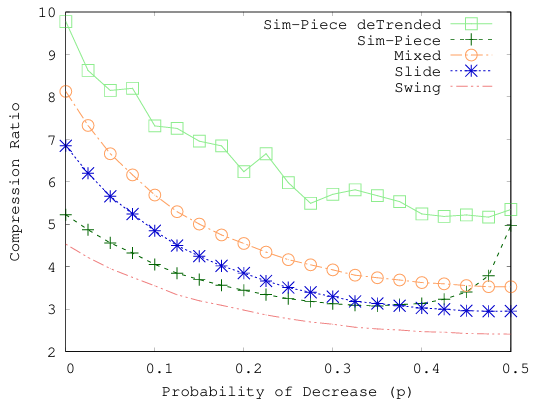
图8 单调性的程度的影响
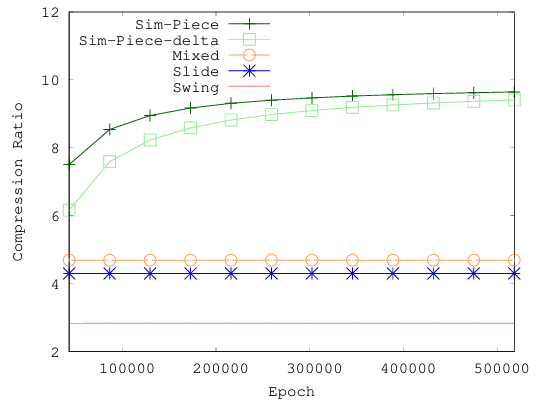
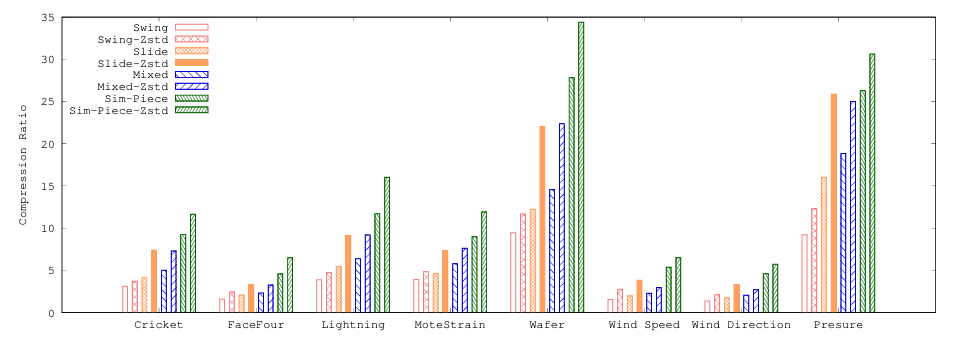
表3 0.5%和5%
Epsilon下的执行时间(ms)
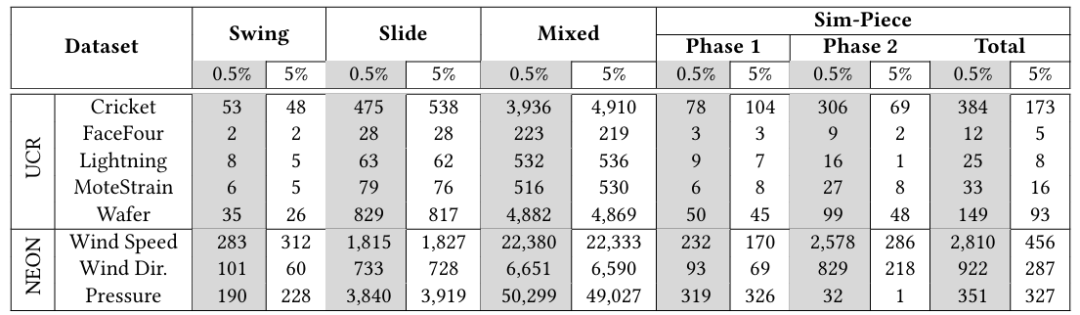
图11 显示了Sim‑Piece的优越性,它说明了压缩时间和比率之间的平衡权衡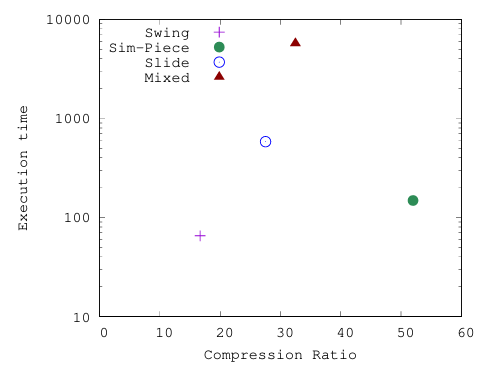
图11 对于各种算法,在压缩时间(ms)和空间(压缩率)之间的权衡介绍了Sim-Piece,一种利用PLA产生的线段之间的相似性,以提供多个线段的联合表示。Sim-Piece算法,在很大范围内提供了更好的空间节省,包括当可接受的误差界很小时。这一点尤为重要,因为最近的无损算法已被证明在这种设置下优于早期的有损方法。使用真实和合成数据集算法进行的实验评估表明,对于所有可接受的误差范围,获得的压缩比远远优于第二好的方法。此外,即使在强单调增加或减少输入信号的极端情况下,Sim-Piece也优于过去的PLA方法,并设法利用季节性组件提供额外的节省。就执行时间而言,在压缩比方面,Sim-Piece比第二优的方法快150×,在空间和速度方面提供了总体上显著提高的效率。
鲁茹芸 重庆大学计算机科学与技术专业本科在读学生,重庆大学Start Lab成员。主要研究方向:时空数据压缩 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有3~5名研究生名额,欢迎计算机、GIS等相关专业的学生报考!
图文|鲁茹芸
编辑|徐小龙
审核|李瑞远
审核|杨广超