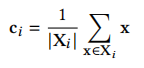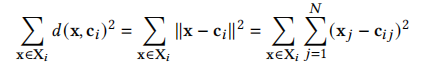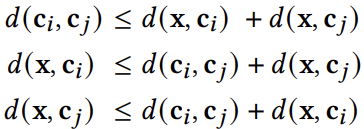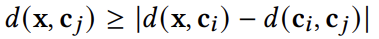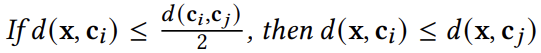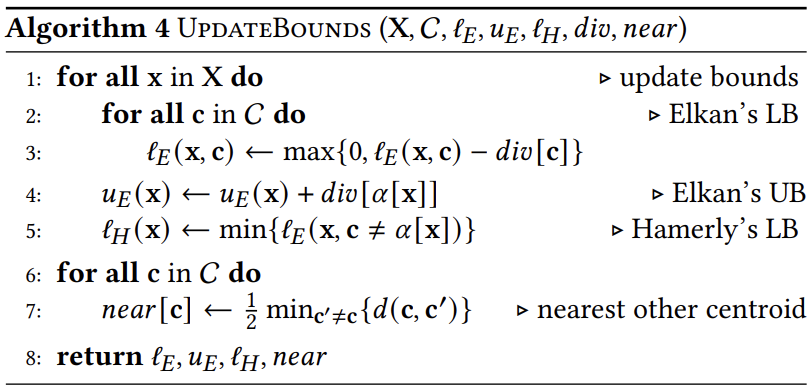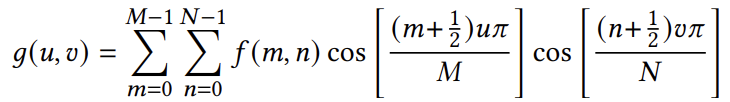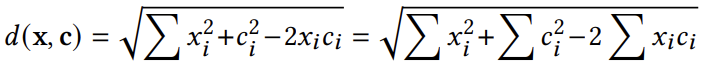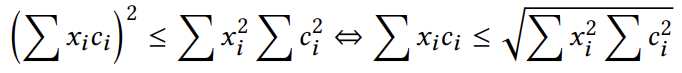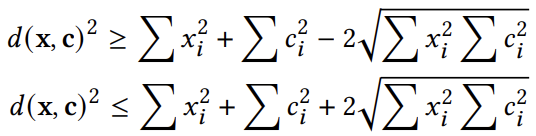k-means聚类算法通过迭代减少簇内欧氏距离来聚类数据,直到收敛。在这个过程中点与质心之间的欧氏距离需要重复计算,使得它在高维数据中的应用受到了阻碍。本次为大家带来的国际顶级会议VLDB 2023上的论文《ARIGOLD: Efficient k-means Clustering in High Dimensions》,它提出了一种高维k-means聚类算法MARIGOLD,能够有效地聚类高维数据,比现有技术实现了大约一个数量级的提升。

高维空间中的数据通常出现在健康科学、天文学、金融等学科和应用中。为了分析这些数据,我们需要针对高维空间定制相应的数据科学方法。k-means聚类算法用于自动发现原始数据分布中的分组。作为一种无监督的方法,它不需要对原始数据进行任何标注作为输入,随后通过迭代减少簇内欧氏距离来聚类数据,直到收敛,最终将数据划分为k个不相交的集群。虽然k-means聚类在选择k的值、初始化集群中心和处理许多小集群方面都得到了广泛的应用和增强,但这些方法回避了k-means解决方案扩展到非常高的维度的问题。主要瓶颈在于聚类过程中点与质心之间的欧氏距离需要重复计算。现有的工作有的专注于高维数据记录的方法,而有的方法在处理中会完全计算距离,只不过在计算之前通过某种筛选步骤进行了处理,旨在避免直接计算高维距离。因此,目前还没有旨在部分为了提高时间效率而计算高维距离,且不影响 k-means聚类结果的方法。本论文提出了一种高维k-means聚类算法MARIGOLD,它是LLOYD算法的一种修剪密集的改良形式,它利用基于三角不等式的界限,同时还采用了轻量级的预处理和紧凑的双边界方案,以及通过能量集中转换进行逐步距离计算,以在迭代过程中修剪高维度距离计算。在对真实数据集进行的全面实验研究后,证明了MARIGOLD能够有效地聚类高维数据,比现有技术实现了大约一个数量级的改进。在高维数据中扩展k-means的需求出现在角分辨光电发射谱学(ARPES)中。在ARPES实验中,通过紫外光利用光电效应激发样品中的电子。空间分辨ARPES,也称nanoARPES,具有很高的分辨率。如图1所示,聚焦的光斑在样品上进行栅格扫描,每个位置产生一个光电发射强度图像,记录强度为电子能量 Ekin 和发射角θ的函数,光谱编码了材料的能带结构和电子性质。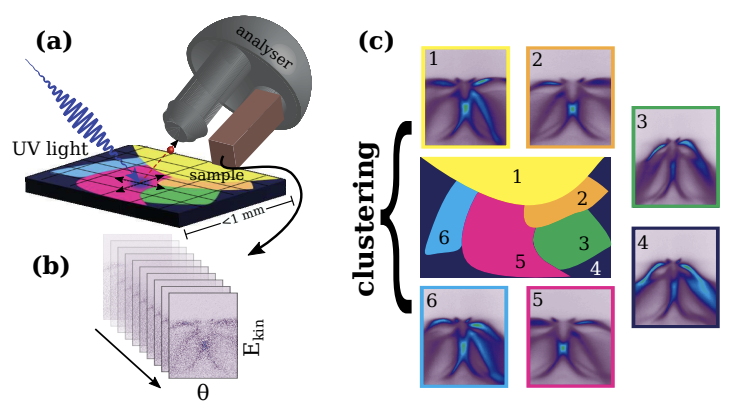
图1 k-means用于nanoARPES:(a) 光脉冲照射样品以发射电子;(b)光电发射强度图像;(c) k-means检测电子结构区域机器学习方法在检测和分析ARPES数据的差异方面被证明是有效的,但它们采用了可能会错过关键特征的降维方法。由于采集成本仍然很高,而获得所需光源的时间有限,物理学家需要快速从高维度的光电发射图像堆栈中提取簇,以在实验数据收集会话期间实时决策如何进行。为此,论文的目标是加速在nanoARPES中产生的高维数据上的k-means聚类。(1)质心:聚类将一组N维点X划分为不相交的聚簇。在k-means中,簇Xi⊆X用质心ci作为其中点的平均值表示,公式表示为: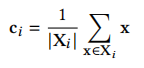
(2)紧密度:簇i的紧密度是簇中的点与其质心之间的欧氏距离的平方和,公式表示为: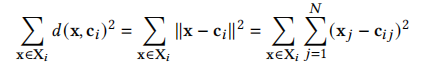
(3)k-means算法:找到一个包含k个簇的聚类C,以最小化总体的紧密度。k-means是NP-难问题,需采用启发式方法进行解决。Lloyd's算法从一组k个初始质心开始,通过欧几里得距离将每个点分配到最近质心的簇中,并重新计算每个质心的位置,直到收敛。实际上,它反复计算点与质心之间的O(kn)个距离;随着维度N的增加,这种计算变得不可行。算法流程如下,算法1呈现了伪代码:

3.2 三角形不等式
Elkan[1]提出可利用三角形不等式修剪O(kn)点到质心的欧几里得距离计算。对于任何点x和质心ci和cj,有如下不等式成立: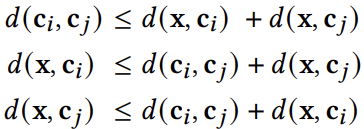
进而可以推出两个引理:
①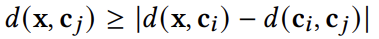
②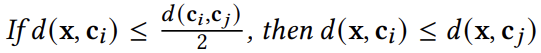
具体推导过程详见论文2.2节。引理说明如果ci到x的距离至多是其到其他任何质心的距离的一半,那么ci是x的最近质心。因此,只有当d(x,ci)>d(ci,cj)/2时,才可以将x从ci重新分配到cj,这样的话就避免重新计算点到质心的距离。引理使用质心间距离和之前的点到质心距离,修剪了重新点到质心距离的计算。
Hamerly[2]则提出了两个条件来避免距离计算。第一个条件使用下界ℓH表示一个点到其未被分配的质心的距离的最小值。在每一轮迭代中,根据引理②可得出,某点x到其当前质心的距离的上界不超过ℓH,则点x依然属于当前质心,那么就无需重新计算。第二个条件使用了类似引理2.2 中的质心到质心的距离,具体可以参考文献[2]。MARIGOLD是一种利用分层的能量集中特征变换,逐步计算特征层次上距离的方法,它同时也基于三角不等式进行修剪。首先说明如其何利用三角不等式,然后说明距离的逐步计算。Elkan和Hamerly都利用了三角不等式来限制距离计算,然而他们的方法尚未被结合。论文整合在算法3中,在将数据点分配给质心时,使用从三角不等式导出的界限来避免距离计算:
算法3
算法4呈现了界限更新子程序:
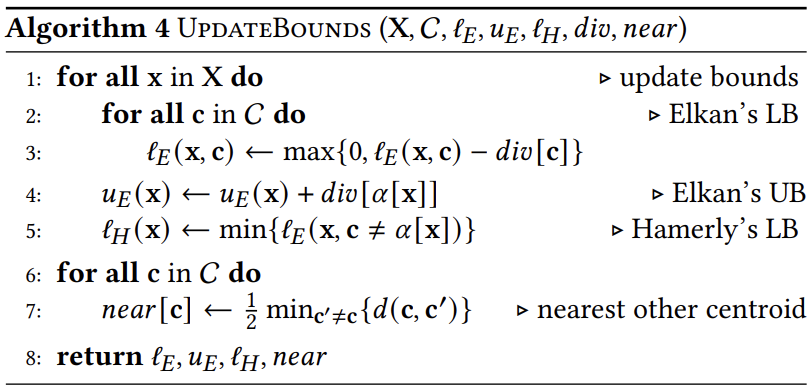
(1)Elkan的下界ℓE(x,c):它限制的是x到质心的距离,d(x,c) ≥ℓE(x,c)。算法3的第8行在每次迭代(除了第一次迭代)计算完距离d(x,α[x])后,将ℓE(x,α[x])重置为x到其质心α[x]的距离。算法3的第11行,如果x到其质心α[x]的距离超过了对于质心c的ℓE(x,c)和引理②导出的界限,则继续检查x是否是更靠近c的。第12行计算d(x,c)并相应地重置ℓE(x,c)。(2)Elkan的上界uE(x):同样限制的是x到质心的距离,即 d(x,α[x])≤uE(x)。算法3的第7行,如果uE(x)不超过从引理②和Hamerly的下界(下面说明)导出的界限,则意味着x到其他任何质心的距离都大于uE(x)。那么在该迭代中x保持最接近α[x],因此可避免计算从x到其它质心的距离。第9行和第15行将uE(x)重置为x到其新质心的距离。(3)Hamerly的下界ℓH(x):限制了x到未分配的质心的距离。如果uE(x)≤ℓH(x),那么x可能会保持其当前质心α[x]。算法3的第7行将ℓH(x)与引理②导出的界限一起与uE(x)进行比较,就像上面讨论的一样。在每次迭代中,算法4的第5行将每个ℓH(x)调整为除α[x]外的质心中ℓE(x,c)的最小值。通过三角不等式进行剪枝可以减少每次迭代中欧几里得距离计算的次数。然而,一旦距离计算通过剪枝阶段,就必须以完整的成本执行。而这一成本在高维情况下增长得非常高,变得难以承受。因此,需要更为激进的措施来丢弃或限制距离计算。论文中使用的是广泛应用于图像压缩的离散余弦变换(DCT)。变换公式如下: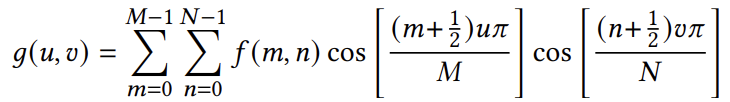
f(m,n)是原始数据矩阵[F]2的元素,而g(u,v)是DCT变换后的矩阵[G]2的元素。DCT在原始数据点的DCT系数向量x上保持变换空间上的欧氏距离,因此,对于点x和质心c之间的欧氏距离,可计算如下: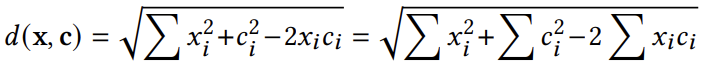
这里的求和是针对所有由i标识的相关DCT(u,v)对。xi²和ci²项可以预先计算,点乘积项∑xi²ci²需要动态计算,但可以通过柯西-施瓦茨不等式对这一项进行约束,即: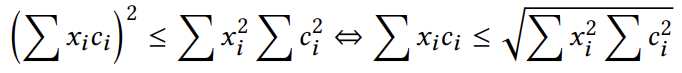
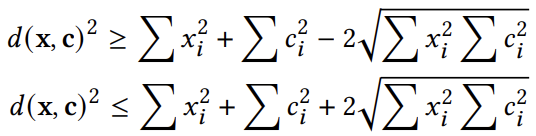
公式中所有项都涉及对x和c的平方和,这些只需计算一次。我们利用这些边界循序渐进地计算点到质心的距离。在每一步中,推导出越来越多的DCT特征的精确距离,其已知部分、上下界和用于递减的剩余未知部分,以逐步扩展对数据的DCT特征的了解。算法5呈现了在DCT变换数据上逐步计算的k-means算法:
关于该算法的说明和更多详细内容可阅读文章4.2节。
上文说明了两种优化距离计算的方法:基于三角不等式的检查和逐步计算。前者是一次性的过滤操作,而后者通过在每次迭代中逐步淘汰质心候选项来逐渐削减距离计算。MARIGOLD将这两种方法合并到一起。在DCT变换的数据上执行逐步距离计算,类似于算法5的做法。它使用与算法3相同的界限,并通过算法4进行更新,同时通过算法2重新计算质心。而且MARIGOLD会跟踪通过逐步计算和基于三角不等式获得的界限中最紧密的那个,因此它比算法5具有更强的剪枝能力。算法8展示了MARIGOLD的具体过程:
(1)数据集:真实世界的图像数据,两个来自nanoARPES研究(gr_flake,misfit:misfit_Se3d,misfit_Bi5d),四个来自其他领域(MNIST、DGLC: DGLC Train、DGLC Validation、DGLC Test)。(2)对比方法:LLOYD、ELKAN、HAMERLY、TRIANGLE-BASED k-MEANS、KMEANS-G∗、STEPWISE和MARIGOLD。(3)衡量标准:距离计算的特征数量;包括预计算在内的运行时间,进行了五次不同的初始化运行,并计算平均值。图2(a)展示了随着DCT特征数量的增加,进入距离计算的特征数量如何变化,其中k=10。所有方法都呈线性增长趋势,但LLOYD、HAMERLY和其他方法存在差距。随着维度的增加,STEPWISE和MARIGOLD成为性能最好的方法。图2(b)展示了在有214个DCT特征的情况下,距离计算的特征数量如何随k的变化而变化。如图所示,随着k的增加,各方法之间的差距加大。MARIGOLD在整体上表现最佳: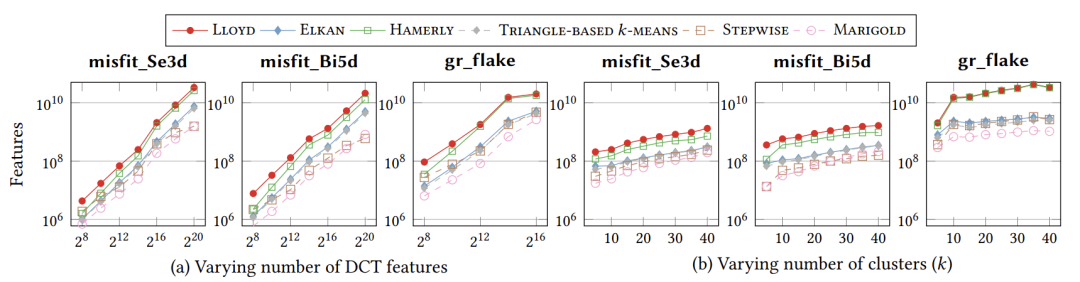
图2
(a)特征数量与DCT特征数(k=10);(b)特征数量与簇数(DCT特征数=214)图3(a)展示了总运行时间随着DCT特征数量的变化而产生的变化,其中k=10。现在的差距比以前更加明显,除在最低维度外,STEPWISE的性能始终优于基于三角不等式的方法。MARIGOLD利用了HAMERLY和ELKAN的界限来优化距离计算,从两种形式的界限中受益,表现最佳。图3(b)展示了在使用214个DCT特征的情况下,运行时间随簇数k的变化。随着簇数的增加,HAMERLY的运行时间接近甚至超过LLOYD。这是合理的,因为更多的簇意味着更大的界限维护开销。STEPWISE和MARIGOLD稳定地优于其它方法。且当每个簇的数据点比例较高时,MARIGOLD更可取,而该比例较低时,STEPWISE占优势:
图3
(a)运行时间与DCT特征数(k=10);(b)运行时间与簇数(DCT特征数=214)图4展示了使用DGLC数据集,随着DCT特征数量和簇数k的增加,运行时间的变化。该图的结果与图3相似,但随着k的增长,STEPWISE和MARIGOLD中逐步距离计算的好处更加明显: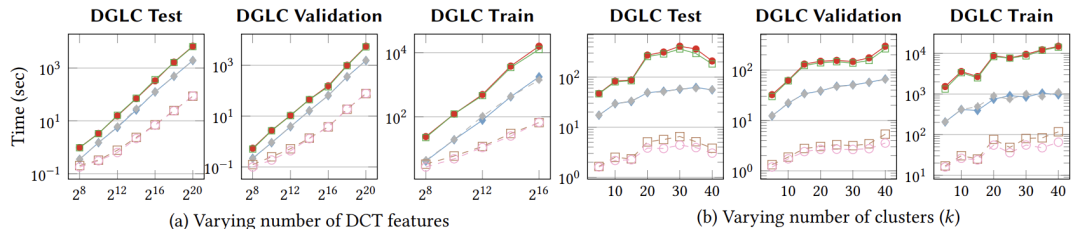
图4
DGLC数据集(a)运行时间与DCT特征数(k=10);(b)运行时间与簇数(DCT特征数=214)在自然科学中,对高维数据进行k-means聚类的需求经常出现。论文设计了MARIGOLD,一种高效的高维度k-means算法。它将基于三角不等式的修剪与强大的逐步距离计算方法整合在一起,后者在维持上下距离界限的同时逐渐细化数据表示粒度,以便修剪质心候选。实验结果表明,MARIGOLD将距离计算的特征数量以及总运行时间减少了大约一个数量级。论文的设计成果为凝聚态物理中的nanoARPES等应用领域提供了实时k-means聚类的可能性。[1]Charles Elkan. 2003.
Using the triangle inequality to accelerate k-means. In ICML. 147-153.[2]Greg Hamerly. 2010.
Making k-means even faster. In SDM. 130-140. 李文慧
重庆大学计算机科学与技术(卓越)专业在读大四学生,重庆大学START团队成员。主要研究方向:时空数据挖掘 |

|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!