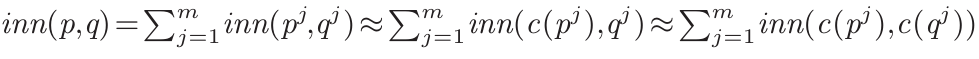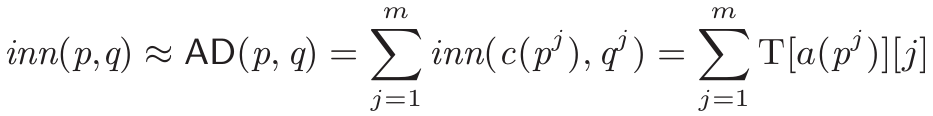鉴于大数据和人工智能的迅猛发展,对高维数据的高效压缩和相似性搜索已成为数据处理和分析中的关键需求。在诸多处理高维数据的方法中,乘积量化作为一种有效的数据压缩技术,因其在降低存储成本和加速数据检索方面的独特优势而受到广泛关注。然而,传统的乘积量化方法通常面临压缩效率不足和难以应对大规模数据集的挑战。为此,本次为大家带来的是数据库顶级国际会议VLDB2020的论文《DeltaPQ: Lossless Product Quantization Code Compression for High Dimensional Similarity Search》。这篇论文提出了一种新的无损乘积量化压缩算法DeltaPQ,成功解决了在处理高维数据时的压缩效率问题。DeltaPQ不仅在提高数据压缩率方面取得显著进展,而且支持在压缩数据上直接进行高效的相似性搜索,极大地增强了数据处理的灵活性和效率。
高维数据无处不在,并在许多应用中发挥着重要作用。然而高维数据的大小通常过大,为缓解这个问题,这篇论文提出来了新的算法来压缩和搜索高维数据。首先应用了一种经典的有损数据压缩方法,即向量量化,它将一个高维向量量化为一系列小整数,即量化代码。然后提出了一种新颖的无损压缩算法DeltaPQ,来进一步压缩这些量化代码。DeltaPQ以树状结构组织量化代码,并存储两个量化代码之间的差异,而不是原始代码。在众多可能的树状结构中,作者设计了一种高效的算法,其时间和空间复杂度与代码数量成线性关系,以找到最优压缩比的结构。近似最近邻搜索查询可以直接在压缩数据上进行处理,空间开销仅为几个字节。该算法支持许多相似性度量,如内积、余弦相似性、欧几里得距离和Lp范数。论文的主要贡献如下:
提出通过在DeltaTree中存储量化代码的差异来压缩量化代码,并形式化定义最优DeltaTree构建问题。
开发了时间和空间复杂度与代码数量成线性关系的最优DeltaTree构建算法。
可以直接在压缩代码上执行近似最近邻搜索,且空间开销极小。
在五个大规模真实数据集上进行的实验结果表明,该算法通常可以实现超过2倍甚至高达5倍的压缩比。
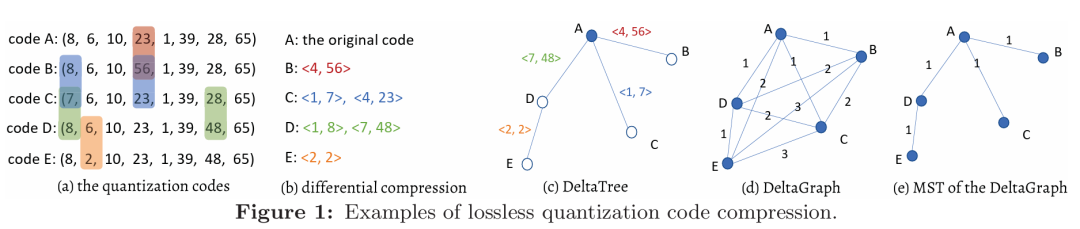
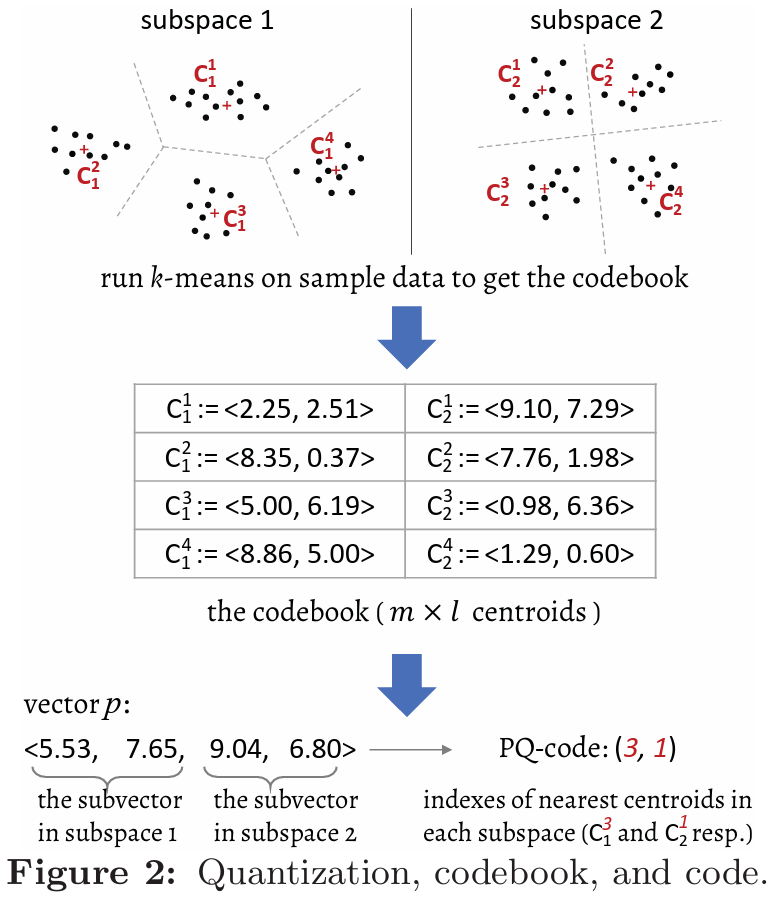
2.1.1乘积量化(Product Quantization)将高维密集向量的每个维度量化为一系列小整数(如YouTube-8M数据集中的32位浮点数量化为1到256之间的整数),如Fig1(a)所示,然后进一步通过乘积量化将原始空间分割为多个子空间并对每个子向量进行量化,从而显著减少数据的存储需求。具体来说,乘积量化将原始空间均匀分割为m个子空间,并相应地将所有(数据和查询)向量分割为m个子向量,如Fig2所示。在每个子空间中,所有子向量都被量化为l个不同的质心,这些质心通过聚类算法(例如,k均值)从数据样本中学习得到。然后,每个原始向量由m个整数的元组表示,这称为其量化代码(简称代码)。所有m×l个质心共同组成乘积量化器的码本。向量之间的相似性可通过inn值来衡量,两个向量的内积可以通过其m个子向量的内积之和来近似计算,也可以通过一个子向量的最近质心和另一个子向量的最近质心之间的内积来近似。具体地,向量p和q的内积可以估算为:后两者被称为非对称距离(AD,由向量和代码计算的距离)和对称距离(SD,由两个代码计算的距离)。SD和AD是对原始空间中inn(q,p)的准确估计,具有有限的失真。SD的误差是AD的两倍,因此在实践中通常使用AD。 给定一个查询向量,PQScan扫描所有代码,计算每个代码到查询向量的非对称距离(AD),并返回具有最大(或最小,取决于使用的度量)AD的代码作为最近邻。由于查询子向量与质心之间的内积频繁被访问,为了实现高性能,事先构建了一个l×m的查找表T,如Fig3所示,其中T[i][j]=inn(c(pj),qj)。然后,任何数据子向量pj与查询子向量qj之间的AD都可以在查找表中找到,我们有: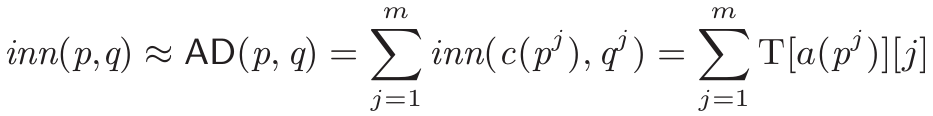

如Fig1(b)所示,通过计算并存储相邻代码之间的差异而非原始代码,来实现更高效的数据存储,伪代码如下图。 
在差分压缩中,需要存储相邻代码之间的差异,差异的数量与存储成本和计算成本成正比。然而,一个代码可能与多个代码“相似”。例如,如Fig1(a)所示,代码A与B、C和D同时相似。而在差分压缩中,A不能与这三个代码都相邻。为了解决这个问题,论文提出在一种称为DeltaTree的树状索引中存储差异。DeltaTree的定义是:给定一组代码,DeltaTree为每个代码设立一个树节点。对于根节点,存储原始代码。对于其他每个树节点,存储该节点与其父节点之间的差异。为找到最优DeltaTree,论文提出了DeltaGraph的概念:给定一组代码,它们的DeltaGraph是一个完全图,每个代码为一个顶点。每条边的权重是两端代码之间的差异数量。可以得出:一组代码的所有可能DeltaTrees可以从它们的DeltaGraph的生成树生成,且生成树的总权重与其n个对应DeltaTrees中的总差异数量完全相同。显然,DeltaGraph的最小生成树(MST)具有最小的总权重,其n个对应的DeltaTrees都是最优的。接下来介绍一个基于Kruskal的在O(2mn)时间和O(n)空间找到MST的算法:即时生成边并按其权重顺序。生成的边会被不相交集合检查,通过检查的边才会被存储,在通过检查并存储了n-1条边后算法终止。这样就避免了生成、存储和排序所有边的需要。可以按升序枚举每个权重w,并在每轮中生成DeltaGraph中所有权重为w的边。因为找到权重为w的边等同于找到具有w个差异的代码对,只需枚举w个坐标的所有组合,并在所有代码中“掩码”这些坐标,掩码后完全相同的代码最多只有w个差异。为了掩码一个代码,可以简单地将代码中的w个坐标设置为零。生成MST的伪代码如图算法3所示。 当一组代码在掩码处理后完全相同时,算法中会枚举并检查这些代码对是否属于同一个连通分量。然而这种检查其实是不必要的,因为在这个列表中的任何一对代码,经过不相交集合检查后必然位于同一个连通分量中。如果它们不在同一个连通分量中,不相交集合会批准这对代码,并将它们之间的边添加到E中。基于上述观察,算法只需枚举并检查列表中相邻代码对,这样列表中所有代码最终必定属于同一个连通分量。 2.3.3固定高度生成树
因为直接在DeltaTree上处理查询的空间开销与DeltaTree的高度成正比,从最小生成树构建的最佳DeltaTree可能高达O(n)。考虑到n是一个大数字,每个查询的空间开销过高。为解决这个问题,需要生成一个固定高度的生成树。实验结果表明,固定高度生成树对应的DeltaTree高度被限制在O(m),其总差异数量几乎与最佳DeltaTree相当,而每个查询的空间开销仅为O(m)几个字节。将结果图G中的每个连通分量视为一棵树。最初每个代码都是一个连通分量本身,同时也是一个根节点。然后,按照它们的权重升序枚举DeltaGraph中的边,但只生成连接连通分量的根节点之间的边。为此,使用n位位图来记录代码是否是一个连通分量中的根节点。当添加一条边到G时,只有一端保持为根节点,另一端成为根节点的子节点。位图相应地进行更新。这样,每个连通分量始终是一棵树。此外,仅当添加边后不会导致树的高度大于w+2时,才向G中添加权重为w的边。这样得到的生成树G的最大高度为w+2。为此,使用一个数组来维护以G中每个代码为根的子树的高度。算法5显示了生成固定高度生成树的伪代码,复杂度与MSTGeneration相同。

一旦生成了固定高度的生成树,就将其转化为相应的DeltaTree并存储在磁盘上。转化过程通过深度优先遍历生成树来完成,并以与差分压缩类似的格式存储差异。该格式包括一个m位的位图,表示差异的位置,以及不同坐标的列表。为了维护树的信息,每个树节点都与两个布尔字段相关联:“is_leaf”表示节点是否是叶节点,“is_last_ child”表示节点是否是其父节点在深度优先顺序中的最后一个子节点。在搜索DeltaTree时,会对压缩的代码进行顺序扫描。维护两个栈h1和h2,其中h1包含源代码,h2存储源代码在h1中与查询向量之间的AD。位于h1顶部的源代码是当前访问代码的父代码。利用位于h2顶部的源代码的AD和差异,可以高效地计算当前访问代码的AD。该算法确保使用“is leaf”和“is last child”布尔字段来保持这两个栈的更新。如果一个节点是叶节点,则不会将其信息推送到这两个栈上。在访问内部节点的最后一个子节点后,会弹出这两个栈。这是因为内部节点的信息将不再被引用,并且两个栈顶部的元素是关于内部节点的信息,因为当前访问的代码是内部节点的子代码。这种方法保持了两个栈的同步。 
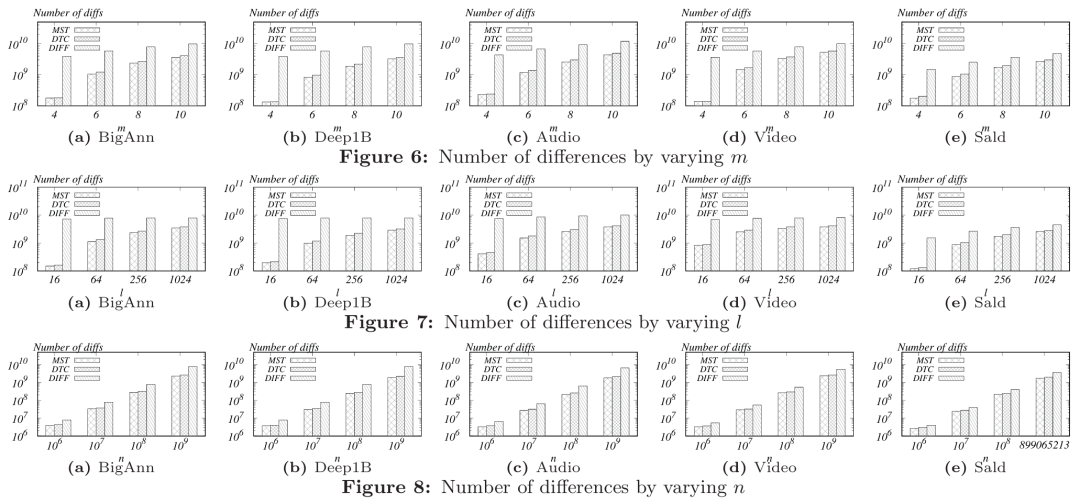
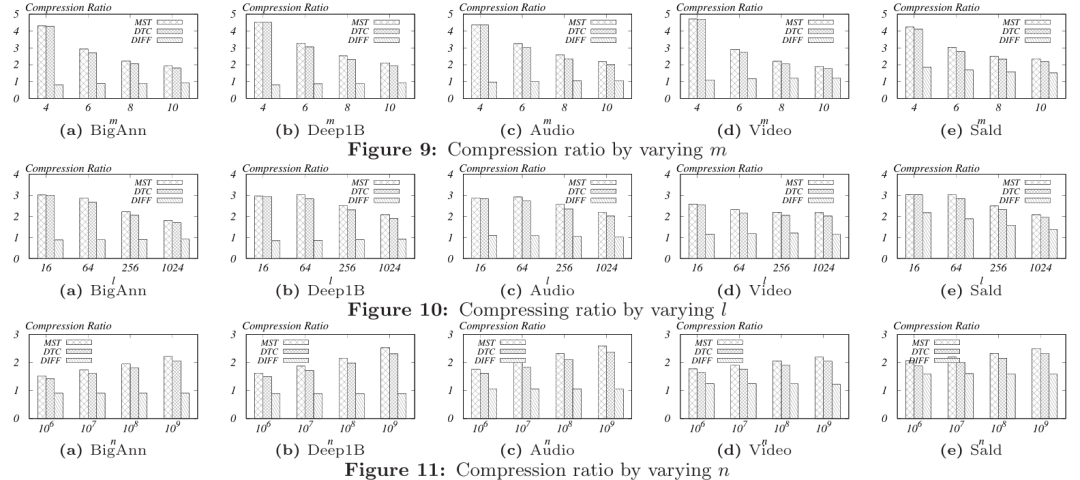
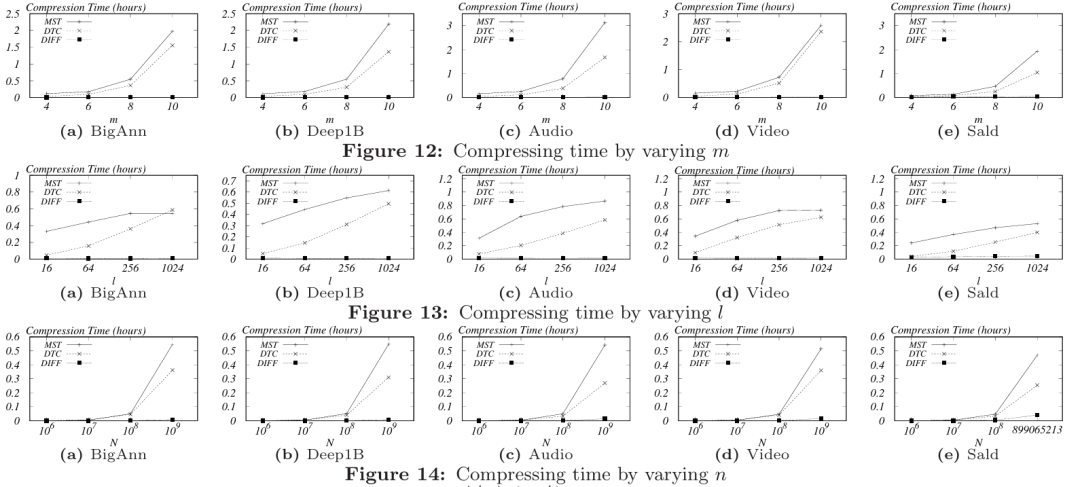
算法6和7提供了DeltaPQ算法的伪代码,该算法以固定高度的生成树作为输入,并在磁盘上生成相应的DeltaTree。算法8展示了在磁盘上搜索DeltaTree的伪代码,首先读取DeltaTree的根节点并计算其与查询的AD,两个栈使用根节点和其AD进行初始化。然后算法依次读取有关每个节点的信息,计算当前访问节点的AD,并相应地维护两个栈。在访问所有节点后,算法返回与查询向量具有最小(或最大)AD的代码。 当一个新向量到达时,先将该向量量化为一个代码,然后将该代码附加到现有的DeltaTree中,作为根节点的最后一个子节点。为处理删除查询,我们使用一个布尔序列来标记每个向量的存在,删除查询只需将相应的代码的存在标记为假。整个DeltaTree需要定期重新构建以优化空间成本。lBigAnn:包含了10亿个128维的SIFT向量,从约100万张图像中提取。lDeep1B:包含10亿个向量,向量从网络上10亿张图像的最后一个全连接层的输出中获得,并经过PCA压缩到96维。lVideo and Audio:分别包含了来自YouTube视频的帧级别视频和音频特征,使用Inception-V3和VGG-like模型从350,000小时的视频中提取的,每个数据集包含约14亿个特征向量。lSALD:包含了神经科学MRI数据,包括了8.99亿个128维的向量。所有方法通过C++实现并使用g++ -std=c++11 -fopenmp with -O3 flag进行编译。压缩算法使用machines with Centos 7, Intel(R) Xeon(R) Gold 6230 CPUs @ 2.10GHz, 192 GB memory. 查询实验使用machine with Ubuntu 18.04, Intel(R) Xeon(R) Gold 6212U CPU @ 2.40GHz, 64 GB memory, and an 8TB hard disk. (1) DIFF采用差分压缩的方式压缩代码。(2) MST将代码编码为最佳DeltaTree。(3) DTC将代码编码为从DeltaGraph的固定高度生成树派生的DeltaTree。实验变化了三个参数m,l,n,并报告了这三种方法的差异数量、压缩时间和压缩比率。每次变化其中一个参数,并将其他两个参数固定为它们的默认值。m变化在[4,6,8,10]范围内,l变化在[16,64,256,1024]范围内,n变化在[106,107,108,109]范围内。默认值为m为8,l为256。如图6,7和8所示,DIFF在三种方法中具有最大数量的差异,MST实现了最小总差异数量,而DTC的差异数量仅略大于MST。这意味着压缩方法DeltaPQ在所有DeltaTree中几乎实现了最佳压缩比。此外,可以观察到随着m和l的增加,所有方法的差异数量都增加了,并且DIFF和MST(DTC)之间的差距减小。这是因为当m和l增加时,代码空间ml(可能的代码数量)增长,两个代码共享公共坐标的机会减少,因此差异数量增加。另外,即使在m和l较小且无法通过增加m和l而变得更糟时,DIFF几乎具有最大可能的差异数量。差异数量随着输入大小n的增加而增加。 图9,10和11展示了不同参数下三种方法的压缩比率,可以看到压缩比率与总差异数量具有相同的趋势。需要注意,DTC的压缩比率只比MST略小,并且在几乎所有情况下都大于2。DIFF的压缩比率甚至小于1,意味着压缩后的数据比原始代码还要大。这是因为DIFF具有太多的差异,并且需要存储差异的位置信息的位图。如图12,13和14所示,DIFF的压缩时间非常小。MST和DTC的压缩时间较长。随着m的增加,MST和DTC的压缩时间呈指数增长,而随着n的增加,压缩时间呈线性增长。在大多数情况下,DTC比MST快大约2倍,因为DTC生成的边比MST少,只在连接组件中是根节点且高度较小的代码之间生成边。 将DeltaPQ与这三种通用无损压缩算法进行比较:RLE(Run-Length-Encoding),LZMA(Lempel-Ziv-Markov chain algorithm),LZ4。从图16(a)可以看出,DeltaPQ在所有数据集上都优于LZMA、LZ4和RLE。图16(b)显示了使用默认设置在五个数据集上的压缩时间。LZ4和RLE有非常高的速度压缩数据,但它们的压缩比接近1。尽管LZMA的压缩比略高于LZ4和RLE,但其压缩时间要长得多。与LZMA相比,DeltaPQ在较少的压缩时间内实现了更好的压缩比。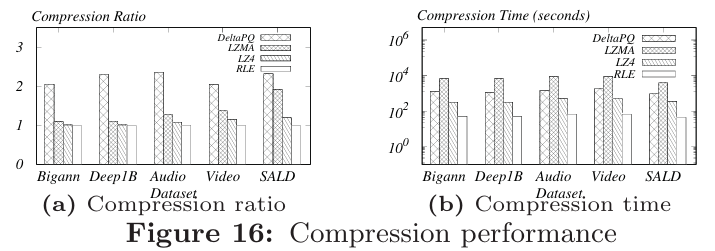
四.总结
这篇论文研究了高维数据管理的无损压缩技术,提出了用于压缩量化代码并直接在压缩数据上执行查询的DeltaPQ压缩算法,并详细地介绍了DeltaPQ的算法设计与实践。实验结果表明,在五个真实数据集上,DeltaPQ优于最先进的通用压缩方法和相似性搜索算法。 | 重庆大学弘深学院2022级计算机拔尖班学生,重庆大学START团队成员。 主要研究方向:时空数据压缩 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!