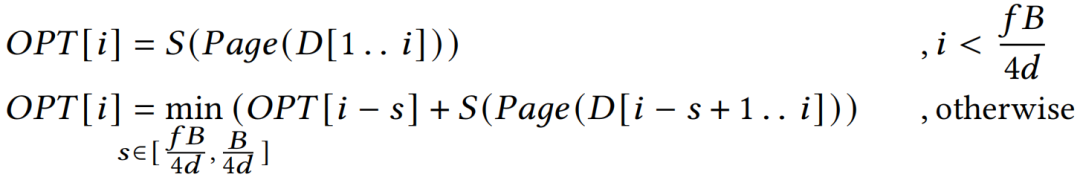最近提出的学习索引引起了广泛关注,因为它们可以适应实际数据和查询分布以获得更好的搜索效率。现有的一些多维索引也建立在学习索引之上以提高查询性能。这些方法往往先使用空间填充曲线或其变体将数据降至一维,然后应用学习索引来优化。然而,在第一步中,通常只能使用固定的空间填充曲线,这限制了学习到的多维索引通过不同的查询工作负载来适应数据分布的潜力。那么如何解除这个限制呢?本次为大家带来数据库领域顶级会议VLDB的论文:《LMSFC: A Novel
Multidimensional Index based on Learned Monotonic Space Filling Curves》如今,多维数据数量较大,种类繁多。例如,基于位置的服务,如谷歌地图,产生了海量的多维数据,这些数据通常是二维(经纬度)的。在这些多维数据集上,常见和最主要的查询类型是窗口查询,它对几个或所有维度施加范围约束。多维索引是有效地为海量的多维数据集回答窗口查询的关键。空间填充曲线(SFC)是多维索引中最常用的方法之一。SFC具有良好的邻近性保持特性,因此它们是数据降维的理想选择。SFC可分为两类:单调SFC和非单调SFC。单调的SFC,如z曲线,可以快速定位搜索范围。然而,非单调的SFC可能会在查询处理过程中导致更多的计算开销。例如,希尔伯特曲线要求枚举查询窗口边界上的所有值,以确定搜索范围。因此,当使用非单调SFC作为线性化方法时,更难进行范围搜索。最近,通过机器学习优化数据库索引的工作激增。这些方法优化了索引在特定数据和查询工作负载实例下的性能。一些工作也对学习型的多维索引进行了研究,最流行的方法是将多维数据点映射到一维空间中,并进一步在一维空间上应用学习索引。然而,这些工作具有以下的缺陷:(1)多维索引的关键部分是从多维空间映射到一维空间,这部分还未被充分学习到。(2)用于存储降维后的数据的真实物理布局并没有被充分优化。现有的方法通常在每个磁盘页中打包固定数量的数据点,这可能会导致每个磁盘页的最小边界边形(MBR)包含很多的死空间或彼此之间的MBR严重重叠。(3)即使上述两个问题可以在索引构建时得到缓解,现有的查询处理方法仍然需要访问许多页面,因为它们的MBR或z地址范围不可避免地与查询的范围重叠。论文提出的LMSFC可以有效地解决上述问题。(1)设计了一个基于SMBO的有效解决方案来学习一个最优/次优的SFC,以适应不同的数据分布和工作负载。(2)使用dp算法求解降维后数据存储优化的问题,并提出了一个启发式算法进一步提高求解速度。(3)除了上述离线优化技术外,还提出了查询分割算法以进行在线优化。多维数据集:多维数据集𝐷由𝑑维欧几里得空间中的𝑛个点组成。每个点𝑥∈𝐷可记为(𝑥(1),···,𝑥(𝑑)),其中𝑥(𝑖)∈ R𝑑为𝑥的第𝑖个维度值。假设通过适当的缩放,每个坐标的域是[0,2k−1]内的一个整数,因此每个点在每个维度的数值都可以用𝐾位二进制来表示。多维窗口是𝑑维空间上中的超矩形,形式化定义为w =[X(1) L, X(1) U] x
… x [X(n) L,
X(n) U],其中,X(i) L<X(i) U(1<=i<=n)。多维窗口查询:给定一个多维数据集𝐷,一个具有窗口约束𝑞.𝑤的多维窗口查询𝑞,返回位于窗口𝑞.𝑤内的点𝑥,即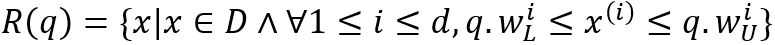 。空间填充曲线(SFC)是一种将多维数据空间映射到一维数据空间的方法。假设原始数据每个维度的数据范围均为[0, 2d-1],相当于在多维空间上共有2kd种可能的点。SFC就是这些点和[0, 2𝐾𝑑−1]内的整数之间的双射函数𝑓。在回答D上的窗口查询q时,以z曲线(一种常用的空间填充曲线)为例,需要首先计算q对应的一维z值的范围qz,接着取出所有z值范围在qz之内的数据,最后过滤掉那些不落在查询窗口q中的点。简单地计算qz的方法是
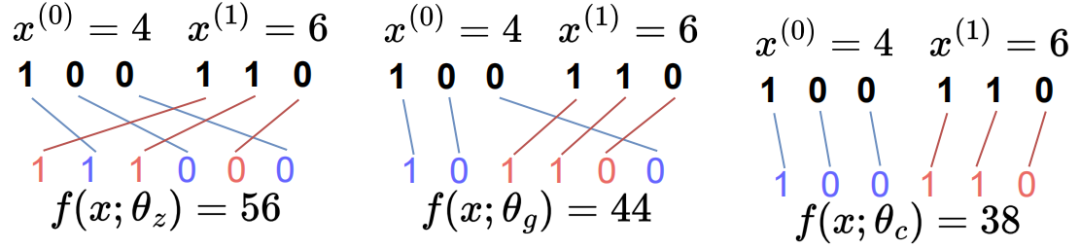
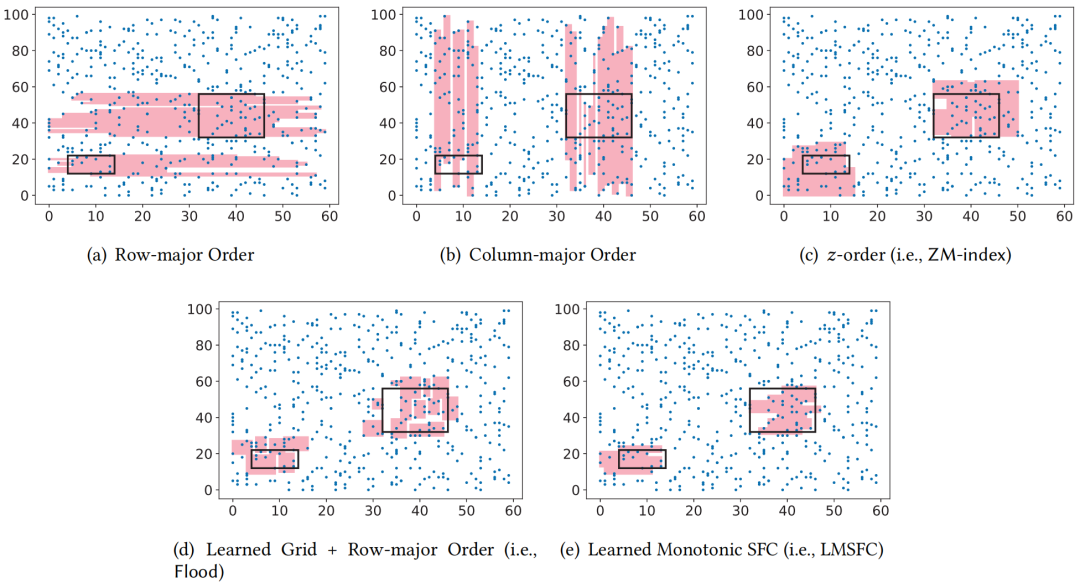
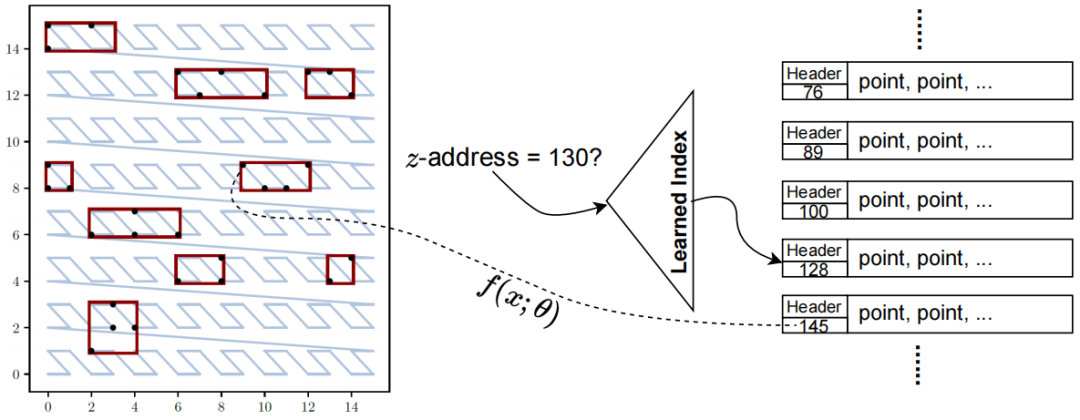
。空间填充曲线(SFC)是一种将多维数据空间映射到一维数据空间的方法。假设原始数据每个维度的数据范围均为[0, 2d-1],相当于在多维空间上共有2kd种可能的点。SFC就是这些点和[0, 2𝐾𝑑−1]内的整数之间的双射函数𝑓。在回答D上的窗口查询q时,以z曲线(一种常用的空间填充曲线)为例,需要首先计算q对应的一维z值的范围qz,接着取出所有z值范围在qz之内的数据,最后过滤掉那些不落在查询窗口q中的点。简单地计算qz的方法是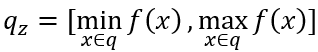 。然而,计算这些极值通常是困难的。在最坏的情况下,可能需要枚举𝑞中的所有𝑥,因此其成本与查询的大小成正比,这与高效查询处理的目的相悖。因此,论文确定了一个SFC的子类(即下面提出的单调空间填充曲线),这样qz就可以在𝑂(𝑑)时间内有效地计算出来,而不依赖于查询的大小。多维空间中的单调函数:记多维数据𝑎≤𝑏为true当且仅当∀𝑖,𝑎(𝑖)≤𝑏(𝑖)。那么一个函数𝑔是单调的,当且仅当对于所有的𝑎和𝑏,如果𝑎≤𝑏,那么𝑔(𝑎)≤𝑔(𝑏)。当某种空间填充曲线对应的映射函数为单调函数,那么称其为单调空间填充曲线。图 1展示了3种常用的空间填充曲线,可以发现,仅z曲线是单调空间填充曲线,即左下角对应的z值为最小的,右上角对应的z值为最大的。受z曲线的单调性的启发,论文提出了一类z曲线,该类曲线中的每个实例都具有独特的属性以支持不同的查询。利用参数θ参数化的SFC表示如下:其中,θ=[θ(1), θ(2)…θ(d)], θ(i)为一个k维的向量,xi j为x的第i维的第j个bit的值,K为xi的最大bit数,θ的作用为将x的第i维的第j个bit映射到z值的二进制位的对应位置。如图 2所示,(a)为传统z曲线使用的交叉编码方式,对应的θ=[[1,4,16],[2,8,32]],最终的z值计算出来就是(0*1+0*4+1*16)+(0*2+1*8+1*32)=56。(b)对应的θ=[[1,16,32],[2,4,8]]。由于不同的SFC将数据集中的点以不同的顺序进行排列,因此在不同的查询负载下查询性能各有不同。这促使我们学习一个好的SFC来适应查询集(详见下一节)。 在图 3中,论文在同一数据集和查询工作负载上,基于不同的SFC,在5个索引上构建和可视化了查询处理成本。首先在一个二维空间中生成了一组随机点,并使用这两个随机生成的查询(表示为粗黑框)作为查询工作负载。图3(a)和图3(b)分别是行排序和列排序,图3(c)使用了z曲线,图3(d)是Flood,一种基于空间的学习网格划分方法,然后使用行序对网格进行排序,图3(e)显示了论文提出的方法LMSFC,它是一个基于学习的单调SFC。查询处理过程中访问到的数据点显示为红色。从图3中可以看出,学习到的索引,即Flood和LMSFC,由于对特定实例进行了学习,访问的数据点更少。基于之前提出的参数化SFC,论文提出了基于学习的单调空间填充曲线LMSFC。如图 4所示,首先学习对应的映射函数f(x;θ),它将采样查询工作负载的查询处理成本最小化。学习到的SFC相当于给定了一个多维数据点的排序顺序。然后,论文提出了一种基于最优动态规划和次优但更快的启发式分页算法来将数据点加载到页面中(图4中的粗红色矩形)。最后,从每个页面中提取最小的z地址来形成一个排序好的数组,并在其上使用一个最先进的学习索引,用于加速根据z地址取出对应数据的过程。学习一个参数化的SFC的目标是找到𝜃∗,从而使所得到的查询处理成本最小化,也就是说,其表示为一个优化问题为:
。然而,计算这些极值通常是困难的。在最坏的情况下,可能需要枚举𝑞中的所有𝑥,因此其成本与查询的大小成正比,这与高效查询处理的目的相悖。因此,论文确定了一个SFC的子类(即下面提出的单调空间填充曲线),这样qz就可以在𝑂(𝑑)时间内有效地计算出来,而不依赖于查询的大小。多维空间中的单调函数:记多维数据𝑎≤𝑏为true当且仅当∀𝑖,𝑎(𝑖)≤𝑏(𝑖)。那么一个函数𝑔是单调的,当且仅当对于所有的𝑎和𝑏,如果𝑎≤𝑏,那么𝑔(𝑎)≤𝑔(𝑏)。当某种空间填充曲线对应的映射函数为单调函数,那么称其为单调空间填充曲线。图 1展示了3种常用的空间填充曲线,可以发现,仅z曲线是单调空间填充曲线,即左下角对应的z值为最小的,右上角对应的z值为最大的。受z曲线的单调性的启发,论文提出了一类z曲线,该类曲线中的每个实例都具有独特的属性以支持不同的查询。利用参数θ参数化的SFC表示如下:其中,θ=[θ(1), θ(2)…θ(d)], θ(i)为一个k维的向量,xi j为x的第i维的第j个bit的值,K为xi的最大bit数,θ的作用为将x的第i维的第j个bit映射到z值的二进制位的对应位置。如图 2所示,(a)为传统z曲线使用的交叉编码方式,对应的θ=[[1,4,16],[2,8,32]],最终的z值计算出来就是(0*1+0*4+1*16)+(0*2+1*8+1*32)=56。(b)对应的θ=[[1,16,32],[2,4,8]]。由于不同的SFC将数据集中的点以不同的顺序进行排列,因此在不同的查询负载下查询性能各有不同。这促使我们学习一个好的SFC来适应查询集(详见下一节)。 在图 3中,论文在同一数据集和查询工作负载上,基于不同的SFC,在5个索引上构建和可视化了查询处理成本。首先在一个二维空间中生成了一组随机点,并使用这两个随机生成的查询(表示为粗黑框)作为查询工作负载。图3(a)和图3(b)分别是行排序和列排序,图3(c)使用了z曲线,图3(d)是Flood,一种基于空间的学习网格划分方法,然后使用行序对网格进行排序,图3(e)显示了论文提出的方法LMSFC,它是一个基于学习的单调SFC。查询处理过程中访问到的数据点显示为红色。从图3中可以看出,学习到的索引,即Flood和LMSFC,由于对特定实例进行了学习,访问的数据点更少。基于之前提出的参数化SFC,论文提出了基于学习的单调空间填充曲线LMSFC。如图 4所示,首先学习对应的映射函数f(x;θ),它将采样查询工作负载的查询处理成本最小化。学习到的SFC相当于给定了一个多维数据点的排序顺序。然后,论文提出了一种基于最优动态规划和次优但更快的启发式分页算法来将数据点加载到页面中(图4中的粗红色矩形)。最后,从每个页面中提取最小的z地址来形成一个排序好的数组,并在其上使用一个最先进的学习索引,用于加速根据z地址取出对应数据的过程。学习一个参数化的SFC的目标是找到𝜃∗,从而使所得到的查询处理成本最小化,也就是说,其表示为一个优化问题为: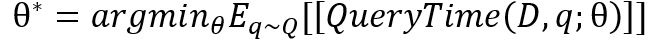 。其中,Q表示查询工作负载的分布,而𝑞是该负载中的一个样例,𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数返回在给定数据集上的实际查询执行时间。为了优化该方程,可以首先应用有限样本近似,即从Q中获取采样查询,用样本平均值代替期望。然而,𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数很难精确地建模或近似,因为它包含了各种复杂的优化。此外,直接评估𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数会产生过高的成本。另外,θ是一个高维离散参数,其搜索量是指数级别。因此在实践中不可能通过暴力算法来解决该优化问题。鉴于上述挑战,论文采用了最先进的贝叶斯优化算法SMBO [1]来近似解决上述优化问题,返回一个平均查询时间较低的高质量SFC。并使用随机森林模型来替代典型的高斯过程模型,这提高了学习速度,并且不依赖于多维高斯假设和核函数的选择。为了适应外部IO并允许额外的优化,需要执行分页,它将数据集𝐷划分为多个页面。假设每个页面的最大大小为𝐵字节,并且必须满足由𝑓∈(0,1]指定的最小填充因子约束。也就是说,在每个页面中使用的字节数必须在[𝑓𝐵,𝐵]字节的范围内。寻找最优的分页方法是NP难问题。传统的基于SFC的索引采用固定分页大小的方法,每次都需要加载同样大小的数据。对于基于SFC的索引来说,分页是很重要的。这是因为可以在每个页面中记录数据点的MBR,并使用MBR来进一步优化查询处理。如果页面的MBR与查询不相交,则可以跳过页面。默认的一维分页方法,如固定大小的分页方法,不知道页面的MBR,也不能对其执行主动优化。基于上述的观察,作者设计了一个评分函数S(P)来表示页面的密度,即S(P)=vol(P)/size(P),其中vol(P)和size(P)分别表示MBR的大小以及该页面内的数据量。然后,将寻找最优分页问题转换成寻找使得S(P)之和最小的分页问题,即
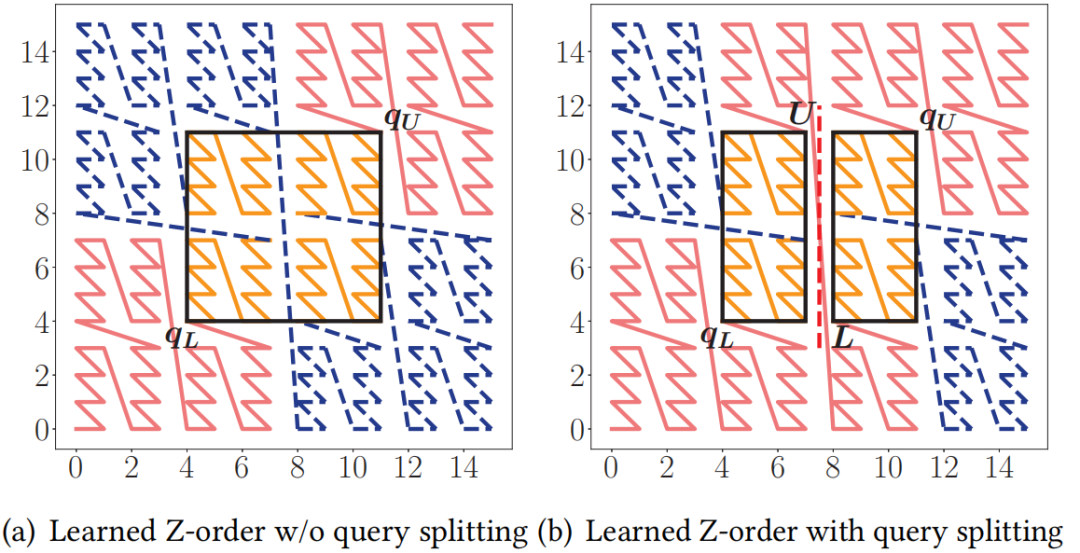
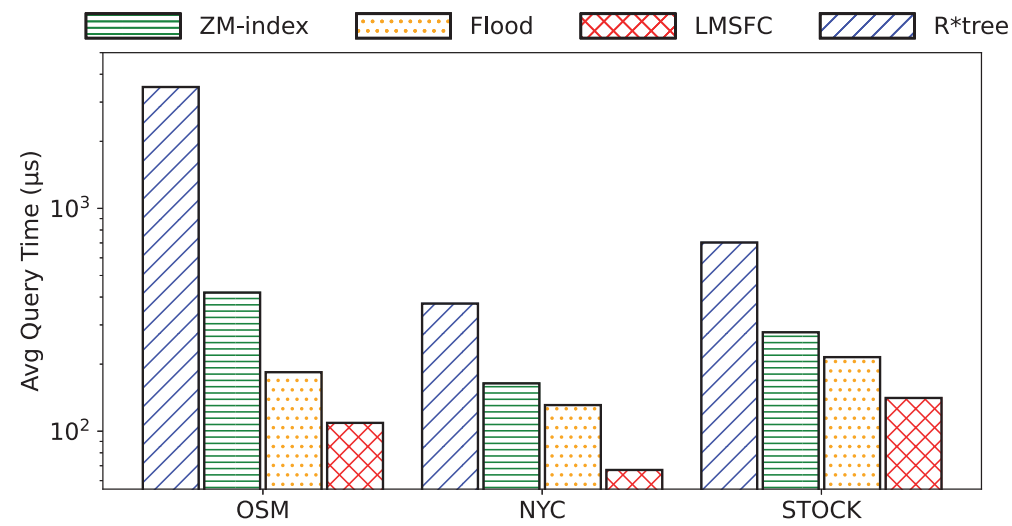
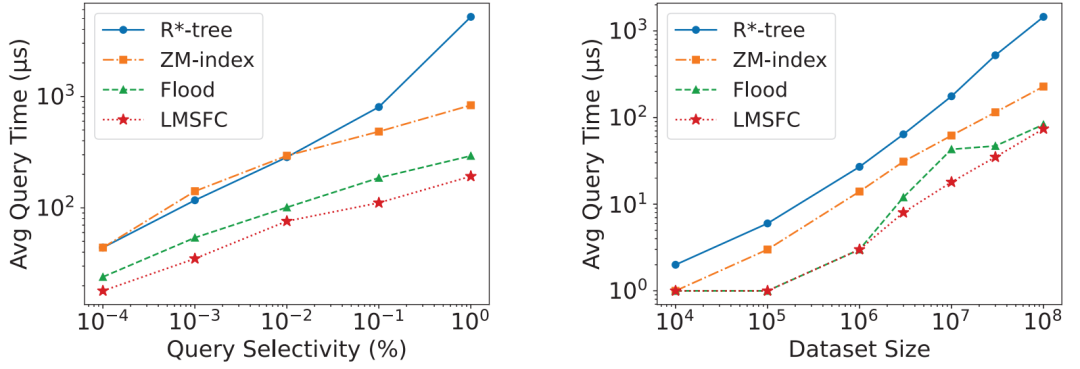
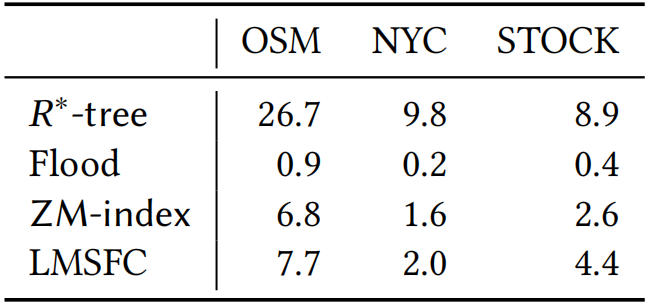
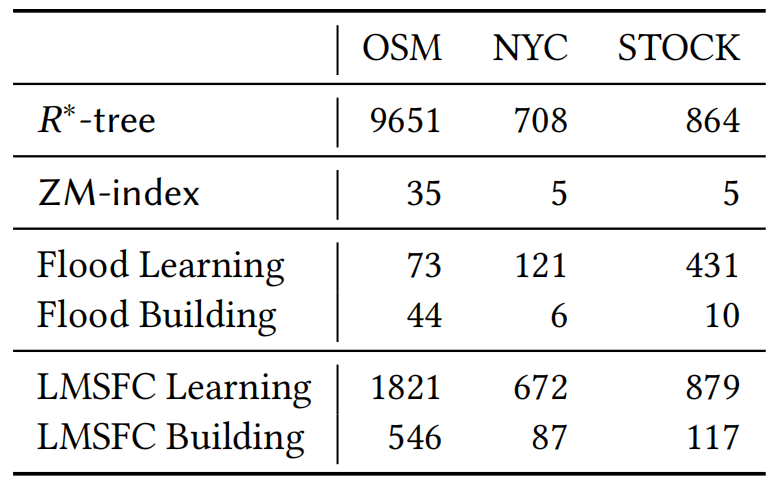
。其中,Q表示查询工作负载的分布,而𝑞是该负载中的一个样例,𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数返回在给定数据集上的实际查询执行时间。为了优化该方程,可以首先应用有限样本近似,即从Q中获取采样查询,用样本平均值代替期望。然而,𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数很难精确地建模或近似,因为它包含了各种复杂的优化。此外,直接评估𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数会产生过高的成本。另外,θ是一个高维离散参数,其搜索量是指数级别。因此在实践中不可能通过暴力算法来解决该优化问题。鉴于上述挑战,论文采用了最先进的贝叶斯优化算法SMBO [1]来近似解决上述优化问题,返回一个平均查询时间较低的高质量SFC。并使用随机森林模型来替代典型的高斯过程模型,这提高了学习速度,并且不依赖于多维高斯假设和核函数的选择。为了适应外部IO并允许额外的优化,需要执行分页,它将数据集𝐷划分为多个页面。假设每个页面的最大大小为𝐵字节,并且必须满足由𝑓∈(0,1]指定的最小填充因子约束。也就是说,在每个页面中使用的字节数必须在[𝑓𝐵,𝐵]字节的范围内。寻找最优的分页方法是NP难问题。传统的基于SFC的索引采用固定分页大小的方法,每次都需要加载同样大小的数据。对于基于SFC的索引来说,分页是很重要的。这是因为可以在每个页面中记录数据点的MBR,并使用MBR来进一步优化查询处理。如果页面的MBR与查询不相交,则可以跳过页面。默认的一维分页方法,如固定大小的分页方法,不知道页面的MBR,也不能对其执行主动优化。基于上述的观察,作者设计了一个评分函数S(P)来表示页面的密度,即S(P)=vol(P)/size(P),其中vol(P)和size(P)分别表示MBR的大小以及该页面内的数据量。然后,将寻找最优分页问题转换成寻找使得S(P)之和最小的分页问题,即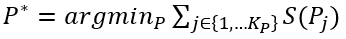 ,其中size(pj) ∈[𝑓𝐵,𝐵]。下面,首先介绍一个基于动态规划(DP)的最优求解上述问题的算法,然后是一个次优但快速的启发式算法。这两种方法都比固定大小的分页实现了更好的分页布局,从而提高了查询性能。由于SFC为数据点提供了一个线性顺序,因此能够通过动态规划最优地求解一维分页问题来规避多维分页问题的NP-hard问题。记𝑂𝑃𝑇[𝑖]是对前𝑖个数据点的最优成本分页算法获得的最优代价。然后,可以推导出以下递归方程:该方法的时间复杂度为𝑂(𝑛𝐵/4𝑑),因为评分函数𝑆可以通过增量计算以𝑂(1)时间进行计算。然而在实践中该方法依旧十分耗时,因为B通常是一个较大的值。因此,论文进一步提出了一个启发式算法来快速计算分页方法。该启发式算法是一种贪心算法,它将尽可能多的数据点打包到当前页面中,直到违反某些条件。该条件规定,新的MBR(通过将当前数据点添加到页面中而形成)不应将旧的MBR放大超过𝛼倍(𝛼>1是一个超参数)。这个条件减少了结果页面的MBR变得太大的机会,其中一个大的MBR可能与很多无用的查询相交。在之前已经提到,使用基于SFC的索引回答查询𝑞,需要两个步骤:1)给定一个空间查询矩形𝑞,确定其在z地址中的扫描范围,记为[𝑓(𝑞𝐿),𝑓(𝑞𝑈)]。2)扫描:所有z地址在此范围内的页面都需要进行扫描。可以使用正向索引找到这些页面。此外,由于LMSFC为每个页面维护了MBR和特定的排序信息,因此可以跳过不相关的页面,并只扫描页面的相关部分。上述框架的主要局限性是,它忽略了由于SFC映射而导致的z地址范围内潜在的大量假阳性数据点。如图 5(a)所示,查询对应的z地址范围可以分成蓝色部分(假阳)和黄色部分,可以看出额外的开销(即蓝色部分)是比较大的。因此,论文提出了基于查询分割的策略来缩小该开销。比如,在图5(a)中考虑相同的查询(黑色矩形)我们可以通过在𝑥轴上的值8处进行切割,将查询分成两部分,如图5(b)所示,可以看到蓝色部分可以被有效地减小。论文首先讨论了如何将一个查询精确地分割为两个子查询,然后将其推广为基于递归的方法以分割成多个子查询。该过程计算比较多,建议参考原论文。实验平台:CPU:i9-7900X;内存:64GB;操作系统:Ubuntu 20.04.4。编程语言:C++。数据集:论文一共使用了3个数据集进行评估,1)OSM:一个空间数据集,由OpenStreetMap数据集中从北美随机采样的250M条记录组成。使用GPS坐标(即经度和纬度)来形成一个二维数据集。2)NYC:从纽约市2018年和2019年的黄色出租车旅行记录中随机抽取。使用上车位置、旅行距离和总量来形成一个三维数据集。3)STOCK:包括从1970年至2018年的每日历史股票价格,包括四个特征:最高价格、最低价格、调整后的收盘价和交易量。具体参数如表 1所示。查询负载:查询通过其在每个维度中的中心和范围进行生成。以以下两种模式之一生成查询中心:1)倾斜,其中查询中心是随机抽样的数据点。2)均匀,其中查询中心在数据空间内随机生成。每个维度中的查询的宽度从0均匀地采样到该维度的数据空间的宽度,其比例为0.05。所有的查询窗口都被剪切为在数据空间内。最终的查询工作负载是通过混合90%的倾斜查询和10%的统一查询来获得的对比方法:1) ZM-index,一个结合Z曲线和学习索引的方法;2) R*-tree,传统的多维索引;3) Flood,较新的多维学习索引。如图 6所示,LMSFC在所有数据集上都优于所有其他索引。与亚军相比,LMSFC在查询时间上提高了1.52×到1.96×。LMSFC相对于基线(即z阶曲线)的主要优点是,学习到的SFC在映射到一维地址空间后,能更好地保持数据的局部性。因此,多维空间中的近距离点更有可能被分配到同一个页面中。选择率(图 7左):对于所有的方法,由于访问了更多的数据点,查询时间近似地随着查询选择性的线性增长。注意到,当查询选择性变大时,R*-tree会恶化;这可能是由于𝑅-tree及其变体需要对每个内部节点执行复杂的MBR交集查询,并可能导致许多回溯(特别是对于更高维的情况),在查询窗口较大时该现象会更加严重。学习型SFC只需要扫描特定z地址范围内的页面,并且没有复杂的交集查询或回溯。与ZM-index相比,Flood效率显著提高,而LMSFC进一步持续提高了查询性能,展示了学习索引的广泛适用性。伸缩性(图 7右):可以看到,所有的索引都与数据大小近似线性扩展,而LMSFC表现最好,其次是Flood、ZM-index,最后是R*-tree。图7 不同查询大小(左图)以及数据大小(右图)实验从表 2中可以看出,论文提出的LMSFC比ZM-index或Flood具有更大的索引大小,其中一个原因是LMSFC为了优化页面布局占用了一定空间。尽管如此,LMSFC的索引大小仍然是可以接受的,因为它仍然明显小于传统的R*-tree。表 3给出了不同索引所需要的构建时间,对于学习索引,论文进一步区分了学习时间和索引建立时间。R*-tree在数据量较大时需要很长的构建时间,因为它在构建的过程中需要对树的结构进行调整。ZM-index具有最快的构建时间,因为不需要学习或优化。Flood比LMSFC的学习和构建时间更快,因为1)Flood的模型更简单,超参数空间比LMSFC要小得多。此外,它还针对学习的成本模型进行优化,因此超参数搜索更快。2)LMSFC还包括其他优化(如基于动态规划的分页),因此也会影响到索引的构建时间。本文介绍了LMSFC,一个基于学习型空间填充曲线的高维索引。论文设计了一个学习一类特殊的空间填充曲线的框架以实现高效的查询处理。此外,LMSFC通过优化数据的存储布局进行离线优化,对查询进行分割实现在线优化,以进一步提高查询处理效率。大量的实验结果表明,在三个真实数据集上,该方法的性能优于非学习索引(如R*-tree)和先进的学习多维索引。一个可能的未来方向是将该方法扩展到非单调性空间填充曲线上,比如希尔伯特曲线。
,其中size(pj) ∈[𝑓𝐵,𝐵]。下面,首先介绍一个基于动态规划(DP)的最优求解上述问题的算法,然后是一个次优但快速的启发式算法。这两种方法都比固定大小的分页实现了更好的分页布局,从而提高了查询性能。由于SFC为数据点提供了一个线性顺序,因此能够通过动态规划最优地求解一维分页问题来规避多维分页问题的NP-hard问题。记𝑂𝑃𝑇[𝑖]是对前𝑖个数据点的最优成本分页算法获得的最优代价。然后,可以推导出以下递归方程:该方法的时间复杂度为𝑂(𝑛𝐵/4𝑑),因为评分函数𝑆可以通过增量计算以𝑂(1)时间进行计算。然而在实践中该方法依旧十分耗时,因为B通常是一个较大的值。因此,论文进一步提出了一个启发式算法来快速计算分页方法。该启发式算法是一种贪心算法,它将尽可能多的数据点打包到当前页面中,直到违反某些条件。该条件规定,新的MBR(通过将当前数据点添加到页面中而形成)不应将旧的MBR放大超过𝛼倍(𝛼>1是一个超参数)。这个条件减少了结果页面的MBR变得太大的机会,其中一个大的MBR可能与很多无用的查询相交。在之前已经提到,使用基于SFC的索引回答查询𝑞,需要两个步骤:1)给定一个空间查询矩形𝑞,确定其在z地址中的扫描范围,记为[𝑓(𝑞𝐿),𝑓(𝑞𝑈)]。2)扫描:所有z地址在此范围内的页面都需要进行扫描。可以使用正向索引找到这些页面。此外,由于LMSFC为每个页面维护了MBR和特定的排序信息,因此可以跳过不相关的页面,并只扫描页面的相关部分。上述框架的主要局限性是,它忽略了由于SFC映射而导致的z地址范围内潜在的大量假阳性数据点。如图 5(a)所示,查询对应的z地址范围可以分成蓝色部分(假阳)和黄色部分,可以看出额外的开销(即蓝色部分)是比较大的。因此,论文提出了基于查询分割的策略来缩小该开销。比如,在图5(a)中考虑相同的查询(黑色矩形)我们可以通过在𝑥轴上的值8处进行切割,将查询分成两部分,如图5(b)所示,可以看到蓝色部分可以被有效地减小。论文首先讨论了如何将一个查询精确地分割为两个子查询,然后将其推广为基于递归的方法以分割成多个子查询。该过程计算比较多,建议参考原论文。实验平台:CPU:i9-7900X;内存:64GB;操作系统:Ubuntu 20.04.4。编程语言:C++。数据集:论文一共使用了3个数据集进行评估,1)OSM:一个空间数据集,由OpenStreetMap数据集中从北美随机采样的250M条记录组成。使用GPS坐标(即经度和纬度)来形成一个二维数据集。2)NYC:从纽约市2018年和2019年的黄色出租车旅行记录中随机抽取。使用上车位置、旅行距离和总量来形成一个三维数据集。3)STOCK:包括从1970年至2018年的每日历史股票价格,包括四个特征:最高价格、最低价格、调整后的收盘价和交易量。具体参数如表 1所示。查询负载:查询通过其在每个维度中的中心和范围进行生成。以以下两种模式之一生成查询中心:1)倾斜,其中查询中心是随机抽样的数据点。2)均匀,其中查询中心在数据空间内随机生成。每个维度中的查询的宽度从0均匀地采样到该维度的数据空间的宽度,其比例为0.05。所有的查询窗口都被剪切为在数据空间内。最终的查询工作负载是通过混合90%的倾斜查询和10%的统一查询来获得的对比方法:1) ZM-index,一个结合Z曲线和学习索引的方法;2) R*-tree,传统的多维索引;3) Flood,较新的多维学习索引。如图 6所示,LMSFC在所有数据集上都优于所有其他索引。与亚军相比,LMSFC在查询时间上提高了1.52×到1.96×。LMSFC相对于基线(即z阶曲线)的主要优点是,学习到的SFC在映射到一维地址空间后,能更好地保持数据的局部性。因此,多维空间中的近距离点更有可能被分配到同一个页面中。选择率(图 7左):对于所有的方法,由于访问了更多的数据点,查询时间近似地随着查询选择性的线性增长。注意到,当查询选择性变大时,R*-tree会恶化;这可能是由于𝑅-tree及其变体需要对每个内部节点执行复杂的MBR交集查询,并可能导致许多回溯(特别是对于更高维的情况),在查询窗口较大时该现象会更加严重。学习型SFC只需要扫描特定z地址范围内的页面,并且没有复杂的交集查询或回溯。与ZM-index相比,Flood效率显著提高,而LMSFC进一步持续提高了查询性能,展示了学习索引的广泛适用性。伸缩性(图 7右):可以看到,所有的索引都与数据大小近似线性扩展,而LMSFC表现最好,其次是Flood、ZM-index,最后是R*-tree。图7 不同查询大小(左图)以及数据大小(右图)实验从表 2中可以看出,论文提出的LMSFC比ZM-index或Flood具有更大的索引大小,其中一个原因是LMSFC为了优化页面布局占用了一定空间。尽管如此,LMSFC的索引大小仍然是可以接受的,因为它仍然明显小于传统的R*-tree。表 3给出了不同索引所需要的构建时间,对于学习索引,论文进一步区分了学习时间和索引建立时间。R*-tree在数据量较大时需要很长的构建时间,因为它在构建的过程中需要对树的结构进行调整。ZM-index具有最快的构建时间,因为不需要学习或优化。Flood比LMSFC的学习和构建时间更快,因为1)Flood的模型更简单,超参数空间比LMSFC要小得多。此外,它还针对学习的成本模型进行优化,因此超参数搜索更快。2)LMSFC还包括其他优化(如基于动态规划的分页),因此也会影响到索引的构建时间。本文介绍了LMSFC,一个基于学习型空间填充曲线的高维索引。论文设计了一个学习一类特殊的空间填充曲线的框架以实现高效的查询处理。此外,LMSFC通过优化数据的存储布局进行离线优化,对查询进行分割实现在线优化,以进一步提高查询处理效率。大量的实验结果表明,在三个真实数据集上,该方法的性能优于非学习索引(如R*-tree)和先进的学习多维索引。一个可能的未来方向是将该方法扩展到非单调性空间填充曲线上,比如希尔伯特曲线。[1]Frank Hutter, Holger H. Hoos, and Kevin Leyton-Brown.
2011. Sequential Model Based Optimization for General Algorithm Configuration.
In LION (Lecture Notes in Computer Science), Vol. 6683. Springer, 507–523.
https://doi.org/10.1007/978-3-642-25566-3_40
| 重庆大学计算机科学与技术专业在读硕士二年级学生,重庆大学START团队成员,主要研究方向:时空数据管理 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!

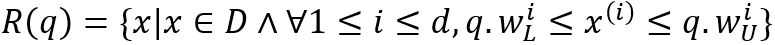 。
。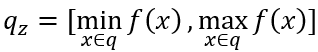 。然而,计算这些极值通常是困难的。在最坏的情况下,可能需要枚举𝑞中的所有𝑥,因此其成本与查询的大小成正比,这与高效查询处理的目的相悖。因此,论文确定了一个SFC的子类(即下面提出的单调空间填充曲线),这样qz就可以在𝑂(𝑑)时间内有效地计算出来,而不依赖于查询的大小。
。然而,计算这些极值通常是困难的。在最坏的情况下,可能需要枚举𝑞中的所有𝑥,因此其成本与查询的大小成正比,这与高效查询处理的目的相悖。因此,论文确定了一个SFC的子类(即下面提出的单调空间填充曲线),这样qz就可以在𝑂(𝑑)时间内有效地计算出来,而不依赖于查询的大小。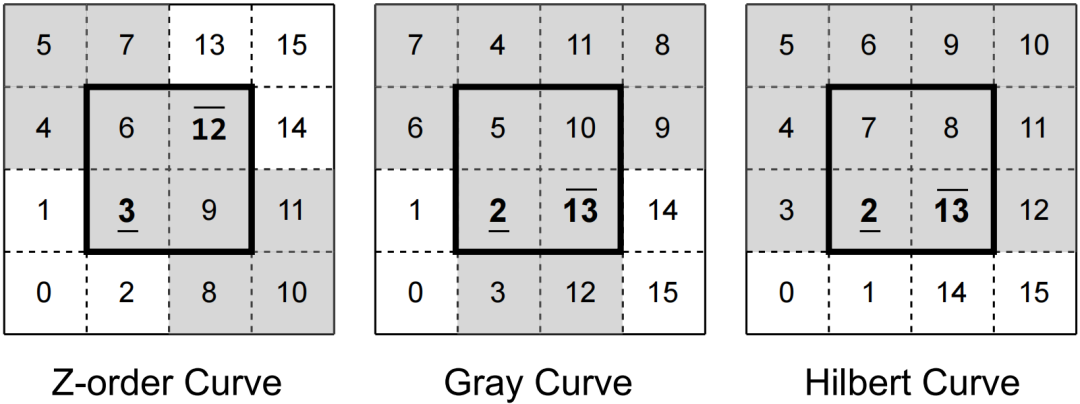
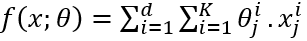
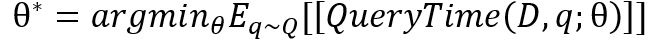 。其中,Q表示查询工作负载的分布,而𝑞是该负载中的一个样例,𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数返回在给定数据集上的实际查询执行时间。为了优化该方程,可以首先应用有限样本近似,即从Q中获取采样查询,用样本平均值代替期望。然而,𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数很难精确地建模或近似,因为它包含了各种复杂的优化。此外,直接评估𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数会产生过高的成本。另外,θ是一个高维离散参数,其搜索量是指数级别。因此在实践中不可能通过暴力算法来解决该优化问题。
。其中,Q表示查询工作负载的分布,而𝑞是该负载中的一个样例,𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数返回在给定数据集上的实际查询执行时间。为了优化该方程,可以首先应用有限样本近似,即从Q中获取采样查询,用样本平均值代替期望。然而,𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数很难精确地建模或近似,因为它包含了各种复杂的优化。此外,直接评估𝑄𝑢𝑒𝑟𝑦𝑇𝑖𝑚𝑒函数会产生过高的成本。另外,θ是一个高维离散参数,其搜索量是指数级别。因此在实践中不可能通过暴力算法来解决该优化问题。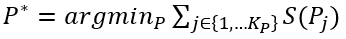 ,其中size(pj) ∈[𝑓𝐵,𝐵]。下面,首先介绍一个基于动态规划(DP)的最优求解上述问题的算法,然后是一个次优但快速的启发式算法。这两种方法都比固定大小的分页实现了更好的分页布局,从而提高了查询性能。
,其中size(pj) ∈[𝑓𝐵,𝐵]。下面,首先介绍一个基于动态规划(DP)的最优求解上述问题的算法,然后是一个次优但快速的启发式算法。这两种方法都比固定大小的分页实现了更好的分页布局,从而提高了查询性能。