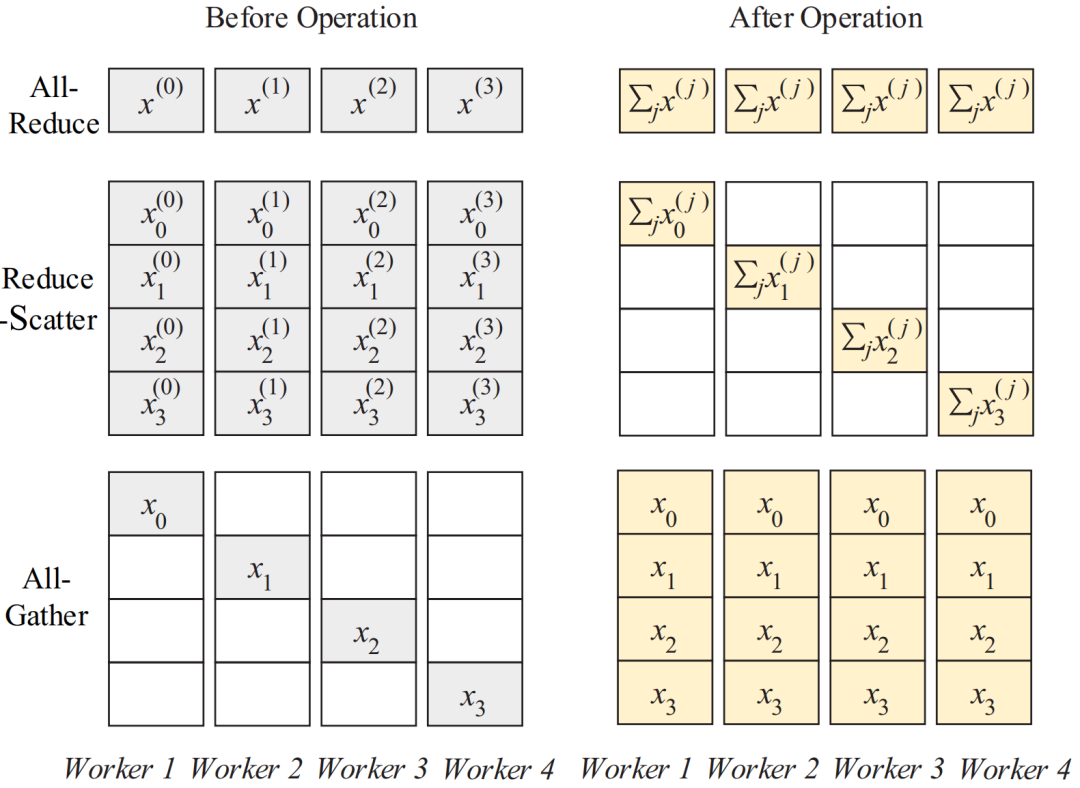
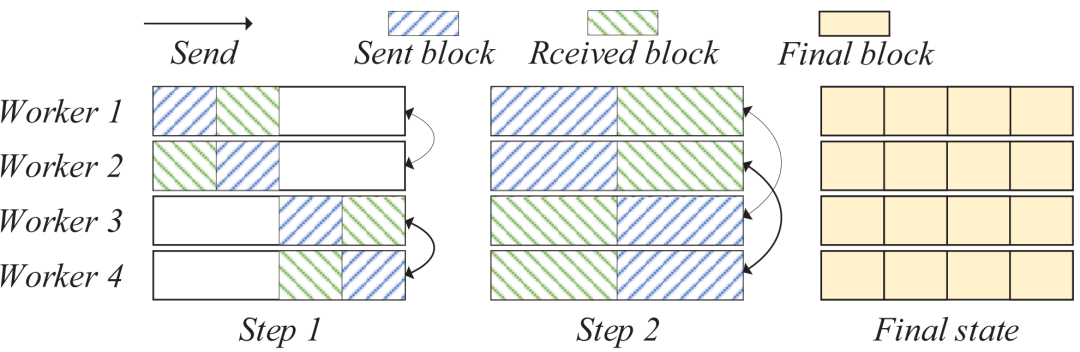
近期,top-k稀疏化技术因其在降低分布式深度学习通信负担方面的效果而受到广泛关注。然而,由于稀疏梯度累积(SGA)问题,这项技术的效果并不总是能达到预期。为了应对SGA问题,研究者们提出了多种解决方案,但这些方法往往存在一些不足,如依赖于效率不高的通信算法,或者需要额外的数据传输步骤。本次为大家带来数据库领域顶级会议ICDE 2024的文章《SparDL: Distributed Deep Learning Training with Efficient Sparse Communication》,论文介绍了一个名为SparDL的分布式深度学习训练框架,它通过结合多个选择过程和Reduce-Scatter操作来解决SGA难题,此外,SparDL使用全局残差收集算法来收集集群中所有丢弃的梯度,确保快速的训练收敛,论文还提出Spar-All-Gather算法进一步提高了SparDL的通信效率。如今,由于数据量巨大以及模型结构复杂,训练深度学习模型变得越来越耗时。为此,许多分布式模型训练技术被提出用于深度学习。其中,数据并行的同步小批量随机梯度下降(S-SGD)被广泛使用。具体来说,当使用S-SGD进行分布式模型训练时,在每次迭代结束时,工作节点通常通过All-Reduce操作同步它们的局部梯度,并使用相同的全局梯度更新它们的训练模型。S-SGD涉及大量的数据通信,Top-k稀疏化是减少通信开销的一种方法,它可以将局部梯度稀疏化为约1%的密度,同时不损害模型收敛性。然而,Top-k稀疏化有时会遭受稀疏梯度累积(SGA)困境。 具体来说,当使用高效的All-Reduce方法同步稀疏化梯度时,所选梯度会经历多次传输和求和步骤以获得全局梯度。由于不同工作节点的稀疏梯度可能来自不同的索引,每次求和都会增加后续传输过程中稀疏梯度的体积,从而导致SGA困境。SGA困境将导致梯度快速增加,甚至可能退化为密集梯度。例如,图1(a)和1(b)分别显示了worker1和worker2的初始3个梯度。在worker2接收到worker1的梯度并将其添加到自己的梯度后,worker2得到5个梯度,如图1(c)所示。随着传输步骤的继续,工作节点的梯度数量增加。SGA困境显著降低了带有稀疏化的分布式模型训练的通信效率。因此,有必要设计一种有效的方法来缓解SGA困境。(a)Worker1的稀疏度 (b)worker2的稀疏度 (c)求和后worker2的稀疏度通信复杂度成本模型: 延迟(α)--带宽(β)模型(α-β模型)被广泛用于分析通信复杂度。在这个成本模型中,α是两个节点之间传输的延迟成本,β是带宽成本。所有通信成本可以建模为xα+yβ,其中x可以视为传输轮数,y可以视为通信过程中一个节点接收的数据总量。All-Reduce、Reduce-Scatter和All-Gather: All-Reduce、Reduce-Scatter和All-Gather是常见的通信操作。图2展示了这些操作,All-Reduce操作通常用于同步和求和来自所有工作节点的梯度,Reduce-Scatter 将梯度各部分归约到对应节点,All-Gather 从所有节点收集梯度各部分。可以看出,依次使用Reduce-Scatter和All-Gather可以实现与All-Reduce相同的结果。 图2 All-Reduce,Reduce-Scatter和All-Gather操作有两种流行的高效All-Gather算法,称为递归倍增(recursive doubling)和Bruck All-Gather,如图3所示。递归倍增算法在工作节点数量为2的幂次方时效果最好,但在数量不是2的幂次方时不能直接使用。相比之下,Bruck All-Gather在任意数量的工作节点上都有较好效果且达到带宽成本下限。对于递归倍增,每个工作节点在第t步与距离为的工作节点通信和交换所有数据。对于BruckAll-Gather,每个工作节点在第t步向一侧距离为的工作节点发送数据,并从另一侧距离为的工作节点接收数据。当工作节点数量为2的幂次方时,递归倍增和BruckAll-Gather的通信复杂度均为: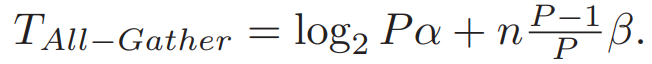
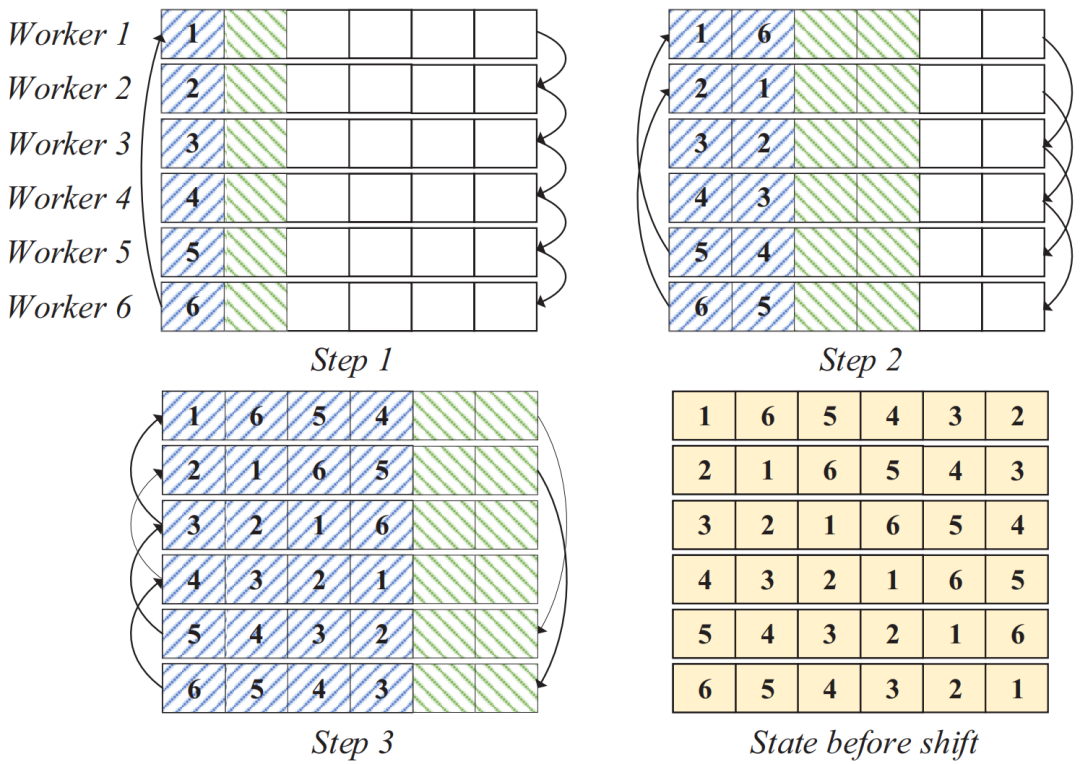
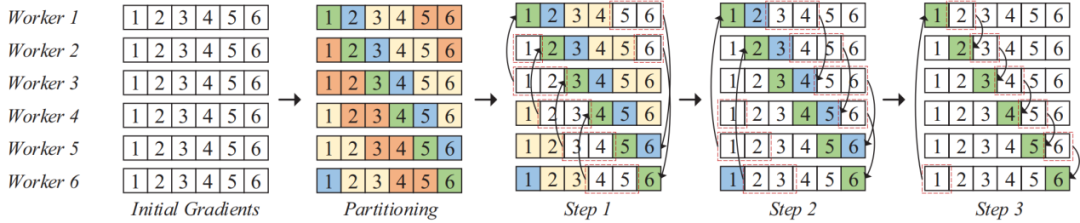
Top-k稀疏化:Top-k稀疏化通常用于高效分布式深度学习中对梯度进行稀疏化,它从密集梯度中选择绝对值最大的k个梯度,其中k通常设置为密集梯度数量的一定比例。Top-k稀疏化不会严重影响学习性能,这已在许多先前的理论和实证研究中得到证明。SparDL框架的如图4所示,对于一个具有P个工作节点的集群,训练开始时,各工作节点通过前向传播和反向传播生成梯度,并结合全局残差收集算法处理梯度。然后,将所有工作节点平均划分为d个组。接着,先利用Spar-Reduce-Scatter算法对每个组内的梯度进行处理,然后通过Spar-All-Gather算法在组间同步梯度,最后在每个组内使用All-Gather操作完成最终的梯度同步,得到全局梯度后各工作节点更新模型。如果设置d=1,则只使用Spar-Reduce-Scatter和一个All-Gather操作就可以完成的梯度同步。在没有其他说明的情况下,这篇论文中的SparDL表示d=1的SparDL。3.2 Spar-Reduce-Scatter算法为了解决SGA困境并且不增加通信复杂度,论文提出了Spar-Reduce-Scatter(SRS)算法,该算法将规约散射(Reduce-Scatter)阶段与多个分块稀疏化过程相结合。此外,论文为Reduce-Scatter提出了一种非递归结构,以确保低通信复杂度,并能在任意数量的工作节点上高效运行,无需额外操作。在这种结构中,一个工作节点的源工作节点和目标工作节点在一次传输步骤中是不同的。图5展示了一个六个工作节点的示例来说明SRS,块中的数字表示块的位置,每个块包含其对应位置的梯度(密集或稀疏)的一部分。 为了阐明SRS算法,论文设d=1,并将SRS分为两个过程:分区和稀疏化传输。对于工作节点 rw(所有P个工作节点中的第w个工作节点),给定第t次迭代(一次迭代包括前向传播和后向传播)的梯度G(w, t)以及上一次迭代(第t-1次)的残差ξwt-1。首先,工作节点 rw 将G(w, t)和ξwt-1相加作为新的G(w, t)。然后,它将G(w, t)划分为P个块{G0(w, t),…,GP(w, t)},并通过选择每个块的前k/P个值来稀疏化其局部密集梯度。然后,将P个块依次划分为一个保存袋B0w和l=⌈log2P⌉个发送袋{B1w,…, Blw}。这些发送袋将在后续传输步骤中用作发送单元,保留保存袋。具体来说,从块G(w, t)开始,将其放入保存袋B0w。然后,将从w+20到w+21的接下来20的个块放入发送袋B1w。重复此过程,直到所有块都放入不同的袋中。请注意,在分区过程中,P个块被视为排成一个圆圈,即如果在分区过程中到达块P,则继续从块1开始放置块。可能剩下的块不足以填满最后一个发送袋Blw,剩余数量将为E=P-2⌈log2P⌉-1。示例 1 图 5 展示了分区过程。假设有 6 个工作节点,以工作节点 1 为例,其中l=3,首先,把第一个块{1}放入保存袋,最后一个发送袋本来应该放置4个块,但工作节点 1 只剩下2个块{5,6}。因此,最后把块{5,6}放入发送袋最后一个发送袋,该袋未满。3.2.2 稀疏化传输(Transmission with sparsification) 将块分区到袋中后,按顺序从最后一个袋Blw到B1w传输所有发送袋中的块。具体来说,对于工作节点rwi中,它将工作节点rw+2^(l-i)视为目标,将工作节点rw+2^(l-i)视为源。它将袋Bl-i+1w发送到工作节点rw+2^(l-i),并从工作节点rw+2^(l-i)接收袋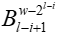 。在从源接收到发送袋后,每个工作节点根据梯度索引将接收的发送袋中的块的稀疏梯度添加到本地剩余块的梯度中。然后,在每个工作节点中利用分块稀疏化,即在求和后的每个本地剩余块中选择前 k/P 个值,并删除未选中的梯度。通过在每一步进行这种稀疏化,发送袋中每个块的梯度数量保持为k/P,从而解决了SGA 困境。示例2 图5也展示了传输和稀疏化过程。以工作节点1为例,l=3,在步骤1,通信距离(通信距离为节点与目标节点的距离同时也是与源节点的距离,即
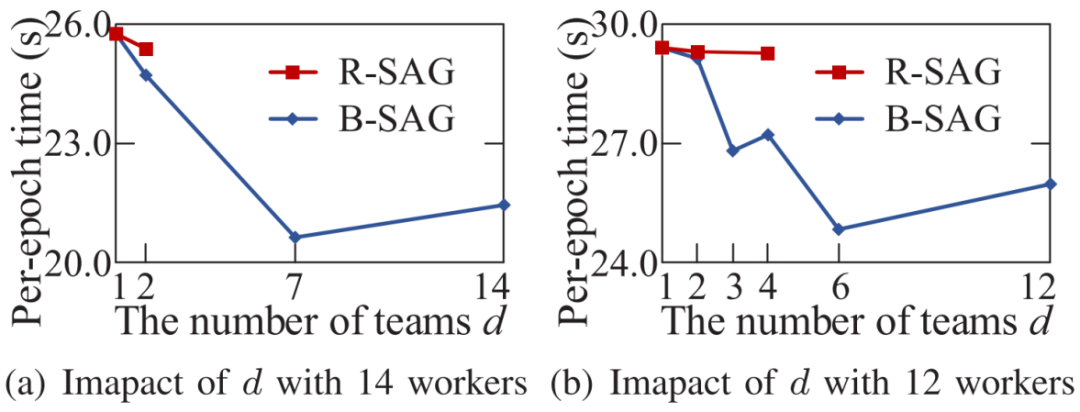
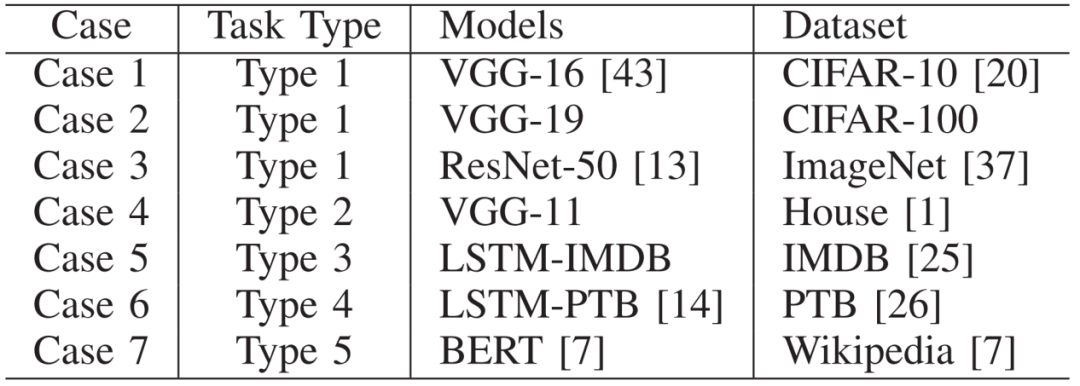
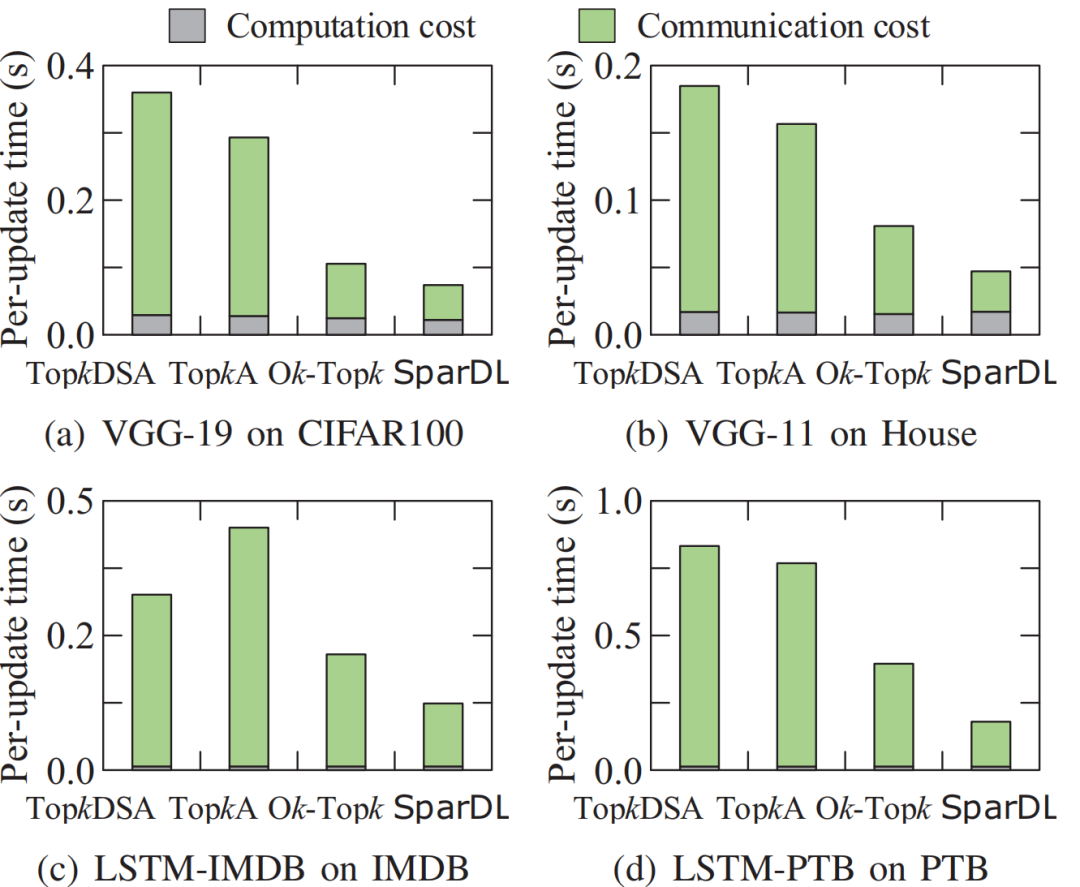
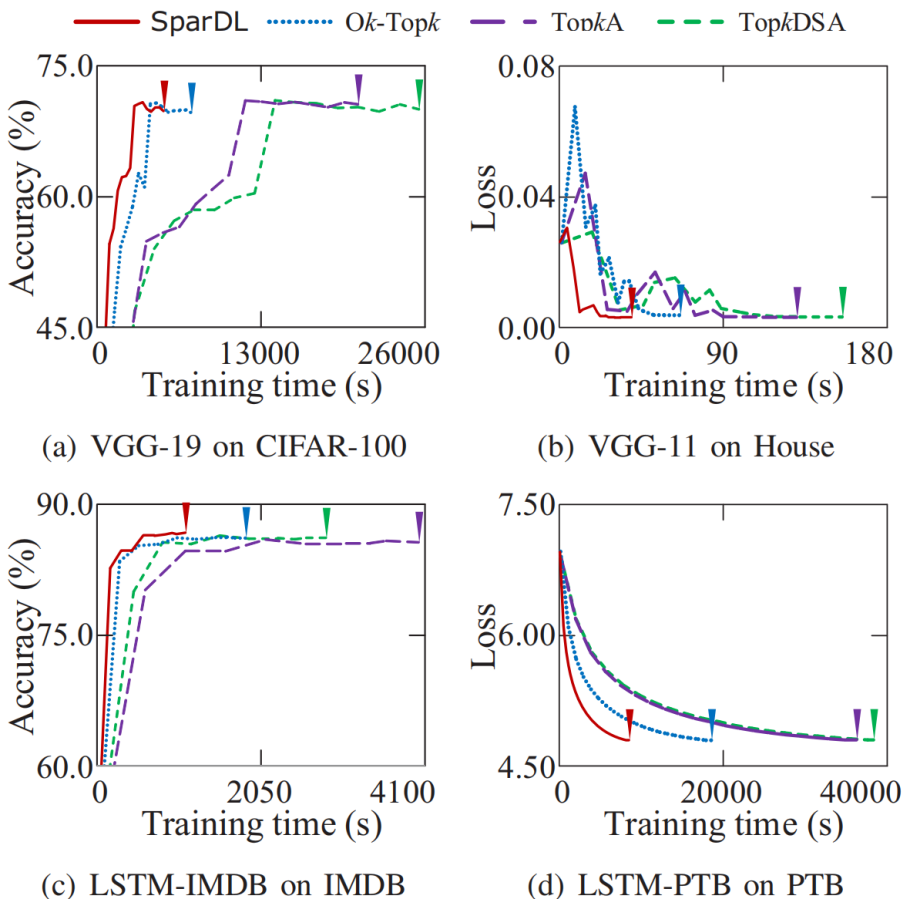
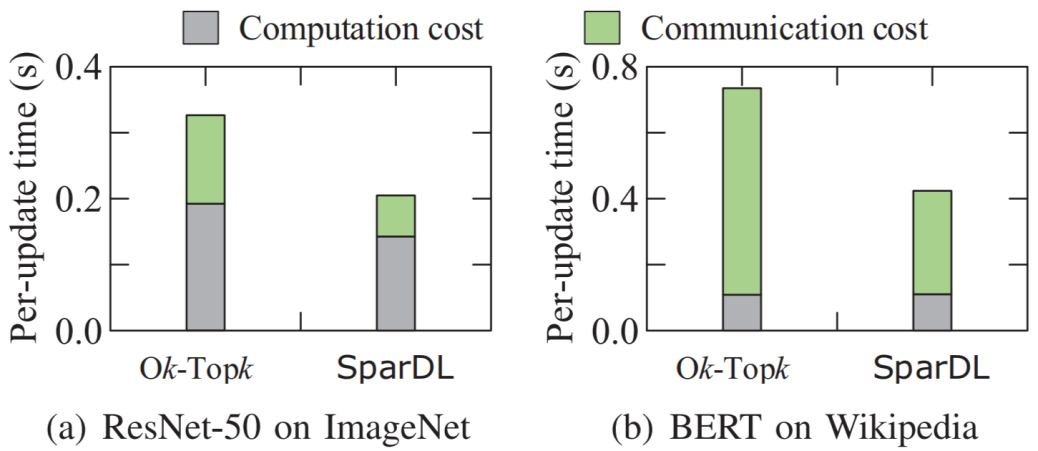
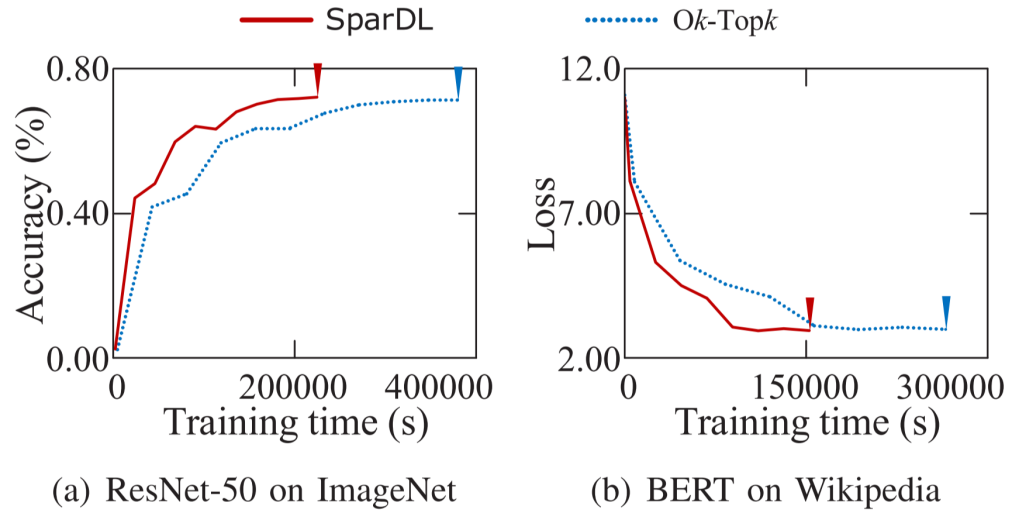
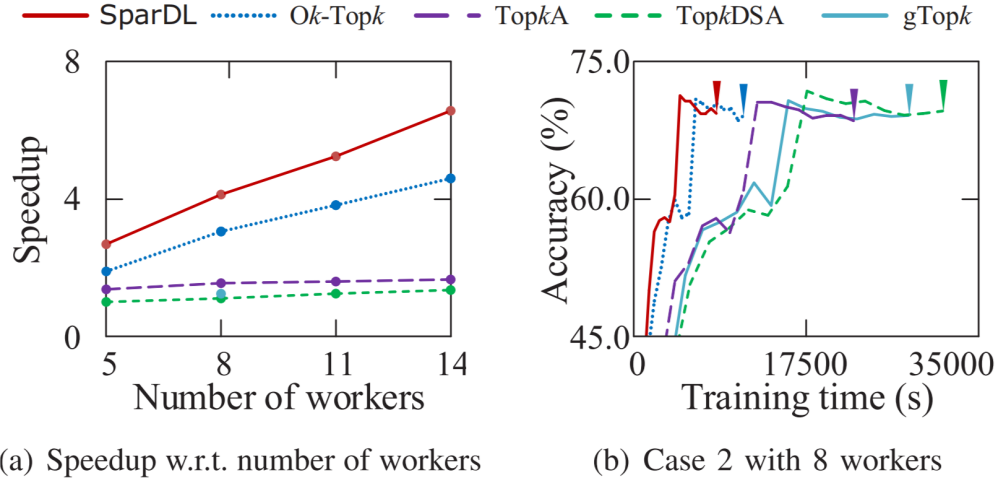
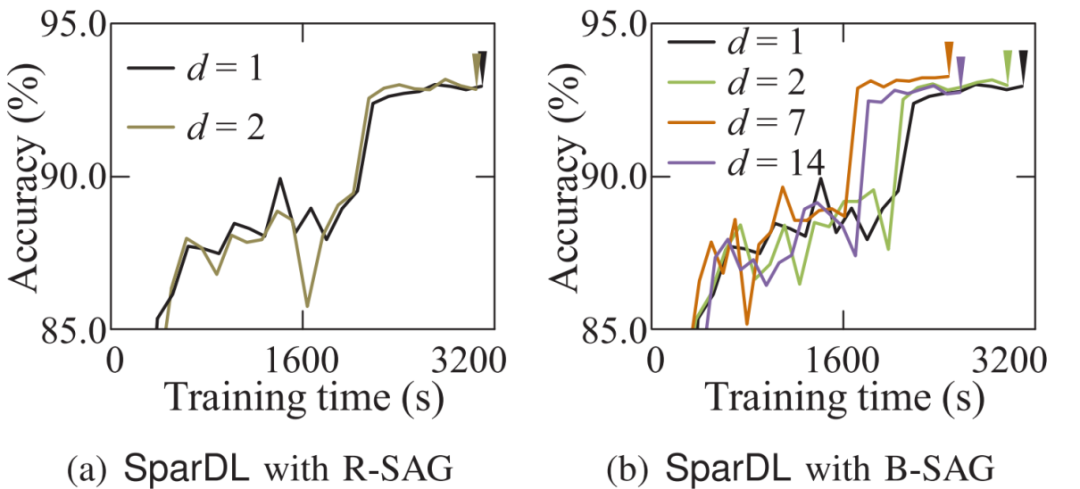
。在从源接收到发送袋后,每个工作节点根据梯度索引将接收的发送袋中的块的稀疏梯度添加到本地剩余块的梯度中。然后,在每个工作节点中利用分块稀疏化,即在求和后的每个本地剩余块中选择前 k/P 个值,并删除未选中的梯度。通过在每一步进行这种稀疏化,发送袋中每个块的梯度数量保持为k/P,从而解决了SGA 困境。示例2 图5也展示了传输和稀疏化过程。以工作节点1为例,l=3,在步骤1,通信距离(通信距离为节点与目标节点的距离同时也是与源节点的距离,即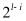 )为4。因此,它将装有2个块的袋B3发送到工作节点5,并从工作节点2接收一个装有2个块的袋。在步骤2,通信距离为2。因此,工作节点1将装有2个块的袋发送到工作节点3,并从工作节点5接收一个装有2个块的袋。在最后一步,工作节点1将装有1个块的袋发送到工作节点2,并从工作节点6接收一个装有1个块的袋。3.3 全局残差收集算法(Global Residual Collection)SparDL在传输步骤之间使用多次top-k选择梯度,虽然解决了SGA困境,但是可能会丢失重要的梯度,继而导致收敛速度变慢。因此,论文提出了全局残差收集算法来存储所有丢弃的梯度,并确保快速收敛。SparDL中有三种类型的丢弃梯度,分别为局部残差、结束残差和过程中残差。局部残差是在每个工作节点本地在传输之前被稀疏化并丢弃的梯度;结束残差和过程中残差都是在传输步骤之间被丢弃的梯度,区别为结束残差的索引不会出现在最终的全局梯度中,而过程中残差的索引仍然存在于最终的全局梯度中。图6展示了过程中残差和结束残差之间的区别,图中,索引为2的丢弃梯度是结束残差,索引为1的丢弃梯度是过程中残差。 现有补偿方法仅收集局部残差或局部和结束残差,但不能收集过程中残差。然而,由于其多次稀疏化过程,SparDL在每个工作节点上会产生大量的过程中残差,这些过程中误差可能会很重要。因此,现有方法不适用于SparDL。为了解决这个问题,论文提出了全局残差收集算法,该算法涵盖了所有三种类型残差的收集。由于过程中残差的索引如同正常的全局梯度一样,仍存在于最终的梯度中,所以无法根据最终索引来收集过程中残差,因此,论文在整个通信过程中对这些残差进行收集。如算法1所示,分两步收集残差。首先,将过程中残差保存在执行稀疏化操作的工作节点上(第8行)。这是因为过程中残差可能来自多个工作节点,收集这些残差需要很高的通信成本,直接将他们保存在执行稀疏化操作的工作节点上可以大大降低通信消耗,尽管这些残差是在处理工作节点上收集的,但从整个训练集群的角度来看,丢弃的梯度仍然被收集,并且迟早会被使用。接着,将局部残差和结束过程残差存储在本地工作节点上(第13-14行)。 3.4 Spar - All - Gather 算法当集群中有大量工作节点时,由于带宽存在上限,带宽成本会收敛到一个常数值,而延迟成本则不会收敛。因此,为了进一步提高SparDL的效率,降低延迟成本并使SparDL能够根据两种成本的重点进行调整十分重要,论文基于分治思想为SparDL提出了Spar-All-Gather(SAG)算法。具体来说,首先将所有P个工作节点平均分成d个组,其中应满足d | P(d整除P)。然后,每个组中的P/d个工作节点并行执行SRS算法。在SRS期间,每个工作节点将其梯度划分为P/d个块,在SRS之后,每个工作节点有一个稀疏梯度块。然后,组之间进行同步操作,同步后的每个组中相同排名的工作节点在有相同的L(k, d, p)=dK/P个稀疏梯度,最后,在每个组中使用Bruck All-Gather。数据集和模型为了全面评估所提出的SparDL在不同场景中的功效,论文采用了五种不同类型的任务:图像分类、图像回归、文本分类、语言建模和语言处理。论文使用了七个不同的真实世界数据集和七个广泛使用的深度学习模型,其中LSTM-IMDB和LSTM-PTB是具有LSTM单元的2层RNN模型,这些模型分别包含1470万、2010万、2350万、920万、3520万、6600万、13350万个参数。深度学习模型和数据集总结在表1中。对比方法论文将所提出的SparDL与四种现有的稀疏全规约(All-Reduce)方法进行比较:gTopk、Ok-Topk、TopkA和TopkDSA。实验设置论文中的所有实验均在PyTorch 1.11.0中使用mpi4py 3.0.3实现。所有实验均在一个具有14台GPU机器的GPU集群中进行评估。每台GPU机器安装有CentOS-7.9、Nvidia驱动程序510.39.01和CUDA 11.6,具有256GB内存、两个Intel(R) Xeon(R) 4314 CPU @ 2.40GHz处理器、一个GeForce RTX A40 GPU。所有机器均以默认设置连接到以太网。4.2 case2、4、5、6在14个节点上训练的性能评估为了验证SparDL框架在通信成本方面的优越性,论文在涉及14个节点的四个不同分布式深度学习案例中将其与Ok-Topk、TopkA和TopkDSA进行比较。这四个案例分别对应图像分类、图像回归、文本分类和语言建模。实验结果如图8所示。从该图中可以观察到,在所有四个案例中,SparDL的通信成本最低。如图8(a),在CIFAR-100上训练VGG-19时,SparDL的通信成本比TopkDSA、TopkA、Ok-Topk分别少6.4倍、5.1倍、1.6倍;在图8(b)中,在House数据集上训练VGG-11时,SparDL是最快的,其通信成本比TopkDSA、TopkA、Ok-Topk分别少5.6倍、4.7倍、2.2倍;从图8(c)和图8(d)中可以看出,在LSTM-IMDB上,SparDL比TopkDSA、TopkA、Ok-Topk分别少2.7倍、3.8倍、1.8倍,在LSTM-PTB上,SparDL比TopkDSA、TopkA、Ok-Topk分别少5.0倍、4.5倍、2.3倍。 为了展示SparDL在减少总体收敛时间方面的能力,论文记录了SparDL相对于基线的训练时间及模型准确率,如图9所示。从实验结果可以看出,SparDL优于所有基线方法,在收敛到与基线方法相似的准确率的同时,展现出最短的训练完成时间。具体而言,如图9所示,对于在VGG-19模型上训练CIFAR100数据集,SparDL分别比TopkA、TopkDSA和Ok-Topk快4.9倍、4.0倍、1.4倍。对于VGG-11模型,SparDL分别比TopkA、TopkDSA和Ok-Topk快3.9倍、3.3倍、1.7倍。对于LSTM-IMDB模型,SparDL分别比TopkA、TopkDSA和Ok-Topk快2.6倍、3.6倍、1.7倍。对于LSTM-PTB模型,SparDLSparDL分别比TopkA、TopkDSA和Ok-Topk快4.6倍、4.3倍和2.2倍。此外,从图9(a)到图9(d)可以看出,使用四种稀疏全规约(All-Reduce)方法训练的模型在相同数量的轮次后都收敛到相似的准确率。 为了进一步验证SparDL的效率,论文使用大型数据集(ImageNet和Wikipedia)以及大型模型(ResNet-50和BERT)对SparDL进行进一步评估。论文将SparDL与Ok-Topk进行比较,Ok-Topk是基线方法中最有效的方法。图10(a)和图10(b)描绘了每次更新的时间。对于ResNet-50,可以看到SparDL相比于Ok-Topk实现了2.3倍的通信成本加速。对于BERT,就通信成本而言,SparDL比Ok-Topk少2.0倍。 图10 ResNet-50 and BERT的每次更新的时间图11(a)和图11(b)分别绘制了ResNet-50和BERT相对于训练时间的测试准确率和训练损失。这些图表明,SparDL在大型数据集上保持了与Ok-Topk相当的收敛速度,同时完成训练过程的速度明显快于Ok-Topk。此外,对于ResNet-50,SparDL比Ok-Topk实现了1.7倍的加速,对于BERT也有类似的1.7倍加速。因此,SparDL在不同任务类型的大型数据集上展示了效率和有效性。图11 ResNet-50 and BERT的训练时间论文将在8个工作节点的集群中使用TopkDSA作为通信方法完成VGG-19单轮训练所需的平均训练时间设为参考时间。随后,计算gTopk、TopkA、TopkDSA和Ok-Topk在不同数量工作节点下相对于该参考时间的加速比。由于gTopk仅在工作节点数量为2的幂次方的集群中有效,论文仅评估8个工作节点时的gTopk。如图12(a)所示,与其他稀疏All-Reduce方法相比,SparDL表现出更优的可扩展性。此外,图12(b)描绘了使用gTopk、TopkA、TopkDSA、Ok-Topk和SparDL在8个工作节点上训练VGG-19时相对于训练时间的测试准确率。很明显,SparDL在速度方面超过了其他方法。 在这组实验中,论文研究了Spar-All-Gather(简称SAG,包括R-SAG和B-SAG)算法对SparDL框架性能的影响。对于R-SAG,论文将d设置为1和2;对于B-SAG,论文将d设置为1、2、7和14。算法的效果是通过在CIFAR-10数据集上训练VGG-16模型来检验的,具体方法是将SparDL框架与R-SAG或B-SAG算法结合使用,作为通信策略。如图13(a)所示,与没有SAG的SparDL(即d = 1的R-SAG或B-SAG)相比,d = 2的R-SAG的SparDL完成训练过程略快。此外,从图13(b)可以看出,所有的B-SAG的SparDL框架都比没有SAG的SparDL快,这表明B-SAG加速了SparDL。特别是d = 7的B-SAG和d = 14的B-SAG分别可以显著提高速度1.25倍和1.2倍。此外,实验结果还表明,带有SAG的SparDL框架与没有SAG的SparDL具有相似的收敛速度。 图13 SparDL在14个节点的集群中使用不同的SAG算法的训练时间接下来,论文观察d不同的值对不同数量工作节点下SAG效率的影响。对于图14(a)中的14个工作节点,R-SAG对SparDL产生这种影响的原因是,2个组的R-SAG在保持带宽成本不变的情况下略微降低了SparDL的延迟成本,从而导致训练时间略有减少。此外,B-SAG极大地提高了速度,因为它不仅降低了SparDL的延迟成本,还降低了带宽成本。还可以观察到d = 14的B-SAG比d = 7的B-SAG慢,这是因为带宽上限随着d的增加而增加,并且当d >
)为4。因此,它将装有2个块的袋B3发送到工作节点5,并从工作节点2接收一个装有2个块的袋。在步骤2,通信距离为2。因此,工作节点1将装有2个块的袋发送到工作节点3,并从工作节点5接收一个装有2个块的袋。在最后一步,工作节点1将装有1个块的袋发送到工作节点2,并从工作节点6接收一个装有1个块的袋。3.3 全局残差收集算法(Global Residual Collection)SparDL在传输步骤之间使用多次top-k选择梯度,虽然解决了SGA困境,但是可能会丢失重要的梯度,继而导致收敛速度变慢。因此,论文提出了全局残差收集算法来存储所有丢弃的梯度,并确保快速收敛。SparDL中有三种类型的丢弃梯度,分别为局部残差、结束残差和过程中残差。局部残差是在每个工作节点本地在传输之前被稀疏化并丢弃的梯度;结束残差和过程中残差都是在传输步骤之间被丢弃的梯度,区别为结束残差的索引不会出现在最终的全局梯度中,而过程中残差的索引仍然存在于最终的全局梯度中。图6展示了过程中残差和结束残差之间的区别,图中,索引为2的丢弃梯度是结束残差,索引为1的丢弃梯度是过程中残差。 现有补偿方法仅收集局部残差或局部和结束残差,但不能收集过程中残差。然而,由于其多次稀疏化过程,SparDL在每个工作节点上会产生大量的过程中残差,这些过程中误差可能会很重要。因此,现有方法不适用于SparDL。为了解决这个问题,论文提出了全局残差收集算法,该算法涵盖了所有三种类型残差的收集。由于过程中残差的索引如同正常的全局梯度一样,仍存在于最终的梯度中,所以无法根据最终索引来收集过程中残差,因此,论文在整个通信过程中对这些残差进行收集。如算法1所示,分两步收集残差。首先,将过程中残差保存在执行稀疏化操作的工作节点上(第8行)。这是因为过程中残差可能来自多个工作节点,收集这些残差需要很高的通信成本,直接将他们保存在执行稀疏化操作的工作节点上可以大大降低通信消耗,尽管这些残差是在处理工作节点上收集的,但从整个训练集群的角度来看,丢弃的梯度仍然被收集,并且迟早会被使用。接着,将局部残差和结束过程残差存储在本地工作节点上(第13-14行)。 3.4 Spar - All - Gather 算法当集群中有大量工作节点时,由于带宽存在上限,带宽成本会收敛到一个常数值,而延迟成本则不会收敛。因此,为了进一步提高SparDL的效率,降低延迟成本并使SparDL能够根据两种成本的重点进行调整十分重要,论文基于分治思想为SparDL提出了Spar-All-Gather(SAG)算法。具体来说,首先将所有P个工作节点平均分成d个组,其中应满足d | P(d整除P)。然后,每个组中的P/d个工作节点并行执行SRS算法。在SRS期间,每个工作节点将其梯度划分为P/d个块,在SRS之后,每个工作节点有一个稀疏梯度块。然后,组之间进行同步操作,同步后的每个组中相同排名的工作节点在有相同的L(k, d, p)=dK/P个稀疏梯度,最后,在每个组中使用Bruck All-Gather。数据集和模型为了全面评估所提出的SparDL在不同场景中的功效,论文采用了五种不同类型的任务:图像分类、图像回归、文本分类、语言建模和语言处理。论文使用了七个不同的真实世界数据集和七个广泛使用的深度学习模型,其中LSTM-IMDB和LSTM-PTB是具有LSTM单元的2层RNN模型,这些模型分别包含1470万、2010万、2350万、920万、3520万、6600万、13350万个参数。深度学习模型和数据集总结在表1中。对比方法论文将所提出的SparDL与四种现有的稀疏全规约(All-Reduce)方法进行比较:gTopk、Ok-Topk、TopkA和TopkDSA。实验设置论文中的所有实验均在PyTorch 1.11.0中使用mpi4py 3.0.3实现。所有实验均在一个具有14台GPU机器的GPU集群中进行评估。每台GPU机器安装有CentOS-7.9、Nvidia驱动程序510.39.01和CUDA 11.6,具有256GB内存、两个Intel(R) Xeon(R) 4314 CPU @ 2.40GHz处理器、一个GeForce RTX A40 GPU。所有机器均以默认设置连接到以太网。4.2 case2、4、5、6在14个节点上训练的性能评估为了验证SparDL框架在通信成本方面的优越性,论文在涉及14个节点的四个不同分布式深度学习案例中将其与Ok-Topk、TopkA和TopkDSA进行比较。这四个案例分别对应图像分类、图像回归、文本分类和语言建模。实验结果如图8所示。从该图中可以观察到,在所有四个案例中,SparDL的通信成本最低。如图8(a),在CIFAR-100上训练VGG-19时,SparDL的通信成本比TopkDSA、TopkA、Ok-Topk分别少6.4倍、5.1倍、1.6倍;在图8(b)中,在House数据集上训练VGG-11时,SparDL是最快的,其通信成本比TopkDSA、TopkA、Ok-Topk分别少5.6倍、4.7倍、2.2倍;从图8(c)和图8(d)中可以看出,在LSTM-IMDB上,SparDL比TopkDSA、TopkA、Ok-Topk分别少2.7倍、3.8倍、1.8倍,在LSTM-PTB上,SparDL比TopkDSA、TopkA、Ok-Topk分别少5.0倍、4.5倍、2.3倍。 为了展示SparDL在减少总体收敛时间方面的能力,论文记录了SparDL相对于基线的训练时间及模型准确率,如图9所示。从实验结果可以看出,SparDL优于所有基线方法,在收敛到与基线方法相似的准确率的同时,展现出最短的训练完成时间。具体而言,如图9所示,对于在VGG-19模型上训练CIFAR100数据集,SparDL分别比TopkA、TopkDSA和Ok-Topk快4.9倍、4.0倍、1.4倍。对于VGG-11模型,SparDL分别比TopkA、TopkDSA和Ok-Topk快3.9倍、3.3倍、1.7倍。对于LSTM-IMDB模型,SparDL分别比TopkA、TopkDSA和Ok-Topk快2.6倍、3.6倍、1.7倍。对于LSTM-PTB模型,SparDLSparDL分别比TopkA、TopkDSA和Ok-Topk快4.6倍、4.3倍和2.2倍。此外,从图9(a)到图9(d)可以看出,使用四种稀疏全规约(All-Reduce)方法训练的模型在相同数量的轮次后都收敛到相似的准确率。 为了进一步验证SparDL的效率,论文使用大型数据集(ImageNet和Wikipedia)以及大型模型(ResNet-50和BERT)对SparDL进行进一步评估。论文将SparDL与Ok-Topk进行比较,Ok-Topk是基线方法中最有效的方法。图10(a)和图10(b)描绘了每次更新的时间。对于ResNet-50,可以看到SparDL相比于Ok-Topk实现了2.3倍的通信成本加速。对于BERT,就通信成本而言,SparDL比Ok-Topk少2.0倍。 图10 ResNet-50 and BERT的每次更新的时间图11(a)和图11(b)分别绘制了ResNet-50和BERT相对于训练时间的测试准确率和训练损失。这些图表明,SparDL在大型数据集上保持了与Ok-Topk相当的收敛速度,同时完成训练过程的速度明显快于Ok-Topk。此外,对于ResNet-50,SparDL比Ok-Topk实现了1.7倍的加速,对于BERT也有类似的1.7倍加速。因此,SparDL在不同任务类型的大型数据集上展示了效率和有效性。图11 ResNet-50 and BERT的训练时间论文将在8个工作节点的集群中使用TopkDSA作为通信方法完成VGG-19单轮训练所需的平均训练时间设为参考时间。随后,计算gTopk、TopkA、TopkDSA和Ok-Topk在不同数量工作节点下相对于该参考时间的加速比。由于gTopk仅在工作节点数量为2的幂次方的集群中有效,论文仅评估8个工作节点时的gTopk。如图12(a)所示,与其他稀疏All-Reduce方法相比,SparDL表现出更优的可扩展性。此外,图12(b)描绘了使用gTopk、TopkA、TopkDSA、Ok-Topk和SparDL在8个工作节点上训练VGG-19时相对于训练时间的测试准确率。很明显,SparDL在速度方面超过了其他方法。 在这组实验中,论文研究了Spar-All-Gather(简称SAG,包括R-SAG和B-SAG)算法对SparDL框架性能的影响。对于R-SAG,论文将d设置为1和2;对于B-SAG,论文将d设置为1、2、7和14。算法的效果是通过在CIFAR-10数据集上训练VGG-16模型来检验的,具体方法是将SparDL框架与R-SAG或B-SAG算法结合使用,作为通信策略。如图13(a)所示,与没有SAG的SparDL(即d = 1的R-SAG或B-SAG)相比,d = 2的R-SAG的SparDL完成训练过程略快。此外,从图13(b)可以看出,所有的B-SAG的SparDL框架都比没有SAG的SparDL快,这表明B-SAG加速了SparDL。特别是d = 7的B-SAG和d = 14的B-SAG分别可以显著提高速度1.25倍和1.2倍。此外,实验结果还表明,带有SAG的SparDL框架与没有SAG的SparDL具有相似的收敛速度。 图13 SparDL在14个节点的集群中使用不同的SAG算法的训练时间接下来,论文观察d不同的值对不同数量工作节点下SAG效率的影响。对于图14(a)中的14个工作节点,R-SAG对SparDL产生这种影响的原因是,2个组的R-SAG在保持带宽成本不变的情况下略微降低了SparDL的延迟成本,从而导致训练时间略有减少。此外,B-SAG极大地提高了速度,因为它不仅降低了SparDL的延迟成本,还降低了带宽成本。还可以观察到d = 14的B-SAG比d = 7的B-SAG慢,这是因为带宽上限随着d的增加而增加,并且当d > 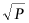 时,带宽下限也随着的增加而增加,因此,与最佳的d = 7相比,较大的d最终会削弱提高速度的效果。对于图14(b)中的12个工作节点,可以观察到R-SAG从2个组增加到4个组时效率的提高小于从1个组增加到2个组时的情况,原因是d = 2的R-SAG在保持带宽成本不变的情况下降低了SparDL的延迟成本,而d = 4的R-SAG在降低相同延迟成本的同时增加了带宽成本。对于B-SAG,d = 4的B-SAG比d = 3的B-SAG慢,这是因为d = 4的B-SAG与d = 3的B-SAG具有相同的延迟成本和相同的带宽成本下限,而d = 4的B-SAG的带宽成本上限更高。此外,如图13(b)所示,d = 14的B-SAG的SparDL达到了最低的测试准确率。这是因为当d等于集群中的工作节点数量(即P)时,会出现所有工作节点在仅进行一次局部top-h操作后就进行聚合,完全不考虑全局梯度。这导致许多全局重要但局部不太重要的梯度被丢弃,从而影响收敛速度。 论文分析了现有稀疏全规约(All-Reduce)框架的低效率问题,并提出了SparDL来解决这些问题。SparDL首次将多次选择过程与规约散射(Reduce-Scatter)操作相结合,以应对稀疏梯度累积(SGA)困境。此外,SparDL使用全局残差收集算法来收集集群中所有被丢弃的梯度,确保训练快速收敛。另外,Spar-All-Gather算法进一步提高了SparDL的通信效率,并使延迟和带宽成本的比例可调。在对广泛的常见深度学习任务进行实验后,论文发现论文的SparDL与最先进的方法相比,速度提升高达4.9倍,同时保持了相当的有效性。
时,带宽下限也随着的增加而增加,因此,与最佳的d = 7相比,较大的d最终会削弱提高速度的效果。对于图14(b)中的12个工作节点,可以观察到R-SAG从2个组增加到4个组时效率的提高小于从1个组增加到2个组时的情况,原因是d = 2的R-SAG在保持带宽成本不变的情况下降低了SparDL的延迟成本,而d = 4的R-SAG在降低相同延迟成本的同时增加了带宽成本。对于B-SAG,d = 4的B-SAG比d = 3的B-SAG慢,这是因为d = 4的B-SAG与d = 3的B-SAG具有相同的延迟成本和相同的带宽成本下限,而d = 4的B-SAG的带宽成本上限更高。此外,如图13(b)所示,d = 14的B-SAG的SparDL达到了最低的测试准确率。这是因为当d等于集群中的工作节点数量(即P)时,会出现所有工作节点在仅进行一次局部top-h操作后就进行聚合,完全不考虑全局梯度。这导致许多全局重要但局部不太重要的梯度被丢弃,从而影响收敛速度。 论文分析了现有稀疏全规约(All-Reduce)框架的低效率问题,并提出了SparDL来解决这些问题。SparDL首次将多次选择过程与规约散射(Reduce-Scatter)操作相结合,以应对稀疏梯度累积(SGA)困境。此外,SparDL使用全局残差收集算法来收集集群中所有被丢弃的梯度,确保训练快速收敛。另外,Spar-All-Gather算法进一步提高了SparDL的通信效率,并使延迟和带宽成本的比例可调。在对广泛的常见深度学习任务进行实验后,论文发现论文的SparDL与最先进的方法相比,速度提升高达4.9倍,同时保持了相当的有效性。| 重庆大学计算机科学与技术专业2022级本科生,重庆大学Start Lab团队成员。 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有3~5名研究生名额,欢迎计算机、GIS等相关专业的学生报考!
图文|刘明星
校稿|李佳俊
编辑|李佳俊
审核|李瑞远
审核|杨广超


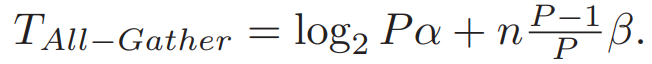

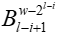 。
。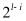 )为4。因此,它将装有2个块的袋B3发送到工作节点5,并从工作节点2接收一个装有2个块的袋。在步骤2,通信距离为2。因此,工作节点1将装有2个块的袋发送到工作节点3,并从工作节点5接收一个装有2个块的袋。在最后一步,工作节点1将装有1个块的袋发送到工作节点2,并从工作节点6接收一个装有1个块的袋。
)为4。因此,它将装有2个块的袋B3发送到工作节点5,并从工作节点2接收一个装有2个块的袋。在步骤2,通信距离为2。因此,工作节点1将装有2个块的袋发送到工作节点3,并从工作节点5接收一个装有2个块的袋。在最后一步,工作节点1将装有1个块的袋发送到工作节点2,并从工作节点6接收一个装有1个块的袋。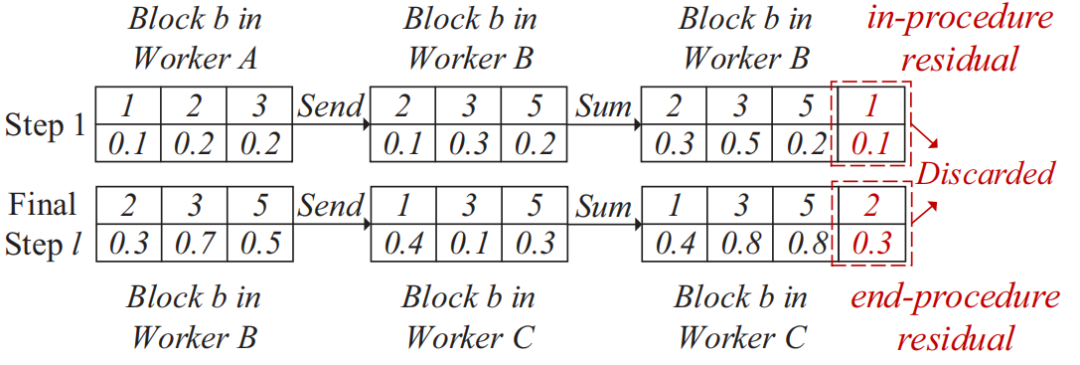

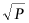 时,带宽下限也随着的增加而增加,因此,与最佳的d = 7相比,较大的d最终会削弱提高速度的效果。对于图14(b)中的12个工作节点,可以观察到R-SAG从2个组增加到4个组时效率的提高小于从1个组增加到2个组时的情况,原因是d = 2的R-SAG在保持带宽成本不变的情况下降低了SparDL的延迟成本,而d = 4的R-SAG在降低相同延迟成本的同时增加了带宽成本。对于B-SAG,d = 4的B-SAG比d = 3的B-SAG慢,这是因为d = 4的B-SAG与d = 3的B-SAG具有相同的延迟成本和相同的带宽成本下限,而d = 4的B-SAG的带宽成本上限更高。此外,如图13(b)所示,d = 14的B-SAG的SparDL达到了最低的测试准确率。这是因为当d等于集群中的工作节点数量(即P)时,会出现所有工作节点在仅进行一次局部top-h操作后就进行聚合,完全不考虑全局梯度。这导致许多全局重要但局部不太重要的梯度被丢弃,从而影响收敛速度。
时,带宽下限也随着的增加而增加,因此,与最佳的d = 7相比,较大的d最终会削弱提高速度的效果。对于图14(b)中的12个工作节点,可以观察到R-SAG从2个组增加到4个组时效率的提高小于从1个组增加到2个组时的情况,原因是d = 2的R-SAG在保持带宽成本不变的情况下降低了SparDL的延迟成本,而d = 4的R-SAG在降低相同延迟成本的同时增加了带宽成本。对于B-SAG,d = 4的B-SAG比d = 3的B-SAG慢,这是因为d = 4的B-SAG与d = 3的B-SAG具有相同的延迟成本和相同的带宽成本下限,而d = 4的B-SAG的带宽成本上限更高。此外,如图13(b)所示,d = 14的B-SAG的SparDL达到了最低的测试准确率。这是因为当d等于集群中的工作节点数量(即P)时,会出现所有工作节点在仅进行一次局部top-h操作后就进行聚合,完全不考虑全局梯度。这导致许多全局重要但局部不太重要的梯度被丢弃,从而影响收敛速度。