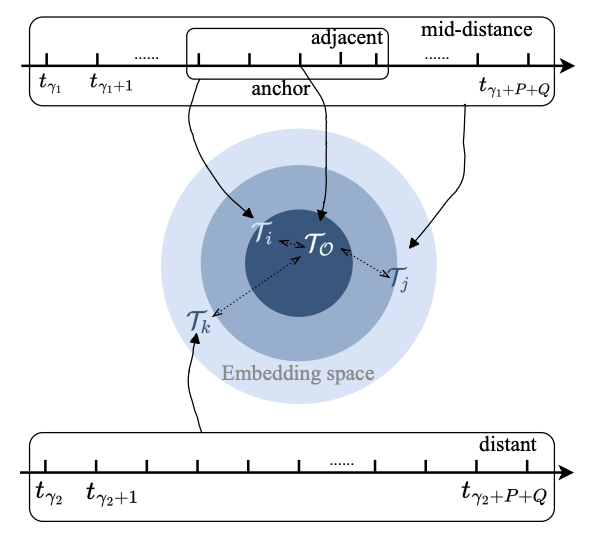
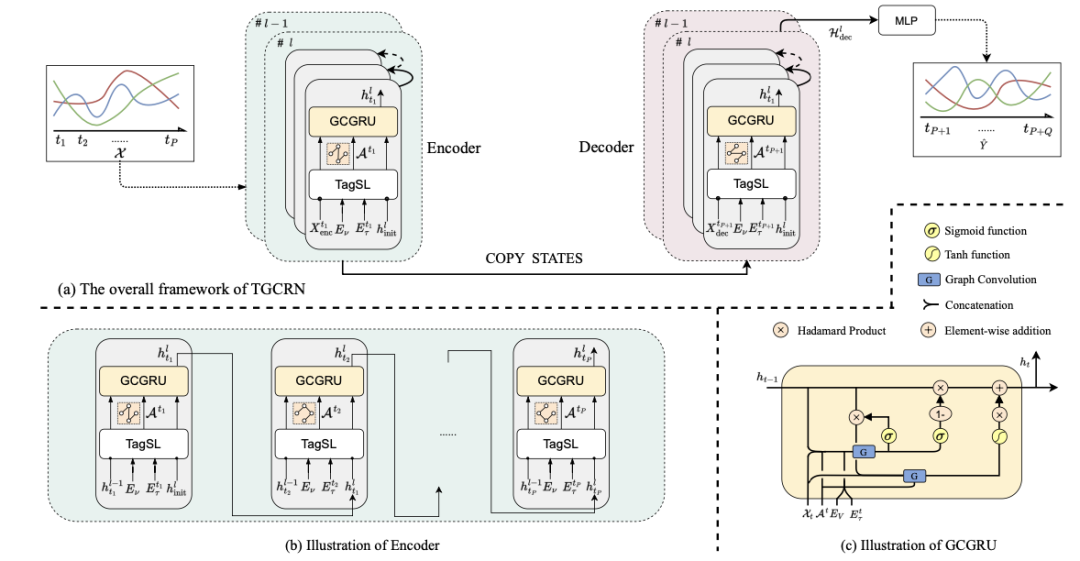
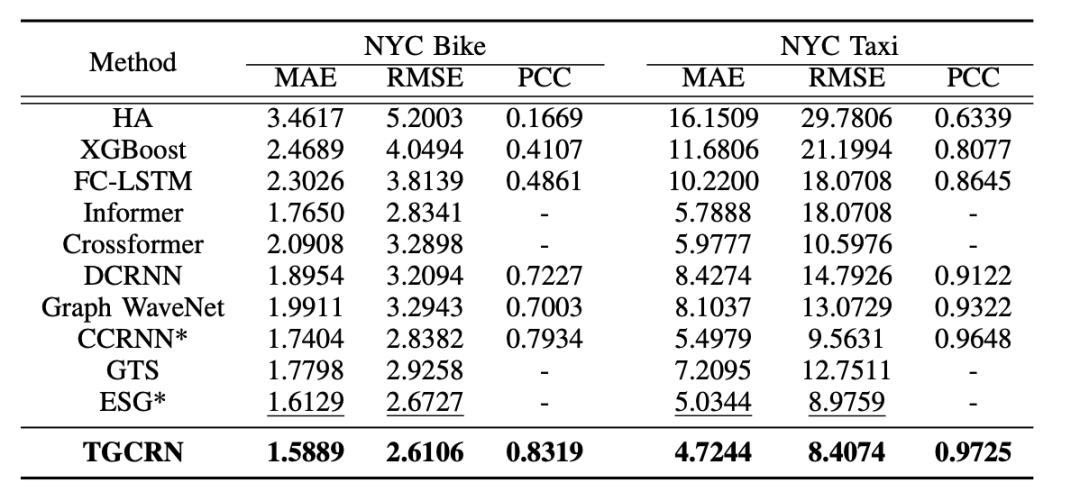
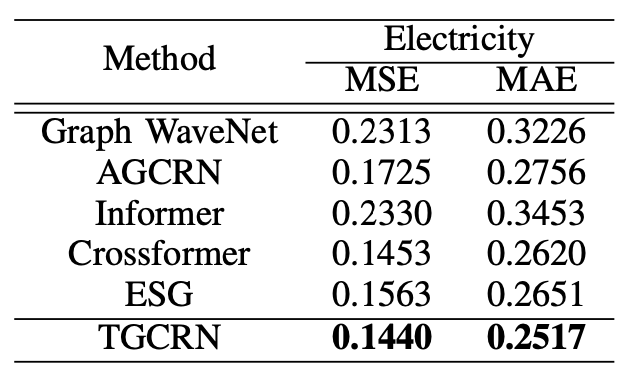
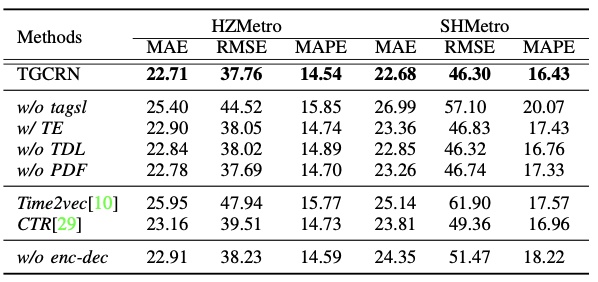
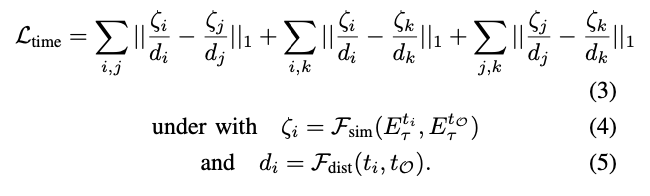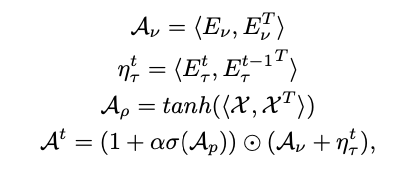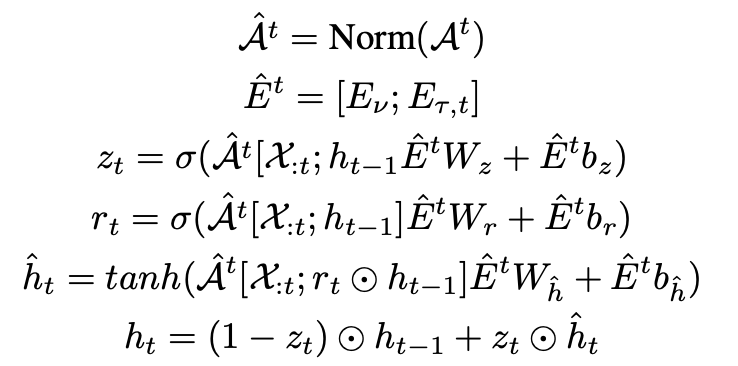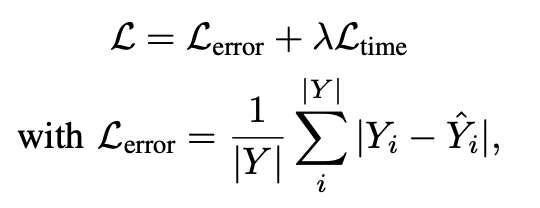信息物理系统(CPS)具有动态响应物理世界中实时变化的能力,在诸如空气质量预测、天气预报等广泛领域有着重要的意义。由空间分布的传感器生成的时间序列预测是CPS的重要组成部分,使其能够做出明智的决策。然而,大多数现有方法依赖于预定义或自学习的图结构,这些图结构要么是静态的,要么是无意中动态的。因此,要建模那些由于CPS中基础过程的规律性所导致的趋势和周期性变化,仍面临一些挑战。本次为大家带来数据库领域顶级会议ICDE 2024的文章《Learning Time-aware Graph Structures for Spatially Correlated Time Series Forecasting 》。由空间分布的传感器生成的时间序列预测对信息物理系统具有重要作用,能够使其动态调整以适应不断变化的物理世界。这最终在诸如空气质量预测、天气预报、交通规划以及船舶碰撞风险预警等广泛领域中提高了整体效率、可靠性和响应能力。现有的时空预测方法表明,当同时考虑时间和空间相关性时,预测的准确性会显著提高。然而,现有的预测解决方案在捕捉空间趋势和周期性方面能力不足。采用预定义图结构的解决方案需要大量计算和存储资源来预计算空间相关性,而且由于先验假设的不完整,可能还会引入不可避免的偏差。采用自学习图结构的解决方案要么难以表示动态性,要么无法显式考虑动态性的规律性。总体而言,有三个挑战需要解决:挑战1: 如何在时空预测中学习具有趋势和周期性的动态图结构?挑战2: 构建能够随时间变化的图结构不可避免地会引入更多的模型参数,如何让模型能够收敛?挑战3:在时间和空间相关性会动态地相互影响与当前的时空状态会受过去状态的影响的背景下,如何学习动态的时空相关性? 为了解决上述三个挑战,论文提出了时间感知图卷积递归网络(TGCRN)框架。首先,论文构建了具有趋势性和周期性的图结构来表示空间相关性。不同于采用复杂的神经网络,本文将图学习分解为节点和时间表示,然后将它们结合起来构建时间感知的图结构。接下来,论文利用基于图卷积的门控循环单元(GRU)来有效捕捉空间和时间依赖性,这种方法将时间感知图结构上的图卷积与用于整合当前输入和先前状态的门控机制结合起来。最后,论文提出了TGCRN,它采用了一个整合了时间感知图结构学习和基于图卷积的门控循环单元的编码器-解码器架构。这种递归集成允许模型有效捕捉时空相关性的趋势和周期性变化。• 时间差异学习:时间编码函数Φ(·)应满足两个标准,以便有效学习空间趋势。首先,它应符合平移变异性,即时间表示的度量在相邻时间步之间应有所不同。假设一个函数⟨Φ(t), Φ(t + c)⟩ := K(t, t + c),则平移变异性可以表示为K(t, t + c)≠ K(t + i∗c, t + (i + 1) ∗c),其中i≠ 0,c表示时间间隔。其次,编码应保留时间步之间的差异性。例如,08:00和09:00之间的表示应该比08:00和10:00之间的表示更加相似。如图1所示,本文设计了一种基于嵌入技术和自监督学习的时间编码函数。考虑到一个最小周期(例如一天),我们首先将无限时间离散化为以一天为周期的时间戳序列,表示为T = [t0, t1, ···, tmax]。然后我们随机初始化这些时间戳的可学习嵌入向量。为了学习时间步向量表示之间的差异,并使它们与时间域中的距离成比例,本文提出了一个基于距离的比例正则化项来约束时间嵌入。如图1所示,存在三种不同的时间步集合:相邻时间步、中距离时间步和远距离时间步。如果两个时间步之间的距离较近,它们的时间表示更加相似;相反,如果两个时间步之间的距离较远,它们的时间表示应表现出更大的差异。因此,本文设计了如下的目标损失函数: 其中Fsim表示时间表示的相似性,Fdist 表示时间步之间的距离。本文使用欧几里得距离作为Fsim以考虑向量空间中的相似性度量,使用L1距离度量Fdist来保证时间步之间距离的对称性。ti, tj和tk分别表示相邻、中距离和远距离的时间步,这些时间步都是相对于锚点时间步tO进行采样的。这种采样策略和目标损失函数的设计旨在帮助模型更好地学习时间表示之间的平移变异性和差异性,从而在时空数据预测任务中提供更准确的结果.• 周期判别函数:为了区分不同的周期并生成捕捉相应空间相关性的图结构,本文设计了一个周期判别函数。我们观察到,在不同的时间周期中,同一日的时间点节点状态差异显著。例如,在交通流量预测中,同一时间点的交通流量在工作日和周末由于旅行需求不同而表现出不同的模式,这些模式可以从观察数据中提取出来以区分这两者。因此,我们提出了一个判别函数,根据当前节点状态来识别相应的周期。具体地,节点状态可以通过分段非线性函数映射到不同的范围,内积操作进一步扩大这些范围。则学习型时间感知图的邻接矩阵可以用如下方程组表示: 其中,Aν和 Aρ∈RN×N表示自学习的周期判别矩阵,ητ是一个标量,表示趋势因子,σ(⋅)是 sigmoid 函数,⊙表示 Hadamard 乘积,α是一个用于调整周期效应对当前空间相关性权重的超参数。大多数最新的提议采用图卷积网络(GCN)来捕捉时间序列之间的空间依赖性,其主要目标是通过信息传递学习节点表示。显著的图卷积操作采用了在谱域中的“切比雪夫多项式扩展”的一阶近似。给定多元时间序列 X∈RN×Cin,其中包含 Cin维特征向量,卷积可以表示为:Z=LsymXW+b,其中 Lsym是对称拉普拉斯正则化矩阵,W和b是可训练参数,Z∈RN×Cout表示卷积后的特征。除了捕捉变量间的相关性,还使用门控循环单元(GRU),即带有门控机制的循环神经网络的一种变体,来捕捉变量内部的时间模式。考虑到空间和时间依赖性,论文提出了一种基于图卷积的门控循环单元,定义如下: 这里,At是在时间步t的时间感知图的邻接矩阵,Norm表示归一化函数,例如 softmax 函数,tanh 表示双曲正切函数,zt,rt,和ht分别是更新、重置和候选激活向量。每个门控单元都会结合前一个隐藏状态和当前输入,使用学习到的参数,包括权重矩阵W∈RCin×Cout 和偏置 b∈RCout 。同时,为了减少参数规模并控制由权重W∈RN×Cin×Cout引起的过拟合,本文采用矩阵分解 W=EW,其中E∈RN×d且d≪N。图2展示了本文提出的TGCRN框架。该框架使用编码器-解码器结构来输出多步的预测。为了增强特征表示的能力,编码器和解码器采用了多层网络,并递归地提取时间感知的时空相关性。具体来说,给定编码器或解码器中第i层的输入Xitj=htj-1i−1,包括前一个隐藏状态 htj−1i、节点嵌入Eν以及在时间tj的时间向量Eτ,tj,首先将它们输入 TagSL 以获得一个时间感知的图结构Atj。然后使用 GCGRU 来聚合由Atj 得出的节点及其邻域之间的空间相关性,并捕捉变量内部的时间相关性。输出的隐藏状态 htji被视为下一个单元的输入。注意,当i=1时,X1tj,enc=Xtj且X1tj,dec=hltj,enc。此外,解码器和编码器的结构是相同的,唯一的区别是在解码器的最后一层上有一个附加的输出层,它将最后一层的隐藏状态[hltP+1, …,hltP+Q]转换为具有所需维度的输出。最后,本文提出了TGCRN的整体学习目标,包括辅助的时间差异学习损失和误差损失。可以表示为: 其中,Lerror衡量了真实值和预测值之间的平均绝对误差,而 λ是一个可调的超参数。总而言之,任务目标是通过最小化联合损失函数来优化所有可训练参数。对比方法. 本文将TGCRN与13个现有的时间序列预测的方案进行比较,包括了最新的时空预测方法和一些基于Transformer的方案。数据集. 论文使用了五个真实数据集HZmetro, SHMetro, NYC-Bike, NYC-Taxi, 和Electricity。平台及设置. 论文在 Intel(R) Xeon(R) Gold 5215 CPU @ 2.50GHz 和两块 Nvidia Quadro RTX 8000 GPU 上进行了所有实验。采用 Adam 优化器来更新模型权重。L2 正则化项的系数为 10−4。初始学习率为 10−3,并在训练轮次达到 [5, 20, 40, 70, 90] 时按 0.3 的比例衰减。对于所有数据集,批量大小设为 16。周期判别函数的饱和因子设为 0.3。编码器和解码器的层数以及 GCGRU 的隐藏单元数分别设置为 2 和 64。 表1和表2展示了五个数据集上的预测性能,不难发现:1.TGCRN在所有指标上始终取得最佳性能,无论是对于所有数据集还是预测时长(Q1);2.捕捉时空关系的方法相比只捕捉时间相关性的方法(如 HA、GBDT 和 FC-LSTM)有显著改进;3.从空间相关性建模的角度来看,TGCRN 优于采用固定、自学习和动态图结构的现有基于 GCN 的方法,包括 DCRNN、AGCRN 和 ESG,这证明了捕捉时间感知空间相关性的有效性。更具体地说,与现有的最先进方法相比,TGCRN 在 HZMetro 上的 MAE 和 RMSE 分别提升了 10.95% 和 14.16%,在 SHMetro 上分别提升了 8.44% 和 7.44%,在 NYC-Taxi 上分别提升了 6.15% 和 6.33%。TGCRN 优于 ESG 的原因在于它增强了捕捉空间相关性常规动态的能力;4.从多步预测的角度来看,TGCRN 始终保持优势。以 FC-LSTM 为基准,可以发现随着时间步长的增加,TGCRN 相较于其他方法展现出越来越显著的预测性能。 表1 各方案在NYCBike和NYC-Taxi数据集上的表现- w/o tagsl:用 AGCRN 的自学习机制替换时间感知图结构学习。
- w/ TE:仅在时间感知图结构学习中使用时间嵌入。
- w/o TDL:移除时间差异学习,以评估学习到的时间表示的效果。
- w/o PDF:移除周期判别函数,以评估其通过捕捉不同周期性效应的贡献。
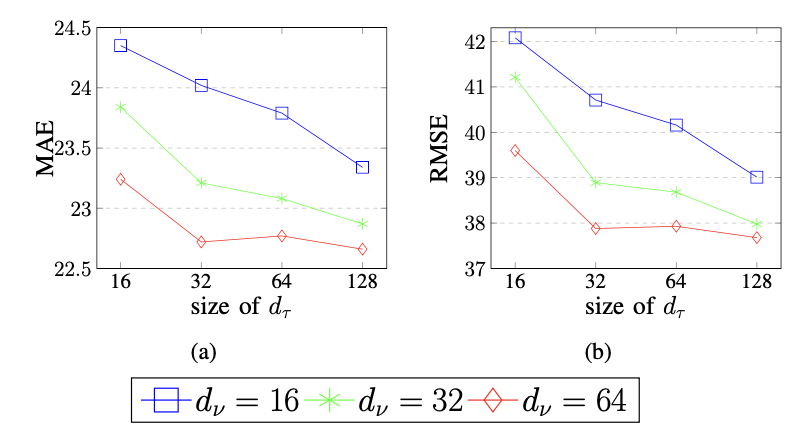
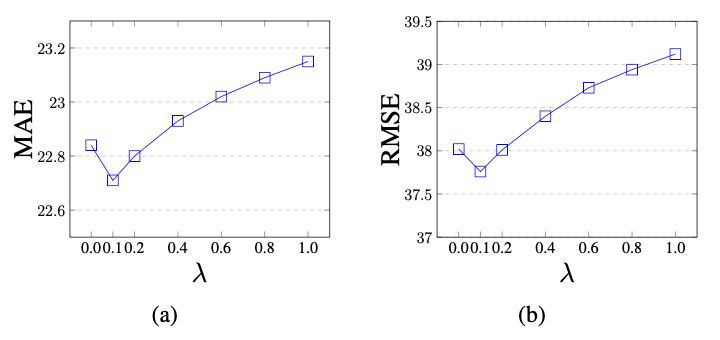
其次,本文采用了最新的显著时间表示方法:Time2vec和连续时间表示来编码时间,以评估本文提到的简单但有效的时间表示的效果。最后,w/o enc-dec 用基于全连接神经网络的直接输出替换递归获得的解码输出。 表3展示了 TGCRN 在 HZMetro 和 SHMetro 上不同变体的结果。不难发现 w/o tagsl 的性能显著下降,这表明时间感知图结构在提供更准确的空间相关性动态方面起到了重要作用。接下来,w/ TE 的结果表明,用于构建时间感知图的离散时间嵌入对于空间模式非常重要。然而,单独利用时间嵌入无法保证学习到有意义的时间表示,因为模型会根据下游任务的预测损失来简单地优化表示。w/o TDL 和 w/o PDF 的结果表明,时间差异学习和周期判别函数对于时空预测都是至关重要的。此外,Time2vec 和 CTR 的结果表明,时间嵌入和时间差异学习的结合更适合该模型。w/o enc-dec 的结果表明,通过多个时间步递归地预测未来值,有助于模型更好地捕捉时空依赖性。表3 数据集HZMetro与SHMetro上的消融实验参数敏感性:本文分析了三个关键参数的影响:节点嵌入维度 dν、时间嵌入维度 dτ和损失权重因子 λ。从图3中可以看出,随着维度的增加,性能持续提高,除了在维度为 64 时(红线)出现轻微波动。TGCRN 在具有较大节点嵌入维度和较大时间嵌入维度时,可以包含更多关于图拓扑和其动态的信息,但同时也会占用更多的参数,这会导致过拟合和更高的计算成本。因此,找到合适参数的一个好的做法是权衡性能和计算成本之间的关系。图 4显示了在 λ=0.1附近的折线出现明显的转折点,这证明了时间差异学习可以相互促进学习到的时间感知图的可解释性和性能的有效性,但不建议将辅助任务的比例设得太大。 论文介绍了TGCRN,一个用于预测空间相关时间序列的新框架。该框架第一个考虑到空间相关时间序列的周期性和趋势动态以进行时间序列预测的研究。作者提出了一种有效的方法,称为时间感知图结构学习,用于利用时间相关的变量间的规律性相关性,并将其表示为图结构。此外,本文提出了 GCGRU 来联合捕捉动态的空间和时间依赖性。最后,作者开发了一个统一的框架,采用编码器-解码器架构,将所提出的图结构学习和 GCGRU 集成在一起,以输出多步预测。在多个真实世界数据集上进行的实验验证了TGCRN相较于最先进的方法表现更优。 | 重庆大学计算机科学与技术专业 (弘深) 2022级本科生,重庆大学Start Lab团队成员。主要研究方向:时空数据挖掘、AI4DB | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有3~5名研究生名额,欢迎计算机、GIS等相关专业的学生报考!
图文|尚游
编辑|李佳俊
审核|李瑞远
审核|杨广超