MD在多个科学领域广泛应用,包括材料科学、生物化学、生物物理学和结构生物学,MD模拟生成大量数据,模拟涉及大量原子(可能高达数万亿)和大量时间步长(高达数亿)。本文是数据库领域顶会ICDE的论文《MDZ: An Efficient Error-bounded Lossy Compressor for
Molecular Dynamics》,论文引入了一个自适应的错误有界有损压缩框架,名为MDZ,该框架旨在保持受控错误水平的同时高效压缩MD模拟数据。

I.介绍
MD模拟被广泛应用于多个领域,包括生物物理学、结构生物学和物理学。科学数据通常可以分为三种类型,包括粒子数据、结构化网格和非结构化网格。MD模拟是最重要和典型的基于粒子的研究之一。随着MD模拟计算规模的增加,模拟期间生成的数据量也急剧增加。
随着科学数据量的迅速增长,科学数据集存储系统面临着重大挑战。为了进行方便的事后分析、管理和传输,科学应用通常将大量数据以文件形式进行存储。为了有效应对存储、管理和传输的挑战,降低生成数据的体积显得尤为重要,通过高效地减少数据量,可以大幅度减轻对存储系统的负担。
设计面向分子动力学(MD)数据集的高效、误差有界的有损压缩器面临多重挑战。首先,MD模拟中的快照可能包含大量粒子,需要进行批处理压缩,因此依赖于时间序列模式的压缩器表现不佳。其次,快照数据通常不平滑,难以使用现有的基于空间数据高平滑性的先进有损压缩器。最后,MD压缩器难以有效利用速度信息来帮助压缩位置数据。为应对这些挑战,论文提出了一种新颖的误差有界有损压缩器,特别适用于MD模拟。
II.相关工作
在科学领域,无损压缩器如Google
Brotli和Facebook Zstandard在工业数据管理系统等领域得到广泛应用。然而,在处理科学数据集时,由于其特殊性质,尤其是浮点数的随机性质,无损压缩的效果通常较差。科学数据集中的随机结尾尾数使得无损压缩器难以捕捉重复模式,因此有损压缩成为更高效的解决方案。有损压缩通过舍弃一些数据信息实现更高的压缩比,在科学领域可能更为有效。
与无损压缩不同,有损压缩在一定信息损失的情况下可达到更高的压缩比。在数据库系统中,已经采用了一些使用有损压缩的方法,例如ModelarDB是一个内置有损压缩的时间序列管理系统,ModelarDB使用基于窗口的方法为每个数据段找到最佳算法;SummaryStore是一个近似的时间序列存储,当达到空间限制时合并旧数据;除了时间序列数据库外,也有一些针对GPS轨迹数据系统的有损压缩研究。
但是数据库系统中的有损压缩器不适合MD数据集。首先,ModelarDB等时间序列数据库使用简单的数据估计方法,没有量化或熵编码过程,因此在MD数据集上的压缩比较低。其次,GPS轨迹压缩器也不适合用于MD数据集,因为MD数据比GPS数据更不受约束。第三,许多数据库系统(如SummaryStore)没有错界设计,因此它们不能保证解压缩数据的质量满足用户的要求。即使是用于科学应用的一般有损压缩器,如ZFP和SZ-Interp,在MD数据集上也表现出次优结果,因为它们是为三维数据设计和优化的。而MD数据集是二维的,并且被分成批次进行压缩。由于上述限制,研究人员正在研究专门为MD数据集设计的有损压缩器。
III.研究背景
A.MD 模拟
MD 是一种 N 体模拟,广泛用于探索材料在纳米尺度上的行为。如图所示,单个MD模拟通常涉及许多时间步长,其中每个时间步长根据原子间力的复杂计算来预测每个粒子的新位置和速度。力计算通常消耗绝大多数计算时间,在根据计算力调整原子位置(如突出显示的箭头所示)后,应用边界条件并协调或计算和写出感兴趣的物理量。
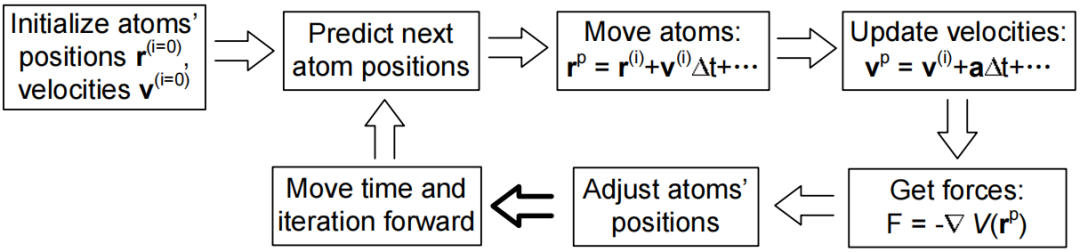
图1经典MD模拟的说明
典型的MD输出主要是沿轨迹存储坐标信息。每个粒子的位置由三个轴(x, y, z)组成,这就是为什么大多数现有的有损轨迹压缩器关注的是位置而不是速度。因此,在下文中,压缩的目标仅是粒子的位置(x, y, z)。
B.SZ误差有界有损压缩框架
文章提出的压缩技术建立在SZ有损误差有界压缩框架的基础上。SZ 框架支持定制的预测阶段,因此能够利用 MD 特定于应用程序的特征和模式来提高压缩质量。SZ 通过四个关键步骤进行,如图所示:(1)数据预测,(2)线性尺度量化,(3)熵编码(即霍夫曼编码)和(4)无损压缩(例如,Zstd)。在大多数应用中,调整第一步对于在特定应用中实现高压缩质量至关重要,因为更高的预测精度将产生更好的量化箱分布,从而在霍夫曼编码下产生更高的压缩比。

图2 SZ压缩框架的说明
IV.问题表述
研究问题可以表述如下:假设一个MD模拟数据集(用D表示)由M个快照组成,每个快照包含N个粒子,在模拟过程中,原子位置(表示为三个轴值{x, y, z})需要存储到磁盘上。论文的研究的目标是在保持足够快的压缩和解压缩速度以进行MD模拟的同时,最大化压缩比,并批量处理M个快照,而不是一次性压缩整个数据集D。
基于上述问题定义,传统的纯轨迹压缩方法是不适合的,因为它们需要收集大量的快照进行压缩,并且解压缩任何一个快照都需要解压缩之前的所有快照。此外,基于单快照的压缩也不是一个理想的解决方案,因为空间粒子数据的非光滑性会导致压缩比较低。为了解决这些问题,论文提出了MDZ,它充分利用了MD数据集在空间和时间维度上的特征,显著提高了压缩比。
V.MD数据集的调查
A.使用的 MD 模拟。
表 I 总结了以下考虑的八个 MD 模拟数据集。
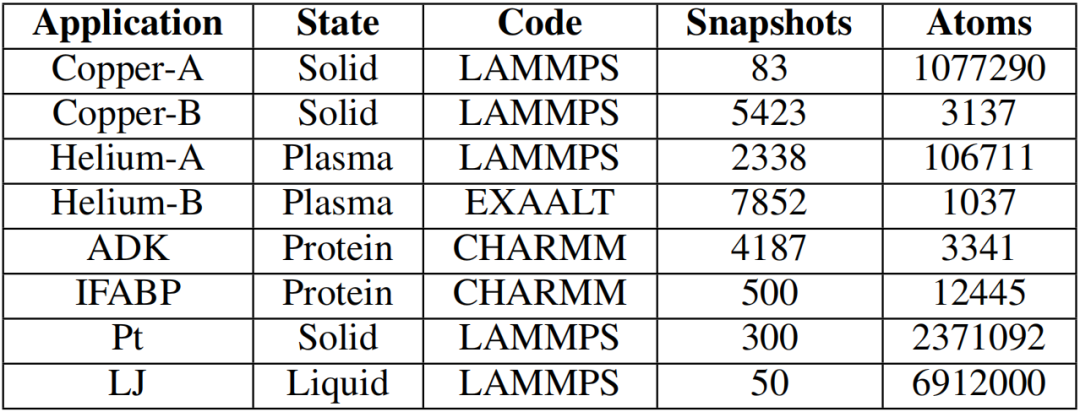
表I 本文研究中的Md模拟数据集
B.空间特征的表征。
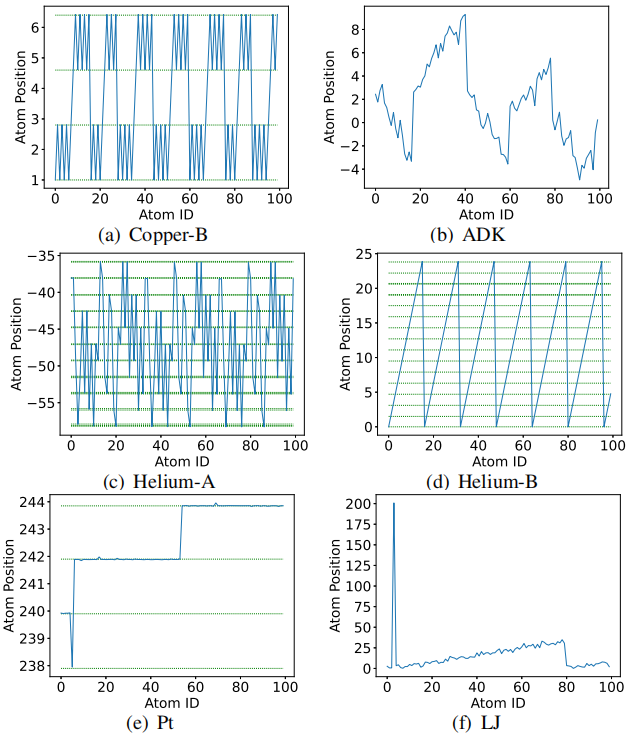
图3 数据的空间相关性的演示
要点1:第一个关键观察是,在许多情况下,MD 数据集在空间域中表现出各种模式。由于空间限制,文章给出了六个典型示例(包括 Cop-B、ADK、Helium-A、Helium-B、Pt 和 LJ),以证明图3中的不同空间模式。如图所示,数据集可能表现出稳定的锯齿形图案(图3 (a) (d))、不稳定的锯齿形图案(图3 (c) (f)、楼梯图案(图3 (e))或随机图案(图3 (b))。
要点2:本文还从图3(a) (c) (d) 中观察到,在许多情况下,数据在整个值范围内聚类成几个等距的离散级别。事实上,对于所有在特定级别上进行聚类的数据点,它们的位置实际上在小范围内振动,并且不是严格恒定的。这些常规模式来自底层材料的晶体结构。
要点3:根据图3,了解到原子坐标可能在整个数据集中从一个离散级别跳转到另一个相邻的级别。由于许多基于预测的压缩器,如SZ,仅仅依赖于前面的数据点来预测每个数据点,而没有显式使用离散级别信息,因此在这种情况下,其预测精度较低,导致较低的压缩比。
C.时间特征的表征
没有突出空间模式的数据集通常表现出特定的时间相关性,可用于实现非常高的压缩比。图 4 显示了时间维度中的位置数据(即原子的轨迹位置) 用于六个数据集。很明显,数据值在时间维度上总是表现出或多或少的相关性。总结有两个相关级别:
(1) 某些数据集(例如Cop-B、ADK和Helium-B)的数据可能相对广泛且频繁变化。
(2) 某些情况下,数据可能会略有变化(例如 Helium-A、Pt和LJ)。
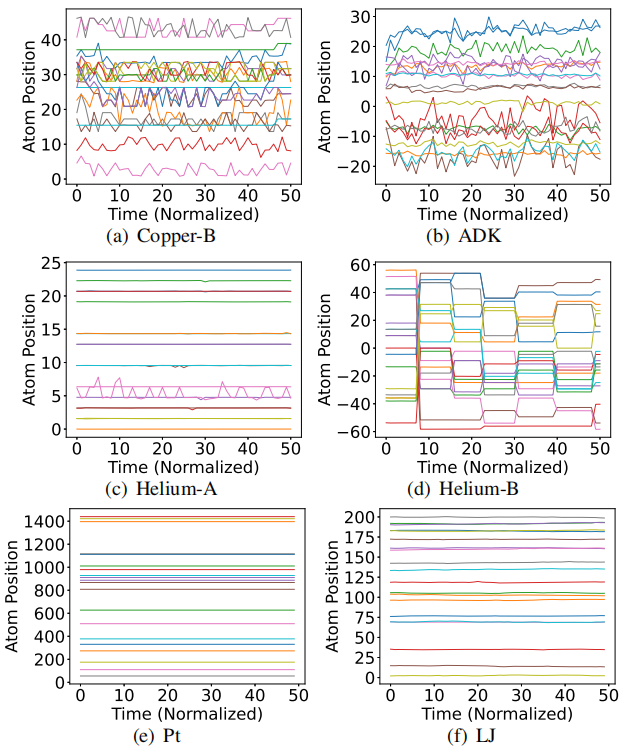
图4 证明原子位置数据中的时间相关性,时间归一化为0-50
要点 4:一个非常有用的观察是,对于表现出低空间模式的数据集,例如 Pt 和 LJ,它们通常在时间维度上具有极强的数据平滑度,并且绝大多数数据在整个模拟过程中在时间维度上非常接近。
基于在表征中探索的四个重要结论,论文为不同的 MD 数据集开发了一种自适应误差有界有损压缩器,可以显着提高现有最先进的 MD 压缩器压缩比。
VI. MDZ:MD 数据集的自适应误差边界损失压缩器
基本设计思想是从三个最适合空间和时间维度上的不同数据特征的压缩器中选择最好的方法。图5总结了MDZ的设计。要压缩的快照存储在缓冲区中,缓冲区大小(BS)定义为缓冲区中要保留的最大快照数量,压缩后的数据将存储到并行文件系统(PFS)中。整个压缩流程包括四个关键步骤:预测、优化量化、编码和Zstd,遵循经典的SZ压缩框架。论文的主要贡献包括对预测和量化阶段的改进。
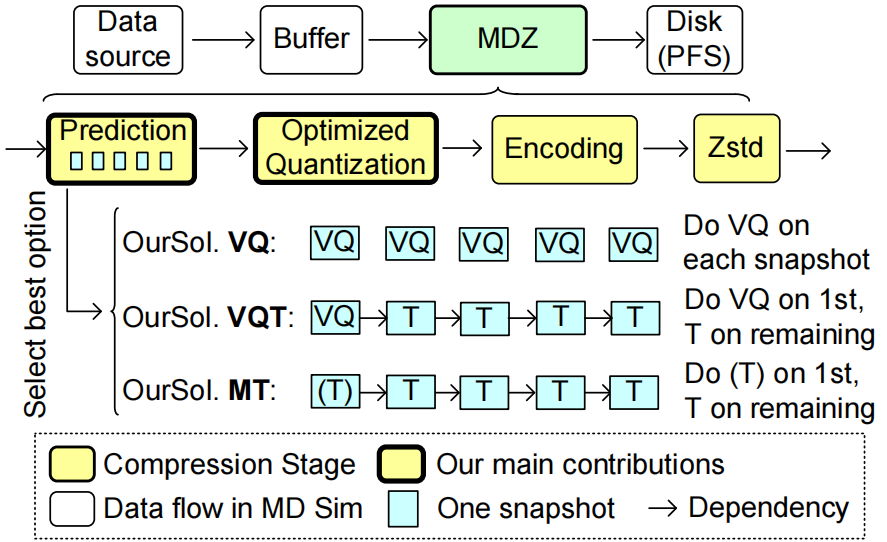
图5 设计概述
具体来说,文章设计了三种有效的MD数据预测策略,以适应MD数据集中不同的数据模式:
(1)基于矢量量化的压缩器(简称VQ):VQ压缩器完全根据空间信息预测数据值,因此任何快照的数据预测对任何其他快照都没有依赖关系,这样任何快照数据都可以非常快地解压缩,而不需要解压缩其他快照。这在时间维度平滑度非常低的数据集上特别有效(见图 4 (a) (b))。
(2)基于矢量量化时间的压缩器(简称VQT):VQT压缩器在缓冲区的第一个快照上采用VQ预测器,并对缓冲区中的所有剩余快照采用基于时间的预测器。该方法专为具有平滑时间维度的数据集而设计,并且在空间中具有很强的多峰分布模式(见图5 (c)和(d))。
(3)基于多级时间的压缩器(简称 MT):MT 压缩器采用一种特殊的数据预测方法——称为基于初始时间的预测(如图6中的符号(T)),并将普通基于时间的预测器应用于缓冲区所有其他剩余快照。这种方法在时间维度上具有非常高的平滑度的数据集特别有效(见图4(e) (f))。
以下为具有优化预测和量化方法的压缩器。
A.基于矢量量化的压缩(VQ和VQT)
VQ算法的基本思想是利用V-B节中描述的空间模式(即要点2和要点3)。要点2表明数据聚类成不同的大致相等距离的离散水平,这促使文章使用每个聚类的质心(aka, center)来预测该聚类内的所有数据值。
图7中说明了VQ压缩算法的关键步骤(数据预测和量化)。图中显示了数据集的片段(i=10→26)。如前所述,数据值聚集在不同的水平上,振动较小,因此文章使用相应水平的质心值来预测每个数据点。因此,量化仓(见图中红色数字3)是根据预测误差(即di−Vi)计算出来的,用向量B存放量化仓,用向量J存放相对索引数。稍后,它们都将被霍夫曼编码压缩。
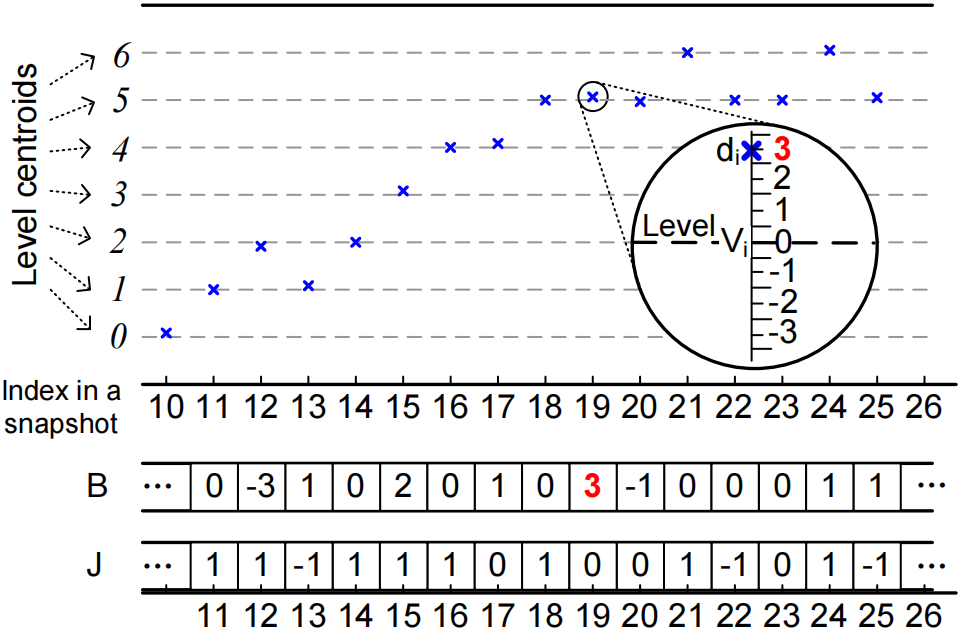
图6 基于VQ的预测+量化的说明
与耗时的 2D K-means 问题不同,将N个排序的一维数据点优化划分为K个组具有多项式时间复杂度解。将排序的数据点定义为d1, d2,..., dN,聚类成本作为数据点与其质心点之间的距离之和。在公式 (1) 中,定义Cost(l, r)为聚类的最优代价d1,…,dr到一组,F (n, k)作为聚类的最优代价d1,…,dn到k组,H(n, k)作为最小化F的参数。
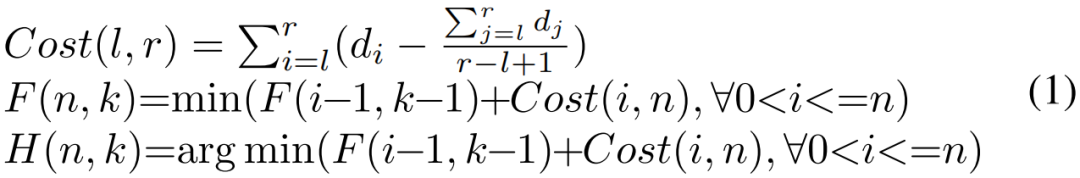
聚类的边界可以从H迭代恢复。求解F (N, K)的na ̈ıve实现具有O(KN2)的时间复杂度,本文采用了一种将计算成本优化为O(KN)的解决方案。
在示例中,集群的数量K是未知的,数据点没有排序。为了提高性能,一方面,在整个模拟过程中只计算一次F,文章在采样数据集上计算它,该数据集具有来自第一个快照的 10% 个数据点。另一方面,请注意 F (N, 1), F (N, 2),…, F (N,
K) 在计算 F (N, K) 时按顺序计算。令G(k)=F(N,k)/F(N,k-1);如果G(κ)显着低于G(κ − 1),则在 κ 处停止F的计算。K的最大测试值设置为150,因为更多的集群会损害矢量量化索引的压缩比。使用从H获得的边界计算水平距离λ和初始水平值μ。
对于VQ压缩方法,文章对每个快照采用VQ算法,如图5所示。相比之下,VQT压缩方法只对每个缓冲区中的第一个快照应用VQ算法,而缓冲区中的所有其他快照将被经典的基于时间的压缩所压缩。具体来说,每个后续数据点将使用前一个时间步中的相应数据值进行预测。这可能会显著提高压缩比,特别是在时间维度上数据相对平滑的情况下(见图4 (c)-(f))。
B.多级基于时间的压缩(MT)
论文提出了一种额外的误差有界压缩方法-称为多层时间压缩(MT),它对时间维度上具有极高平滑度的数据集特别有效。
MT压缩算法也采用了基于预测的压缩模型。MT的特殊设计是缓冲区中的第一个快照将基于整个数据集的初始快照进行预测,这是由于某些数据集中所有模拟快照与初始快照之间存在非常强的相关性。图7显示了所有快照与初始快照(即快照0)的相似度,相似度定义如公式(2)所示。
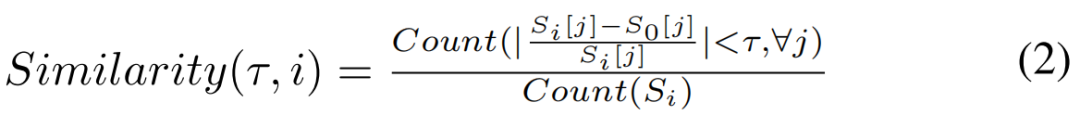
其中τ为阈值,Si为快照i, Si[j]为快照Si中的第j个数据点。相似性公式计算基于某些阈值τ的“未改变”数据点(原子)的百分比。该图清楚地表明,某些数据集中(如Copper-A和Pt)的后续快照总是与初始快照极其相似。
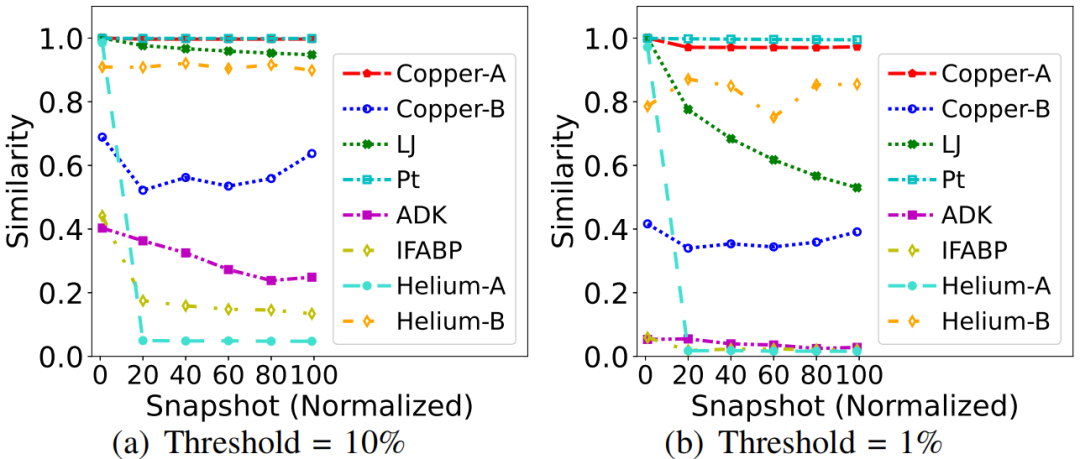
图7 快照与快照的相似性-0(快照归一化为0- 100)
使用特定的基于快照0的预测,预测误差可能远低于Lorenzo-predictor等传统空间预测误差,如表II所示。
C.线性尺度量化优化
在本节中,通过调整两个量化设置来优化线性尺度量化步骤,以进一步提高整体压缩性能和质量。
1)量化尺度的优化:在有损压缩中,作者优化了量化尺度,该尺度控制量化整数的值范围。不同的量化尺度设置会影响压缩比和压缩性能。通过实验证明,将最佳量化尺度设置为1024,可以在保持高压缩比的同时保持较高的压缩性能,确保了最佳的压缩/解压缩速度。
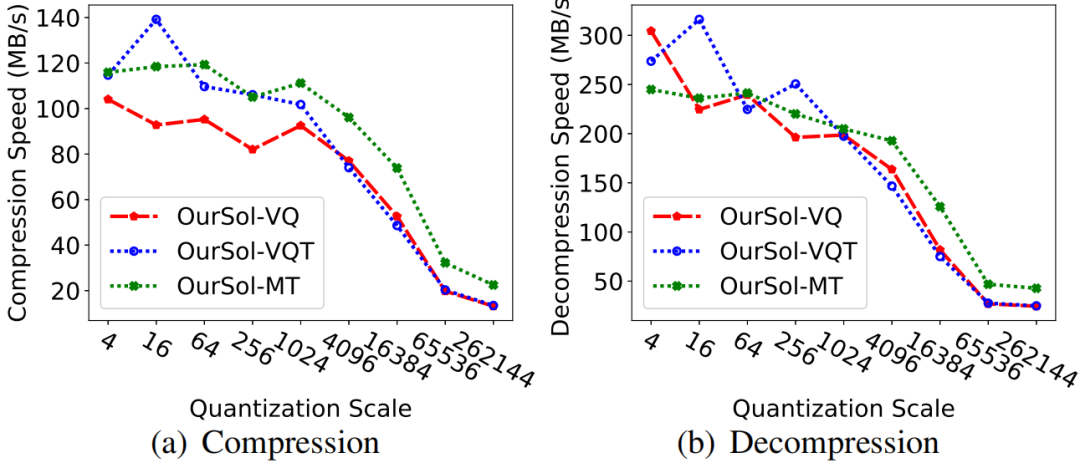
图8 Helium-b数据集量化尺度对压缩机性能的影响
2)量化序列的优化:在量化序列的优化中,研究人员比较了两种不同的序列存储方式:Seq-1和Seq-2。Seq-2方式首先存储一个快照中的所有粒子,然后再存储下一个快照,而Seq-1则是首先存储一个快照,然后再存储下一个快照的所有粒子。由表3可以得出,Seq-2在时间维度上稳定的情况下,尤其是当许多数据点在时间上保持不变时,具有更好的压缩比。因此,在解决方案中选择了Seq-2,提高了在不同轴上的压缩比。

表3 具有不同序列设置的HELIUM-B数据集的压缩比(CR),缓冲区大小(bs)=10(方法=mt)
D.最佳压缩机 (ADP) 的自适应选择
论文提出了一种自适应解决方案(ADP),该解决方案在运行时能够动态选择最佳的压缩器,包括VQ、VQT或MT。实验证明,数据模式在短期内保持不变,但从长远来看可能会发生显著变化。最佳的压缩器在不同的快照上可能表现出优势,如图 9 (a) 所示,MT 在快照400 之前具有最高的压缩比,VQT成为该快照后的最佳压缩器。因此建议通过评估三个压缩器并选择在每个快照上表现最好的压缩器。
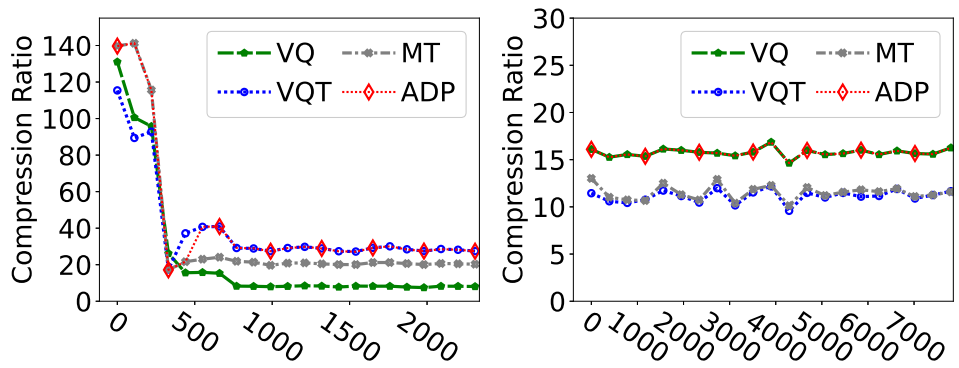
图9 短期内平稳CR和长期内多样化CR的说明(BS=10)。ADP可以在所有的快照中选择最好的压缩机。
VII. 实验评估
A.实验设置
实实验评估了八个真实的分子动力学(MD)模拟数据集。为了与有损压缩器进行比较,实验还评估了六个最先进的无损压缩器,包括Zstd、Brotli和Zlib等广泛用于数据库和文件系统的工具,以及专门针对浮点数据格式的ZFP、Fpzip和FPC等科学数据集的最先进无损压缩器。实验还将提出的解决方案与两个MD数据压缩器、两个广泛使用的科学数据压缩器以及两个最先进的时间序列压缩器进行比较。
B.无损压缩机评价结果与分析
首先评估了六种最先进的无损压缩器,所有无损压缩器都具有极低的压缩比(大约 1∼2)。结果证实无损压缩器不适合科学应用。
C.有损压缩器的评价结果与分析
1)压缩比:
图10展示了本文的解决方案的压缩比。可以观察到ADP在本文的解决方案中具有最高的压缩比不同的数据集和缓冲区大小设置。它进一步证实ADP 可以在运行时从 VQ、VQT 和 MT 准确选择最佳压缩器。
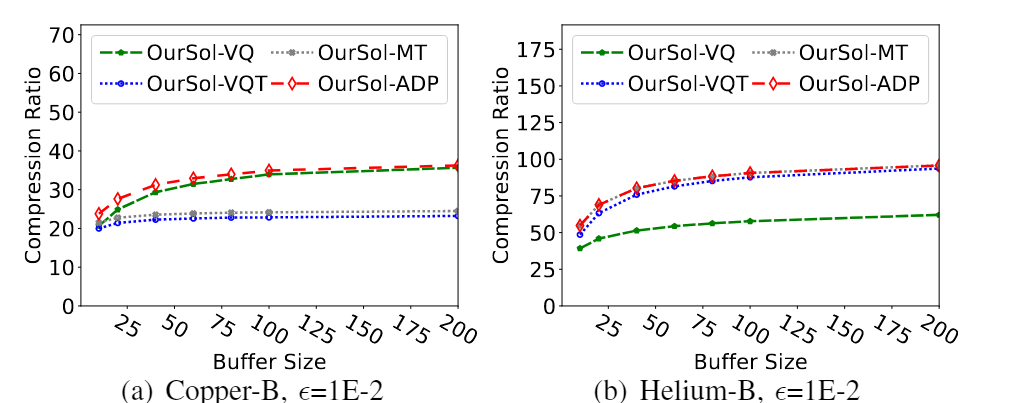
图10 在不同的数据集和缓冲区大小(BS)设置下,本文的自适应解决方案(ADP)比VQ、VQT和MT具有最高的压缩比,因为ADP总是能够准确地选择最佳的压缩方法
图11的实验中,本文的有损压缩解决方案在不同缓冲区大小设置下始终表现出最高的压缩比,对比其他压缩器有着显著的提升。
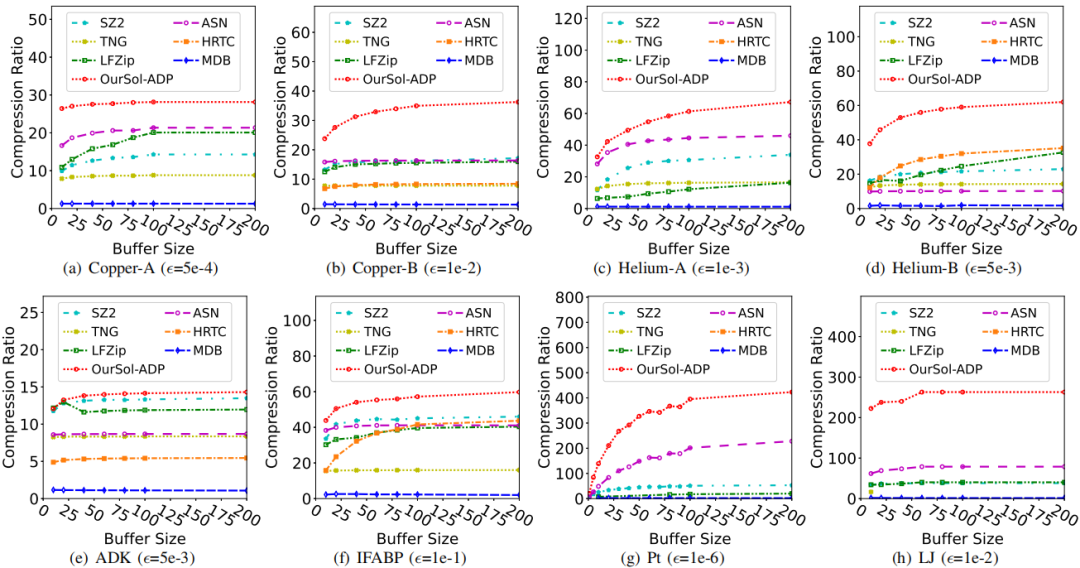
图11本文的解决方案在所有数据集上具有最高的压缩比
2)速率-失真
图12呈现了所有有损压缩器的速率-失真结果。清晰可见,本文的解决方案在相同比特率下具有最佳的PSNR(在大多数情况下提高了约20dB),并且在相同PSNR下具有最低的比特率。
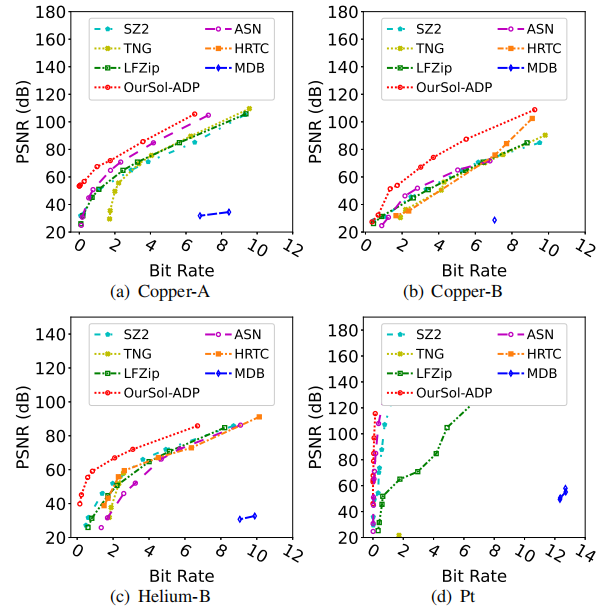
图12速率失真图显示本文的解决方案有最佳压缩质量
3)压缩错误:在有损压缩方面,本文使用最大压缩误差(MaxError)和归一化均方根误差(NRMSE)这两个关键指标评估了不同压缩器的性能,以Copper-B数据集为例。如图13显示,本文的解决方案在所有轴上均表现出最低的MaxError和NRMSE,这些结果验证了本文的解决方案在保持压缩质量的同时维持了数据的物理准确性。
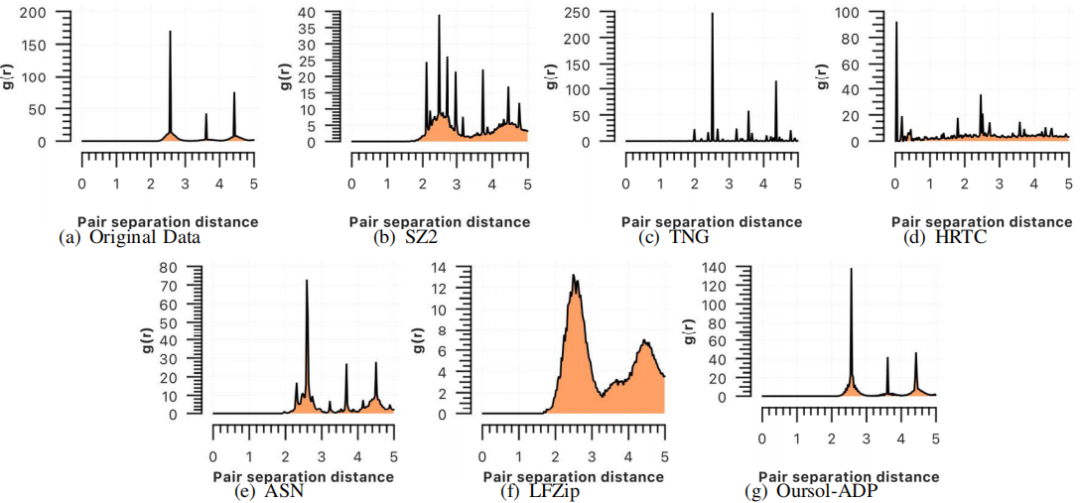
图13只有本文的解决方案在解压缩数据(Copper-B,CR=10,BS=10)上得到正确的径向分布函数(RDF)
4)压缩/解压吞吐量:在图14中,展示了所有有损压缩器的吞吐量比较。显然,文章的解决方案在所有数据集上都是所有有损压缩器中最快的之一。
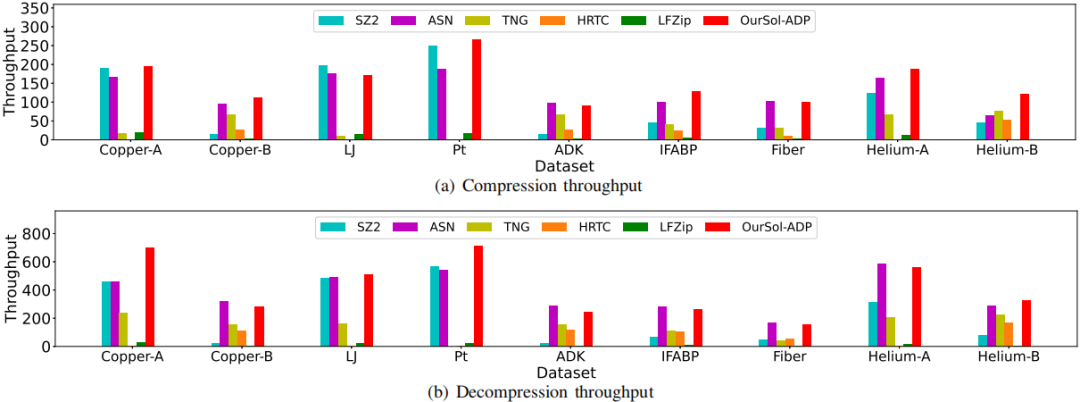
图14 本文的解决方案是唯一一个在所有数据集上始终具有高压缩/解压吞吐量(MB/s)的解决方案。
VIII. 总结
在本文中,作者开发了一种有效的误差有界有损压缩器(称为MDZ)用于MD仿真数据集。其关键思想是基于数据在空间和时间维度上的规律性和相关性来显著提高预测精度。论文提出了基于矢量量化的压缩器VQ和VQT,以及基于多电平时间的压缩器MT,自适应解决方案ADP可以在运行时动态选择最佳压缩器(VQ、VQT或MT)。
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!

图文|许熠
编辑|李政
审核|李瑞远







