最大影响(Max-Inf)查询是空间数据管理中的基础操作。给定一组加权对象,该查询旨在从候选集中找到一个最优位置,以最大化其影响力,即其反向最近邻的总权重。现有的研究通常假设每个对象都在固定的位置上。然而,在现实生活中,有许多驱动服务(例如,餐厅、加油站、自动取款机等)被移动用户(即轨迹)广泛访问,而不是固定的。在轨迹数据中解决Max-Inf查询(MIT)是紧迫和具有挑战性的。本次为大家带来数据库领域顶级会议ICDE的论文:《Towards
Efficient MIT query in Trajectory Data》
随着GPS技术的发展和移动设备的普及,轨迹数据逐渐成为研究的热点之一。轨迹数据可以描述个体或物体在空间上的移动过程,广泛应用于位置服务、交通管理、环境监测、人口流动等领域。与传统的空间数据不同,轨迹数据包含了时序信息,使得数据量巨大、复杂度高,同时也提供了更多的研究价值。其中,最大影响时间(Max-Inf Time)查询是轨迹数据分析中的一个重要问题,指的是在一个时间范围内,查询哪些设施对给定的轨迹有最大的影响。这个问题具有很高的实用性,可以应用于物流路径规划、城市交通分析等场景。然而,MIT查询面临着一些挑战,主要包括:1)轨迹数据量大,难以高效处理;2)设施的数量可能很大,导致搜索空间巨大;3)轨迹的活动区域和移动模式不一定能够很好地对应到设施,造成查询精度降低。为了解决以上问题,研究者提出了一种基于QB-Tree的混合索引方法,该方法可以将轨迹数据按照活动区域和移动模式进行分组,以便更加高效地处理。同时,该方法还采用了分支界定算法(Branch-and-Bound
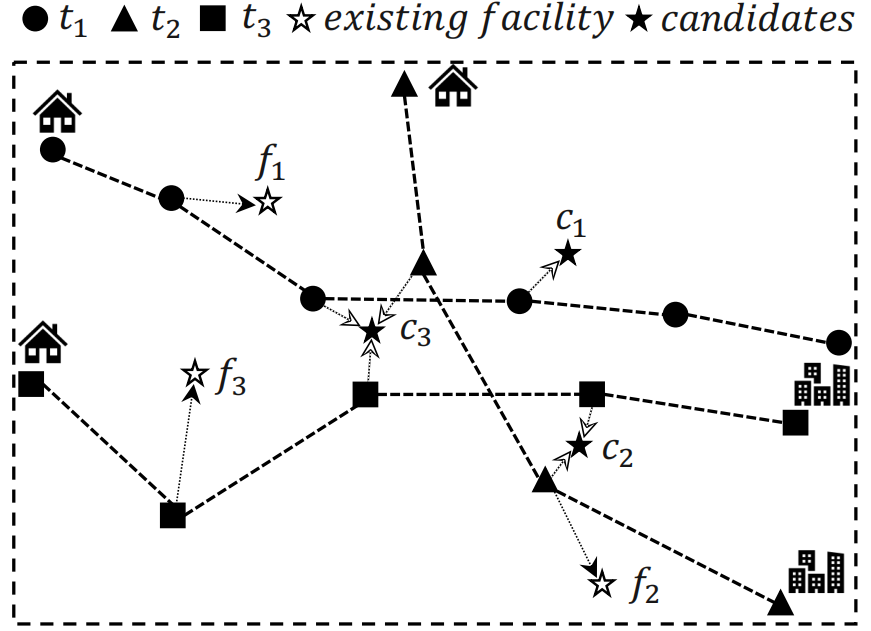
Algorithm)来快速搜索最大影响时间,并利用三级剪枝技术来估计候选设施的上下界。该方法经过了大量实验验证,证明了其在处理轨迹数据时的高效性、可扩展性和通用性。Max-Inf查询是在空间数据中查找具有最高影响力的位置,被广泛应用于基于位置的服务中。图1显示出了针对3个单位加权用户轨迹{t1,t2,t3}、现有设施{f1,f2,f3}和候选设施{c1,c2,c3}的MIT查询的示例。如果c 是t 的最近邻居,则用户t 将受到候选设施c 的影响。因此,c1 影响轨迹t1,c2 影响t2 和t3,c3 影响所有三个轨迹。因此,图 1 中的候选设施 c3 是MIT 查询的最佳解决方案。
此外,还研究了Max-Inf查询的其他变体,如在移动对象上的概率Max-Inf查询、连续MaxRS查询、MaxBRkNN查询等。研究人员们开发了各种近似和精确算法,以平衡查询效率和结果准确性。对于MIT查询,这些算法并不能高效地处理,因为它们假设候选项是与现有设施相辅相成而不是竞争的。本文提出了一种基于连续轨迹的MIT查询,以高效地找到具有最高影响力的位置,解决了一些实际问题。问题定义:给定一个在二维空间R2中的加权轨迹集合T,其中轨迹t记录一个点序列,表示为t =< p1,p2,…,pn>,其中pi =(xi,yi)是笛卡尔坐标系中的点。文章假设不同的轨迹与不同的用户相关联。在现实生活中,对于某种服务(例如,汽车快餐),不同的用户具有不同的重要性(例如,潜在购买力)。设w(t)为轨迹t的权重,表示用户的重要性。文章还定义轨迹t与设施f之间的距离d(t, f)为:其中distϵ(pi, f)表示pi和f之间的欧几里得距离。定义1(影响):给定一个轨迹t =
<p1,p2,…,pn>和R2中的一个现有设施f∈F,t被f影响(吸引),即f是t的吸引子,对于t,当且仅当∀f′∈ F\{f}, d(t, f′) ≥ d(t, f)。令 ad(t) 为轨迹t∈ T 的吸引子距离,即:定义 2(潜在影响权重)给定一组候选设施C和一组加权轨迹T在R2,对于任何候选 c ∈ C,潜在的影响权重c是受c影响的所有轨迹的总权重,即:定义 3(MIT 查询)给定一组现有设施F,一组候选C和一组加权轨迹T在R2中,MIT 查询找到一个最佳位置c∗∈ C 到最大化潜在影响权重,定义为:显然,Max-Inf 查询是 MIT 查询的一个特例其中每个轨迹的权重为 1,并且只包含一点。MIT 查询的一个直观解决方案是详尽地比较所有可能的候选轨迹对。然而,这种方法在大规模轨迹中非常昂贵。启发作者的两个关键观察结果如下:(i)具有相似活动区域和运动模式的轨迹可能会受到同一设施的影响,(ii)轨迹通常不受距离它们相对较远的设施的影响。文章提出了一种高效新颖的索引 QB‑tree,以实现高效的查询处理。QB-tree 是一个集成了四叉树、哈希桶和排序列表的三层索引。四叉树划分空间来分层组织空间相似的轨迹。哈希桶进一步对同一节点内的轨迹进行分类。(1)四叉树Qt:Qt利用[1]中算法将空间递归划分为四个不相交的子空间,然后将不同位置和长度的轨迹划分到Qt中的不同子空间(节点),每个节点代表R2中的一个矩形区域。QB 树的关键思想是采用分层组织策略将空间相似的轨迹分组在一起。具体来说,对于任何轨迹t ∈ T,其MBR表示为MBR(t),t存储在Qt 完全覆盖MBR(t) 的最小节点中。给定用户指定的阈值α,它控制QB 树的高度。直到该节点存储的轨迹数不大于α,或者不存在经过当前节点的多个子节点的轨迹时,终止对该节点的划分。对于QB 树的节点 Ni,它的形式是(MBRi ,ad , ad, ws, ptr)。 (i) MBRi 是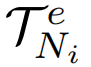 中所有轨迹的最小边界矩形。(ii)
中所有轨迹的最小边界矩形。(ii)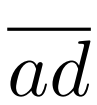 是
是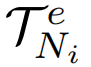 中轨迹的吸引子距离的上限,即:(iii)ad是 T 中轨迹的吸引子距离的下限,即:(iv)ws表示
中轨迹的吸引子距离的上限,即:(iii)ad是 T 中轨迹的吸引子距离的下限,即:(iv)ws表示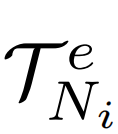 中轨迹的权重和,即:
中轨迹的权重和,即:
(v)ptr是指向存储 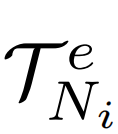 轨迹的桶的指针图(a)显示了单位权重轨迹T = {t1, t2,
..., t9} 的四叉树分割示例,假设α = 2,首先将节点N 划分为N1, .., N4。那么TSN = {t1, t2, t3} .由于N4只包含一条轨迹,并且N1和N3中没有包含轨迹,这些节点不需要进一步划分。TsN4 = {t8}。N2是进一步划分为四个节点,TsN2 = {t4,
t5, t9}。然后,TsN23 ={t6, t7},划分结束。
轨迹的桶的指针图(a)显示了单位权重轨迹T = {t1, t2,
..., t9} 的四叉树分割示例,假设α = 2,首先将节点N 划分为N1, .., N4。那么TSN = {t1, t2, t3} .由于N4只包含一条轨迹,并且N1和N3中没有包含轨迹,这些节点不需要进一步划分。TsN4 = {t8}。N2是进一步划分为四个节点,TsN2 = {t4,
t5, t9}。然后,TsN23 ={t6, t7},划分结束。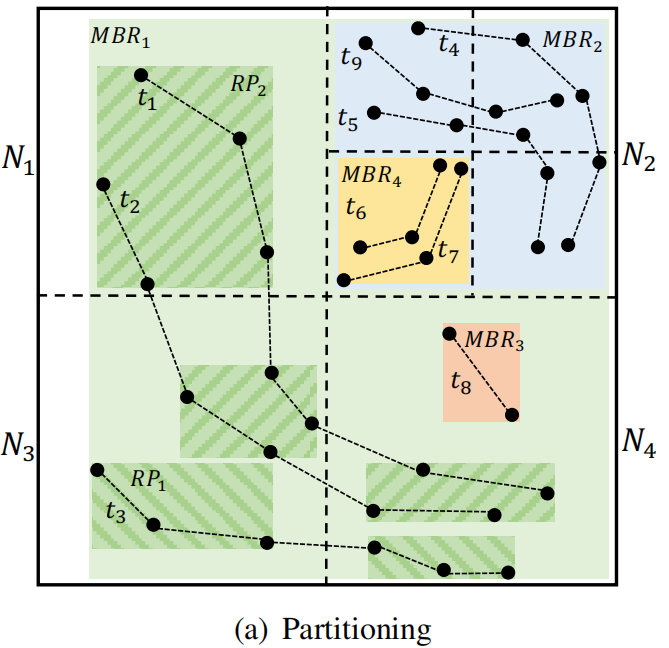
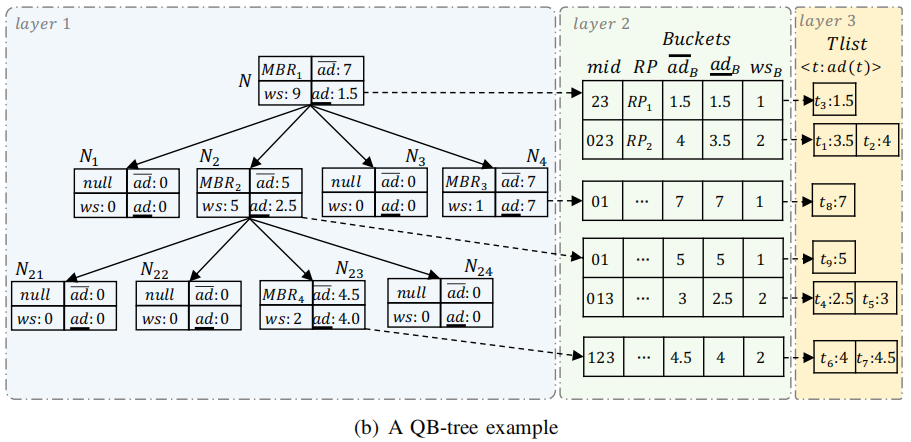
(2)哈希桶Bh:由于包含大量不相关的区域,轨迹MBR 过于粗略,无法有效剪枝MIT 查询的不必要计算。具有相似轨迹的MBR运动模式(例如,图(a) 中的t1、t2)包含类似的内容不相关的领域。受此启发,文章在同一个节点中根据他们的运动模式对存储的轨迹进行分类,然后,对同一桶内的轨迹构造直线多边形,以大大减少不相关的MBR 中的区域。给定一个 QB 树节点Ni,对于∀t∈TsNi,文章使用基于Morton的方法对t的mid进行编码,它简要描述了它的运动模式。然后,将TsNi 中具有相同mid的轨迹散列到相同的桶B 中,表示为 TB,即: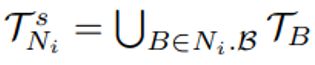
具体来说,Ni中的桶B 是以下的五元组(RP、adB、adB、wsB、Tlist)。(i)RP 是构建于TB之上的直线多边形,注意TB中的所有轨迹都通过Ni的多个相同子节点,不失一般性,文章假设这些子节点是NB={Ni1, ..., Nim},然后,∀t ∈ TB, t被分成m个子轨迹st1, ..., stm,分别圈在Ni1,...,Nim。TB 被子区域Nij ∈NB切割的子轨迹集表示为 STBNij = {stj | ∀t∈ TB}。则B 的直线多边形RP 表示为:可以通过联合子轨迹集的所有MBR 来计算。(ii)adB是TB里轨迹的吸引子距离的上限,即:(iii)adB是TB里轨迹的吸引子距离的下限,即:(v)Tlist 是一个有序列表,其中轨迹按吸引子距离的升序排序。考虑节点N,由上可知TsN = {t1, t2, t3}。在图 (b) 中,t1 和t2都经过三个编码为 0、2 和 3的子区域。不同的是,t3仅通过通过2和3的两个子区域。因此,t3被散列进入 mid = 23 的桶B1,t1 和t2 被散列进入mid= 023的桶B。每个桶的Tlist排序按ad升序排列。此外,RP1 和 RP2 是分别在B1 和 B2 上构建的直线多边形。算法 1 提供了构建QB 树的细节。输入由轨迹集T和用户指定的α 组成,它控制QB树的高度。在第 1 行,文章初始化QB 树的根节点。为了计算Qt 和Bh,文章遍历T中的所有轨迹。在第 2-9 行中,对于每个T中的轨迹t,首先以自上而下的方式找到包围t的最小节点node,同时更新MBR,ad,ad和ws在从根到存储t的节点的路径上。当遇到存储t的节点,根据t的中间节点将t插入桶中并更新直线。第 10-11 行中的多边形RP、adB、adB和wsB。如果节点是叶子节点,当满足以下两个条件时,(i)的个数节点存储的轨迹超过α,(ii)有轨迹在通过多个子节点的节点中,满足于同时,进一步拆分当前节点(第 12-14 行)。插入一条轨迹t:插入过程以自上而下的方式进行。首先定位包含t的最小节点N,并更新从root到存储t的N路径上的MBR、ad、ad和ws。然后,将 t 插入N的桶中,并以与构造过程相同的方式检查是否满足拆分条件(第 10-14 行)。删除一条轨迹t:删除过程与插入相反,分为以下三个步骤。Step1: 首先找到存储 t的节点N。同时,从根到N的路径上的任何节点的ws中减去w(t)。根据t的中值,文章从N的桶中删除t并更新RP、adB、adB和wsB。Step2:调整N.MBR使其紧紧包围TeN 中的所有剩余轨迹,然后更新N.ad和N.ad如下:Step3: 如果在步骤 2 中更新了 N的某些字段,文章需要迭代地对N 的父级执行步骤 2;否则删除终止。4.2 分支定界算法(Branch-and-Bound)Branch-and-Bound方法是一种搜索算法,通过分割搜索空间来快速找到最优解。该算法会将搜索空间分成多个子空间,然后根据一些特定的规则来选择哪个子空间先进行搜索。在这个过程中,算法会不断更新当前最优解,并剪枝那些不能产生更优解的子空间,以减少搜索空间的大小。论文中的Branch-and-Bound方法包括以下步骤:1. 预处理:对于数据集中的每个轨迹Ti,计算其与其他轨迹的相似度Sim(Ti,Tj),并将结果存储在相似度矩阵S 中。根据相似度矩阵,可以设置相似度阈值th,用于确定轨迹是否需要进一步计算。2. 划分子空间:将轨迹空间划分成多个子空间,每个子空间包含一部分轨迹。作者提出了一种基于簇的划分方法,称为Cluster-BB,该方法使用 K-Means 算法将轨迹划分成多个簇,并将每个簇视为一个子空间。每个子空间的上下界可以通过计算子空间内的轨迹与查询轨迹的相似度来得到。3.分支定界搜索:将轨迹空间划分成多个子空间后,可以对每个子空间进行分支定界搜索。搜索过程中,需要维护一个当前最优解best,用于剪枝和更新最终结果。具体而言,对于每个子空间C,可以计算其上下界LBC和UBC,其中: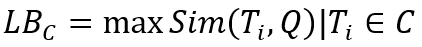 表示子空间中轨迹与查询轨迹的最大相似度;
表示子空间中轨迹与查询轨迹的最大相似度;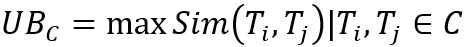 表示子空间内任意两个轨迹之间的最大相似度。如果UBC <= best,则可以剪枝,因为该子空间中的轨迹无法提供更优的解。如果LBC > th,则可以进一步划分该子空间。如果LBC <=
best且UBC > best,则需要在该子空间中搜索,以查找可能更优的解。4.更新最优解:在搜索过程中,如果找到一个比当前最优解更优的解,则需要更新最优解best。具体而言,如果查询轨迹与当前轨迹Ti的相似度Sim(Q,Ti)大于当前最优解best,则更新best =
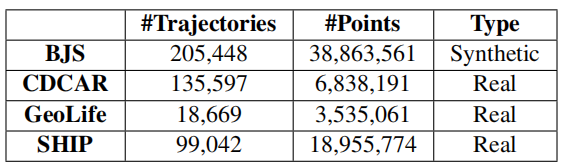
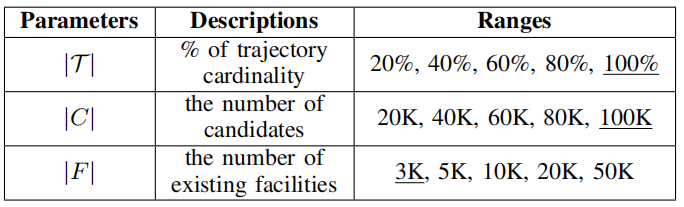
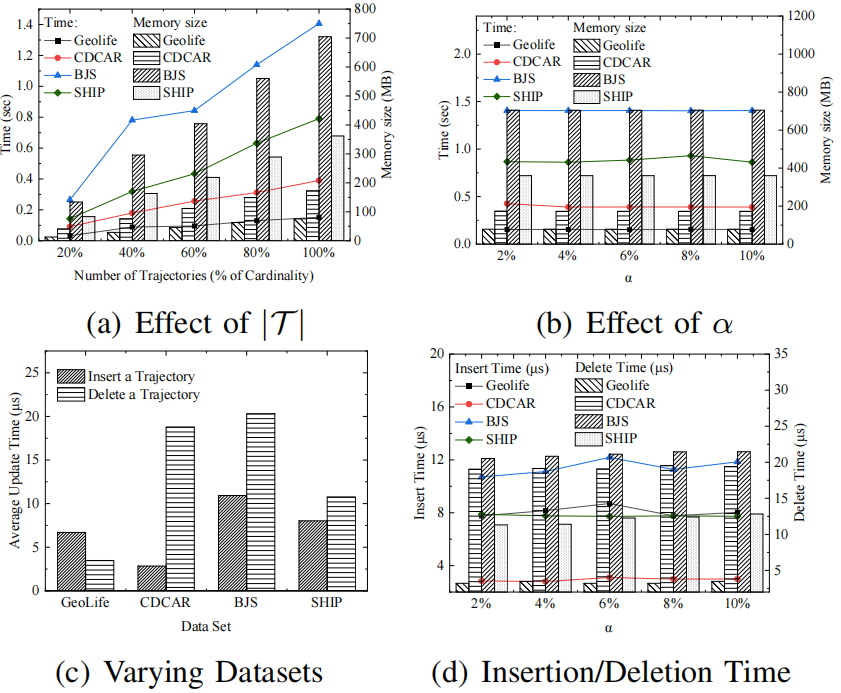
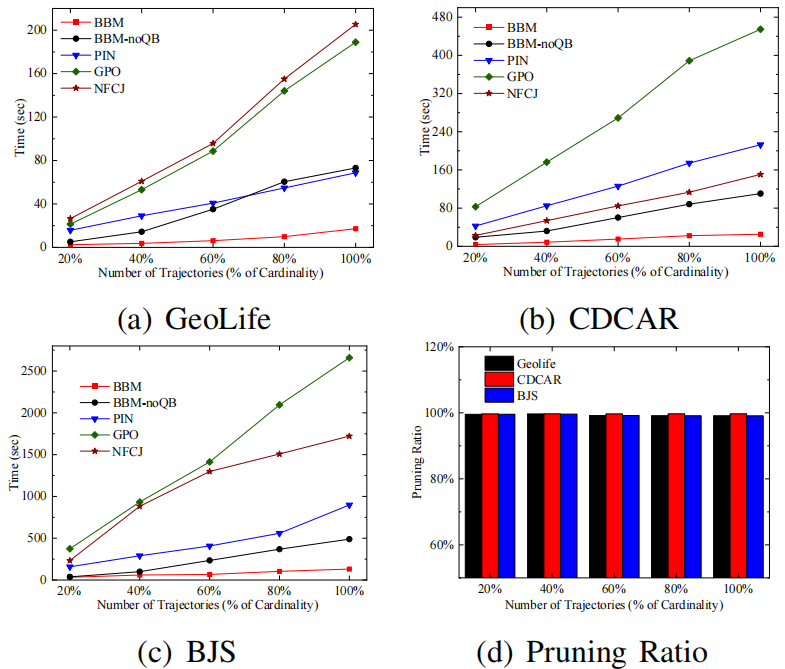
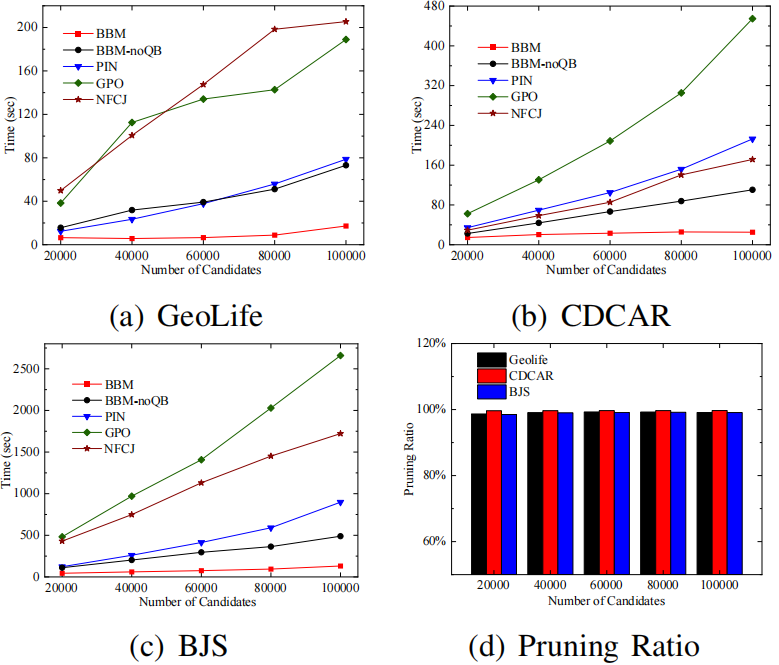
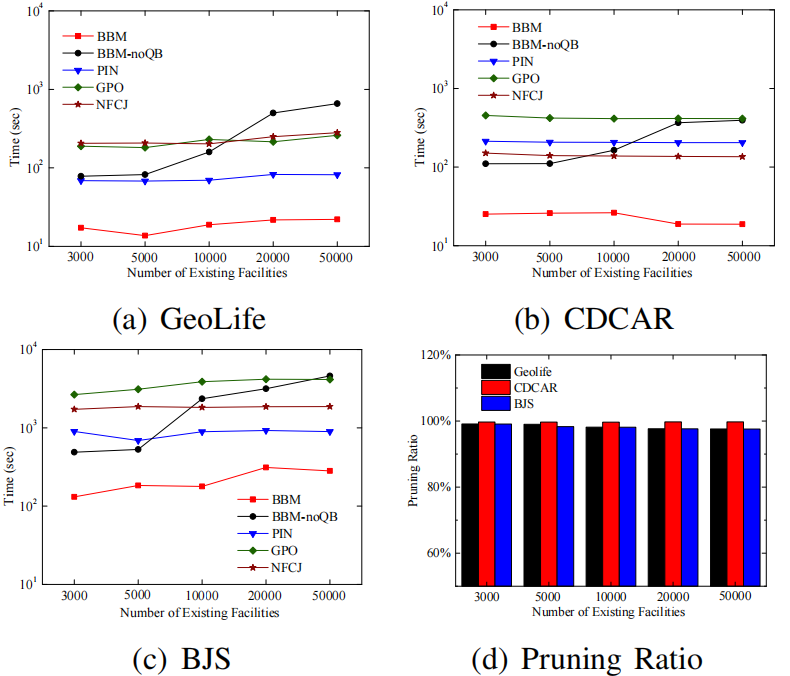
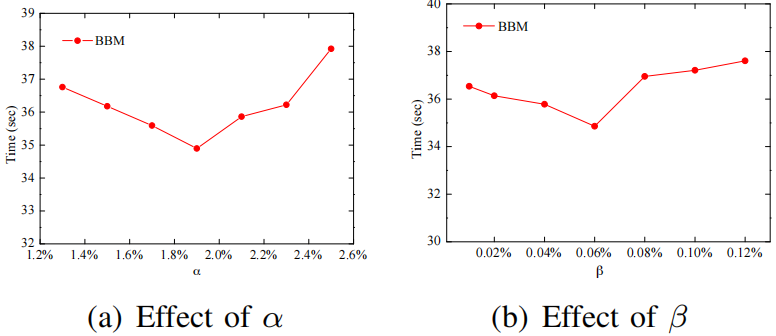
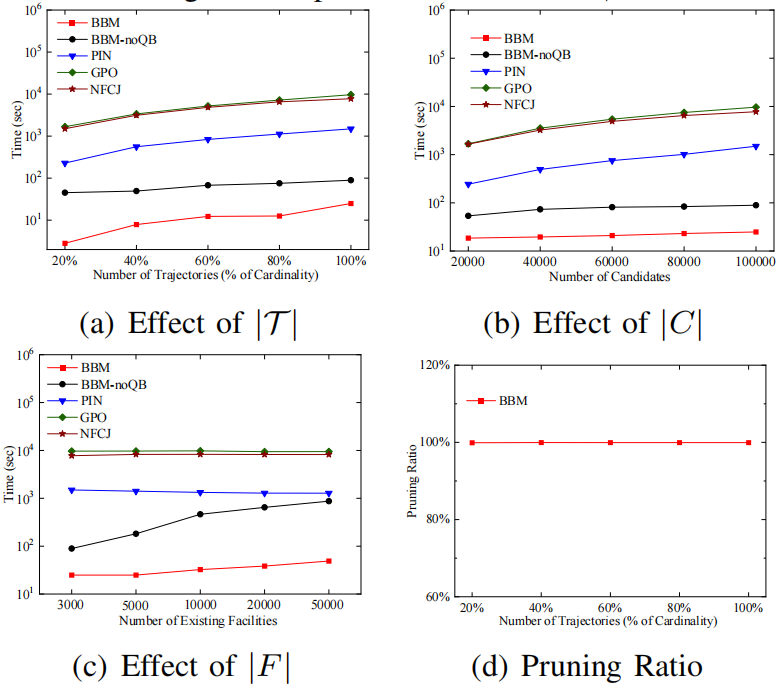
Sim(Q,Ti)。BBM算法如算法2所示。它以一组候选者和一棵QB树作为输入,并返回具有最大影响值的查询结果三级剪枝策略是 BBM 算法中用于减少搜索空间的重要技术,包括基本剪枝、时间剪枝和距离剪枝。1.基本剪枝(basic pruning):该剪枝策略基于最小外接矩形(Minimum Bounding Rectangle,MBR)的概念。对于每个子空间Si,使用 MBR来计算其上下界,即子空间的最小和最大时间戳、经度和纬度范围。如果子空间的MBR与查询范围Q没有交集,那么子空间可以被剪枝,因为它不可能包含任何解。2.时间剪枝(temporal pruning):该剪枝策略基于时间戳的先后顺序。对于每个子空间Si,如果子空间的最小时间戳晚于查询结束时间,或者最大时间戳早于查询开始时间,则该子空间可以被剪枝。3.距离剪枝(spatial pruning):该剪枝策略基于查询点到子空间 MBR 的距离。对于每个子空间Si,如果查询点到子空间MBR 的最短距离大于查询范围Q的半径,则该子空间可以被剪枝。算法3显示了如何使用 QB 树计算区域边界的伪代码。输入是一个区域R 和一个 QB 树,边界更紧的区域作为输出返回。基本剪枝是最基本的剪枝策略,可以剪枝一部分子空间,但无法剪枝所有不可能包含解的子空间。时间剪枝和距离剪枝可以进一步减少搜索空间,特别是当查询范围较小且轨迹数据集分布比较集中时,可以大幅度提高算法效率。三级剪枝策略的组合可以在保证正确性的前提下,显著减少算法的计算和搜索时间。所有实验均在配备Intel Xeon E3-1225 v6 3.3GHz和32GB RAM,运行64 位Windows 10 Education的PC上进行,所有算法均由C++实现。论文采用合成和真实轨迹数据集进行实验,表一总结了所有数据集的详细信息。论文通过改变几个参数来研究提出的方法的效率、可扩展性和有效性。表二总结了具体的参数设置,默认值带有下划线。在所有实验中,仅改变一个参数,同时将其余参数保持为默认值。α和|T|是所有数据集中轨迹基数的比例,β是候选基数的比例。QB 树是一种基于内存的索引结构。如图3(a)所示,随着 |T| 的值越大,QB-tree的构建时间增长缓慢并且与 |T| 成正比,内存开销也是如此。在图3(b)中,随着α 的增加,构建时间略有减少,索引的内存成本几乎保持不变。这是因为,随着α的增加,QB-tree的高度降低,使得将轨迹插入索引的成本降低。即使在大规模BJS 上,构建QB 树也只需要大约 1.4 秒和 704.5 MB 的存储空间。索引仅需几秒钟即可建立,因此与索引实现的性能提升相比,QB树的开销可以忽略不计。如图3(c)和图3(d)所示。在BJS 数据集上,平均插入时间为 10 微秒,平均删除时间为 20 微秒。随着α的增加,更新时间基本趋于平稳,文章提出的索引可以有效地支持更新。这组实验证了论文提出的MIT 查询算法的效率和可扩展性,考虑了不同参数设置的影响。(1)轨迹数量的影响:通过改变参数|T|来评估方法的效率,划分数据集使轨迹的比例分别约为 0.2、0.4、0.6、0.8 和 1.0。图4所示,无论|T|如何变化,BBM的时间增⻓缓慢,在所有数据集中,BBM的剪枝率超过 90%,最大值为 99.8%,实验评估表明,BBM在可扩展性和效率方面具有较高的性能,更适用于大型轨迹数据集。(2)候选设施数量的影响:实验评估了算法在不同|C|上的性能, 从20K到100K。如图5所示,当|C|增加,PIN、GPO 和NFCJ 的查询时间增长迅速,BBM-noQB略优于PIN。显然,BBM在所有情况下总是优于五种算法中最好的,这意味着分支定界框架显着受益于基于QB树的三级剪枝。此外,BBM 的查询时间会增加,因为|C|增加,根据扫描剩余候选者的方法,需要改进的候选轨迹对的数量增加。在所有数据集中,BBM 的剪枝率都在 90% 以上,最高可达 99.7%。验证了分支定界技术的有效性。(3)现有设施数量的影响:该实验评估了算法在不同 |F|上的性能。从 3K到50K,结果如图6所示。总体而言,BBM算法仍然大大优于所有竞争对手。然后,用|F|随着时间的推移,BBM 的查询时间略有波动,但基本趋于平稳。当|F|增加,每条轨迹的吸引子距离可能减小,则三级剪枝的效果略有波动。相比之下,由于粗MBR 剪枝的性能下降,BBM-noQB 增长迅速。在所有情况下,剪枝率都保持在 98% 左右。(4)α和β的作用:参数α控制在轨迹数据库上构建的QB-tree树的高度,参数β控制划分树的高度。图7所示,随着α(β)的增大,BBM的查询时间先减少后逐渐增加。显然,图8(a)和图8(b)中均存在盈亏平衡点。在图7(a)中,随着α的增加,三级剪枝计算边界所需的额外时间逐渐超过其在细化阶段节省的时间。同样,随着β的增加,分支定界技术的额外成本逐渐超过BBM 的收益。因此,当α和β分别取其盈亏平衡点的值时,BBM算法的查询性能最佳。(5)其他场景下的结果:以上结果均在城市轨迹场景下进行评估。为了充分展示通用性,文章还在海洋场景的SHIP 数据集中评估了文章的算法。与其他数据集相比,SHIP 中轨迹的活跃区域更大。在图 8(a) 中,当 |T|增加,BBM 的时间增长缓慢。相比之下,其他竞争对手增长迅速。这是因为在三级剪枝中检查了在QB 树中预先组织的所有轨迹。显然,在图8(b) 中,BBM 在所有情况下总是优于五种算法,这得益于分支定界技术。在图8(c)中,|F| 增加,BBM 仍然大大优于所有竞争对手,这与其他数据集的结果一致。在所有情况下,BBM 的剪枝率都在 90% 以上,最高可达 99.8%。Max-Inf 查询是空间数据库的一项基本功能。本文探索了轨迹数据 (MIT) 中的Max-Inf 查询,超出了每个对象都固定在一个点的限制性假设。文章通过将影响的概念扩展到轨迹数据来提出MIT 查询的定义。然后,提出了一种称为QB-tree 的混合索引,它能够将具有相似活动区域的轨迹组织在一起进行后续统一处理,然后根据运动模式将同一节点内的轨迹分类到多个桶中。对于每个桶,文章使用其中的轨迹构建一个直线多边形,以排除 MBR 中一些不相关的区域。基于QB 树,文章开发了一种称为 BBM的分支定界方法,其中包含剪枝策略以有效处理MIT 查询。最后,文章进行了广泛的实验,以在效率、可扩展性和通用性方面评估提出的索引和算法。
表示子空间内任意两个轨迹之间的最大相似度。如果UBC <= best,则可以剪枝,因为该子空间中的轨迹无法提供更优的解。如果LBC > th,则可以进一步划分该子空间。如果LBC <=
best且UBC > best,则需要在该子空间中搜索,以查找可能更优的解。4.更新最优解:在搜索过程中,如果找到一个比当前最优解更优的解,则需要更新最优解best。具体而言,如果查询轨迹与当前轨迹Ti的相似度Sim(Q,Ti)大于当前最优解best,则更新best =
Sim(Q,Ti)。BBM算法如算法2所示。它以一组候选者和一棵QB树作为输入,并返回具有最大影响值的查询结果三级剪枝策略是 BBM 算法中用于减少搜索空间的重要技术,包括基本剪枝、时间剪枝和距离剪枝。1.基本剪枝(basic pruning):该剪枝策略基于最小外接矩形(Minimum Bounding Rectangle,MBR)的概念。对于每个子空间Si,使用 MBR来计算其上下界,即子空间的最小和最大时间戳、经度和纬度范围。如果子空间的MBR与查询范围Q没有交集,那么子空间可以被剪枝,因为它不可能包含任何解。2.时间剪枝(temporal pruning):该剪枝策略基于时间戳的先后顺序。对于每个子空间Si,如果子空间的最小时间戳晚于查询结束时间,或者最大时间戳早于查询开始时间,则该子空间可以被剪枝。3.距离剪枝(spatial pruning):该剪枝策略基于查询点到子空间 MBR 的距离。对于每个子空间Si,如果查询点到子空间MBR 的最短距离大于查询范围Q的半径,则该子空间可以被剪枝。算法3显示了如何使用 QB 树计算区域边界的伪代码。输入是一个区域R 和一个 QB 树,边界更紧的区域作为输出返回。基本剪枝是最基本的剪枝策略,可以剪枝一部分子空间,但无法剪枝所有不可能包含解的子空间。时间剪枝和距离剪枝可以进一步减少搜索空间,特别是当查询范围较小且轨迹数据集分布比较集中时,可以大幅度提高算法效率。三级剪枝策略的组合可以在保证正确性的前提下,显著减少算法的计算和搜索时间。所有实验均在配备Intel Xeon E3-1225 v6 3.3GHz和32GB RAM,运行64 位Windows 10 Education的PC上进行,所有算法均由C++实现。论文采用合成和真实轨迹数据集进行实验,表一总结了所有数据集的详细信息。论文通过改变几个参数来研究提出的方法的效率、可扩展性和有效性。表二总结了具体的参数设置,默认值带有下划线。在所有实验中,仅改变一个参数,同时将其余参数保持为默认值。α和|T|是所有数据集中轨迹基数的比例,β是候选基数的比例。QB 树是一种基于内存的索引结构。如图3(a)所示,随着 |T| 的值越大,QB-tree的构建时间增长缓慢并且与 |T| 成正比,内存开销也是如此。在图3(b)中,随着α 的增加,构建时间略有减少,索引的内存成本几乎保持不变。这是因为,随着α的增加,QB-tree的高度降低,使得将轨迹插入索引的成本降低。即使在大规模BJS 上,构建QB 树也只需要大约 1.4 秒和 704.5 MB 的存储空间。索引仅需几秒钟即可建立,因此与索引实现的性能提升相比,QB树的开销可以忽略不计。如图3(c)和图3(d)所示。在BJS 数据集上,平均插入时间为 10 微秒,平均删除时间为 20 微秒。随着α的增加,更新时间基本趋于平稳,文章提出的索引可以有效地支持更新。这组实验证了论文提出的MIT 查询算法的效率和可扩展性,考虑了不同参数设置的影响。(1)轨迹数量的影响:通过改变参数|T|来评估方法的效率,划分数据集使轨迹的比例分别约为 0.2、0.4、0.6、0.8 和 1.0。图4所示,无论|T|如何变化,BBM的时间增⻓缓慢,在所有数据集中,BBM的剪枝率超过 90%,最大值为 99.8%,实验评估表明,BBM在可扩展性和效率方面具有较高的性能,更适用于大型轨迹数据集。(2)候选设施数量的影响:实验评估了算法在不同|C|上的性能, 从20K到100K。如图5所示,当|C|增加,PIN、GPO 和NFCJ 的查询时间增长迅速,BBM-noQB略优于PIN。显然,BBM在所有情况下总是优于五种算法中最好的,这意味着分支定界框架显着受益于基于QB树的三级剪枝。此外,BBM 的查询时间会增加,因为|C|增加,根据扫描剩余候选者的方法,需要改进的候选轨迹对的数量增加。在所有数据集中,BBM 的剪枝率都在 90% 以上,最高可达 99.7%。验证了分支定界技术的有效性。(3)现有设施数量的影响:该实验评估了算法在不同 |F|上的性能。从 3K到50K,结果如图6所示。总体而言,BBM算法仍然大大优于所有竞争对手。然后,用|F|随着时间的推移,BBM 的查询时间略有波动,但基本趋于平稳。当|F|增加,每条轨迹的吸引子距离可能减小,则三级剪枝的效果略有波动。相比之下,由于粗MBR 剪枝的性能下降,BBM-noQB 增长迅速。在所有情况下,剪枝率都保持在 98% 左右。(4)α和β的作用:参数α控制在轨迹数据库上构建的QB-tree树的高度,参数β控制划分树的高度。图7所示,随着α(β)的增大,BBM的查询时间先减少后逐渐增加。显然,图8(a)和图8(b)中均存在盈亏平衡点。在图7(a)中,随着α的增加,三级剪枝计算边界所需的额外时间逐渐超过其在细化阶段节省的时间。同样,随着β的增加,分支定界技术的额外成本逐渐超过BBM 的收益。因此,当α和β分别取其盈亏平衡点的值时,BBM算法的查询性能最佳。(5)其他场景下的结果:以上结果均在城市轨迹场景下进行评估。为了充分展示通用性,文章还在海洋场景的SHIP 数据集中评估了文章的算法。与其他数据集相比,SHIP 中轨迹的活跃区域更大。在图 8(a) 中,当 |T|增加,BBM 的时间增长缓慢。相比之下,其他竞争对手增长迅速。这是因为在三级剪枝中检查了在QB 树中预先组织的所有轨迹。显然,在图8(b) 中,BBM 在所有情况下总是优于五种算法,这得益于分支定界技术。在图8(c)中,|F| 增加,BBM 仍然大大优于所有竞争对手,这与其他数据集的结果一致。在所有情况下,BBM 的剪枝率都在 90% 以上,最高可达 99.8%。Max-Inf 查询是空间数据库的一项基本功能。本文探索了轨迹数据 (MIT) 中的Max-Inf 查询,超出了每个对象都固定在一个点的限制性假设。文章通过将影响的概念扩展到轨迹数据来提出MIT 查询的定义。然后,提出了一种称为QB-tree 的混合索引,它能够将具有相似活动区域的轨迹组织在一起进行后续统一处理,然后根据运动模式将同一节点内的轨迹分类到多个桶中。对于每个桶,文章使用其中的轨迹构建一个直线多边形,以排除 MBR 中一些不相关的区域。基于QB 树,文章开发了一种称为 BBM的分支定界方法,其中包含剪枝策略以有效处理MIT 查询。最后,文章进行了广泛的实验,以在效率、可扩展性和通用性方面评估提出的索引和算法。[1] H. Samet, Foundations of multidimensional and metric data structures, ser. Morgan Kaufmann series in data management systems. Academic Press, 2006.
本文作者 唐永昕 重庆大学START团队成员。主要研究方向:流式轨迹数据管理。 | |
时空艺术团队(START,Spatio-Temporal Art)来自重庆大学时空实验室,旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!

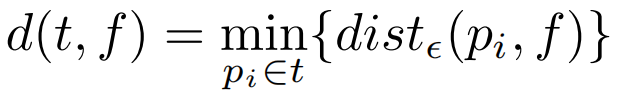
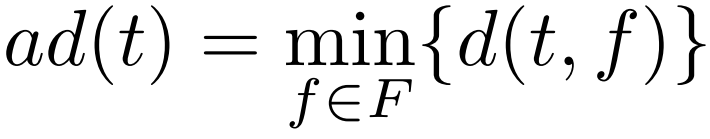
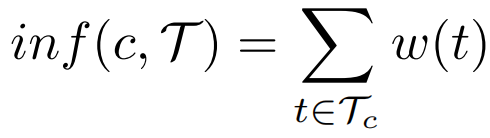
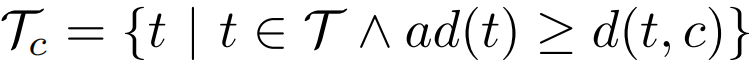
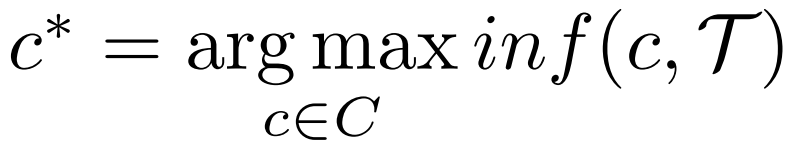
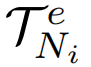 中所有轨迹的最小边界矩形。(ii)
中所有轨迹的最小边界矩形。(ii)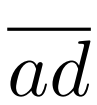 是
是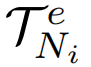 中轨迹的吸引子距离的上限,即:
中轨迹的吸引子距离的上限,即: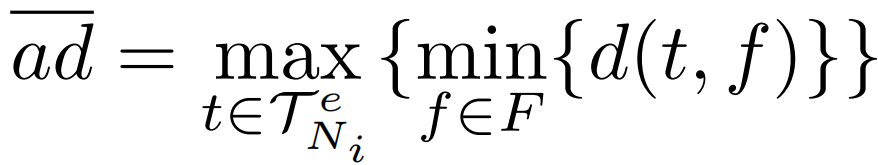
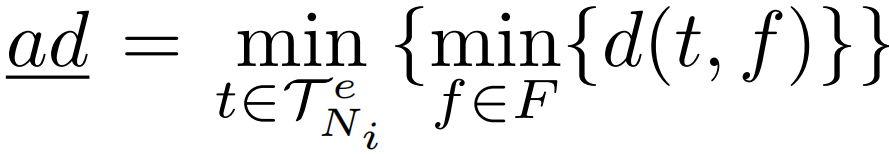
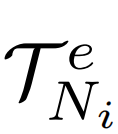 中轨迹的权重和,即:
中轨迹的权重和,即: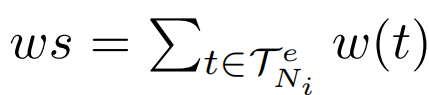
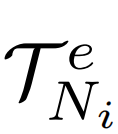 轨迹的桶的指针
轨迹的桶的指针
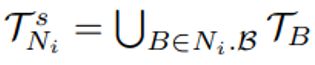
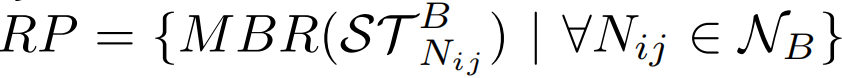
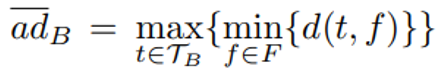
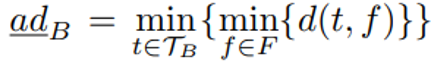
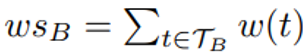
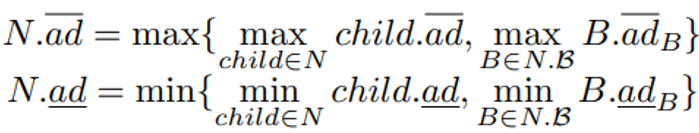

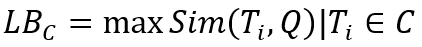 表示子空间中轨迹与查询轨迹的最大相似度;
表示子空间中轨迹与查询轨迹的最大相似度;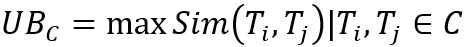 表示子空间内任意两个轨迹之间的最大相似度。如果UBC <= best,则可以剪枝,因为该子空间中的轨迹无法提供更优的解。如果LBC > th,则可以进一步划分该子空间。如果LBC <=
best且UBC > best,则需要在该子空间中搜索,以查找可能更优的解。
表示子空间内任意两个轨迹之间的最大相似度。如果UBC <= best,则可以剪枝,因为该子空间中的轨迹无法提供更优的解。如果LBC > th,则可以进一步划分该子空间。如果LBC <=
best且UBC > best,则需要在该子空间中搜索,以查找可能更优的解。