数据科学与SQL：如何利用SQL计算线性回归系数？

会飞的一十六 2024-12-28

412

点击上方【蓝色】字体关注我们

01 线性回归模型基础

02 数据准备

假设我们有一个名为 regression_data
的表，表中包含两列：x
（自变量）和 y
（因变量），示例数据如下：

x	y
1	2
2	3
3	4
4	5
5	6

CREATE TABLE regression_data (
    x INT,
    y INT
);


INSERT INTO regression_data VALUES
(1, 2),
(2, 3),
(3, 4),
(4, 5),
(5, 6);

03 问题分析

第一步：计算 x
和 y
的均值

SELECT AVG(x) AS x_mean, AVG(y) AS y_mean
FROM regression_data;

中间结果展示：

x_mean	y_mean
3	4

第二步：计算分子部分

这里使用SUM
聚合函数结合分析函数LAG
来实现，LAG
函数可以获取当前行的前一行数据，方便我们计算差值的乘积并求和。

-- 第一步：在子查询中计算每行对应的 (x - x_mean) 和 (y - y_mean) 以及整体的均值，方便后续计算
SELECT 
    x,
    y,
    AVG(x) OVER() AS x_mean,
    AVG(y) OVER() AS y_mean,
    (x - AVG(x) OVER()) AS x_diff_mean,
    (y - AVG(y) OVER()) AS y_diff_mean
FROM regression_data;


-- 第二步：基于第一步的结果，计算 (x - x_mean) * (y - y_mean) 并求和得到分子部分
SELECT SUM(x_diff_mean * y_diff_mean) AS numerator
FROM (
    SELECT 
        x,
        y,
        AVG(x) OVER() AS x_mean,
        AVG(y) OVER() AS y_mean,
        (x - AVG(x) OVER()) AS x_diff_mean,
        (y - AVG(y) OVER()) AS y_diff_mean
    FROM regression_data
) subquery;

在上述代码中：

首先在子查询里通过OVER()使用分析函数AVG计算出整个数据集里x和y的均值，分别命名为x_mean和y_mean，并将其与原始的x、y列一起返回。

然后在外层查询中，利用这些带有均值的数据列，按照回归系数计算分子部分的公式，计算出(x - x_mean) * (y - y_mean)的总和，即得到分子的值。

第一步中间结果展示（部分示例数据，实际会展示全部行）：

x	y	x_mean	y_mean	x_diff_mean	y_diff_mean
1	2	3	4	-2	-2
2	3	3	4	-1	-1

第二步中间结果展示：

numerator
10

第三步：计算分母部分

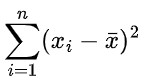
线性回归模型的一般形式为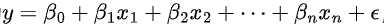，其中y是因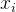变量，是自变量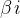，是回归系数，是误差项。在简单线性回归（只有x一个自变量）中，模型为。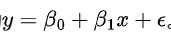
计算回归系数的目的是找到一条最佳拟合线，使得预测值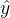与实际值y之间的误差平方和最小。这个方法称为最小二乘法。

-- 第一步：在子查询中计算每行对应的 (x - x_mean) 以及整体的均值，方便后续计算
SELECT 
    x,
    AVG(x) OVER() AS x_mean,
    (x - AVG(x) OVER()) AS x_diff_mean
FROM regression_data;


-- 第二步：基于第一步的结果，计算 (x - x_mean) * (x - x_mean) 并求和得到分母部分
SELECT SUM(x_diff_mean * x_diff_mean) AS denominator
FROM (
    SELECT 
        x,
        AVG(x) OVER() AS x_mean,
        (x - AVG(x) OVER()) AS x_diff_mean
    FROM regression_data
) subquery;

这里的思路和计算分子部分类似，先在子查询里通过分析函数AVG
获取x
的均值（命名为x_mean
），然后在外层查询中计算(x - x_mean) * (x - x_mean)
的总和，也就是分母部分的值。

第一步中间结果展示（部分示例数据，实际会展示全部行）：

x	x_mean	x_diff_mean
1	3	-2
2	3	-1

第二步中间结果展示：

denominator
10

第四步：计算回归系数（斜率）

-- 计算斜率beta_1，分子除以分母
SELECT numerator  denominator AS beta_1
FROM (
    SELECT 
        SUM(x_diff_mean * y_diff_mean) AS numerator,
        SUM(x_diff_mean * x_diff_mean) AS denominator
    FROM (
        SELECT 
            x,
            y,
            AVG(x) OVER() AS x_mean,
            AVG(y) OVER() AS y_mean,
            (x - AVG(x) OVER()) AS x_diff_mean,
            (y - AVG(y) OVER()) AS y_diff_mean
        FROM regression_data
    ) subquery
) final_subquery;

结果展示：

beta_1
1

先通过前面步骤计算出的分子和分母部分的子查询结果，组合在一个子查询里，然后再从这个子查询结果中获取分子除以分母的值，就是回归系数中的斜率beta_1
。

第五步：计算截距

-- 计算截距beta_0，根据公式 beta_0 = y_mean - beta_1 * x_mean
SELECT y_mean - beta_1 * x_mean AS beta_0
FROM (
    SELECT 
        AVG(y) AS y_mean,
        AVG(x) AS x_mean,
        (SELECT numerator  denominator AS beta_1
         FROM (
            SELECT 
                SUM(x_diff_mean * y_diff_mean) AS numerator,
                SUM(x_diff_mean * x_diff_mean) AS denominator
            FROM (
                SELECT 
                    x,
                    y,
                    AVG(x) OVER() AS x_mean,
                    AVG(y) OVER() AS y_mean,
                    (x - AVG(x) OVER()) AS x_diff_mean,
                    (y - AVG(y) OVER()) AS y_diff_mean
                FROM regression_data
            ) subquery
         ) final_subquery
        ) AS beta_1
    FROM regression_data
) beta_0_subquery;

结果展示：

beta_0
1

最后，根据已经算出的y的均值、x的均值以及斜率beta_1，按照截距的计算公式beta_0 = y_mean - beta_1 * x_mean来计算出截距beta_0。

通过上述使用分析函数的方式，整体上可以更有条理且相对简洁地完成简单线性回归系数的计算，不过对于多元线性回归，还需要进一步拓展代码逻辑以及可能借助更多自定义函数等方式来模拟矩阵运算等复杂操作来计算回归系数。

04 小结

本文利用SQL分析了线性回归技术的求解方法，在计算回归系数的过程中，多次使用了分析函数（如AVG(x) OVER()
）来计算数据列的均值。这种方式使得在子查询中可以方便地获取整体数据集的均值，并且能够与每行数据一起进行后续计算。例如，在计算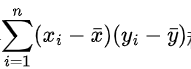

分子部分和分母部分

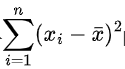
时，通过分析函数计算出的均值可以直接在子查询中与每行的x
、y
值进行差值计算，避免了复杂的嵌套查询或多次扫描数据集来获取均值。

线性回归技术应用及使用场景

使用场景特点：
存在线性关系假设：线性回归技术基于因变量和自变量之间存在线性关系的假设。在实际应用中，需要先通过数据探索性分析（如绘制散点图等）来初步判断变量之间是否大致呈现线性关系。如果变量之间的关系是非线性的，直接使用线性回归可能会导致模型不准确。
需要足够的数据量：为了得到可靠的回归系数，通常需要足够的样本数据。数据量过少可能会导致回归模型过拟合或系数估计不准确。例如，在销售预测中，如果只有少数几个月的数据来建立广告投入和销售额之间的线性回归模型，可能会因为数据的局限性而无法准确反映真实的市场规律。
用于预测和趋势分析：线性回归主要用于预测和趋势分析场景。它可以帮助用户根据已知的自变量变化情况来预测因变量的变化趋势。例如，在资源分配场景中，通过对生产数量和成本的线性回归分析，企业可以预测在不同生产规模下的成本变化趋势，从而提前做好资源调配和预算规划。
线性回归的优缺点

优点

简单易懂


线性回归模型的数学形式简单，其基本方程（以多元线性回归为例）直观易懂。对于有基本数学知识的人来说，很容易理解因变量和自变量之间的线性关系是如何通过回归系数来体现的。这种简单性使得它在解释变量之间的关系时非常直观，例如在简单线性回归中，斜率直接表示了自变量每变化一个单位，因变量的变化量。


计算高效


计算线性回归系数的算法相对简单且成熟。对于普通规模的数据，通过最小二乘法可以高效地计算出回归系数。例如，在简单线性回归中，通过计算和等统计量来确定回归系数，计算过程不复杂，并且可以在较短时间内完成计算。许多统计软件和编程语言（包括 SQL 通过一定的函数组合）都能够快速实现线性回归的计算。


广泛的适用性


在很多领域都能找到线性回归的应用场景。如在经济领域，用于预测股票价格、分析市场需求；在医疗领域，进行疾病风险预测和药物剂量 - 疗效研究等。只要变量之间大致呈现线性关系，就可以尝试使用线性回归模型进行分析和预测。而且，当自变量和因变量之间的关系不是严格线性时，通过一些数据变换（如对数变换、多项式变换等），有时也可以将其转化为线性关系，从而使用线性回归方法。


模型可解释性强


回归系数能够提供关于自变量对因变量影响程度的量化信息。例如，在一个预测房价的线性回归模型中，回归系数可以告诉我们房屋面积、房龄、周边配套设施等自变量每变化一个单位，房价会相应地变化多少。这种可解释性对于理解数据背后的关系以及做出决策非常有帮助，比如房地产开发商可以根据这些系数来确定房屋的定价策略，或者购房者可以了解不同因素对房价的影响程度。

缺点

线性关系假设的局限性


线性回归模型假设自变量和因变量之间是线性关系，但在实际数据中，很多关系是非线性的。例如，生物种群的增长通常呈现出 S 型曲线，这种情况下使用线性回归模型会导致拟合效果差，不能准确地描述变量之间的真实关系。如果强行使用线性回归，可能会得到错误的结论或不准确的预测。


对异常值敏感


由于线性回归是基于最小二乘法来拟合数据的，它对异常值非常敏感。异常值可能会对回归系数的计算产生较大影响，从而改变模型的拟合直线。例如，在一个关于员工工资和工作年限的线性回归模型中，如果存在一个工作年限很短但工资极高（可能是由于特殊奖励或数据录入错误等原因）的异常点，这个点可能会拉高回归直线的斜率，导致模型对正常数据的拟合效果变差，降低模型的准确性和可靠性。


多重共线性问题


当自变量之间存在高度相关性（多重共线性）时，会导致回归系数的估计不稳定，其标准误差增大。例如，在一个预测汽车油耗的模型中，如果将汽车的重量和车身尺寸同时作为自变量，由于它们之间可能存在较强的相关性，这会使得回归系数的解释变得困难，并且可能会使模型对新数据的预测性能下降。在这种情况下，很难确定每个自变量对因变量的独立影响。


预测能力有限


线性回归模型是基于历史数据建立的，对于复杂多变的现实世界，其预测能力有一定的局限性。尤其是在数据分布发生变化或者出现新的影响因素时，线性回归模型可能无法及时适应这种变化。例如，在市场需求预测中，如果出现了新的竞争对手或者消费者偏好发生了重大变化，之前建立的线性回归模型可能就无法准确地预测市场需求了。

应用领域：
销售预测：在商业领域，线性回归可以用于预测产品的销售额。例如，将广告投入作为自变量x，销售额作为因变量y，通过历史数据建立线性回归模型，计算出回归系数后，就可以根据未来的广告投入计划来预测销售额。这样企业可以合理安排广告预算，以达到预期的销售目标。
金融分析：在股票市场中，线性回归可以用来分析股票价格与某些经济指标（如利率、通货膨胀率等）之间的关系。通过建立线性回归模型，投资者可以尝试预测股票价格的走势，辅助投资决策。例如，以利率作为自变量，股票价格作为因变量，回归系数可以帮助投资者了解利率变动对股票价格的影响程度。
资源分配和成本估算：在生产制造行业，线性回归可以用于估算生产成本。例如，将生产数量作为自变量，总成本作为因变量，通过线性回归分析，可以确定单位产品的变动成本（回归系数）和固定成本（截距），从而帮助企业进行成本控制和资源分配。例如，企业可以根据预测的生产数量来估算总成本，进而制定合理的生产计划和定价策略。

会飞的一十六
微信号：ddan_hashcode
扫描右侧二维码关注我们

点个【在看】你最好看