数据科学与SQL：如何利用本福特法则识别财务数据造假？

会飞的一十六 2025-01-09

399

点击上方【蓝色】字体关注我们

01 场景描述

本福特法则（Benford's Law）指出，在许多自然产生的数字数据集中，首位数字（最左边的非零数字）出现的概率不是均匀分布的。具体来说，数字 1 作为首位数字出现的概率约为 30.1%，数字 2 出现的概率约为 17.6%，数字 3 约为 12.5%，以此类推，数字 9 出现的概率约为 4.6%。这种分布规律在各种数据场景如财务数据、人口统计数据等中广泛存在。当数据不符合本福特法则的预期分布时，可能意味着数据存在异常，例如数据造假、数据录入错误等。

02 数据准备

-- 创建表
CREATE TABLE financial_data (
    id INT,
    amount DECIMAL(20, 2)
);


-- 插入示例数据
INSERT INTO financial_data VALUES
(1, 1234.56),
(2, 2345.67),
(3, 345.67),
(4, 4567.89),
(5, 567.89),
(6, 678.90),
(7, 789.01),
(8, 890.12),
(9, 901.23),
(10, 1012.34),
(11, 1123.45),
(12, 2234.56),
(13, 3345.67),
(14, 4456.78),
(15, 5567.89),
(16, 6678.90),
(17, 7789.01),
(18, 8890.12),
(19, 9901.23),
(20, 100.00);

03 问题分析

步骤1：提取首位数:

使用 Hive 中的函数来提取每个财务数据金额的首位数字，将其作为一个新的字段，方便后续统计分析。这里使用substr
和cast
函数实现提取，并使用count
分析函数结合over
子句计算总记录数。

-- 提取首位数字并添加总记录数列（用于后续计算频率）
SELECT
    id,
    amount,
    -- 通过转换为字符串后取第一个字符，再转回数字类型来获取首位数字
    CAST(SUBSTR(CAST(amount AS STRING), 1, 1) AS INT) AS first_digit,
    COUNT(*) OVER () AS total_count
FROM financial_data;

id	amount	   first_digit	 total_count
1	1234.56	 1	20
2	2345.67	 2	20
3	345.67	        3	20
4	4567.89	 4	20
5	567.89	        5	20
6	678.90	        6	20
7	789.01	        7	20
8	890.12	        8	20
9	901.23	        9	20
10	1012.34	1	20
11	1123.45	1	20
12	2234.56	2	20
13	3345.67	3	20
14	4456.78	4	20
15	5567.89	5	20
16	6678.90	6	20
17	7789.01	7	20
18	8890.12	8	20
19	9901.23	9	20
20	100.00	       1	20

在这个中间结果集中，我们不仅提取出了首位数字，还通过分析函数计算出了数据的总记录数，为后续计算每个首位数字的频率做准备。

步骤2：计算首位数字的实际频率分布

利用分析函数count结合partition by来对首位数字进行分组统计出现次数，再结合前面得到的总记录数计算频率，这样无需嵌套子查询来分组统计和计算频率。

-- 计算首位数字的频率分布
SELECT
    first_digit,
    COUNT(*) AS digit_count,
    -- 计算频率，每个首位数字出现的次数除以总记录数
    COUNT(*)  total_count AS frequency
FROM (
    SELECT
        id,
        amount,
        CAST(SUBSTR(CAST(amount AS STRING), 1, 1) AS INT) AS first_digit,
        COUNT(*) OVER () AS total_count
    FROM financial_data
) subquery
GROUP BY first_digit, total_count;

这里展示了每个首位数字在我们的财务数据样本中出现的实际次数以及对应的频率，接下来就可以将这些实际频率与本福特法则的理论频率进行对比了。

步骤3：比较实际频率与本福特法则理论频率（最终判断）

本福特法则中首位数字 1 - 9 的理论概率分别为约 30.1%（0.301）、17.6%（0.176）、12.5%（0.125）、9.7%（0.097）、7.9%（0.079）、6.7%（0.067）、5.8%（0.058）、5.1%（0.051）、4.6%（0.046）。我们将实际频率与这些理论频率进行对比，通过计算差异等方式来判断是否存在异常，这里简单通过查看频率差异较大的首位数字来初步判断（实际应用中可结合更严格的统计检验方法）。

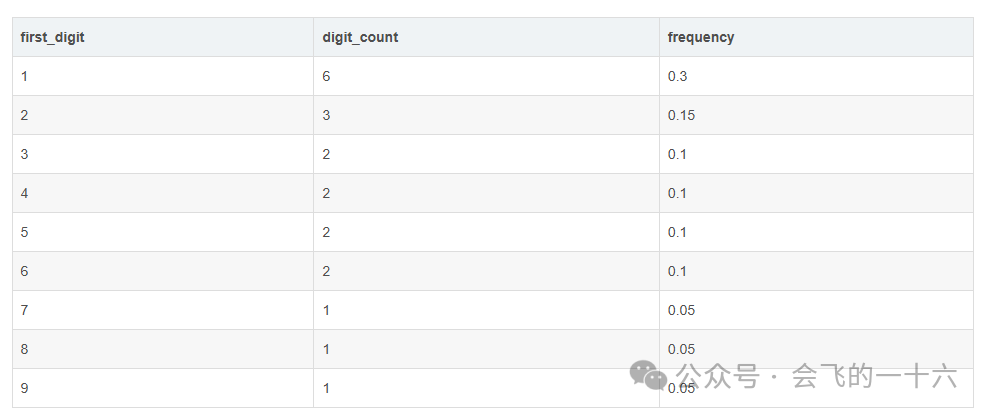
-- 定义本福特法则理论频率表（这里简单示例，可根据更精确要求完善）
CREATE TABLE benford_expected_frequencies (
    first_digit INT,
    expected_frequency DECIMAL(5, 3)
);


INSERT INTO benford_expected_frequencies VALUES
(1, 0.301),
(2, 0.176),
(3, 0.125),
(4, 0.097),
(5, 0.079),
(6, 0.067),
(7, 0.058),
(8, 0.051),
(9, 0.046);


-- 连接实际频率表和理论频率表，计算频率差异并判断异常（这里简单以较大差异判断，实际可细化标准）
SELECT
    actual.first_digit,
    actual.digit_count,
    actual.frequency,
    expected.expected_frequency,
    -- 计算实际频率与理论频率的差值绝对值
    ABS(actual.frequency - expected.expected_frequency) AS frequency_difference
FROM (
    SELECT
        first_digit,
        COUNT(*) AS digit_count,
        COUNT(*)  total_count AS frequency
    FROM (
        SELECT
            id,
            amount,
            CAST(SUBSTR(CAST(amount AS STRING), 1, 1) AS INT) AS first_digit,
            COUNT(*) OVER () AS total_count
        FROM financial_data
    ) subquery
    GROUP BY first_digit, total_count
) actual
JOIN benford_expected_frequencies expected ON actual.first_digit = expected.first_digit
WHERE ABS(actual.frequency - expected.expected_frequency) > 0.05; -- 可根据实际调整差异阈值

在这个简单示例中，我们看到首位数字 2 和 7 的实际频率与理论频率差异相对较大（这里以大于 0.05 作为简单判断阈值，实际需更严谨评估），这可能提示对应的数据存在异常情况，但还需要结合更多的财务背景知识、其他分析方法等来综合判断是否存在财务数据造假的情况，毕竟数据的差异可能由多种合理原因导致，不能仅凭此就下定论。

04 小结

本福特法则计算步骤及思路如下：
提取首位数字的过程
在许多编程语言和数据库环境中，首先要将数值型数据转换为字符型数据，这样才能方便地提取首位数字。例如，在 Python 中，如果数据存储在一个列表data_list中，使用str()函数将每个数值转换为字符串：string_data = [str(i) for i in data_list]。
在 SQL 中，也有类似的函数用于数据类型转换。以 MySQL 为例，使用CAST()函数，如CAST(numeric_column AS CHAR)（假设numeric_column是存储数值的列）。
提取首位数字：
对于转换为字符格式的数据，使用字符串操作函数来提取首位数字。在 Python 中，可以使用索引操作来提取字符串的第一个字符，例如first_digits = [int(i[0]) for i in string_data]，这里将提取的字符再转换为整数类型并存入first_digits列表。
在 SQL 中，使用SUBSTR()（不同数据库可能函数名略有不同，如SUBSTRING()）函数来提取子串。例如，在 Oracle 中可以使用SUBSTR(CAST(numeric_column AS VARCHAR2), 1, 1)来提取数值列numeric_column转换为字符后的第一个字符，再通过CAST()将提取的字符转换回数字类型。
计算首位数字的频率分布
统计首位数字的出现次数：
在编程语言中，通常使用数据结构来统计每个首位数字的出现次数。例如，在 Python 中，可以使用字典来实现。初始化一个空字典digit_count = {}，然后遍历提取的首位数字列表first_digits，对于每个数字，如果它已经在字典中，就将其对应的计数加 1，否则将其添加到字典中并设置计数为 1，如for digit in first_digits: if digit in digit_count: digit_count[digit]+=1 else: digit_count[digit] = 1。
在数据库中，使用GROUP BY和COUNT()函数来实现分组统计。例如，在 SQL 中，查询语句可能是SELECT first_digit, COUNT(*) AS count FROM (SELECT CAST(SUBSTR(CAST(numeric_value AS CHAR), 1, 1) AS UNSIGNED) AS first_digit FROM data_table) subquery GROUP BY first_digit（假设data_table是包含数据的表，numeric_value是数值列）。
计算频率：
计算每个首位数字的频率，即每个首位数字的出现次数除以数据的总个数。在 Python 中，计算总个数可以使用len(data_list)，然后对于字典digit_count中的每个键值对，计算频率frequency = {k: v/len(data_list) for k, v in digit_count.items()}。
在数据库中，在前面统计出现次数的查询基础上，通过子查询或者其他方式计算总记录数。例如，在 SQL 中可以修改前面的查询为

将数值转换为字符格式（如果需要）：

```
SELECT first_digit, COUNT(*) AS count, COUNT(*)/ (SELECT COUNT(*) FROM data_table) AS frequency FROM (SELECT CAST(SUBSTR(CAST(numeric_value AS CHAR), 1, 1) AS UNSIGNED) AS first_digit FROM data_table) subquery GROUP BY first_digit。
```
比较实际频率与本福特法则理论频率
确定本福特法则理论频率值：
根据本福特法则，首位数字 1 - 9 的理论概率分别约为 30.1%（0.301）、17.6%（0.176）、12.5%（0.125）、9.7%（0.097）、7.9%（0.079）、6.7%（0.067）、5.8%（0.058）、5.1%（0.051）、4.6%（0.046）。可以将这些理论频率值存储在一个数组或者表格结构中，方便后续比较。例如，在 Python 中可以创建一个字典benford_frequencies = {1:0.301, 2:0.176, 3:0.125, 4:0.097, 5:0.079, 6:0.067, 7:0.058, 8:0.051, 9:0.046}。
比较分析：
逐个比较实际频率和理论频率。可以通过计算差值（实际频率 - 理论频率）或者差值的绝对值来观察差异程度。在 Python 中，可以遍历实际频率字典和理论频率字典，计算差值，如for digit in digit_count.keys(): difference = abs(digit_count[digit] - benford_frequencies[digit])。
除了简单的差值比较，还可以使用统计检验方法来更科学地判断实际频率和理论频率之间的差异是否显著。例如，卡方检验是一种常用的方法。卡方值的计算公式为，其中是实际观测值（实际频率），是理论期望值（理论频率）。在 Python 中，可以使用scipy.stats库中的chisquare函数来进行卡方检验，如from scipy.stats import chisquare; observed = [digit_count[i] for i in range(1, 10)]; expected = [benford_frequencies[i]*len(data_list) for i in range(1, 10)]; chisquare(observed, f_exp = expected)。
结果解读与决策
判断数据是否异常：
如果实际频率与理论频率的差异较小，或者通过统计检验没有发现显著差异，那么数据在首位数字分布上基本符合本福特法则，数据可能是正常的。
如果差异较大，尤其是在多个首位数字上都出现明显差异，或者统计检验显示差异显著，那么数据可能存在异常情况。但这并不绝对意味着数据造假，可能是数据本身的特殊性导致的，如数据集中在某个特定的范围（例如，公司的大部分交易金额都在某个固定区间内）或者受到特殊业务模式的影响。
综合考虑其他因素：
即使首位数字分布异常，也不能仅凭此就判定财务数据造假。需要结合其他财务分析工具和方法，如比率分析（如偿债比率、盈利比率等）、趋势分析（观察财务数据在多个期间的变化趋势是否合理）、审计线索（如是否存在异常的交易对手、不合规的审批流程等）以及行业特点和公司经营策略等来综合判断。例如，如果首位数字分布异常且同时发现公司有财务压力、业绩考核不合理等情况，那么财务数据造假的嫌疑可能会增加。