六种数据分析方法
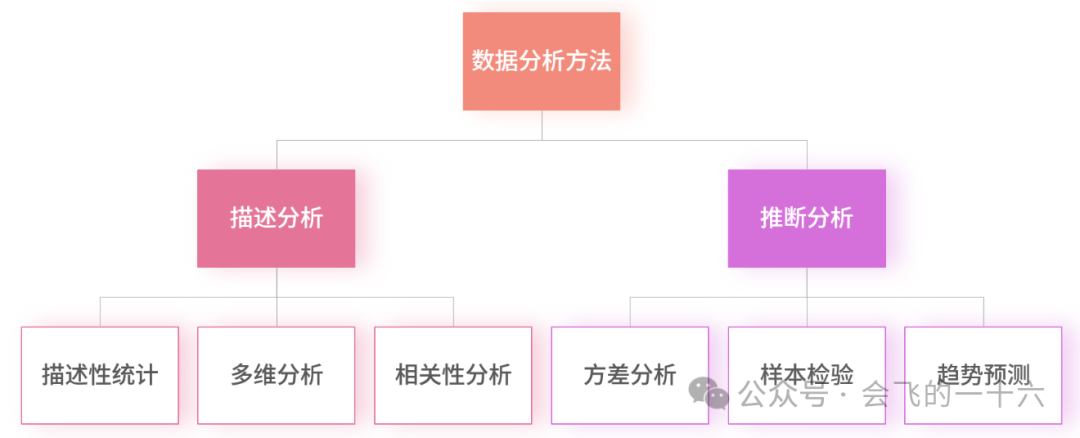
描述分析
主要用于分析数据的整体情况,重点着眼于分析数据本身的分布和特征,主要包括描述性统计、多维分析和相关性分析等分析方法。
例如分析产品的 DAU 时,通常用描述分析对 DAU 的分布、趋势和组成进行初步分析,以了解掌握 DAU 总体的特征情况。
一般而言,拿到一份数据或报表时,通常首先进行描述性分析,看看整体情况如何之后再进行其他更为深入的分析。

推断分析
主要通过分析少量数据的特征,来推断整体数据特征的方法,主要包括方差分析、样本检验和趋势预测。
例如,判断影响营销活动效果的有效因素、分析对指定客群投放营销活动后的真实效果、A/B 测试中选取的客群能否代表整体用户特征等等,这些都是推断分析去解决的场景。一般而言,推断分析是在描述分析之后,深入探索数据特征,寻找数据归因的重要分析方法。
闲话休提,今天我们先深入探讨第一类描述分析中的第一种分析方法:描述性统计。
什么是描述性统计?
大多数同学每天到公司第一件事,就是看各种各样的报表以了解产品运营的情况。特别是当我们打开一份有十几列,几万行的明细数据时,那种感觉我相信用铺天盖地、头晕目眩来形容是再合适不过了。
面对如此令人崩溃的场景,必须要求我们要求能够快速找到数据的特征。描述性统计正是为此而生,它通过几个简单的分析方法就能在几秒钟内提取出指标背后的数据特征,快速建立整体全面的认知,并帮助我们寻找到分析的突破口。
为了能够高效的发现数据的特征,描述性统计为我们提供了三个非常有用的分析工具,分别是:
并且还提供了一个分析图表——箱线图来辅助分析。
分析工具 1:用“中位数和平均数”分析数据的分布情况
1.数学定义和业务含义
平均数的特点是极易受到极大值或极小值的影响,从而会变得不客观,所以在计算平均数时,一般都要看看这组数据的最大值和最小值是否偏离太大,如果偏离太大需要剔除后再计算平均值。
比如,要评估 11 月中 30 天的日均销售额,显然双 11 极高的销售额会把整月的日均销售额拉高,无法真实反映 11 月的日均销售额。所以需要除去双 11 的数据后,再计算 11 月的日均销售额。
特别需要强调的是,算术平均数和几何平均数的适用场景完全不同。
几何平均数适用于指标是百分比的数据,例如计算不同渠道的平均转化率、不同客群的平均留存率、不同品类的平均付费率、月均增长率等,只能用几何平均数来计算。
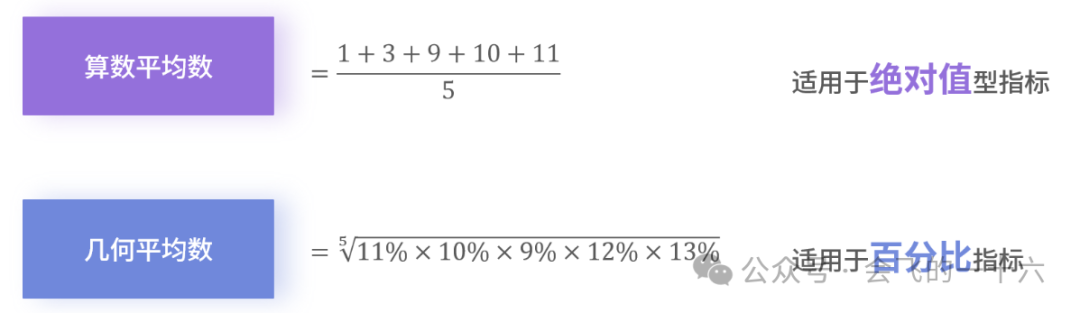
2.使用指南
数据中偏大的居多,抬高了整体的均值,导致平均数大于中位数;
数据中出现了个别极小值,拉低了整体的均值,导致平均数小于中位数。
为什么要这么去看?因为很多场景下两组数据的总和和平均数相差无几,难以评估谁好谁坏;而通过“中位数与平均数”的对比,可以发现很多有趣的业务问题,例如下面这个例子。
3.应用示例
在电商行业中经常需要分析不同品类产品的销售情况。
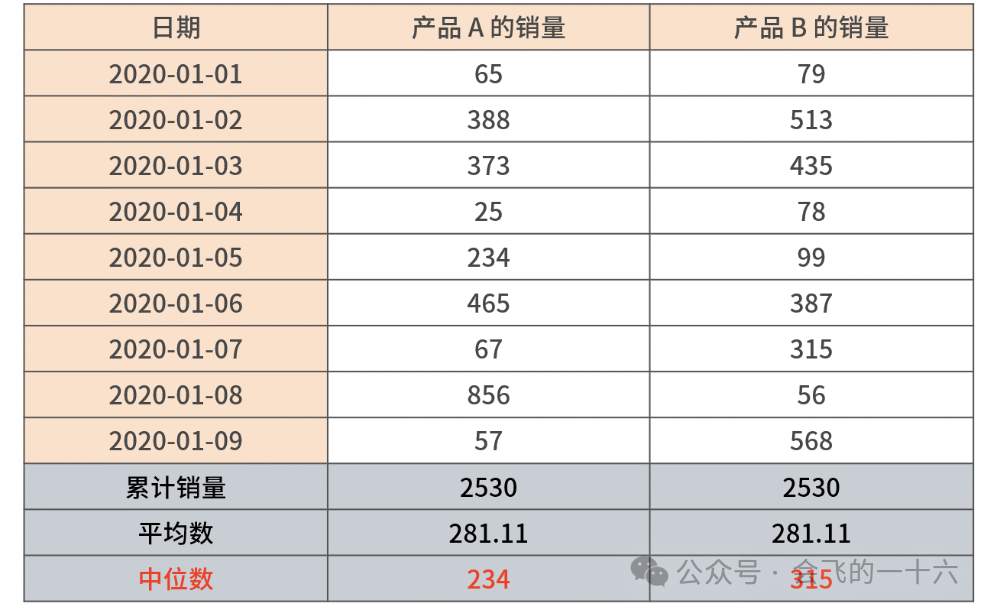
由上表可以看出,产品 A 和产品 B 的累计销售额完全一样,日均销售额也完全一样,仅看这两个指标无法得出任何业务结论;但是我们试着看看产品 A 和产品 B 的平均数和中位数,情况就有趣了。
产品 A 的日均销售额为 281.11,每日销售额的中位数是 234,即平均数大于中位数。
意味着产品 A 的每日销售额偏高的居多,可能是产品 A 的客单价较高,可能是某一天的销售额很高,拉高了平均数。
产品 B 的日均销售额为 281.11,每日销售额的中位数是 315,即平均数小于中位数。
意味着产品 B 的每日销售额偏低的居多,可能是产品 B 的客单价较低,可能是某一天的销售额很低,拉低了平均数。
分析工具 2:用“方差和标准差”来分析指标的波动情况
1.数学定义和业务含义
方差,是指数据的离散程度,是一组数据与这组数据平均数之差的平方值的平均数;而标准差,是方差的开方值。这些都是简单的基本概念,我们了解下方差和标准差的业务含义。
方差和标准差代表了业务指标的波动情况,即业务稳定性的高低,也即业务经营风险的大小;
当方差和标准差变大,意味着指标波动变大,业务稳定性降低,业务经营风险升高;
当方差和标准差变小,意味着指标波动变小,业务稳定性升高,业务经营风险降低;
方差和标准差可以将微小的变化显著放大,即更直观和更直接地观察到业务经营风险。
2.使用指南
方差和标准差的使用非常简单,只需要留意以下两点即可。
方差没有量纲,即没有任何单位,不具备任何业务含义,就是一个纯数字。不能说11月的销售额方差是多少万元,只能说方差是多少数字。所以单看一个方差没有任何业务价值,而是需要做各种对比来看方差的变化,从变化中找到可能的数据问题。
例如,连续两周的每周 DAU 方差都在变大,意味着 DAU 的波动不断变大,背后的原因或者是投放的运营活动数量和节奏出现问题,或者是产品稳定性出现问题,或者是外部竞品抢用户等等。
因为方差会将数据微小的波动放得很大,所以在某些情况下方差的数据可以到 8 位甚至 9 位数,这对视觉体验非常不友好。所以更多数情况下我们是考察标准差,因为数字显示得不会太大,同时具备业务意义。
3.应用示例
渠道是重要的获客方式,渠道的获客稳定性非常重要,波动过大的渠道一般其客群质量也不会太高,对于产品而言会造成获客资源的浪费,以及加大后续运营资源的压力。如果要评估渠道的获客稳定性,那么我们就要用方差/标准差来评估。
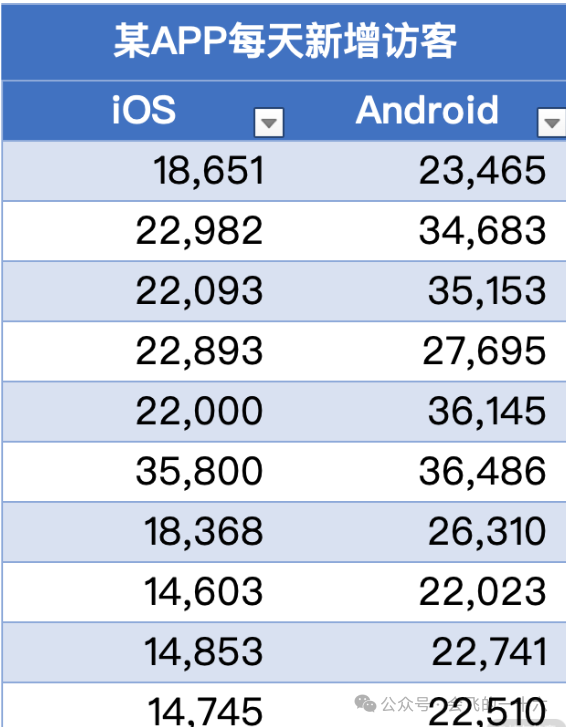
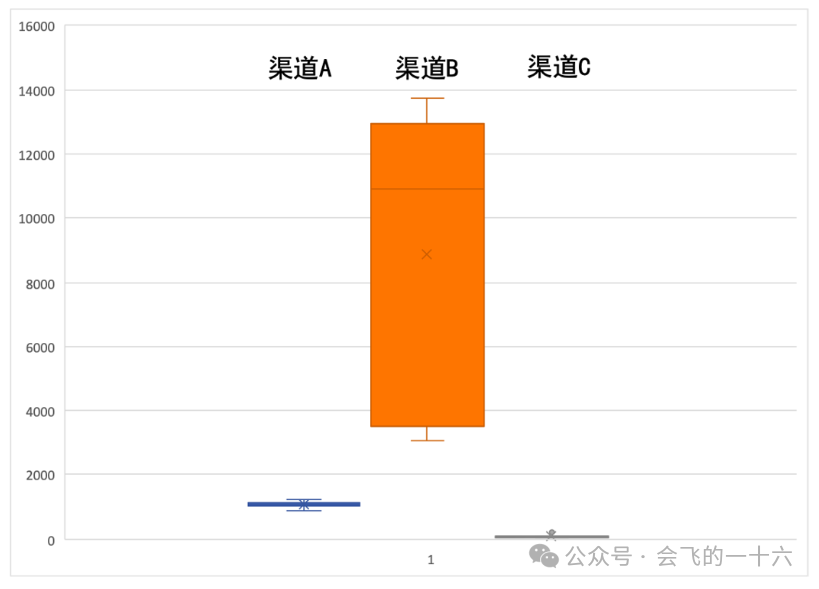
例如,要分析如下三个渠道的新增用户稳定性,考察其每日新增用户数的方差,看看能否得出有趣的结论。
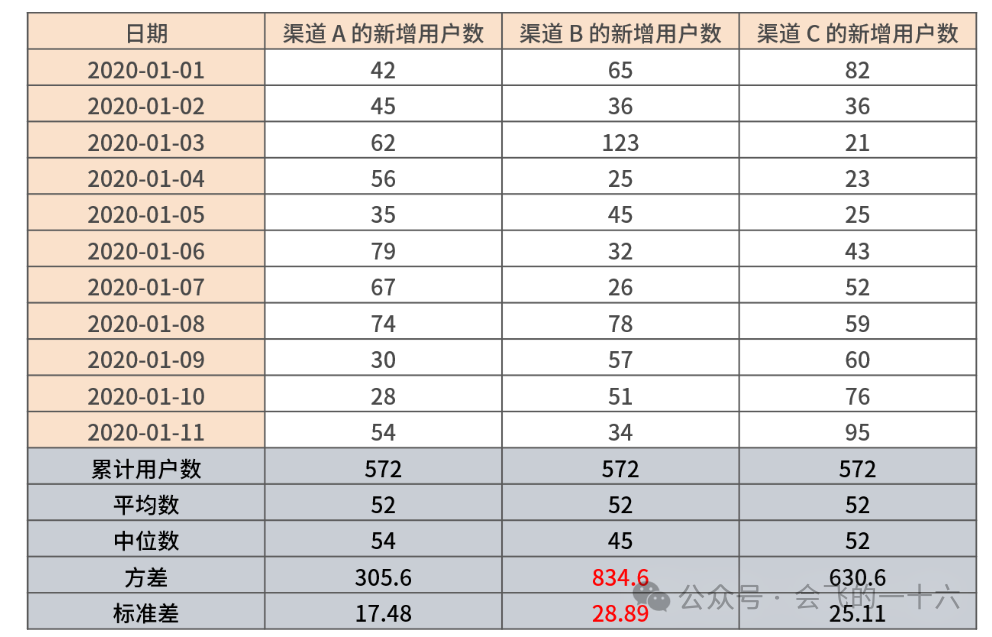
从上表可以看出,仅分析这三个渠道的累计新增用户数、日均新增用户数无法得出任何业务结论,同时分析各个渠道自己的平均值和中位数也难以评估渠道的获客稳定性。
于是,我们发现:因为渠道 B 的每日新增用户数方差和标准差最大,可以认为在这 3 个渠道中,渠道 B 的获客能力波动最大,稳定性最差,后续的风险也在 3 个渠道中最高(相对),接下来的运营需要更多的关注渠道 B 的运营情况;而渠道 A 和渠道 C 的获客能力相对波动较小,获客较稳定,保持中优先级的关注即可。
分析工具 3:用“分位数和异常值”来寻找异常数据
1.数学定义和业务含义
分位数,是指将一组有序数据分为几个具有相同长度的区间,常用的有中位数、四分位数等。
统计学中,把所有数值由小到大排列并分成四等份,处于三个分割点位置就是分位数,通常用 Q1、Q2、Q3 来表示一分位(前25%)、二分位(前 50%)、三分位(前 75%),其中二分位数就是中位数。
异常值,即在数据集中存在过高或过低的值。特别注意的是,当我们说“这个月 DAU 的最大值是 190 万”,其中的“最大值”是指剔除异常值后剩下数据中的最大值(最小值也同理)。
若数据大于 Q3+1.5(|Q3-Q1|) ,则数据为异常值;
异常值,通常需要单独排查和分析,在很多互联网公司都会设置一个职位专门跟进分析异常值,它们叫 Bad Case;
异常值不能说好,也不能说不好,要根据实际业务情况来看。双 11 这天的销售数据,对比其他日期的销售,显然是一个异常值。但对于这个异常值,当然希望越大越好,也就是越异常越好。
2.使用指南
在异常值的算法中,IQR 前面的系数是重要的运营手段。在实际工程应用中,IQR 前面的系数 1.5 被认为是一个经验值,可根据业务实际情况在 1.0~2.0 之间调节,越大意味着异常值标准越宽松,越小意味着异常值标准越严格。
为了找出正常值范围以及异常值,除了用基于 IQR 的算法外,还可以通过箱线图更直观地找出异常值。
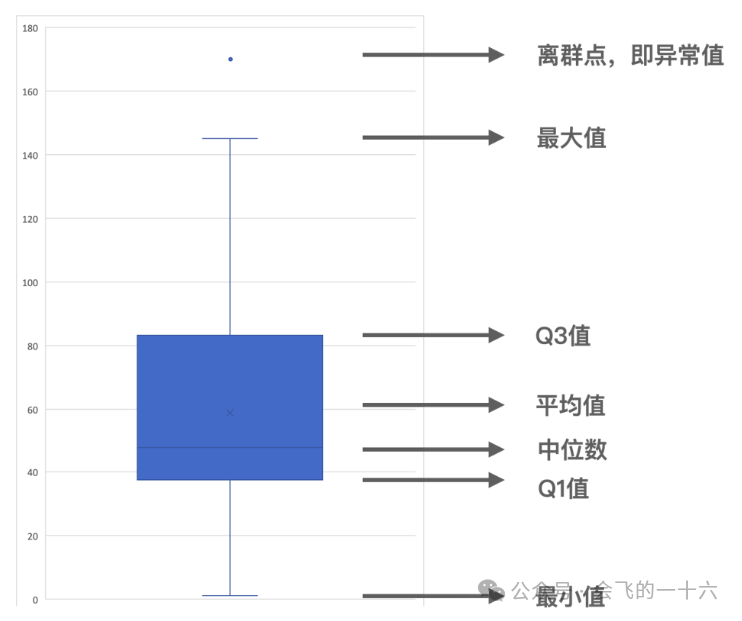
3.应用示例
渠道是重要的获客资源,其获客能力的趋势非常重要。若要分析如下三个渠道的新增用户情况,考察其每日新增用户数有无异常情况,看看能否得出有趣的结论。
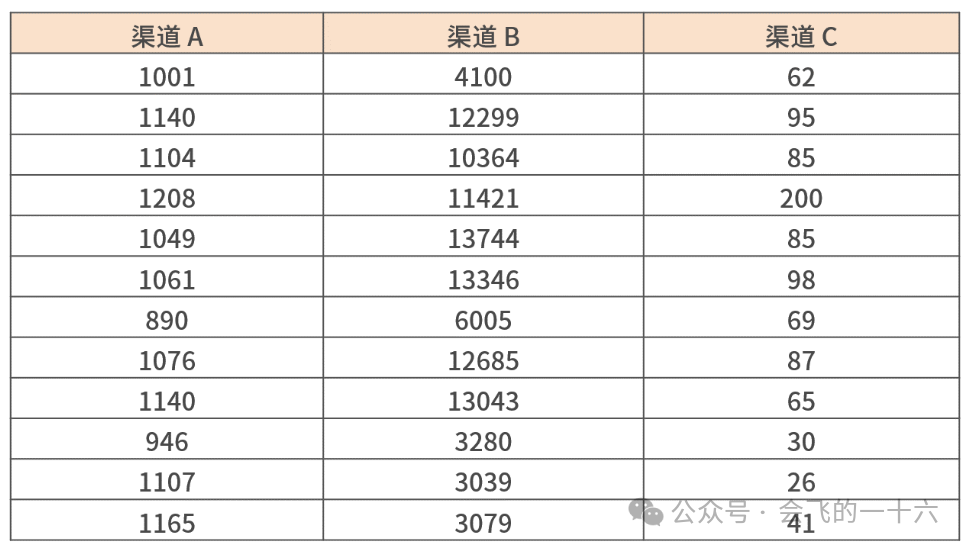
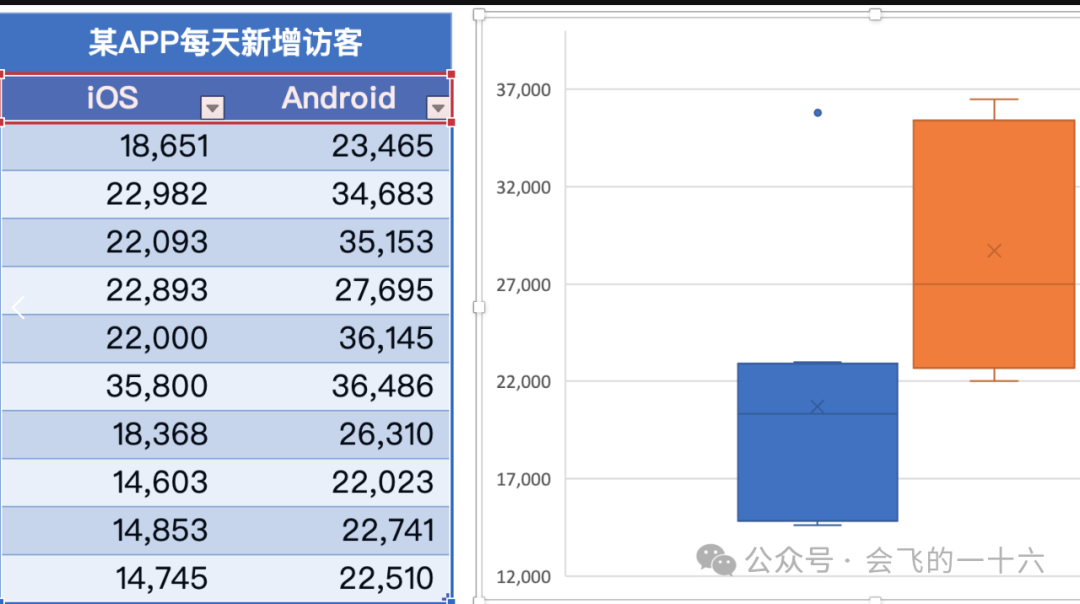
我们为这三个渠道做了如下箱线图,可以看出:
渠道 A 的获客能力排位第二,因为它的箱线图位置在渠道 B 和渠道 C 之间,同时稳定性对比其他两个渠道也较好,整体运营正常,并无异常值出现;
渠道 B 的获客能力排位第一,因为它的箱线图位置最上,同时稳定性也最差,因为箱线图中的箱体高度最高,整体运营正常,并无异常值出现;
渠道 C 的获客能力排位第三,因为它的箱线图位置最下,同时整体运营有一定问题,因为出现了一个异常值,需要单独排查原因,是否是拉新活动、渠道联合活动等因素导致的。\
操作:在 Excel 中实现描述性统计
Excel 作为最重要的数据分析平台,已内置了描述性统计的所有分析工具,能够简单快速地完成上述分析,并且结果极易解读。
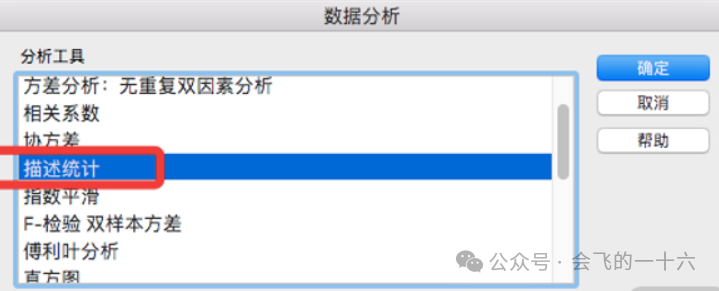
1.用 Excel 的“数据分析”工具包实现描述性统计

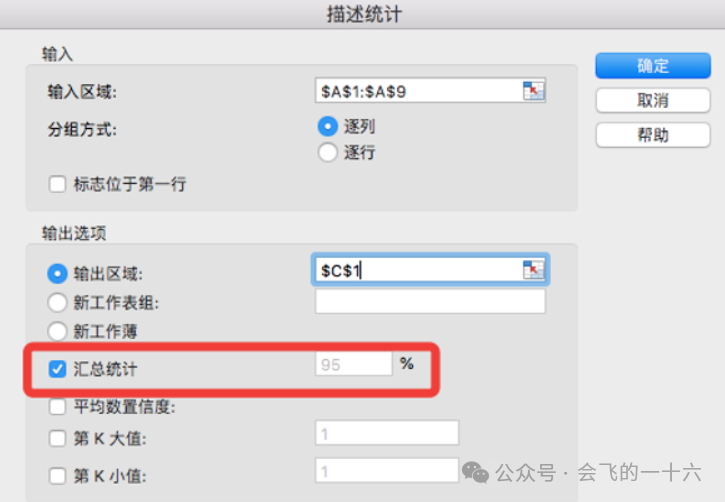
第二步:点击“描述统计”。
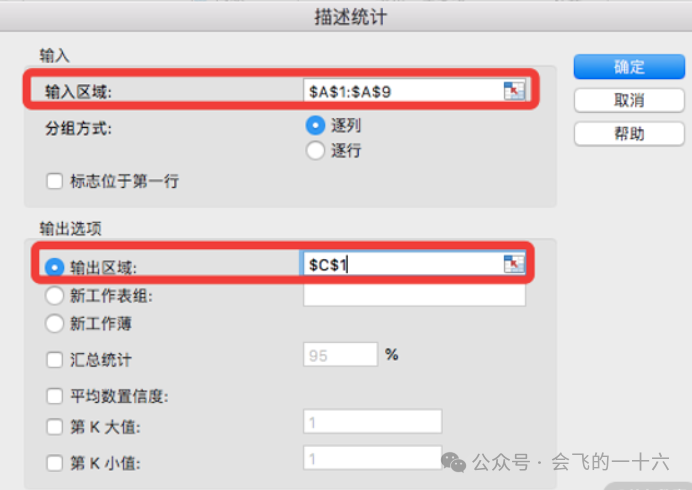
第四步:勾选“汇总”选项卡,其他默认即可。
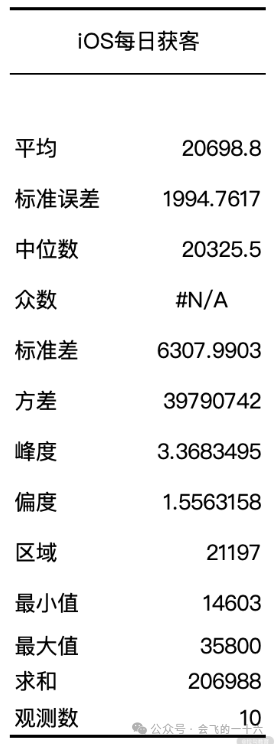
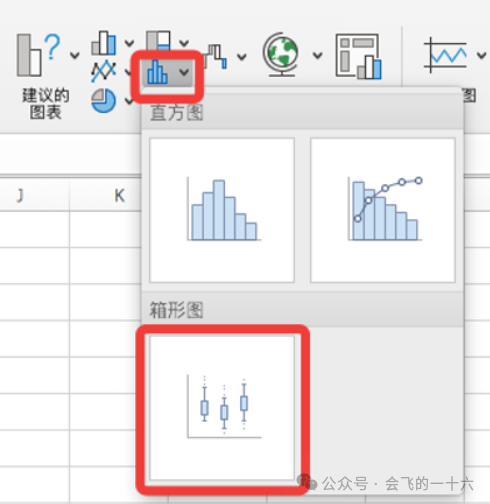
2.用 Excel 的“箱线图”分析异常值
在前文讲述分位数和异常值的算法时,可以通过计算公式和箱线图两种方法来寻找异常值。事实上,Excel 也提供了箱线图工具来帮助我们快速查找异常值。