
作者介绍
司马辽太杰,目前就职于一家国有企业,10余年数据库架构和运维管理经验,擅长常见关系型、NoSQL、MPP 等类型数据库。杭州桐庐人,业余热爱历史、足球,偶尔读点闲书。欢迎关注个人公众号“程序猿读历史”。

关系型数据库中的表连接(Join),是数据库重要的功能和常见的操作。然而广大多开发者却对 Join 却“爱之深、恨之切”。一方面是 Join 方便、简洁、高效,另一方面大部分公司的开发规范通常不允许过多表的 Join,比如网上广泛流传的阿里巴巴开发手册规范中就有一条:
【强制】禁止超过三个表Join。需要Join的字段,数据类型必须绝对一致;多表关联查询时,保证被关联的字段需要有索引。
那么数据库 Join 是什么,又是哪些实现方式?不同的实现的优缺点以及使用场景各是什么?本文以多篇经典数据库论文为材料,试着回答以上问题。由于个人能力有限,如有错误,请各位读者大大轻喷。

数据库中 Join,是指将数据库两个及以上的表数据关联的操作。 通过 Join,可以把两个及以上的表根据关联字段将它们的数据合并在一起,从而进行业务上更复杂的查询和分析操作。常见 Join 类型有 内连接、外连接(含左、右、全外连接)、交叉连接。内连接返回满足连接条件的行;外连接保留一侧或两侧表所有行,匹配行对应字段为空;交叉连接则是笛卡尔积。
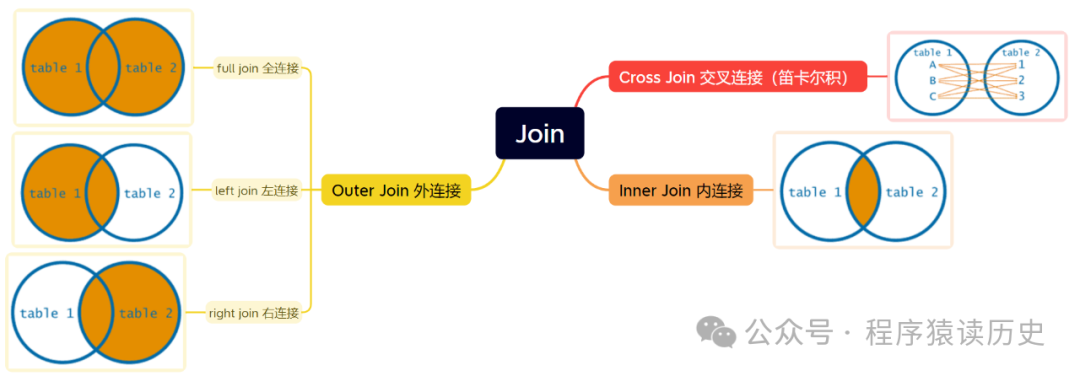
了解数据库 Join 前,先熟悉数学集合论中的笛卡尔积 。笛卡尔积是数学集合论中的一个重要概念,定义如下:两个集合 A 和 B,它们的笛卡尔积记作 A * B,即所有有序对 (a,b)的集合。其中 a ∈ A 且 b ∈ B,它的数学表达式是:
A * B = {(a,b)∣a∈A ∧ b ∈ B}。
代码示例如下:
function crossJoin(tableA, tableB):result = [] # 用于存储笛卡尔积的结果for rowA in tableA: # 遍历表 A 的每一行for rowB in tableB: # 遍历表 B 的每一行combinedRow = rowA + rowB # 将两行组合成一个新的结果行result.append(combinedRow) # 将结果行添加到结果集中return result # 返回结果集
笛卡尔积有两个重要特性:
集合中的元数是有序的,即(a,b) ≠ (b,a),除非 a=b。
集合 A 的元素个数是 m,集合 B 是 n,那么集合A 和 B的笛卡尔积的是 m * n。
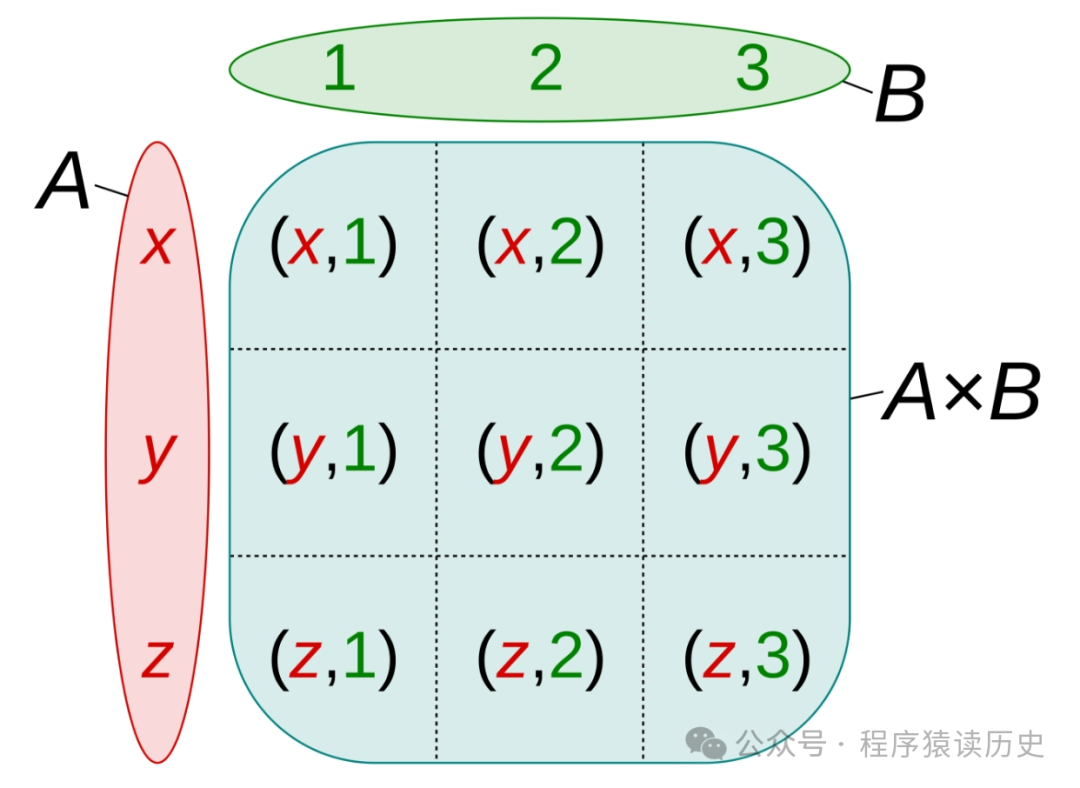
图来自Wikipedia
理解了数学中的笛卡尔积,也就明白了数据库的交叉连接(Cross Join)。数学中的集合对应数据库中表的所有行(tuples),集合中的一个元数就对应表的某一行(tuple)。当两个表进行交叉连接时,两表行数相乘的结果集就是笛卡尔积。
根据定义和特性可知,交叉连接算法的时间复杂度为 O(n * m),其中n和m分别是两个表的行数,因此笛卡尔积会使数据指数级增长,在数据库的实际生产中通常是要避免。但在一些特定场景下仍然有其应用价值,如构建测试数据、生成所有可能的组合、计算统计学中的概率问题、组合推荐算法中的产品配对等场景都可能使用笛卡尔积。
数据库的Join 算法有非常多类型,常见的主要有以下三种:Nested Loop Join、Hash Join、Sort Merge Join。下面将逐一介绍这三种算法的原理以及优缺点和使用场景。

2.1 算法原理
有了笛卡尔积的基础知识后,数据库 Join 的第一个算法 嵌套循环(Nested Loop Join,NLP) 自然就有了。当两个及以上的表Join时,先循环遍历表 A 的每一行,再对每一行循环遍历表 B 的每一行,检查它们是否满足连接条件,如果满足连接条件,就将这对行作为连接结果。通常我们将表A认为是驱动表或外部表、表B是被驱动表或内部表。

来自:Join Processing in Relational Databases
相信不少程序猿都听说过这样的告诫:两表Join时,最好将小表放在前面,大表放在后面,这样SQL性能会更好。可是根据定义,嵌套循环相比于笛卡尔积只是多了一个条件判断,其时间复杂度仍然是O(m * n),为什么非得要小表放前面呢?
确实从数学层面讲,NLP 算法的 时间复杂度是 O(m * n)( m 是外部表的行数,n 是内部表的行数,下同),它的性能与两表的连接顺序(Join Ordering)没有关系,这是纯数学理论。在计算机工程领域,算法的性能还需要考虑不同介质运行效率。
在数据库实际执行时,外部表小则可以更好地利用内存。比如外部表较小时,一次扫描就可以将外部表的数据加载到内存中,然后依次将逐行行数据与内部表匹配,从而有效的减少磁盘IO,提高数据库性能。另外,根据相关研究,计算机的指令执行机制对不同的执行顺序也会影响执行性能。这块我也不是特别懂,可以参考钱林松、张延清老师的《C++反汇编与逆向分析技术揭秘》 一书介绍,如下图。

图来自《C++反汇编与逆向分析技术揭秘》
2.2 相关变种算法
NLP 算法的思想非常朴实,工程实现也相对简单,在不少数据库中能看到他的身影,如 MySQL InndoDB 引擎在8.0.18 版本以前主要是使用NLP 算法。但是仔细分析 MySQL InnoDB 引擎,我们知道其是采用了NLP 的变种算法,NLP 算法的变种有块嵌套循环 (Block Nested Loop Join,BNLP)、索引嵌套循序 Index Nested Loop Join(INLP)等。
BNLP
BNLP和NLP区别,在于它不是每次读取外部表的 一行,而是读取外部表的 一块 block (又称页 apge) 数据 ,然后将这个块的数据与内部表进行匹配。这个过程可以显著减少对外部表的磁盘IO,从而大幅提升查询效率。BNLP 算法的时间复杂度是O(b * n),其中 b是外部表块数,n 为内部表行数。

来自:《Eficient Join Algorithms For Large Database Tables in a Multi-GPU Environment》
例如在BNLP 算法中,如果外部表包含 100万行,BNLP 一次读取多个页面(通常为几百行到千行,取决于表中一行存储的字符数),然后用这些行与内部表进行匹配,而不是每次都从磁盘读取一行外部表。MySQL InnoDB 块的默认大小为16kb。
因此,BNLP是比较适合 外部表大,内部表相对小,且有较多的内存进行缓存。在这种情况下,外部表会被分成多个块进行扫描,而每次扫描的外部表数据量较大,可以减少 I/O ,显著提高查询性能。
INLP
INLP 和NLP区别,是对内部表相关联字段添加 索引。当内部表上的连接字段有索引时,数据库可以快速定位到匹配行,避免全表扫描内部表,从而大大减少了扫描的次数和 I/O 开销。我们知道MySQL 表中的 B-tree 查询的时间复杂度是 O(log n)。 INLP 算法的时间复杂度是O(m * logn)。
INLP 是比较适合外部表小,内部表大、有索引,且是等值查询时,能高效的支持。在这种情况下,通过使用索引,避免了不必要的全表扫描,可以减少磁盘 I/O ,显著提高查询性能。
| 算法 | 时间复杂度 | 适用场景 | 优点 |
|---|---|---|---|
| Nested Loop Join (NLP) | O(m*n) | 外部表没有索引或连接条件复杂,不能利用索引加速查找。 | 实现简单、通用 |
| Index Nested Loop Join (INLP) | O(m*logn) | 外部表小,内部表大,且内部表有索引支持的连接条件。 | 通过索引加速查找匹配行,减少了全表扫描,提高了性能。 |
| Block Nested Loop Join (BNLP) | O(b*n),其中 b是外部表快数 | 外部表较大,内部表较小 | 通过每次扫描块查找匹配行,减少磁盘IO,提高性能 |
2.3 小结
从上可知,嵌套循环算法的原理是外循环遍历一张表,内循环遍历另一张表,逐行匹配。他的优点是简单直观,适用性很强,几乎可以适用于任何场景;缺点是性能并不高效。基于NLP而来的块嵌套循环、索引嵌套循环,则分别从按块处理减少 I/O 次数以及利用索引数据的有序性快速查找所需行,都在一定程度上优化了其性能 。

3.1 算法原理
通过前面 NLP 算法分析可知,它虽然朴实、简单、通用,但是扫描次数过多,复杂度是O(m * n),性能并不高。但根据其变种 INLP 算法分析可知,如果表中的数据是有序的,那么数据库匹配、扫描次数会大幅度降低,能避免很多无意义的计算。因此对于有序表数据进行 Join ,是否有其他算法呢?于是有了排序合并连接(Sort Merge Join,SMJ)算法。
SMJ 算法分两个阶段,先是对两个表进行排序,然后按照连接字段的顺序扫描两个表,将满足连接条件的元组(tuple)合并成单个关系。它的实现方式如下所描述:

来自:Join Processing in Relational Databases
将连接分为排序(Sort)和合并(Merge)两个阶段实现。对于一些有序的数据,比如索引、主键等列,已经具备了有序性,因此省略了Join 时排序(Sort)阶段的消耗。这也能解释阿里巴巴开发手册中,表Join时要求关联的字段必须建立索引。由上可知,SMJ 算法时间复杂度为,排序是:O(m * log(m) + n * log(n)),合并是:O(m + n)。对于有索引保证数据有序的场景,时间复杂度变为O(m + n)。
明白了SMJ 实现原理,它的特点和实现场景就不难理解了。有序的数据、小内存等条件下,SMJ 算法通常是会比NLP 更高效。
3.2 相关变种算法
同NLP算法类似,在计算机工程上SMJ 也有多个优化算法,比如基于块的排序合并连接(Block Sort Merge Join,BSMJ)、全局排序合并连接(Global Sort Merge Join,GSMJ)。
Block Sort Merge Join
BSMJ 以数据块为单位进行处理。对于没有顺序的数据,在排序阶段,将连接的表划分成若干个数据块,依次将这些数据块读入内存,对每个数据块按连接列进行排序。排序完成后,将排序好的数据块写回磁盘。在合并阶段,
合并已排序的数据块,每次从参与Join的表中各读取一个或几个数据块到内存中,使用类似双指针的方法对这两个数据块进行合并。再依次处理,直到其中一个数据块的指针到达末尾时,说明该数据块已处理完毕。此时,如果另一个数据块还有剩余记录,继续处理剩余记录,直到两个数据块都处理完。
因此,BSMJ的算法时间复杂度为,排序是:O(m * log(b) + n * log(b)),其中b是一次Join 内存中块的数量。合并是:O(2mn b )。对于有索引保证数据有序的场景,时间复杂度变为O(2mn b)。
Global Sort Merge Join
这些年相关学者提出了利用多 GPU 的并行计算 能力,从而提高SMJ 的算法查询性能。 在《Eficient Join Algorithms For Large Database Tables in a Multi-GPU Environment》一文中,提出了全局排序合并连接(Global Sort Merge Join,GSMJ)。
将输入关系分成等大小的块,其大小适合单个GPU的全局内存。每个GPU每次都以固定的速度从主机内存中取出一个块,然后使用高效的内核GPU基数排序算法在本地对块进行排序,并将其传回主机内存。所有GPU并行工作,直到对所有块进行排序。对于这一段我也不甚了解,想知道更细节的同学建议阅读原文。
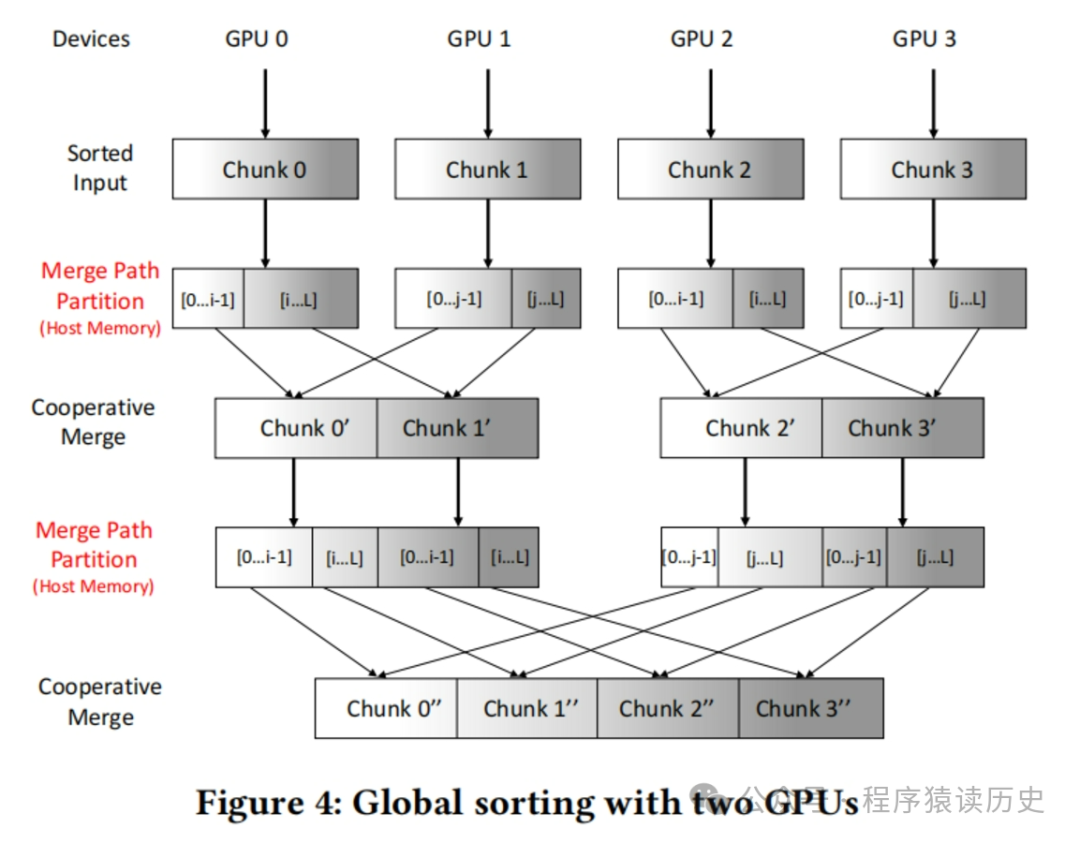
图来自:Eficient Join Algorithms For Large Database Tables in a Multi-GPU Environment
3.3 小结
在数据有序、数据规模就较大、内存有限时,排序合并连接 SMJ 相比于嵌套循环连接 NLP 性能效率更高,但是NLP 使用范围更广、简单、通用,在数据无序、内存较大情况下,NLP及其变种算法也可以有更高的效率。因此,在实际使用中需要根据具体情况判断,哪种算法更高效。

4.1 算法原理
排序合并连接(SMJ)是典型的空间换时间的算法。通过有序的索引,从而实现多表Join时的效率问题。然而维护索引本身也需要成本,业务系统的数据库中不可能在每个字段都添加索引。那在海量数据且又无序的Join时该如何处理?这就需要大名鼎鼎的哈希连接(Hash Join,HJ)出场了。其实现方式如下所描述:

来自:Join Processing in Relational Databases
哈希连接也是分为阶段,分别是构建(build )、探测(probe)。数据库会先选择一张表作为构建表,来构建哈希表。另外一张表作为探测表,同样对连接列的值计算哈希,使用这个哈希值与构建的哈希表中匹配。如果在哈希表中找到具有相同哈希值的行,则表示找到了当前行,生成连接结果。
因此,哈希连接算法的总体时间复杂度,构建和探测这两个阶段时间复杂度之和。在理想情况下(不考虑哈希值冲突,因此哈希算法非常关键),其时间复杂度为 O( m + n) 。
哈希连接是数据库常见和重要的算法之一,在大表、无序数据、等值的连接查询中有着非常高效的表现,也是Oracle、MySQL(8.0.18版本后)等数据库中常见的Join实现。
4.2 相关变种算法
传统的哈希连接也存在一些问题,比如哈希值冲突、内存溢出,并不能满足现代数据库的业务要求。另外,传统的哈希连接,即使在多线程处理,会出现多个线程将操作一个相同的 hash 表,此时线程之间就会争抢资源。这种情况数据库通常用加锁的方式解决,那么等锁的开销就会成为一大热点。
分区哈希连接 Partitioned Hash Join
分区哈希连接(Partitioned Hash Join ,PHJ)算法是基于现代CPU多核架构上演变出来的。和传统哈希算法一样,PHJ 算法共用了完全相同的 build 和 probe 两个步骤,但是 PHJ 在 build 之前会先对输入 relation 进行 partition,然后针对每个 partition 应用传统哈希算法。这充分使用了现代多核CPU的硬件优势。
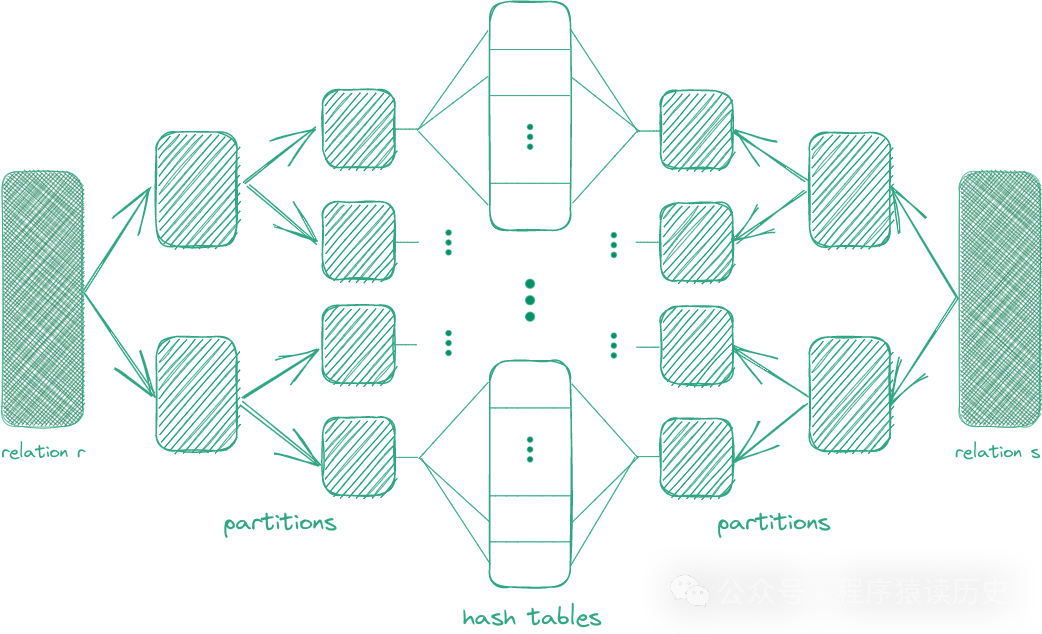
图来自:github.com/themisvaltinos/Partitioned-Hash-Join
除了利用多核CPU的分区优化,现在前沿的哈希算法,在单指令多数据的向量引擎(SIMD)、NUMA-aware、FPGA/GPU 加速等方面均有新的优化方案。对这块有兴趣的同学,可以找相关文章学习了解。
混合哈希连接 Hybrid Hash Join
传统的哈希连接,面对大数据量或者内存较小时,可能会出现OOM甚至系统崩溃。混合哈希连接在构建哈希表过程中,内存不能容纳所有数据块,会将部分哈希表数据溢出到磁盘,而在后续探查阶段,若需要访问溢出到磁盘的哈希表部分,再将其读入内存。如下图左边部分所示。
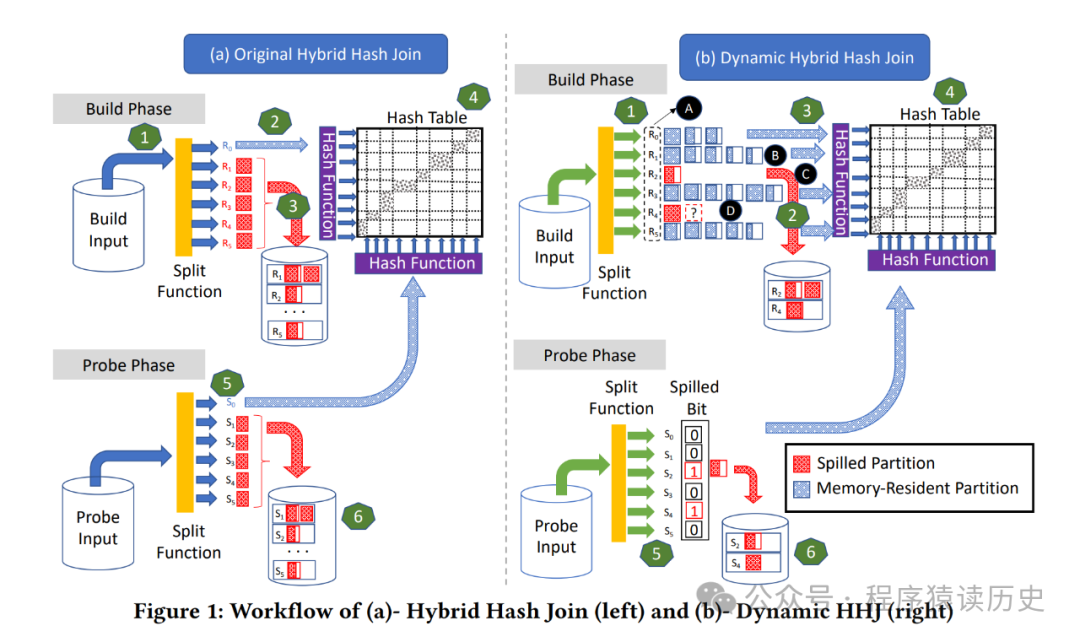
图来自:Design Trade-offs for a Robust Dynamic Hybrid Hash Join
在实际的数据库设计中,为了解决内存不足、动态控制hash 表大小,相关学者提出了动态混合哈希索引(Dynamic Hybrid Hash Join),上图右边部分所示。它增加了动态提出分区的操作,从而更加高效的利用内存特性。这块更详细的介绍请阅读原文。
4.3 小结
哈希连接的算法因其效率高,相对易实现,使用范围广特点,不仅在传统的关系型OLTP数据库,在MPP、分布式等领域也被广泛的使用。针对哈希连接海量数据性能低下、内存溢出等问题,也有相关优化方案,如分区哈希连接、混合连接等方案,来平衡内存与效率问题,也优化了常规哈希连接在不同条件下的性能 。

数据库多表 Join 的查询性能,除了连接算法以外,Join 表的顺序、路径选择、成本计算等对SQL 也有重要的影响。早在1979年一篇数据库优化领域的经典文章《Access Path Selection in a Relational Database Management System》,介绍了关系型数据库鼻祖——IBM System R 的优化器结构,这篇文章也被认为是数据库优化器的开山之作。
当多表 Inner Join 时,是具有结合律、交换律特性的,即内连接不同表的 Join 顺序在逻辑上是等价的,但不同的顺序连接方案,其执行代价可能大相径庭。如何从这若干种方案中,选择一个执行代价最低的策略,即是著名关系型数据库表连接顺序问题(Join Order Problem)。限于篇幅,这方面更多信息可以参考System R 文章。
最后简单概括下本文,本文主要介绍了数据库 Join 三种经典算法:Nested Loop Join、Sort Merge JOIN、Hash Join。他们各有优缺点,比如NLP通常性能较低,但其算法朴实、简单、通用,适用于大部分场景的的连接;SMJ则对有顺序数据,在Join时性能非常好;HJ 则对大数据量通常性能最好,但也要考虑内存溢出、哈希值重复等问题,并且哈希连接通常只处理等值查询(equijoin),对非等值查询,如 c1 > c2 等非等值查询下并不是最优选择。
参考
Join Processing in Relational Databases
《C++反汇编与逆向分析技术揭秘》钱林松、张延清
Eficient Join Algorithms For Large Database Tables in a Multi-GPU Environment
Design Trade-offs for a Robust Dynamic Hybrid Hash Join
Access Path Selection in a Relational Database Management System
https://docs.oracle.com/cd/E17952_01/mysql-8.0-en/nested-loop-joins.html






