 点击蓝字,关注我们
点击蓝字,关注我们

▍本文为TuGraph社区读者供稿。作者:罗元凯(北京航空航天大学PhD在读,香港理工大学联合培养PhD在读。他的博士研究方向是图神经网络、图表示学习 )
论文题目:Node Identifiers: Compact, Discrete Representations for Efficient Graph Learning
作者:罗元凯,李宏康,刘奇煚,时磊,吴晓明
单位:北京航空航天大学、香港理工大学、伦斯勒理工学院
日期:2025年2月25日
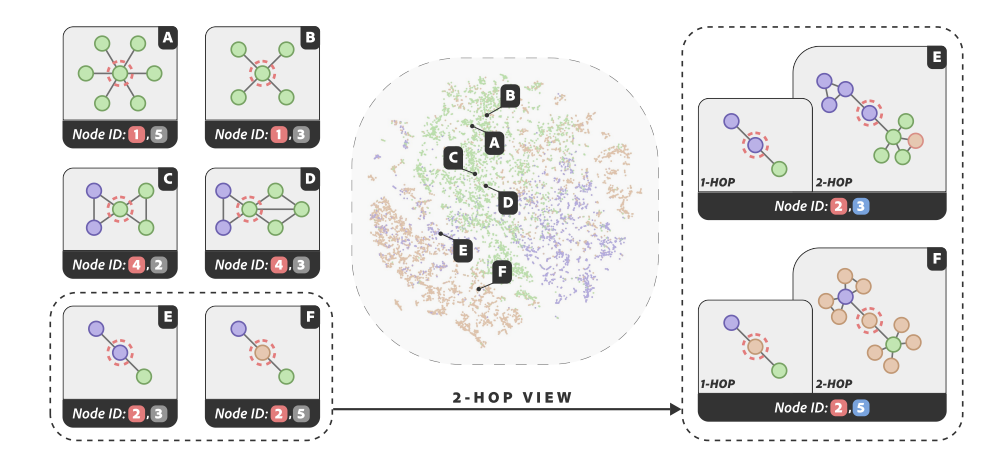
Node ID 示意图
我们简要介绍了一种名为 Node Identifiers(Node IDs) 的新型节点离散表示学习框架。该框架利用向量量化(Vector Quantization,VQ)技术,将经典图神经网络(GNNs)在多层邻域信息聚合后生成的连续嵌入(embeddings),压缩成高效、紧凑(通常6-15维)、并且可解释的离散表示(int4类型)。通过对34个基准任务(涵盖节点分类、图分类、链接预测及图聚类任务)的实证研究,Node IDs 在保证性能表现的同时显著降低了内存占用并加速了推理过程。更重要的是,这些 Node IDs 不依赖可以无缝结合现有的无监督和有监督 GNNs 方法,从而兼顾预测性能与高效推理。本研究为图表示学习在大规模场景下的应用提供了新的思路。
论文链接:https://openreview.net/forum?id=t9lS1lX9FQ
代码链接:https://github.com/LUOyk1999/NodeID
1、引言
在图数据上进行机器学习时,通常要考虑图的结构以及节点/边特征,这广泛应用于节点分类、图分类、链接预测及推荐系统等。现有的大部分图神经网络(GNNs)通过消息传递(message passing)迭代聚合节点邻域的信息,在众多任务上取得了优异的性能。然而,GNNs 在大规模场景中的推理效率往往受限于以下方面:
消息传递的高开销:推理时需要加载完整的图结构,对大规模图(可能包含数十亿条边)会带来巨大的计算与存储压力。
连续嵌入维度高且可解释性差:典型的GNN嵌入通常维度较高(128或256维),不仅影响存储和计算效率,也在一定程度上缺乏可解释性。
为此,我们提出了一个端到端的向量量化框架 NID,可在自监督或有监督训练过程中,不引入重构损失的前提下,将多层 GNN 嵌入直接量化为若干离散编码(Node IDs)。这些 Node IDs 具有以下特点:
1、紧凑与高效:通常只有6-15维,且类型为 int4,可显著提升推理速度并降低内存占用。
2、信息保留充分:在34个数据集的节点分类、图分类、链接预测和带属性图聚类任务中,Node IDs 在高效推理的同时,性能与最先进模型相当或更优。
3、可解释性:由于 Node IDs 以离散码本(codebook)的形式表示多层邻域结构,易于通过码字索引理解节点的聚类模式与语义差异。
基于此,我们的发现表明了 GNN 嵌入存在显著的冗余,而生成的紧凑离散 Node IDs 提供了图数据的高级抽象,这一发现可能为图数据的标记化处理和涉及大模型的应用提供帮助。
2、方法介绍
2.1 Node IDs 的生成

GNN 不同层节点表征的 t-SNE 可视化
上图展示了 GNN 在不同层次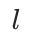 生成的节点表示的不同聚类模式。这种多样性来自于每一层图卷积的连续应用所造成的平滑效应 [1]。为了生成结构感知的 Node IDs,我们采用一个
生成的节点表示的不同聚类模式。这种多样性来自于每一层图卷积的连续应用所造成的平滑效应 [1]。为了生成结构感知的 Node IDs,我们采用一个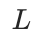 层的 GNN 来捕获多阶邻居结构。在每一层中,我们使用向量量化将 GNN 生成的节点嵌入编码为
层的 GNN 来捕获多阶邻居结构。在每一层中,我们使用向量量化将 GNN 生成的节点嵌入编码为 个代码(整数索引)。对于每个节点
个代码(整数索引)。对于每个节点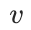 ,我们将 Node ID 定义为由
,我们将 Node ID 定义为由 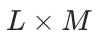 个代码组成的元组,结构如下:
个代码组成的元组,结构如下:
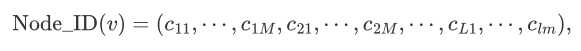
其中 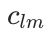 表示第
表示第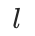 层的第
层的第 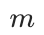 个代码。
个代码。
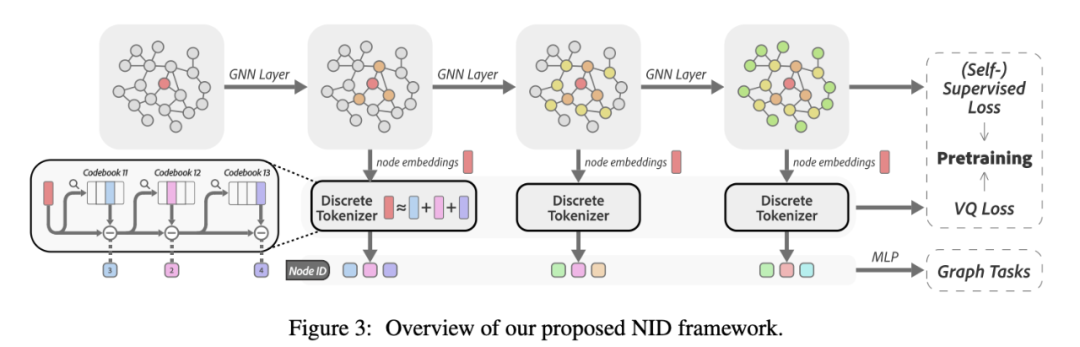
NID 架构图
如上图所示,在 GNN 的每一层
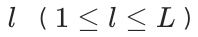 中,我们使用 RVQ [2]对节点嵌入进行量化,为每个节点
中,我们使用 RVQ [2]对节点嵌入进行量化,为每个节点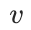 生成
生成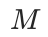 层次的代码。每个代码
层次的代码。每个代码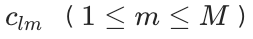 是由不同的 codebook
是由不同的 codebook 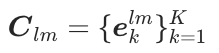 生成的,其中
生成的,其中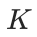 是 codebook 的大小。因此,总共有
是 codebook 的大小。因此,总共有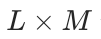 个 codebook,按
个 codebook,按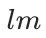 索引。设
索引。设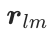 表示待量化的向量。请注意,
表示待量化的向量。请注意,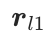 是 GNN 生成的节点嵌入
是 GNN 生成的节点嵌入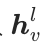 。当
。当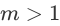 时,
时,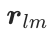 表示残差向量。然后,
表示残差向量。然后,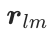 通过其对应codebook
通过其对应codebook 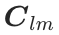 中的最近代码向量进行近似:
中的最近代码向量进行近似:
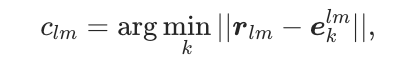
生成代码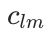 ,即最近代码向量的索引。
,即最近代码向量的索引。
我们提出了一个简单的通用框架,通过联合训练 GNN 和 codebook 来学习Node IDs(代码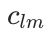 ),并使用以下损失函数:
),并使用以下损失函数:
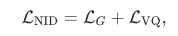
其中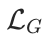 是(自监督/监督)图学习目标,
是(自监督/监督)图学习目标,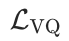 是向量量化损失。
是向量量化损失。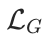 旨在训练 GNN 生成有效的节点嵌入,而
旨在训练 GNN 生成有效的节点嵌入,而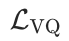 确保 codebook 向量与节点嵌入对齐。对于单个节点
确保 codebook 向量与节点嵌入对齐。对于单个节点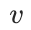 ,
,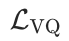 定义为:
定义为:
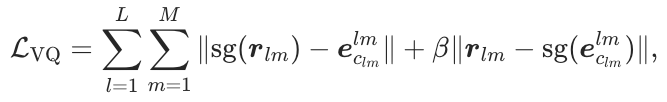
其中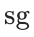 表示停止梯度操作,
表示停止梯度操作,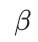 是权重参数。上式中的第一项是 codebook loss [3],它仅影响 codebook,使所选代码向量与节点嵌入接近。第二项是commitment loss [3],它仅影响节点嵌入,并确保节点嵌入与所选代码向量接近。
是权重参数。上式中的第一项是 codebook loss [3],它仅影响 codebook,使所选代码向量与节点嵌入接近。第二项是commitment loss [3],它仅影响节点嵌入,并确保节点嵌入与所选代码向量接近。
总结:
我们的 NID 框架与 VQ-VAE [3]及类似方法(如 VQGraph [4])在 codebook 学习方面有所不同,我们的训练目标 不涉及使用代码向量(
不涉及使用代码向量(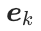 )进行重建任务,而是通过图学习任务(
)进行重建任务,而是通过图学习任务(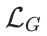 )引导 codebook 学习过程。
)引导 codebook 学习过程。
近期研究 [5,6] 表明,经过合适调参的经典 GNNs 在节点分类和图分类任务中仍能达到 SOTA 方法的竞争性表现。因此在实验中,我们使用了经典 GNNs(GCN、GAT、SAGE、GIN)进行 Node IDs 生成。
2.2 Node IDs 在下游任务中的应用
生成的 Node IDs 可以视为高度紧凑的节点表示,并直接用于各种下游图学习任务,如下所述。
节点预测任务包括节点分类和节点聚类。对于节点分类,图中的每个节点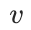 都与一个标签
都与一个标签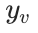 相关联,表示其类别。我们可以直接利用带标签节点的 Node IDs 训练 MLP 网络进行分类。预测公式为:
相关联,表示其类别。我们可以直接利用带标签节点的 Node IDs 训练 MLP 网络进行分类。预测公式为:
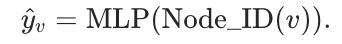
对于节点聚类,可以直接将基于向量的聚类算法,如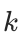 -means,应用于 Node IDs 以获得聚类结果。
-means,应用于 Node IDs 以获得聚类结果。
边预测任务通常涉及链接预测。目标是预测任意节点对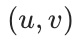 之间是否应存在一条边。预测可以通过以下方式进行:
之间是否应存在一条边。预测可以通过以下方式进行:
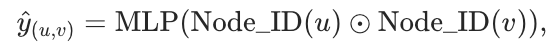
其中 表示 Hadamard 积。
表示 Hadamard 积。
图预测任务包括图分类和图回归。这些任务涉及为整个图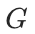 预测类别标签或数值。预测可以表达为:
预测类别标签或数值。预测可以表达为:
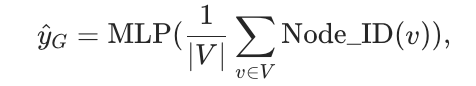
其中对所有 Node IDs 应用全局均值池化函数,生成图 的表示,然后输入 MLP 进行预测。
的表示,然后输入 MLP 进行预测。
注意,选择读取函数(如均值池化)被视为一个超参数。
3、实验结果
学习得到的 Node IDs 通常由 6-15 个 int4 整数组成,可作为高效的节点表示。在多个任务中,它们表现出与 SOTA 方法相当或更优的性能,同时显著提升计算速度和内存效率。
3.1 监督表示学习
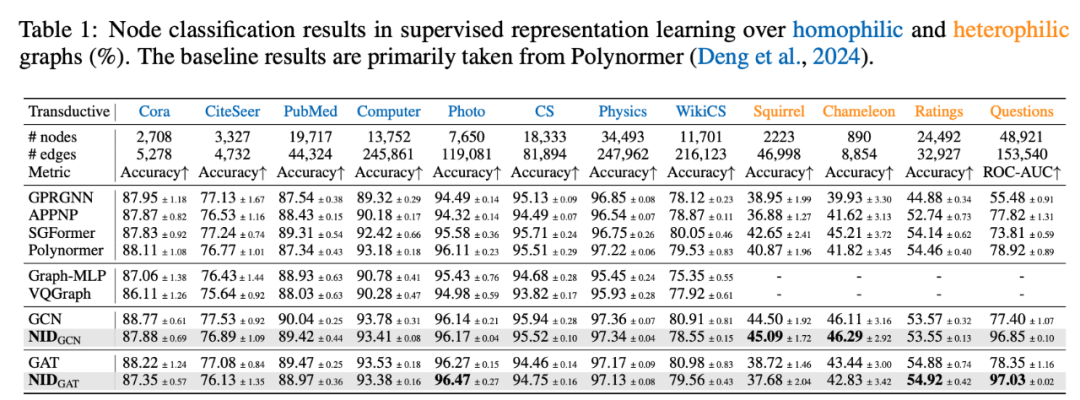
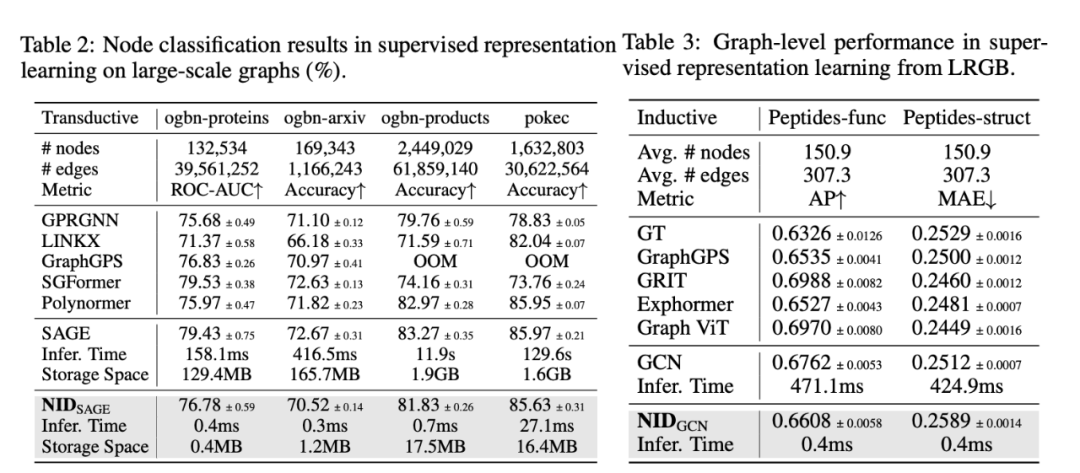
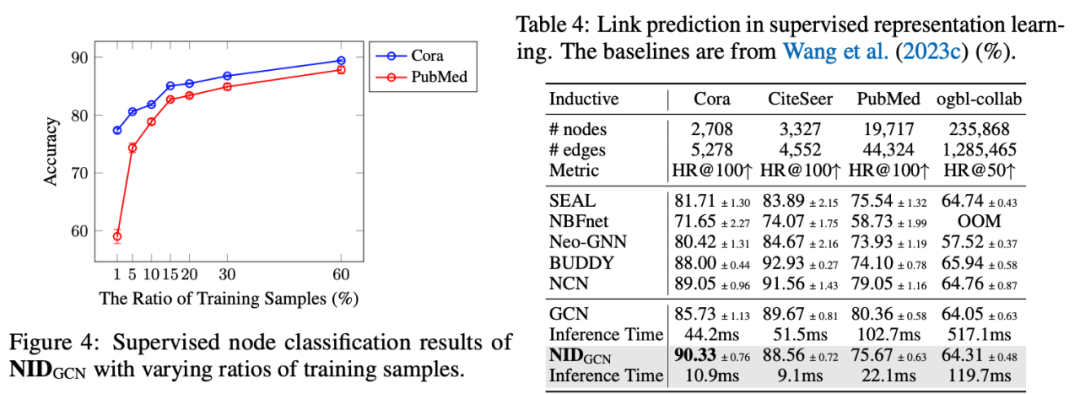
监督学习实验结果
3.2 无监督表示学习
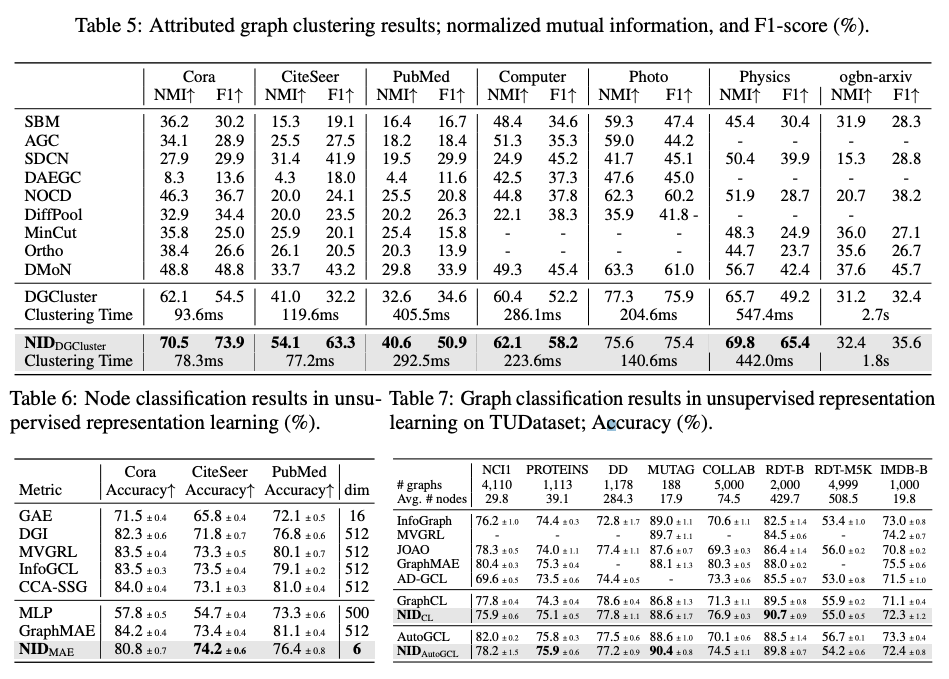
无监督学习实验结果
3.3 Node IDs 的分析
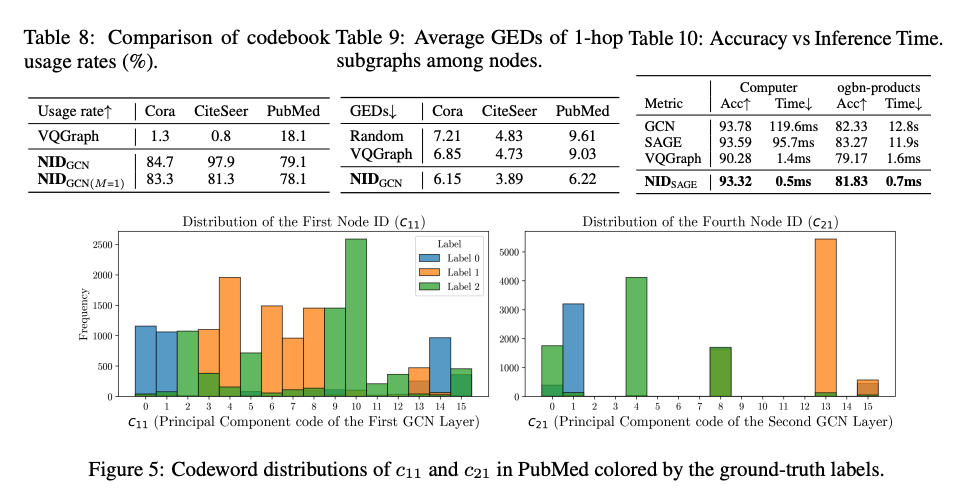
Codebook崩:发现 VQGraph 存在严重的 codebook 崩溃问题,即大多数节点被量化为少数几个代码向量,导致大部分 codebook 未被使用。相比之下,NID实现了高 codebook 使用率,有效避免了 codebook 崩溃。
可解释性:观察 Node IDs 的码字索引分布,发现其可以有效区分不同类别的节点,具有较强的语义可解释性。
子图检索:利用 Node IDs的Hamming距离 进行子图匹配,效果优于现有的 VQGraph 的结果。
推理加速:在 ogbn-products (节点数百万级)上,NID 推理时间从11.9s降至0.7ms。
4、总结
我们提出的 NID 框架可在自监督或有监督训练过程中,不引入重构损失的前提下,将多层 GNN 的连续嵌入直接量化为紧凑、离散且可解释的 Node IDs。通过广泛的实验与消融研究,我们验证了 Node IDs 在多任务、多数据集上的 高效性与实用性。相比传统 GNN 嵌入,Node IDs 不仅大幅降低推理时的内存与计算开销,而且在一系列场景中保 持了有竞争力甚至更佳的预测性能。这一方法为在大规模图上实现实时、高效的推理提供了新的⻅解,也为后续在图数据与大模型结合(如图标记化、LLMs 应用)带来了新的思路。
[1] Qimai Li, Zhichao Han, and Xiao-Ming Wu. Deeper insights into graph convolutional networks for semi- supervised learning. In Thirty-Second AAAI conference on artificial intelligence, 2018.
[2] Julieta Martinez, Holger H Hoos, and James J Little. Stacked quantizers for compositional vector compression. arXiv preprint arXiv:1411.2173, 2014.
[3] Aaron Van Den Oord, Oriol Vinyals, et al. Neural discrete representation learning. Advances in neural information processing systems, 30, 2017.
[4] Ling Yang, Ye Tian, Minkai Xu, Zhongyi Liu, Shenda Hong, Wei Qu, Wentao Zhang, Bin CUI, Muhan Zhang, and Jure Leskovec. VQGraph: Rethinking graph representation space for bridging GNNs and MLPs. In The Twelfth International Conference on Learning Representations, 2024.
[5] Yuankai Luo, Lei Shi, and Xiao-Ming Wu. Classic gnns are strong baselines: Reassessing gnns for node classification. arXiv preprint arXiv:2406.08993, 2024.
[6] Yuankai Luo, Lei Shi, and Xiao-Ming Wu. Unlocking the potential of classic gnns for graph-level tasks: Simple architectures meet excellence. arXiv preprint arXiv:2502.09263, 2025.

·END·

欢迎关注TuGraph代码仓库✨
https://github.com/tugraph-family/tugraph-db
https://github.com/tugraph-family/tugraph-analytics






