随着语言模型规模的不断增长，模型对于计算资源的消耗呈指数级增长，推理成本和访问效率已成为限制大模型规模应用的关键瓶颈。尤其是在实时应用程序中，资源受限的条件下，这一问题尤其突出。为了应对这一挑战，专家学者们提出了多种解决方案，如专家混合模型（Mixture of Experts, MoE）和乘积键存储（Product Key-based Memory, PKM）。然而这些方法在推理过程中仍然会高内存占用，消耗大量的计算资源。基于这一背景，本次为大家带来深度学习领域顶级会议ICLR 2025的文章《Ultra-Sparse Memory Network》。这是字节跳动豆包大模型团队近日发布的一种全新的稀疏模型架构——超稀疏存储网络（Ultra-Sparse Memory Network）。通过引入大规模、超稀疏的存储层，显著降低了推理延迟，同时保持了模型的性能。实验表明，UltraMem不仅在推理速度上超越了MoE模型，还具有更优秀的规模扩展性，为未来构建更大规模的模型铺平了道路。
一. 引言
在大预言模型（Large Language Models，LLMs）的推动下，自然语言处理（Natural Language Procressing，NLP）领域的最新研究成果在扩展时往往会产生指数级的计算资源消耗，这在实时应用程序中构成了严重的挑战。为了解决这一计算难题，MoE和PKM相继问世。MoE有选择地激活参数，显著提高了训练效率，但由于存储访问增加而延长了推理时间；PKM以更少的值嵌入保持常数级的存储访问，但其推理效果明显比MoE差。
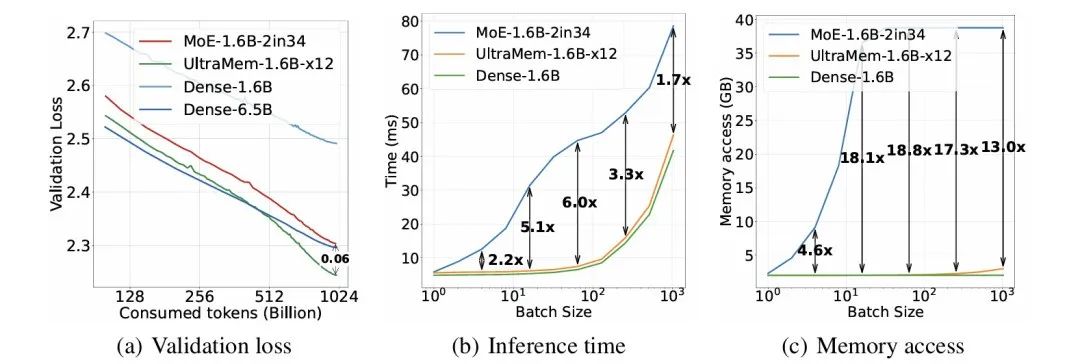
图1 MoE 和 UltraMem 在相同计算量下的验证损失、推理时间和内存访问对比
正如上图（b）所示，尽管MoE模型具有相同的计算成本（有十二倍的总参数量但每次激活的参数量相同），但根据批量大小的不同，MoE模型的推理运行速度要慢2到6倍。如上图（c）所示，这种推理缓慢源于高存储访问需求，凸显了其在推理场景中的效率低下。因此，目前主要挑战是如何达到甚至超越MoE模型的输出质量，同时保持与密集模型相当的存储访问效率。
在本文中，作者介绍UltraMem，这是一种建立在PKM理念之上并有所改进的架构。UltraMem集成了大规模、超稀疏存储层，可以显着提高计算效率并减少推理延迟，同时保持甚至改进各种基准测试的模型性能。该架构不仅支持在资源有限的环境中部署高效的语言模型，而且还为构建更大的模型开辟了新的途径，而无需在此之前被认为是必需的高昂推理成本。
总而言之，这篇文章作出了如下贡献：
1. UltraMem较PKM的推理质量有了大幅增强，并且在同等规模上优于MoE。与PKM相比，UltraMem真正具备在大量计算资源上训练大规模模型的先决条件，并经过了全面的实验验证。
2. 与MoE相比，UltraMem在推理期间的存储访问成本显着更低。 在常见的推理批量大小下，在相同的参数和计算下，它的速度最多比MoE快6倍。UltraMem的推理速度几乎与计算资源相同的稠密模型相同。
3. 论文验证了UltraMem的扩展能力。与MoE类似，UltraMem具有很强的扩展能力，甚至观察到比MoE更强的扩展能力。
二. 相关工作
• 专家混合模型（MoE）：在2017年Shazeer团队提出的MOE，在2022年Fedus团队在大语言模型中引入了MoE。其基本工作方式是：模型中每个词元（token）每次匹配一位专家进行推理，从而在不增加计算量的情况下增加模型参数量。在2022年Rajbhandari团队引入了“共享专家”的概念，其中每个token利用一些共有的专家和一些独有的专家。后来的研究集中于改进MoE的门控功能，包括token选择、不可训练的token选择和专家选择，这些改进主要是为了解决专家不平衡的问题。在2024年Liu团队和Dai团队选择将专家分成更小的部分，同时每个token激活更多的专家，实现了显著的性能改进。同时Krajeski团队进行的研究仔细探索了粒度和增加专家数量的好处，同时调查了与MoE相关的规模定律。在本文中，使用细粒度的MoE作为基线，其中MoE的粒度设置为2。这意味着每个专家的大小是原始多层感知器(MLP)的一半，每个token有两个专家被激活。
• 大型存储层（Large Memory Layer，LML）：Lample团队在2019年首次引入了大型存储层的概念，称为PKM（Product key memory），可以类比地理解为MoE的最小化切分。Kim和Jung在2020年引入了类似于MoE中共享专家的概念，允许PKM和MLP并行运作。Csordas团队在2023年通过删除Softmax操作对PKM进行了轻微改进。2024年PEER技术改进了PKM中参数的激活策略，激活内部维度为1的小专家，实现了显着的效果提升。然而，目前对PKM的研究仅限于较小的模型规模，即使是PKM的最新改进版本也只在某些情况下优于MoE。此外，目前的PKM还不具备适合大规模训练的特征。
• 张量分解（Tensor Decomposition）：张量分解技术将原本较大的张量分解为一系列小矩阵或张量。在深度学习研究中，此类方法通常用于在训练期间作为大张量的近似压缩，达到节省计算和参数的目的。Jegou团队在2010年提出了乘积量化（Product quantization）技术，该技术将一个向量分解为多个子向量，使人们能够使用更少的子向量重建原始向量，从而减少模型参数。在2024年Bershatsky团队使用了多个矩阵和一个核心张量，在微调阶段训练这些参数，并在训练结束时以塔克分解（Tucker Decomposition）的方式重建原始的张量，以降低训练成本。作者团队借用了这一方法来改进PKM的键值检索。
三．UltraMem
3.1预备知识
这里论文首先介绍了原版的基于Product key的大存储层（LML），它是作者团队提出的方法的基础。PKM的概念是在之前的工作中由Lample团队提出的。在他们的方法中，作者将外部存储模块整合到语言模型中，扩展模型参数的同时保持类似常数的计算复杂性。总体结构图如（b）所示。
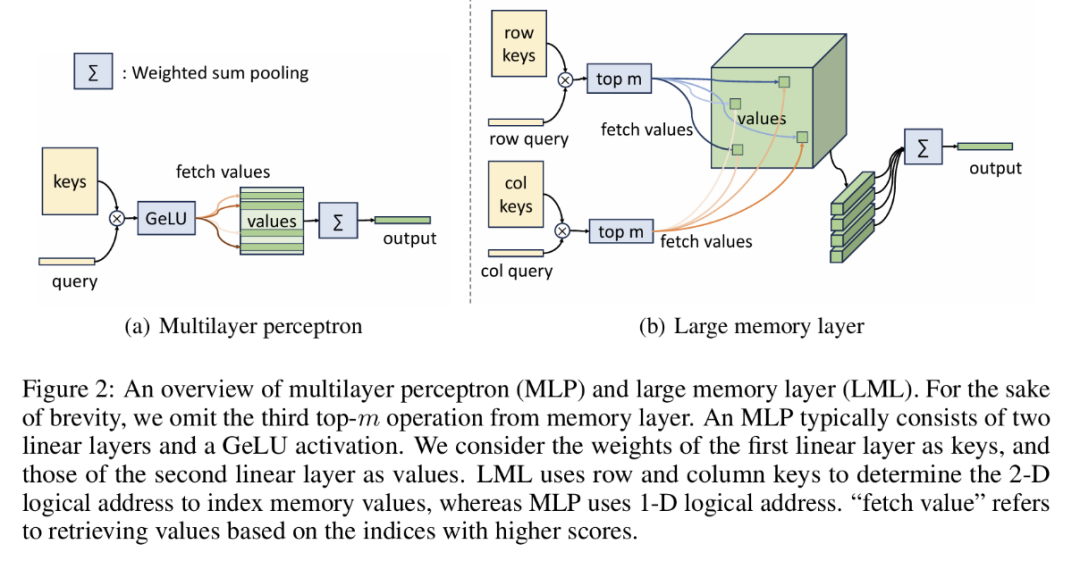
图2 MLP和LML结构
一个存储层大致包含两部分：键向量和值向量。为了从存储层中检索信息，需要将查询向量与键向量相乘来获得评分，评分越高这个键所对应的值的价值越高。形式化表示为：
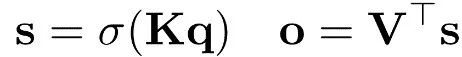
其中s表示评分，σ是一个非线性激活函数，o是输出。注意力层和多层感知器层（Multilayer perceptron，MLP）都遵循上述公式。其中注意力层负责存储上下文信息，激活函数使用SoftMax；MLP层存储通用的世界记忆，激活函数使用GeLU函数。PKM将上述两个存储层的参数量扩展到N>106，但每次只激活评分最高的前m个值向量，其中m是一个用来控制模型稀疏程度的超参数。尽管值向量可以有选择性地获取，但是和值向量的数量一样多的键向量确需要全部参与计算，因为要选出评分前m的值向量。为了减少键向量的计算量，乘积键技术应运而生。借鉴乘积量化的思想，该技术使用了二维的逻辑地址来进行存储信息的提取。二维逻辑地址一般是一个n*n的矩阵，其中n=√N，其中 (i, j) 的值表示物理地址在n*i+j
的存储数据。基于上述策略，逻辑评分被表示为一个矩阵，并且可以被进一步分解为行分数和列分数的求和：
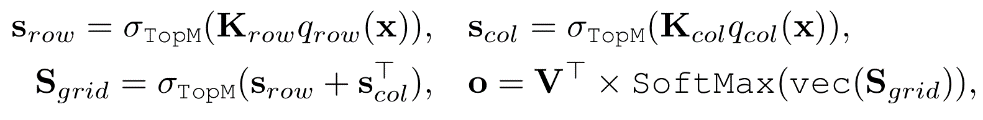
其中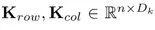
，而函数
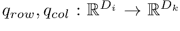将内部参数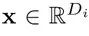
转化成行查询和列查询，函数
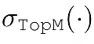保留输入中前m个最大元素，并将其余元素设置为负无穷，然后通过广播机制实现矩阵形状不匹配的矩阵加法。值得注意的是，从上面的第二个式子中移除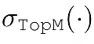函数对结果没有任何影响，使用这个函数的唯一理由只是减少Sgrid的计算成本。
3.2 架构改进
• 大量改进PKM：
1) 移除了原公式中的SoftMax函数，这种方法已经在其他研究中得到了充分的验证；
2) 在查询和键的部分使用层归一化技术，用来保证训练的稳定性；
3) PKM建议使用0.001的恒定学习率来学习这些参数，这比其他参数的学习率高得多。实践证明，逐渐减小学习率会带来更多的训练优势；
4) PKM使用线性层来生成查询，在该线性层之前添加因果深度卷积层来增强查询；
5) 与群组查询注意力（Group Query Attention，Ainslie et al，2023）类似，在两个关键集中共享查询。这可以将生成查询的计算成本减少一半，而对性能的影响很小。
6) 通过将值的维度数减半，将值的数量就增加一倍。在保持激活值参数不变的情况下，增加了激活值的多样性，模型效果进一步提高。为了使输出与隐藏层维度保持一致，作者在聚合输出上添加了线性层。
• UltraMem整体架构
下图展示了基于预层归一化（Pre-LayerNorm）Transformer 架构的 PKM 和改进的 UltraMem 结构。PKM 替换 MLP 或与更深层中的 MLP 并行操作（Kim & Jung, 2020），然后用记忆层替换 MLP。
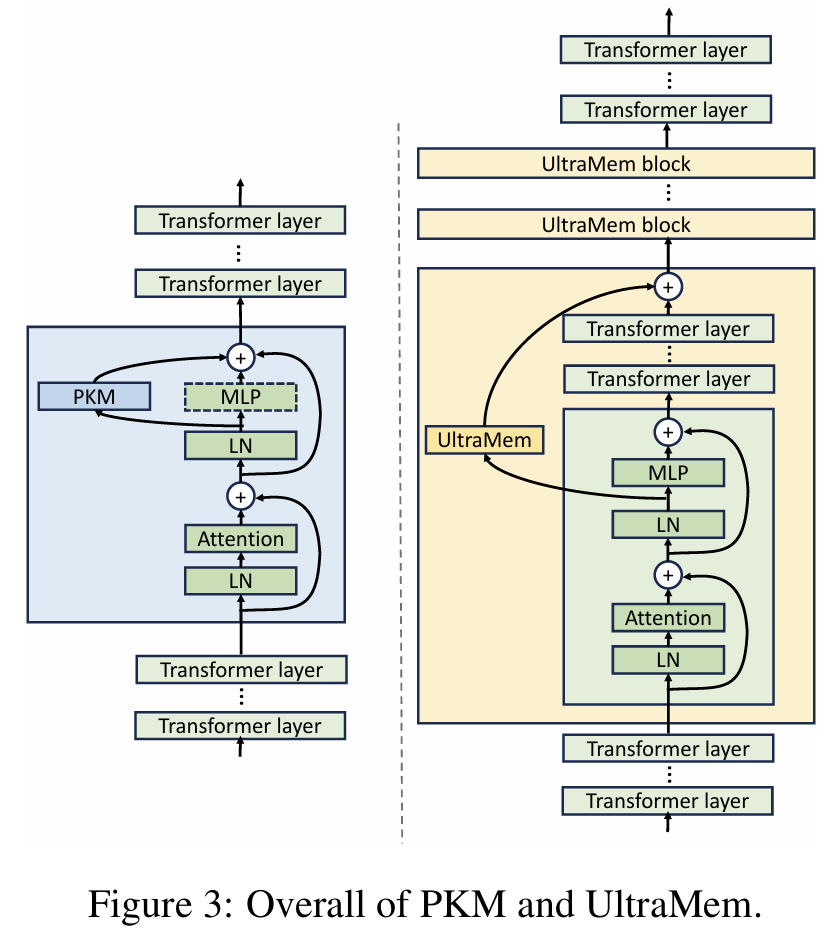
图3 PKM和UltraMen整体结构图
论文注意到 PKM 有三个缺点：
1.随着值大小N显著增加，查询可能更难找到正确的值。
2.乘积键分解在检索拓扑上引入了偏差。例如，假设(i, j) 是 top-1 分数的逻辑地址，那么 top-2 分数必须位于行 i 或列 j ，这大大限制了 top-m 选择的多样性。
3.在大规模参数训练期间，存在多 GPU 计算和通信不平衡的问题，因为完整的模型参数无法放在单个 GPU 上。
为了缓解问题1和3，论文将这个大记忆层分解为多个较小的记忆层，这些层分布在 Transformer 层的固定间隔中。此外，这种跳跃层结构允许论文重叠执行记忆层和 Transformer 层，因为记忆层在训练期间主要是内存密集型的。
• Tucker分解查询关键字检索（TDQKR）。这里探索了一种更复杂的乘法方法来缓解问题1和问题2，其中采用了Tucker分解（Malik & Becker, 2018）来代替乘积量化。TDQKR的整个过程如下图所示。具体来说，Tucker分解通过秩为r的矩阵乘法来估计网格评分。
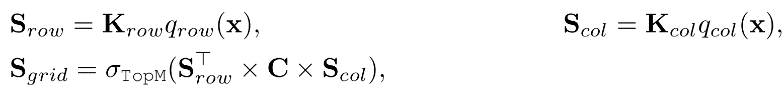
其中Srow ,Scol∈Rr×n 且C∈Rr×n 是Tucker 核心，这是一个具有随机初始化的可学习参数。为了生成形状为r×n的行和列分数，查询和键的维度被重新塑形对应于下图的步骤1。
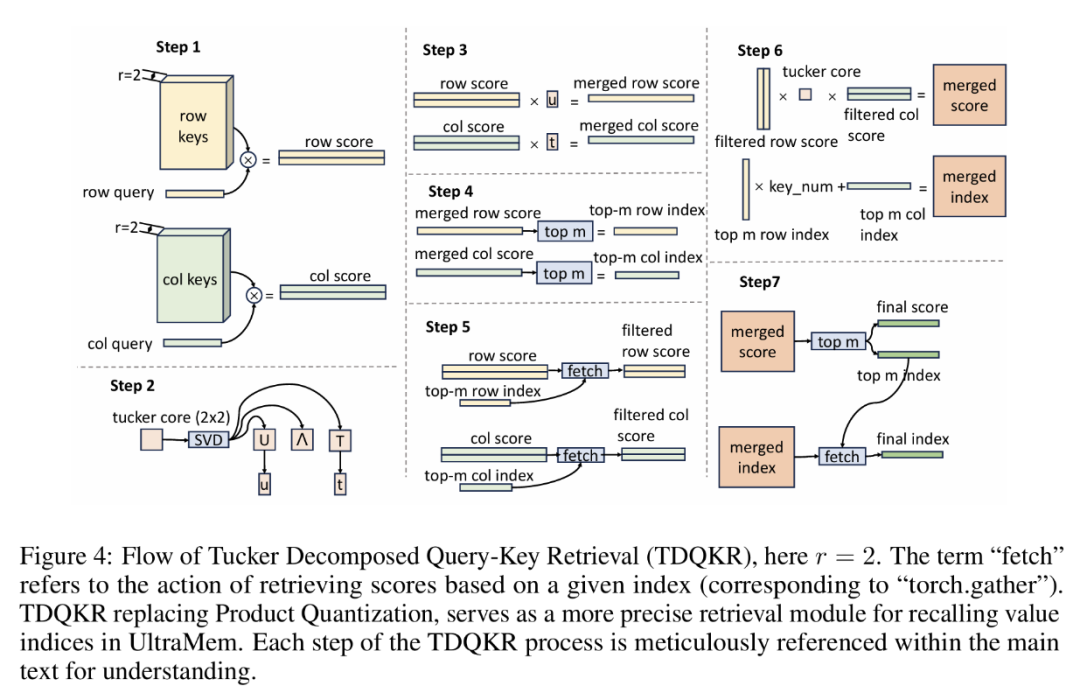
图4 TDQKR流程图
然而Sgrid 的计算方式在实际应用中效率不高，因为top-m操作无法像乘积量化那样通过等效的两阶段top-m技术来简化。因此，论文提出了一种近似的top-m算法来解决这个问题。关键是对Tucker核心进行秩为1的近似，这样整体的top-m就可以通过以下方式来近似：
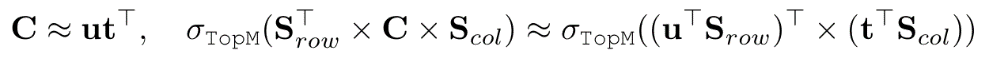
其中u, t ∈ Rr×1。注意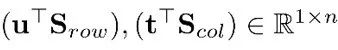
是行向量，那么两阶段的 top- m 技术涉及到近似目标
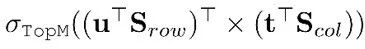，对应于上图的步骤3。总的来说，论文在行和列分数上进行近似的 top-m 操作，过滤掉非顶部元素，然后作者在Sgrid上使用具体的最终 top-m 操作，保持索引评分的精确性：
其中 ITP(·)是一个二值函数，它将前m个元素转换为 1，其余元素转换为 0。公式8和9对应于上图的步骤4和5，公式10对应于图4的步骤6和7。至于秩为1 的近似，论文利用奇异值分解（SVD）来分解 Tucker 核心，其中 u 和 t 分别是对应于主要奇异值的左奇异向量和右奇异向量，这对应于上图图的步骤2。
最后同样重要的是，当非最大奇异值与最大奇异值一样大时，应该关注近似误差。为了缓解这个问题，在训练过程中引入了一个辅助损失，通过约束非最大特征值来控制引入的近似误差：
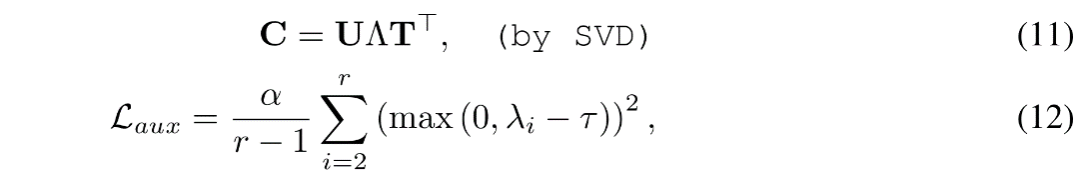
其中, Λ表示矩阵C的特征值，按降序排列，τ作为一个边界值，以防止C退化为秩为1的矩阵，α是损失的系数。
• 隐式值扩展（Implicit Value Expansion，IVE）。尽管使用了稀疏架构，但由于大量的内存访问，维护一个大型内存表在训练过程中仍然很昂贵。为了减少内存访问并扩大内存大小，论文提出使用虚拟内存作为隐式值扩展。给定一个虚拟扩展率 E > 1，虚拟内存将内存表扩展到 E 倍的大小。作者将虚拟内存设计为原始内存值V的多个重新参数化，将其称为物理内存。然后，利用 E 个线性投影器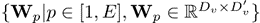
，对应于第p次重新参数化的虚拟内存块可以定义为：
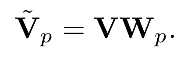
然后，整体的虚拟内存是虚拟块的连接，表示为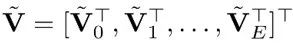
。注意，虚拟值的维度并不一定与物理值的维度一致。
应用虚拟内存是直观的，为了适应虚拟内存的大小，键的大小扩展为√E 倍。此外，建议对虚拟内存进行随机打乱，以消除之前由行和列评分引入的一些不必要的索引拓扑。具体来说，如果虚拟内存表通过连接合并，每个内存值及其扩展将位于逻辑地址中的同一列，因此可以更频繁地同时选择。
对于虚拟内存的简单重新参数化仍然引入了大量的计算，即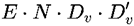
，以及 E 次 GPU 内存访问。一个更好的方法是按需进行重新参数化。也就是说，论文将逻辑地址扩展为三元组 (i, j, p)，其中 (i, j) 是原始逻辑地址，p 是虚拟内存块的索引，然后同时进行求和池化和计算虚拟内存值。因此，原公式被重写为：
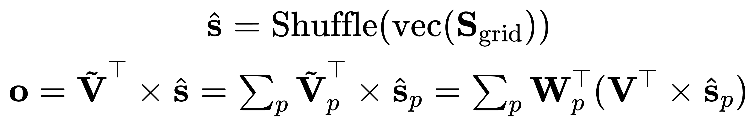
其中， 表示对应于第 p 个虚拟内存块的分数。通过上述公式，可以根据虚拟块索引首先查找和汇总值，然后将减少的物理值直接转换为减少的虚拟值。这个技巧将额外计算从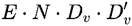
减少到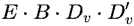
，其中 B 是批次中的标记数，并且除了线性投影器外几乎没有额外的GPU内存访问。下图显示了IVE的流程。
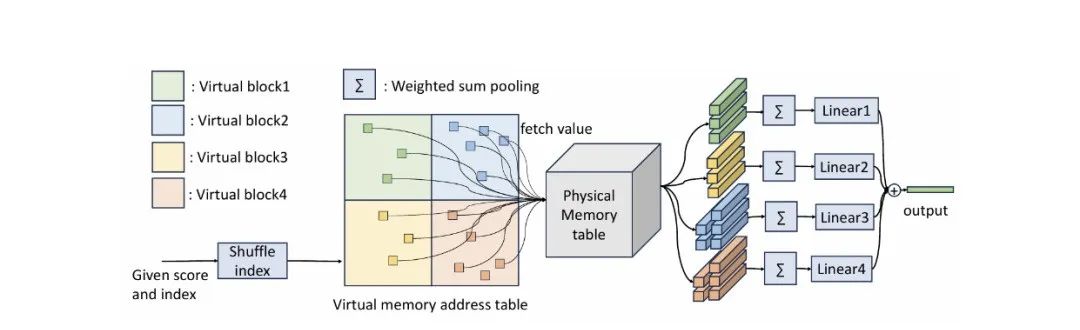
图5 IVE流程图
• 多核评分机制（Multi-core Scoring，MCS）。PKM在每个值的维度上共享一个单一的评分。实践证明，为单个值分配多个评分可以提高性能。因此，论文将Tucker核心 C 重写为一系列组件核心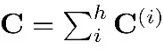
。这允许作者使用
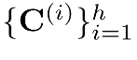来生成单独的分数映射 。显然，
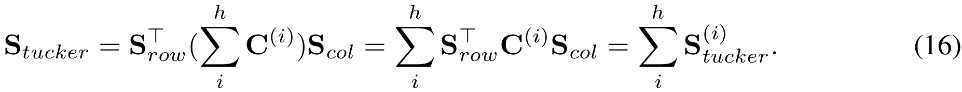
在保留在聚合分数Stucker上进行的前m个操作，同时在垂直分割的值表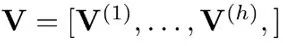
上应用单独的分数
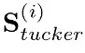，其中
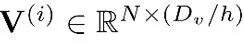，也就是说
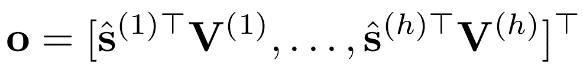
当这种技术与IVE（信息价值评估）结合时，实现了分割物理内存值而不是虚拟内存值，以保持计算的等价性。
• 改进初始化。PKM 使用高斯分布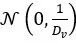
来初始化值。由于PKM对分数应用了 Softmax，因此池化输出的方差为
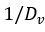。作者认为 LML 应该被视为类似于 MLP 的组件，因此应该使用类似于 MLP 的初始化方法。在训练之前，MLP 的输出通常遵循高斯分布
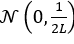，其中 L 是总层数。文章使用
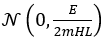来初始化值，其中 m 是激活值的数量，H 是头数，E 是值扩展次数。作者为了确保 UltraMem 的输出分布是
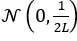，需要确认 top-m 分数的平均值为1。
四．总结
本文介绍了 UltraMem是一种新型的超稀疏存储网络架构，旨在解决大规模 Transformer 模型在推理时面临的高内存访问成本和计算复杂性问题。UltraMem 通过引入大规模超稀疏存储层，显著降低了推理延迟，同时保持甚至提升了模型性能。其主要创新包括：Tucker 分解查询键检索（TDQKR）、隐式值扩展（IVE）和多核评分（MCS）。实验表明，UltraMem 在推理速度上比 MoE 快高达6倍，且在扩展性和模型性能上优于现有方法。该架构不仅适用于资源受限的实时应用，还为构建更大规模的语言模型提供了新的可能性。
 |
图文｜莫 然
校稿｜李 政
编辑｜李佳俊
审核｜李瑞远
审核｜杨广超
