DSE精选文章 | TSQ：一种高效响应时间序列查询的优化框架

1. 时序数据降维相关定义

定义1（时间序列）对于多维时间序列，本文提供一个全面的定义：

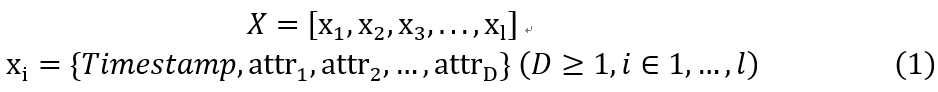
具体的说，查询序列（记为q）是一个长度相对较短的序列，长度为n，而目标序列（记为T）则是一个长度较长的序列，长度为m（n≪m）。

定义2（降维函数）降维函数 f_DR 实现以下效果：

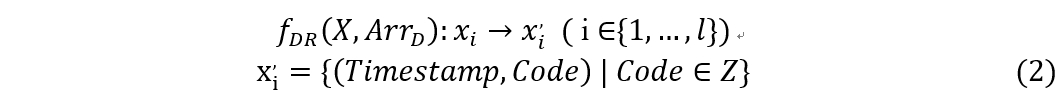
在通过 f_DR  处理序列 X 中的数据点后，每个数据点 x_i 将变为一个二元的 x_i' ，仅包含时间戳和一个整数编码 Code。生成的序列 X 将采用以下形式：

定义3（降维后的时间序列）降维后的时间序列 X'：

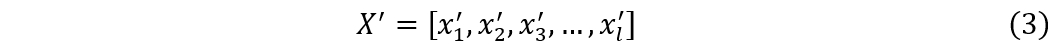
X' 由定义2中的降维处理得到的 x_i 组成。

2. 时序数据相似性查询相关定义

定义4（候选时间序列）c 是目标序列 T 中长度为 n 的子序列，从位置 i 开始（1 ≤ i ≤ m - n + 1），其序列长度等于 q 的长度。

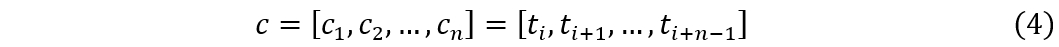
定义5（Top-k 相似性查询）使用欧几里得距离的top-k 相似性查询函数：

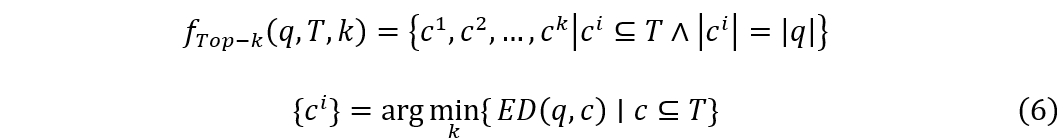
给定查询序列 q、目标序列 T、搜索数量 k 和相似性度量 ED(·,·)。top-k 查询函数 f_(Top-k) 将返回 T 中与 q 最相似的 k 个子序列 cⁱ。

3. TSQ框架

TSQ框架结构如图 1 所示。本文将 DR 和 SQ 模块集成到数据库内核中，作为 SQL 引擎的组成部分，使用户在数据查询时能够随时调用这些模块。具体来说，当用户发送各种查询请求时，SQL 引擎会根据查询类型动态选择并调用适当的模块。例如，如果用户提交一个相似性查询语句：SELECT SimilarityQuery('q','T')，系统会识别目标序列 T 中与查询序列 q 最匹配的序列。随后将完整的结果序列提取后存储在数据库中。

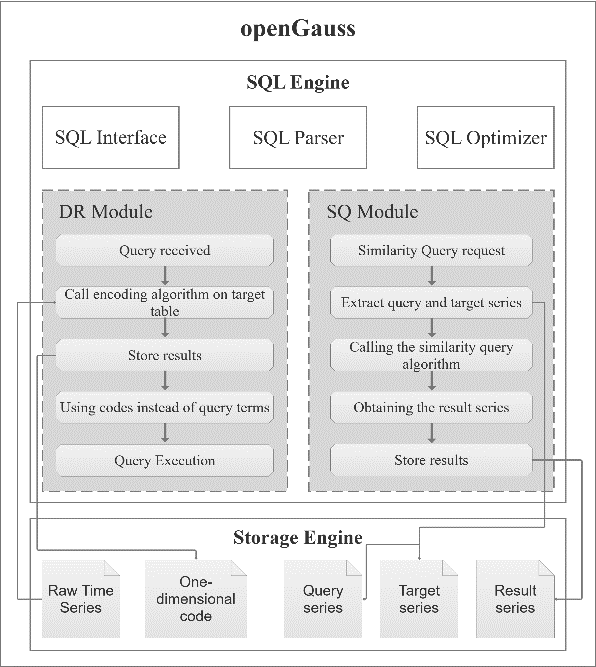
图1. TSQ的结构

4. G-Hilbert算法

空间填充曲线能够很好地保留数据的空间局部性，以确保有效的数据查询性能。本文基于传统希尔伯特曲线提出了更通用的G-Hilbert算法，通过预处理函数预估数据精度，设置合适的曲线阶数。G-Hilbert算法分为以下三个部分：

（1）精度确认函数PC

在处理大规模数据集时，G-Hilbert会优先调用PC函数来获取数据集的规模，并采用随机采样的方式来预估数据集多维度下的最高小数位数并返回。

（2）编码函数HEncoding

HEncoding的主要目标是将多维坐标转换为一维编码。该函数的实现基于递归，处理方式随维度而变化。对于二维坐标直接基于传统的希尔伯特曲线计算。对于超过两维的坐标，首先旋转除第一个坐标以外的所有坐标，然后递归调用HEncoding 处理剩余的维度。最后，将结果组合以获得一维希尔伯特编码。

（3）G-Hilbert

算法首先读取序列X及其相关信息，利用指针来指示X中每个维度的值。此后，在通过PC函数获取缩放因子F并随后编码后，将浮点数转换为整数。对于Hilbert曲线的阶数，定义公式log2(F)  Num + 1进行计算，有助于确保曲线覆盖数据范围。整数数组指针以及曲线阶数n和维数Num作为参数传递给HEncoding算法，以获得每行记录的编码。总体时间复杂度为O（n*logn）。

5. 相似性查询优化策略

关于传统的基于距离的相似性查询算法，特别是基于欧几里得距离的相似性查询，本文总结了一些可行的优化策略：（1）省略公式的平方根计算；（2）提前放弃策略；（3）采用在线标准化技术，使用滑动窗口来实现。

通过从目标序列中逐步提取每个可能的候选序列，相似性算法同步执行 Z 标准化和距离计算。如果累积距离超过当前的最佳距离（bsf），算法会提前终止计算。该策略通过减少对多个候选序列的不必要标准化，从而提高计算效率。

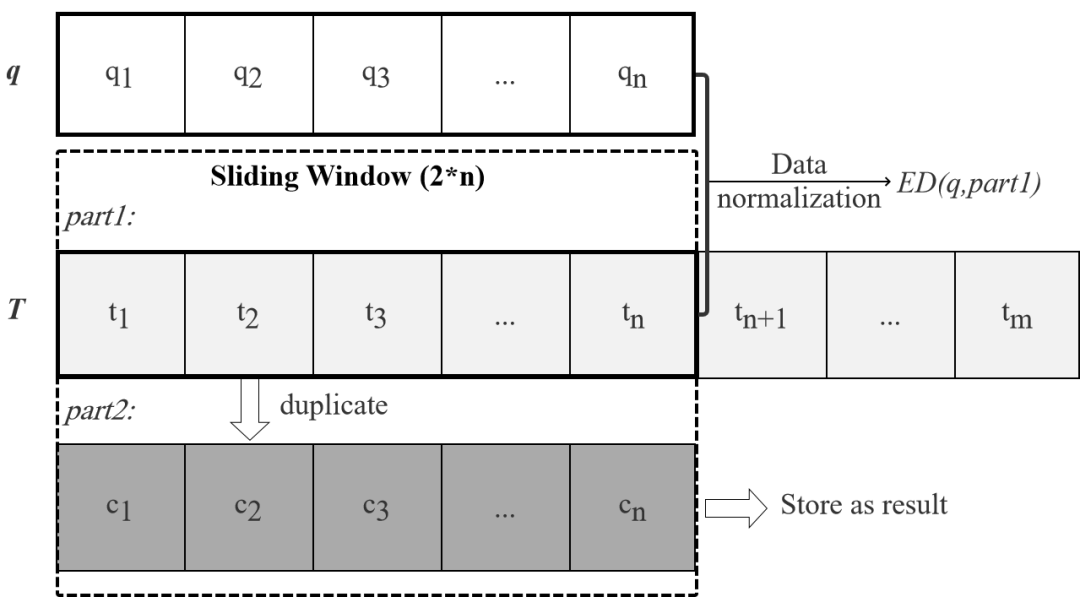
图2. 滑动窗口用于时序数据的相似性查询

滑动窗口长度设置为查询序列q的两倍。窗口将等长于q的候选序列提取到part1，并将原始数据复制到part2。仅当累计距离小于bsf时，执行对part1中数据的Z标准化后计算与q的距离，并且可以直接将part2保留为临时查询结果。并且滑动窗口的使用对于新的候选序列的标准化计算也有帮助。

6. 相似性查询算法

简单介绍了优化策略之后，正式提出优化的相似性查询算法UCR-ED-W和top-k相似性查询算法。本文引入了一个辅助函数ST，用于相似性查询在读取序列中的每个数据点时跳过时间戳信息。

（1）ST函数

该函数主要用于距离计算时跳过时间维度，使用输入的time_index和位置i读取数值维度。对于序列X中的每个数据点x_i，该函数将时间戳分配给变量temp的时间属性，并将第（i+1）维度的值分配给temp的数值属性。

（2）UCR-ED-W

在相似性查询算法中，查询序列q和目标序列T作为输入。首先对q提取相关信息。ST函数将时间信息和每个维度下的值存储到变量temp的两个不同属性中。计算每个维度下的和ex与平方和ex²，从而方便标准化。对目标序列T，定义了长度两倍于q的滑动窗口C和结果数组R。获得temp后将其值放置在C的适当位置。当计数器与查询序列长度相等时，将相关变量传递给DC函数计算距离，如果距离小于bsf，则bsf和结果序列都会更新。反之滑动窗口向后移动一个单位，读取新的数据点。重复该过程直到扫描完整个序列。

（3）DC函数

该算法利用传入的ex和ex²计算每个数值维度的平均值μ和标准偏差σ。建立双层循环来实现在线Z标准化。具体来说，对于每个循环，如果当前距离仍然小于bsf，则继续标准化并计算C到Q中对应点的距离。一旦超过bsf后，标准化和距离计算终止，扫描至下一个候选序列。

（4）top-k相似性查询

top-k相似度查询算法的整体逻辑与UCR-ED-W一致，区别在于top-k查询需要一系列变量来维护top-k的查询结果。每次对新的候选序列与查询序列q调用DC函数后，第k个序列的距离会作为新的bsf进行比较和更新。在更新过程中，采用循环来确定新序列的插入位置。最终算法返回与q最相似的k个序列以及相关信息。

本文实验在真实时序数据集上进行。表 1 提供了这些数据集的详细信息。

表1. 时间序列数据集及其属性

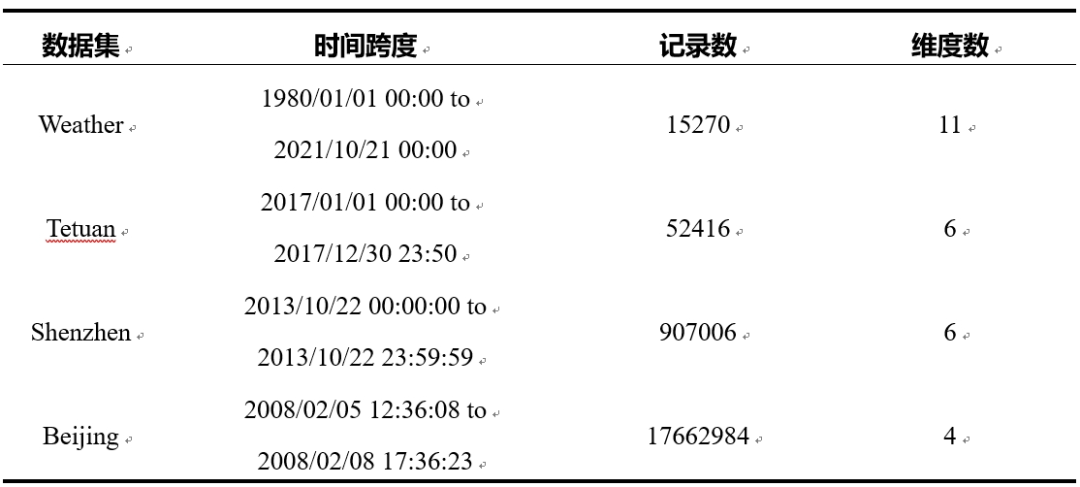
首先选择了两个较大的数据集“Shenzhen”和“Beijing”，以评估本文降维编码算法与基准算法的性能差异。并且使用数据空间局部性保持作为算法降维的质量评估指标，再次进行对比实验。两次实验结果如图3所示：

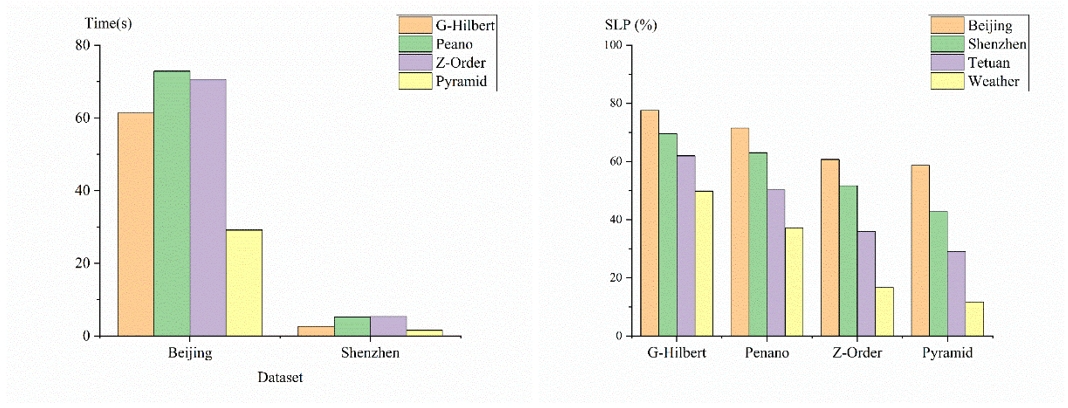
图3. 降维时间比较与空间局部性保留

对比实验表明，G-Hilbert 在保持空间局部性方面表现更为优越。与其他基准算法相比，本文的方法表现出最优的空间局部性保留效果。本文在降维后的二元组(Timestamp,Code)上构建了B-树索引，并在“Beijing”和“Shenzhen”数据集上进行了实验。评估了四种方法在点查询和范围查询中的时间效率（图4）。

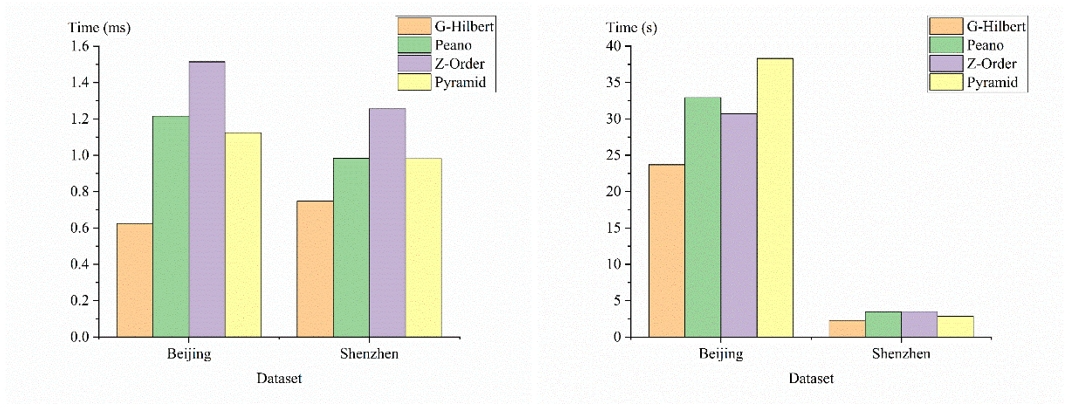
图4. 降维时间比较与空间局部性保留

相似性查询实验首先测试并验证了本文优化策略对于各种传统相似性查询算法的提升（表2）。为测试算法对于不同长度的序列的通用性，设置了长度从16到256的查询序列进行实验（图5）。

表2. 本文优化策略对于各种相似性算法的提升

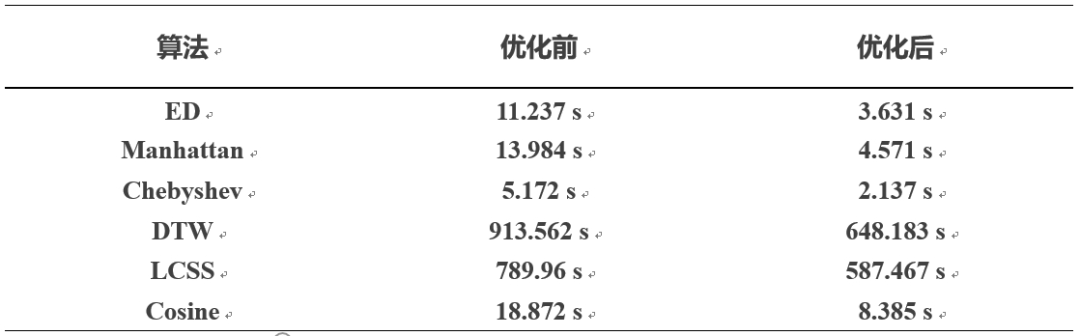
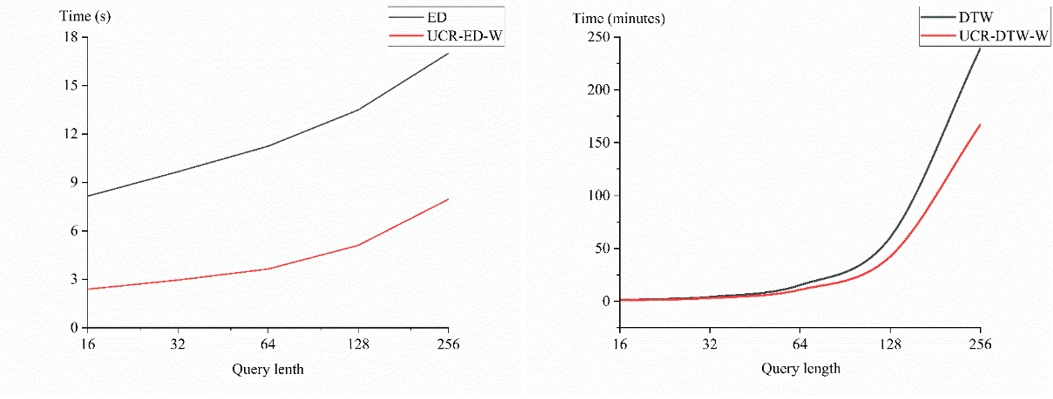
图5. 相似性查询算法随序列长度增长的时间变化

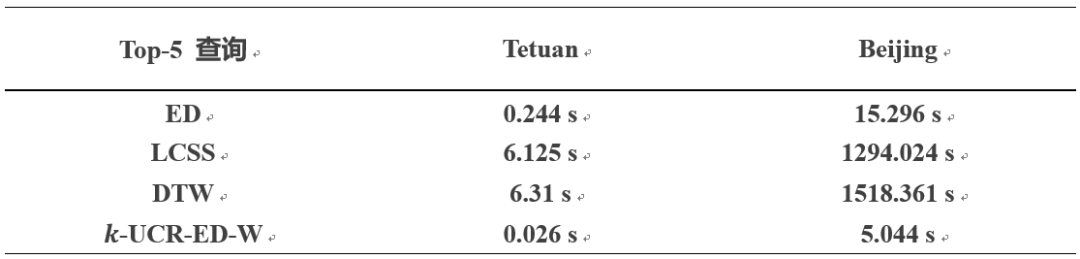
随着查询序列长度的增加，本文方法的优势愈加显著。当长度超过128时，原始欧几里得距离（ED）算法的计算时间显著增加。对于top-k 相似性查询。实验设置了相同的 k 值和查询序列长度（|q| = 64），以观察并比较本文的优化方法在不同算法中优化效果（表3）。

表3. Top-k 查询时间，k=5，∣q∣=64

Data Science and Engineering（DSE）是由中国计算机学会（CCF）主办，数据库专业委员会承办，施普林格·自然（Springer Nature）出版的开放获取（Open Access）期刊。DSE致力于发表与数据科学与工程领域相关的关键科学问题与前沿研究热点，以大数据为研究重点，建设国际学术交流的重要平台，推动学术界和企业界的深度融合。征稿范畴主要包括：数据库系统、大数据管理与分析、大数据治理等相关基础理论、关键技术与系统实践。现任主编（Editors-in-Chief）为数据科学与工程领域的知名专家北京大学崔斌教授和意大利英苏布里亚大学Elena Ferrari教授，现任执行主编(Managing Editor)为数据库专业委员会主任、华东师范大学周傲英教授和浙江大学高云君教授。

目前期刊已被EI、ESCI与SCOPUS收录，2023年CiteScore为10.4，影响因子（Impact factor）为5.1，在计算机科学应用领域排名前12%(92/817)、计算机软件领域排名前12%(49/407)、信息系统领域排名前13%(51/394)，人工智能领域排名前17%(58/350)。稿件处理费由赞助商中新赛克（Sinovatio）承担，欢迎大家免费下载阅读期刊全文，并积极投稿。

原文链接：

https://link.springer.com/article/10.1007/s41019-024-00273-8