谓词下推（Predicate Pushdown）是一种广泛应用的查询优化技术。先前的研究和现有的系统大多使用模式匹配规则来决定何时可以谓词下推通过某些操作符（如连接或分组）。然而，在优化数据科学管道时，由于广泛使用的非关系型操作符和用户自定义函数（UDF），现有规则往往难以覆盖，从而带来了挑战。本次为大家带来数据库领域顶级会议SIGMOD 2023的文章《Predicate Pushdown for Data Science Pipelines》。
一. 背景
由于机器学习和数据驱动的商业智能等新兴应用的出现，数据科学管道和ETL管道如今变得越来越普遍。这些管道需要处理日益增长的数据量，因此高效性变得至关重要，同时也充满挑战。尽管将关系型数据处理中的成熟优化技术应用到数据科学管道中是一个显而易见的想法，但由于两个主要差异，这一过程面临挑战。首先，数据科学管道通常包含非关系型操作符，例如电子表格操作符（如pivot和unpivot）以及更改模式的操作符（如drop-column和change-column-type）。其次，用户自定义函数（UDF）被广泛使用，尤其是在使用Python或R等语言开发管道的系统中，这些语言具有丰富的语法和大量的库。如果简单地将SQL查询优化技术应用到数据科学管道中，就无法达到最佳效果，因为这些非关系型操作符和UDF经常会被忽略，而实际上它们可以与关系型操作符一起进行优化。可以总结为以下三个主要挑战：
挑战1：如何在数据科学管道中设计一种通用的谓词下推技术，使其能够处理非关系型操作符和用户自定义函数（UDF）？
挑战2：如何验证谓词下推的正确性，确保其适用于不同规模的数据表，同时避免规则匹配方法的复杂性和局限性？
挑战3：如何优化管道中无法直接下推的谓词，并尽可能减少数据加载量以提升性能？
为了解决上述三个挑战，论文提出了一种新颖的谓词下推优化方法。首先，针对第一个挑战，论文提出了一种基于搜索和验证的谓词下推技术，能够覆盖数据科学管道中的非关系型操作符和UDF。通过符号执行（Symbolic Execution）技术，系统可以验证谓词下推的正确性，而无需依赖传统的规则匹配方法。其次，针对第二个挑战，论文引入了小模型性质（Small Model Property, SMP）的前置条件，通过在有限大小的符号表上验证正确性，归纳证明其适用于任意规模的表，从而实现了高效且全面的验证机制。最后，针对第三个挑战，论文设计了一个搜索算法，用于在管道的输入表上寻找最具选择性的谓词，同时提出了额外的优化技术，例如在无法直接下推时生成附加谓词以减少数据加载量，并处理UDF中的黑盒函数和空值（NULL）等特殊情况。
通过上述方法，论文提出了一个名为MagicPush的谓词下推优化器。MagicPush能够自动搜索和验证谓词下推的正确性，并在数据科学管道中实现高效的优化。实验结果表明，MagicPush在操作符和UDF的支持范围上具有显著优势。
二. 准备工作
2.1数据科学管道
通过多个处理步骤，数据科学管道能将原始数据转换为可用于回答业务问题或训练机器学习模型的形式。过程的每步都表示为一个操作符（如连接、分组），这些操作符通过数据流连接。关系查询的逻辑查询计划也是一个由操作符组成的管道。
2.1操作符
操作符主要分为三类：1.常见操作符（如Filter、InnerJoin、GroupBy），具有特定语义，嵌入UDF用于局部计算。2.子管道操作符（GroupedMap、RowIterPipeline），嵌入的UDF定义表处理逻辑，类似于SQL子查询。3.其他操作符（如表1中的“Other”），如转置，谓词无法下推。
2.1嵌入操作符中的UDF
表1 主要几种MagicPush实现的操作符
MagicPush支持嵌入操作符的UDF，其输入输出类型如表1所列。操作符和UDF的语法如上所述。第一类操作符嵌入的UDF接受具有常量大小的参数（行的某种类型r-param），并返回常量大小的r-param。第二类操作符，GroupedMap和RowIterPipeline，嵌入其中的UDF可能接收表（t-param）作为参数。此类UDF的主体是由其他操作符（即op）组成的子管道，其语法与普通管道中的语法相同。
图1 操作符示例
三. 方法介绍
3.1单个操作符的谓词下推
论文首先介绍MagicPush如何通过单个操作符将谓词下推，即给定F(谓词）和Op，找到一个最具选择性的谓词G，使得F(Op(T))=Op(G(T))成立。论文还考虑一种情况，即当F无法下推时，可以在不删除或移除F的情况下，额外添加谓词G到输入中。（即F(Op(T)=F(Op(G(T))），这仍然可以通过减少Op处理的数据量来提升性能。为了便于说明，我们将前者称为等价下推，后者称为超集下推。
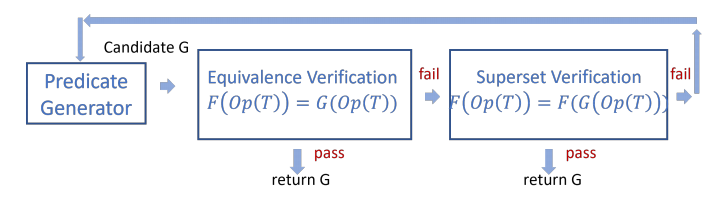图2 MagicPush 在给定Op和F的情况下搜索G
图2展示了谓词搜索模块每次按选择性顺序（选择性高的优先）返回一个候选谓词 G的流程。随后会通过等价验证，检查每个候选G是否满足F(Op(T)) = Op(G(T))。如果通过，MagicPush返回这个谓词G并停止；否则，继续进行超集验证谓词G。如果两者都失败，MagicPush 就会生成下一个候选谓词。由于MagicPush优先验证更具选择性的候选谓词，因此它总是返回最具选择性且正确的G（无论是等价下推还是超集下推）。在MagicPush尝试有限数量的候选谓词后，如果未找到正确的谓词，则返回一个“真过滤器”（即不过滤任何行）。
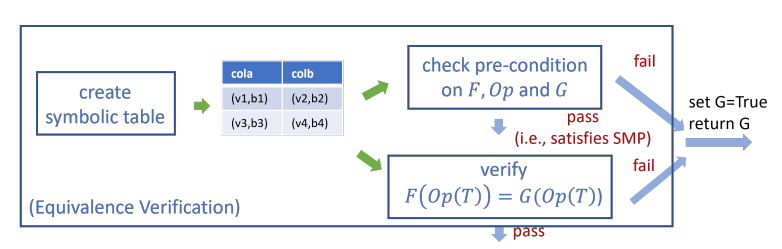
图3 MagicPush验证候选词G的流程
在验证候选谓词时（如图3所示），MagicPush基于输入表的模式创建一个符号表。它在该符号表上运行符号执行，检查F、Op和G是否满足小模型属性的预条件。如果不满足，MagicPush无法保证G的正确性，直接判定G失败。然后，MagicPush继续在符号表上检查验证是否满足F(Op(T))=Op(G(T))，并返回失败或通过。超集验证的过程是类似的，只是替换了预条件和验证目标。
3.1.1 使用SMT求解器进行有限验证
通过符号执行验证F(Op(T))=Op(G(T))。MagicPush在固定大小的符号表上计算该等式，生成一个逻辑公式，并使用SMT求解器求解。具体来说，论文引入了两个额外的符号：与每个单元格值关联的NULL指示符和与每行关联的行存在指示符，并修改符号执行以支持这两个符号的计算。
· 符号表表示
图4 展示带有NULL指示符和行存在指示符的符号执行过程
论文中使用符号表示表中的值，而不是具体值。同时添加了一个NULL指示符，即附加到每个值一个符号，表示该值是否不为NULL。还为每行添加了一个符号行存在指示符，其值为真时表示该行存在。该符号在初始符号表中为真，并在应用过滤器F或G后重新计算。
· 运行过滤器
过滤器运行在符号表而非具体表上，某行是否通过过滤器取决于该行的符号值。由于引入了行存在指示符，运行过滤器只需重置该符号。例如，图4(5)展示了运行过滤器G后，行存在指示符的更新。
· 符号操作符执行
论文构建了一个支持符号执行的Python解释器，允许运行任意符合Python语法的UDF，并用Python实现每个操作符。与标准符号程序执行不同，MagicPush计算与每个值关联的NULL指示符。具体来说，在每条计算字节码（如二元加法）处，MagicPush 返回一对值：一个if-else表达式，根据两个输入是否为NULL选择四种可能的结果；以及一个表达式作为结果的NULL指示符。例如，图4(3)中黄色阴影区域。行存在指示符可能影响NULL指示符，因为符号表中的行可能不存在，因此实际的NULL指示符是其原始NULL指示符与对应行存在值通过逻辑与运算的结果。例如，图4(6)。
· 检查F(Op(T)) = Op(G(T))
等价检查通过约束求解器比较运行F(Op(T))和Op(G(T))后输出符号表中每个单元格的值对是否等价。两个单元格相等仅当它们的NULL指示符相等，且当NULL指示符为真时它们的值相等（即只有在值不为NULL时，值才重要）。
3.1.2 扩展有限验证到完全验证
使用SMT求解器的验证是有限的，所以要通过预条件将其扩展到完全验证。简而言之，我们为小模型属性（SMP）找到预条件：只要Op、F和G满足预条件，在小型有限表上验证F(Op(T))=Op(G(T))即可实现完全验证。此外，预条件是一个从Op、F和G计算得出的表达式，其本身也满足SMP。通过这种预条件，我们只需检查预条件，然后在小型有限符号表上验证F(Op(T))=Op(G(T))，即可获得完全验证。这种预条件的核心在于它能够对F(Op(T))=Op(G(T))归纳证明。当预条件满足且等价性在所有 | T | ≤ N 的表上成立时，我们可以证明其在所有 | T ′| = N + 1 的表上也成立。通过这种证明，我们只需在基础案例（即行数较少的表）上展示等价性，归纳证明即可保证所有表的正确性。
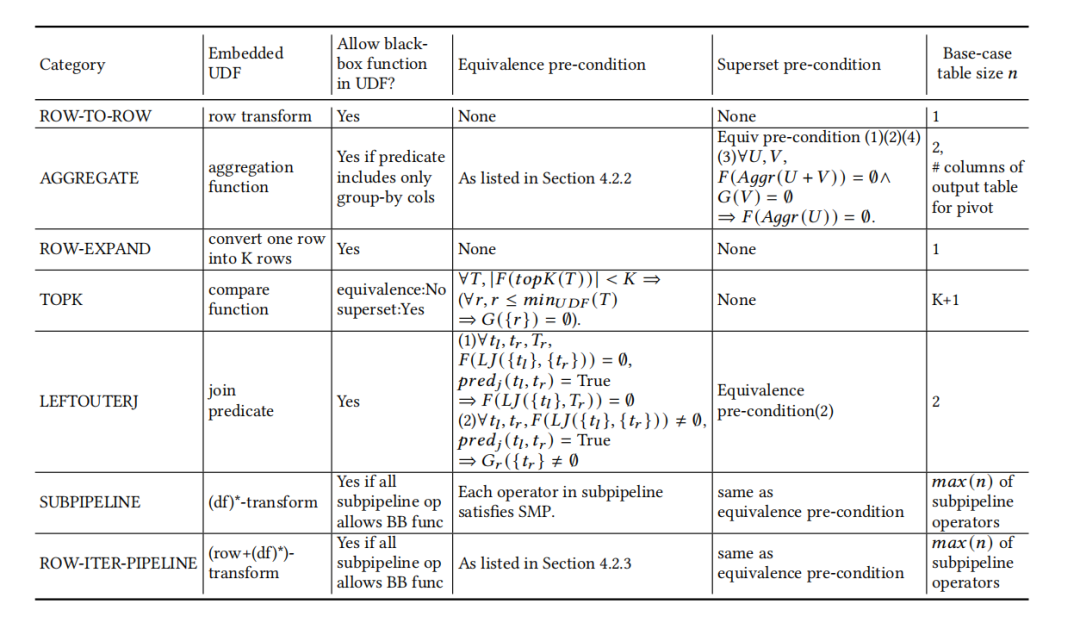
这些预条件因操作符而异。核心操作符总结为6类，其预条件和基础案例表大小列于表2中。超集验证（ F(Op(T) = F(Op(G(T))）与此类似，只是预条件不同，这些预条件也列于表2中。
表2 每种类别的预条件、基础案例表大小，以及是否允许黑箱函数
3.1.3 处理不可解释函数
库函数在管道UDF中被广泛使用。库函数可以在不实际计算的情况下通过验证，例如，一个RowTransform操作符为表添加一个新列day，该列通过从原始列date计算dayofweek得到（df.day=dayofweek(df.date)），并且在其输出上有一个选择周末的过滤器F（df.day in [6,7]）。MagicPush会生成一个候选谓词G：dayofweek(date) in [6,7]。通过利用SMT求解器中的未解释函数，MagicPush能够验证G的正确性，表达式为(dayofweek(date)) in [6,7] == dayofweek(date) in [6,7]（左侧是F (Op (T))的计算行存在符号，右侧是Op(G (T))），而无需展开dayofweek函数。
然而，并非所有黑箱函数都可以保持未展开状态，某些操作符可能需要实际计算才能验证。黑箱函数是否允许取决于验证过程，论文在表2中总结了经验上允许的情况。
3.1.4 谓词搜索
我们现在介绍如何搜索候选谓词G。MagicPush根据选择性枚举候选谓词，并在找到正确的谓词时停止，可以在不验证所有候选的情况下返回最具选择性的G。
主要挑战在于如何确保良好的覆盖范围，使得最佳的正确G被包含并尽早枚举。MagicPush从F和Op中提取谓词组件，然后通过使用合取（conjunction）和析取（disjunction）组合这些组件来合成候选G。
（1）谓词组件提取
MagicPush从输出谓词F和操作符Op中提取候选组件，解决表模式变更问题：
直接映射：输出列c′直接对应输入列c。表达式映射：c′由输入列表达式生成，提取仅依赖表字段的子表达式。无映射：若c′被删除，移除相关比较并替换为true或false。多列映射：c′对应多列，生成析取或合取表达式组合。操作符内条件：提取UDF分支条件及其否定形式，或Filter操作符的谓词。
（2）候选谓词G合成
快捷生成：优先生成高选择性候选：若无操作符组件，直接返回重写后的F；否则返回F与操作符组件的合取（避免冲突条件如l与¬l共存）。枚举策略：首先生成所有无冲突的合取组合，按字面量数量排序（越多越优先）。再生成析取组合，按子集元素数由少到多枚举（如先a ∧ b，再a ∨ b）。
3.2 管道中的谓词下推
本节介绍MagicPush如何将管道中间的谓词下推到其输入，特别是在数据流分叉或条件执行的情况下。同时，我们还将介绍如何处理包含子管道的操作符（如GroupedMap和RowIterPipeline）的下推过程。
3.2.1 数据流中的下推
图4展示了在处理多输入/输出流和分支时，数据流和谓词下推的不同场景。图中使用不同的箭头来表示数据流、谓词下推和控制流。以下是对每个子图的解释：
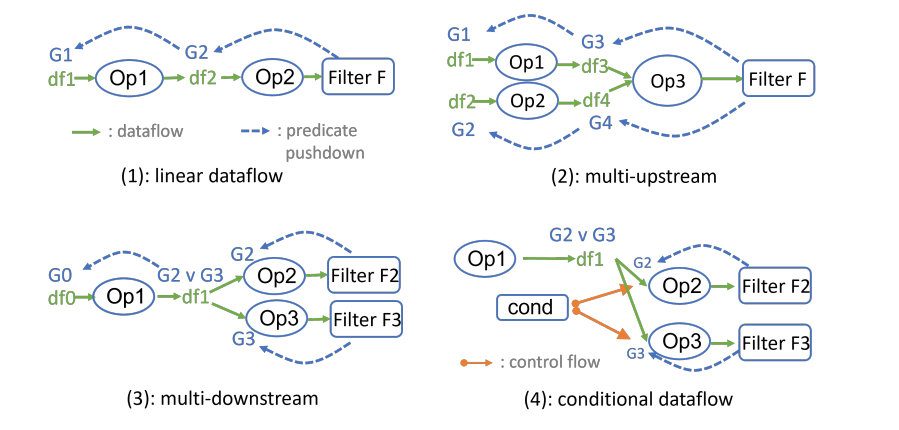
图5 处理多输入/输出流和分支
（1）线性数据流：数据从Op1流向Op2，然后经过过滤器Filter F。数据流（绿色箭头）：表示数据从一个操作符流向下一个操作符。谓词下推（蓝色虚线箭头）：表示谓词`F`可以被下推到更早的操作符Op1，以便更早地过滤数据。
（2）多上游：操作符Op3从两个上游操作符Op1和Op2接收数据，然后经过过滤器Filter F。谓词F可以被下推到Op1和Op2，以便在数据到达Op3之前进行过滤。
（3）多下游：一个操作符Op1向两个下游操作符Op2和Op3发送数据，每个下游操作符都有自己的过滤器Filter F2和Filter F3。谓词可以分别被下推到Op2和Op3，以便在各自的过滤器中进行处理。
（4）条件数据流 ：数据从Op1流出，根据条件cond，流向不同的下游操作符，每个操作符都有自己的过滤器。控制流（橙色箭头）：表示条件cond控制数据流向。
在满足条件的路径上，谓词可以被下推到对应的操作符。
3.2.2 子管道操作符的下推
与其他操作符不同，包含子管道的操作符的G搜索过程需要将谓词逐操作符下推，直到子管道的输入。如图6所示，黄色背景区域表示数据处理管道中可以进行优化的部分，通过下推谓词来减少不必要的数据处理。
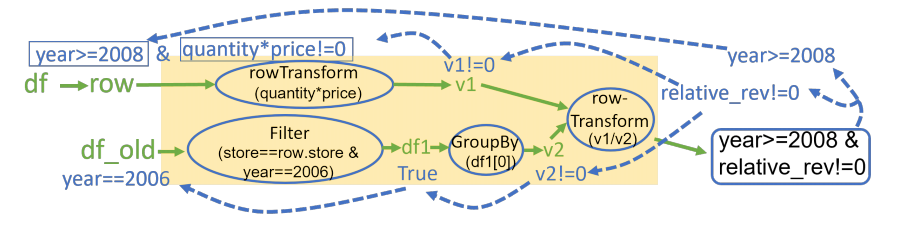
图6 子管道操作符的下推流程
四．实验
4.1实验设置
配备 2.4GHz 处理器和 64GB 内存的服务器，使用Pandas 1.1.4。
原型解析器：将带有Pandas API的Python代码翻译成MagicPush的语法。
4.2 效率和效果研究
下表是关于MagicPush系统在处理操作符和用户自定义函数（UDF）时的覆盖率：
表3 MagicPush系统在处理操作符和用户自定义函数（UDF）时的覆盖率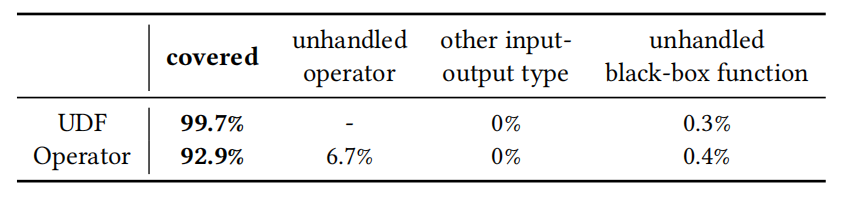
表3显示：MagicPush的UDF覆盖率达99.7%，未处理的黑盒函数仅有0.3%。操作符覆盖率达92.9%，未处理的操作符仅占6.7%，未处理的黑盒函数仅占0.4%。该结果展示了MagicPush在处理不同类型的操作符和UDF时的有效性，表明其对大多数操作符和UDF的良好支持。
表4 200个采样管道的特征分析
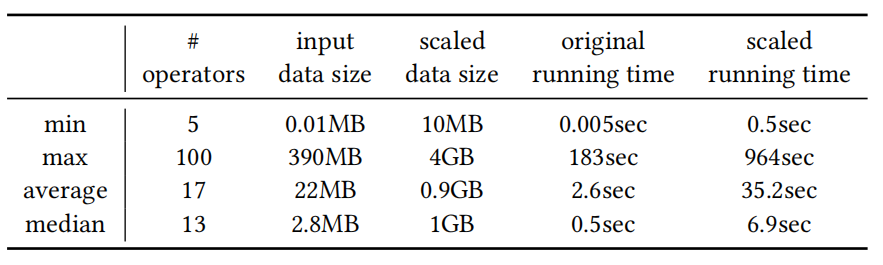
表4显示：在原始数据上，由于许多管道处理的数据量较小，运行时间较短，中位数为 0.5 秒。在扩展数据上：数据上运行的时间更长，中位数为 28 秒，且运行时间更加稳定。
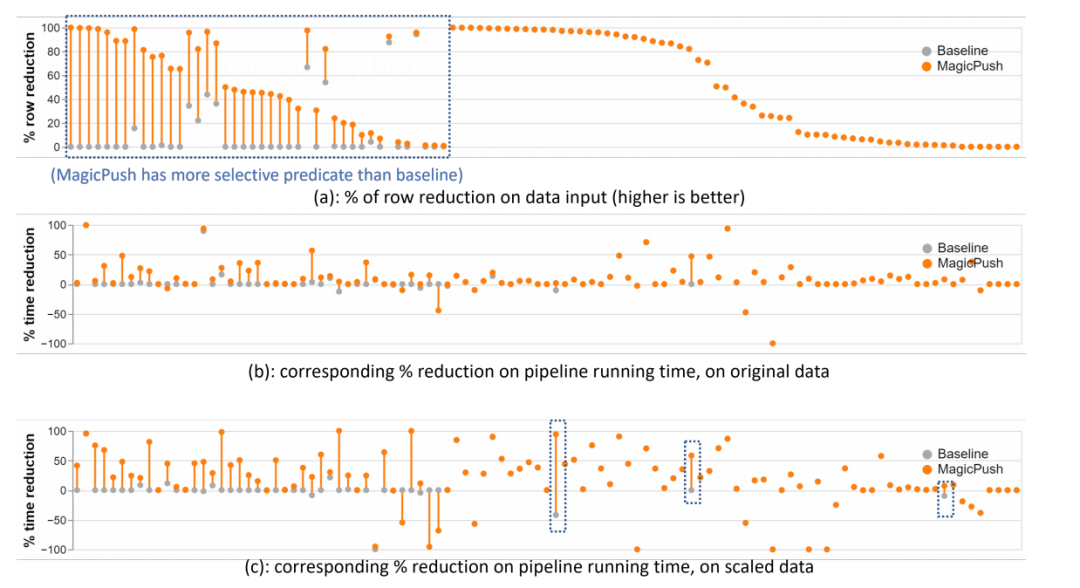
图7 改进在真实世界数据管道上的表现
图7表明：
（a）展示了通过下推谓词减少的数据量，用处理的行数来衡量。结论：MagicPush的下推能力明显优于基准系统，能够显著减少数据处理量。
（b）展示了在原始数据规模下，MagicPush对管道运行时间的端到端性能提升。结论：MagicPush在处理原始数据时，能够有效减少管道运行时间，提高处理效率。
（c）展示了在扩展数据规模下，MagicPush对管道运行时间的端到端性能提升。结论：MagicPush在处理扩展数据时，能够更显著地减少管道运行时间，大幅提高处理效率。
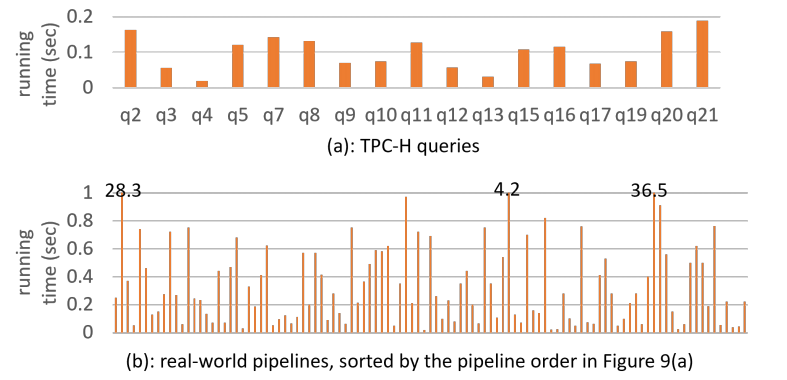
图8 MagicPush的运行时间
图8中展示了MagicPush从接收Python脚本到生成优化后的Python管道的端到端运行时间。它的效率非常高，优化TPC-H查询的时间<0.2秒（平均0.1秒），优化98个管道的时间<0.8秒（平均0.33秒）。
五．总结
本研究中，论文提出了MagicPush方法，用于决定在包含关系型和非关系型操作符以及嵌入式UDF的数据管道中如何进行谓词下推。论文展示了MagicPush的创新性搜索-验证方法优于传统的下推规则，MagicPush在TPC-H查询和采样的真实世界管道中发现了更多的下推机会，同时能够为其优化提供完整的正确性保证。
 |
图文｜白玉韬
校稿｜何 翔
编辑｜朱明辉
审核｜李瑞远
审核｜杨广超
