DSE精选文章
Computing Prominent Skyline on Massive Data
文章介绍
方法框架
1. P-skyline定义
给定一个包含n个元组的表T(A1, …, AM),对任意t∈ T,设t.Ai为t的属性Ai的值。不失一般性,设ASsky= {A1, …, Am}为Skyline标准,在该标准下定义元组之间的支配关系。支配和Skyline的定义如下。
定义1(支配):对于任意t1, t2∈T,t1支配t2(记作t1≻t2),当且仅当,对于所有i (1≤i≤m),t1.Ai≤t2.Ai,并且存在某个i(1≤i≤m),使得t1.Ai<t2.Ai。
定义2(Skyline):Skyline查询返回T的一个子集SKY,其中每个元组都不被其他元组支配。
给定近似因子𝜖(0≤𝜖<1),p-支配和P-skyline定义如下。
定义3(p-支配):对于任意t1, t2∈T,t1元组p支配t2元组(记作t1 ≻p t2),当且仅当,对于所有i (1≤i≤m),(1-ϵ)×t1.Ai≤t2.Ai,并且存在某个i (1≤i≤m),使得(1-ϵ)×t1.Ai<t2.Ai。
定义4(P-skyline): P-skyline查询返回T的一个子集SKYP,其中每个元组都不被其他元组p-支配。
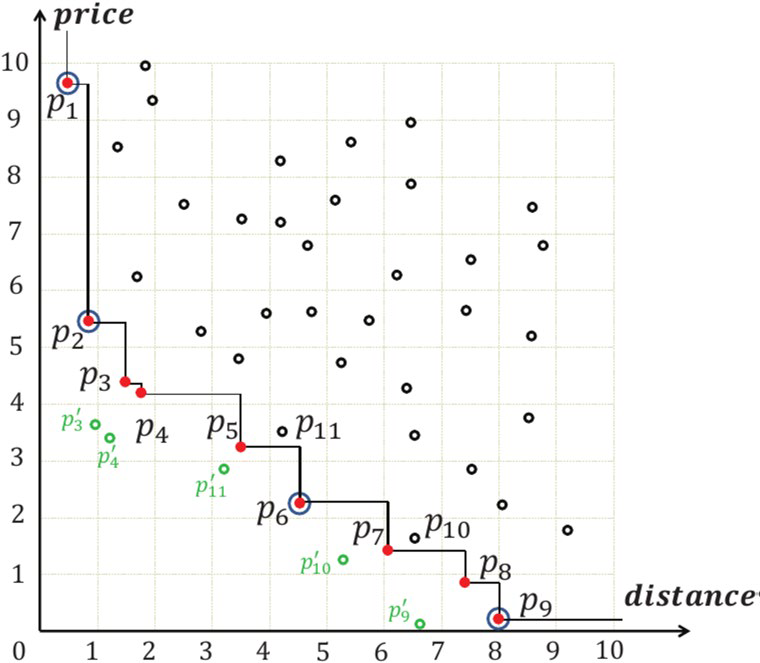
图1. 一个Skyline例子图示
如图1所示,P-skyline返回Skyline结果的一个子集,SKYP⊆ SKY,p-支配的定义增强了元组的支配能力。随着𝜖值的增大,指定的元组会更接近坐标原点,可能支配更多的元组。如果𝜖 = 0,则P-skyline返回传统的Skyline元组。如果ϵ→1,P-skyline可能返回一个空集。随着𝜖从0增加到1,P-skyline的结果单调地从传统Skyline结果减少到空集。
2. 构建所需的结构
我们的目标是设计一个高效的算法在海量数据上发现P-skyline结果,大幅减少I/O成本和计算成本。
定义5(有前景的元组):可能成为P-skyline结果的元组称为有前景的元组。
剪枝效果是通过p-支配的定义来实现的。其直观的思路是,通过仅检索有前景的元组并进行必要的p-支配检查来计算P-skyline。如何快速确定有前景的元组是高效执行的关键。为此,一些有用的数据结构被预先构建。
定义 6(p-支配得分):对于任意t∈T,t的p-支配得分是T⧵t中被t所p-支配的元组的数量。
令每个元组的MPIL属性表示该元组在每个属性的有序列表中的最小位置索引,表T可以根据MPIL执行预排序操作。在PT的构建过程中,具有较小MPIL的元组更有可能具有较高的p-支配得分,因为它们至少在一个属性上表现良好。这些元组被排在PT的前面。
3. PSTP算法
本文提出PSTP算法,该算法利用预构建的结构,在海量数据上高效计算P-skyline。PSTP算法的执行包括两个阶段:获取候选元组和精炼结果。由于p-支配关系的非传递性,任何被某些元组p-支配的元组都可以用来p-支配其他元组。PSTP算法只在第1阶段保留候选元组C。在第2阶段,候选元组经过精炼,去掉被p-支配的候选元组。这个过程通过两次表扫描实现。为了提高计算效率,PSTP算法仅检索PT中必要的元组,并通过有效的剪枝策略在有限的候选元组上执行p-支配检查。
(1) 第1阶段:候选元组的获取
在第1阶段,PSTP算法通过在PT上进行选择性检索来获取P-skyline结果的候选元组。PSTP算法中的检索操作按轮次进行。在第一轮,PSTP算法按顺序检索PT中的前B1个元组。设当前检索的元组为t,PSTP遍历C中的每个元素,并将t和当前候选元组进行比较,并根据比较结果执行相应处理。后续轮次。在第k轮(k≥2)的开始,PSTP首先检索ℝ中的每个元组,设tr为当前的ℝ元组。第k轮中被tr所p-支配的元组应当直接跳过。
随着PSTP算法的执行,ℝ中的元组所带来的剪枝效果会逐渐提高,直到为每个大的子空间找到最优剪枝元组。这也是我们将PSTP算法的执行分为多个轮次的原因,在每个轮次中处理一组连续的元组。在本文中,B1被设置为32K。一方面,剪枝的位向量在每轮开始时计算,这避免了每次更新剪枝元组时都需要频繁计算位向量。另一方面,B1远小于海量数据中的n,即使第一轮没有涉及剪枝操作,PSTP算法仍然可以跳过大部分后续元组。在第1阶段,如果PT中的所有元组都被检索或跳过,PSTP算法就会获取P-skyline结果的候选元组。本文分析结果表明,PSTP算法可以利用提前终止条件提前终止执行。
(2) 第2阶段:结果的精炼
在第2阶段,PSTP算法通过对PT的再次选择性检索来精炼第1阶段获得的候选元组。
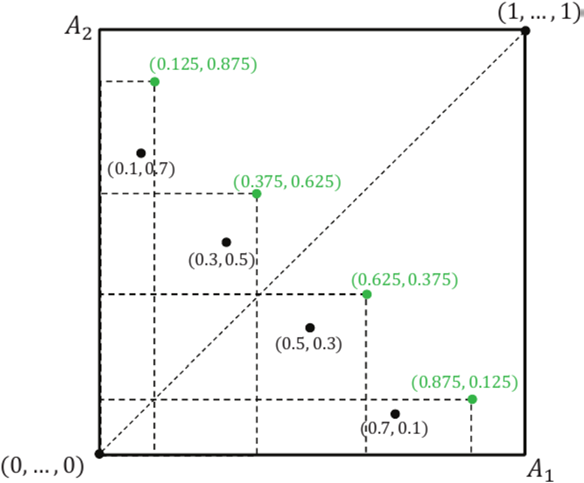
图2. 候选元组的图示,用于选择性检索,其中C={(0.1,0.7),(0.3,0.5),(0.5,0.3),(0.7,0.1)}和ε= 0.2。
选择性检索。如图2所示,PSTP算法仅在每个大的子空间中选择一个候选元组,用于确定无法p-支配任何候选元组的表元组,并在扫描过程直接跳过它们。
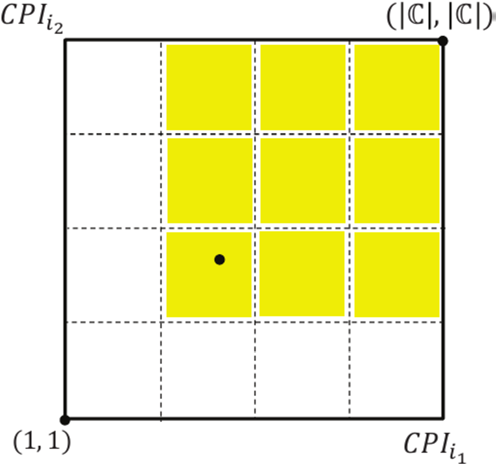
图3. 元组可能p-支配区域的网格划分图示
选择性p-支配检查。设当前检索的元组为t,PSTP算法利用t去移除C中被它p-支配的候选元组。一种简单的方法是遍历C并将t与每个候选元组进行比较。如果|C|不够小,这将导致较高的计算成本。在这部分中,PSTP算法在第2阶段开发了选择性p-支配检查,其灵感来自于一个直观的想法:如图3所示,每个检索到的元组只能p-支配一部分候选元组。换句话说,t不需要与C中的所有候选元组进行比较。
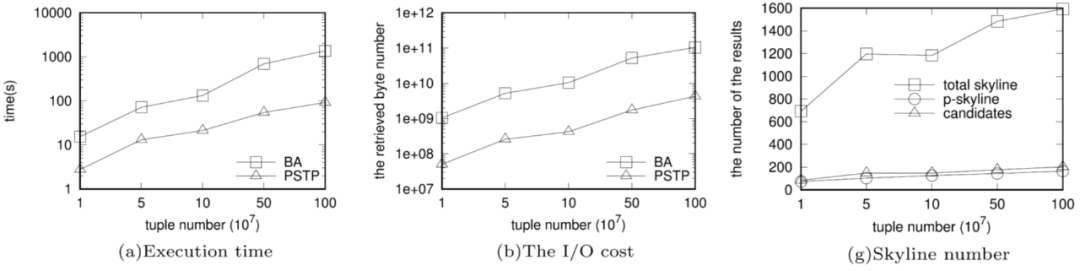
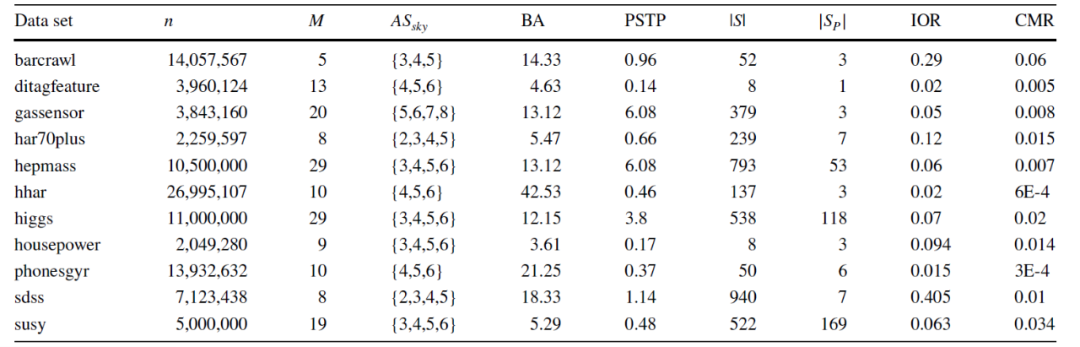
实验效果
结语
作者简介
期刊简介










