突破性能瓶颈：深度解析PolarDB-X列存分页查询原理（二）

PolarDB-X的并行Top-K优化

PolarDB-X引入了并行Top-K处理方案，采用了L1、L2、L3三层Top-K算子的特殊结构。每一层次分别负责不同阶段的Top-K汇总与优化，相比于简单的堆合并方法降低了计算复杂度。此外，通过多线程共同更新全局第K大值（Kth），加速阈值的收敛过程，提升数据过滤的效率。上下游算子之间的紧密协作机制，使得查询处理更加流畅高效。Top-K算子内部的执行流程也经过了重新设计，包含堆顶清理和动态过滤等步骤。

(一) 并行Top-K的DAG执行结构

PolarDB分布式数据库的计算集群中有N个节点，其中有一个master节点（主节点）用于发起查询并充当协调者的角色，其他节点为worker节点；master节点也承担worker节点的功能。

当用户发起一次Top-K查询时，数据库实例根据计算节点总数N和总并行度m，创建一个执行的有向无环图（DAG）。假设并行度均匀分配在各个计算节点上，具体步骤如下：

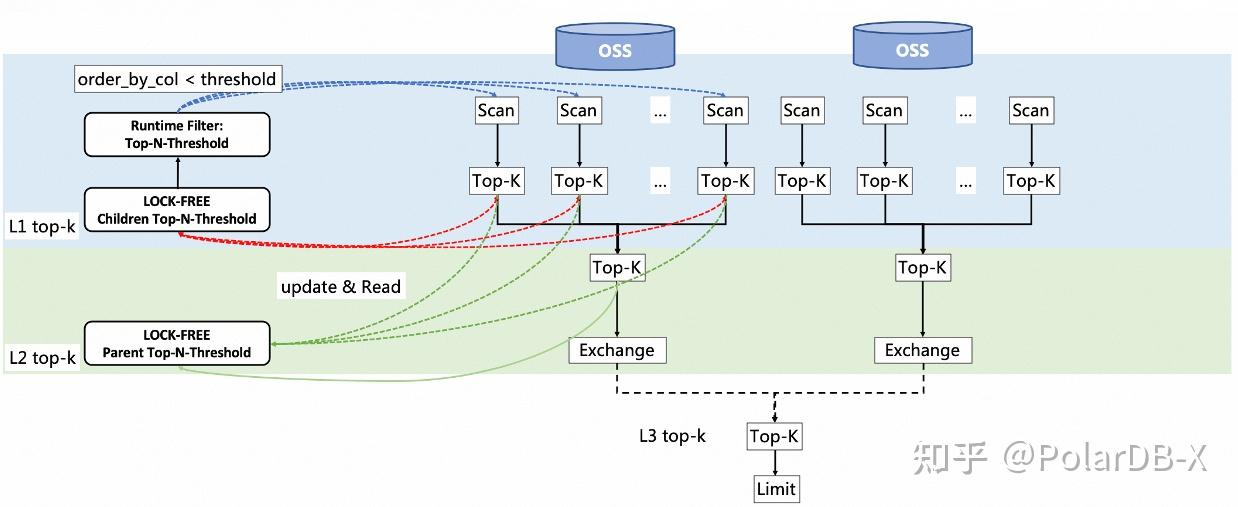
1. 在N个计算节点上创建m个扫描（Scan）算子，每个节点上m/N个，负责从各自分区中拉取数据。
2. 设定每个计算节点内的扫描算子，将数据输出到下游的m/N个Top-K算子（一级Top-K，L1 Top-K）。
3. 每个节点内部的m/N个Top-K算子接收上游扫描算子的数据，并通过内部维护的最小堆计算各自输入数据的Top-K值。
4. 每个节点内部的m/N个Top-K算子在计算完毕后，立即将结果输出到下游的一个Top-K算子（即二级Top-K，L2 Top-K）。每个节点仅包含一个L2 Top-K算子。
5. 每个节点内部的L2 Top-K算子在接收到全部L1 Top-K算子的计算结果后，计算得到该节点的Top-K数据。然后，通过下游的交换（Exchange）算子，发起网络传输，将计算结果汇聚到主节点的三级Top-K算子（L3 Top-K）。
6. 主节点上仅有一个L3 Top-K算子，它接收各工作节点汇聚的Top-K数据，并计算最终的Top-K结果。
7. L3 Top-K算子输出结果到限制（Limit）算子。例如，对于“select * from table order by xx limit offset, len”语句，K = offset + len，而Limit算子负责输出从offset开始的len行数据。

在上述步骤中，所有层级的Top-K算子 （L1, L2, L3 Top-K 算子）内部都维护了一个大小为K的小顶堆。

下图展示了上述并行调度的工作流程：每个节点的扫描算子输出数据到一级Top-K算子，一级Top-K算子的结果汇聚到二级Top-K算子，再由二级Top-K算子的结果通过交换算子传输至主节点的三级Top-K算子，最终实现Top-K的并行计算。

• 为什么要设计L1, L2, L3 Top-K算子
• L1 Top-K算子是为了充分利用并行计算的优势，通过多核性能来优化整体的Top-K效率，具体的设计方案在下文详述。
• L2 Top-K算子是为了在节点内进行各个并行度上L1 Top-K结果的汇总，得到节点内的总的Top-K结果。这一步避免了把所有L1 Top-K算子结果数据通过网络传输到master节点上再进行整体的汇总，从而大幅降低网络传输数据量和网络开销。
• L3 Top-K算子是为了汇总各个节点上的Top-K结果，从而计算得到整体的执行结果。

• 相比于单核Top-K处理的性能优势
• 对于总数据量为n，单核求解Top-K问题的时间复杂度是： $O\left(nlogK\right)$
• 单节点内，对于总数据量为n，假设使用m个线程，每个线程平均处理n/m行数据，m个最小堆各自处理Top-K问题且m个堆的大小都是K。此外，有一个堆负责将这m个最小堆的top-K结果进行汇总，得到最终的top-k结果，它的时间复杂度分析：

1. 每个线程处理 n/m 行数据，维持一个大小为 K 的最小堆来处理Top-K问题。对一个数据流维护一个大小为K的最小堆，其单次操作的时间复杂度是O(logK)。因此，每个线程在处理 n/m 条数据时，总时间复杂度是： $O\left(\frac{n}{m}logK\right)$
2. 最终，我们需要将 m 个大小为 K 的最小堆合并成一个最终的最小堆，以得到总体数据的top-K。这个部分的计算复杂度可以通过将 m 个堆（每个大小为 KK ）合并来分析: $O\left(Klogm\right)$
3. 因此总的复杂度是 $O(\frac{n}{m}logK+Klogm)$

(二) L1 Top-K算子之间的协作

本节介绍 L1 Top-K算子的在节点内和跨节点间的协作，帮助更快提升和收敛全局第K大值Kth，减少堆的写入次数，提升top-k计算效率。

所有并行度之间共同维护一个变量 Kth，它表示当前全局已知的第K大值，可能是一个单列的列值 val_col，也可能是多列的数值共同组成的向量 {val_col1, val_col2, ..., val_colx} 。随着不同并行度间的算子协作，Kth逐渐收敛到真实的总体第K大值Kth'。而Kth->Kth'速度越快，过滤掉数据的概率就越大，写入堆的数据越少，整体性能就越高。

1. 起始状态：L1 Top-K算子刚初始化时，全局元素数量为0，此时无法计算得到当前第K大值
2. 元素总数更新：在L1 Top-K算子内部，每写入一行，就会更新该节点内写入所有L1 Top-K算子的元素总数，这个更新过程是原子性的、并发安全的。
3. Kth值初始化：当全局元素总数等于K 时，对于所有L1 Top-K算子内部维护的大小为K的堆，获得堆顶元素， $min\left(H_i\right)$ 计算得到它们的最小值，就是当前全局的第K大值Kth。此时，完成了Kth数值的初始化。

• 第3步的原理是，对于多个节点上的多个线程，总线程数为m，每个线程维护一个堆 $H_i$ ，那么，当m个线程上的堆元素大小之和等于K时，这些堆他们共同组成了一个大小为K的元素集合，设 $min\left(H_i\right)$ 是每个线程上堆元素的最小值（堆顶）
• 那么对于他们共同组成的大小为K的元素集合S，S的第K大元素为： $K_{th}=min\left(min\right(H_1),min(H_2),...min(H_m\left)\right)$

4. 节点内Kth值的并发更新：当Kth数值初始化之后，各个并行度开始并发安全地更新Kth值。在所有并行度上，每当写入一个元素到Top-N算子时，都尝试比较和更新 Kth 值，以期尽可能提高Kth值并更快速地收敛，从而过滤更多数据，避免无必要的堆写入。具体过程如下：

1. 一个线程上的一个L1 Top-K算子写入一个数据a时，将其与全局的Kth值进行比较；
2. 如果 a < Kth，则丢弃 a（因为 a 不可能进入最终的 top-k ）。
3. 否则，并发安全地将Kth值更新为a。接着，将a写入到该线程L1 Top-K算子内的小顶堆中。

第4步的原理是，由于单个元素写入堆的时间复杂度是O(logK)，而元素比较的时间复杂度为O(1)，因此尽可能地利用全局的Kth过滤掉不必要的堆写入。虽然堆顶元素的比较与替换也可以减少堆的写入，但是全局Kth值往往比单个线程上或单个L1 Top-K算子内部的堆顶值更大，更新频率更高，收敛速度更快。Kth和每个线程上写入元素a的关系是： $K_{th}=max(a,K_{th})$

为了确保Kth值的更新是并发安全的，对于每个线程，执行的过程伪代码如下，其中利用了CAS机制确保更新的原子性：

Function update_Kth_value(a):
    Loop forever:
        needUpdate = cmp(a, Kth_value) > 0
        If not needUpdate OR cas_compare_and_set_Kth_value(Kth_value, a):
            Break from loop
    End Loop

5. 跨节点Kth值更新：当各个节点内的Kth值初始化并不断更新后，每个节点会定时（通常是几十毫秒）将本节点当前Kth_i值广播到其他节点，每个节点会求取Kth最大值，更新到本地的Kth值中：（N=节点总数）

$K_{th}=max(K_{th1},K_{th2},...K_{thN})$

这一步骤进一步加速了整个计算集群Kth值的收敛。

(三) 上下游算子间的协作

本节描述L1 Top-K、L2 Top-K、L3 Top-K以及Scan算子之间的协同工作流程。

在并行调度章节，详细描述了执行DAG的基本情况。上下游算子间除了输入上游数据，和输出数据到下游外，还存在着其他的协作关系。这些协作关系的设计是本方案的重点之一，对整体top-k查询处理性能提升起到关键作用。

1. runtime-filter 帮助过滤scan算子中的数据：PolarDB分布式数据库的查询引擎支持runtime-filter机制，这是一种动态变化的表达式，由上层算子构建并传递给Scan算子，作为谓词条件来过滤扫描数据。在本方案中，如果用户的Top-K查询语句中使用了"ORDER BY col1, col2, ..., colx LIMIT offset, len"的格式，那么可以结合L1 Top-K算子所维护的Kth值，形成一个谓词条件：(col1, col2, ..., colx) >= Kth，其中Kth值是动态变化的，对应x个列值的向量：Kth = {val_col1, val_col2, ..., val_colx}。具体过程如下：
1. 在创建DAG执行结构时，将L1 Top-K算子共享的Kth对象包装为runtime-filter：func={(col1, col2, ..., colx) >= Kth} 并传递给所有Scan算子。
2. 刚开始执行时，Kth尚未初始化，runtime-filter不生效，Scan算子忽略runtime-filter；
3. 当Kth初始化并不断更新时，runtime-filter开始生效，Scan算子会感知到runtime-filter的生效以及Kth值的动态变化，每次使用最新的Kth值形成谓词条件 (col1, col2, ..., colx) >= Kth来过滤Scan算子中的数据，从而提升整体性能。
2. L2 Top-K和L3 Top-K算子利用上游算子输出Chunk的有序性：在L2 Top-K和L3 Top-K算子内部，由于其上游分别是L1 Top-K和L2 Top-K算子，其输出的结果是有序的序列{Chunk_ij}，其中Chunk是数据库执行器中的基本数据单元，一般包含1024行数据；i代表Chunk来自于第i个线程/算子，j代表Chunk在i线程/算子内的序号。虽然来自不同线程的Chunk_ij之间没有顺序关系，但Chunk_ij内部显然是有序的，按照排序列递减排列。因此，当L2 Top-K和L3 Top-K算子在处理中遇到Chunk_ij中的某一行数据小于当前Kth值时，接下来的所有行数据也必然小于Kth值，可以直接丢弃，从而提高处理效率。
3. L2 Top-K算子维护的Kth_parent用于过滤上游L1 Top-K算子：L2 Top-K算子中实时维护的当前第K大值Kth_parent是单调递增的，并且对L1 Top-K算子可见；L1 Top-K算子可以检查Kth_parent值的大小以帮助过滤输入元素，原理与Kth值过滤相同。由于L2 Top-K与L1 Top-K的输入元素序列顺序不同，Kth_parent和Kth值的收敛速度也可能不同。因此，有一定的概率Kth_parent的收敛速度更快，即其值更大，从而能够展现更优的过滤性能。

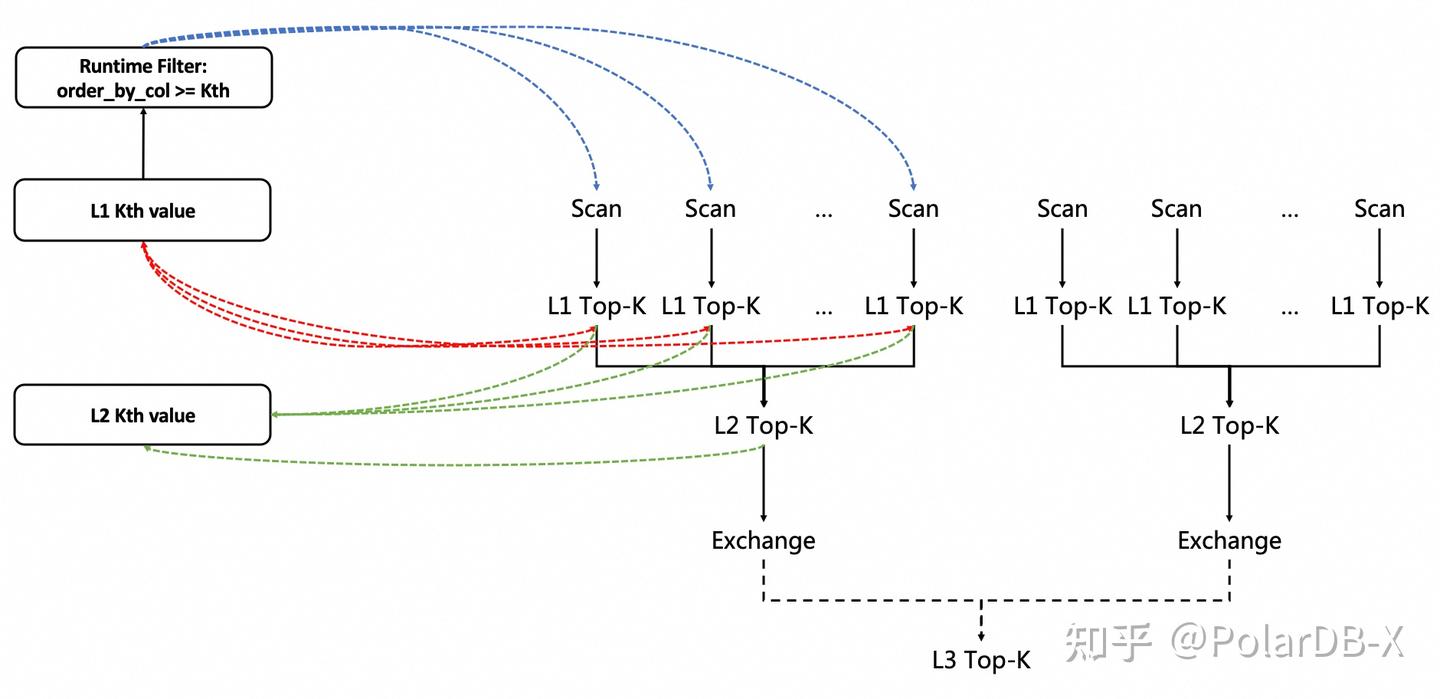
下图表示在并行Top-K查询处理执行过程中，并行度之间以及上下游算子之间的协作关系：

1. 红线代表L1 Top-K算子共享和更新Kth值，同时也使用Kth值来过滤Scan输入的数据；
2. 蓝线代表Scan算子使用runtime filter : {col >= Kth}来过滤数据，同时由 L1 Top-K算子来更新维护谓词条件中的Kth值；
3. 绿线代表L2 Top-K算子维护Kth值，并供L1 Top-K算子做额外过滤

(四) Top-K算子内部执行流程

1. 算子初始化：
1. 根据order by 列类型的不同，创建相应的比较器。比较器的原理与“方案背景-经典Top-K算法实现-应用到Top-K查询”章节提到的比较器原理相同
2. 算子内部构建小顶堆min-heap对象，大小即Top-K查询中的K值。
3. 对于L1，L2, L3 Top-K算子，每个计算节点内的每个层级，会分别构建全局Kth对象，并且在各个并行度的Top-K算子间共享。
2. 写入Chunk数据到各个并行度的Top-K算子中。L1，L2, L3 Top-K算子共用一套执行逻辑，但是内部会通过标记来区分算子所处的级别。
1. 堆顶清理：写入流程的第一步，并不会对Chunk本身做任何处理，而是每个Top-K算子首先对小顶堆 min-heap对象进行清理：
1. 不断地检查小顶堆的堆顶元素，如果本层级的Kth对象已经初始化，则利用比较器，进行堆顶元素和Kth对象值的比较；如果堆顶元素小于Kth当前对象值，执行pop heap操作，移除堆顶元素，小顶堆自动选出新的堆顶；
2. 如果步骤1中堆顶没有被本层级Kth值过滤掉，则尝试使用高一层级的Kth对象进行过滤，方法和步骤1相同。
3. 如果步骤1，2中堆顶被移除，则继续检查新的堆顶；否则，结束堆顶清理流程。
2. Kth值比较和过滤：对写入的Chunk，检查其每一行，
1. 如果当前层级的Kth值已经初始化，则获取Kth值与该行数据进行比较；如果小于Kth值，则该行不可能属于最终的Top-K结果，丢弃该行；
2. 如果第1步中该行没有被过滤掉，则尝试使用高一层级的Kth对象进行过滤，方法同上。
3. 如果1，2步骤中该行数据被过滤掉，并且算子被告知输入Chunk的内部是有序的，则接下来所有行都将会被直接丢弃 （见“上下游算子协作”章节）
3. 写入小顶堆：如果上一步中，该行没有被Kth值过滤掉，则将该行包装为堆元素对象a，尝试写入小顶堆：
1. 如果堆元素数量小于K，将对象a直接写入堆中；
2. 如果堆元素数量大于等于K，利用比较器，将对象a和堆顶进行比较，如果对象a小于堆顶，丢弃对象a；否则，将堆顶移除，写入a元素，小顶堆将重新选出堆顶。
4. 更新Kth值：对于每一行数据，如果在上一步“写入小顶堆”成功写入了小顶堆中，并且小顶堆的元素数量大于等于K，那么获取小顶堆的堆顶，更新到Kth对象里，具体方法见“L1 Top-K算子之间的协作-节点内Kth值并发更新”章节。
5. 更新元素总数：计算上述步骤中成功写到小顶堆中的元素总数，并更新到一个全局的元素计数中。如果总元素数量达到或刚刚超过K，则初始化Kth值。具体方法见“L1 Top-K算子之间的协作-Kth值初始化” （触发初始化的时候，意味着第iv步是无法更新Kth值的，因为此时整体节点每个层次内元素数量才刚达到K，所以每个算子内的堆大小一定不会超过K，不满足更新Kth的条件）
3. 算子完成并输出：对于每个层级的Top-K算子（L1/L2/L3），如果输入数据全部完成了写入流程，就意味着该算子进入完成状态。此时，堆中元素总数是小于等于K的，因为有Kth值的堆顶清理、比较与过滤等流程，帮助识别和丢弃不可能存在于最终Top-K结果中的元素。对此时的堆不断进行堆顶移除操作，直到堆被清空；收集得到的堆顶元素是基于比较器按照倒序排序的有序元素序列 S_sorted = {a1, a2, ... an}，n <= K。将有序序列分割为一个个Chunk向下游算子输出，具体情况如下：
1. 对于每个计算节点内的L1 Top-K算子，当它所属分区的数据被读取和计算完毕，意味该算子完成了Top-N计算流程；在每个L1 Top-K算子完成后，立即以Chunk为单位输出有序序列到L2 Top-K算子；该过程是通过内存与L2 Top-K算子进行数据传递的。
2. 对于每个计算节点内的L2 Top-K算子，从接收第一个L1 Top-K算子的数据开始，直到接收完最后一个L1 Top-K算子的数据为止，就完成了Top-N计算过程，并开始利用Exchange算子发起网络传输，向L3 Top-K算子传输数据。
3. 对于master计算节点上的L3 Top-K算子，从接收第一个L2 Top-K算子的数据开始，直到接收完最后一个L2 Top-K算子的数据为止，就完成了Top-N计算过程。不断收集堆顶元素得到大小为K的有序序列，从其中第offset位置开始，获取len个元素，就是Top-K查询 order by xxx limit offset , len的最终结果。

Part2. Top-K执行调度与提前终止

上文已经介绍了PolarDB-X并行Top-K优化的具体实现。现在，对于这样一类多表连接再分页的复杂查询，假设R, T, S表的行数都在亿级别，如何做到100ms内得到执行结果呢？

select * from R inner join S on S.A = R.A inner join T on T.B = R.B
where R.condition_1 and S.condition_2 and T.condition_3
order by R.col1 asc , R.col2 desc limit offset, len;

显然，先执行完复杂查询，物化后再求top-k，不能满足性能需要。需要数据库在设计好调度、扫描的基础上，内部自动识别出正确的位点，一旦达到分页输出要求，立即停止扫描。我们需要解决几个技术挑战

1. 需要识别出形如scan-join-topk的流水线，并得到top-k与sort key的顺序关系。
2. 列存存储 只能有一种顺序（sort key），不能添加各种覆盖索引。因此需要一种普适性的方案，通过一种sort key来适应各种order by列组合 和 各种正反顺序组合。
3. 列存存储 不存在全局顺序性或分区内顺序，只能依赖每个文件内部的顺序性，因此需要精确控制文件的调度和扫描过程。

接下来，我们将详细介绍PolarDB-X对复杂查询分页的提前终止优化。

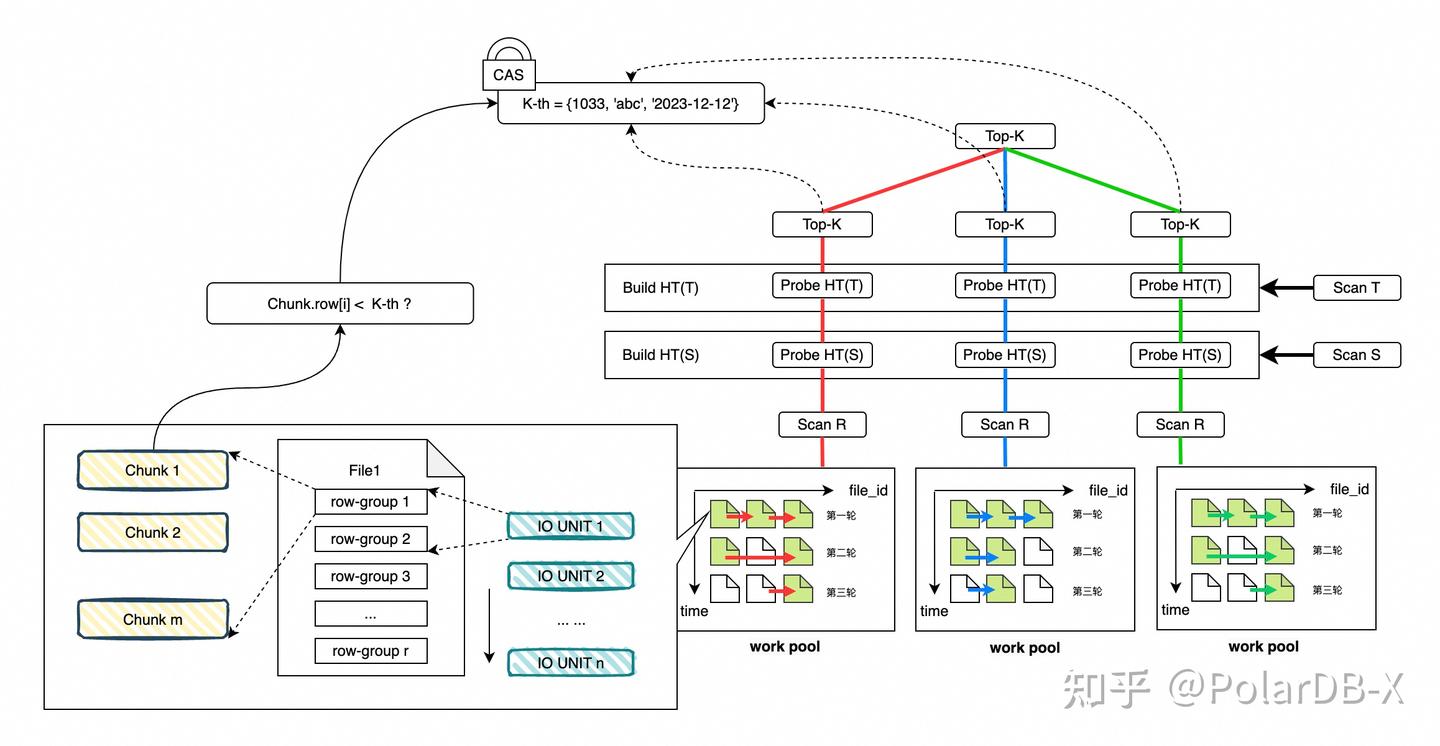
一、执行片段匹配

(一) 匹配条件

首先，识别和匹配能够应用提前终止策略的执行片段。该执行片段需要满足以下条件：

1. 能够形成pipeline流水线的执行片段；
2. pipeline流水线的起始算子是Scan算子，最后一个算子是Top-K算子；
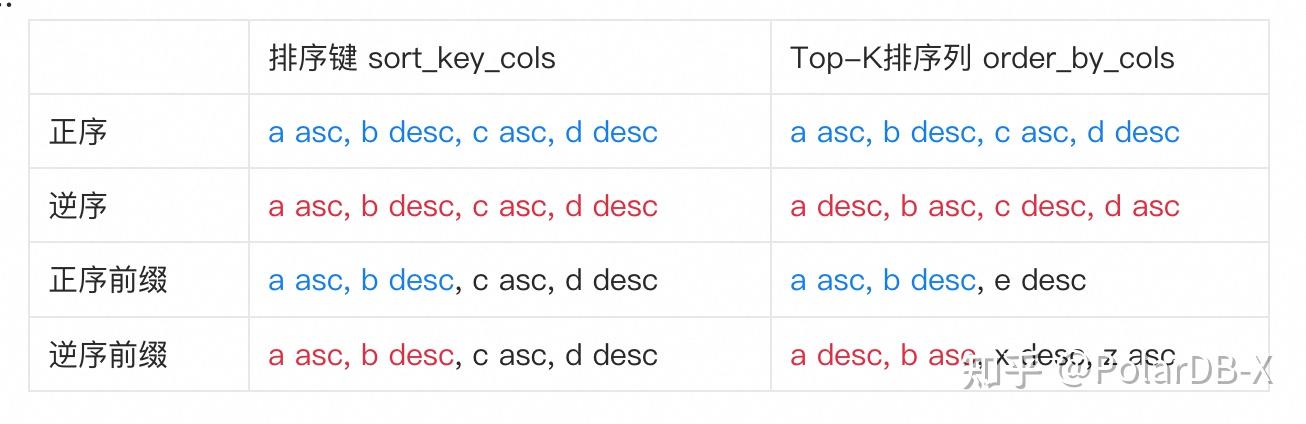
3. Top-K的排序列order_by_cols: (order_by_col1 asc|desc, order_by_col2 asc|desc, order_by_col3 asc|desc .. ) ，和Scan算子所查询表的排序键 sort_key_cols: (sort_key_col1 asc|desc, sort_key_col2 asc|desc, sort_key_col3 asc|desc .. ) ，具有以下四种关系之一：
1. 正序, TOTOAL_ORDER_ASC: order_by_cols和sort_key_cols顺序完全一致
2. 逆序, TOTOAL_ORDER_DESC: order_by_cols和sort_key_cols顺序正好完全相反（）
3. 正序前缀, PREFIX_ORDER_ASC: order_by_cols和sort_key_cols具有公共前缀，并且order_by_cols的公共前缀和sort_key_cols的公共前缀顺序正好相同
4. 逆序前缀，PREFIX_ORDER_DESC: order_by_cols和sort_key_cols具有公共前缀，并且order_by_cols的公共前缀和sort_key_cols的公共前缀顺序正好相反。

举例来说：

(二) 匹配过程

对于用户发起的SQL，首先经过解析器进行语法分析，并转换为一种中间表示形式，通常是一棵解析树（AST, abstract smantics tree）。然后，AST被传递给查询优化器，优化器选择成本最低的执行计划，生成一个执行计划或执行树。执行计划详细描述了数据库引擎如何执行查询，包括操作的顺序、使用的算法和数据结构。数据库执行引擎根据执行计划执行查询，返回结果给用户。

例如，对于本章节提到的查询，会形成下列树形结构，含义是：

1. 对R, S, T表执行扫描，并分别根据条件condition_1, condition_2, condition_3进行过滤；
2. 过滤后的S表数据作为join（R inner join S on S.A = R.A）的build端，T表数据作为join (R inner join T on T.B = R.B)的build端
3. 过滤后的R表数据作为probe端，依次执行上述两个join算子的匹配计算。最后对计算结果做Top-K运算。这里的K=offset+len。

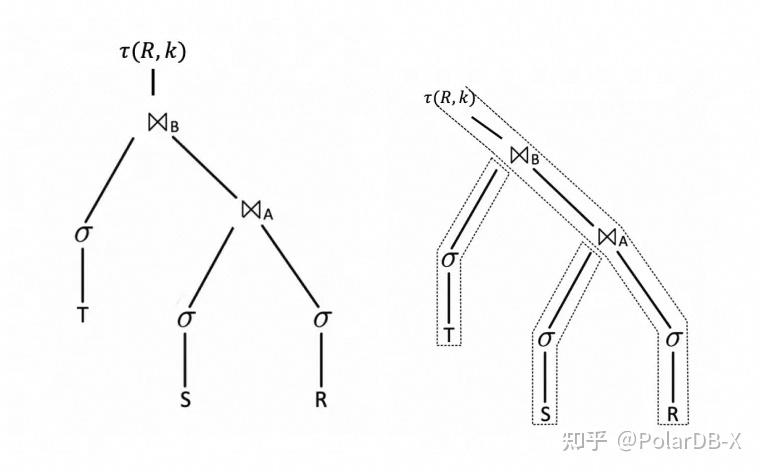
数据库中的pipeline执行框架（也称为执行管道或查询管道）是指在数据库查询处理中，对执行计划的组件或操作以流水线的形式组织和执行的一种策略。在数据库系统中，查询的执行涉及许多步骤，包括多个算子（如连接操作、选择操作、投影操作等），每个算子可能需要处理大量数据。

这些算子可以串行执行，即一个操作完成后，开始下一个操作。然而，这种方式可能导致效率不高，因为某些操作可能要等待前面的操作完成后才能开始。相反，pipeline执行框架允许当一个操作正在处理当前的数据批次时，另一个操作可以同时开始处理上一个操作的输出结果，从而提高数据库查询的整体性能。

Pipeline执行的基本概念类似于计算机科学中的指令流水线技术，后一个算子不需要等待前一个算子处理完所有的数据就可以开始执行。

pipeline框架中包含两种算子执行模式：

1. 阻塞性（Blocking）执行：即某个操作需要等待其所有输入都被处理之后才可以执行
2. 非阻塞性（Non-blocking）执行：算子可以立即处理上游算子的输出，而不需要等待所有输入处理完成。

Pipeline执行大幅提高了资源的利用率和整个查询处理的并行度，因为它允许在多个核心/处理器上同时处理不同的查询阶段。多数现代数据库系统（如PostgreSQL, MySQL, Oracle等）在执行查询时采用某种形式的Pipeline执行策略，以优化性能。

(三) 匹配符合条件的pipeline

1. 寻找起始算子是Scan并且终止算子是Top-K的pipeline；
2. 收集排序信息，包括Top-K的排序列order_by_cols: (order_by_col1 asc|desc, order_by_col2 asc|desc, order_by_col3 asc|desc .. ) ，和Scan算子所查询表的排序键 sort_key_cols: (sort_key_col1 asc|desc, sort_key_col2 asc|desc, sort_key_col3 asc|desc .. )
3. 判断Top-K排序列和Scan排序键的关系属于正序、逆序、前缀正序、前缀逆序中的哪一种。