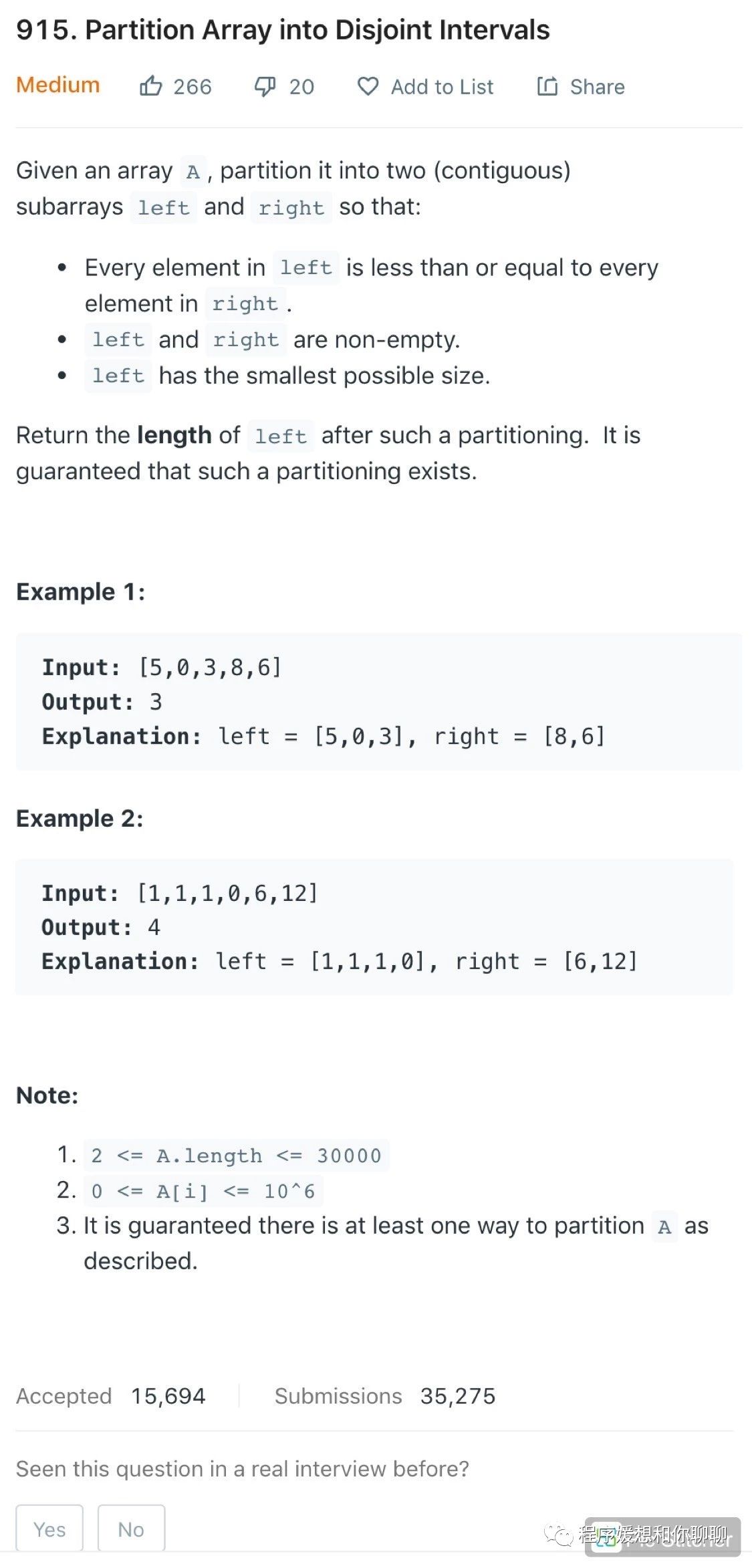
给了一个数组A,让我们分成两个相邻的子数组 left 和 right,使得 left 中的所有数字小于等于 right 中的,并限定了每个输入数组必定会有这么一个分割点,让返回数组 left 的长度。
思路:
遍历每个数字,更新当前最大值 curMax,并且判断若当前数字 A[i] 小于 preMax,说明这个数字也一定是属于 left 数组的,此时整个遍历到的区域应该都是属于 left 的,所以 preMax 要更新为 curMax,并且当前位置也就是潜在的分割点,所以 partitionIdx 更新为i。
curMax是遍历过的元素中的最大值,而preMax表示 left 中的最大值,curMax的作用主要是为了更新preMax,这样的话,是不是说curMax是preMax和A[i]中的较大值?不是的,如:A = {2, 3, 1, 7, 8},当i=1的时候,curMax=3,而preMax不变=2,当i=2的时候,curMax=3还是等于3,而不是等于Math.max(preMax, A[2]}=Math.max{2, 1}=2,而此时preMax要更新为curMax的值,等于3。
这道题,其实只要出现后面的元素比前面的小,那这个后面的元素就肯定得归到left里面。如果出现递增,是不确定的,因为有可能后面还会遇到一个更加小的元素,这时递增的那对都得归到left中。
时间复杂度:O(N), 空间复杂度:O(1)。
1/**
2 * @author lxn
3 * @description 915. Partition Array into Disjoint Intervals
4 * @create 2020-01-18 17:02
5 */
6public class Algorithm915 {
7 public static void main(String[] args) {
8 int[] A = {5, 0, 3, 8, 6};
9 int res = new Solution915().partitionDisjoint(A);
10 }
11}
12
13class Solution915 {
14 public int partitionDisjoint(int[] A) {
15 int partitionIdx = 0; // 分割点的位置
16 int preMax = A[0]; // left中的最大值
17 int curMax = preMax; // 当前的最大值
18 for (int i = 1; i < A.length; ++i) {
19 curMax = Math.max(curMax, A[i]); // 当前的最大值。本例中,i=3的时候,A[i]=8, curMax更新为A[i]的值8
20 if (A[i] < preMax) { // 小于,当前的元素A[i]肯定属于left
21 preMax = curMax;// 更新left的最大值
22 partitionIdx = i;// 更新分割点的位置
23 }
24 }
25 return partitionIdx + 1; // 左边的长度为index+1
26 }
27}
文章转载自程序媛的梦想,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






